Low-Voltage Ride-Through of the Novel Voltage Source-Controlled PMSG-Based Wind Turbine Based on Switching the Virtual Resistor
Abstract
:1. Introduction
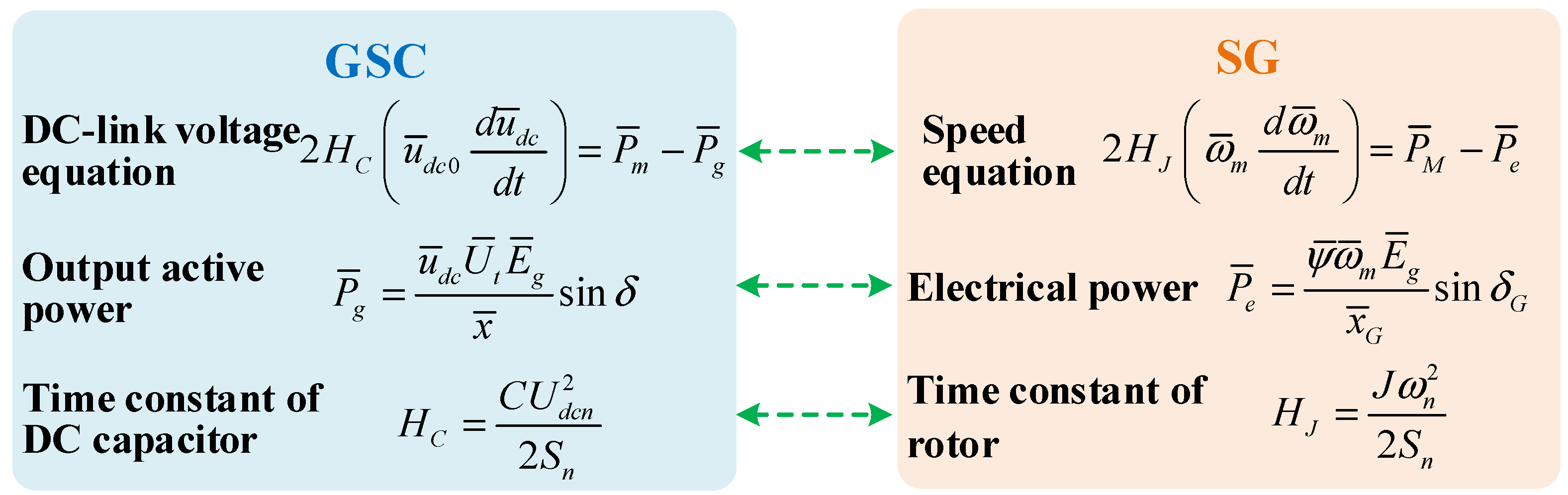
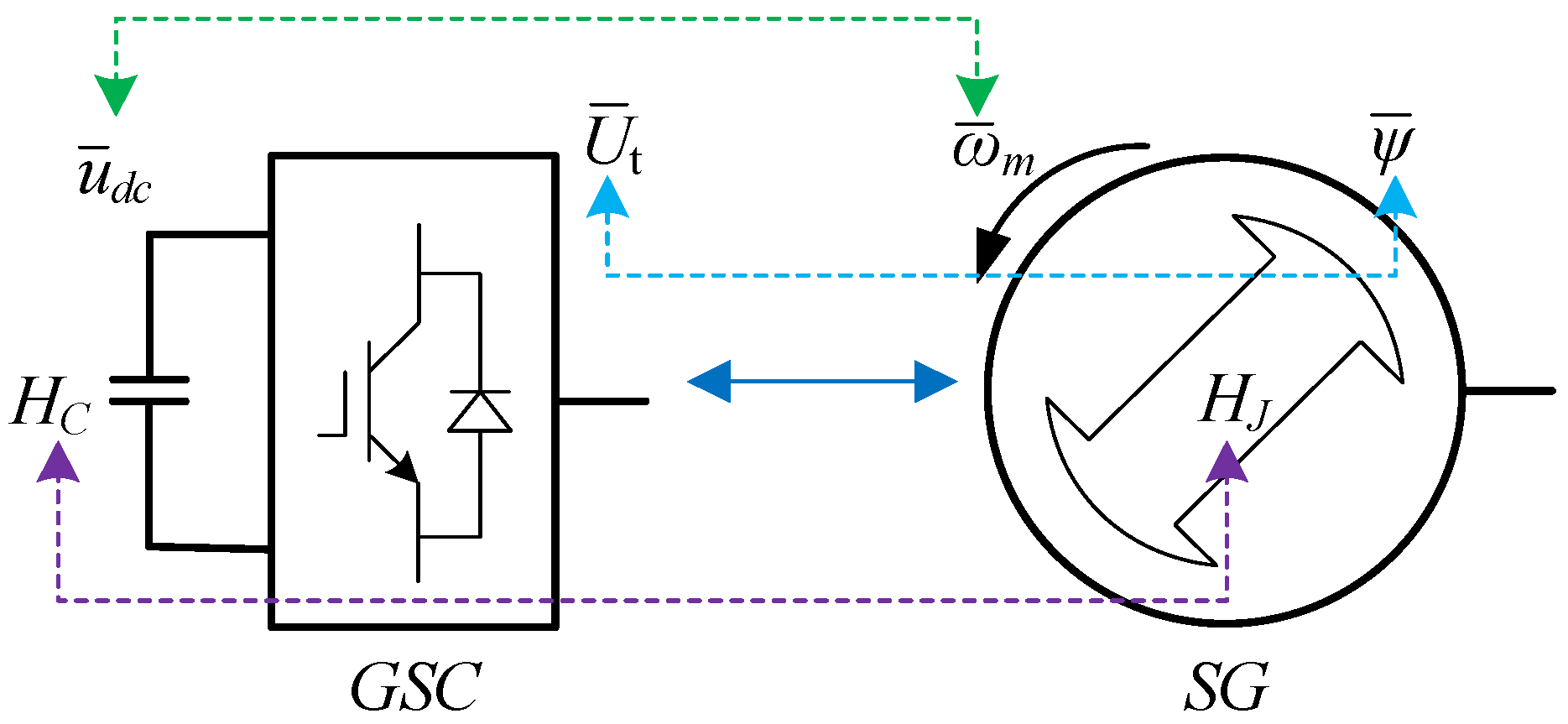
2. Kinetic Similarity between SG and GSC
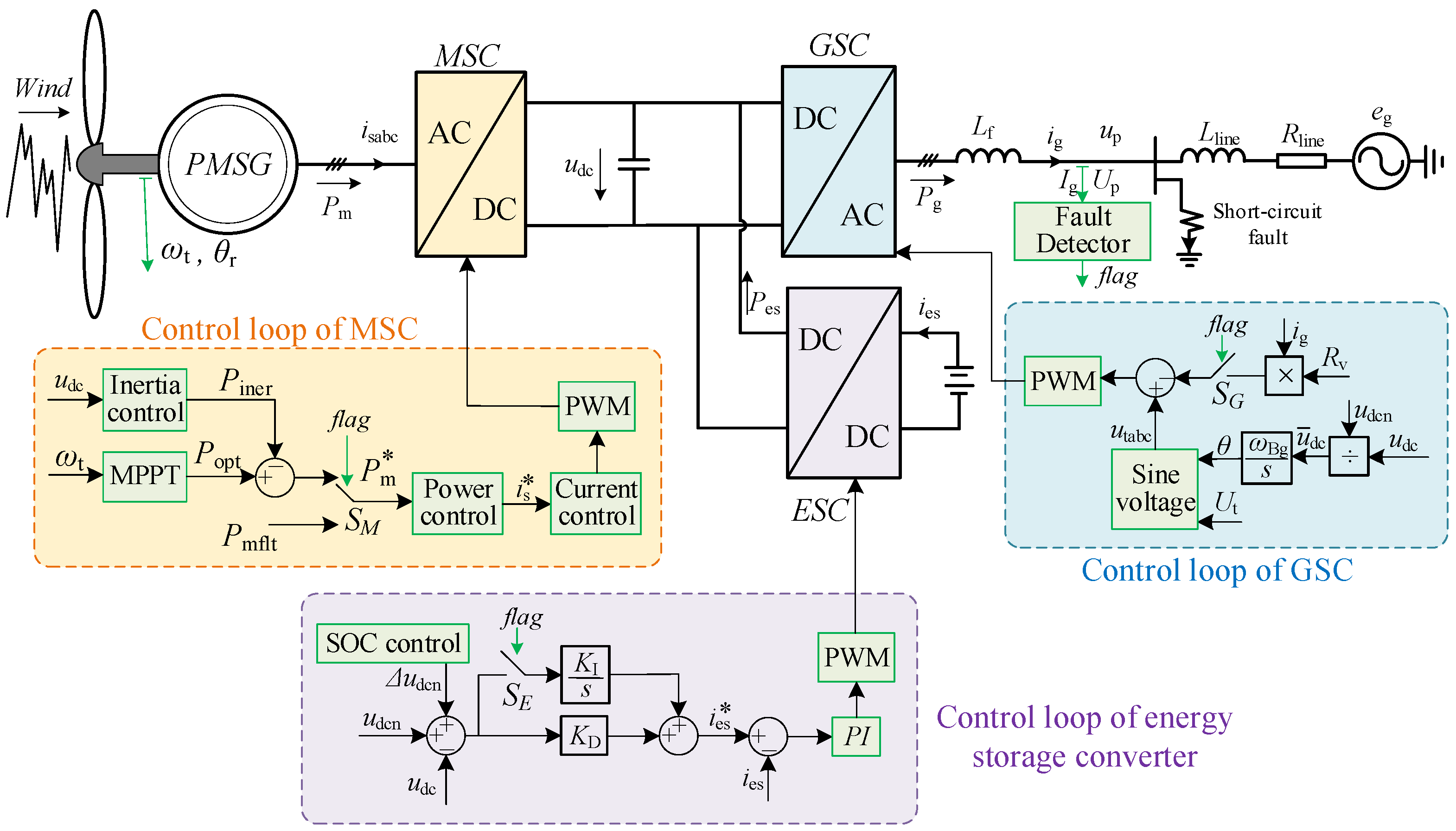
3. System Control Structure
3.1. Control Strategy of the GSC
3.2. Control Strategy of the MSC
3.3. Control Strategy of the Energy Storage Converter
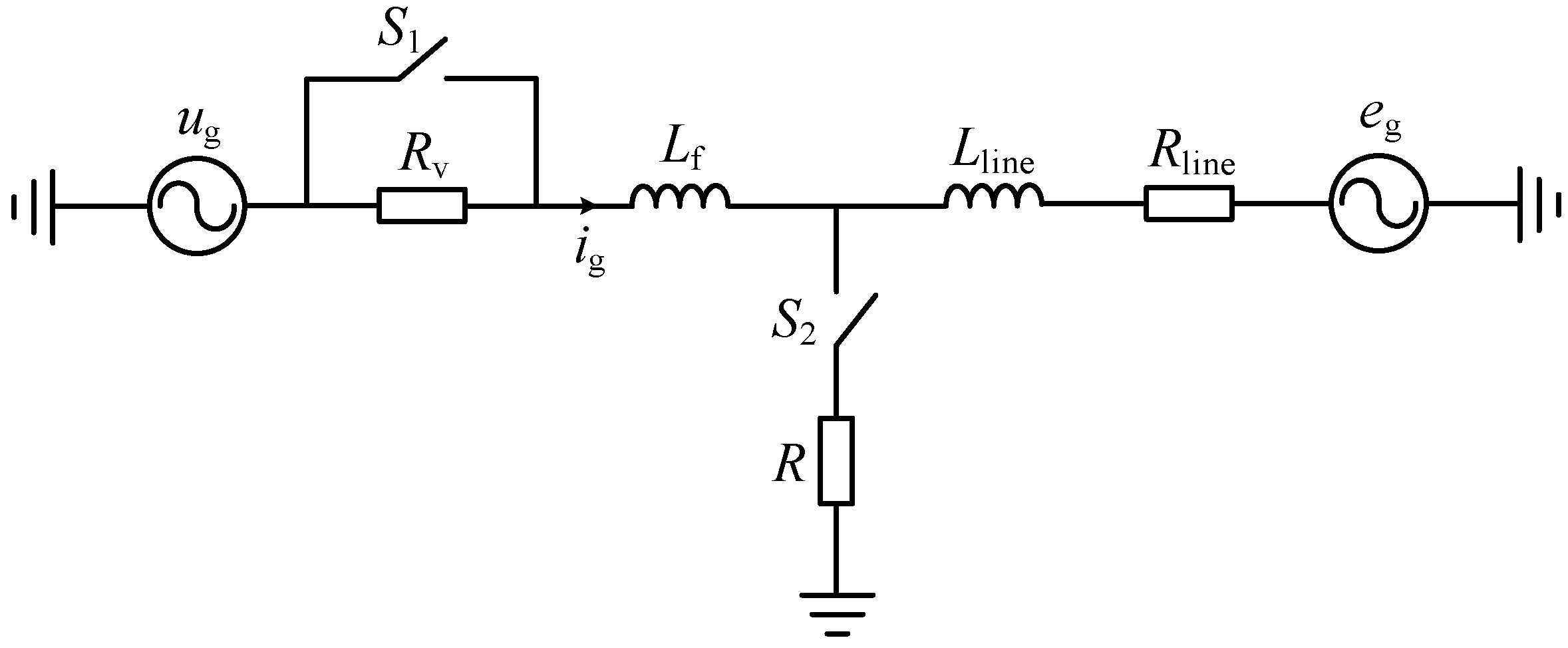
4. Transient Current Characteristics of Wind Turbines after Short-Circuit Fault
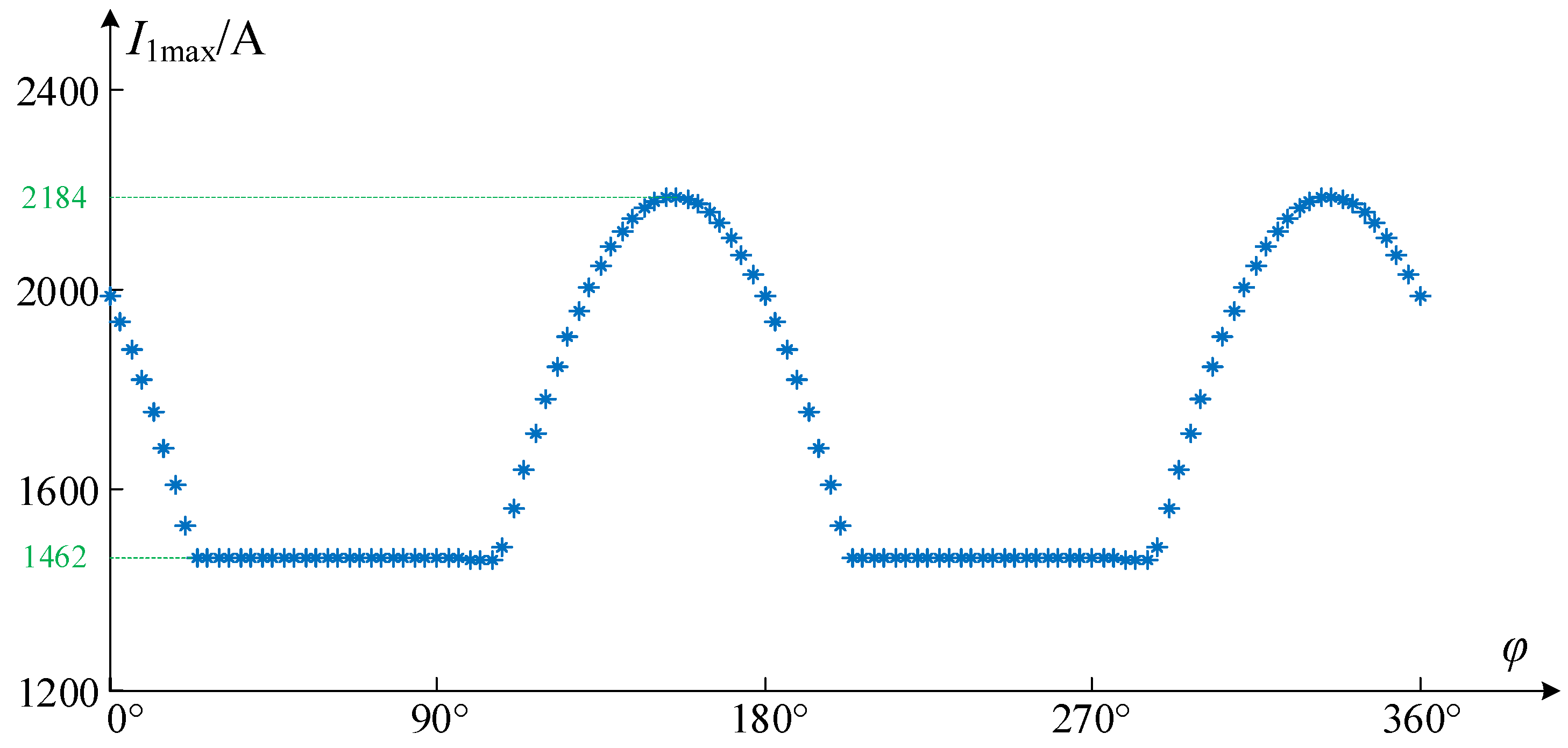
5. Design of the Virtual Resistor
5.1. Steady-State Current of the Wind Turbine after the Fault
5.2. Virtual Resistance Range to Avoid Overcurrent
6. Simulation Verification
6.1. Verification of the Inertial Response and Primary Frequency Regulation
6.2. Verification of the Wind Turbine’s Transient Current Characteristics
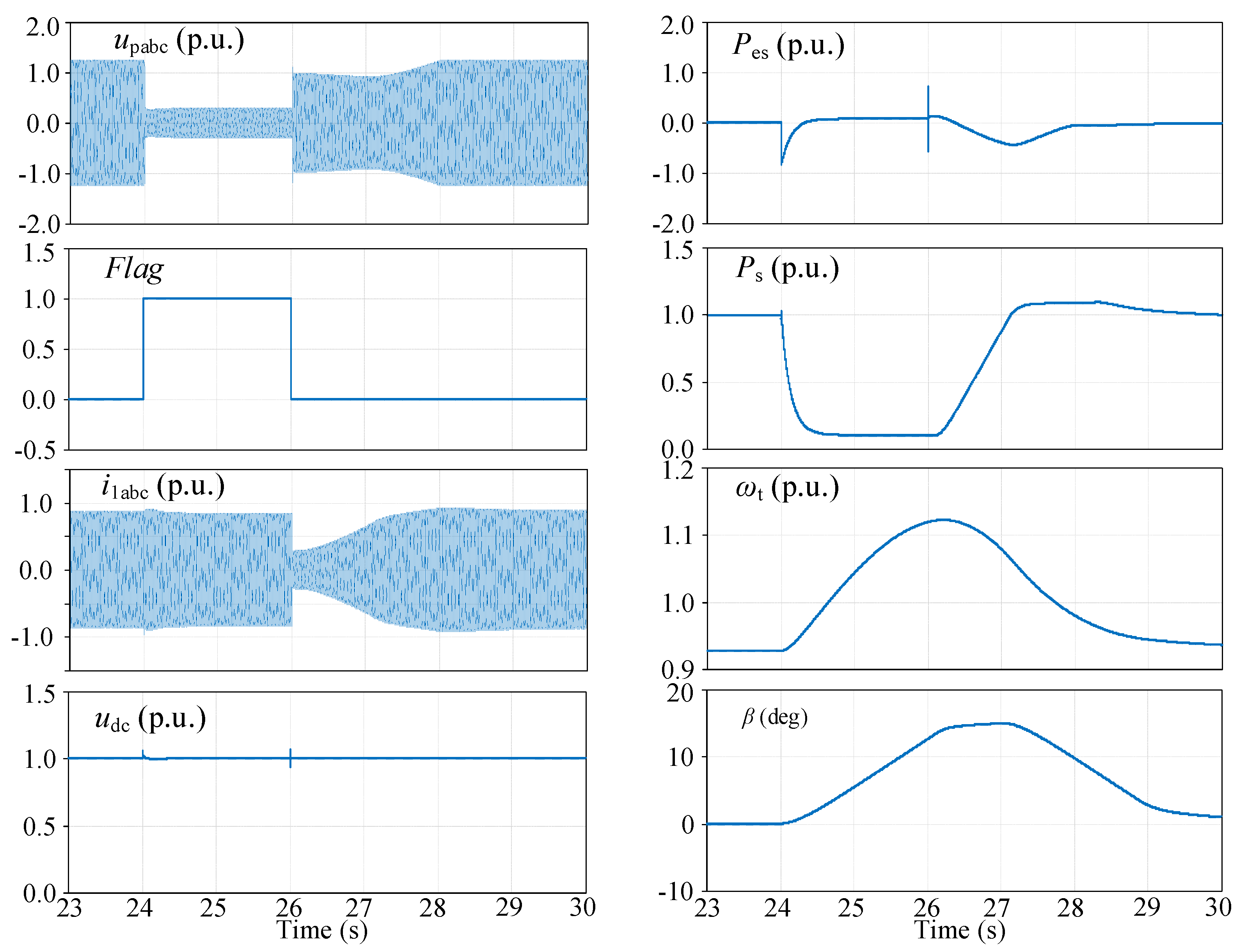
6.3. Verification of the LVRT Control Strategy
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Singh, S.; Fozdar, M.; Malik, H.; Fernández Moreno, M.d.V.; García Márquez, F.P. Influence of Wind Power on Modeling of Bidding Strategy in a Promising Power Market with a Modified Gravitational Search Algorithm. Appl. Sci. 2021, 11, 4438. [Google Scholar] [CrossRef]
- Probst, O.; Minchala, L.I. Mitigation of Short-Term Wind Power Ramps through Forecast-Based Curtailment. Appl. Sci. 2021, 11, 4371. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.; Lee, J.; Jang, G. Novel Coordinated Control Strategy of BESS and PMSG-WTG for Fast Frequency Response. Appl. Sci. 2021, 11, 3874. [Google Scholar] [CrossRef]
- Chen, X.; Wu, W.; Gao, N.; Chung, H.S.-H.; Liserre, M.; Blaabjerg, F. Finite Control Set Model Predictive Control for LCL-Filtered Grid-Tied Inverter with Minimum Sensors. IEEE Trans. Ind. Electron. 2020, 67, 9980–9990. [Google Scholar] [CrossRef]
- Gajewski, P.; Pieńkowski, K. Control of the Hybrid Renewable Energy System with Wind Turbine, Photovoltaic Panels and Battery Energy Storage. Energies 2021, 14, 1595. [Google Scholar] [CrossRef]
- Huynh, V.V.; Minh, B.L.N.; Amaefule, E.N.; Tran, A.-T.; Tran, P.T.; Phan, V.-D.; Pham, V.-T.; Nguyen, T.M. Load Frequency Control for Multi-Area Power Plants with Integrated Wind Resources. Appl. Sci. 2021, 11, 3051. [Google Scholar] [CrossRef]
- Deng, F.; Chen, Z.; Khan, M.R.; Zhu, R. Fault detection and localization method for modular multilevel converters. IEEE Trans. Power Electron. 2015, 30, 2721–2732. [Google Scholar] [CrossRef]
- Sang, S.; Gao, N.; Cai, X.; Li, R. A Novel Power-Voltage Control Strategy for the Grid-Tied Inverter to Raise the Rated Power Injection Level in a Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 219–232. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; pp. 1–1161. [Google Scholar]
- Tan, Y.; Muttaqi, K.M.; Ciufo, P.; Meegahapola, L. Enhanced Frequency Response Strategy for a PMSG-Based Wind Energy Conversion System Using Ultracapacitor in Remote Area Power Supply Systems. IEEE Trans. Ind. Appl. 2017, 53, 549–558. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Cai, X.; Amin, M.; Molinas, M. Sub-synchronous oscillation mechanism and its suppression in MMC-based HVDC connected wind farms. IET Gener. Transm. Distrib. 2018, 12, 1021–1029. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.; Meng, K.; Huang, J.; Dong, Z.Y.; Zhang, W.; Xie, X. Development of HVRT and LVRT Control Strategy for PMSG-Based Wind Turbine Generators. Energies 2020, 13, 5442. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Engelken, S.; Mendonca, A.; Fischer, M. Inertial response with improved variable recovery behaviour provided by type 4 WTs. IET Renew. Power Gener. 2017, 11, 195–201. [Google Scholar] [CrossRef]
- Zhang, C.; Cai, X.; Rygg, A.; Molinas, M. Sequence Domain SISO Equivalent Models of a Grid-Tied Voltage Source Converter System for Small-Signal Stability Analysis. IEEE Trans. Energy Convers. 2018, 33, 741–749. [Google Scholar] [CrossRef]
- Zhu, K.; Sun, P.; Zhou, L.; Du, X.; Luo, Q. Frequency-Division Virtual Impedance Shaping Control Method for Grid-Connected Inverters in a Weak and Distorted Grid. IEEE Trans. Power Electron. 2020, 35, 8116–8129. [Google Scholar] [CrossRef]
- Mousavi, S.Y.; Jalilian, A.; Savaghebi, M.; Guerrero, J.M. Autonomous Control of Current and Voltage Controlled DG Interface Inverters for Reactive Power Sharing and Harmonics Compensation in Islanded Microgrids. IEEE Trans. Power Electron. 2018, 33, 9375–9386. [Google Scholar] [CrossRef]
- Zhong, Q.; Weiss, G. Synchronverters: Inverters that mimic synchronous generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-Synchronization Control of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Syst. 2010, 25, 809–820. [Google Scholar] [CrossRef]
- Sang, S.; Zhang, C.; Cai, X.; Molinas, M.; Zhang, J.; Rao, F. Control of a Type-IV Wind Turbine With the Capability of Robust Grid-Synchronization and Inertial Response for Weak Grid Stable Operation. IEEE Access 2019, 7, 58553–58569. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Optimal Transient Search Algorithm-Based PI Controllers for Enhancing Low Voltage Ride-Through Ability of Grid-Linked PMSG-Based Wind Turbine. Electronics 2020, 9, 1807. [Google Scholar] [CrossRef]
- Saurabh, M.T.; Amar, N.T.; Deependra, S. Low-voltage-ride-through Enhancement with the ω–and T–Control of PMSG in a Grid-integrated Wind Generation System. IET Gener. Transm. Distrib. 2019, 13, 1979–1988. [Google Scholar]
- Yan, X.; Cui, S.; Sun, X.; Sun, Y. Transient modelling of doubly-fed induction generator based wind turbine on full operation condition and rapid starting period based on low voltage ride-through testing. IET Renew. Power Gener. 2021, 15, 1069–1084. [Google Scholar] [CrossRef]
- Yan, X.; Yang, L.; Li, T. The LVRT Control Scheme for PMSG-Based Wind Turbine Generator Based on the Coordinated Control of Rotor Overspeed and Supercapacitor Energy Storage. Energies 2021, 14, 518. [Google Scholar] [CrossRef]
- Kim, C.; Kim, W. Enhanced Low-Voltage Ride-Through Coordinated Control for PMSG Wind Turbines and Energy Storage Systems Considering Pitch and Inertia Response. IEEE Access 2020, 8, 212557–212567. [Google Scholar] [CrossRef]
- Zhang, C.; Cai, X.; Rygg, A.; Molinas, M. Modeling and analysis of grid-synchronizing stability of a Type-IV wind turbine under grid faults. Int. J. Electr. Power Energy Syst. 2020, 117, 105544. [Google Scholar] [CrossRef]

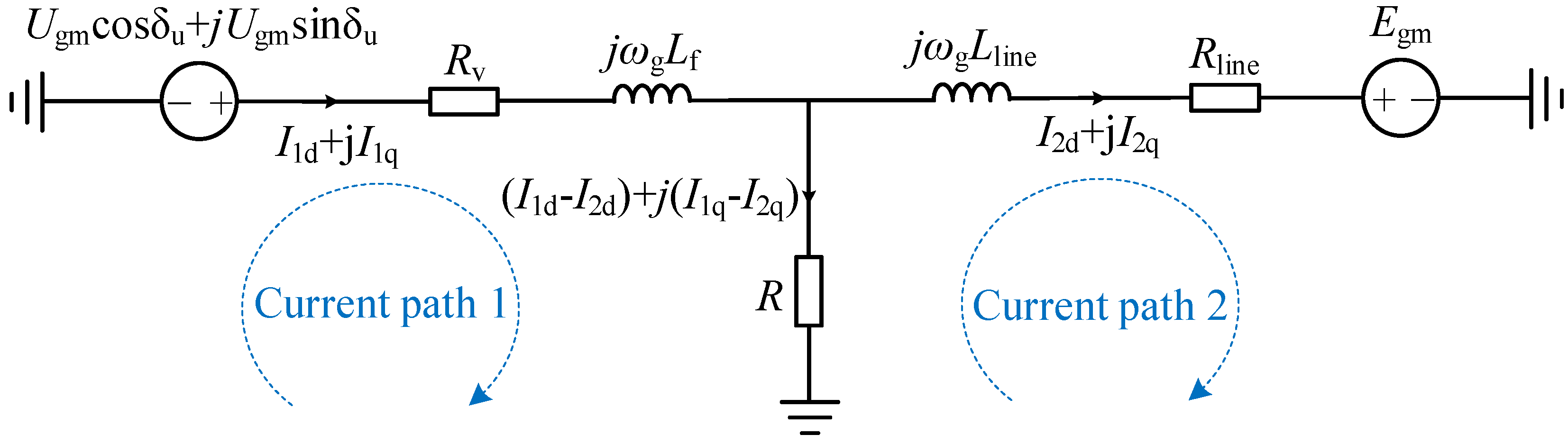



| Symbols | Parameters | Value/Unit |
|---|---|---|
| SN | Rated power value | 2 MW |
| UN | Rated value of AC phase voltage | 0.563 kV |
| udcn | Rated value of DC-link voltage | 1.1 kV |
| ωBm | Rated value of stator angular frequency | 84.6 rad/s |
| ωBg | Rated value of grid angular frequency | 314 rad/s |
| fN | Rated frequency of PMSG | 13.47 Hz |
| P | Pole pairs of PMSG | 42 |
| ψr | Magnetic flux linkage of rotor | 0.896 p.u. |
| Ls | Synchronous inductance of PMSG | 0.5495 p.u. |
| Rs | Stator resistance of PMSG | 0.00387 p.u. |
| HWT | Inertia constant of wind turbine and PMSG Inertia constant of DC-link capacitor | 4 s |
| HC | 3.6 ms | |
| uEdcn | Rated value of battery voltage Switching frequency of GSC and MSC | 0.78 kV |
| fs | 2 kHz | |
| fEs | Switching frequency of ESC | 10 kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, S.; Pei, B.; Huang, J.; Zhang, L.; Xue, X. Low-Voltage Ride-Through of the Novel Voltage Source-Controlled PMSG-Based Wind Turbine Based on Switching the Virtual Resistor. Appl. Sci. 2021, 11, 6204. https://doi.org/10.3390/app11136204
Sang S, Pei B, Huang J, Zhang L, Xue X. Low-Voltage Ride-Through of the Novel Voltage Source-Controlled PMSG-Based Wind Turbine Based on Switching the Virtual Resistor. Applied Sciences. 2021; 11(13):6204. https://doi.org/10.3390/app11136204
Chicago/Turabian StyleSang, Shun, Binhui Pei, Jiejie Huang, Lei Zhang, and Xiaocen Xue. 2021. "Low-Voltage Ride-Through of the Novel Voltage Source-Controlled PMSG-Based Wind Turbine Based on Switching the Virtual Resistor" Applied Sciences 11, no. 13: 6204. https://doi.org/10.3390/app11136204
APA StyleSang, S., Pei, B., Huang, J., Zhang, L., & Xue, X. (2021). Low-Voltage Ride-Through of the Novel Voltage Source-Controlled PMSG-Based Wind Turbine Based on Switching the Virtual Resistor. Applied Sciences, 11(13), 6204. https://doi.org/10.3390/app11136204







