DR-Transformer: A Multi-Features Fusion Framework for Tropical Cyclones Intensity Estimation
Abstract
:1. Introduction
- We propose a distance-consistency loss function, which is a general loss function, especially suitable for constructing image features with continuous labels.
- We apply a transformer for aggregating temporal correlation features, which is a multi-task model to make a better effect in the estimation and prediction of TC intensity.
- Extensive experiments on the TCIR dataset demonstrate the effectiveness of our proposed approach, which outperforms the existing methods.
2. Related Works
2.1. Tropical Cyclone Intensity Estimate
2.2. Metric Learning
2.3. Transformer
3. Methods
3.1. Image-to-Intensity Feature Learning
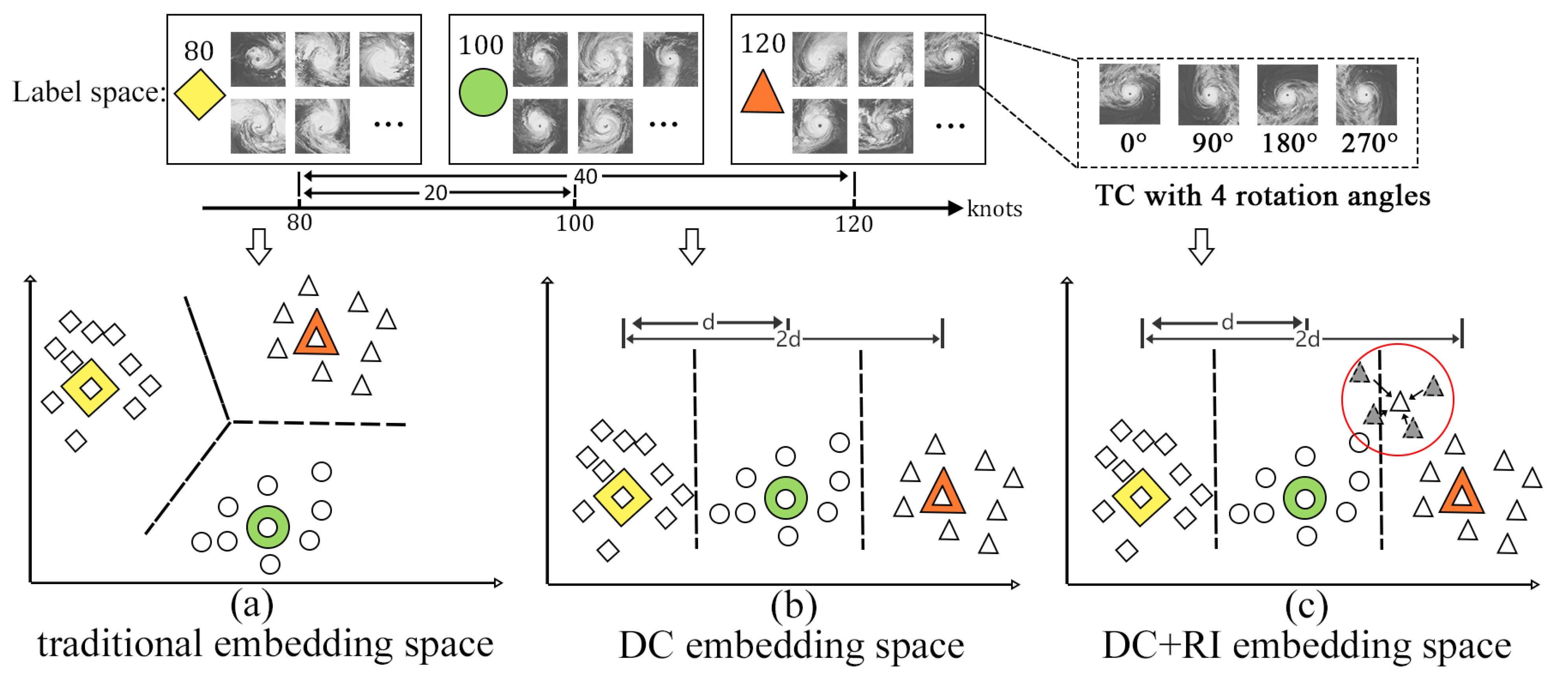
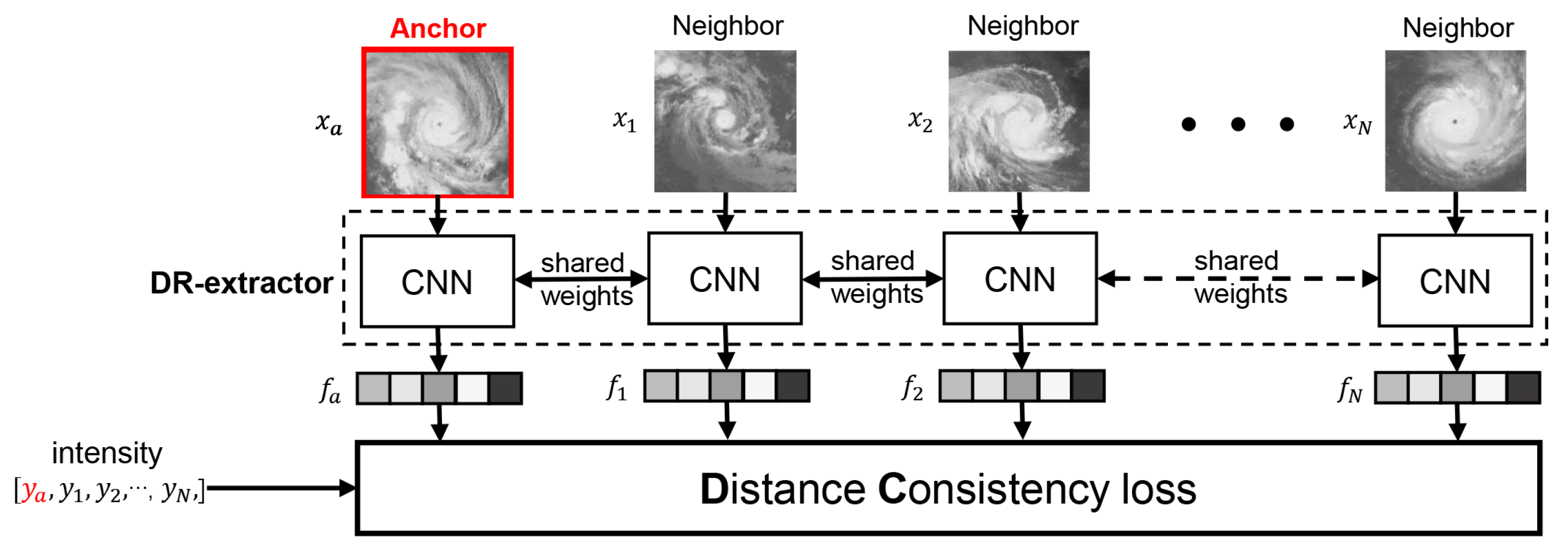
3.1.1. Distance Consistency Feature Learning
3.1.2. Rotation-Invariance Feature Learning
3.2. Temporal Correlation Learning via Transformer
3.3. Inference Stage
4. Experiment
4.1. Experimental Settings
4.2. Comparison to the Baseline
4.3. Analysis of the Loss
4.4. Ablation Studies
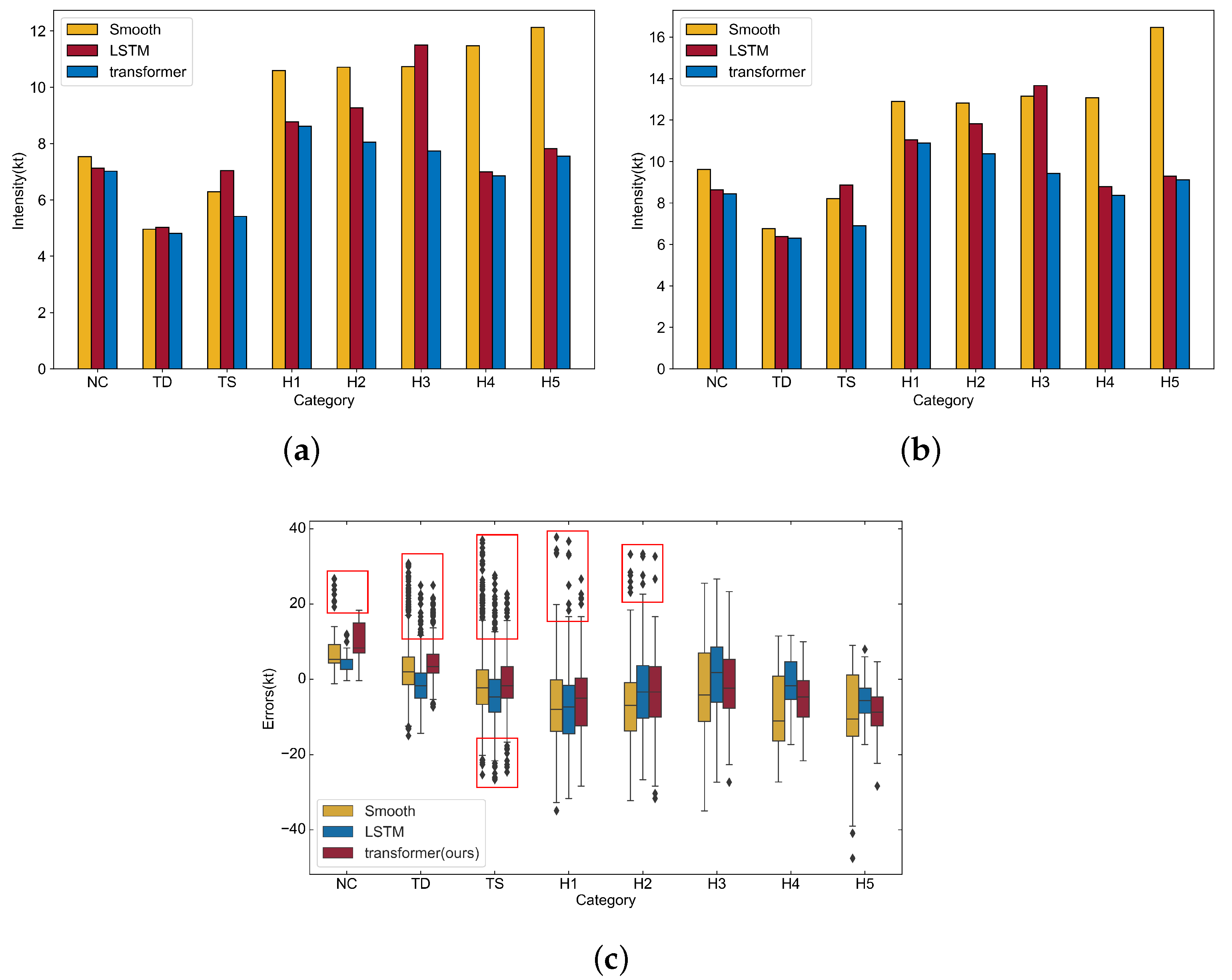
4.5. Intensity Estimation and Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TC | Tropical Cyclone |
| DC | Distance Consitency |
| RI | Rotation Invariance |
| DR | Distance consitency and Rotation invariance |
References
- Dvorak, V.F. Tropical Cyclone Intensity Analysis and Forecasting from Satellite Imagery. Mon. Weather Rev. 1975, 103, 420–430. [Google Scholar] [CrossRef]
- Pradhan, R.; Aygun, R.S.; Maskey, M.; Ramachandran, R.; Cecil, D.J. Tropical Cyclone Intensity Estimation Using a Deep Convolutional Neural Network. IEEE Trans. Image Process. 2018, 27, 692–702. [Google Scholar] [CrossRef]
- Chen, B.; Chen, B.F.; Lin, H.T. Rotation-blended CNNs on a New Open Dataset for Tropical Cyclone Image-to-intensity Regression. In Proceedings of the 24th ACM SIGKDD International Conference, London, UK, 19–23 August 2018. [Google Scholar]
- Chen, B.; Chen, B.; Lin, H.T.; Elsberry, R.L. Estimating Tropical Cyclone Intensity by Satellite Imagery Utilizing Convolutional Neural Networks. Weather Forecast. 2019, 34, 447–465. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Xu, Y.; Yang, H.; Cheng, M.; Li, S. Cyclone intensity estimate with context-aware cyclegan. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 3417–3421. [Google Scholar]
- Chen, B.; Chen, B.F.; Chen, Y.N. Real-time Tropical Cyclone Intensity Estimation by Handling Temporally Heterogeneous Satellite Data. arXiv 2020, arXiv:2010.14977. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Bromley, J.; Bentz, J.; Bottou, L.; Guyon, I.; Lecun, Y.; Moore, C.; Sackinger, E.; Shah, R. Signature Verification using a “Siamese” Time Delay Neural Network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 539–546. [Google Scholar] [CrossRef]
- Hadsell, R.; Chopra, S.; Lecun, Y. Dimensionality Reduction by Learning an Invariant Mapping. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Proceedings of the International Workshop on Similarity-based Pattern Recognition, Copenhagen, Denmark, 12–14 October 2015. [Google Scholar]
- Schroff, F.; Kalenichenko, D.; Philbin, J. FaceNet: A Unified Embedding for Face Recognition and Clustering. arXiv 2015, arXiv:1503.03832. [Google Scholar]
- Sohn, K. Improved Deep Metric Learning with Multi-Class N-Pair Loss Objective. In NIPS’16: Proceedings of the 30th International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 1857–1865. [Google Scholar]
- Sun, Y.; Cheng, C.; Zhang, Y.; Zhang, C.; Zheng, L.; Wang, Z.; Wei, Y. Circle Loss: A Unified Perspective of Pair Similarity Optimization. arXiv 2020, arXiv:2002.10857. [Google Scholar]
- Kim, S.; Seo, M.; Laptev, I.; Cho, M.; Kwak, S. Deep Metric Learning Beyond Binary Supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. arXiv 2019, arXiv:1910.10683. [Google Scholar]
- Parmar, N.; Vaswani, A.; Uszkoreit, J.; Kaiser, L.; Shazeer, N.; Ku, A. Image Transformer. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Wu, B.; Xu, C.; Dai, X.; Wan, A.; Zhang, P.; Yan, Z.; Tomizuka, M.; Gonzalez, J.; Keutzer, K.; Vajda, P. Visual Transformers: Token-based Image Representation and Processing for Computer Vision. arXiv 2020, arXiv:2006.03677. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-End Object Detection with Transformers. arXiv 2020, arXiv:2005.12872. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the Variance of the Adaptive Learning Rate and Beyond. arXiv 2020, arXiv:1908.03265. [Google Scholar]
- Olander, T.; Velden, C. The Advanced Dvorak Technique (ADT) for Estimating Tropical Cyclone Intensity: Update and New Capabilities. Weather Forecast. 2019, 34, 905–922. [Google Scholar] [CrossRef]
- Kidder, S.; Goldberg, M.; Zehr, R.; Demaria, M.; Purdom, J.; Velden, C.; Grody, N.; Kusselson, S. Satellite Analysis of Tropical Cyclones Using the Advanced Microwave Sounding Unit (AMSU). Bull. Am. Meteorol. Soc. 2000, 81. [Google Scholar] [CrossRef] [Green Version]
- Herndon, D.; Velden, C. A Consensus Approach for Estimating Tropical Cyclone Intensity from Meteorological Satellites: SATCON. Weather Forecast. 2020, 35, 805–922. [Google Scholar]
- Fetanat, G.; Homaifar, A.; Knapp, K.R. Objective Tropical Cyclone Intensity Estimation Using Analogs of Spatial Features in Satellite Data. Weather Forecast. 2013, 28, 1446–1459. [Google Scholar] [CrossRef]
- Ritchie, E.A.; Wood, K.M.; Rodríguez-Herrera, O.G.; Pieros, M.F.; Tyo, J.S. Satellite-Derived Tropical Cyclone Intensity in the North Pacific Ocean Using the Deviation-Angle Variance Technique. Weather Forecast. 2014, 29, 505–516. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.C.; Liu, C.Y.; Lin, T.H.; Chen, L.D. A satellite-derived typhoon intensity index using a deviation angle technique. Int. J. Remote Sens. 2015, 36, 1216–1234. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, C.; Sun, R.; Wang, Z. A Multiple Linear Regression Model for Tropical Cyclone Intensity Estimation from Satellite Infrared Images. Atmosphere 2016, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.; Maskey, M.; Berendes, T. Using Deep Learning for Tropical Cyclone Intensity Estimation. In Proceedings of the 2017 American Geophysical Union (AGU) Fall Meeting, New Orleans, LA, ISA, 11–15 December 2017; p. IN11E-05. [Google Scholar]


| Approach | Temporal | Rmse (kt) | |
|---|---|---|---|
| 1 | FASI [31] | - | 12.70 |
| 2 | Improved DAV-T [32] | - | 12.70 |
| 3 | TI index [33] | - | 9.34 |
| 4 | Y. Zhao (2016) [34] | - | 12.01 |
| 5 | J. Miller (2017) [35] | - | 10.00 |
| 6 | R. Pradhan (2018) [2] | - | 10.18 |
| 7 | CNN-TC [3] | - | 10.18 |
| 8 | Cross-entropy | - | 10.36 |
| 9 | Npair [14] | - | 10.75 |
| 10 | log-ratio [16] | - | 10.21 |
| 11 | Ours (DC + RI) | - | 8.88 |
| 12 | ADT [28] | smooth | 11.79 |
| 13 | AMSU [29] | smooth | 14.10 |
| 14 | SATCON [30] | smooth | 9.21 |
| 15 | CNN-TC(S) [4] | smooth | 8.39 |
| 16 | Ours (DR + smooth) | smooth | 9.16 |
| 17 | Ours (DR + LSTM) | LSTM | 8.67 |
| 18 | Ours (DR + transformer) | transformer | 7.76 |
| Category | Intensity Range | Numbers | Approach | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cross-Entropy | Npair | Log-Ratio | Ours (DC + RI) | |||||||
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |||
| H5 | ≥137 kt | 41 | 9.09 | 10.89 | 7.43 | 9.53 | 7.43 | 8.79 | 5.41 | 6.44 |
| H4 | 113–136 kt | 93 | 7.96 | 10.10 | 10.79 | 13.32 | 7.44 | 9.41 | 6.82 | 9.26 |
| H3 | 96–112 kt | 130 | 12.22 | 15.18 | 15.13 | 18.63 | 11.98 | 15.36 | 9.87 | 12.35 |
| H2 | 83–95 kt | 243 | 11.98 | 15.71 | 13.61 | 16.82 | 10.83 | 13.66 | 10.33 | 12.86 |
| H1 | 64–82 kt | 468 | 11.35 | 14.05 | 11.34 | 14.15 | 10.56 | 13.08 | 10.19 | 12.40 |
| TS | 34–63 kt | 1735 | 7.84 | 10.01 | 8.15 | 10.34 | 7.76 | 9.95 | 6.35 | 8.20 |
| TD | 20–33 kt | 1501 | 5.01 | 7.44 | 5.50 | 7.25 | 6.78 | 8.43 | 5.43 | 7.03 |
| NC | <20 kt | 89 | 8.69 | 9.39 | 5.76 | 7.23 | 3.75 | 6.54 | 6.70 | 8.09 |
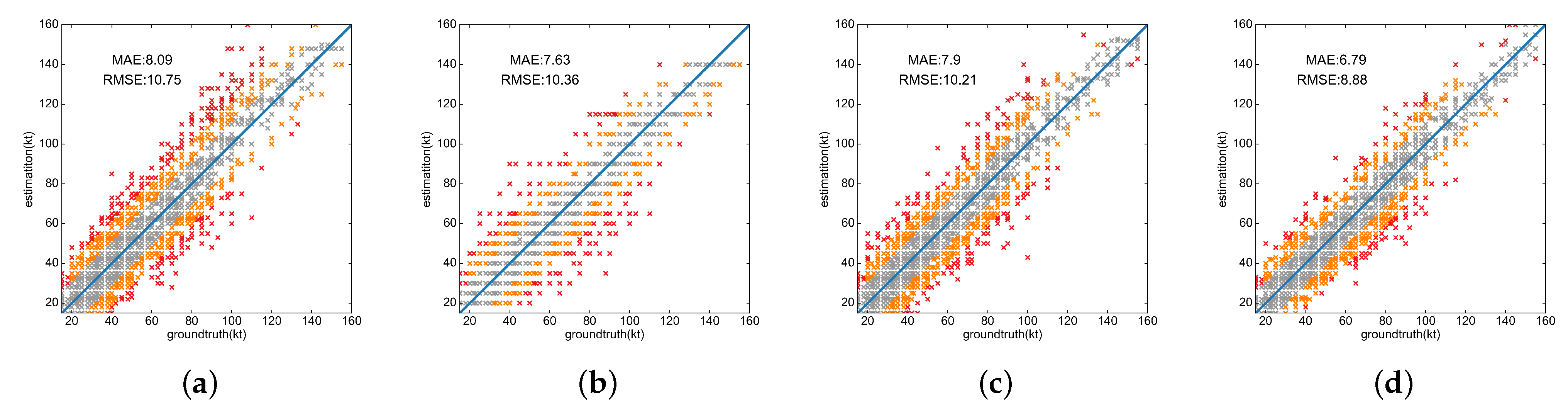
| Total | - | 4300 | 7.63 | 10.36 | 8.09 | 10.75 | 7.90 | 10.21 | 6.79 | 8.88 |
| Loss | MAE | RMSE | |
|---|---|---|---|
| (a) | CE | 7.63 | 10.36 |
| (b) | DC | 7.44 | 9.71 |
| (c) | DC + RI | 6.79 | 8.88 |
| (d) | DC + RI + smooth | 6.87 | 9.16 |
| (e) | DC + RI + transformer | 6.06 | 7.76 |
| Apporach | T = 3 | T = 4 | T = 5 | T = 6 | T = 7 | T = 8 | T = 9 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| ours (3 h-predict) | 6.46 | 8.53 | 6.45 | 8.52 | 6.41 | 8.44 | 6.58 | 8.84 | 6.42 | 8.51 | 6.47 | 8.54 | 6.30 | 8.09 |
| ours (6 h-predict) | 7.31 | 9.80 | 7.00 | 9.35 | 7.11 | 9.46 | 7.14 | 9.67 | 6.93 | 9.30 | 7.04 | 9.93 | 6.53 | 8.55 |
| ours (12 h-predict) | - | - | 9.23 | 12.65 | 8.92 | 12.41 | 8.57 | 11.85 | 8.66 | 11.91 | 7.65 | 10.52 | ||
| ours (24 h-predict) | - | - | - | - | - | - | 12.12 | 17.16 | ||||||
| ours (estimate) | 6.13 | 7.96 | 6.08 | 7.82 | 6.11 | 7.91 | 7.92 | 8.04 | 6.01 | 7.76 | 6.16 | 7.93 | 6.79 | 8.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Xu, Y.; Li, S.; Qian, Q.; Xiao, B. DR-Transformer: A Multi-Features Fusion Framework for Tropical Cyclones Intensity Estimation. Appl. Sci. 2021, 11, 6208. https://doi.org/10.3390/app11136208
Luo Y, Xu Y, Li S, Qian Q, Xiao B. DR-Transformer: A Multi-Features Fusion Framework for Tropical Cyclones Intensity Estimation. Applied Sciences. 2021; 11(13):6208. https://doi.org/10.3390/app11136208
Chicago/Turabian StyleLuo, Yicheng, Yajing Xu, Si Li, Qifeng Qian, and Bo Xiao. 2021. "DR-Transformer: A Multi-Features Fusion Framework for Tropical Cyclones Intensity Estimation" Applied Sciences 11, no. 13: 6208. https://doi.org/10.3390/app11136208
APA StyleLuo, Y., Xu, Y., Li, S., Qian, Q., & Xiao, B. (2021). DR-Transformer: A Multi-Features Fusion Framework for Tropical Cyclones Intensity Estimation. Applied Sciences, 11(13), 6208. https://doi.org/10.3390/app11136208






