Structural Performance of R-Type Steel Damper Used in Reinforced Concrete Members

Abstract

This study proposes a steel damper with a simple shape and excellent energy dissipation capacity. The proposed damper has a rectangular shape (R-type) and has an energy dissipation part and a load transmission part. The energy dissipation part dissipates external energy through the yielding of the steel material; it comprises a vertical member and upper and lower horizontal members. This study performed two-phase experiments to verify the structural performance of the proposed damper. The Phase I test was performed to evaluate the load history characteristics and energy dissipation capacity of the damper and the Phase II test was performed to confirm the structural performance of reinforced concrete members with the proposed damper. The experimental results showed that the proposed R-type steel damper had high-energy dissipation performance despite having a simple shape.

1. Introduction

The seismic design concepts traditionally recommended in building codes are aimed at ductility to ensure that people have enough time to evacuate during a strong earthquake [1]. Building structures can dissipate energy during an earthquake by exploiting the inelastic behavior and damping capacity of each constituent structural system. However, after a strong earthquake, the building structure undergoes permanent deformation and failure owing to its inelastic behavior. In this case, the damage recovery cost increases, repair and rehabilitation become difficult, and environmental pollution is caused if the building must be demolished.

In order to avoid these problems and render building design sustainable, economical, and safe, damping and isolation systems for earthquakes have attracted increasing interest. A damping system contains an energy dissipation device that absorbs most of the earthquake energy, thereby minimizing damage to the building. Furthermore, such systems are economical and ecofriendly because only this energy dissipation device needs to be replaced after an earthquake. As a result, the building lifecycle is greatly increased and, in turn, the consumption of natural resources such as natural aggregates, mineral resources, and wood for a new construction is greatly reduced. This design method thus effectively addresses current social needs.

Damping systems were first studied in 1956 with a seismic design method using Housner’s energy method. In 1981, a steel damper that dissipates external energy by yielding steel was first used in reinforced concrete (RC) piers in New Zealand. In 1987, a friction damping system proposed in New Zealand in the early 1970s was first applied to a library at the University of Montreal. Since the 1990s, fluid-based viscous dampers have been proposed and applied for the first time in a three-story building in Sacramento.

Damping systems are of active and passive types. Passive dampers are relatively economical and easy to install. They are divided into metal yield dampers or friction dampers for which hysteresis characteristics depend on displacement and viscous dampers or viscoelastic dampers for which hysteresis characteristics depend on speed. In general, dampers that depend on displacement are mainly used for seismic design and those that depend on speed are mainly used for wind resistance design. Recently, remarkable developments have been made in passive dampers that use the energy dissipation capacity of steel because they are relatively easy to manufacture and install and have excellent energy dissipation capability. In particular, with environmental protection becoming a key issue in the recent years, yield-type steel dampers are being increasingly used because they are relatively less damaging to existing buildings during earthquakes and are, therefore, advantageous for building repair and rehabilitation.

Various types of steel dampers have been developed thus far. Whittaker et al. [2] and Shih and Sung [3] developed added damping and stiffness (ADAS) dampers and Tsai et al. [4] developed triangular ADAS (TADAS) dampers. Lee et al. [5] developed a steel honeycomb damper. Nakashima [6], Foti et al. [7], and Choi and Abebe [8] developed a shear panel damper with low yield strength and evaluated its hysteresis characteristics. Di Sarno and Manfredi [9] performed an experimental study on the full-scale RC frames retrofitted with buckling-restrained braces. Teruna et al. [10,11] theoretically investigated the use of a steel damper for improving the seismic performance of RC frames and then experimentally determined the geometric shape of steel dampers.

Bagheri et al. [12], Jamkhaneh et al. [13], and Sravya and Manchalwar [14] developed U-shaped steel dampers in different forms. Lee and Kim [15] developed a box-shaped steel slit damper. Shen et al. [16] conducted theoretical and experimental studies on a transverse steel damper (TSD). Abebe et al. [17] performed finite element (FE) analysis to evaluate the hysteresis behavior of a circular hollow steel damper (CHSD) and verified its applicability through comparisons with experimental results. Naeem and Kim [18] developed a multi-slit damper (MSD) that connects weak and strong slit dampers. Qiu et al. [19] developed a damper using a shape memory alloy and steel and performed its FE analytical and experimental evaluation.

Yield-type steel dampers are being studied continuously to improve their energy dissipation capacity as well as to simplify their form to make their manufacturing process and installation easier. This study proposes a steel damper with a relatively simple shape and excellent energy dissipation capacity. Experiments and FE analysis are performed on this damper itself to verify its structural performance. Furthermore, the superiority of this damper is experimentally verified through evaluations of the performance of structural members with this damper.

2. Experimental Program

This study involved two experimental phases to develop a steel damper with a simple shape and excellent energy dissipation capacity that is easy to manufacture as well as to verify its performance. In the Phase I test, the performance of the proposed steel damper was evaluated and, in the Phase II test, the performance of a structural member with this damper was verified.

2.1. Phase I Test Program

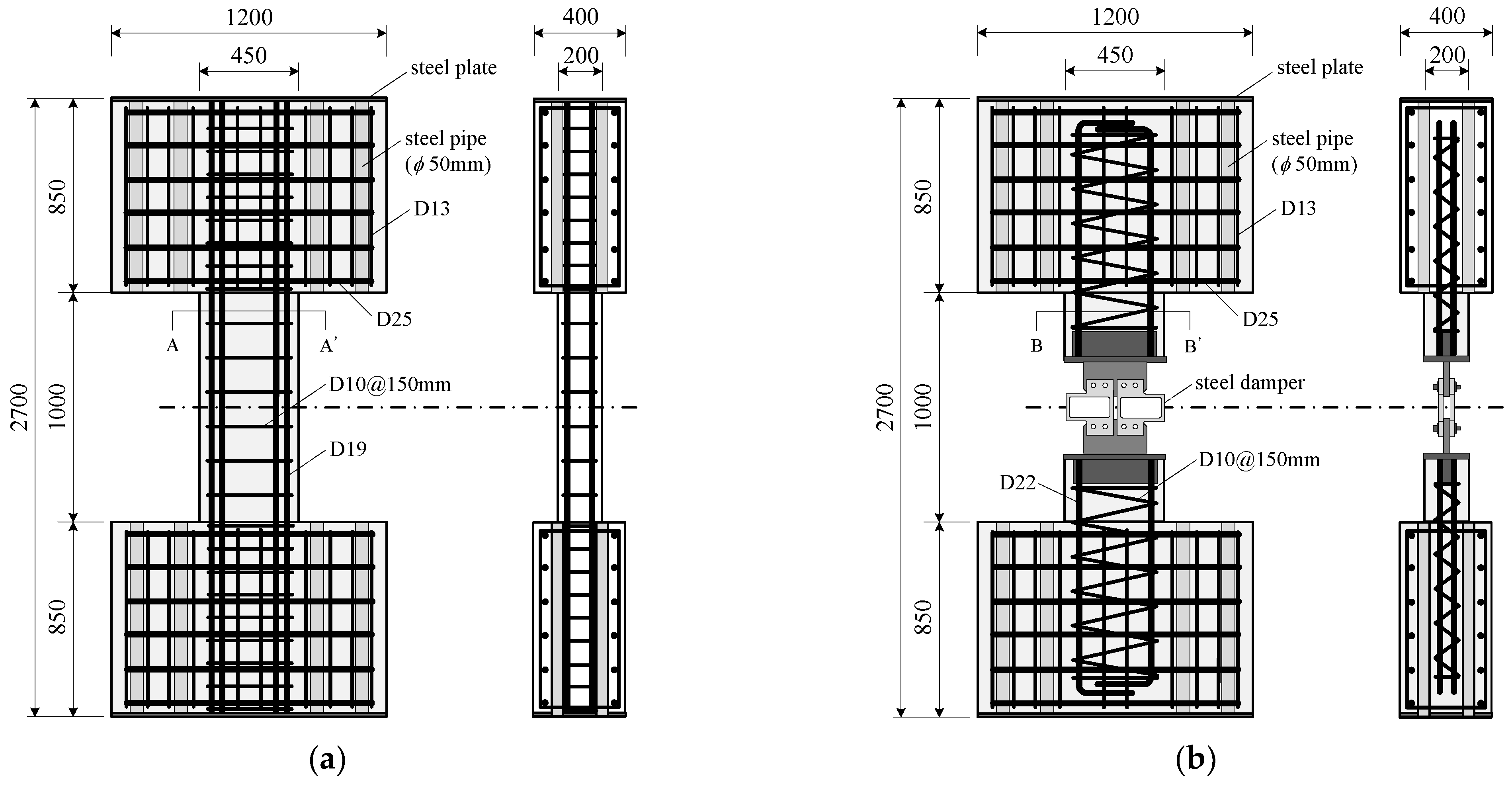
2.1.1. Design of Phase I Test Specimens

As shown in Figure 1, two types of dampers were designed in this study. In order to prevent eccentricity, four steel dampers were connected to the front and rear of each specimen. Tension tests of the steel used in the damper were performed according to ASTM E8 [20]. As a result, the yield and tensile strengths were 245 and 420 MPa, respectively, and the yield strain was 0.00147, as shown in

Table 1. Mechanical properties of materials.

Steels	Yield Strength (MPa)	Tensile Strength (MPa)	Yield Strain	Elastic Modulus (×105 MPa)
Steel damper	245	420	0.00147	1.67
D10 (stirrup)	461	600	0.00242	1.90
D10 (spiral)	554	607	0.00275	2.01
D19	520	662	0.00260	2.00
D22	518	672	0.00258	2.01

.

As shown in Figure 1a, Specimen D1 comprises four angled U-shaped dampers. This specimen was designed to compare the structural performance and characteristics of the rectangular-type (R-type) steel damper proposed in this study. The steel damper used in the experiment had an energy dissipation part and a load transmission part. The energy dissipation part dissipates external energy through the yielding of the steel. It comprises a vertical member and upper and lower horizontal members. The upper horizontal member allows the vertical member to stably undergo plastic deformation through bending while dissipating energy through plastic deformation. The lower horizontal member is directly connected to the load transfer plate to improve the load resistance capability of the damper and to dissipate energy. Figure 1 shows the dimensions and shape of this damper.

2.1.2. Test Setup and Loading Procedure

Figure 2 shows the test setup of the Phase I test specimen. The damper was bolted to the T-shaped steel plate for load transmission located on the left and right sides. In turn, this plate was bolted to each of the two L-shaped load frames. One of the L-shaped load frames was fastened with a 2000 kN universal testing machine (UTM) on the top and the other was fastened with the steel frame on the bottom. Rollers were installed in the upper and lower parts where the L-shaped frame meets to apply a shear force to the specimen in the vertical direction.

Four identical dampers were applied for each specimen to prevent eccentricity and to evaluate the actual applicable load resistance performance. In order to measure the relative displacement of the specimens, a linear variable differential transformer (LVDT) with a capacity of 50 mm was installed on both the front and the rear of the specimen, as shown in Figure 2. A load was gradually applied to the specimens by the displacement control method five times in both the positive and the negative directions up to the target displacement of 15 mm.

2.2. Phase II Test Program

2.2.1. Design of Phase II Specimens

In the Phase II test, the proposed R-type damper was applied to an RC member to evaluate its structural performance. The proposed damper can be applied in various manners wherever a passive vibration damper can be applied, for example, a wall type, a coupling beam connecting the shear wall, and a brace type, etc. In this study, an RC coupling beam was selected as the structural member as it is relatively simple and can be used to verify the performance of the proposed damper. The coupling beam is a structural member that exists between the shear walls and is easily damaged by lateral load. The experimental results in this study can be applied to many places where shear force due to lateral load is transmitted to the damper as well as the coupling beams.

As shown in Figure 3, Specimens M1 and M2 without and with the proposed damper, respectively, were designed for the Phase II test. The specimens had stiff stubs at both ends to realize relatively high rigidity compared to that of the coupling beam because many reinforcing bars are placed in the shear wall to withstand the lateral and axial forces. The beam of the specimen had a width, height, and length of 200 mm, 450 mm, and 1000 mm, respectively. Furthermore, the stub has a cross section of 400 × 850 mm² and length of 1200 mm.

A compression test revealed that the concrete used in the specimens had a strength of 26.0 MPa and the damper was made of the same steel as that used in the Phase I test. As shown in Figure 3, in Specimen M1, eight D19 (286.7 mm² × 8 ea.) rebars were placed in a section of the test region as the main reinforcement and the effective height of the beam was 370 mm. The stirrup was designed to dominate the shear by placing D10 (71.3 mm²) rebars at 150 mm intervals.

In Specimen M2 with the proposed R-type steel dampers, the yielding of the damper is designed to precede the flexural yielding of the specimen. In addition, four D22 (387.1 mm² × 4 ea.) steel bars were placed in the test region of specimen M2 as the main reinforcing bars, reflecting the reduced factored-external load by installing dampers. The T-shaped steel plate to which the damper is fastened and the main reinforcing bar were welded together. In addition, for simplifying the construction, the stirrup was spirally reinforced with D10 reinforcing bars at 150 mm intervals.

2.2.2. Test Setup and Loading Procedure

In order to evaluate the applicability of the proposed damper to structural members, an antisymmetric moment due to seismic loads was designed to act on the specimen. Figure 4 shows the test setup of the Phase II test specimen. The antisymmetric moment was implemented using a horizontal holding device. The lateral load was applied to the specimen using an electric actuator with a capacity of 1000 kN that was installed at the mid-height of the specimen. The lateral load actuator was bolted to the loading frame connected to the specimen. In order to simulate the damper resisting the shear force induced by the lateral load caused by the earthquake, a 1000 kN hydraulic actuator connected to the upper part of the load frame was used to prevent axial force from acting on the specimen.

As shown in Figure 4b, two LVDTs were installed to measure the drift angle of the specimen. Another two LVDTs were installed at the front and rear of the damper to evaluate its behavior. Strain gauges were attached at the position where the maximum strain rate was expected to evaluate the deformation characteristics of the longitudinal reinforcing bars, stirrups, and the proposed dampers. Repetitive loading was performed two times, each with drift angles of 1/400, 1/200, 1/100, 1/75, 1/50, and 1/30.

3. Phase I Test Results

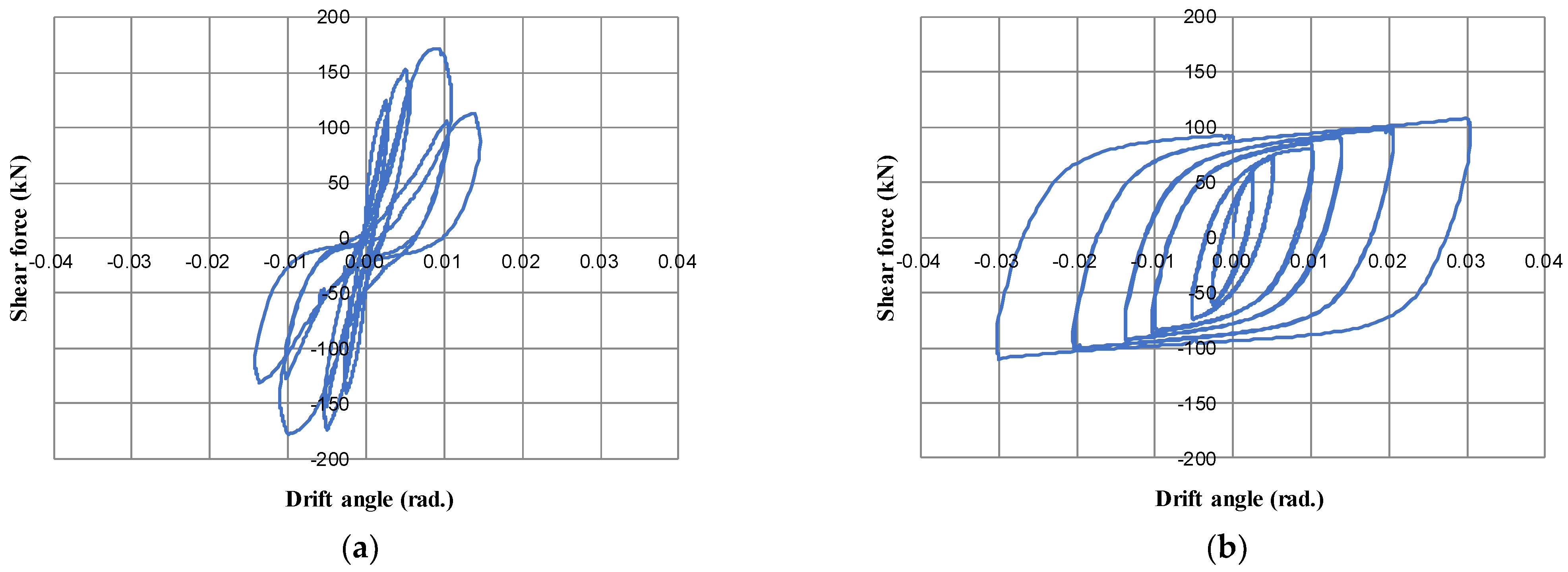
3.1. Behavior of Specimens

The shear force-displacement curve obtained from the Phase I test is shown in Figure 5. Specimens D1 and D2 showed stable elasticity and plastic behavior up to the target displacement of ±15 mm. As shown in

Table 2. Experimental results of Phase I test.

Specimens	At First Yield			${\mathit{P}}_{\mathit{i}}/{\mathit{P}}_{\mathit{y}} \mathbf{at} \mathbf{Target} \mathbf{Displacement} \mathbf{for} \mathbf{Each} \mathbf{Cycle}$
	Cycle	$\mathbf{Load} \left({\mathit{P}}_{\mathit{y}}\right)$ (kN)	Disp. (mm)	Directions	1st	2nd	3rd	4th	5th
D1	+1st	+18.1	+1.85	Positive Negative	1.28 −1.56	1.50 −1.65	1.54 −1.66	1.55 −1.66	1.55 −1.66
D2	+1st	+36.0	+0.57	Positive Negative	2.51 −2.77	2.79 −2.93	2.84 −2.91	2.84 −2.90	2.84 −2.88

, D1 first yielded in the first cycle at a displacement of 1.85 mm and load of 18.1 kN. By contrast, D2, with an additional lower horizontal member, first yielded in the first cycle at a displacement of 0.57 mm and a load of 36 kN. In other words, D2 had 6.4 times higher rigidity than D1 owing to the addition of the lower horizontal member. This means that a damper with higher initial rigidity can dissipate external energy more quickly when the external load is transmitted to the structure.

As shown in Figure 5 and Table 2, D2 had a higher rate of strength increase after yielding than D1. That is, in D1, the load at target displacement of the first cycle was 1.56 times the yield load, whereas in D2, it was 2.77 times. However, there was no significant difference in the load at the target displacement for each of the specimens during five cycles. Furthermore, D1 and D2 showed little decrease in stiffness and strength during five repeated loads. In the first forward cycle, D1 showed strength of up to 23.3 kN, whereas D2 showed strength of up to 90.5 kN (i.e., 3.9 times higher load resistance capacity). In the fifth cycle, D2 showed around 3.6 and 3.4 times higher strength in the positive and negative directions than compared to D1, respectively. The shear force-displacement curve in Figure 5 and the deformation state at the target displacement in Figure 6 confirms that the deformation of the specimen is stable and no in-plane and out-of-plane buckling were found even after the experiment was completed. Therefore, the experimental results confirmed that D2 has excellent load resistance and deformation capacity even though it has a relatively simple shape.

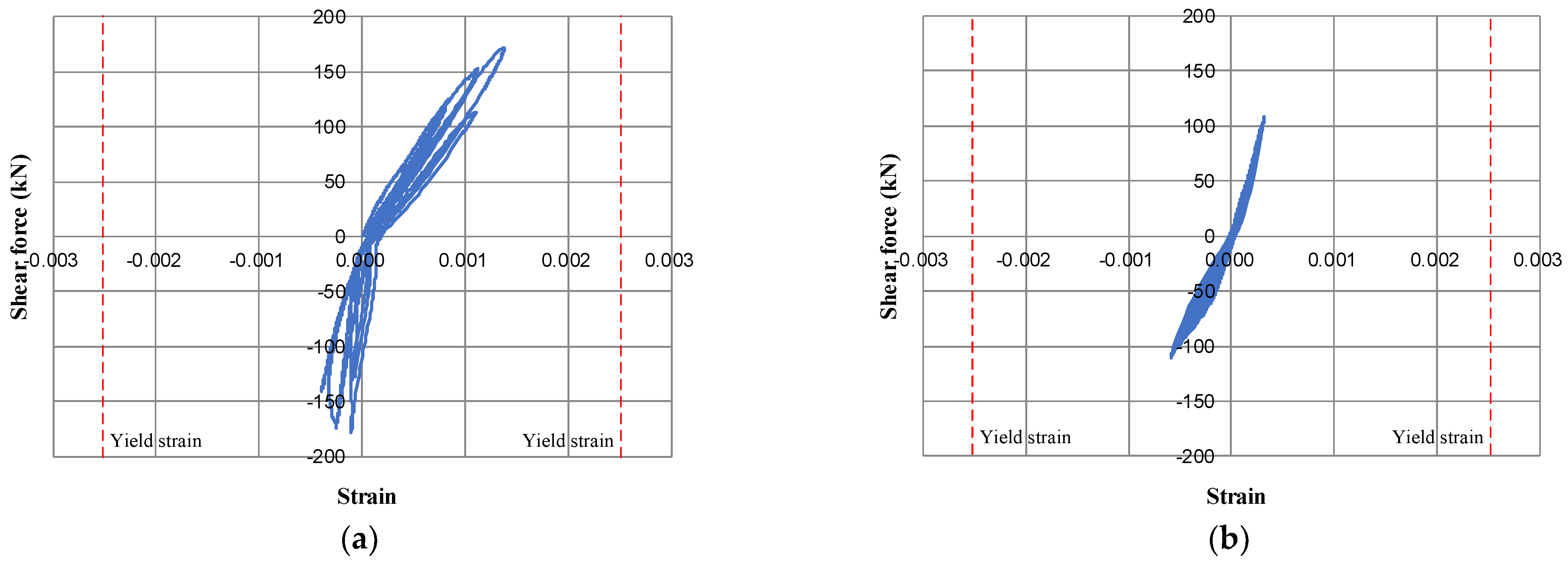
3.2. Strain Distribution

The analysis of the deformation characteristics of each specimen using attached strain gauges showed that D1 first reached a yield strain of 0.00147 in the vertical member during the first positive loading cycle and then yielding occurred in the horizontal member as well. In D2, the yielding of the vertical member occurred shortly after the initial yield of the lower horizontal member and the following yielding occurred in the upper horizontal member. D2, similar to D1, yielded in all energy-dissipating members during the first positive loading cycle.

As shown in Figure 7, D1 has a maximum strain of approximately 0.021 in the vertical member. At both ends of the horizontal member, it was deformed to a maximum strain of 0.0018. D2 showed maximum deformations of 0.05 in the lower horizontal member, 0.02 in the vertical member, and 0.0022 in the upper horizontal member. These experimental results reveal that in D1, most energy is dissipated in the vertical member, whereas in D2, most energy is dissipated in the lower horizontal member as well as the vertical member.

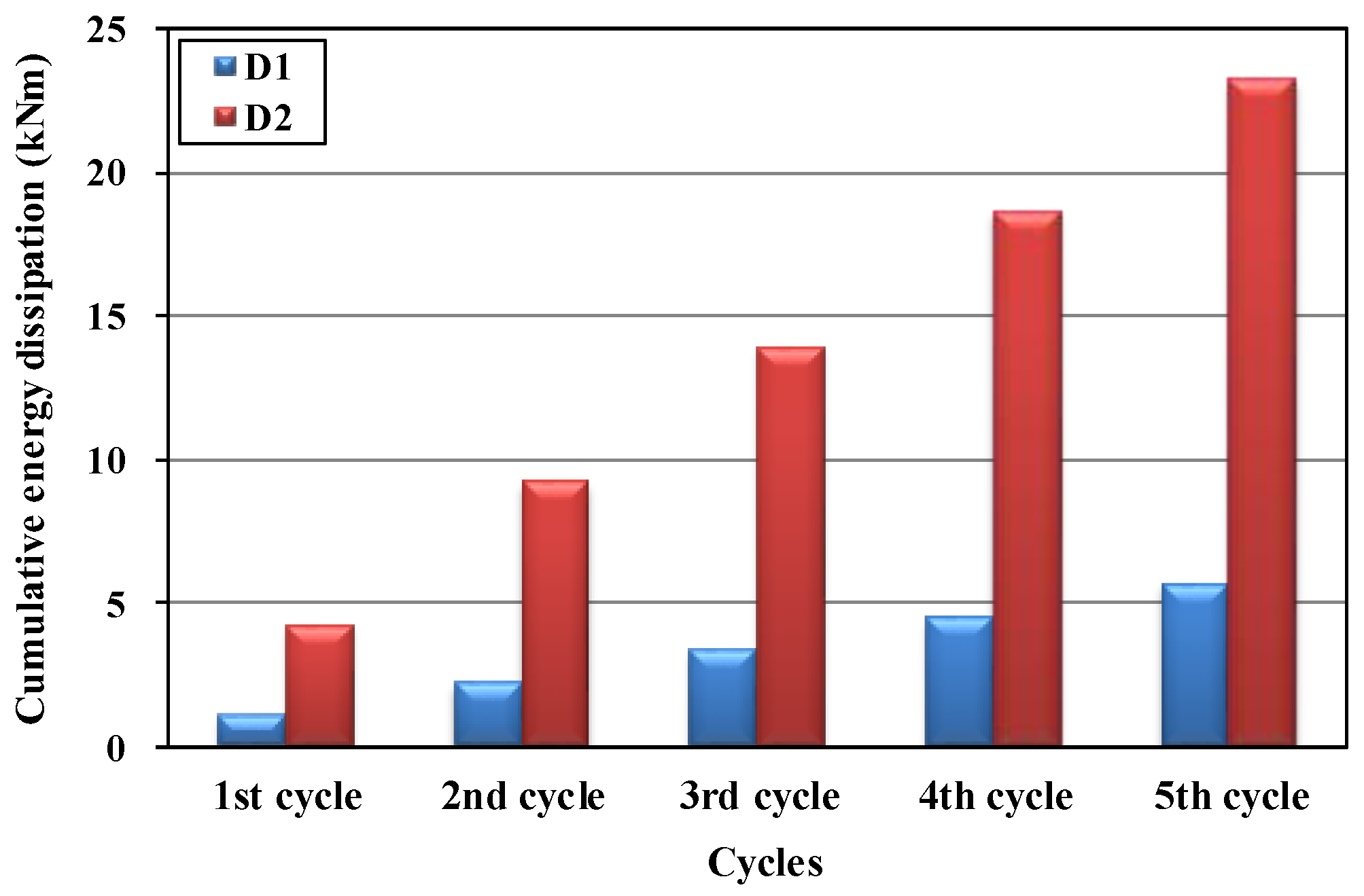
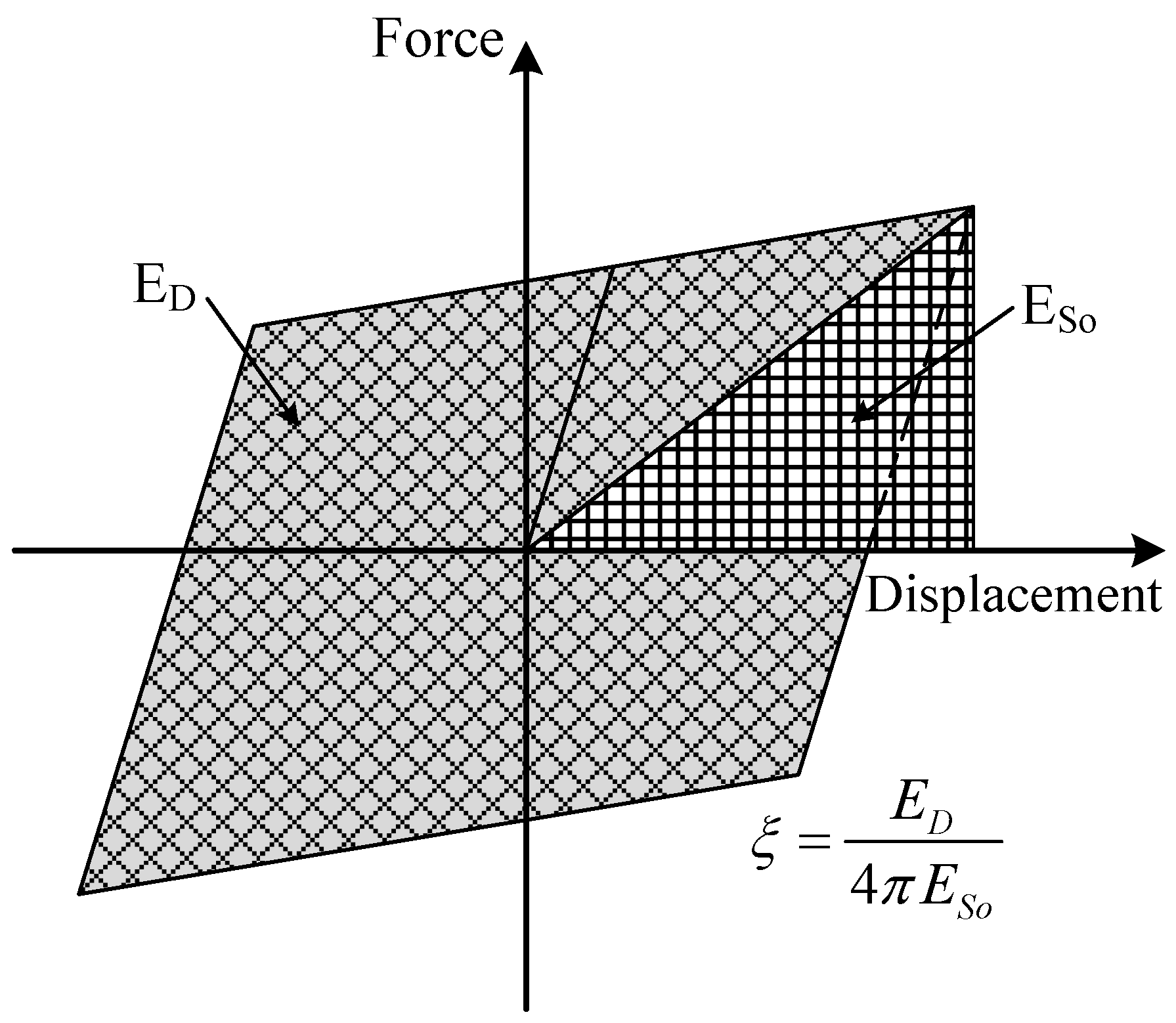
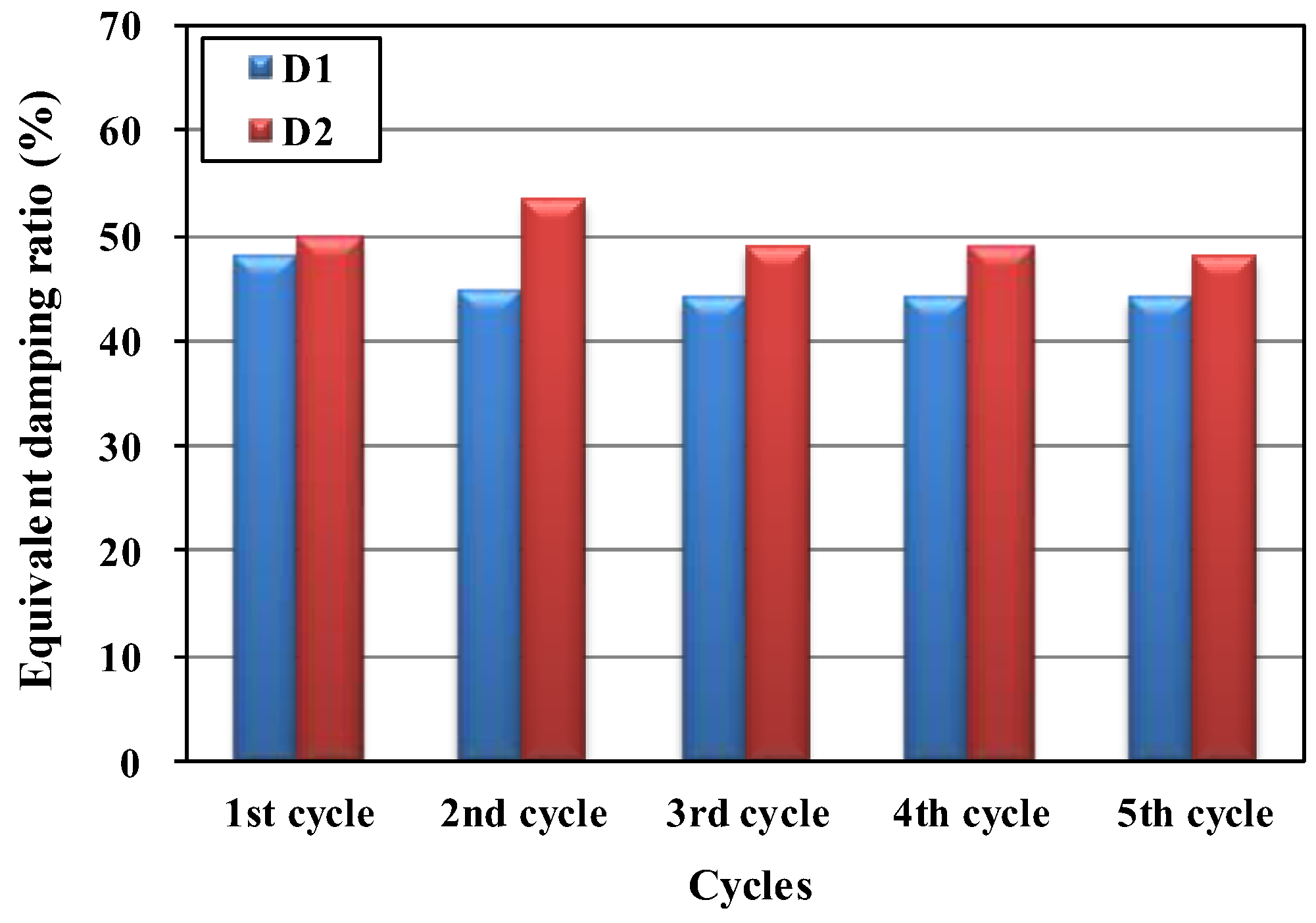
3.3. Energy Dissipation and Damping Capacities

Figure 8 shows the cumulative energy dissipation area of D1 and D2 for each cycle. In the first cycle, D1 showed an area of 1050.6 kN·mm, whereas D2 showed an area of 4235.9 kN·mm (i.e., around four times higher). A similar trend was seen in all five cycles. In the fifth cycle, the energy dissipation areas of D1 and D2 increased by approximately 10% compared to those in the first cycle. The accumulated energy dissipation of D1 and D2 during the five cycles was 5650.2 and 23,262.1 kN·mm, respectively. In addition, the energy dissipation area did not decrease from the first to the fifth cycles in all specimens. These experimental results confirmed that the proposed R-type steel damper has high load resistance capability and very good energy dissipation capability.

In this study, in order to evaluate the damping capacity of the specimen, the equivalent damping ratio $\xi$ was calculated as the following [21]:

$$\xi =\frac{E_D}{4\pi E_{So}}$$

(1)

where $E_D$ is the internal area of the first cycle history of the specimen and $E_{So}$ is the maximum strain energy; they are obtained as shown in Figure 9. Furthermore, Figure 10 shows the result calculated using Equation (1). D1 and D2 showed high equivalent attenuation ratios of 44% ~ 48% and 48.1% ~ 53.4%, respectively, and these values are close to the ideal case of elastic–plastic behavior. It can be confirmed that the proposed R-type damper maintained a high damping capacity through the vertical and upper horizontal members and had high load resistance capability through the addition of the lower horizontal members.

3.4. Stress Distribution by FE Analysis at Target Displacement

In this study, the FE analysis program MIDAS-NFX [22] was used to analytically confirm the energy dissipation area of the D1 and D2 dampers used in the Phase I test. This program can be applied to single materials such as steel and aluminum and it can be used to perform 3D analyses that consider material and geometric nonlinearities. The kinematic hardening model considering the Bauschinger effect is used as the constitutive relationship of the steel damper.

Figure 11 shows the FE analysis modeling of the damper used in the Phase I test. A 3D solid hexahedron element with a size of approximately 4 mm was used to model the steel damper. In order to induce a shear force, the bolted part of one steel plate was fixed and then a displacement was induced in the bolted part so that the other steel plate was moved only in the vertical direction. Figure 12 shows the stress distribution when the target displacement is reached; the red color indicates that the yield stress has been reached. As in the experiment, no buckling was found. The FE analytical results in Figure 12 and the experimental results were similar in the region where the yielding occurred. In other words, most energy dissipation of the angled U-shaped D1 damper occurred in the vertical member. The upper horizontal member participates in energy dissipation at both ends where the moment is at the maximum. In the R-type D2 damper, most vertical and lower horizontal members participate in energy dissipation and the upper horizontal member showed similar results to the D1 damper. The FE analytical results showed sufficient agreement with the experimental results, thereby confirming their reliability.

4. Phase II Test Results

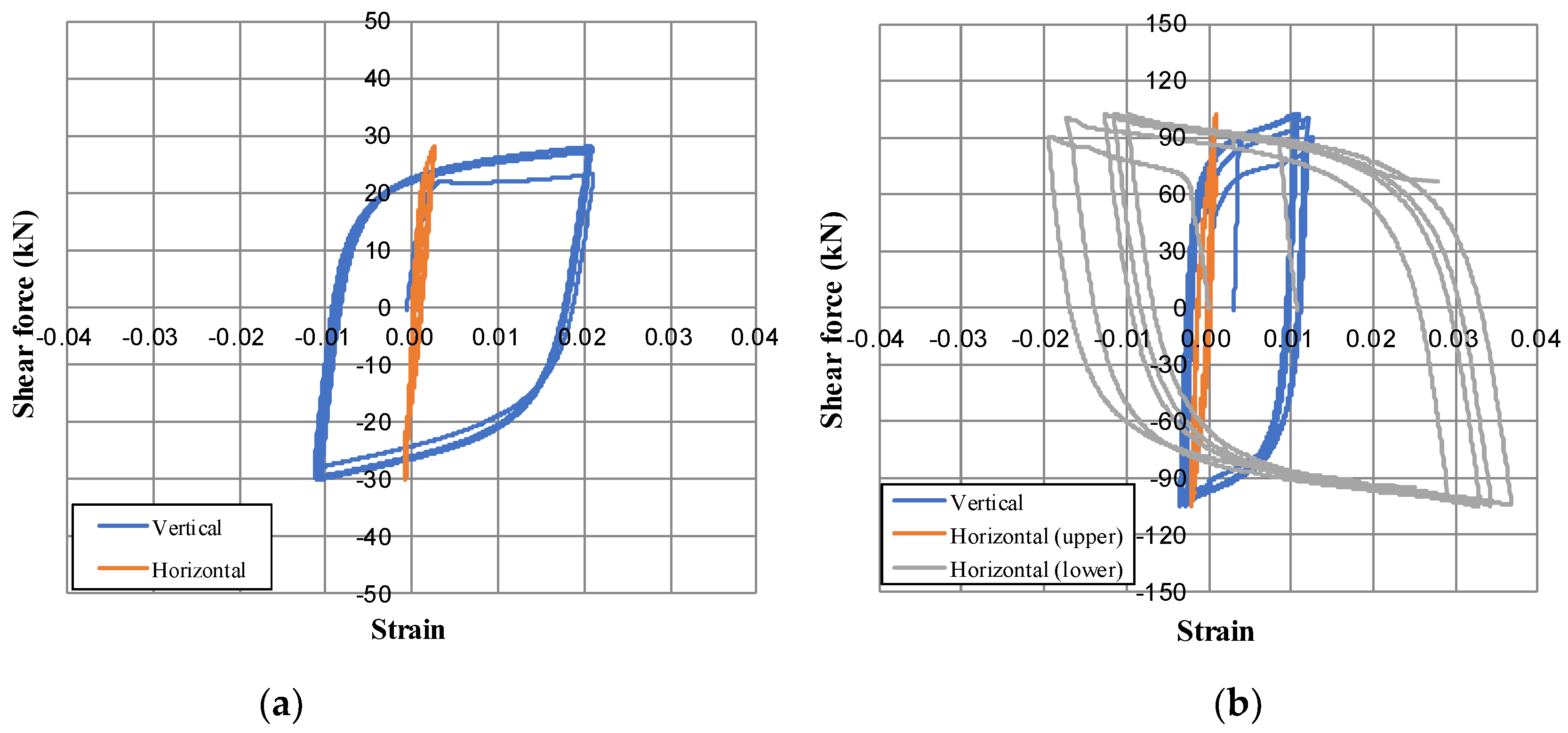
4.1. Shear vs. Drift Angle Relationships

Figure 13 shows the shear force vs. drift angle relationships obtained from the Phase II test for evaluating the applicability of the proposed R-type damper. Figure 14a shows that in Specimen M1 without a damper, the RC member resisted the entire external shear force and this resulted in brittle fracture owing to shear and bond cracks. As shown in

Table 3. Experimental results of Phase II test. (Unit: kN, rad.)

Speci-mens	Directions	Peak Load and Drift Angle at First Loading of Each Cycle
		1/400	1/200	1/100	1/75	1/50	1/30
M1	Positive	124.7 (0.0025)	153.0 (0.005)	171.4 (0.0088)	112.8 (0.0139)	-	-
	Negative	−140.3 (−0.0025)	−174.4 (−0.005)	−177.8 (−0.010)	−131.4 (−0.0137)	-	-
M2	Positive	55.3 (0.0025)	71.2 (0.005)	81.0 (0.010)	90.6 (0.0135)	98.4 (0.02)	108.0 (0.03)
	Negative	−60.9 (−0.0026)	−73.2 (−0.0051)	−83.2 (−0.010)	−91.9 (−0.0134)	−100.5 (−0.02)	−110.1 (−0.03)

, M1 had a maximum load of 171.4 kN at a drift angle of 0.0088 rad in the 1/100 cycle in the positive direction and −177.8 kN at a drift angle of −0.01 rad in the −1/100 cycle in the negative direction. In the 1/75 cycle, the test was terminated as the applied load decreased to approximately 65% of the maximum load. As shown in Figure 15a, the longitudinal reinforcement of M1 did not yield.

In Specimen M2 with the proposed R-type steel dampers, the yielding and energy dissipation of the steel damper occurred before the RC member was damaged. Hardly any cracks formed in the RC member and ductile behavior was observed for a drift angle of up to 3%. As shown in Figure 15b, the longitudinal reinforcement of M2 remained at a strain of at most 0.0006. The damper yielded in the first 1/400 cycle and the load and drift angle at that time were 52.1 kN and 0.002 rad, respectively. Initially, the vertical member of the steel damper yielded and, immediately after, the lower horizontal member of the steel damper yielded at a drift angle of 0.0025 rad. The upper horizontal member of the steel damper yielded in the 1/200 cycle and the load and drift angle at that time were 68.8 kN and 0.004 rad, respectively.

4.2. Crack Patterns and Failure Modes

As shown in Figure 14a, which is the view after M1 failure, the shear and bond cracks are more prominent than the flexural cracks. In M1, flexural and shear cracks were observed in the 1/400 cycle. As the drift angle increased further, the number and width of shear cracks increased. Shear and bond cracks developed significantly with a load of 171.4 kN at a drift angle of 0.0088 rad in the 1/100 cycle, resulting in brittle shear-bond failure. This is because the short shear span ratio of the coupling beam is very vulnerable to shear and bond due to lateral forces such as earthquake loads.

Figure 14b shows the appearance at the maximum drift angle of M2 with the proposed R-type steel dampers. Hardly any cracks were observed in the test region and all deformations were concentrated in the damper. These experimental results confirmed that the proposed damper performs very well when applied to a structural member.

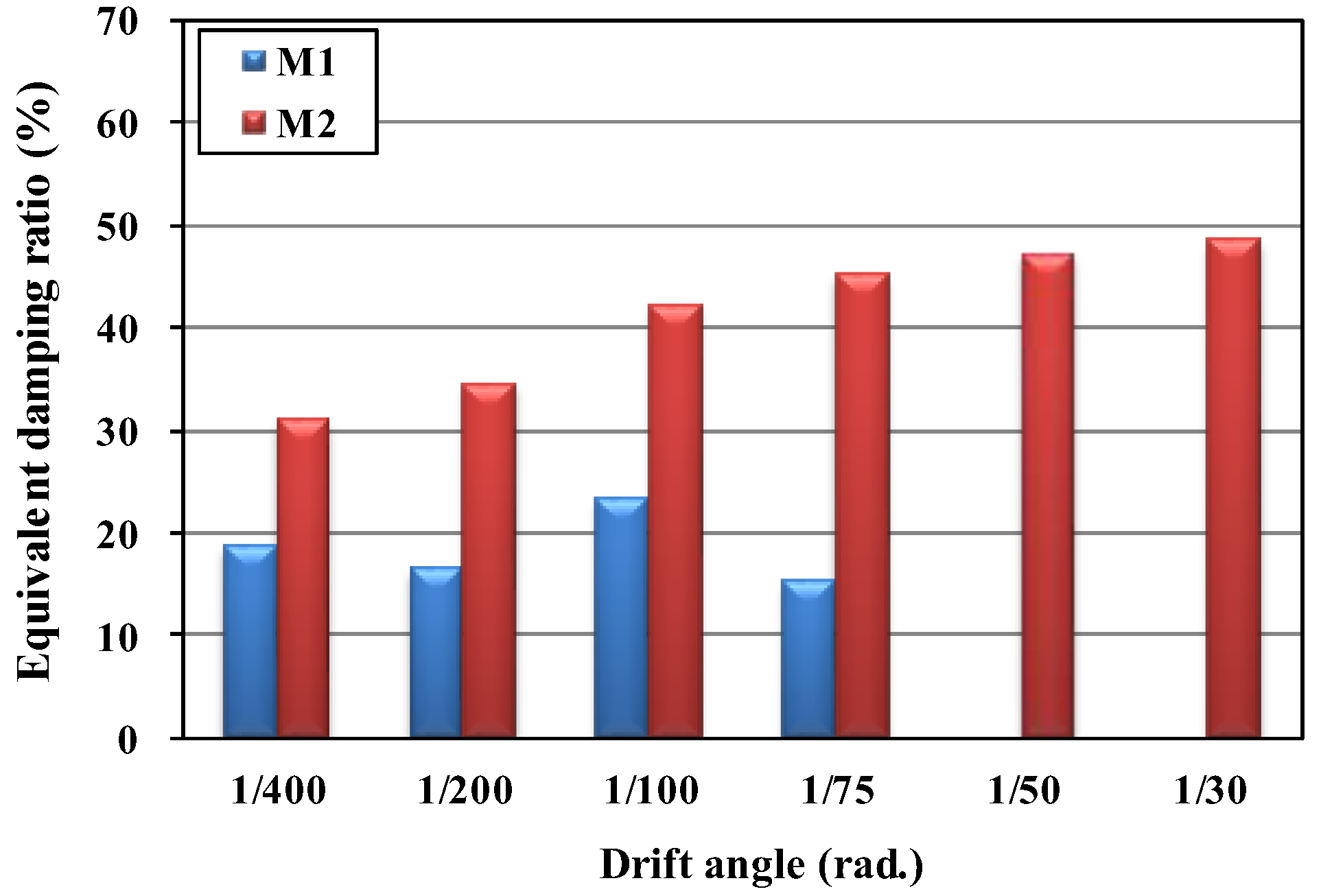
4.3. Energy Dissipation and Damping Capacities

Figure 16 shows the cumulative energy dissipation area, which is calculated as described in Section 3.3, of M1 and M2 for each cycle. M1 and M2 showed a similar cumulative energy dissipation up to a drift angle of 1% and the energy dissipation ability of M1 became lower than that of M2 at a drift angle of 1.3%. Then, where M1 showed structural failure owing to shear and bond cracks, the energy dissipation capacity of M2 improved greatly as the drift angle increased. For example, at a drift angle of approximately 3%, the cumulative energy dissipation capacity of M2 was around 4.5 times higher than that of M1. These experimental results confirmed that the proposed R-type damper has high energy dissipation capacity even when applied to structural members.

Figure 17 shows the equivalent damping/attenuation ratio, which is calculated as described in Section 3.3, of the Phase II test specimens for each cycle. M1 showed an equivalent damping ratio of approximately 20%, whereas M2 with the proposed R-type damper showed an equivalent damping ratio of 30.8% in the first cycle with a low degree of deformation. As the drift angle increased, this ratio increased continuously up to 48.6%. These experimental results confirmed the excellent damping ability of the proposed R-type damper.

5. Conclusions

In this study, an R-type steel damper with a simple shape and excellent load resistance and energy dissipation capacities was proposed. A two-phase experimental study and an analytical study using FE analysis program were conducted to evaluate its structural performance. In the Phase I test, shear force was applied directly to the damper. In the Phase II test, the proposed damper was applied to an RC member to verify its structural performance. Based on the experimental and analytical studies, the following results were obtained.

(1)

The shape of the proposed damper is easy to manufacture and the number and cross-sectional dimensions of the dampers can be changed freely according to the required structural performance. Tests of the structural performance of the proposed damper showed that the strength and stiffness were maintained without decreasing while a repeated load was applied five times up to the target displacement. In addition, no buckling was observed until the end of the experiment.

(2)

In the proposed damper, the vertical and upper horizontal members are involved in the ductile behavior and energy dissipation and the lower horizontal member is involved in strength enhancement and energy dissipation. The experimental results of the angled U-shaped steel damper showed that the strength and initial rigidity of the proposed R-type steel damper were increased by around 3.5 and 6.4 times, respectively.

(3)

In the Phase I test, the energy dissipation capacity of the proposed damper did not decrease during five repeated loads. In addition, the proposed damper showed an equivalent damping ratio of up to 53.4%, indicating high damping capacity. Similar characteristics were observed in the Phase II test. The Specimen M2 with the proposed damper showed an equivalent damping ratio of up to 48.6%, indicating excellent damping ability.

(4)

The region in which energy is dissipated in the damper was similar in the FE analytical and experimental results. Most vertical and lower horizontal members of the proposed damper yielded and showed high strain in the experiment. On the other hand, the upper horizontal member yielded in some areas but contributed to the stable and ductile behavior of the damper.

(5)

In the Phase II test, an excellent energy dissipation capacity was measured. In the M1 specimen without the damper, excessive cracking and damage occurred because the RC member resisted the external lateral load. By contrast, the M2 specimen with the proposed R-type steel dampers showed ductile behavior without strength deterioration for a drift angle of up to 3% because the damper effectively dissipated the energy of the external lateral load. Furthermore, hardly any cracks or damage were observed in the M2 specimen. Based on the experimental results, the proposed steel damper can be applied excellently to structures as an energy dissipating device.