Effect of Configuration and Yield Strength of Transverse Reinforcement on Lateral Confinement of RC Columns
Abstract
:1. Introduction
2. Experimental Plan
3. Experimental Results
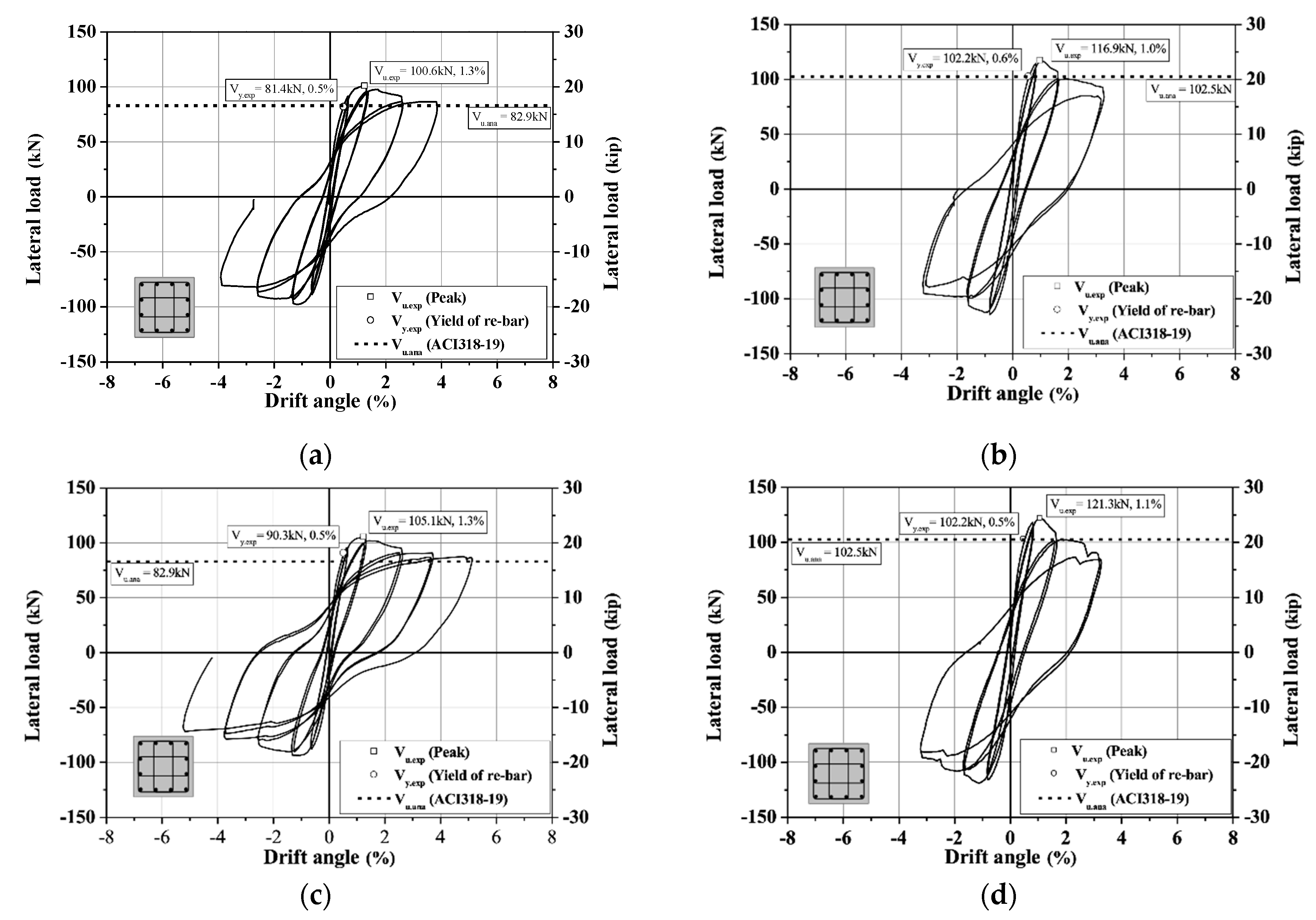
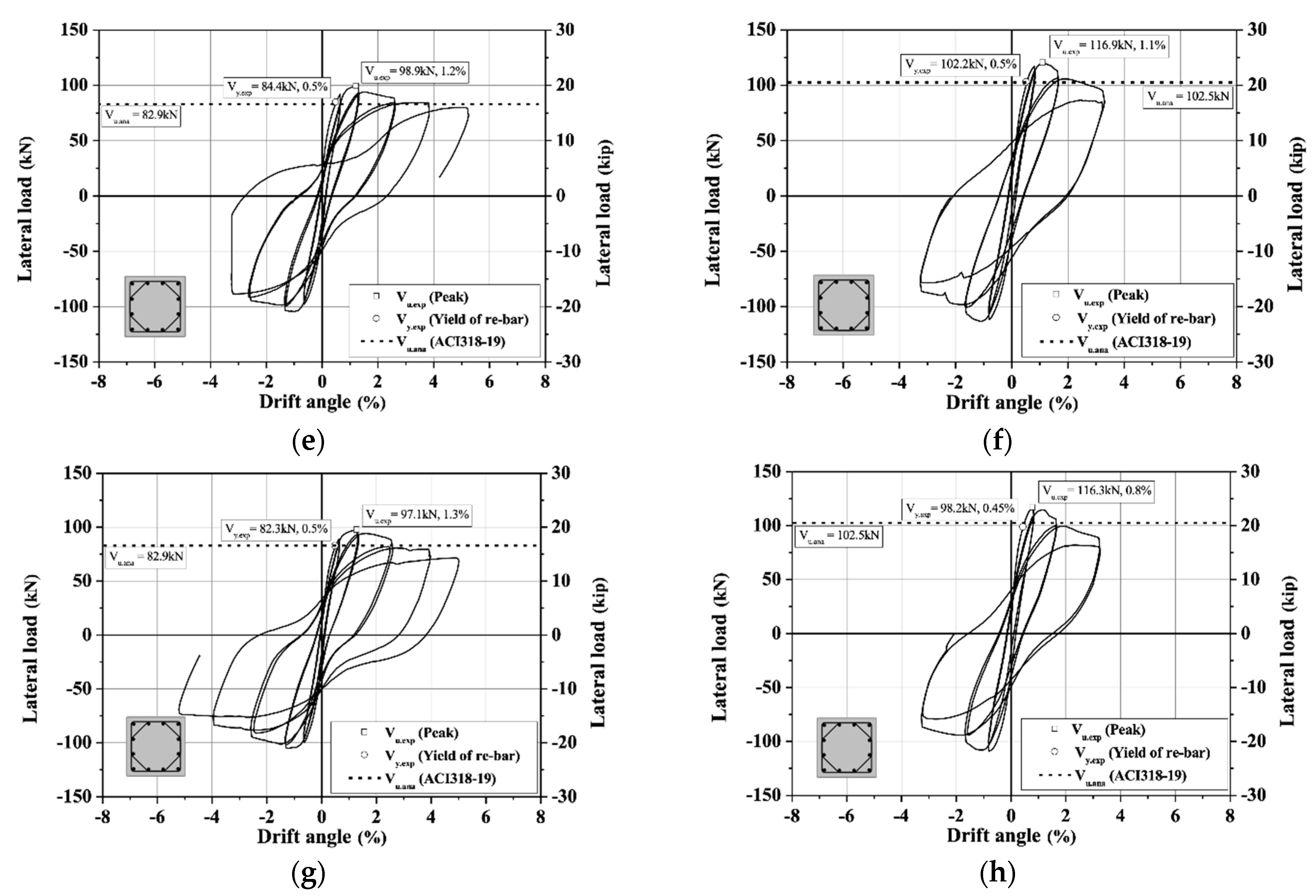
3.1. Relationship of Lateral Load-Drift Angle
3.2. Crack Patterns and Failure Shapes
4. Analysis of Experimental Results
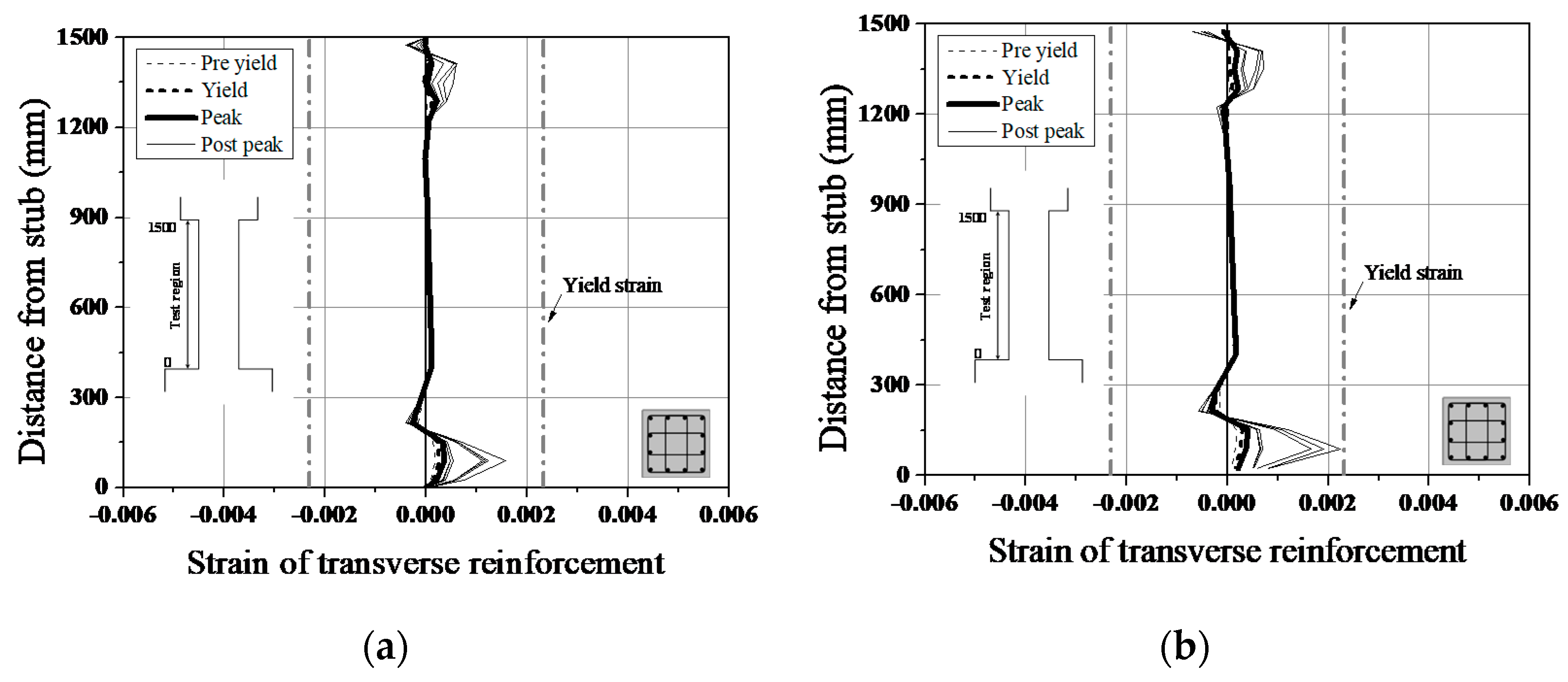
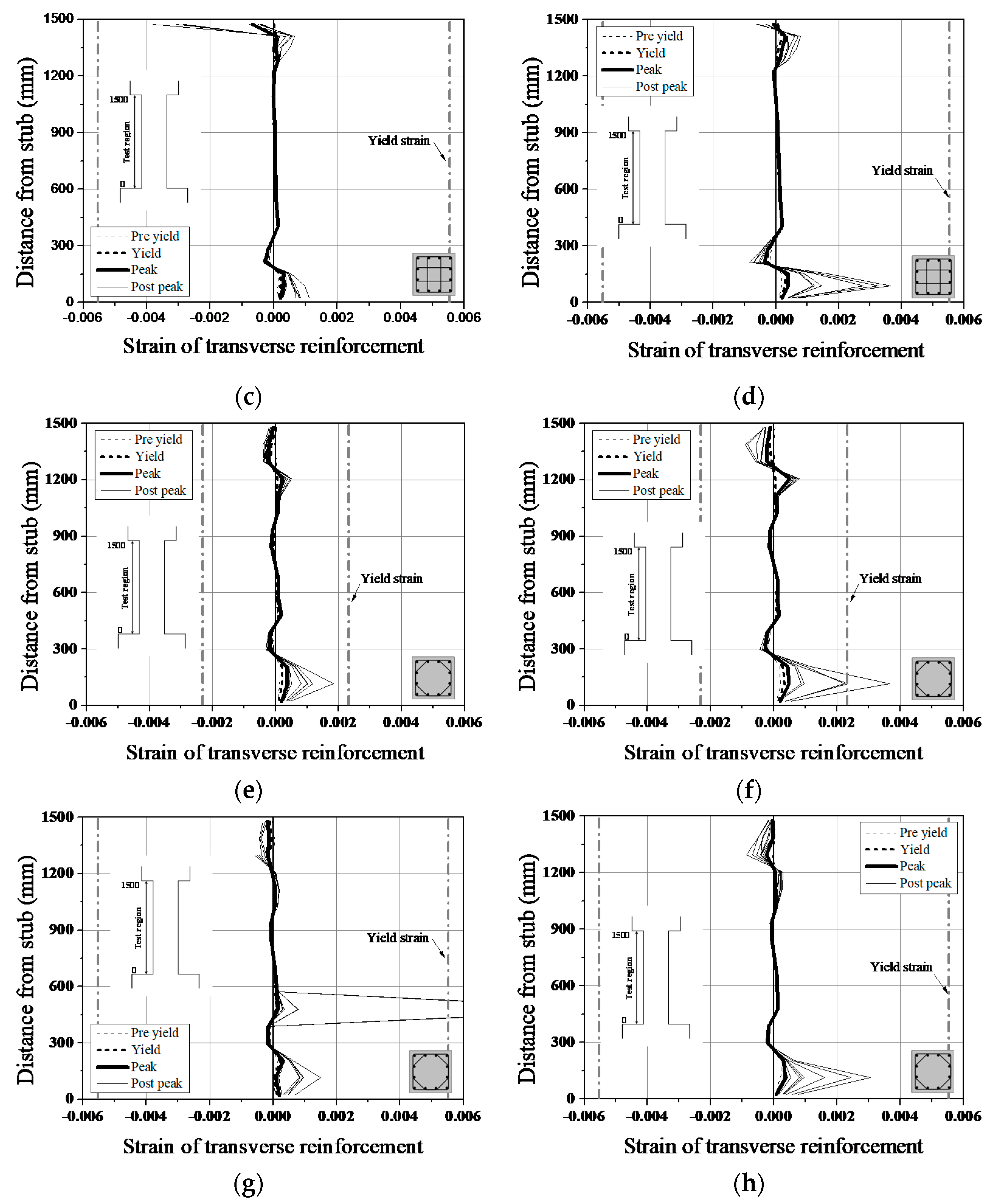
4.1. Strain Distribution in the Reinforcement
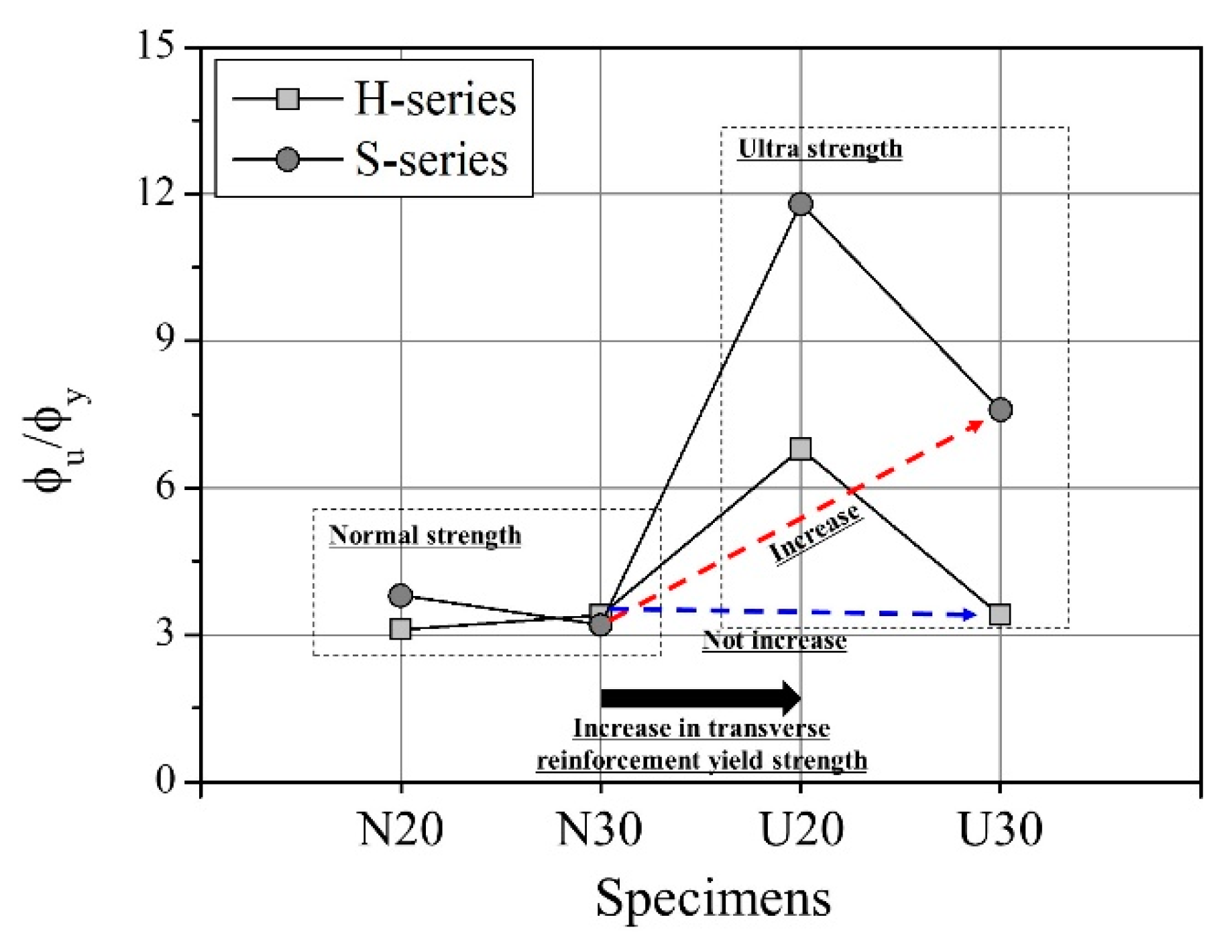
4.2. Flexural Strength and Ductility
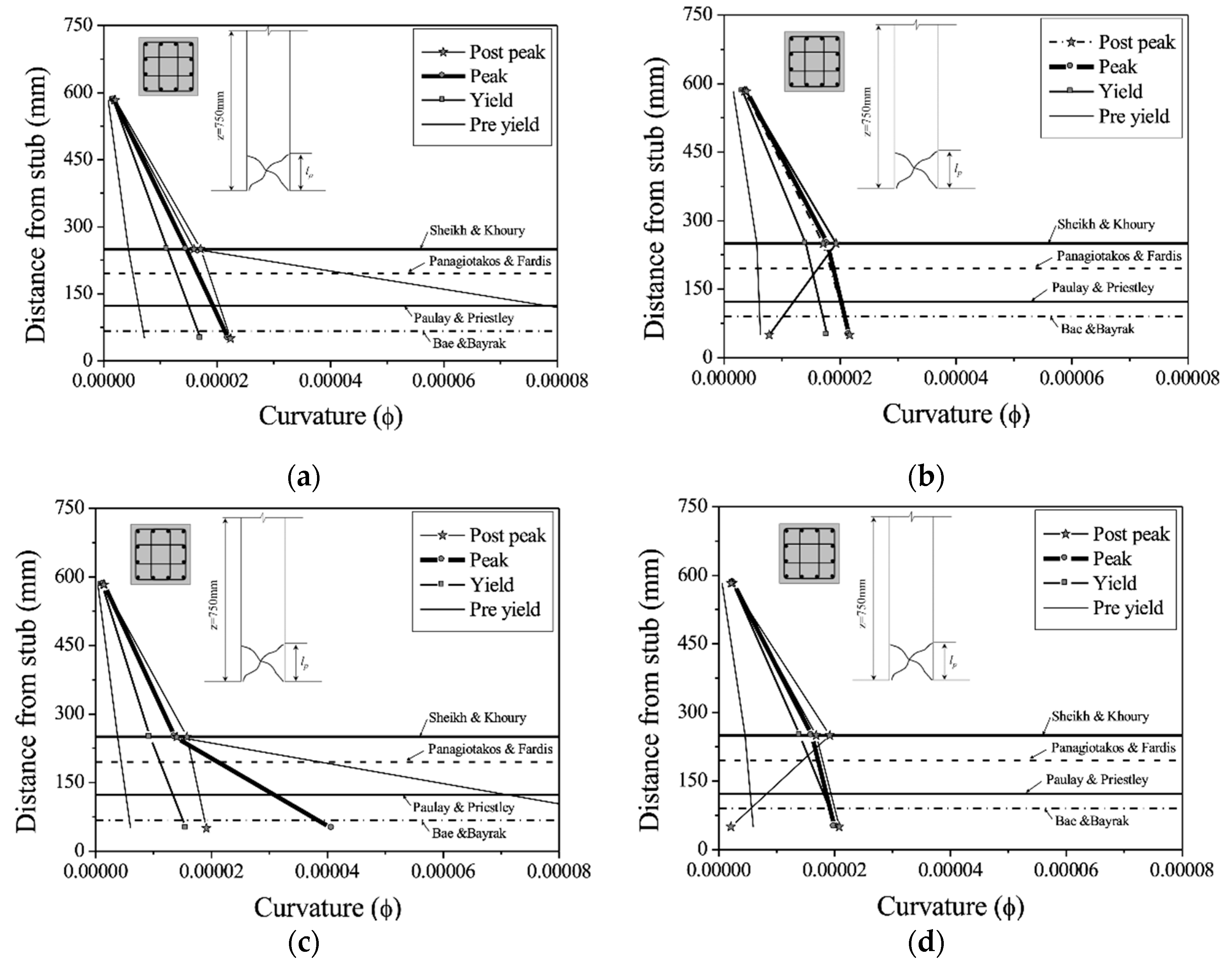
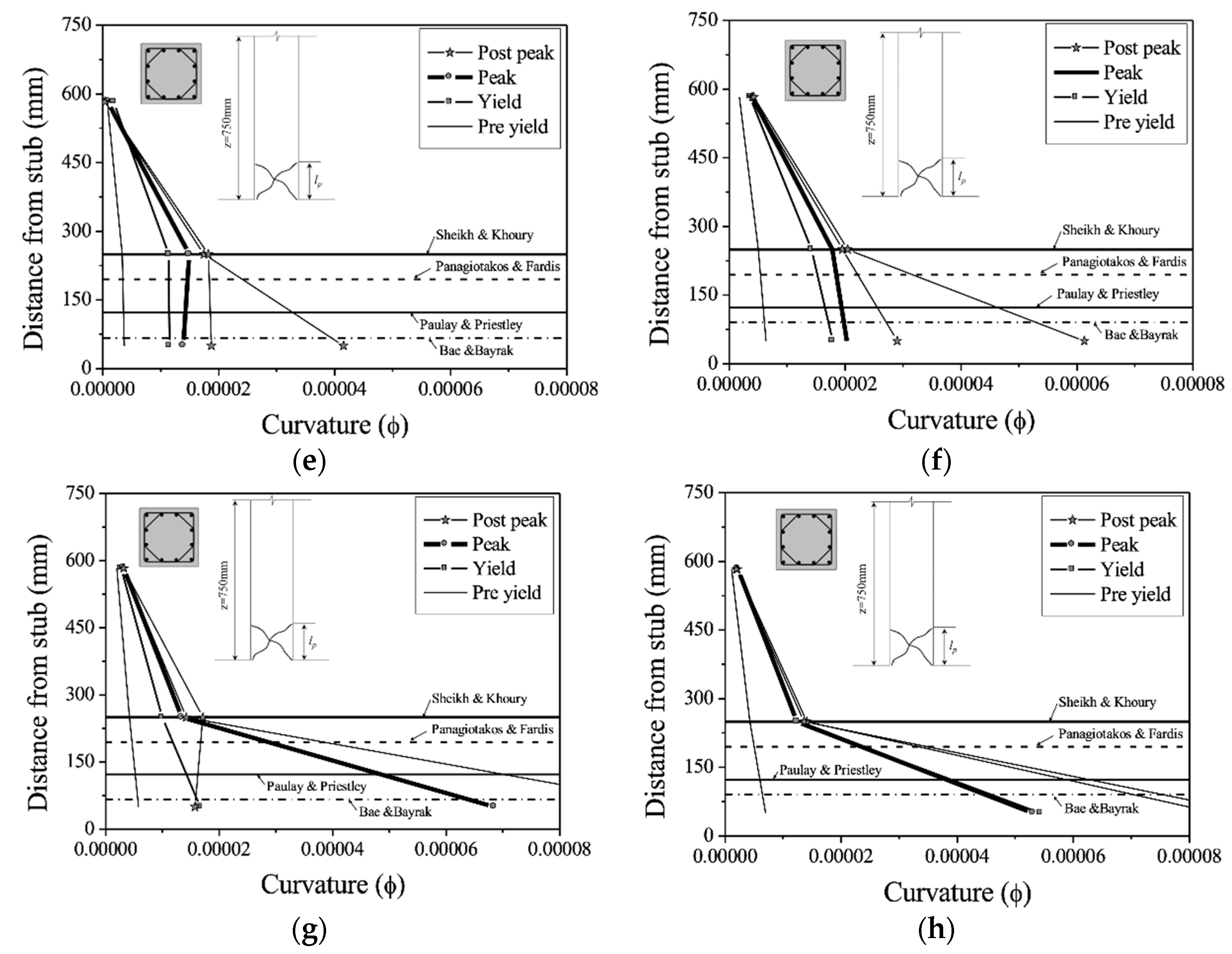
4.3. Plastic Hinge Length
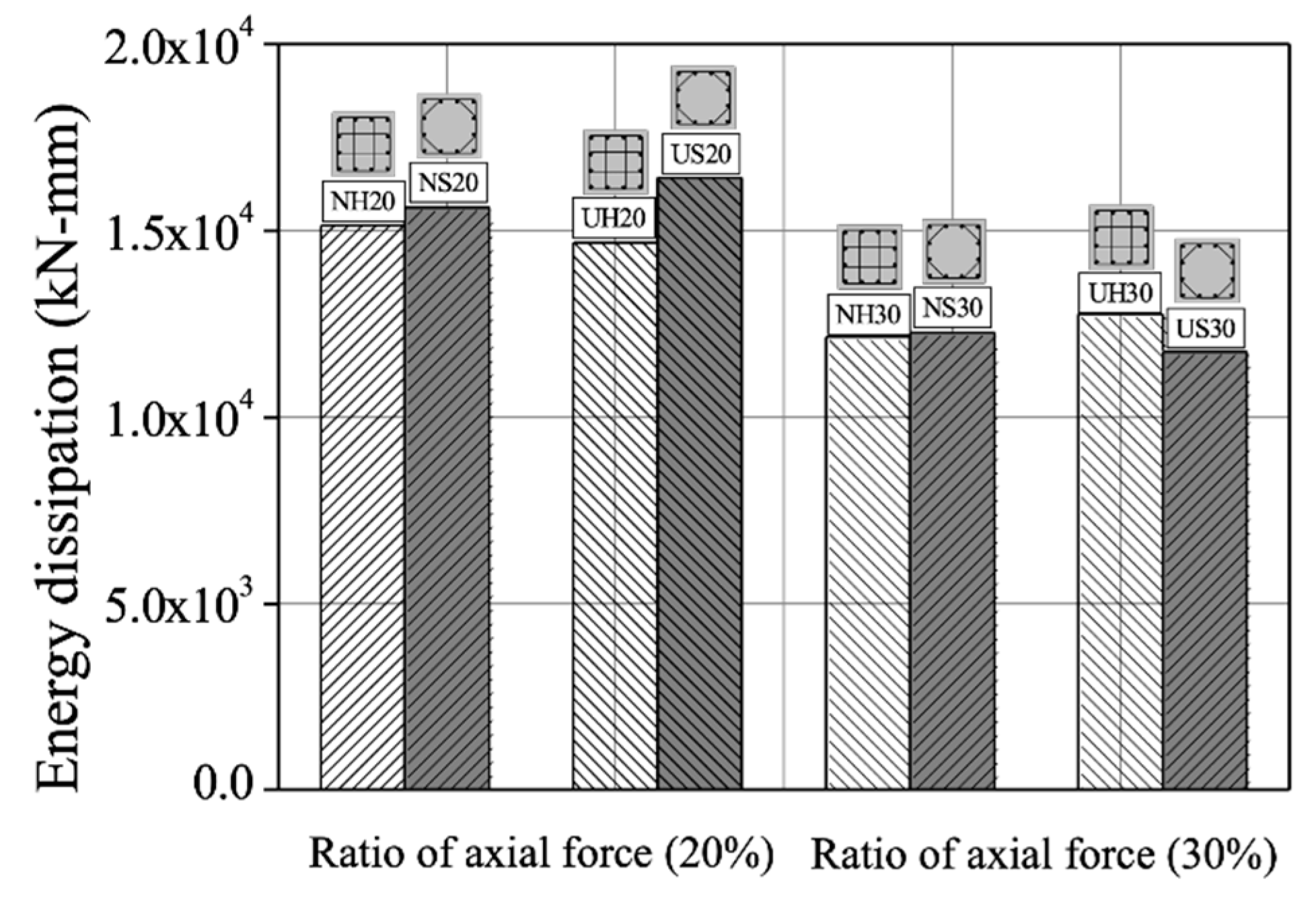
4.4. Energy Dissipation
5. Conclusions
- S-series specimens with alternating square and octagonal shapes showed maximum strength values similar to those of the H-series confined with square ties, even with a 55% decrease in transverse reinforcement amount. The spiral S-series transverse reinforcement effectively prevented buckling of longitudinal reinforcement and provided lateral confinement to the core concrete, thereby allowing specimens to exhibit ductile behavior.
- Compared to the H-series, the S-series had a 1.1 to 2.2 times higher ductility factor. The S-series showed superior ductile performance even under high axial force ratio when the yield strength of transverse reinforcement was increased. The curvature in the plastic hinge zone was high for the S-series, comprised of high-strength transverse reinforcement. The use of high-strength spiral transverse reinforcement in RC members subject to high axial force is expected to significantly improve the lateral confinement, and improve the ductility.
- Compared to the H-series, the S-series specimens except US30 showed similar or higher energy dissipation capacity, and were thus verified as effective against seismic loads.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notations
- = Depth of equivalent rectangular stress block
- = Area of longitudinal reinforcement
- = Effective area of cross-section
- = Gross area of concrete section
- = Area of tension longitudinal reinforcement
- = Cross-sectional of longitudinal reinforcement in each layer
- = Area of transverse reinforcement
- = Width of compression face of member
- = Distance from extreme compression fiber to centroid of longitudinal tension reinforcement
- = Diameter of longitudinal reinforcement
- = Distance from extreme compression fiber to centroid of longitudinal compression reinforcement
- = Compressive strength of concrete (MPa)
- = Yield strength of longitudinal reinforcement (MPa)
- = Yield strength of transverse reinforcement (MPa)
- = Overall height of member
- = Layer of longitudinal reinforcement
- = Applied axial force
- = Nominal axial load capacity as per ACI318-19
- = Spacing of transverse reinforcement (mm)
- = Perimeter of transverse reinforcement per 1 pitch (mm)
- = Distance from critical section to point of contraflexure
- = longitudinal strain of compression zone
- = Longitudinal strain of tension zone
- = Transverse reinforcement ratio ()
- = Amount of transverse reinforcement
- = Curvature of specimen
References
- Mattock, A.H. Redistribution of design bending moments in reinforced concrete continuous beams. Proc. Inst. Civ. Eng. 1959, 13, 35–46. [Google Scholar] [CrossRef]
- Carmo, R.; Lopes, S.M. Ductility and linear analysis with moment redistribution in reinforced high-strength concrete beams. Can. J. Civ. Eng. 2005, 32, 194–203. [Google Scholar] [CrossRef]
- Eom, T.S. Redistribution of Negative Moments in Beams Subjected to Lateral Load. J. Korea Concr. Inst. 2011, 23, 731–740. (In Korean) [Google Scholar] [CrossRef]
- SSheikh, A.; Yeh, C.C. Tied concrete columns under axial load and flexure. ASCE J. Struct. Eng. 1990, 116, 2780–2800. [Google Scholar] [CrossRef]
- Wang, Q.; Zhoo, G.; Lin, L. Effect of axial load ratio and stirrups volume ratio on ductility of high-strength concrete columns. Spec. Publ. 1994, 149, 433–448. [Google Scholar]
- Park, J.W.; Woo, J.H.; Kim, B.I.; Lee, J.Y. Plastic Hinge Length of Reinforced Concrete Columns with Low Height-to-Width Ratio. J. Korea Concr. Inst. 2010, 22, 675–684. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Lee, J.M.; Lee, Y.J.; Jung, Y.J.; Park, J.H.; Lee, B.S.; Kim, K.H. Ductile capacity of reinforced concrete columns with electric arc furnace oxidizing slag aggregate. Constr. Build. Mater. 2018, 162, 781–793. [Google Scholar] [CrossRef]
- Watson, S.; Park, R. Simulated seismic load tests on reinforced concrete columns. ASCE J. Struct. Eng. 1994, 120, 1825–1849. [Google Scholar] [CrossRef]
- Sakai, K.; Sheikh, S.A. What do we know about confinement in reinforced concrete columns. ACI Struct. J. 1989, 86, 192–207. [Google Scholar]
- Paultre, P.; Légeron, F. Confinement reinforcement design for reinforced concrete columns. ASCE J. Struct. Eng. 2008, 134, 738–749. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, S.W.; Lee, J.Y.; Lee, J.M.; Kim, H.G.; Kim, K.H. Prediction of stress–strain behavior of spirally confined concrete considering lateral expansion. Constr. Build. Mater. 2016, 102, 743–761. [Google Scholar] [CrossRef]
- Wang, P.; Shi, Q.; Wang, F.; Wang, Q. Seismic behaviour of concrete columns with high-strength stirrups. Earthq. Struct. 2020, 18, 15–25. [Google Scholar]
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley and Sons: New York, NY, USA, 1992. [Google Scholar]
- Abdel-Halim, M.A.; Abu-Lebdeh, T.M. Analytical study for concrete confinement in tied columns. ASCE J. Struct. Eng. 1989, 115, 2810–2828. [Google Scholar] [CrossRef]
- Sheikh, S.A.; Yeh, C.C. Flexural behavior of confined concrete columns. ACI Struct. J. 1986, 83, 389–404. [Google Scholar]
- Sheikh, S.A.; Khoury, S.S. Confined concrete columns with stubs. ACI Struct. J. 1993, 90, 414. [Google Scholar]
- Mo, Y.L.; Wang, S.J. Seismic behavior of RC columns with various tie configurations. ASCE J. Struct. Eng. 2000, 126, 1122–1130. [Google Scholar] [CrossRef]
- Lukkunaprasit, P.; Thepmangkorn, J. Load history effect on cyclic behavior of reinforced concrete tied columns. ASCE J. Struct. Eng. 2004, 130, 1629–1633. [Google Scholar] [CrossRef]
- Samra, R.M.; Deeb, N.A.; Madi, U.R. Transverse steel content in spiral concrete columns subject to eccentric loading. ACI Struct. J. 1996, 93, 412–419. [Google Scholar]
- Kim, M.J.; Kim, D.H.; Kim, D.H.; Kim, S.W.; Lee, J.Y.; Kim, K.H. Evaluation of flexural performance of RC columns according to configuration of transverse reinforcement. J. Archit. Inst. Korea Struct. Constr. 2012, 28, 3–10. (In Korean) [Google Scholar]
- American Concrete Institute. ACI Committee 318 Building Code Requirements for Structural Concrete (ACI 318M-19) and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley and Sons: New York, NY, USA, 1975. [Google Scholar]
- Panagiotakos, T.B.; Fardis, M.N. Deformations of reinforced concrete members at yielding and ultimate. ACI Struct. J. 2001, 98, 135–148. [Google Scholar]
- Bae, S.; Bayrak, O. Plastic hinge length of reinforced concrete columns. ACI Struct. J. 2008, 105, 290–300. [Google Scholar]
- Elmenshawi, A.; Brown, T. Hysteretic energy and damping capacity of flexural elements constructed with different concrete strengths. Eng. Struct. 2010, 32, 297–305. [Google Scholar] [CrossRef]

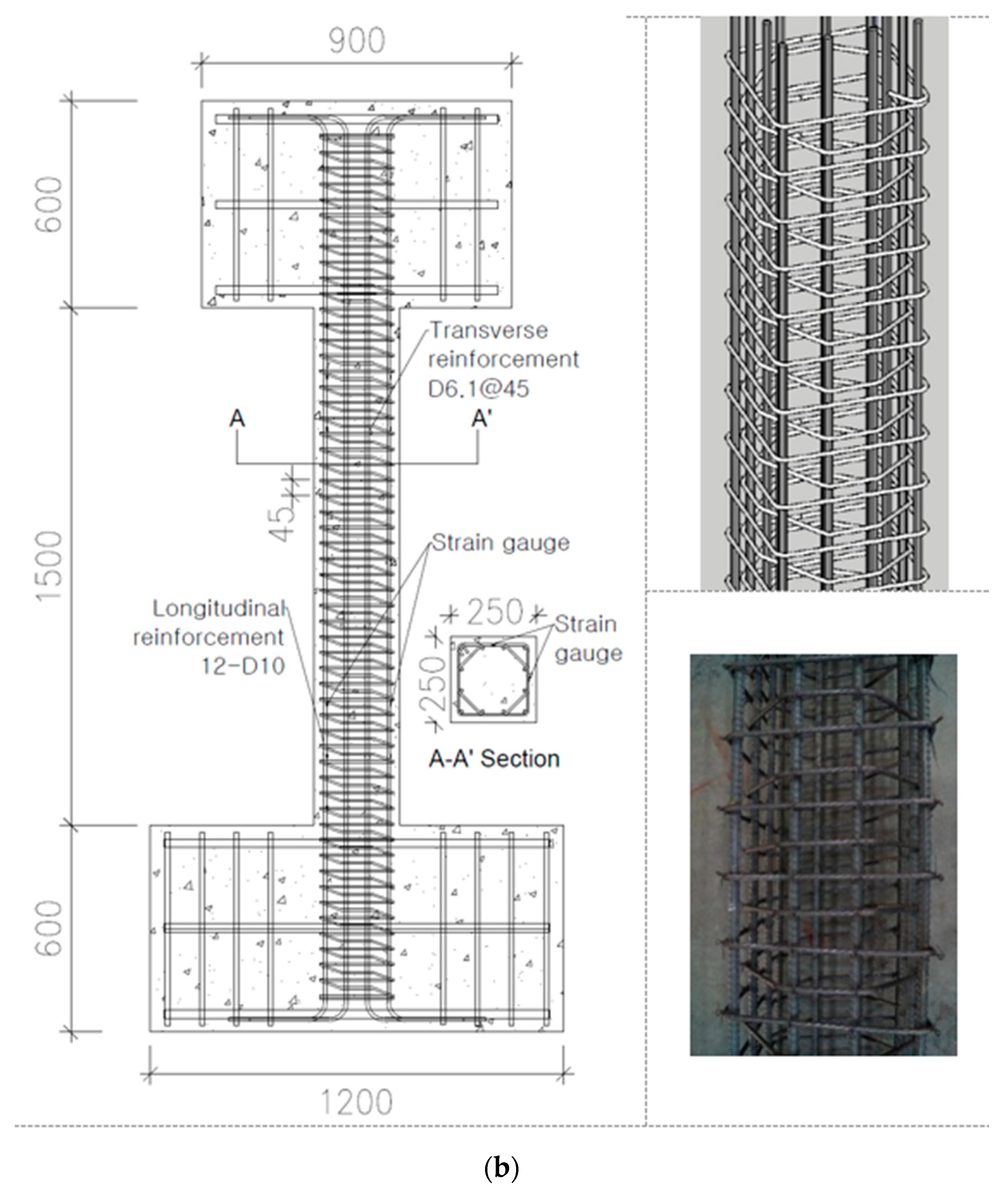

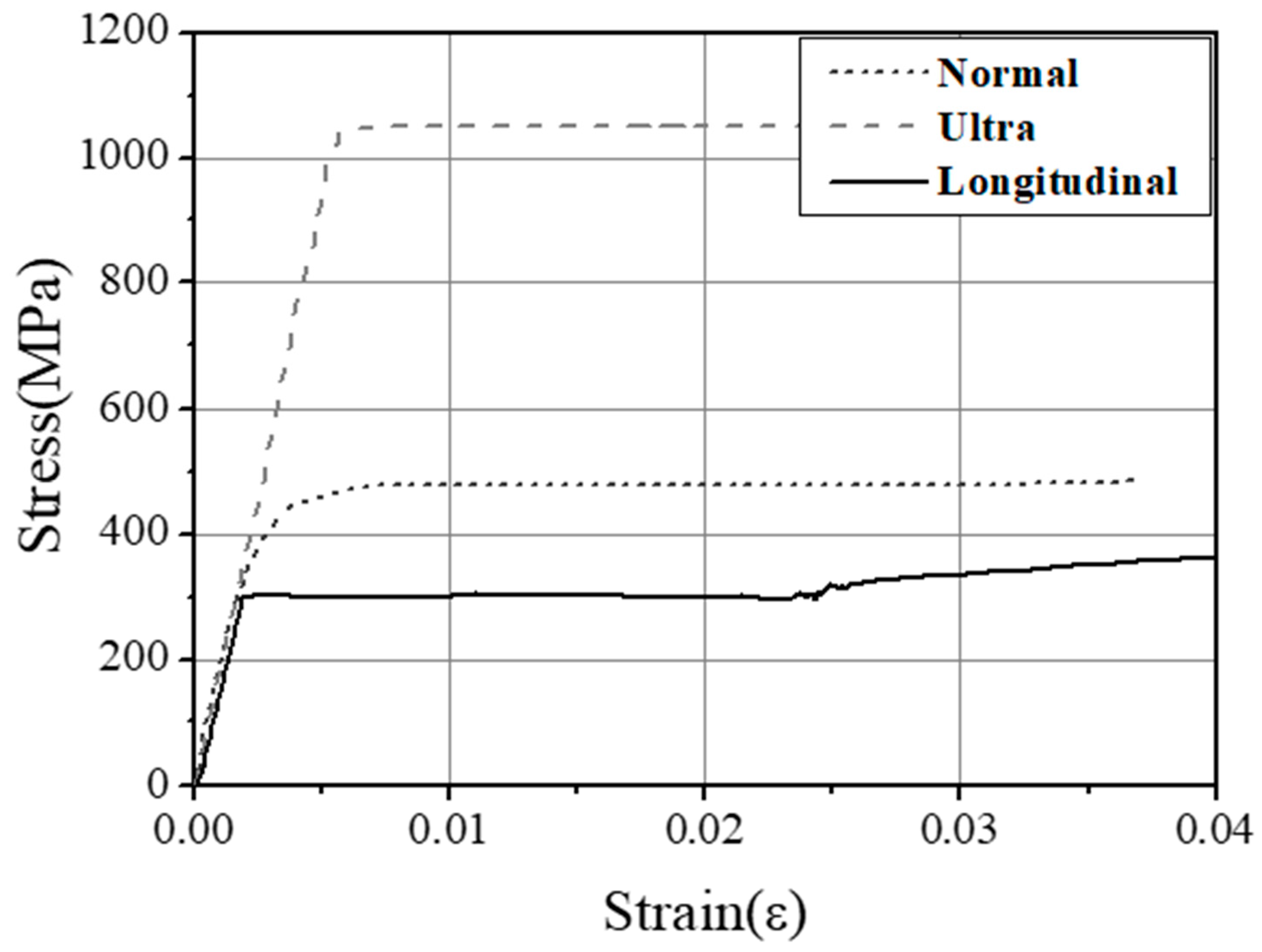
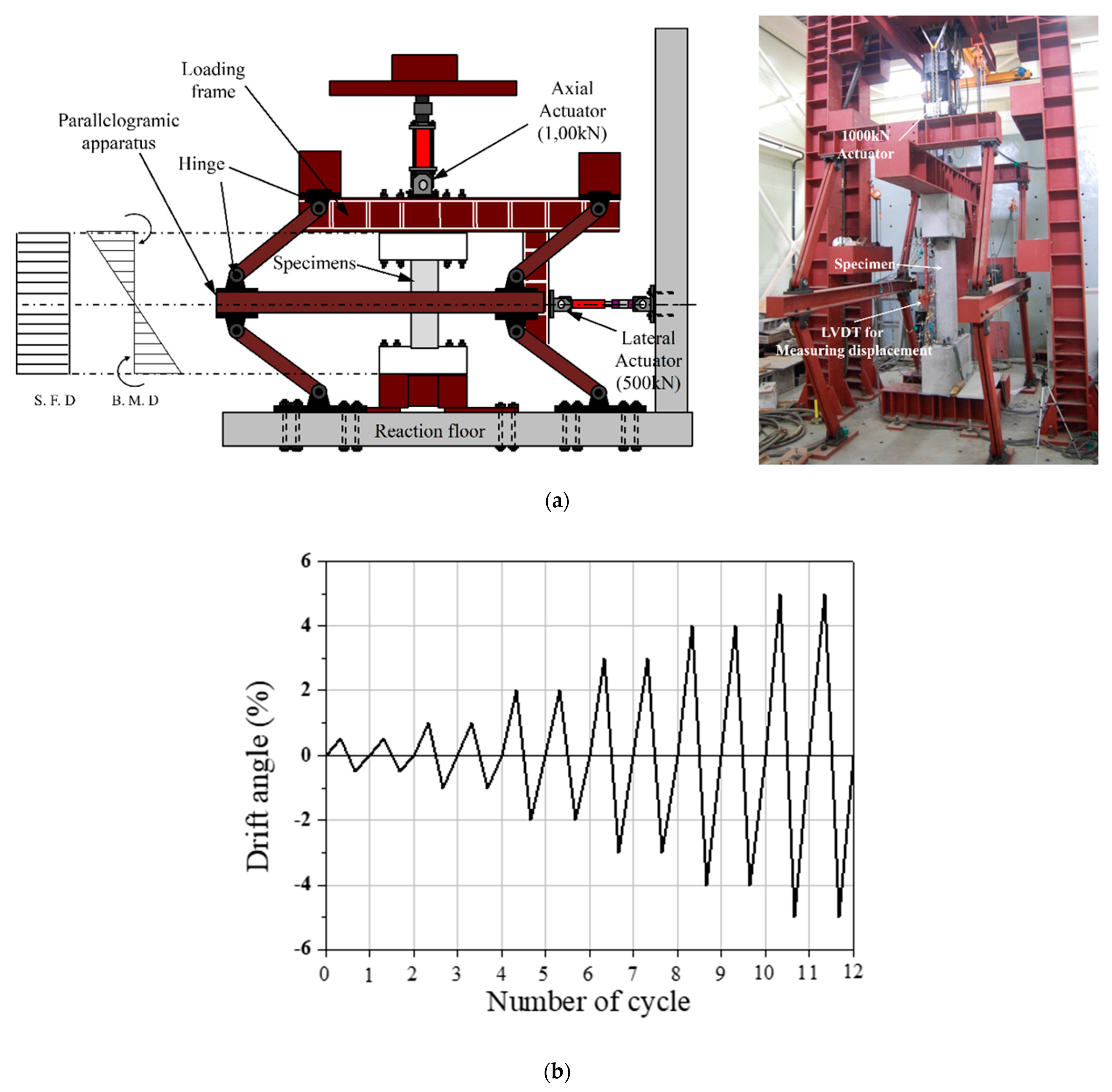





| Specimens | Longitudinal Reinforcement | Transverse Reinforcement | (mm2) | Axial Load (kN) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
(mm2) | (MPa) | (mm2) | (mm) | (MPa) | (%) | (MPa) | |||||
| Hoop type | NH20 | 36 | 71.3 (12-D10) | 300 ( = 0.0017) | 28 (D6.1) | 63.3 ( = 1680 mm) | 453 | 1.20 | 5.43 | 62,500 | 450 |
| NH30 | 453 | 5.43 | 675 | ||||||||
| UH20 | 1050 | 12.6 | 450 | ||||||||
| UH30 | 1050 | 12.6 | 675 | ||||||||
| Spiral type | NS20 | 45.3 ( = 754 mm) | 453 | 5.43 | 38,680 | 450 | |||||
| NS30 | 453 | 5.43 | 675 | ||||||||
| US20 | 1050 | 12.6 | 450 | ||||||||
| US30 | 1050 | 12.6 | 675 | ||||||||
| Specimens | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Drift Angle | |||||||||||
| NH20 | 81 | 0.5% (7.6 mm) | 101 | 1.3% (18.8 mm) | 61 | 7.2 × 10−6 | 76 | 2.2 × 10−5 | 3.1 | 62 | 1.23 |
| NH30 | 102 | 0.6% (8.6 mm) | 117 | 1.0% (15.0 mm) | 77 | 6.3 × 10−6 | 88 | 2.2 × 10−5 | 3.4 | 77 | 1.14 |
| UH20 | 90 | 0.5% (7.6 mm) | 105 | 1.3% (18.8 mm) | 68 | 6.0 × 10−6 | 79 | 4.1 × 10−5 | 6.8 | 62 | 1.27 |
| UH30 | 102 | 0.5% (7.8 mm) | 121 | 1.1% (17.0 mm) | 77 | 5.9 × 10−6 | 91 | 2.1 × 10−5 | 3.4 | 77 | 1.18 |
| NS20 | 84 | 0.5% (7.5 mm) | 99 | 1.2% (18.5 mm) | 63 | 3.1 × 10−6 | 74 | 1.4 × 10−5 | 3.8 | 62 | 1.19 |
| NS30 | 102 | 0.5% (8.6 mm) | 117 | 1.1% (15.0 mm) | 77 | 6.4 × 10−6 | 88 | 2.0 × 10−5 | 3.2 | 77 | 1.14 |
| US20 | 82 | 0.5% (7.4 mm) | 97 | 1.3% (19.0 mm) | 62 | 5.1 × 10−6 | 73 | 6.9 × 10−5 | 11.8 | 62 | 1.18 |
| US30 | 98 | 0.45% (6.5 mm) | 116 | 0.8% (11.9 mm) | 74 | 7.0 × 10−6 | 87 | 5.3 × 10−5 | 7.6 | 77 | 1.13 |
| Researcher Reference | Plastic Hinge Length Model |
|---|---|
| Paulay and Priestley (1992) | (for RC columns) |
| Sheikh and Khoury (1993) | (for columns under high axial loads) |
| Panagiotakos and Fardis (2001) | (for RC beams and columns) |
| Bae and Bayrak (2008) | (for columns) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-J.; Lee, B.-S.; Kim, D.-H.; Han, S.-P.; Kim, K.-H. Effect of Configuration and Yield Strength of Transverse Reinforcement on Lateral Confinement of RC Columns. Appl. Sci. 2021, 11, 6696. https://doi.org/10.3390/app11156696
Kim M-J, Lee B-S, Kim D-H, Han S-P, Kim K-H. Effect of Configuration and Yield Strength of Transverse Reinforcement on Lateral Confinement of RC Columns. Applied Sciences. 2021; 11(15):6696. https://doi.org/10.3390/app11156696
Chicago/Turabian StyleKim, Min-Jun, Bum-Sik Lee, Dong-Hwan Kim, Sang-Pil Han, and Kil-Hee Kim. 2021. "Effect of Configuration and Yield Strength of Transverse Reinforcement on Lateral Confinement of RC Columns" Applied Sciences 11, no. 15: 6696. https://doi.org/10.3390/app11156696
APA StyleKim, M.-J., Lee, B.-S., Kim, D.-H., Han, S.-P., & Kim, K.-H. (2021). Effect of Configuration and Yield Strength of Transverse Reinforcement on Lateral Confinement of RC Columns. Applied Sciences, 11(15), 6696. https://doi.org/10.3390/app11156696







