Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm
Abstract
:1. Introduction
2. General Assumptions in the Machine Location Tracking Problem
- Loading the cargo box at the mining face;
- Hauling material to the dumping point with a grid;
- Unloading cargo box into a grid;
- Returning to the loading zone at the mining face.
- Gyroscope drift, being the integral of two components: a slow-changing bias instability and a higher frequency noise—angular random walk (ARW).
- Unreliable readings from the magnetometer working in underground conditions.
- with possibly a hardened surface, the characteristics of which are relatively constant over time, e.g., when leaving the heavy machinery chamber, or segments with a rock surface that is not quickly damaged or deformed.
- that would be characteristic—signals from the passage of a given section should make it possible to distinguish them from other sections of the route in an unambiguous manner and thus enable the location of a given section in space. Therefore, they cannot be, for example, flat sections of the route, on which the machine vibrations generated while driving will be practically indistinguishable.
- Issue 1: The different trajectory of vehicle movement within one pattern:
- Solution: Create a “pattern catalog”:
- Issue 2: Different speed when covering the same sections of the route and signal length:
- Solution: DTW—Dynamic Time Warping:
- Issue 3: Unexpected stoppages:
- Solution: DTW—Dynamic Time Warping:
- Issue 4: Different machine speed and its influence on vibration level:
- Solution: Use of the road quality classification algorithm:
- Issue 5: Vehicle load and its influence on the vibration level:
- Solution: Using the algorithm for identifying the road quality or limiting the method to only run with an empty or full cargo box:
3. Materials and Methods
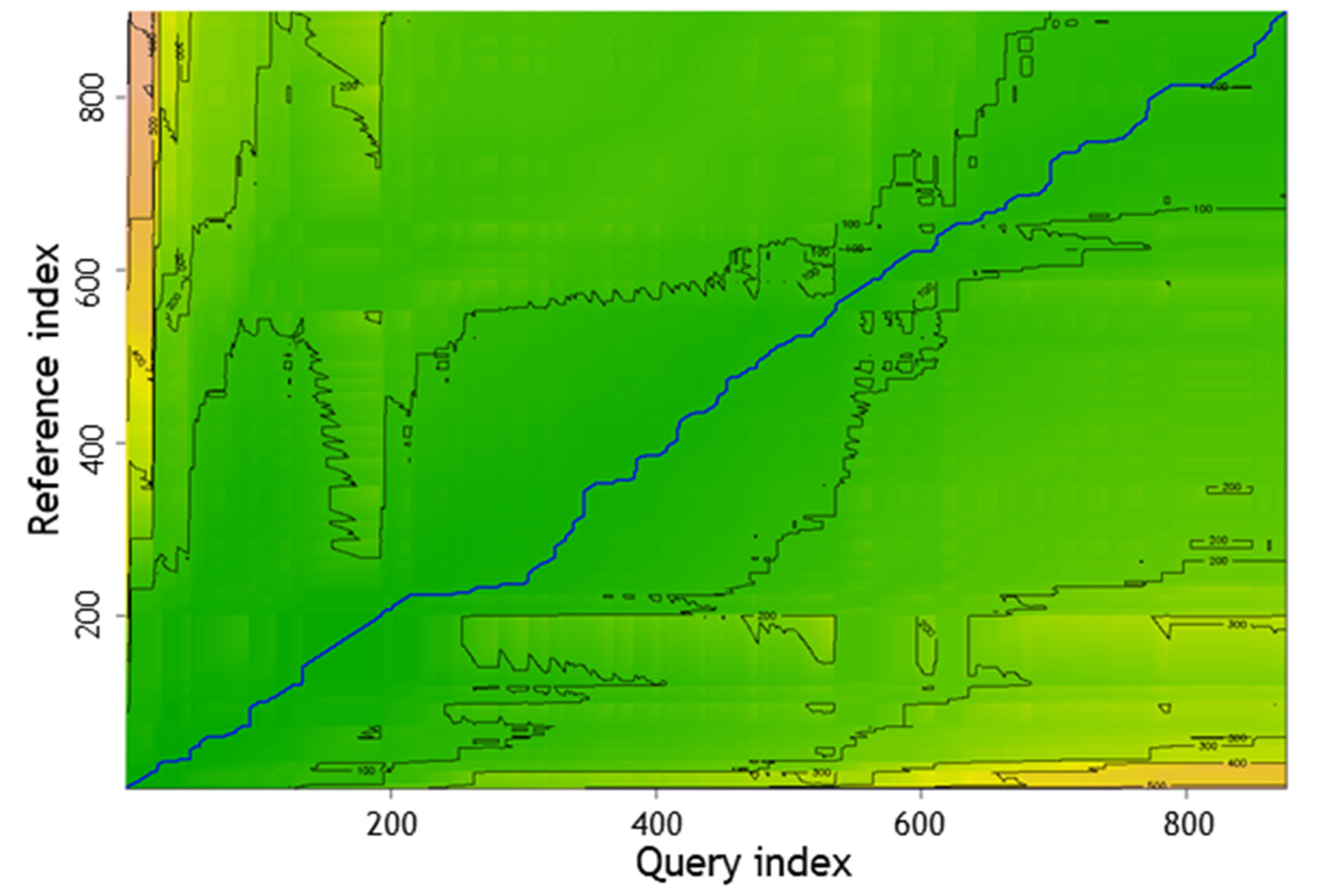
3.1. Dynamic Time Warping
| Algorithm 1. Dynamic Time Warping algorithm pseudo-code [55] |
| //v1 = (a1,…,an), v2 = (b1,…,bm)—time series with n and m observations respecitvely DTW(v1, v2) { Let a two dimensional data matrix S be the store of similarity measures such that S[0,…,n, 0,…,m], and i, j, are loop index, cost is an integer. // data matrix initialization S[0, 0] := 0 FOR i := 1 to m DO LOOP S[0, i] := ∞ END FOR i := 1 to n DO LOOP S[i, 0] := ∞ END // incrementally fill in the similarity matrix with the differences of the two time series FOR i := 1 to n DO LOOP FOR j := 1 to m DO LOOP // d function measures the distance between the two points cost := d(v1[i], v2[j]) S[i, j] := cost + MIN(S[i-1, j], S[i, j−1], S[i-1, j−1]) END END RETURN S[n, m] } |
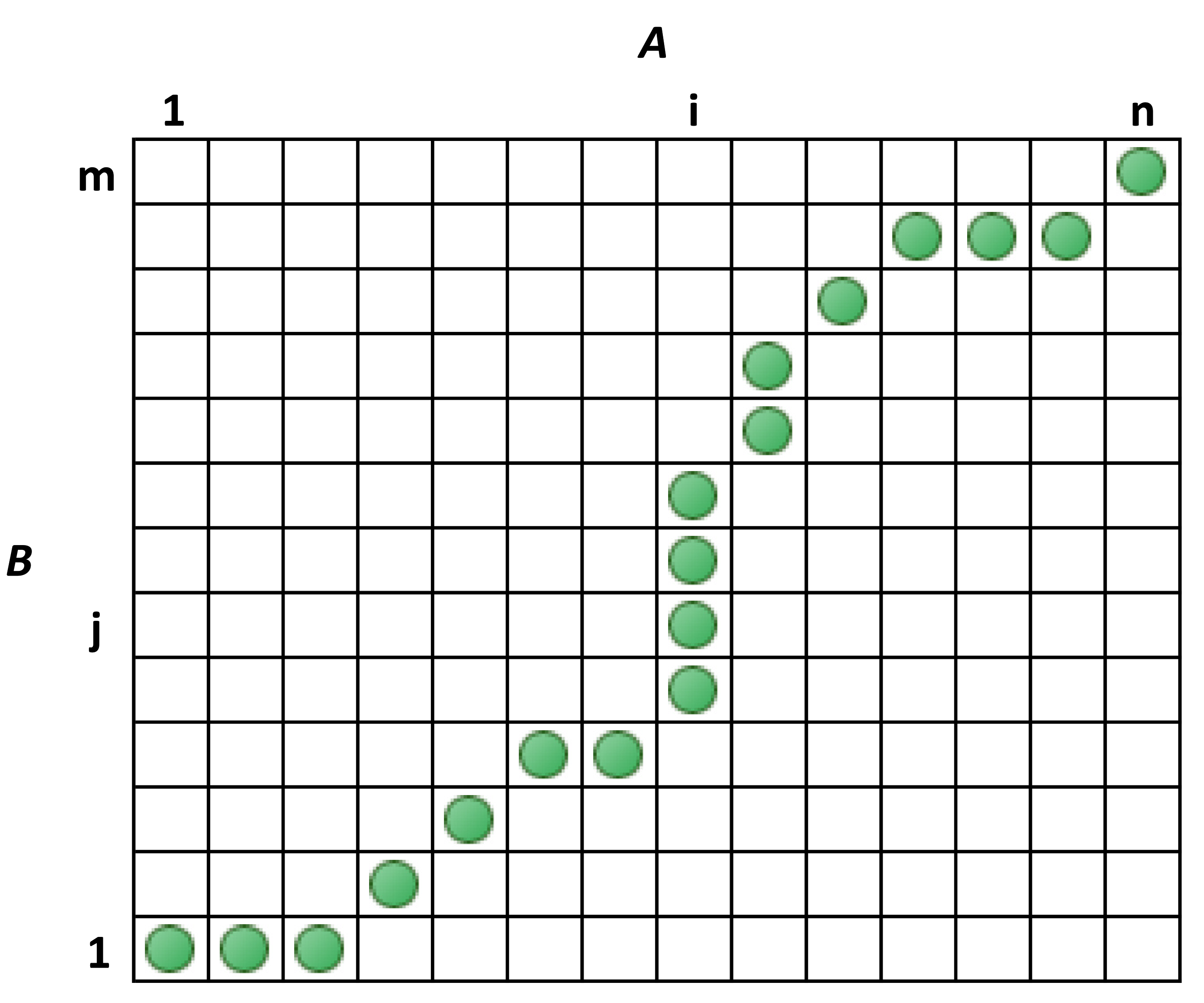
3.2. The Idea of Recognizing the Pattern of the Road
- Creating a catalog of patterns concerning various types of road fragments.
- Iterative comparison of successive cut signal fragments with the directory using DTW.
- Recording the value of the normalized DTW distance for each of the patterns from the catalogs in the subsequent fragments of signals.
- Choosing the best match among the patterns in the catalog to the tested signal.
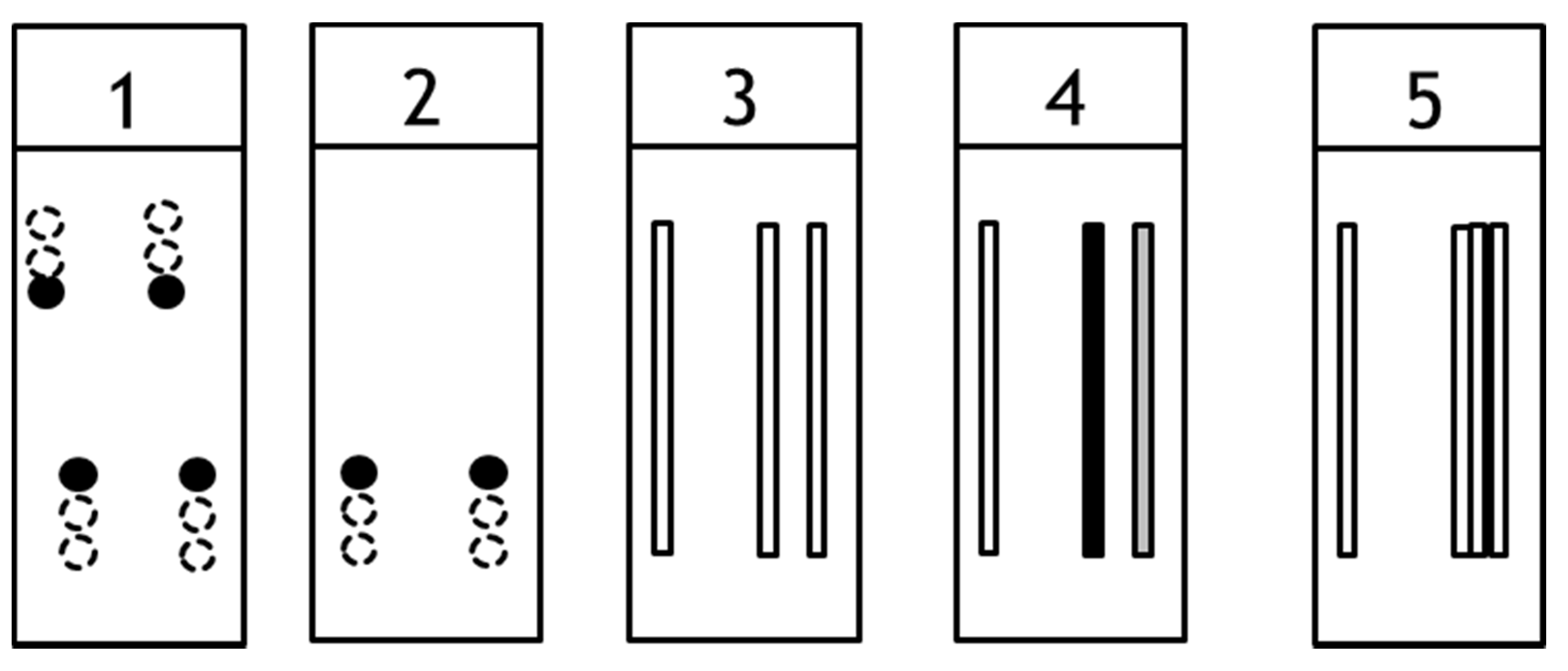
3.3. Description of the Experiment in Laboratory Conditions
- (a)
- panels 1–5 arranged directly one after the other,
- (b)
- panels 1, 3, and 5 arranged directly one after the other,
- (c)
- isolated panels 1, 3, and 5.
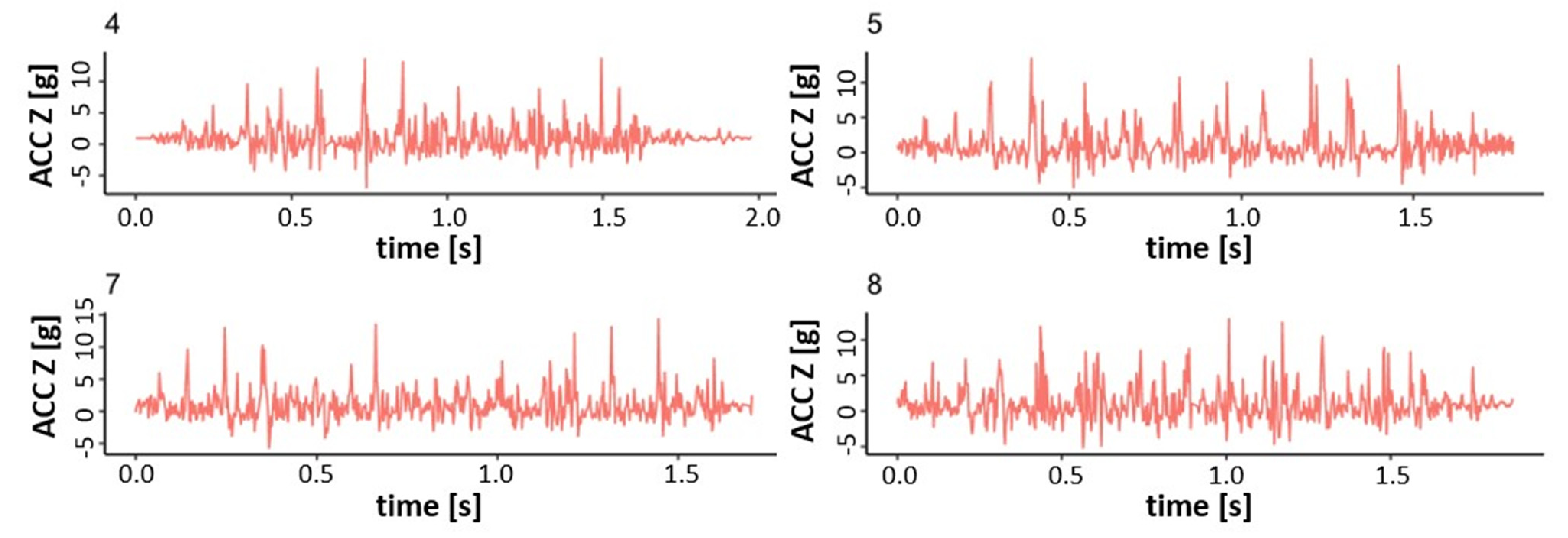
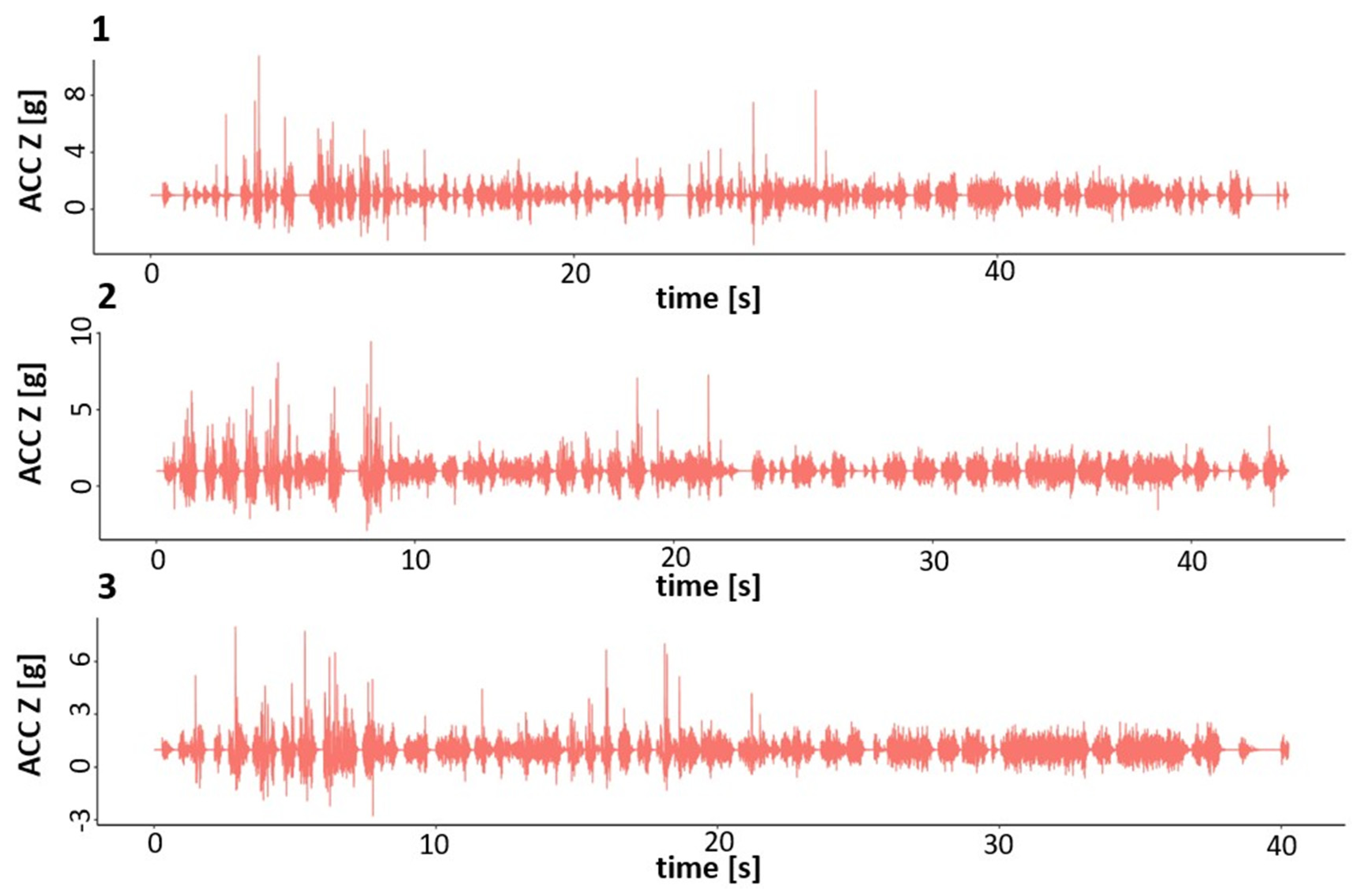
3.4. Application of the Algorithm
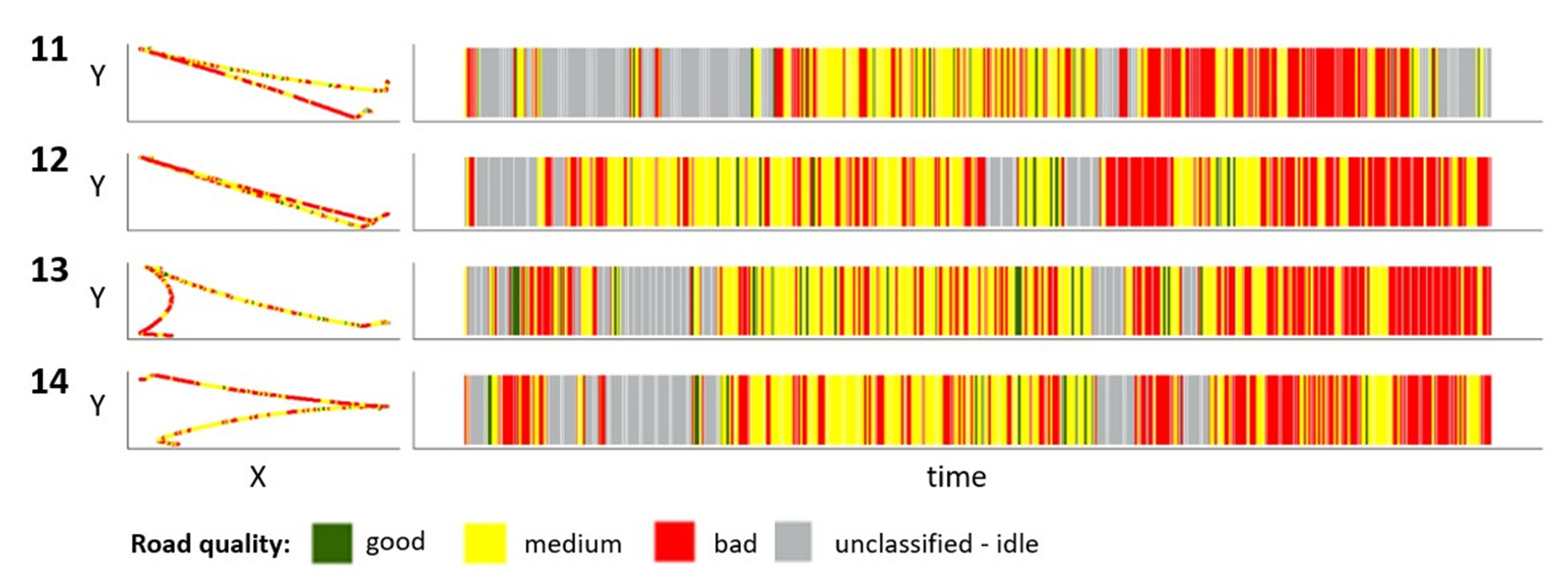
4. Application to Industrial Data
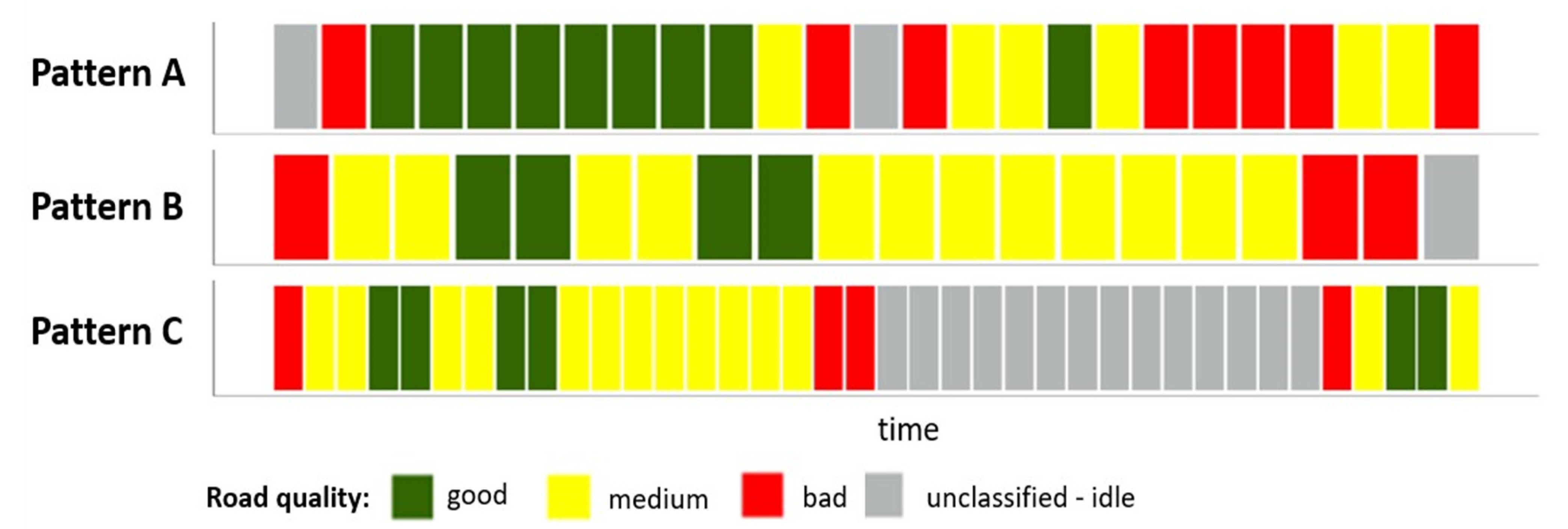
4.1. Creating Patterns
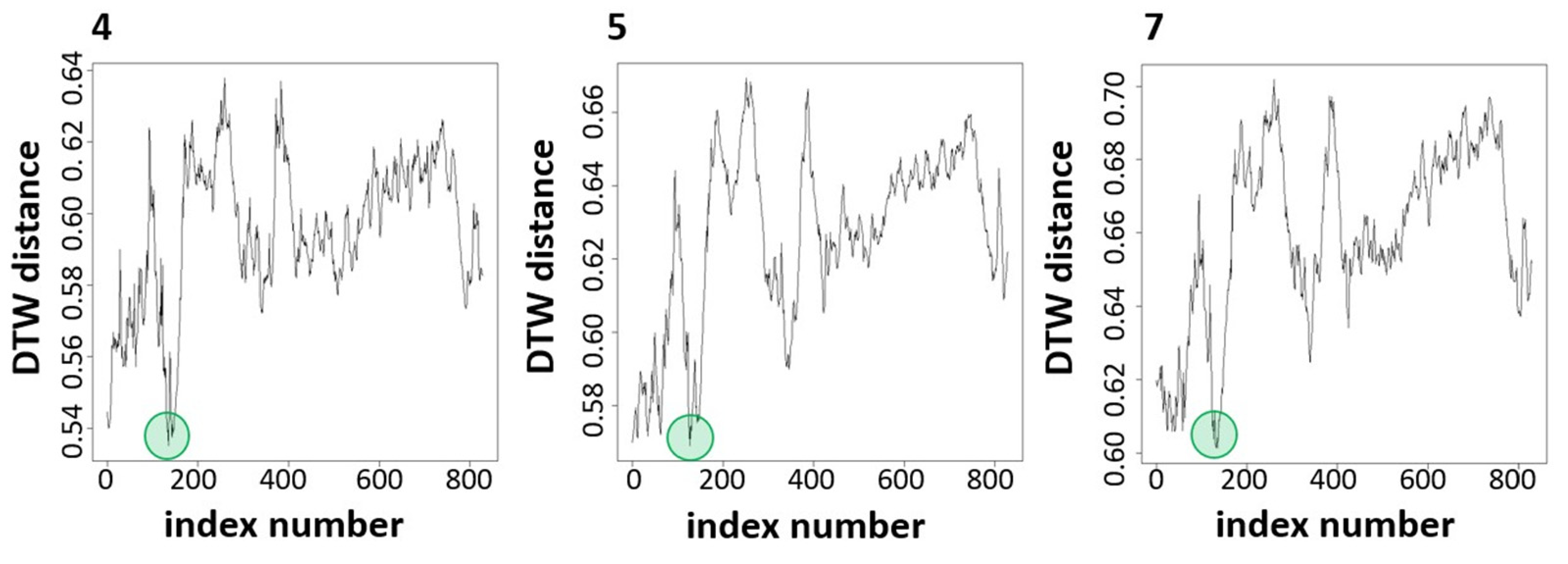
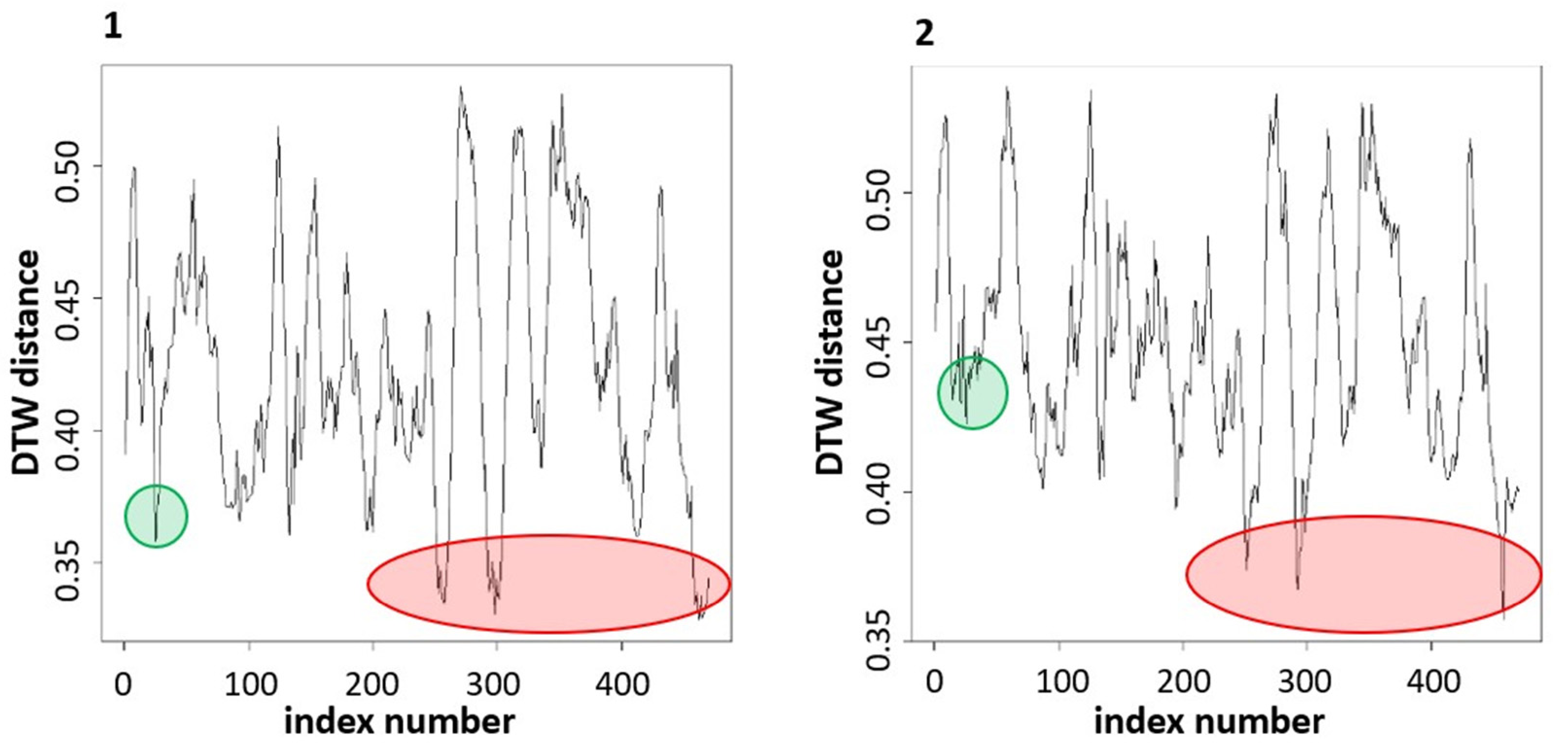
4.2. Pattern Detection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brzychczy, E.; Gackowiec, P.; Liebetrau, M. Data Analytic Approaches for Mining Process Improvement—Machinery Utilization Use Case. Resources 2020, 9, 17. [Google Scholar] [CrossRef] [Green Version]
- Wojaczek, A.; Wojaczek, A. Monitoring the environment and machines in underground mine. Zesz. Nauk. Inst. Gospod. Surowcami Miner. Pol. Akad. Nauk. 2017, 99, 57–70. [Google Scholar]
- Stefaniak, P.K.; Zimroz, R.; Sliwinski, P.; Andrzejewski, M.; Wyłomanska, A. Multidimensional signal analysis for technical condition, operation and performance understanding of heavy duty mining machines. In Proceedings of the International Conference on Condition Monitoring of Machinery in Non-Stationary Operation, Lyon, France, 15–17 December 2014; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2014; pp. 197–210. [Google Scholar]
- Gustafson, A.; Paraszczak, J.; Tuleau, J.; Schunnesson, H. Impact of technical and operational factors on effectiveness of automatic load-haul-dump machines. Min. Technol. 2017, 126, 185–190. [Google Scholar]
- Wodecki, J.; Stefaniak, P.; Michalak, A.; Wyłomańska, A.; Zimroz, R. Technical condition change detection using Anderson–Darling statistic approach for LHD machines–engine overheating problem. Int. J. Min. Reclam. Environ. 2018, 32, 392–400. [Google Scholar] [CrossRef]
- Paraszczak, J.; Gustafson, A.; Schunnesson, H. Technical and operational aspects of autonomous LHD application in metal mines. Int. J. Min. Reclam. Environ. 2015, 29, 391–403. [Google Scholar]
- Kawalec, P. How Will the 4th Industrial Revolution Influences the Extraction Industry? Inżynieria Miner. 2019, 21, 327–334. [Google Scholar]
- Whittaker, W. Utilization of position and orientation data for preplanning and real time autonomous vehicle navigation. In Proceedings of the IEEE/ION PLANS, San Diego, CA, USA, 25–27 April 2006; pp. 372–377. [Google Scholar]
- Roberts, J.M.; Duff, E.S.; Corke, P.I. Reactive navigation and opportunistic localization for autonomous underground mining vehicles. Inf. Sci. 2002, 145, 127–146. [Google Scholar] [CrossRef]
- Hemami, A. A conceptual approach to automation of LHD-loaders. In Proceedings of the 5th Canadian Symposium on Mining Automation, Vancouver, BC, Canada, 27–29 September 1992; pp. 178–183. [Google Scholar]
- Hemami, A. Motion trajectory study in the scooping operation of an LHD-loader. IEEE Trans. Ind. Appl. 1994, 30, 1333–1338. [Google Scholar] [CrossRef]
- Labonte, F.; Cohen, P. Perceptual aspects of mining equipment teleoperation. In Proceedings of the 6th Canadian Symposium on Mining Automation, Montreal, QC, Canada, 16–19 October 1994. [Google Scholar]
- Labonte, F.; Giraud, J.; Polotski, V. Telerobotics issues in the operation of a LHD vehicle. In Proceedings of the Third Canadian Conference on Computer Applications in the Mineral Industry, Montreal, QC, Canada, 22–25 October 1995; pp. 672–681. [Google Scholar]
- Baiden, G. Multiple LHD teleoperation and guidance at Inco Limited. In Proceedings of the International Mining Conference; 1993. [Google Scholar]
- Hurteau, R.; St-Amant, M.; Laperrière, Y.; Chevrette, G. Optical guidance system for underground mine vehicles. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; IEEE Computer Society: Washington, DC, USA, 1992; pp. 639–640. [Google Scholar]
- Amdahl, K.; Lundström, M. Automatic Truck Saves Money Underground; World Mining: London, UK, 1972; pp. 40–44. [Google Scholar]
- Steele, J.P.H.; Ganesh, C.; Kleve, A. Control and scale model simulation of sensor-guided LHD mining machines. IEEE Trans. Ind. Appl. 1993, 29, 1232–1238. [Google Scholar] [CrossRef]
- Mäkelä, H.; Lehtinen, H.; Rintanen, K.; Koskinen, K. Navigation System for LHD machines. In Intelligent Autonomous Vehicles 1995; Pergamon Press: Oxford, UK, 1995; pp. 295–300. [Google Scholar]
- Scheding, S.; Dissanayake, G.; Nebot, E.M.; Durrant-Whyte, H. An experiment in autonomous navigation of an underground mining vehicle. IEEE Trans. Robot. Autom. 1999, 15, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, G. Automatic loading and dumping using vehicle guidance in a Swedish mine. In Proceedings of the 1st International Symposium on Mine Mechanization and Automation, Golden, CO, USA, 10–13 June 1991; Volume 2, pp. 15–33. [Google Scholar]
- Ishimoto, H.; Tsubouchi, T.; Sarata, S. A practical trajectory following of an articulated steering type vehicle. In Field and Service Robotics; Springer: London, UK, 1998; pp. 397–404. [Google Scholar]
- Hemami, A.; Polotski, V. Path tracking control problem formulation of an LHD loader. Int. J. Robot. Res. 1998, 17, 193–199. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. A real-time algorithm for mobile robot mapping with applications to multi-robot and 3D mapping. In Proceedings of the 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 1, pp. 321–328. [Google Scholar]
- Duff, E.S.; Roberts, J.M.; Corke, P.I. Automation of an underground mining vehicle using reactive navigation and opportunistic localization. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No. 03CH37453), Las Vegas, NV, USA, 27–31 October 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 3775–3780. [Google Scholar]
- Larsson, J.; Broxvall, M.; Saffiotti, A. Laser based intersection detection for reactive navigation in an underground mine. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2222–2227. [Google Scholar]
- Mäkelä, H. Overview of LHD navigation without artificial beacons. Robot. Auton. Syst. 2001, 36, 21–35. [Google Scholar] [CrossRef]
- Bakambu, J.N.; Polotski, V. Autonomous system for navigation and surveying in underground mines. J. Field Robot. 2007, 24, 829–847. [Google Scholar] [CrossRef]
- Yulong, Q.; Qingyong, M.; Xu, T. Research on Navigation Path Planning for an Underground Load Haul Dump. J. Eng. Sci. Technol. Rev. 2015, 8, 102–109. [Google Scholar] [CrossRef]
- Skoczylas, A.; Stefaniak, P. Localization System for Wheeled Vehicles Operating in Underground Mine Based on Inertial Data and Spatial Intersection Points of Mining Excavations. In Intelligent Information and Database Systems, Proceedings of the 13th Asian Conference, ACIIDS 2021, Phuket, Thailand, 7–10 April 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 824–834. [Google Scholar]
- Witulska, J.; Stefaniak, P.; Jachnik, B.; Skoczylas, A.; Śliwiński, P.; Dudzik, M. Recognition of LHD Position and Maneuvers in Underground Mining Excavations—Identification and Parametrization of Turns. Appl. Sci. 2021, 11, 6075. [Google Scholar] [CrossRef]
- Walas, K.; Kanoulas, D.; Kryczka, P. Terrain classification and locomotion parameters adaptation for humanoid robots using force/torque sensing. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 133–140. [Google Scholar]
- Mrva, J.; Faigl, J. Feature Extraction for Terrain Classification with Crawling Robots. In ITAT; Charles University: Prague, Czech Republic, 2015; pp. 179–185. [Google Scholar]
- Dallaire, P.; Walas, K.; Giguere, P.; Chaib-draa, B. Learning terrain types with the pitman-yor process mixtures of gaussians for a legged robot. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3457–3463. [Google Scholar]
- Filitchkin, P.; Byl, K. Feature-based terrain classification for littledog. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1387–1392. [Google Scholar]
- Walas, K. Terrain classification and negotiation with a walking robot. J. Intell. Robot. Syst. 2015, 78, 401–423. [Google Scholar] [CrossRef] [Green Version]
- Skoczylas, A.; Stachowiak, M.; Stefaniak, P.; Jachnik, B. Terrain Classification Using Neural Network Based on Inertial Sensors for Wheeled Robot. In Recent Challenges in Intelligent Information and Database Systems; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Gustafson, A. Automation of Load Haul Dump Machines; Luleå Tekniska Universitet: Luleå, Sweden, 2011. [Google Scholar]
- KGHM ZANAM. Available online: https://www.kghmzanam.com/en/produkty/mining-machinery/haul-trucks/haul-truck-cb4p-24k/ (accessed on 21 July 2021).
- Stefaniak, P.; Anufriiev, S.; Skoczlas, A.; Bartosz, J.; Sliwinski, P. Method to haulage path estimation and road-quality assessment using inertial sensors on LHD machines. Vietnam. J. Comput. Sci. 2020. [Google Scholar] [CrossRef]
- Deibe, Á.; Antón Nacimiento, J.A.; Cardenal, J.; López Peña, F. A Kalman Filter for Nonlinear Attitude Estimation Using Time Variable Matrices and Quaternions. Sensors 2020, 20, 6731. [Google Scholar] [CrossRef]
- Skoczylas, A.; Stefaniak, P.; Anufriiev, S.; Jachnik, B. Road Quality Classification Adaptive to Vehicle Speed Based on Driving Data from Heavy Duty Mining Vehicles. In Proceedings of the International Conference on Intelligent Computing & Optimization, Hua Hin, Thailand, 22–23 April 2021; Springer: Cham, Germany, 2020; pp. 777–787. [Google Scholar]
- Fu, T.C. A review on time series data mining. Eng. Appl. Artif. Intell. 2011, 24, 164–181. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using dynamic time warping to find patterns in time series. In Proceedings of the KDD Workshop, Seattle, WA, USA, 31 July–1 August 1994; Volume 10, pp. 359–370. [Google Scholar]
- Vintsyuk, T.K. Speech discrimination by dynamic programming. Cybernetics 1968, 4, 52–57. [Google Scholar] [CrossRef]
- Muda, L.; Begam, M.; Elamvazuthi, I. Voice recognition algorithms using mel frequency cepstral coefficient (MFCC) and dynamic time warping (DTW) techniques. arXiv 2010, arXiv:1003.4083. [Google Scholar]
- Prasad, V. Voice recognition system: Speech-to-text. J. Appl. Fundam. Sci. 2015, 1, 191. [Google Scholar]
- Jančovič, P.; Köküer, M.; Zakeri, M.; Russell, M. Unsupervised discovery of acoustic patterns in bird vocalisations employing DTW and clustering. In Proceedings of the 21st European Signal Processing Conference (EUSIPCO 2013), Marrakech, Morocco, 9–13 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Chen, G.; Wei, Q.; Zhang, H. Discovering similar time-series patterns with fuzzy clustering and DTW methods. In Proceedings of the Joint 9th IFSA World Congress and 20th NAFIPS International Conference (Cat. No. 01TH8569), Vancouver, BC, Canada, 25–28 July 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 4, pp. 2160–2164. [Google Scholar]
- Iwana, B.K.; Frinken, V.; Uchida, S. DTW-NN: A novel neural network for time series recognition using dynamic alignment between inputs and weights. Knowl. Based Syst. 2020, 188, 104971. [Google Scholar] [CrossRef]
- Vlachos, M.; Kollios, G.; Gunopulos, D. Discovering similar multidimensional trajectories. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 673–684. [Google Scholar]
- Hirschberg, D.S. Algorithms for the longest common subsequence problem. J. ACM JACM 1977, 24, 664–675. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; pp. 491–502. [Google Scholar]
- Chen, L.; Ng, R. On the marriage of lp-norms and edit distance. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004; Volume 30, pp. 792–803. [Google Scholar]
- Marteau, P.F. Time warp edit distance with stiffness adjustment for time series matching. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 306–318. [Google Scholar] [CrossRef] [Green Version]
- Fong, S. Using hierarchical time series clustering algorithm and wavelet classifier for biometric voice classification. J. Biomed. Biotechnol. 2012, 2012, 215019. [Google Scholar] [CrossRef] [Green Version]






| Euclidean Distance | Cross-correlation | Longest Common Subsequence | Edit Distance for Real Sequences | Edit Distance for Real Penalty | Time Warp Edit Distance | Dynamic Time Warping | |
|---|---|---|---|---|---|---|---|
| Applies to signals of different length |  |  |  |  |  |  |  |
| Resistance to shortening/lengthening pattern fragments (different vehicle speed) |  |  |  |  |  |  |  |
| Resistance to inserting large fragments of same patterns (vehicle stoppages) |  |  |  |  |  |  |  |
| Noise immunity |  |  |  |  |  |  |  |
| No need for arbitrary selection of parameters |  |  |  |  |  |  |  |
| Pattern Length | 5 Panels (5 × 18 cm = 90 cm) | 3 Panels (3 × 18 cm = 54 cm) | 1 Panel (18 cm) |
|---|---|---|---|
| % of correctly recognized patterns | 100% (3 out of 3 drives) | 100% (3 out of 3 drives) | 0% (0 out of 3 drives) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefaniak, P.; Jachnik, B.; Koperska, W.; Skoczylas, A. Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm. Appl. Sci. 2021, 11, 6751. https://doi.org/10.3390/app11156751
Stefaniak P, Jachnik B, Koperska W, Skoczylas A. Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm. Applied Sciences. 2021; 11(15):6751. https://doi.org/10.3390/app11156751
Chicago/Turabian StyleStefaniak, Paweł, Bartosz Jachnik, Wioletta Koperska, and Artur Skoczylas. 2021. "Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm" Applied Sciences 11, no. 15: 6751. https://doi.org/10.3390/app11156751
APA StyleStefaniak, P., Jachnik, B., Koperska, W., & Skoczylas, A. (2021). Localization of LHD Machines in Underground Conditions Using IMU Sensors and DTW Algorithm. Applied Sciences, 11(15), 6751. https://doi.org/10.3390/app11156751






