Analytical Investigation of Viscoelastic Stagnation-Point Flows with Regard to Their Singularity
Abstract
:1. Introduction
2. Model Equations
2.1. Conservation Equations
2.2. The Oldroyd 8-Constant Model
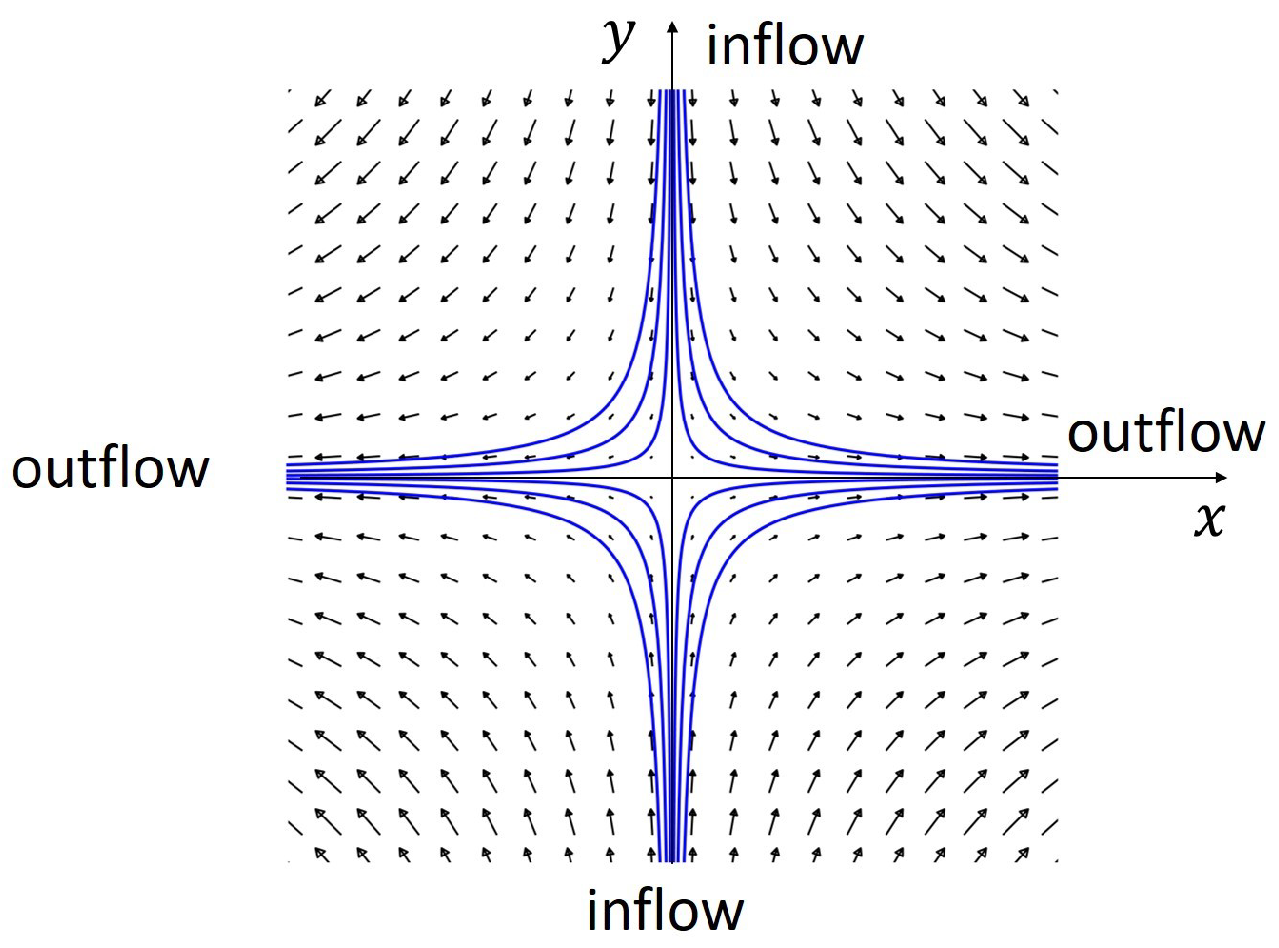
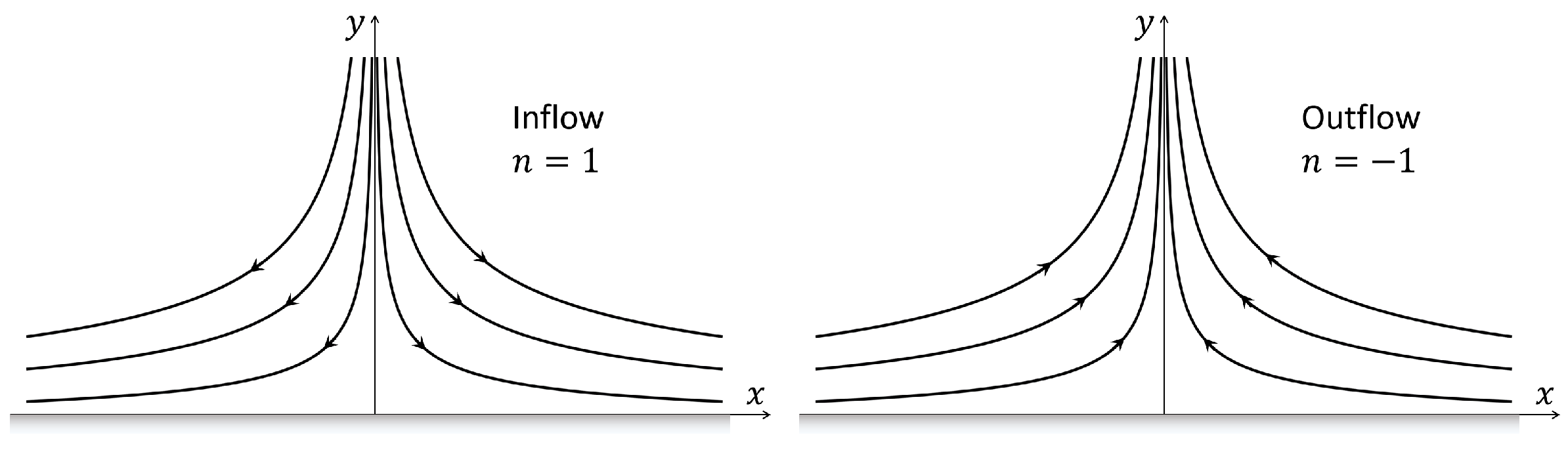
3. Analytical Solutions of a Wall-Free Stagnation-Point Flow and Their Singularities
3.1. Case
3.1.1. Case
- (i)
- Hence, and can be related to bywhere , , and are arbitrary constants, and is still an arbitrary function of . To avoid the integral terms emerging in the above relations, we replace by another arbitrary function as follows:Substituting (30) into (28), (29) and then into (22)–(24), results in the final solutions of the stress tensor:In a recent investigation by [17], the solution of a wall-free stagnation-point flow for the Maxwell fluid with satisfying the momentum equation was discovered. This corresponds to our solutions (31)–(33) with and . Physically, the components of the stress tensor should be limited everywhere, including at the stagnation point and at infinity. Hence, further restrictions on the arbitrary constants , , , and the arbitrary function in the solutions are needed. To avoid the singularity of the stress tensor, Ref. [17] suggested the choice:where and . However, this choice (34) cannot prevent the singularity as was claimed. To demonstrate this, as an example, we substitute (34) into (33) resulting in:where , and are constant coefficients. For , the particular solution (33) has the following properties:
- •
- Along the characteristic curves and , , no singularity occurs.
- •
- Along the characteristic curve , where is a non-zero finite constant, the value of is a bounded constant , while is singular at . An infinite shear stress arises in the region far away from the stagnation point () and near the y-axis ().
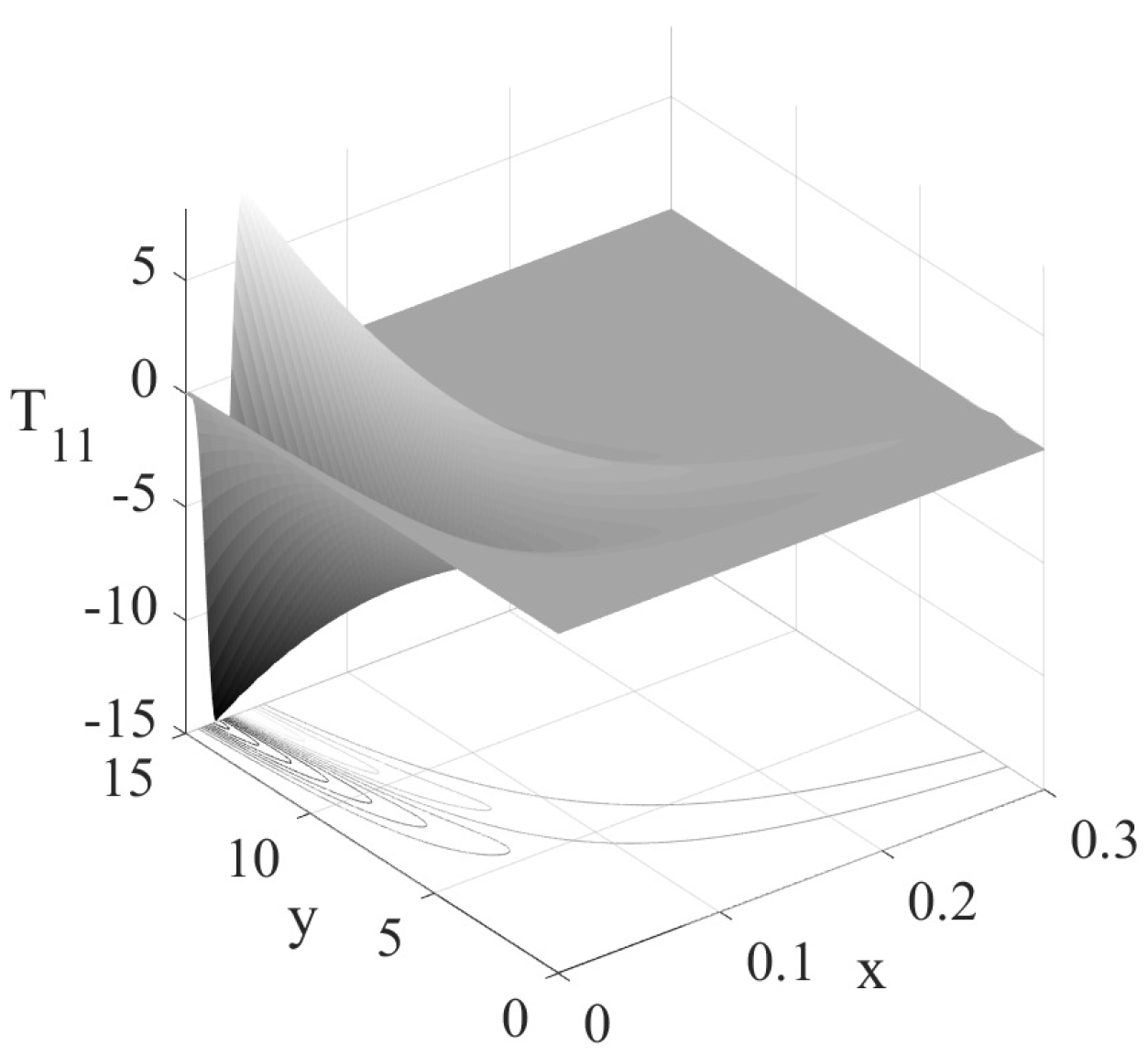
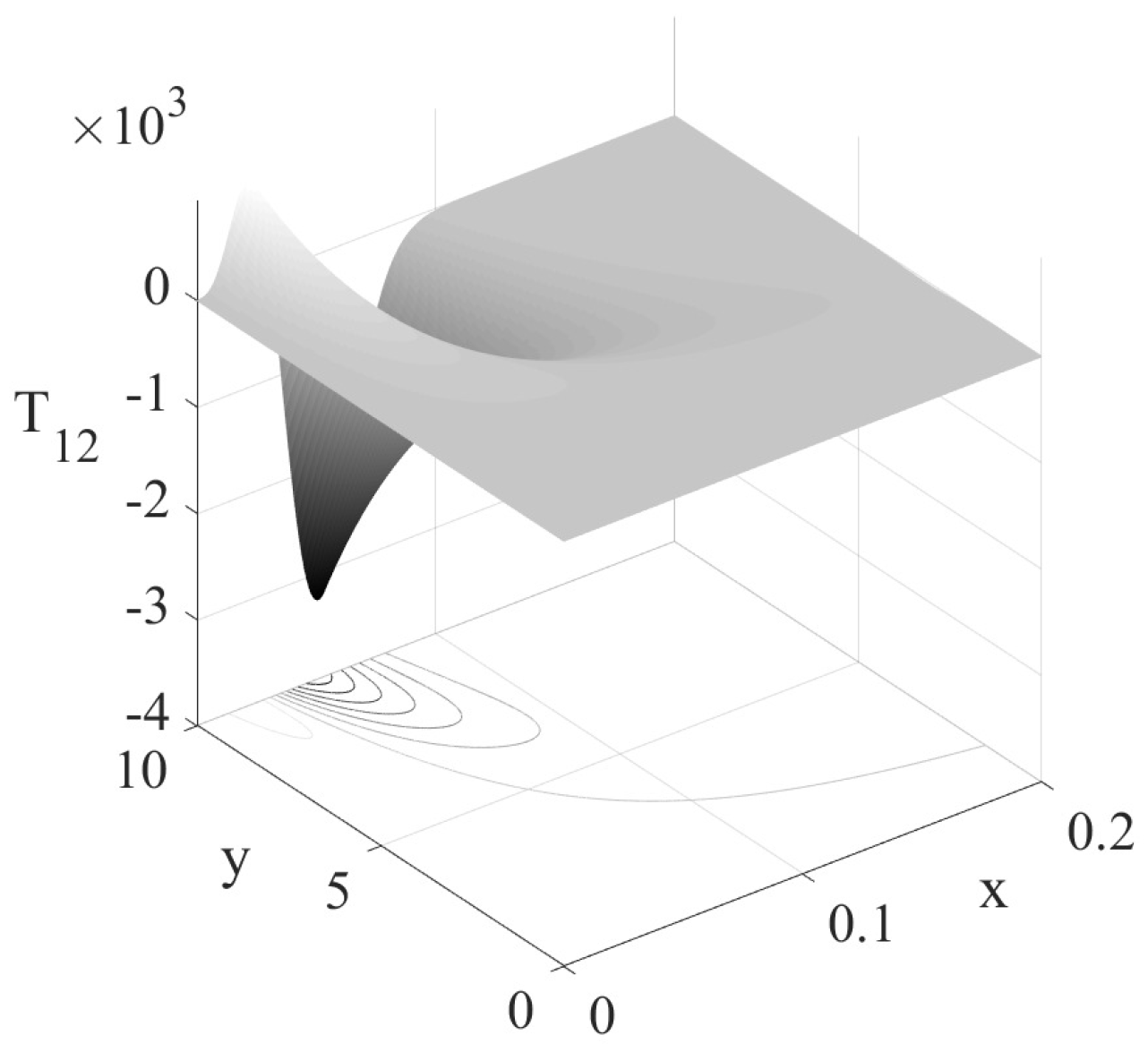
With the choice (34), similar singularities also appear in the stress tensor components and far away from the stagnation point, for (but ) or (but ). As an example, the corresponding stress components and excluding the constant part are presented in Figure 2 and Figure 3 for the case , and with a much finer spatial resolution than [17] used. The present figures show that a singularity in the stress field may arise in the region far away from the stagnation point () and near the y axis (), as previously analytically recognized, while in [17], this tendency was invisible due to the rather coarse resolution employed.Actually, the appearance of the singularity at or is independent from the choice of the arbitrary function . This can be easily recognized by observing the distribution of the stresses (31)–(33) along an arbitrary characteristic curve , where is non-zero finite constant. As an example, the term tends to be infinite at for or at for . These singularities are independent from the choice of and thus non-removable. However, possible singularity near the stagnation point can be effectively prevented by choosing a reasonable function , e.g., (34). This ensures that no singularity occurs in the stress field near the stagnation point. For a stagnation-point flow with the velocity field given by (13), the velocity becomes unbounded at or and is thus physically no longer meaningful. The singularity arising in the far field at or may not be relevant when a bounded stagnation-point flow is investigated. We should then focus on the analysis of singularity in a bounded area near the stagnation point. - (ii)
- If , performing the similar steps as for the above case gives the solutions:Similarly, by reasonably choosing of () and , singularity near the stagnation point can be avoided.
- (iii)
- If , we obtain four equations for , and from (25). Solving them and then substituting them into (22)–(24) yield:To prevent the singularity near the stagnation point , only one of , and one of , need to be zero according to the relative relationship between and . This results in a stress distribution that depends on only one coordinate x or y.
3.1.2. Case
- (i)
- If , we obtain the solutions:The logarithmic singularity in caused by at can only be avoided when , i.e., . In this case, the choice (34) for the arbitrary constants () and arbitrary function is still suitable to prevent the singularity near the stagnation point.However, for the Oldroyd model, i.e., the case of with and for the Maxwell model, i.e., the case of , the logarithmic singularity at the Weissenberg number is unavoidable. The similar conclusion was also drawn by [11] for Maxwell fluid.
- (ii)
- If :The singularity caused by the term can only be avoided if . In addition, also has to be zero to prevent the singularity at . This choice will cause a uniform stress field, which may be physically disputable.
3.1.3. Case
- (i)
- If :where the logarithmic singularity caused by in could only be avoided with the extra restriction . However, for the Oldroyd model there is at with and for the Maxwell model , so that logarithmic singularity is non-removable. The similar conclusion was also drawn by [11] for a Maxwell fluid.
- (ii)
- For :Similar to the last cases, the singularity in and can only be avoided at with (). This again corresponds to a uniform stress field and thus may be physically disputable.
3.2. Case
- (i)
- If , and are real numbers with , we obtain:
- (ii)
- If , i.e., , we obtain:
- (iii)
- If , with are conjugates complex numbers, the homogeneous solution of is given by
- (i)
- If , we obtain:
- (ii)
- If , the particular solution takes the form:
- (i)
- If and :
- (ii)
- If , the solutions take the form:
- (iii)
- If :
- (iv)
- If :
4. Analytical Solutions of a Near-Wall Stagnation-Point Flow
4.1. Analytical Solutions of the Model Equation
4.2. Compatibility Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giesekus, H. Phänomenologische Rheologie: Eine Einführung; Springer: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Dillen, S.; Oberlack, M.; Wang, Y. Analytical investigation of rotationally symmetrical oscillating flows of viscoelastic fluids. J. Non–Newton. Fluid Mech. 2019, 272, 104168. [Google Scholar] [CrossRef]
- Ma, B.; Wang, Y.; Kikker, A. Analytical solutions of oscillating Couette-Poiseuille flows for the viscoelastic Oldroyd B fluid. Acta Mech. 2019, 230, 2249–2266. [Google Scholar] [CrossRef]
- Saengow, C.; Giacomin, A.J.; Kolitawong, C. Exact analytical solution for large-amplitude oscillatory shear flow from Oldroyd 8-constant framework: Shear stress. Phys. Fluids 2017, 29, 043101. [Google Scholar] [CrossRef] [Green Version]
- Schlichting, H. Boundary-Layer Theory, 6th ed.; McGraw-Hill: New York, NY, USA, 1968; p. 96. [Google Scholar]
- Phan-Thien, N. Plane and axi-symmetric stagnation flow of a Maxwellian fluid. Rheol. Acta 1983, 22, 127–130. [Google Scholar] [CrossRef]
- Phan-Thien, N. Stagnation flows for the Oldoryd-B fluid. Rheol. Acta 1984, 23, 172–176. [Google Scholar] [CrossRef]
- Renardy, M. A comment on smoothness of viscoelastic stresses. J. Non–Newton. Fluid Mech. 2006, 138, 204–205. [Google Scholar] [CrossRef]
- Thomas, B.; Shelley, M. Emergence of singular structures in Oldroyd-B fluids. Phys. Fluids 2007, 19, 103103. [Google Scholar] [CrossRef] [Green Version]
- Cruz, D.O.A.; Pinho, F.T. Analytical solution of steady 2D wall-free extensional flows of UCM fluids. J. Non–Newton. Fluid Mech. 2015, 223, 157–164. [Google Scholar] [CrossRef]
- Meleshko, S.V.; Moshkin, N.P.; Pukhnachev, V.V.; Samatova, V. On steady two-dimensional analytical solutions of the viscoelastic Maxwell equation. J. Non–Newton. Fluid Mech. 2019, 270, 1–7. [Google Scholar] [CrossRef]
- Becherer, P.; van Saarloosa, W.; Morozovb, A.N. Stress singularities and the formation of birefringent strands in stagnation flows of dilute polymer. J. Non–Newton. Fluid Mech. 2008, 157, 126–132. [Google Scholar] [CrossRef] [Green Version]
- Van Gorder, R.A.; Vajravelu, K.; Akyildiz, F.T. Viscoelastic stresses in the stagnation flow of a dilute polymer solution. J. Non–Newton. Fluid Mech. 2009, 161, 94–100. [Google Scholar] [CrossRef]
- Van Gorder, R.A. Do general viscoelastic stresses for the flow of an upper convected Maxwell fluid satisfy the momentum equation? Maccanica 2012, 47, 1977–1985. [Google Scholar] [CrossRef]
- Saengow, C.; Giacomin, A.J.; Grizzuti, N.; Pasquino, R. Startup steady shear flow from the Oldroyd 8-constant framework. Phys. Fluids 2019, 31, 063101. [Google Scholar] [CrossRef] [Green Version]
- Oldroyd, J.G. Non–Newtonien effects in steady motion of some idealized elastico-viscous liquids. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1958, 245, 278–297. [Google Scholar]
- Meleshko, S.V.; Moshkin, N.P.; Pukhnachev, V.V. On exact analytical solutions of equations of Maxwell incompressible. Int. J. Non-Linear Mech. 2018, 105, 152–157. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. Magnetorheological Fluids: Qualitative comparison between a mixture model in the Extended Irreversible Thermodynamics framework and an Herschel–Bulkley experimental elastoviscoplastic model. Int. J. Non-Linear Mech. 2020, 118, 103288. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Oberlack, M.; Wang, Y. Analytical Investigation of Viscoelastic Stagnation-Point Flows with Regard to Their Singularity. Appl. Sci. 2021, 11, 6931. https://doi.org/10.3390/app11156931
Liu J, Oberlack M, Wang Y. Analytical Investigation of Viscoelastic Stagnation-Point Flows with Regard to Their Singularity. Applied Sciences. 2021; 11(15):6931. https://doi.org/10.3390/app11156931
Chicago/Turabian StyleLiu, Jie, Martin Oberlack, and Yongqi Wang. 2021. "Analytical Investigation of Viscoelastic Stagnation-Point Flows with Regard to Their Singularity" Applied Sciences 11, no. 15: 6931. https://doi.org/10.3390/app11156931
APA StyleLiu, J., Oberlack, M., & Wang, Y. (2021). Analytical Investigation of Viscoelastic Stagnation-Point Flows with Regard to Their Singularity. Applied Sciences, 11(15), 6931. https://doi.org/10.3390/app11156931






