A Form-Finding Method for Branching Structures Based on Dynamic Relaxation
Abstract
:1. Introduction
2. Method
2.1. Governing Equation
2.2. Element Cluster
3. Characteristics of the Element-Clustered Method
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nerdinger, W.; Meissner, I.; Möller, E.; Grdanjski, M. Complete Works: Lightweight Construction—Natural Design; Birkhäuser: Berlin, Germany; Basel, Switzerland, 2005. [Google Scholar]
- Özdemir, N.B.; Selçuk, S.A. Tree metaphor in architectural design. Int. J. Archit. Urban Stud. 2016, 1, 64–76. [Google Scholar]
- Rian, I.M.; Sassone, M. Tree-inspired dendriforms and fractal-like branching structures in architecture: A brief historical overview. Front. Archit. Res. 2014, 3, 298–323. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Jiang, B. A morphogenesis method for shape optimization of framed structures subject to spatial constraints. Eng. Struct. 2014, 77, 109–118. [Google Scholar] [CrossRef]
- Cui, J.; Zhou, G.; Ohsaki, M. Design of tree-type support structure of free-form shell generated using fractal geometry. In Proceedings of the IASS Annual Symposia, Tokyo, Japan, 26–30 September 2016. [Google Scholar]
- Bao, D.; Yan, X.; Snooks, R.; Xie, Y. Design and Construction of an Innovative Pavilion Using Topological Optimization and Robotic Fabrication. In Proceedings of the IASS Annual Symposia, Barcelona, Spain, 7–10 October 2019. [Google Scholar]
- Chen, Z.; Liu, H.; Wang, X.; Zhou, T. Establishment and application of cable-sliding criterion equation. Adv. Steel Constr. 2011, 7, 131–143. [Google Scholar]
- Zhang, Q.; Chen, Z.; Wang, X.; Liu, H. Form-finding of tree structures based on sliding cable element. J. Tianjin Univ. Sci. Technol. 2015, 48, 362–372. (In Chinese) [Google Scholar]
- Wu, Y.; Zhang, J.; Cao, Z. Form finding analysis and engineering application of branching structures. J. Build. Struct. 2011, 32, 162–168. (In Chinese) [Google Scholar]
- Wu, Y.; Xu, Y.; Li, Q. Effective length factors for branching structures. J. Build. Struct. 2018, 39, 53–60. (In Chinese) [Google Scholar]
- Eguchi, C.; Sugiura, N.; Tagawa, H. Architectural and Structural Design of Tree Structure Supporting Free-surface Shell Roof using Hanging Upside-down Model. In Proceedings of the IASS Annual Symposia, Boston, MA, USA, 16–20 July 2018. [Google Scholar]
- Eguchi, C.; Sugiura, N.; Tagawa, H. Proposal of design method of natural and rational tree-structure based on computational hanging upside-down simulation. In Proceedings of the IASS Annual Symposia, Barcelona, Spain, 7–10 October 2019. [Google Scholar]
- Zhao, Z.; Liang, B.; Liu, H.; Sun, Q. A novel numerical method for form-finding analysis of branching structures. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2241–2252. [Google Scholar] [CrossRef]
- Barnes, M.R. Form finding and analysis of tension structures by dynamic relaxation. Int. J. Space Struct. 1999, 14, 89–104. [Google Scholar] [CrossRef]
- Richardson, J.N.; Adriaenssens, S.; Coelho, R.F.; Bouillard, P. Coupled form-finding and grid optimization approach for single layer grid shells. Eng. Struct. 2013, 52, 230–239. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, D.; Qian, H. Computational method for the deformation mechanism of non-prestressed cable net structures based on the vector form intrinsic finite element method. Eng. Struct. 2021, 231, 111788. [Google Scholar] [CrossRef]
- Su, Y.; Wu, Y.; Ji, W.; Shen, S. Shape Generation of Grid Structures by Inverse Hanging Method Coupled with Multi-objective Optimization. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 498–509. [Google Scholar] [CrossRef]
- Yu, Y.; Paulino, G.H.; Luo, Y. Finite Particle Method for Progressive Failure Simulation of Truss Structures. ASCE J. Struct. Eng. 2011, 137, 1168–1181. [Google Scholar] [CrossRef] [Green Version]
- Hangai, Y.; Kawaguchi, K. Analysis of shape-finding process of unstable link structures. Bull. Int. Assoc. Shell Spat. Struct. 1989, 30, 116–128. [Google Scholar]
- Hangai, Y.; Wu, M. Analytical method of structural behaviours of a hybrid structure consisting of cables and rigid structures. Eng. Struct. 1999, 21, 726–736. [Google Scholar] [CrossRef]
- Zhang, T.; Kawaguchi, K.; Wu, M. A folding analysis method for origami based on the frame with kinematic indeterminacy. Int. J. Mech. Sci. 2018, 146–147, 234–248. [Google Scholar] [CrossRef]
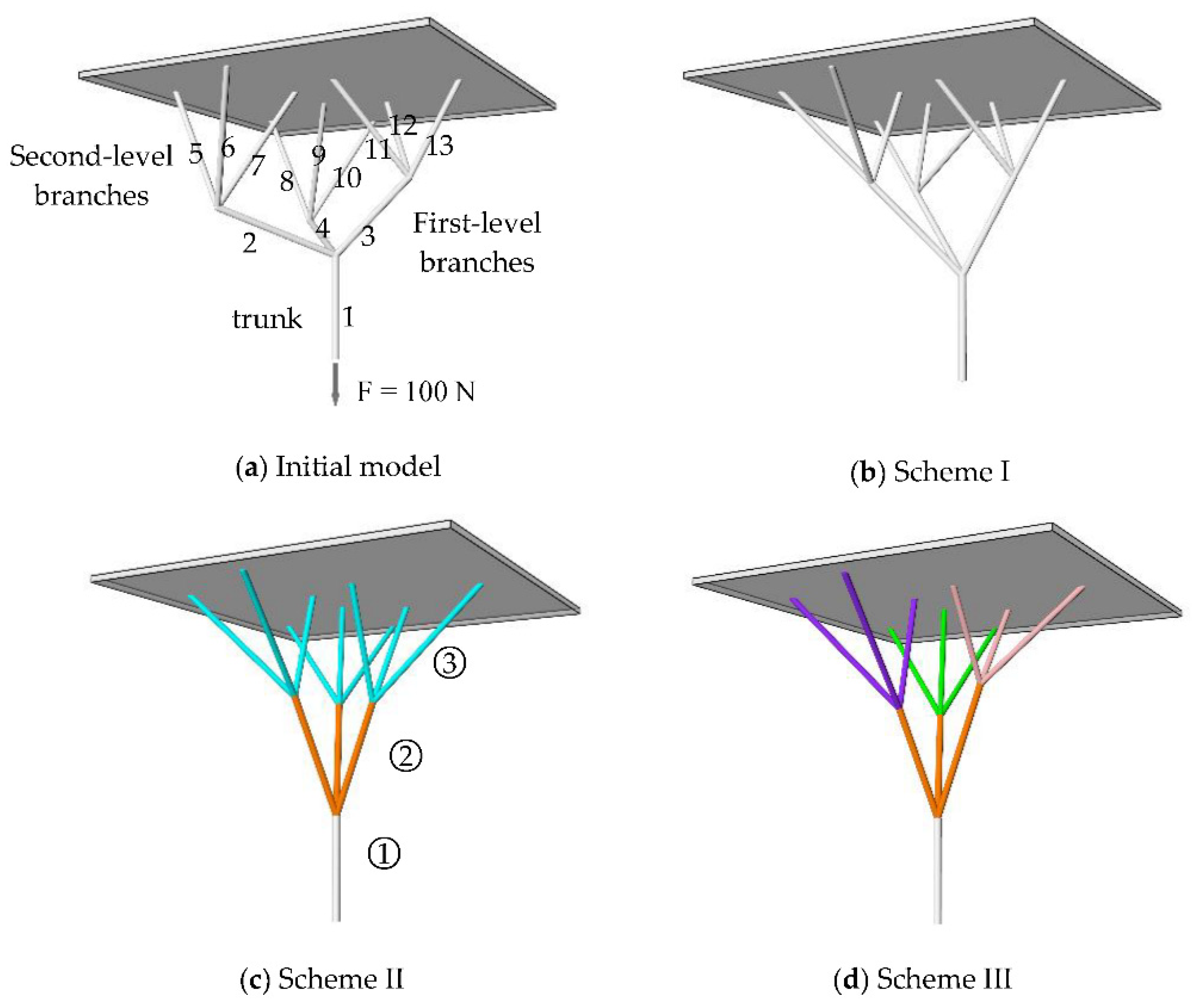





| Position of Elements | Shape Scheme I AF/N | Shape Scheme II AF/N | Shape Scheme III AF/N |
|---|---|---|---|
| Trunk | 100.00 | 100.00 | 100.00 |
| First-level branches | 28.631 | 35.970 | 35.988 |
| 68.901 | 35.992 | 35.914 | |
| 28.631 | 35.970 | 35.988 | |
| Second-level branches | 0.000 | 14.007 | 13.683 |
| 28.633 | 14.010 | 13.717 | |
| 0.002 | 13.995 | 13.688 | |
| 68.900 | 14.028 | 14.999 | |
| 0.001 | 14.008 | 15.006 | |
| 0.001 | 14.008 | 15.006 | |
| 0.000 | 14.007 | 13.683 | |
| 0.002 | 13.995 | 13.688 | |
| 28.633 | 14.010 | 13.717 |
| Mechanical Parameters | Structure Generated by Traditional DR | Structure Generated by Element Clustered Method |
|---|---|---|
| Average axial force | −89,737 N | −92,146 N |
| Average bending moment | 560.10 N·m | 491.49 N·m |
| Maximum axial force | −1.08 × 106 N | −1.11 × 106 N |
| Maximum bending moment | 21,285 N·m | 22,029 N·m |
| Average vertical displacement | −0.088 m | −0.089 m |
| Maximum vertical displacement | −0.164 m | −0.171 m |
| Strain energy | 94,825 N·m | 96,617 N·m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, G.; Chen, C.; Gong, Z.; Wang, Y. A Form-Finding Method for Branching Structures Based on Dynamic Relaxation. Appl. Sci. 2021, 11, 7165. https://doi.org/10.3390/app11157165
Tu G, Chen C, Gong Z, Wang Y. A Form-Finding Method for Branching Structures Based on Dynamic Relaxation. Applied Sciences. 2021; 11(15):7165. https://doi.org/10.3390/app11157165
Chicago/Turabian StyleTu, Guigang, Chen Chen, Zaijing Gong, and Yueren Wang. 2021. "A Form-Finding Method for Branching Structures Based on Dynamic Relaxation" Applied Sciences 11, no. 15: 7165. https://doi.org/10.3390/app11157165







