Risk-Sensitive Rear-Wheel Steering Control Method Based on the Risk Potential Field
Abstract
:1. Introduction
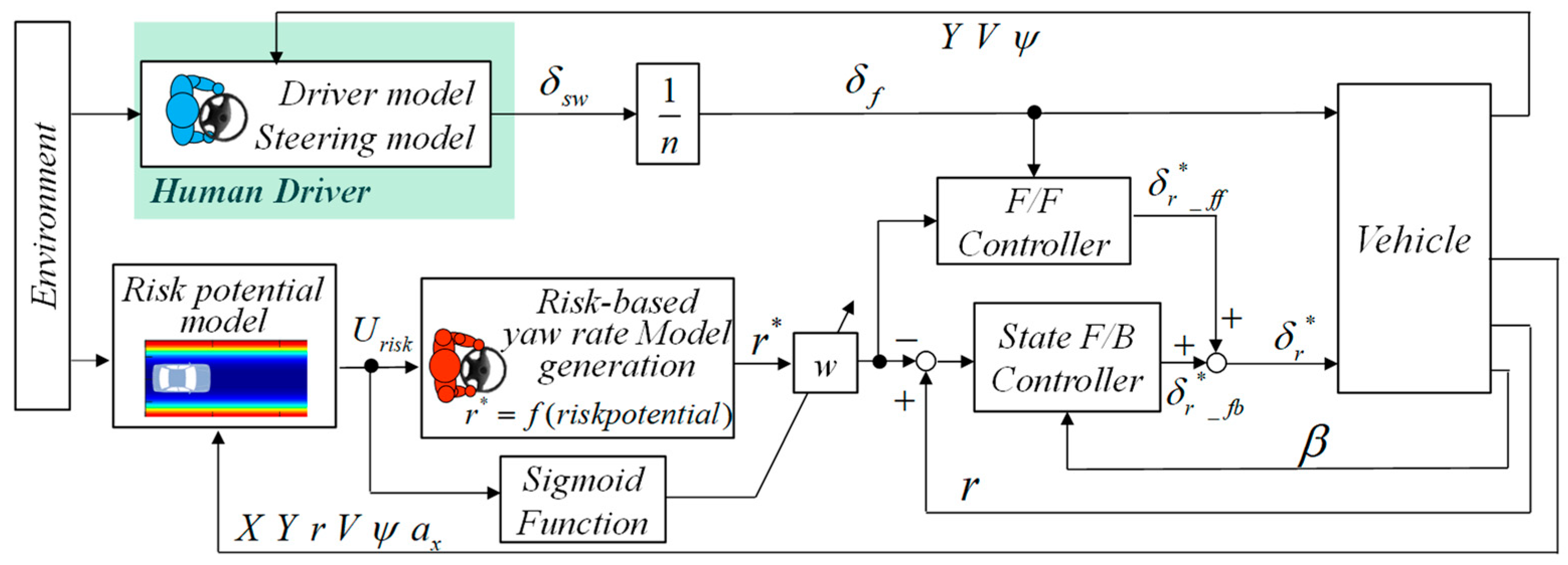
2. Design of Rear-Wheel Steering Control Based on the Risk Potential Field
2.1. Design of the Risk Potential Field
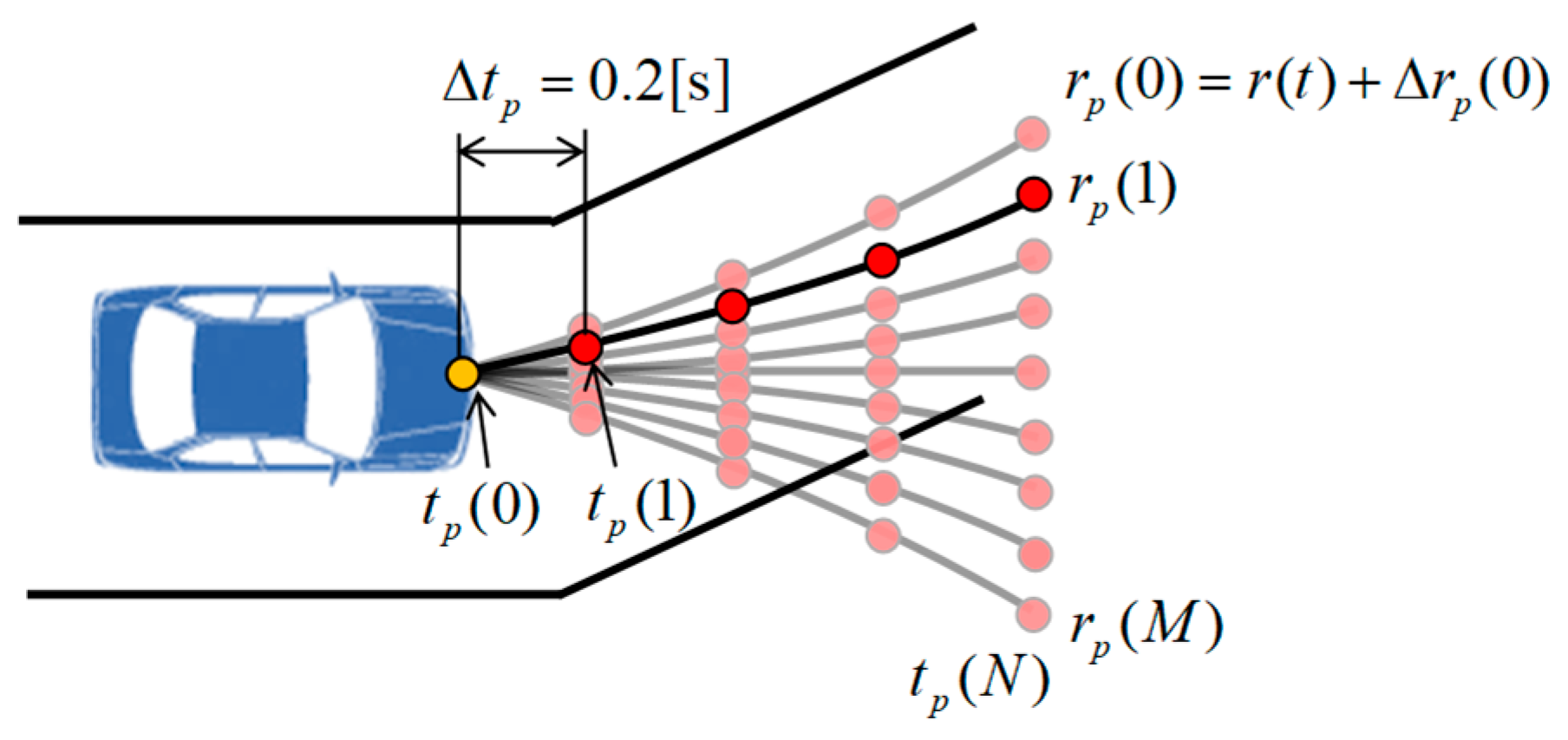
2.2. Optimization of the Reference Yaw Rate
2.3. Linear Vehicle Model
2.4. Feedforward Controller
2.5. Feedback Controller
3. Model Effectiveness Verification Using a Simulation
3.1. Nonlinear Four-Wheel Vehicle Model
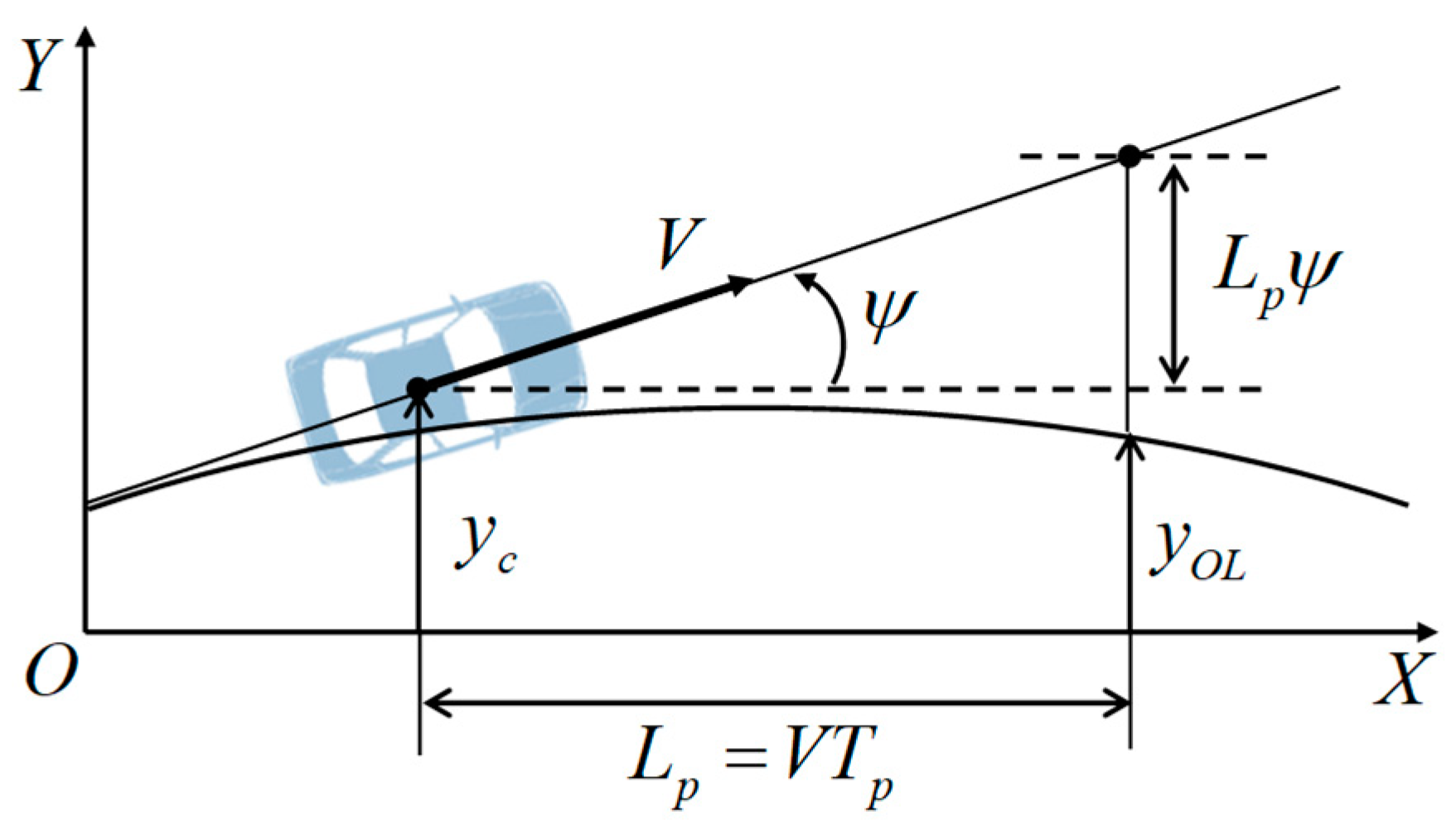
3.2. Reference Driver Model
3.3. Zero-Sideslip Angle 4WS
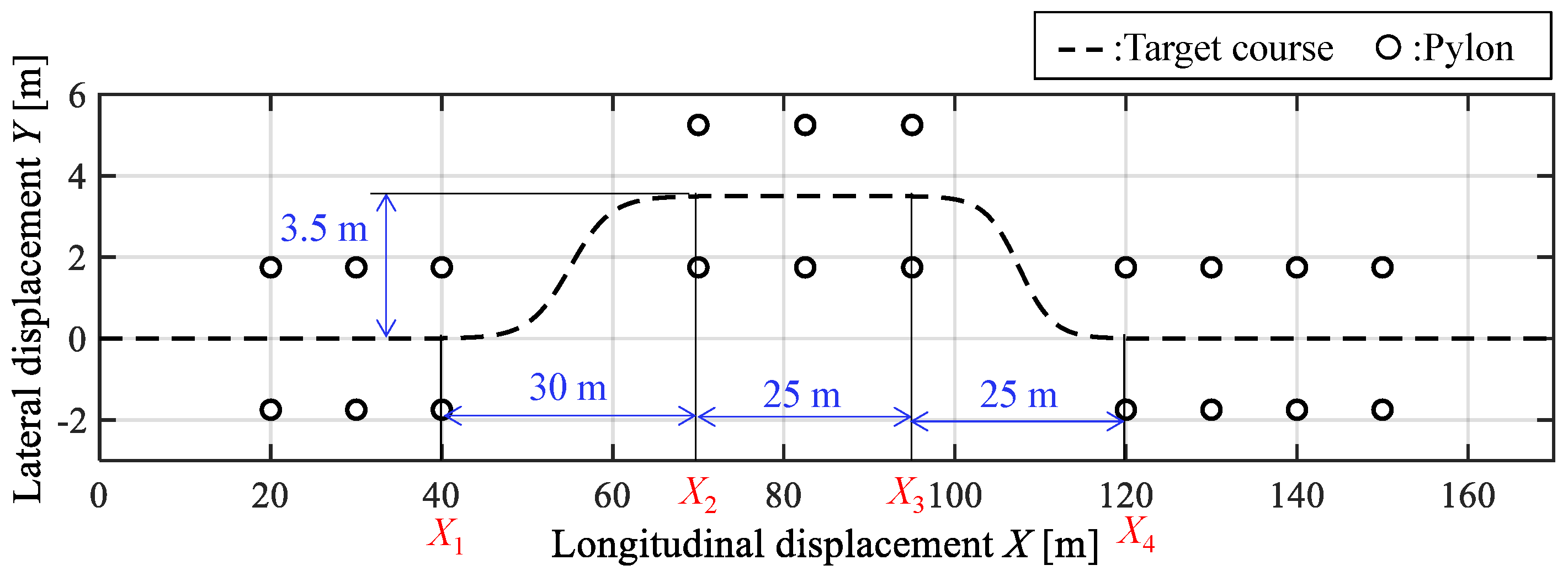
3.4. Simulation Conditions
- 2WS based on the reference driver model;
- 2WS without control;
- Zero-sideslip angle 4WS;
- Risk potential field 4WS (the proposed system).
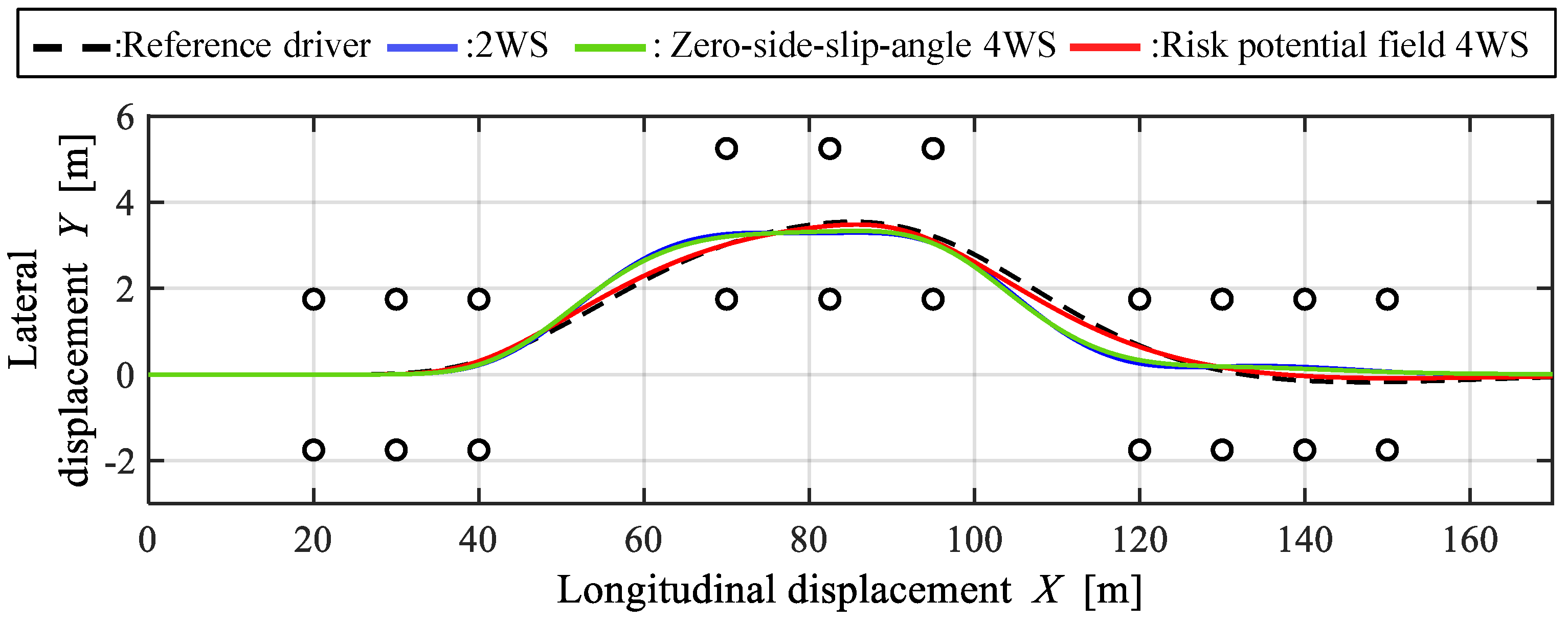
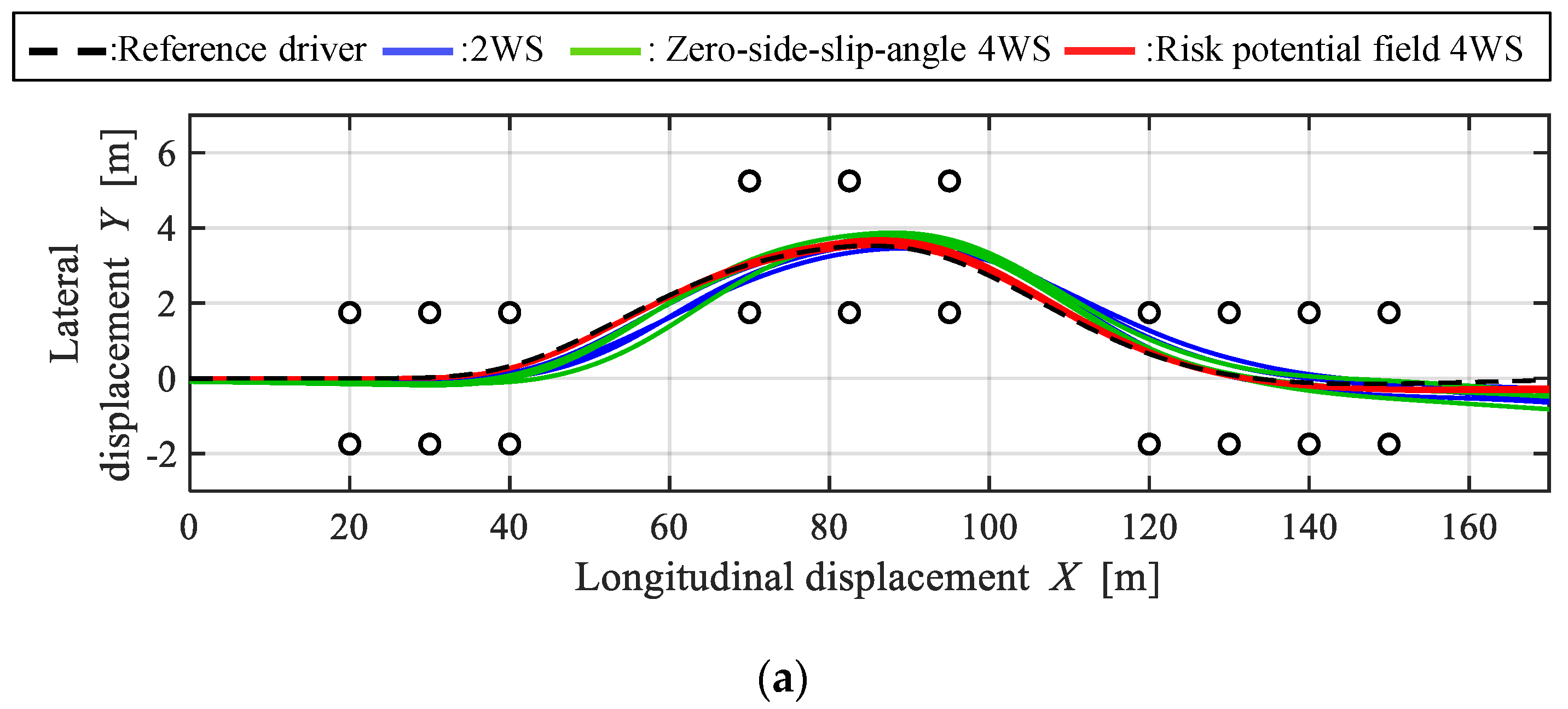
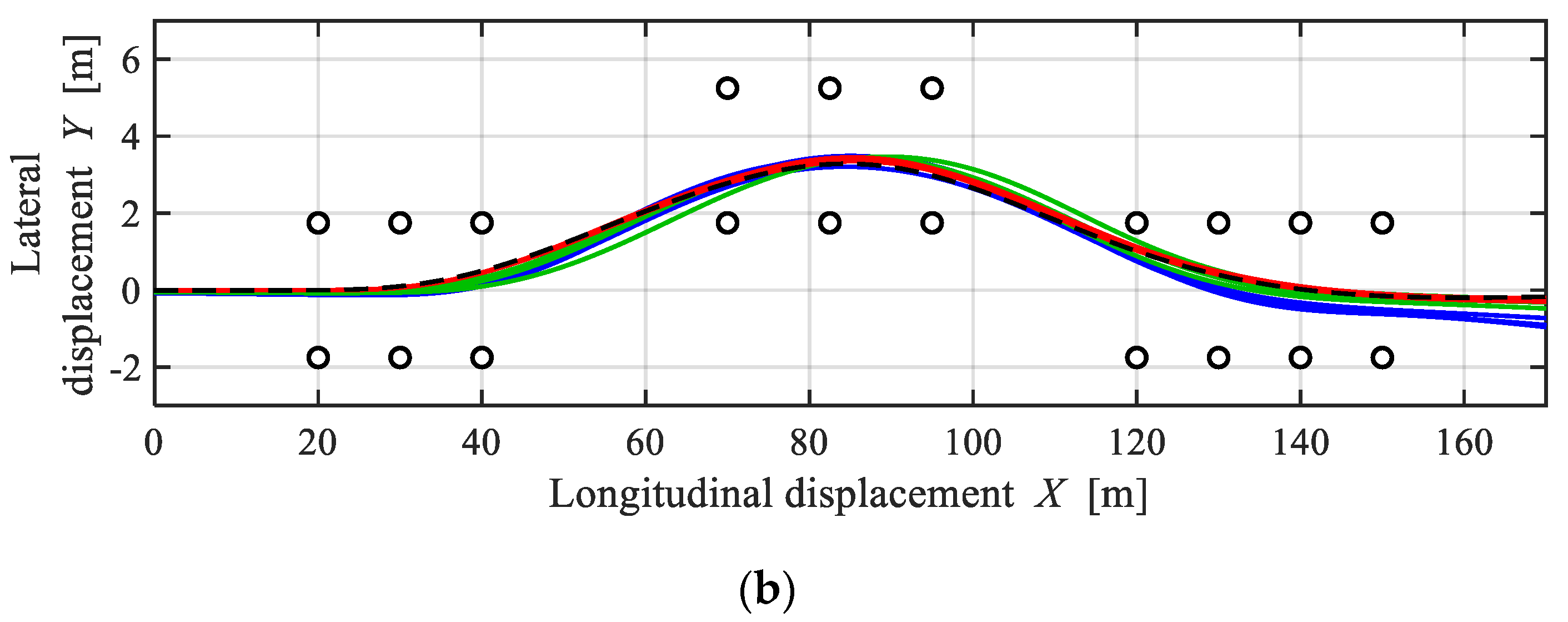
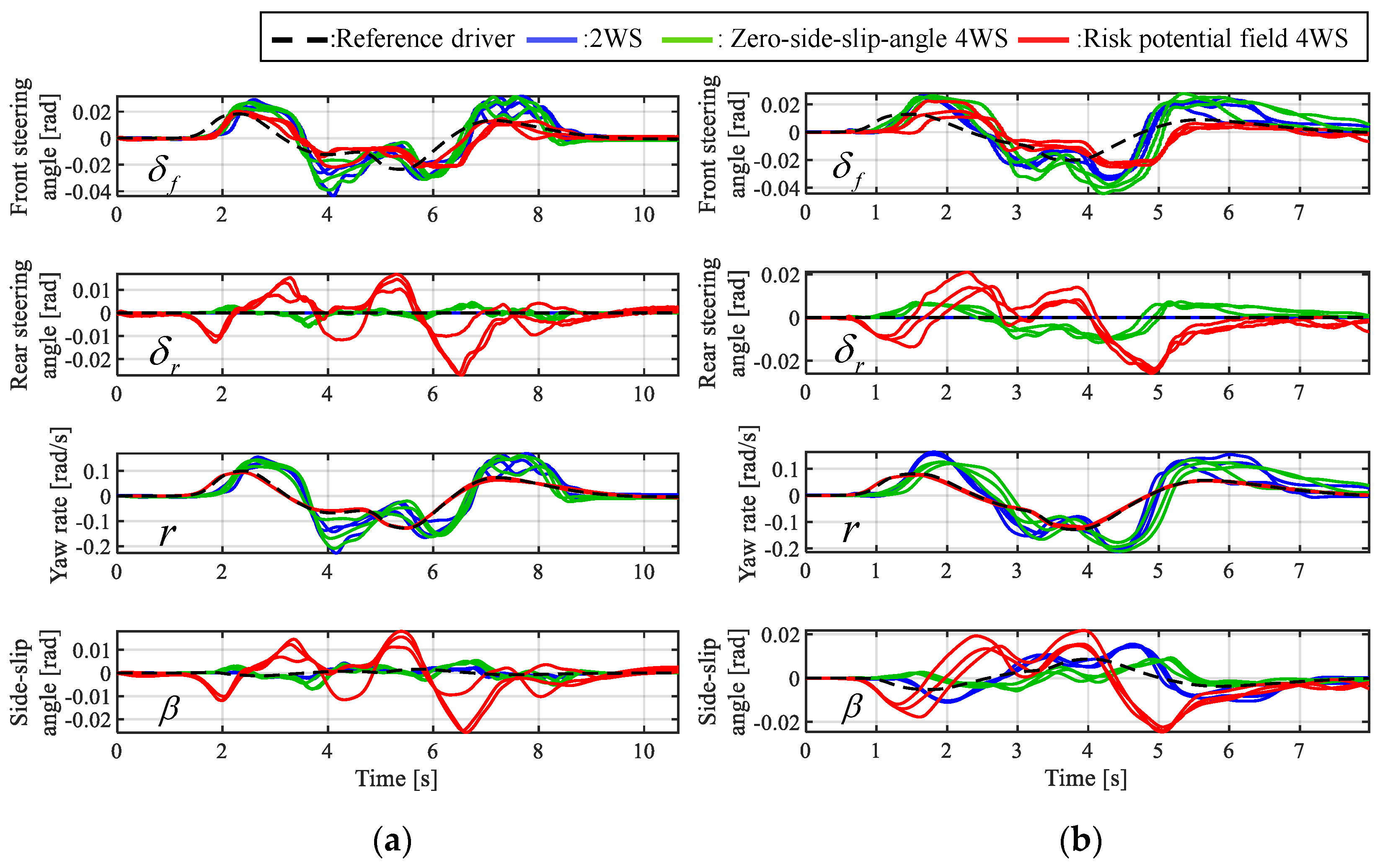
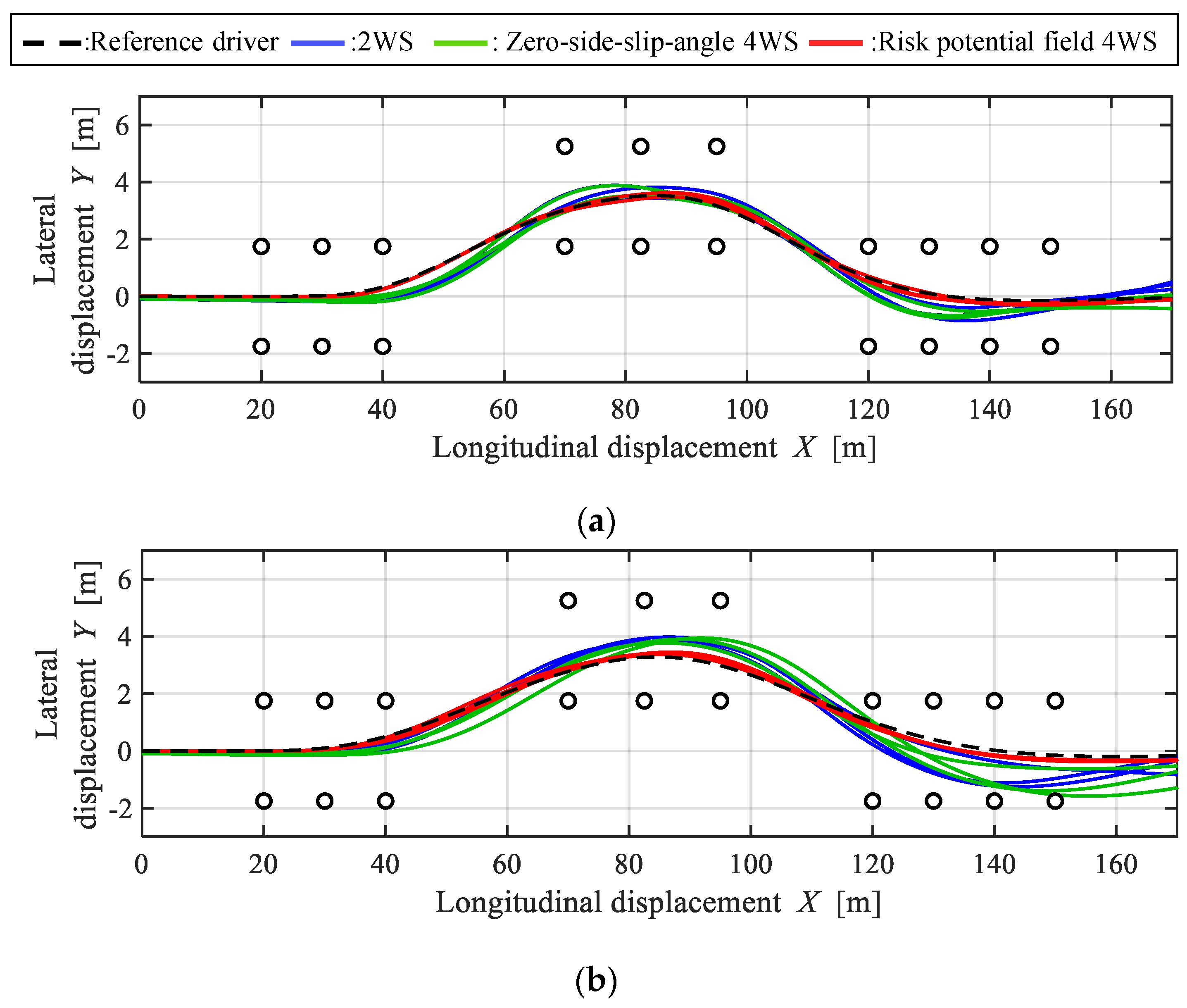
3.5. Simulation Results
4. Experimental Study Using a Driving Simulator
4.1. Experimental Conditions
- 2WS without control;
- Zero-sideslip angle 4WS;
- Risk potential field 4WS (the proposed system).
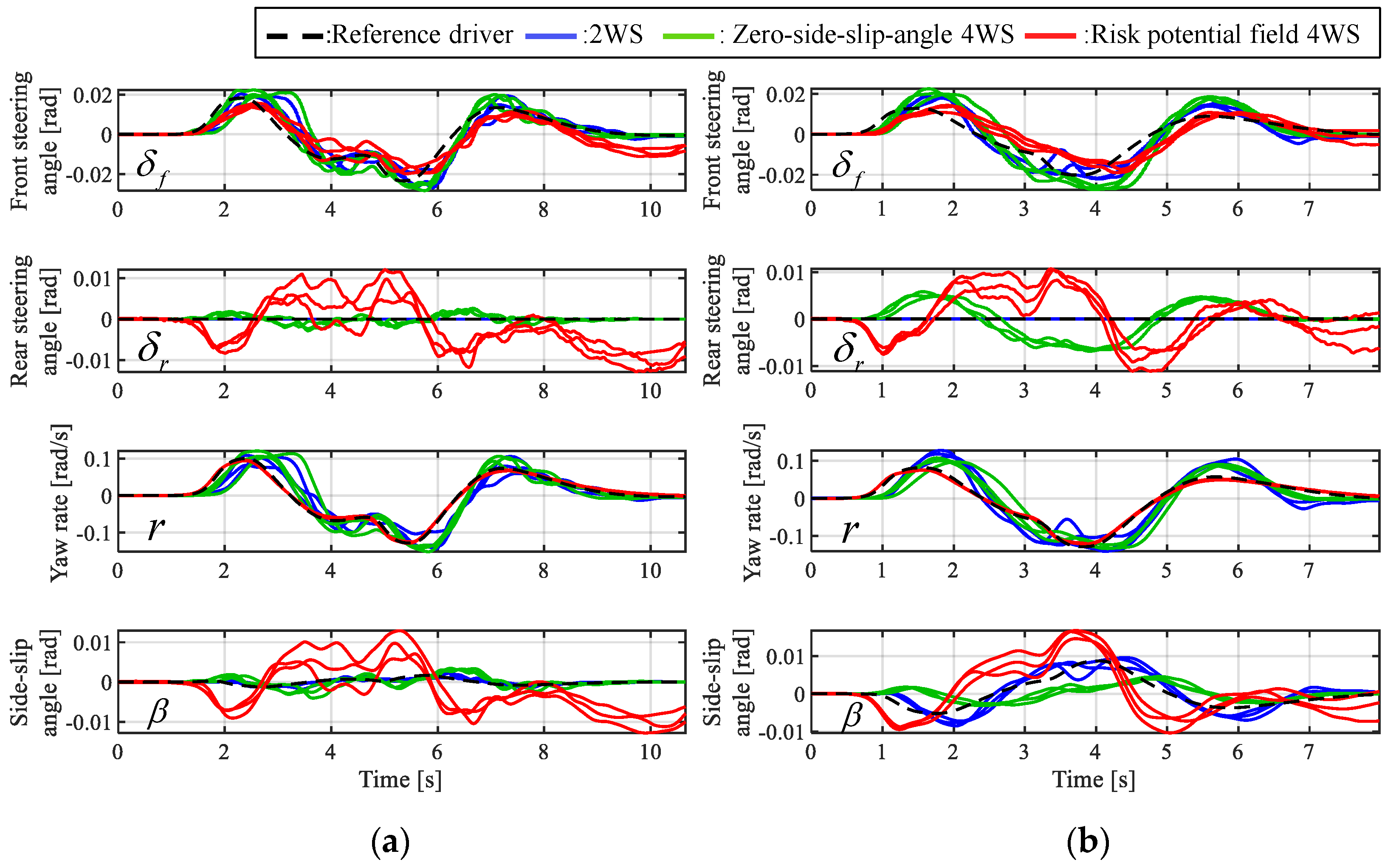
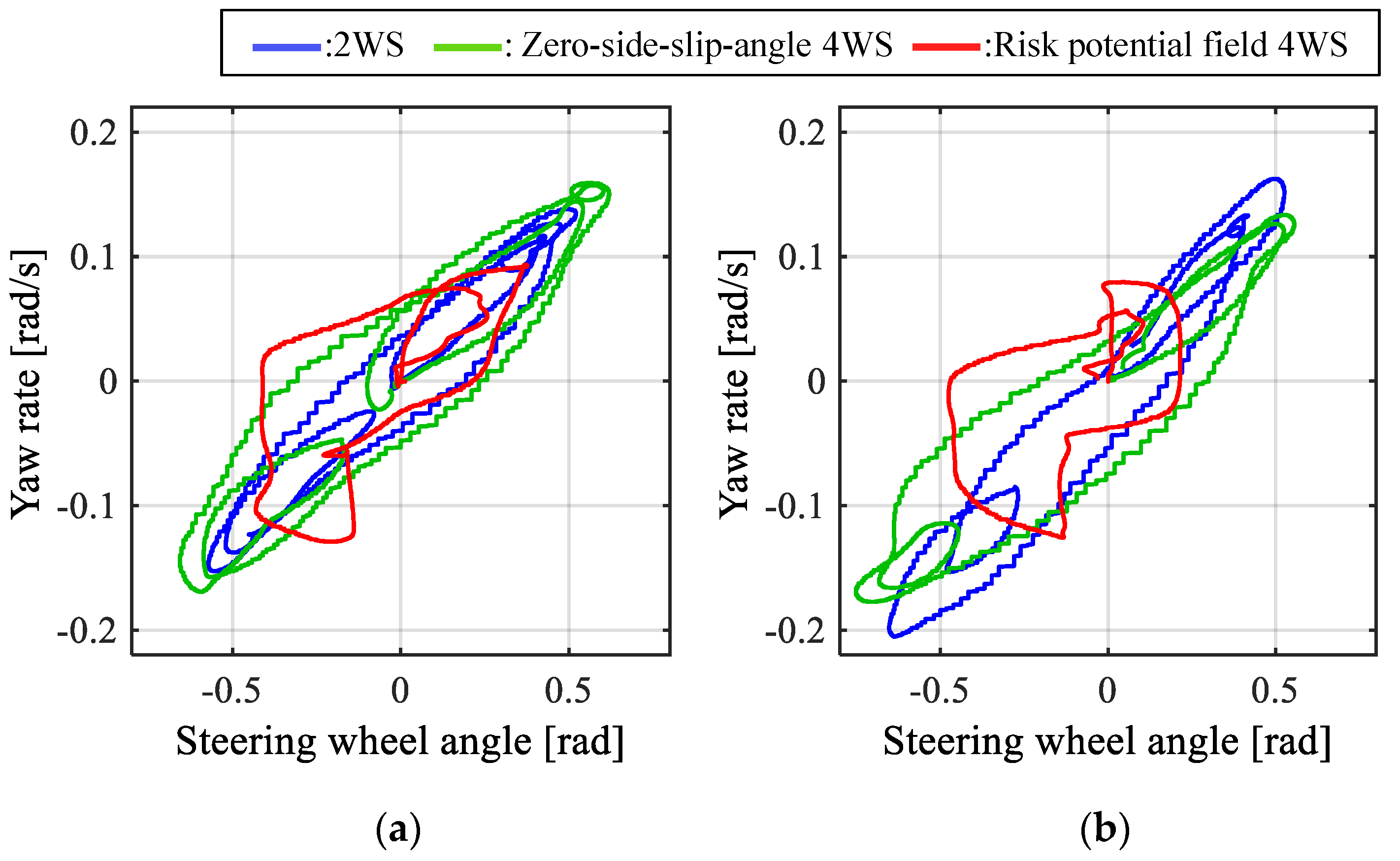
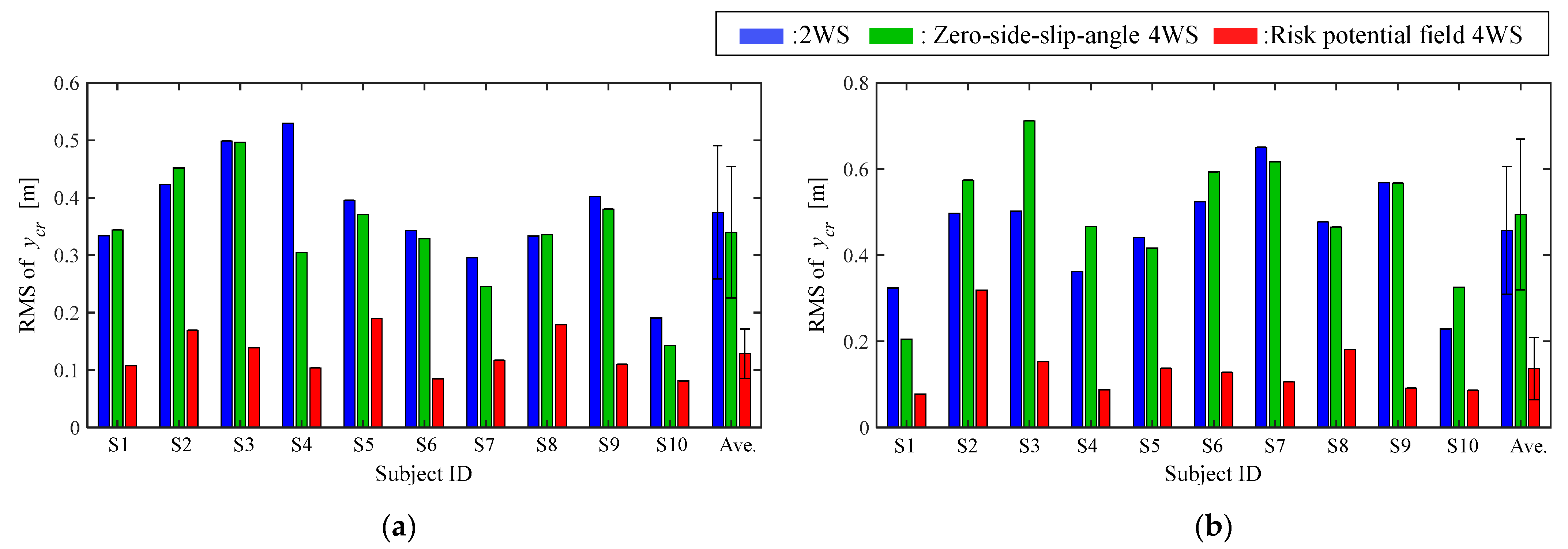
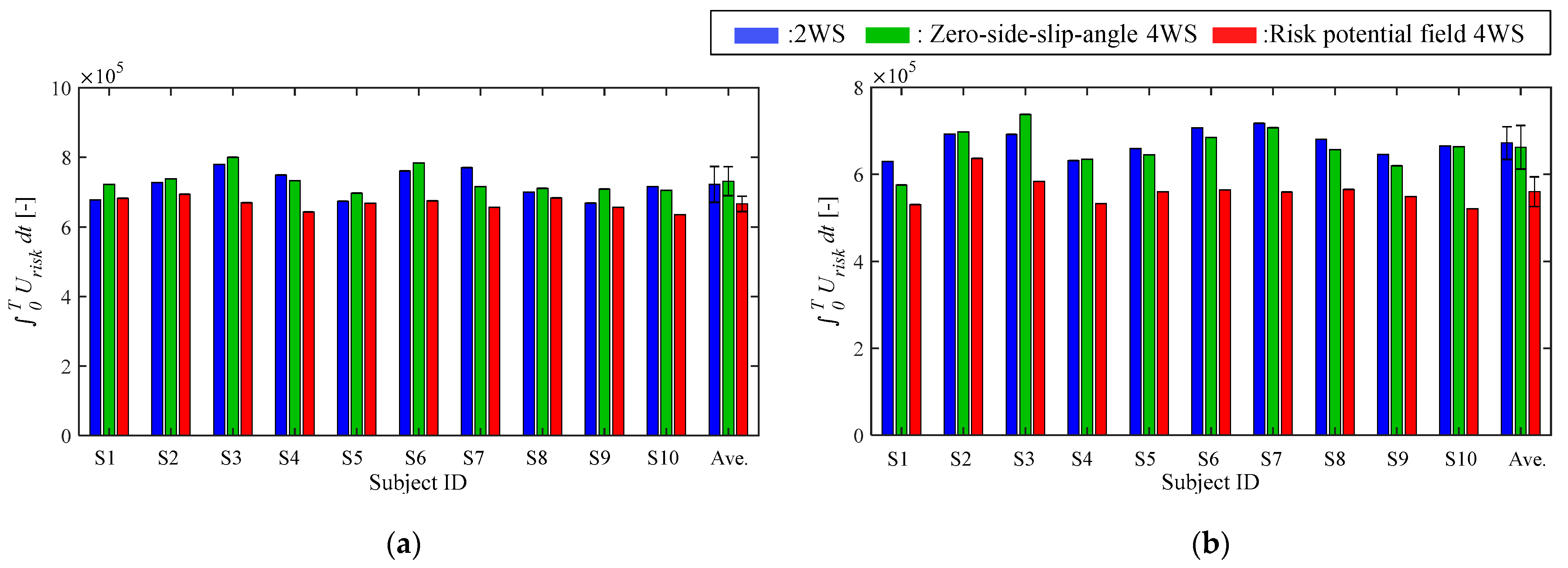
4.2. Results
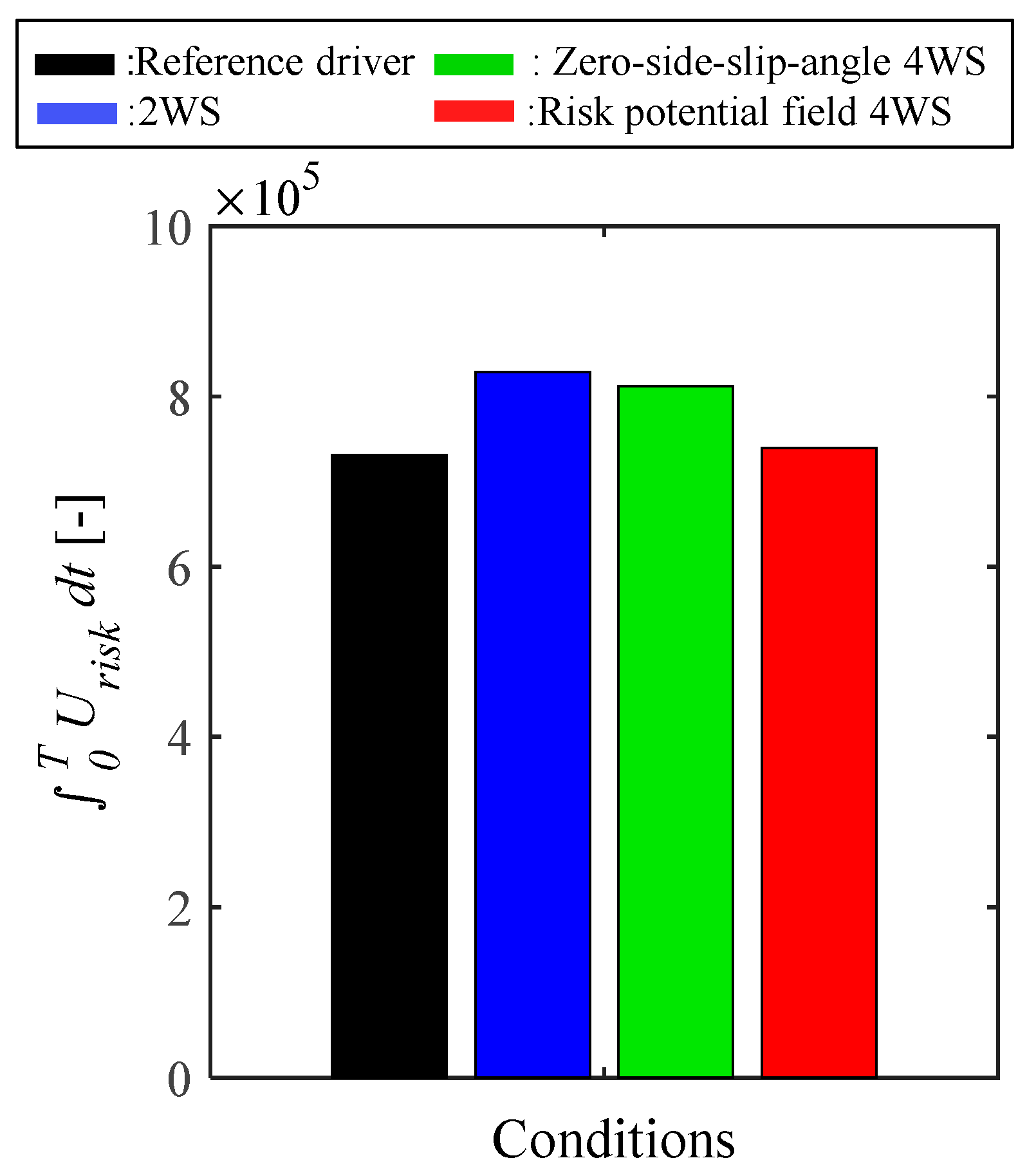
4.3. Evaluation Index
4.4. Discussion
5. Conclusions
- (1)
- The vehicle could generate a yaw rate equivalent to that of the reference driver and derive a safe and smooth trajectory in a double lane change test by applying the risk potential field 4WS.
- (2)
- The experiments were conducted three times under each condition, and the trajectory variation became smaller when the risk potential field 4WS was applied.
- (3)
- The corrective steering and steering burden of the driver were reduced by applying the risk potential field 4WS in comparison with the 2WS and conventional 4WS. Consequently, the handling quality and emergency avoidance performance were enhanced.
- (4)
- The amount of steering support for the rear wheels in the proposed method was adjusted while considering the driving characteristics. Hence, the system could guide the driver to safety while maintaining the driver’s vehicle control authority.
- (5)
- In this study, the simulation was conducted under the assumption that the risk potential field was generated accurately from the road environment information. However, for practical use, it was necessary to conduct experimental verification while actually obtaining information from the sensors and maps in real time. In addition, there were obstacles such as pedestrians and other vehicles in the actual driving environment. Therefore, if the effectiveness of the proposed control could be confirmed after defining the obstacle potential, its feasibility would be further enhanced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, K.; Zheng, J.; Huang, K. Robust active steering control for vehicle rollover prevention. Int. J. Model. Identif. Control. 2019, 32, 70–84. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Hasegawa, T.; Nagai, M. Motion Planning and Control of Autonomous Driving Intelligence System Based on Risk Potential Optimization Framework. Int. J. Automot. Eng. 2016, 7, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Sato, D.; Nunobiki, E.; Inoue, S.; Raksincharoensak, P. Motion Planning and Control in Highway Merging Maneuver Based on Dynamic Risk Potential Optimization. In Proceedings of the 5th International Symposium on Future Active Safety Technology toward Zero-Traffic-Accidents (FAST-Zero’19), Blacksburg, VA, USA, 9–11 September 2019. [Google Scholar]
- Inoue, S.; Kinoshita, T.; Mio, M.; Raksincharoensak, P.; Nagai, M.; Inoue, H. Study on Haptic Steering Shared Control between Driver and ADAS by Using Risk Potential Optimization Theory. In Proceedings of the 4th International Symposium on Future Active Safety Technology toward Zero-Traffic Accidents (FAST-Zero’17), Nara, Japan, 18–22 September 2017. [Google Scholar]
- Kobayashi, Y.; Kageyama, I.; Tsubouchi, A.; Kitaki, Y.; Ito, K. Study on Construction of Driver Model for Obstacle Avoidance Using Risk Potential. Trans. Soc. Automot. Eng. Jpn. 2019, 50, 109–115. [Google Scholar] [CrossRef]
- Raksincharoensak, P. Vehicle Dynamics Control for Obstacle Avoidance by Risk Potential Prediction. J. SICE 2015, 54, 820–823. [Google Scholar] [CrossRef]
- Kanai, K.; Fujishiro, T. Research Trends in Four Wheel Steering System. J. SICE 1989, 28, 252–260. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Mouri, H.; Nagai, M. Evaluation of Four-Wheel-Steering System from the Viewpoint of Lane-Keeping Control. Int. J. Automot. Technol. 2004, 5, 69–76. [Google Scholar]
- Hirose, T.; Tsuchiya, Y.; Limpibunterng, T.; Miyazaki, H. The Development of VDIM Step 5. In Proceedings of the 3rd International Munich Chassis Symposium (Chassis Tech Plus), Munich, Germany, 21–22 June 2012. [Google Scholar]
- Alleyne, A. A Comparison of Alternative Obstacle Avoidance Strategies for Vehicle Control. Veh. Syst. Dyn. 1996, 27, 371–392. [Google Scholar] [CrossRef]
- Eckert, A.; Hartmann, B.; Rieth, P. Emergency Steer Assist: Advanced Driver Assistance System for Emergency Lane Change Maneuvers. In Proceedings of the FISITA World Congress 2010, F2010E017, Budapest, Hungary, 30 May–4 June 2010. [Google Scholar]
- Deng, B.; Zhao, H.; Shao, K.; Li, W.; Yin, A. Hierarchical Synchronization Control Strategy of Active Rear Axle Independent Steering System. Appl. Sci. 2020, 10, 3537. [Google Scholar] [CrossRef]
- Deng, B.; Shao, K.; Zhao, H. Adaptive Second Order Recursive Terminal Sliding Mode Control for a Four-Wheel Independent Steer-by-Wire System. IEEE Access 2020, 8, 75936–75945. [Google Scholar] [CrossRef]
- Rau, M.; Michalski, R.; Spangemacher, B. Innovative Rear Axle Steering with Large Angles. In Proceedings of the Chassis Tech Plus 2021 Symposium, Munich, Germany, 29–30 June 2021; pp. 1–12. [Google Scholar]
- Reichardt, D.; Schick, J. Collision Avoidance in Dynamic Environments Applied to Autonomous Vehicle Guidance on the Motorway. In Proceedings of the IEEE Intelligent Vehicles Symposium, Paris, France, 24–26 October 1994; pp. 1–6. [Google Scholar]
- Kageyama, I.; Pacejka, H.B. On a New Driver Model with Fuzzy Control. Veh. Syst. Dyn. Suppl. 1992, 20, 314–324. [Google Scholar] [CrossRef]
- Kageyama, I.; Kuriyagawa, Y.; Tsubouchi, A. Study on Construction of Driver Model for Obstacle Avoidance Using Risk Potential. In Proceedings of the 25th International Symposium on Dynamics of Vehicles on Roads and Tracks (IAVSD 2017), Rockhampton, Queensland, Australia, 14–18 August 2017; Volume 1, pp. 233–238. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2007. [Google Scholar]
- Ohtsuka, T. A continuation/GMRES method for fast computation of nonlinear receding horizon control. Automatica 2004, 40, 563–574. [Google Scholar] [CrossRef]
- Abe, M. Automotive Vehicle Dynamics Theory and Applications, 2nd ed.; Tokyo Denki University Press: Tokyo, Japan, 2017; pp. 223–231. [Google Scholar]
- Raksincharoensak, P.; Sato, D.; Lidberg, M. Direct Yaw Moment Control for Enhancing Handling Quality of Lightweight Electric Vehicles with Large Load-To-Curb Weight Ratio. Appl. Sci. 2019, 9, 1151. [Google Scholar] [CrossRef] [Green Version]
- Maeda, T.; Irie, N.; Hidaka, K.; Nishimura, H. Performance of Driver-Vehicle System in Emergency Avoidance. SAE Trans. 1977, 86, 518–541. [Google Scholar]
- Hirano, Y.; Ono, E. Non-linear Robust Control for an Integrated System of 4WS and 4WD. JSAE Rev. 1995, 16, 213. [Google Scholar]
- Andreasson, J.; Bunte, T. Global chassis control based on inverse vehicle dynamics models. Veh. Syst. Dyn. 2006, 44, 321–328. [Google Scholar] [CrossRef]
- Ivanov, V.; Savitski, D. Systematization of Integrated Motion Control of Ground Vehicles. IEEE Access 2015, 3, 2080–2099. [Google Scholar] [CrossRef]
- Rasekhipour, Y.; Khajepour, A.; Chen, S.-K.; Litkouhi, B. A Potential Field-Based Model Predictive Path-Planning Controller for Autonomous Road Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1255–1267. [Google Scholar] [CrossRef]
- Dang, T.; Desens, J.; Franke, U.; Gavrila, D.; Schafers, L.; Ziegler, W. Steering and Evasion Assist. In Handbook of Intelligent Vehicles; Eskandarian, A., Ed.; Springer: London, UK, 2012; pp. 759–782. [Google Scholar] [CrossRef]
- Wang, B.; Abe, M.; Kano, Y. Influence of driver’s reaction time and gain on driver–Vehicle system performance with rear wheel steering control systems: Part of a study on vehicle control suitable for the aged driver. JSAE Rev. 2002, 23, 75–82. [Google Scholar] [CrossRef]
- Iwano, K.; Raksincharoensak, P.; Yamasaki, A.; Mouri, H.I.; Nagai, M. Study on Driver-Vehicle Cooperative Characteristics of Autonomous Driving Intelligence System by Using Steer-by-Wire. Trans. Soc. Automot. Eng. Jpn. 2015, 46, 503–508. [Google Scholar] [CrossRef]
- Raksincharoensak, P.; Iwano, K.; Yamasaki, A.; Mouri, H.I.; Nagai, M. Study on Human-Machine Shared Driving Characteristics of Autonomous Driving Intelligence System in Obstacle Avoidance Maneuver. Trans. Soc. Automot. Eng. Jpn. 2015, 46, 1137–1143. [Google Scholar] [CrossRef]
- Nagai, M.; Yamanaka, S.; Hirano, Y. Integrated Control of Active Rear Wheel Steering and Yaw Moment Control Using Braking Forces. JSME Int. J. C Mech. Syst. 1999, 42, 301–308. [Google Scholar] [CrossRef] [Green Version]
- Hirano, Y.; Fukatani, K. Development of Robust Active Rear Steering Control for Automobile. JSME Int. J. C Mech. Syst. 1997, 40, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Horiuchi, S.; Hirao, R.; Okada, K.; Nohtomi, S. Optimal Steering and Braking Control in Emergency Obstacle Avoidance. Trans. Jpn. Soc. Mech. Eng. C 2006, 18, 3250–3255. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, Y.; Furukawa, Y.; Suzuki, T. An Examination of Assist System in the Scene of Collision Avoidance Steer. Trans. Soc. Automot. Eng. Jpn. 2006, 37, 33–38. [Google Scholar]
- Iwano, K.; Raksincharoensak, P.; Nagai, M. A Study on Shared Control between the Driver and an Active Steering Control System in Emergency Obstacle Avoidance Situation. In Proceedings of the IFAC World Congress, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Inoue, S.; Nasu, T.; Hayashi, T.; Sasaki, H.; Inoue, H.; Raksincharoensak, P.; Nagai, M. A Shared-Control-Based Driver Assistance System Using Steering Guidance Torque Combined Direct Yaw-Moment Control. In Proceedings of the 25th Inte·rnational Symposium on Dynamics of Vehicles on Roads and Tracks (IAVSD 2017), Rockhampton, Queensland, Australia, 14–18 August 2017; Volume 1, pp. 135–140. [Google Scholar]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kojima, T.; Raksincharoensak, P. Risk-Sensitive Rear-Wheel Steering Control Method Based on the Risk Potential Field. Appl. Sci. 2021, 11, 7296. https://doi.org/10.3390/app11167296
Kojima T, Raksincharoensak P. Risk-Sensitive Rear-Wheel Steering Control Method Based on the Risk Potential Field. Applied Sciences. 2021; 11(16):7296. https://doi.org/10.3390/app11167296
Chicago/Turabian StyleKojima, Toshinori, and Pongsathorn Raksincharoensak. 2021. "Risk-Sensitive Rear-Wheel Steering Control Method Based on the Risk Potential Field" Applied Sciences 11, no. 16: 7296. https://doi.org/10.3390/app11167296
APA StyleKojima, T., & Raksincharoensak, P. (2021). Risk-Sensitive Rear-Wheel Steering Control Method Based on the Risk Potential Field. Applied Sciences, 11(16), 7296. https://doi.org/10.3390/app11167296





