A Review of Self-Coherent Optical Transceivers: Fundamental Issues, Recent Advances, and Research Directions
Abstract
:1. Introduction
1.1. Review of Related Works
1.2. Contributions
- (i)
- An extensive analysis of the associated short-reach system features and enabling technologies that demand novel transceiver architectures and DSP techniques are presented. In this context, an overview of high-speed short-reach systems regarding their classifications, advanced optoelectronic devices, potential modulation formats, requirements, and challenges are well considered;
- (ii)
- A comprehensive tutorial on the optical transceiver architectures and their classifications based on the DoF is presented. Furthermore, research efforts towards simplified and cost-effective architectures are well discussed. Furthermore, the requirements for a simplified transceiver architectural evolution from 1D to 4D and the related technical challenges are discussed with potential solutions being proffered;
- (iii)
- In addition to a comparison among different detection schemes, we present a detailed SCOH system classification based on the detection schemes, as well as the adopted polarization and modulation schemes at the transmitter. Furthermore, we give a comprehensive discussion of their relative advantages compared to the conventional IM-DD and COH systems. Furthermore, their respective technical limitations are considered, and potential solutions are proffered;
- (iv)
- Moreover, besides the presented comprehensive studies on the carrier and optical SSB signal generation, a distinct classification of the schemes based on the adopted generation approaches is provided. Furthermore, the related features of the schemes are extensively discussed considering the required frequency gap, associated CSPR, achievable SE, required optical filter, and hardware complexity;
- (v)
- Furthermore, apart from an in-depth discussion on the SSBN mitigation concepts, the SSBN mitigation/receiver-based digital linearization schemes for the direct-detection-based systems are clearly presented with the main focus on the performance of transmitter-based EDC (Tx-EDC) and receiver-based EDC (Rx-EDC) systems;
- (vi)
- Moreover, the KK algorithm is comprehensively presented, and due attention is paid to the related effects of different factors such as chromatic dispersion, the optoelectronic frontend, and IQ imbalance on the KK scheme;
- (vii)
- A comprehensive tutorial on various approaches by which the conventional KK system challenges regarding the spectral broadening, high CSPR value, and associated additional sensitivity penalty can be attended to considering factors such as the system complexity and latency is presented;
- (viii)
- Apart from different potential systems for 100 G and beyond applications that have been considered in the other review papers, we also present different SCOH-based experimental demonstrations that are capable of supporting high-speed short- and medium-reach use cases; Furthermore, an overview of recent research and development efforts on the enabling technologies to support 100 Gb/s and beyond (Tb/s) per wavelength is presented;
- (ix)
- Additionally, we address further research directions and future optical network considerations for performance enhancement. In this context, advancement towards high-baud-rate transmission is presented, and the photonic integrated circuit (PIC) exploitation for low-cost, low-power consumption, and low-footprint schemes is comprehensively discussed. We highlight the need for tremendous synergy between photonic technologies and the software-defined networking (SDN) programmability to facilitate the functionalities of flexible transceiver systems that will be able to support the content-aware future transmission systems. An in-depth discussion on how the synergy can facilitate advanced functionalities and ensure full exploitation of photonic technology’s potentialities and available resources is presented.
1.3. Organization
2. Beyond 100 Gb/S Era
2.1. The Need for per Wavelength AIR Enhancement
2.2. Why the Need for a Simplified System?
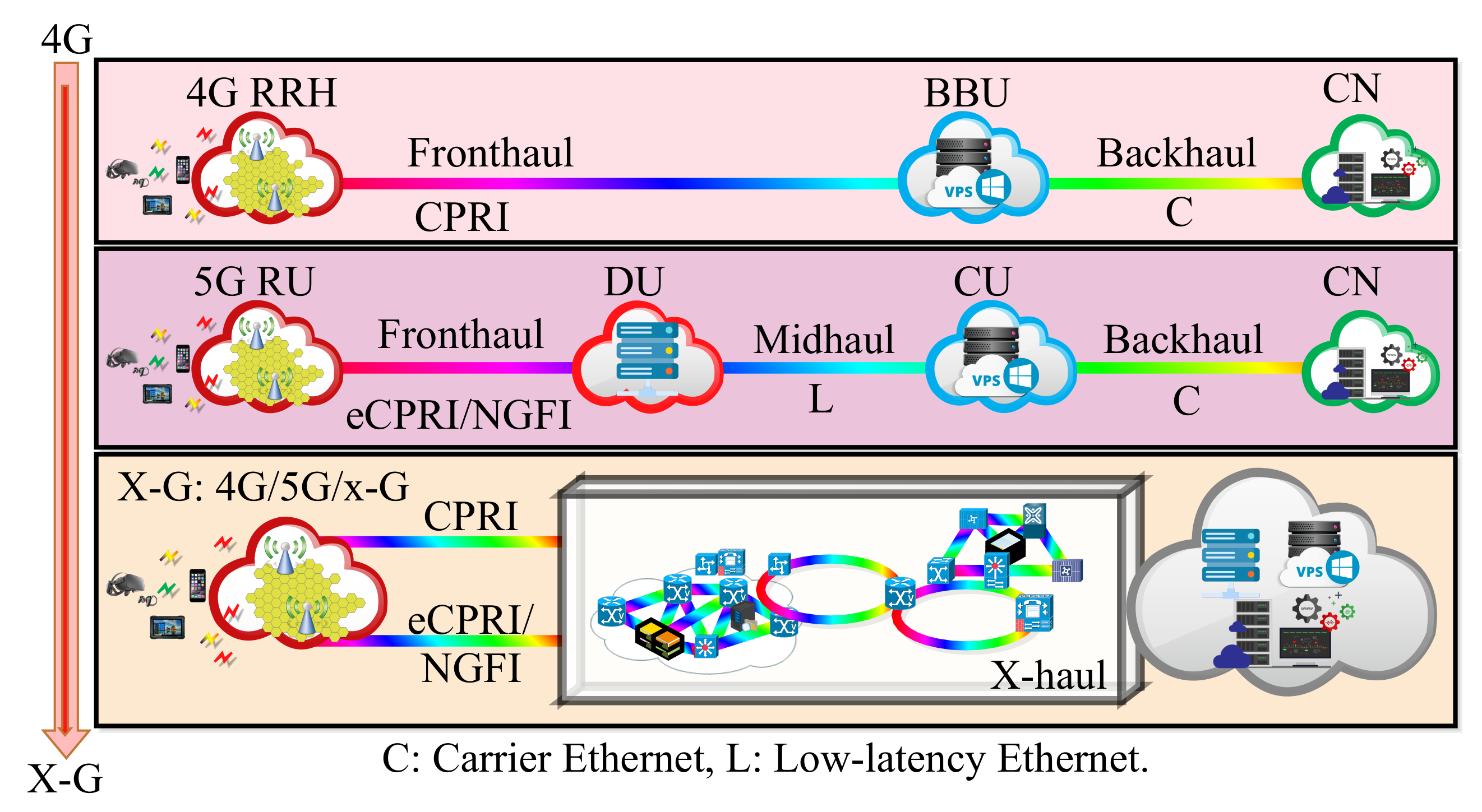
2.3. Ethernet Standards and Optical Transceiver Applications
2.3.1. Optical Transceivers and the Related Ethernet Standards
2.3.2. Ethernet Standards and Optical Transceiver Applications
3. Short-Reach Systems Classification and Enabling Technologies
3.1. Short-Reach Systems’ Overview and Classification
3.1.1. Intra-Data Center or Server-to-Server Links
3.1.2. Inter-Data Center Links
3.1.3. Extended Reach Inter-Data Center, Access, and Metro Links
3.2. Data Center Network Requirements and Challenges
3.2.1. Resilience
3.2.2. Energy Consumption
3.2.3. Traffic
3.2.4. Scalability
3.2.5. Latency
3.3. Enabling Technologies for Short-Reach System
3.3.1. Potential Modulation Formats
Pulse Amplitude Modulation
Carrierless Amplitude and Phase Modulation
Discrete Multitone Modulation
Multicarrier Entropy Loading
Optical Single-Sideband Modulation
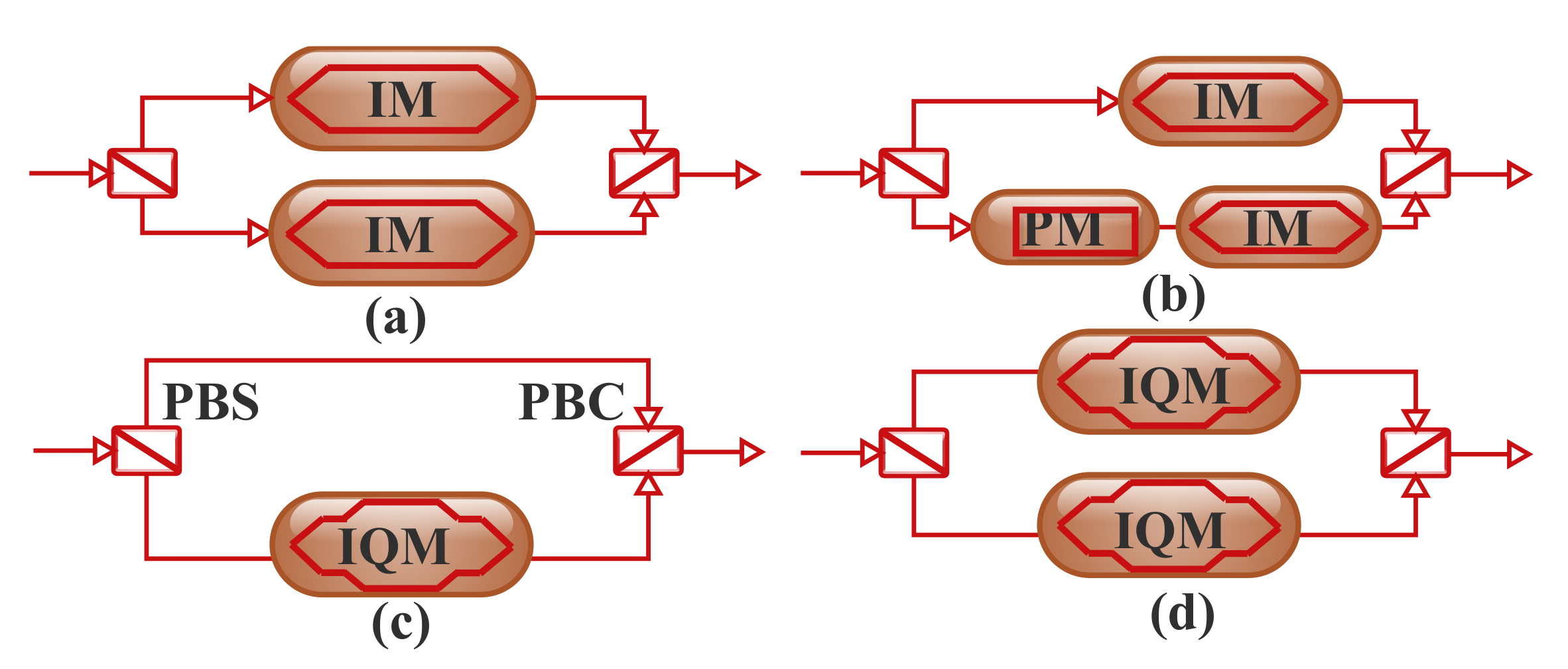
3.3.2. Advanced Optoelectronic Devices for High-Speed DCIs
Vertical-Cavity Surface-Emitting Lasers
Directly Modulated Laser
Mach–Zehnder Modulator
Double-Sided Electro-Absorption Modulated Lasers
Electro-Absorption Modulator Integrated with a Distributed Feedback Laser
Semiconductor Optical Amplifier-PIN/Transimpedance Amplifier Receiver
High-Bandwidth APD Receiver
Optoelectronic Oscillator
3.3.3. Optoelectronic Devices and Modulation Formats’ Applications in the 5G Network
3.3.4. Requirements and Challenges
Cost
Form Factor
Other Challenges of Short-Reach Systems
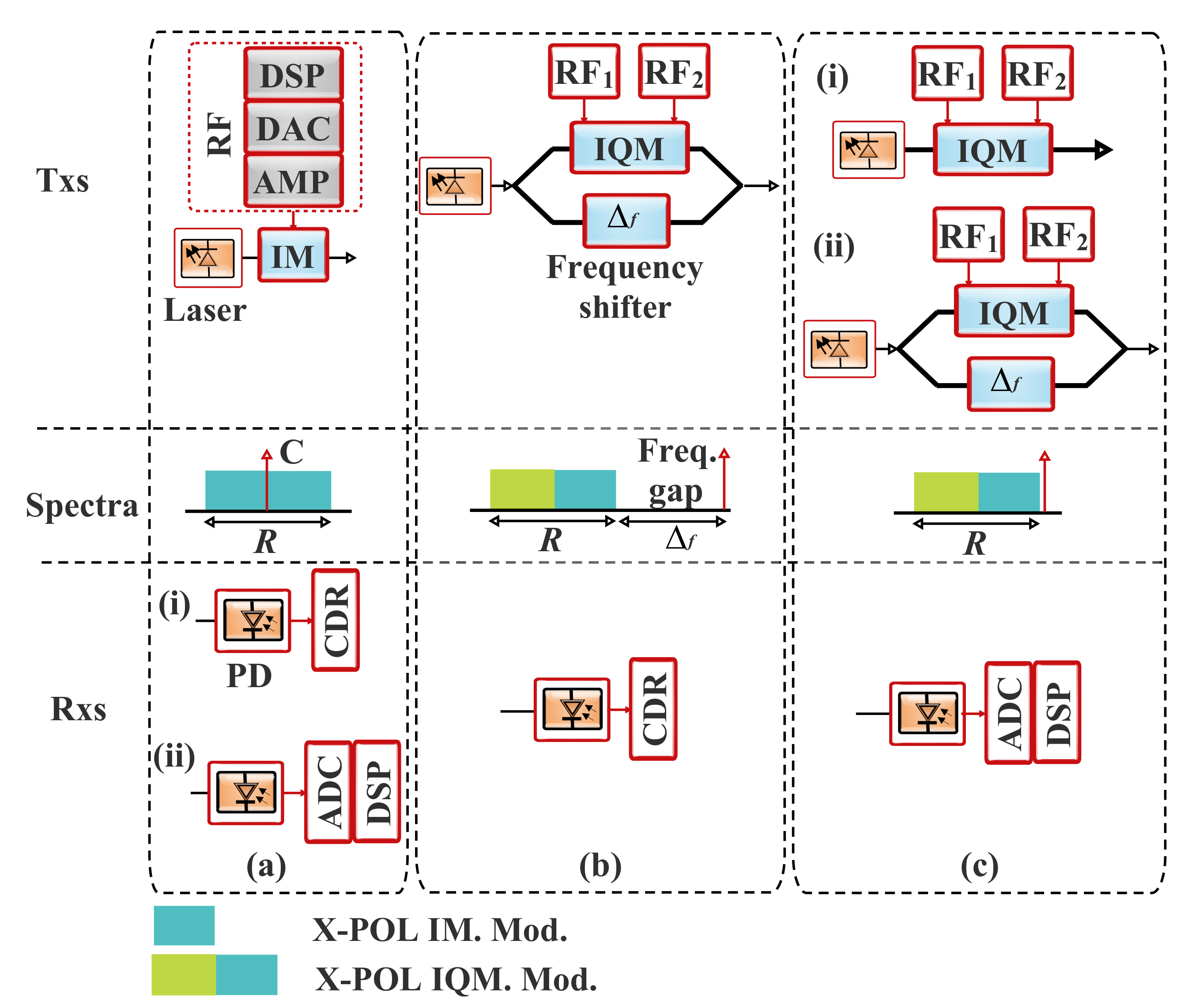
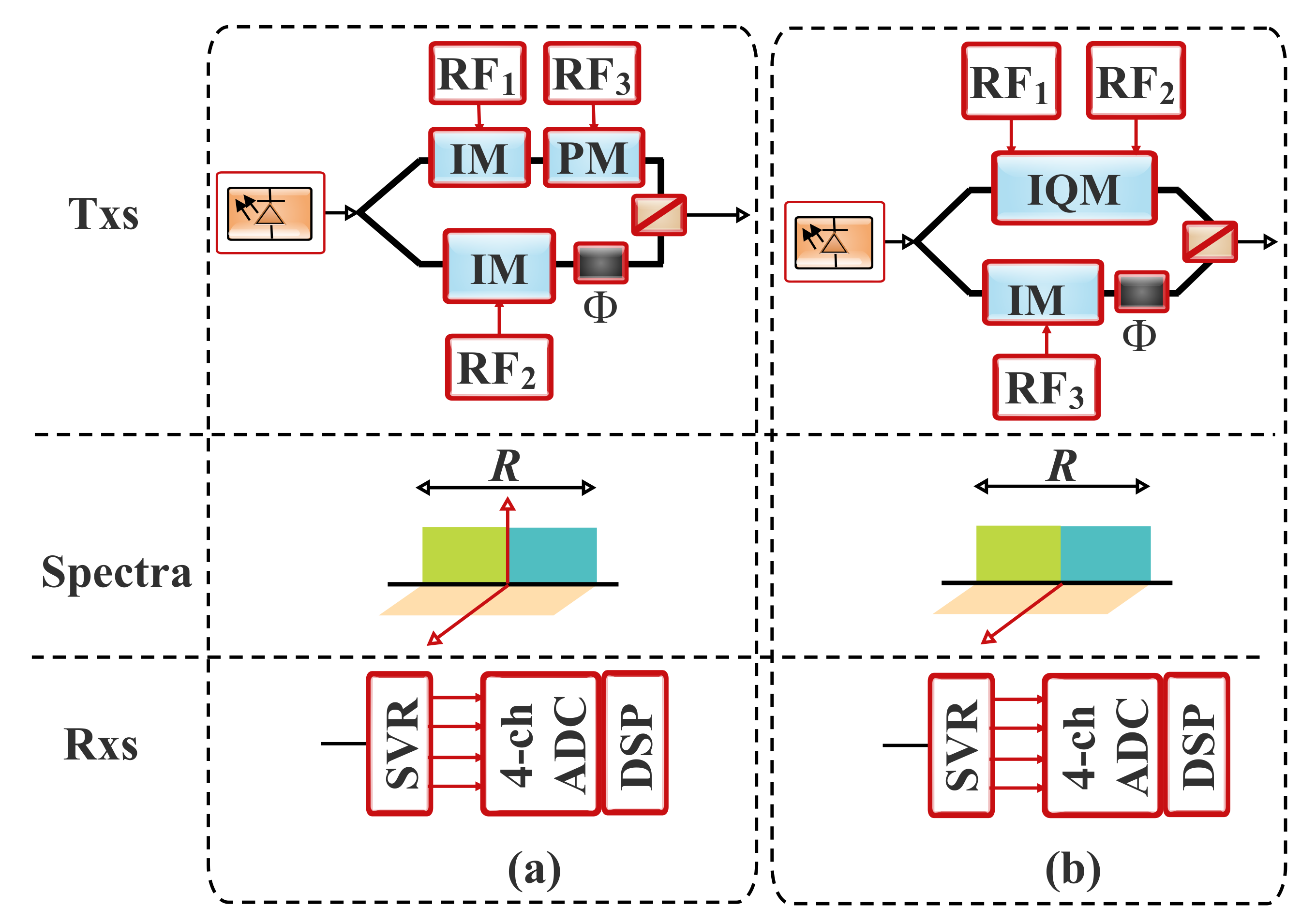
4. SSB Signal Generation and SSBN Mitigation Techniques
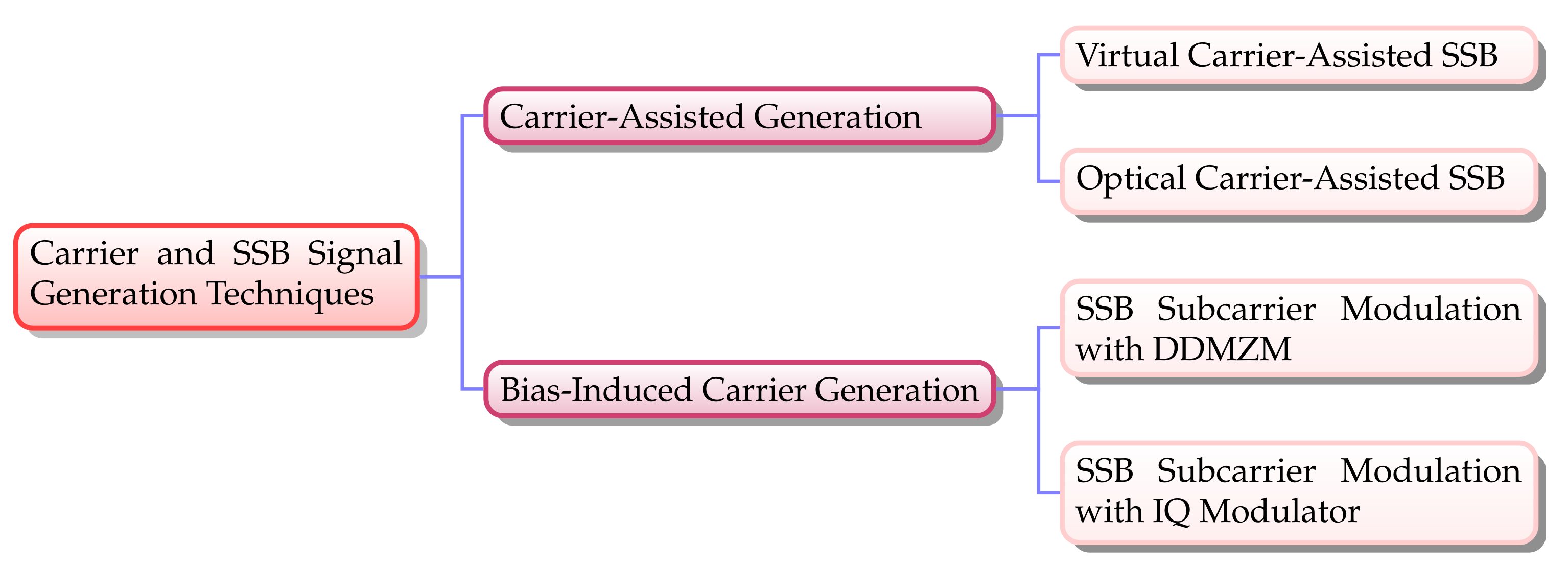
4.1. Carrier and SSB Signal-Generation Techniques
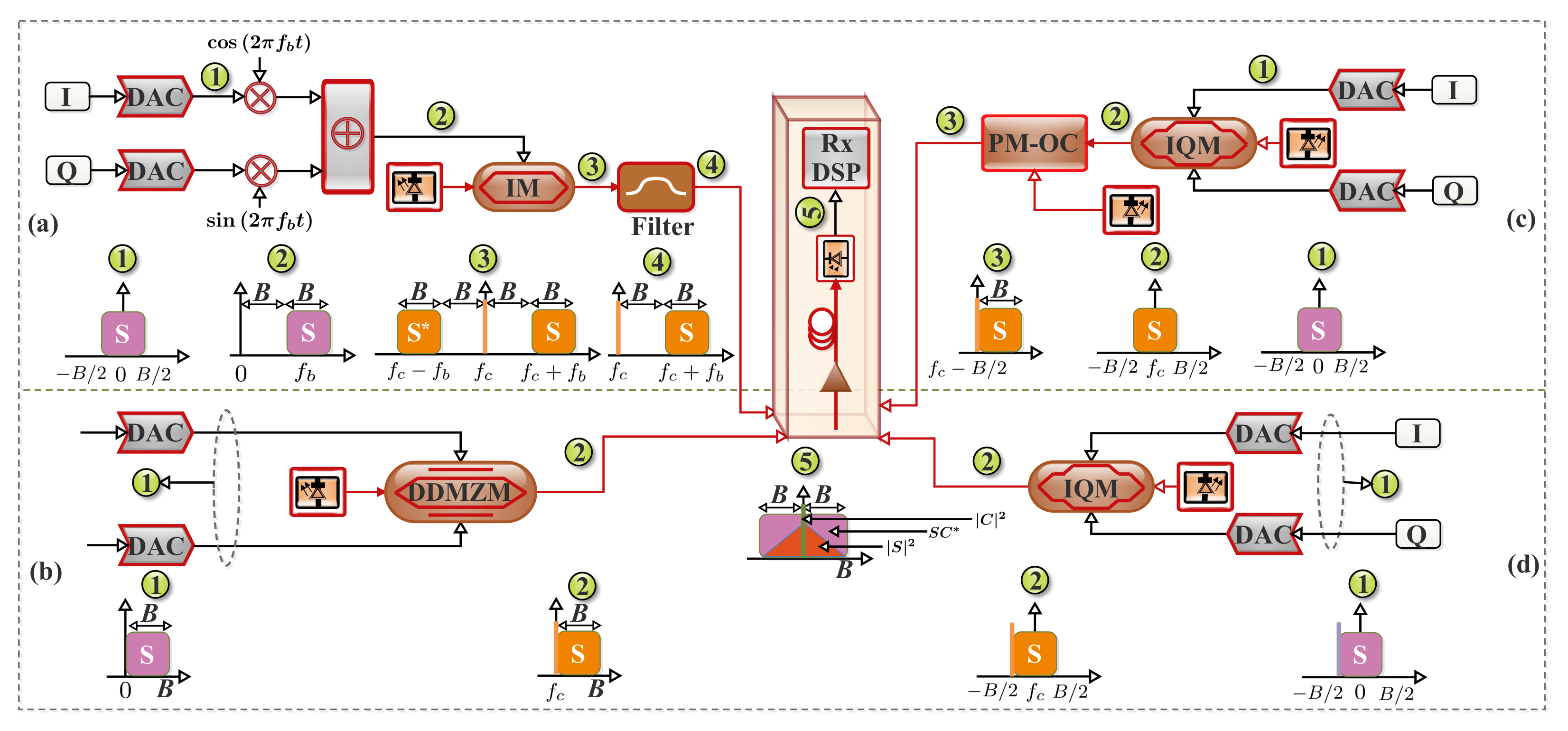
4.1.1. Bias-Induced Carrier Generation Scheme
SSB Subcarrier Modulation with the IQ Modulator
SSB Subcarrier Modulation with the DDMZM
4.1.2. Carrier-Assisted Generation Scheme
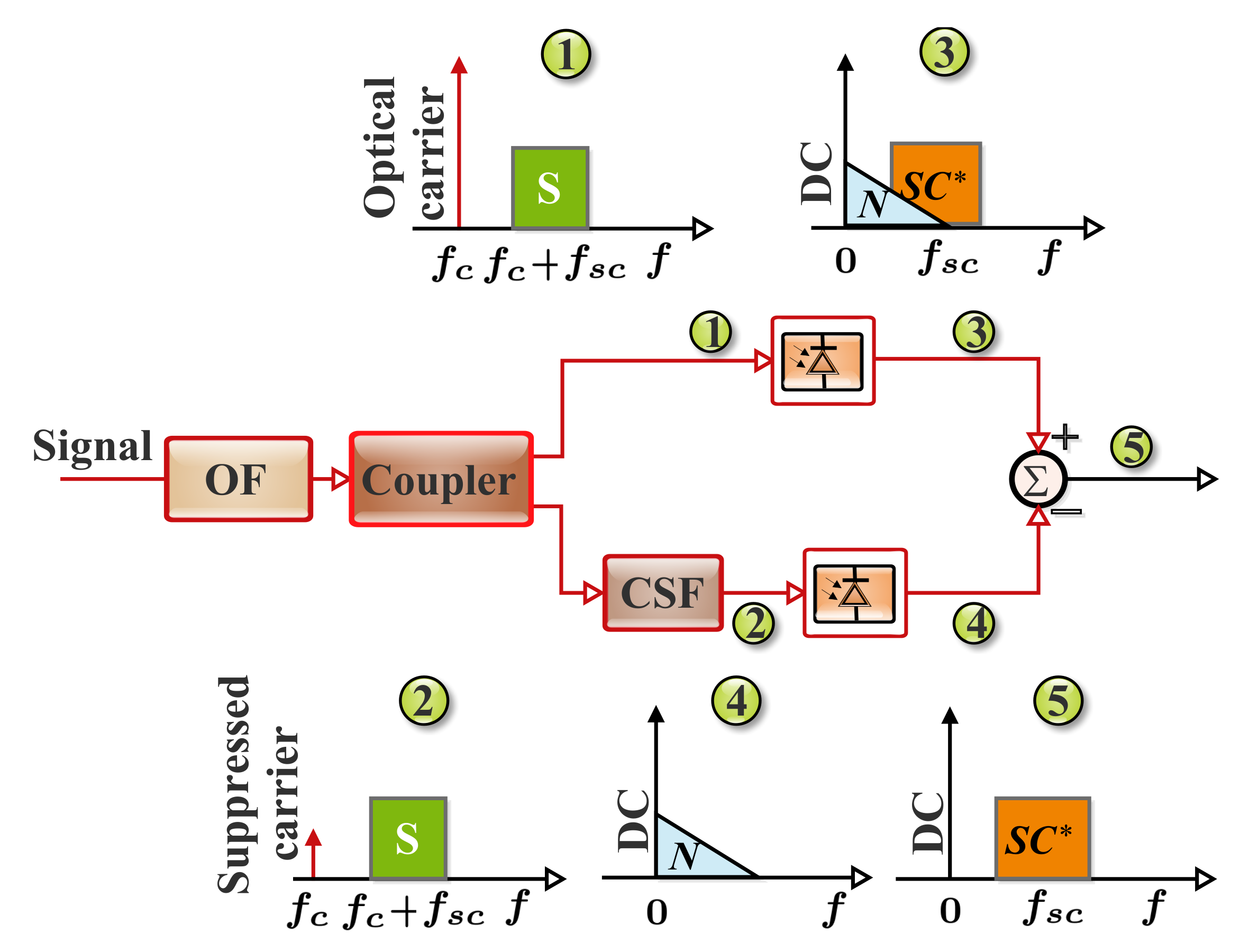
Optical Carrier-Assisted SSB
Virtual Carrier-Assisted SSB
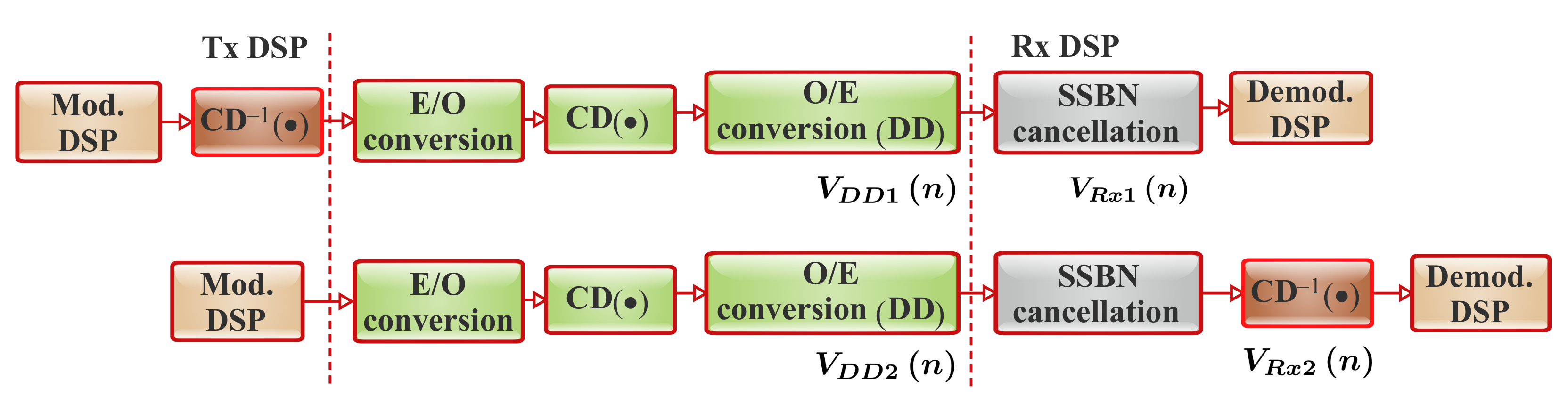
4.2. Optical SSBN Mitigation
4.2.1. Optical SSBN Mitigation Concepts
4.2.2. Optical SSBN Mitigation Approaches
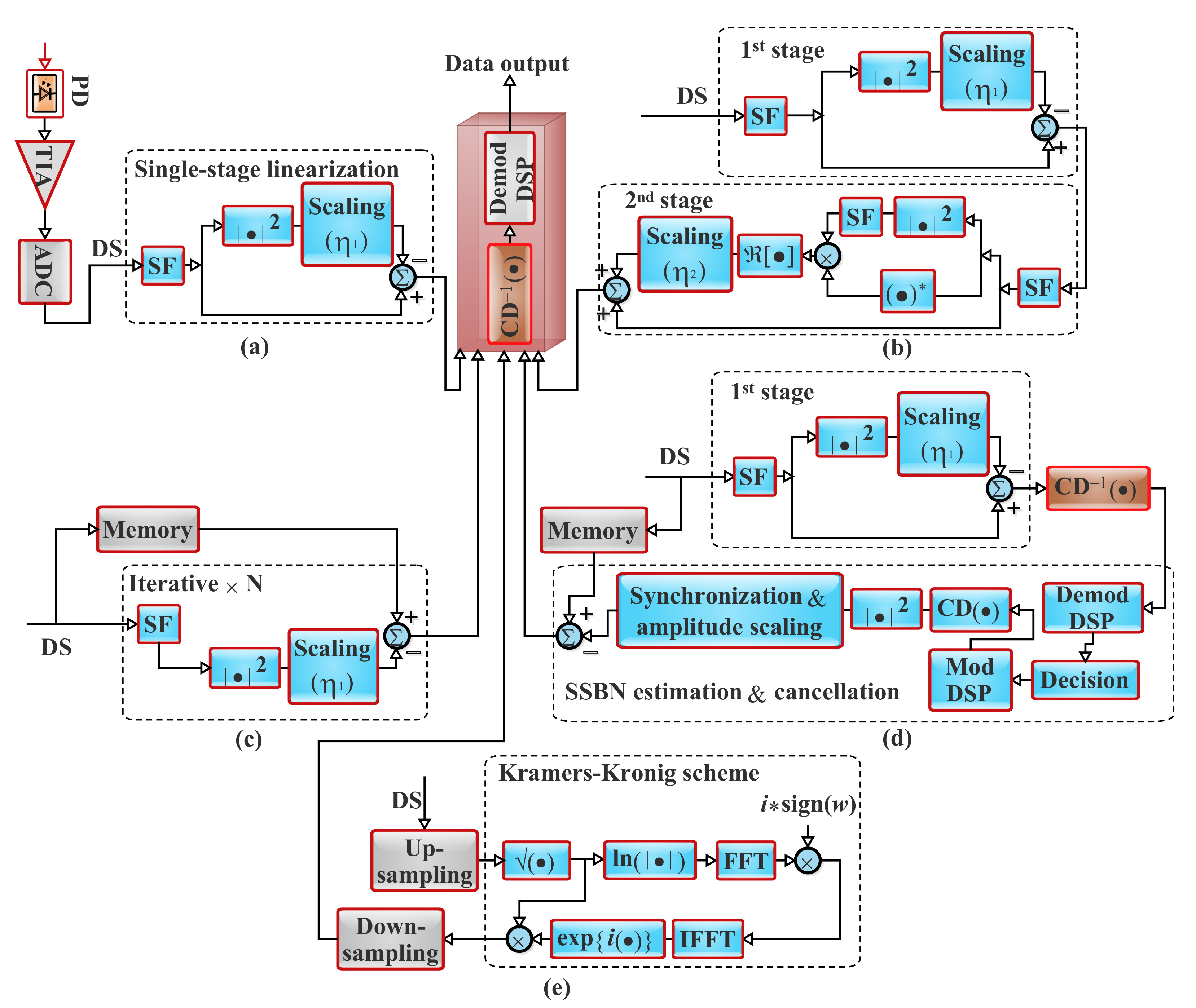
Single-Stage Linearization Filter Approach
Two-Stage Linearization Filter Approach
Iterative Linearization Filter Approach
SSBN Estimation and Cancellation Approach
Kramers–Kronig Approach
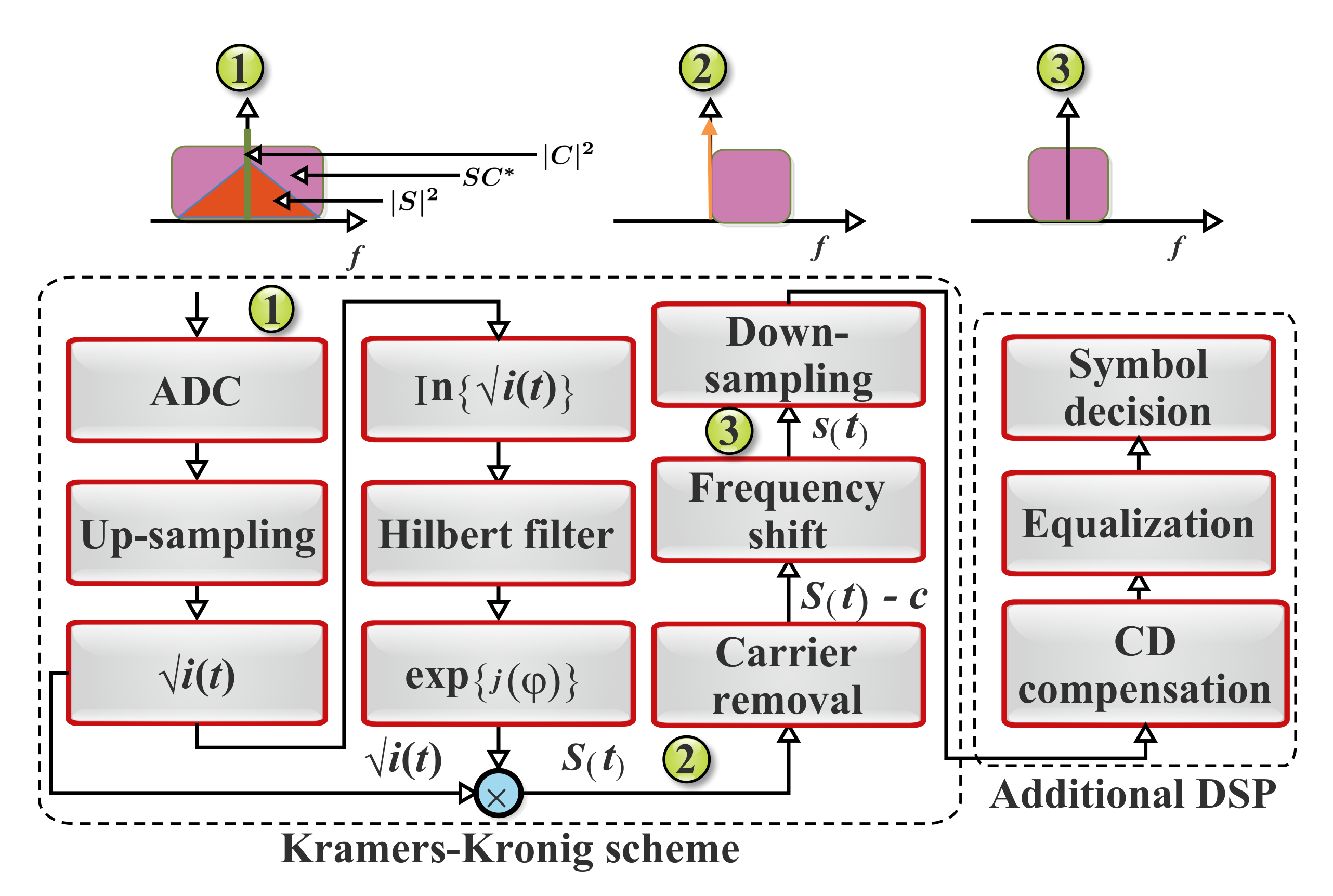
5. Kramers–Kronig Detection Scheme
5.1. Principles of the KK Algorithm
5.1.1. Conventional KK Algorithm
5.1.2. Modified KK Algorithms
5.2. Related Impact on the KK Scheme
5.2.1. Opto-Electronic Frontend
5.2.2. Laser-Related Effects
5.2.3. Fiber Dispersion
5.2.4. IQ Imbalance
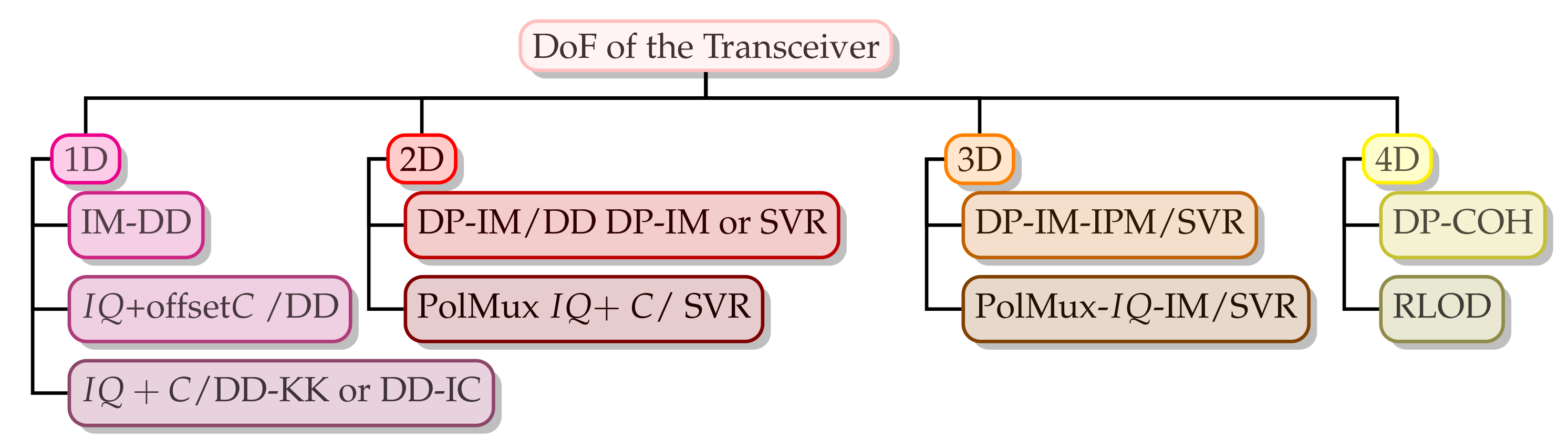
6. Transceiver Architectures’ Classification and Basic Concepts
6.1. 1D-Based Architectures
IM-DD
IG + Offset C/DD
IQ + C/DD-KK or DD-IC
6.2. 2D-Based Architectures
6.2.1. DP-IM/DD DP-IM or the Stokes Vector Receiver
6.2.2. PolMux + Carrier (C)/Stokes Vector Receiver
6.3. 3D-Based Architectures
6.4. 4D-Based Architectures
7. Towards a Simplified Optical Transceiver
7.1. Full Coherent Optical System
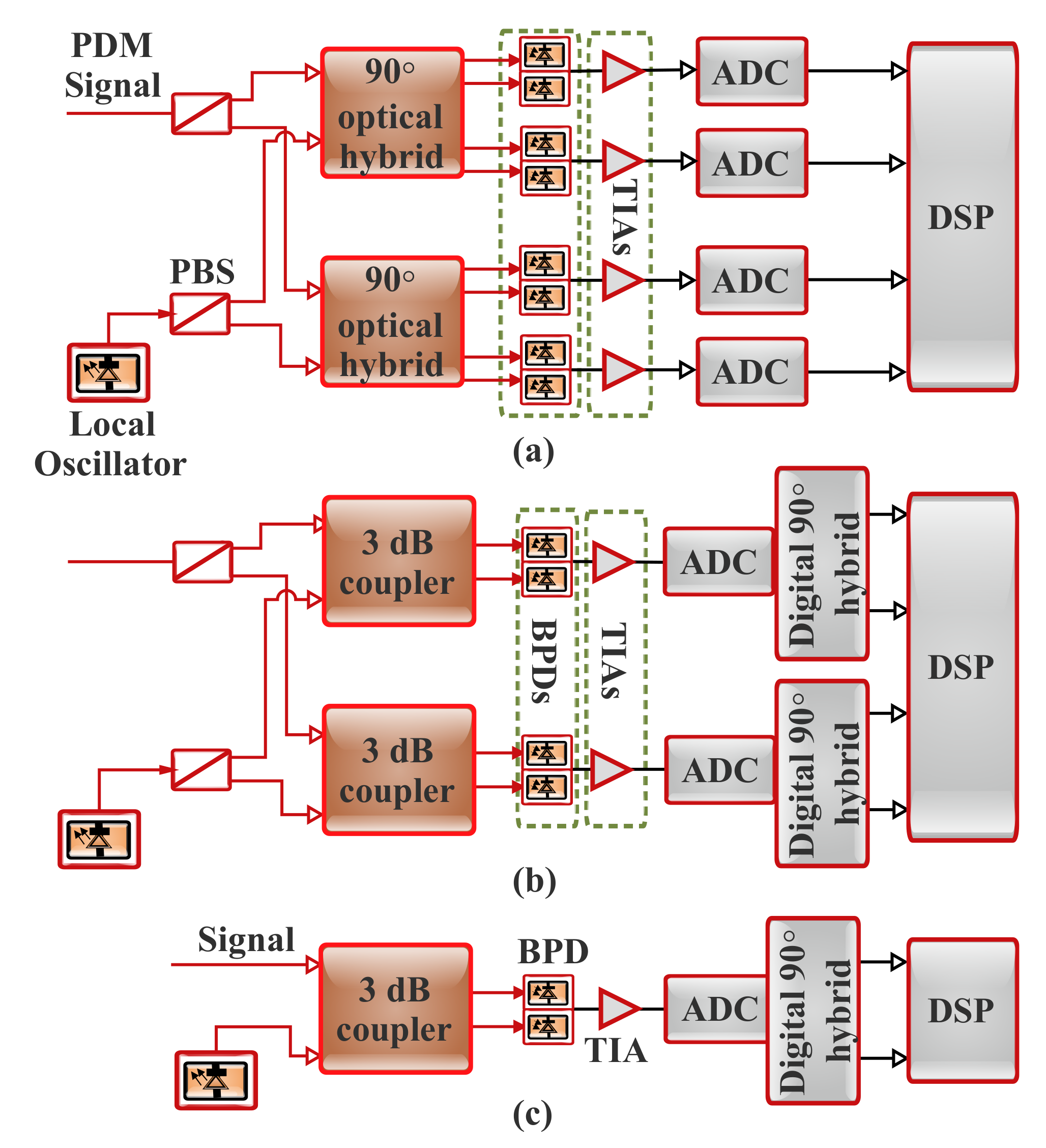
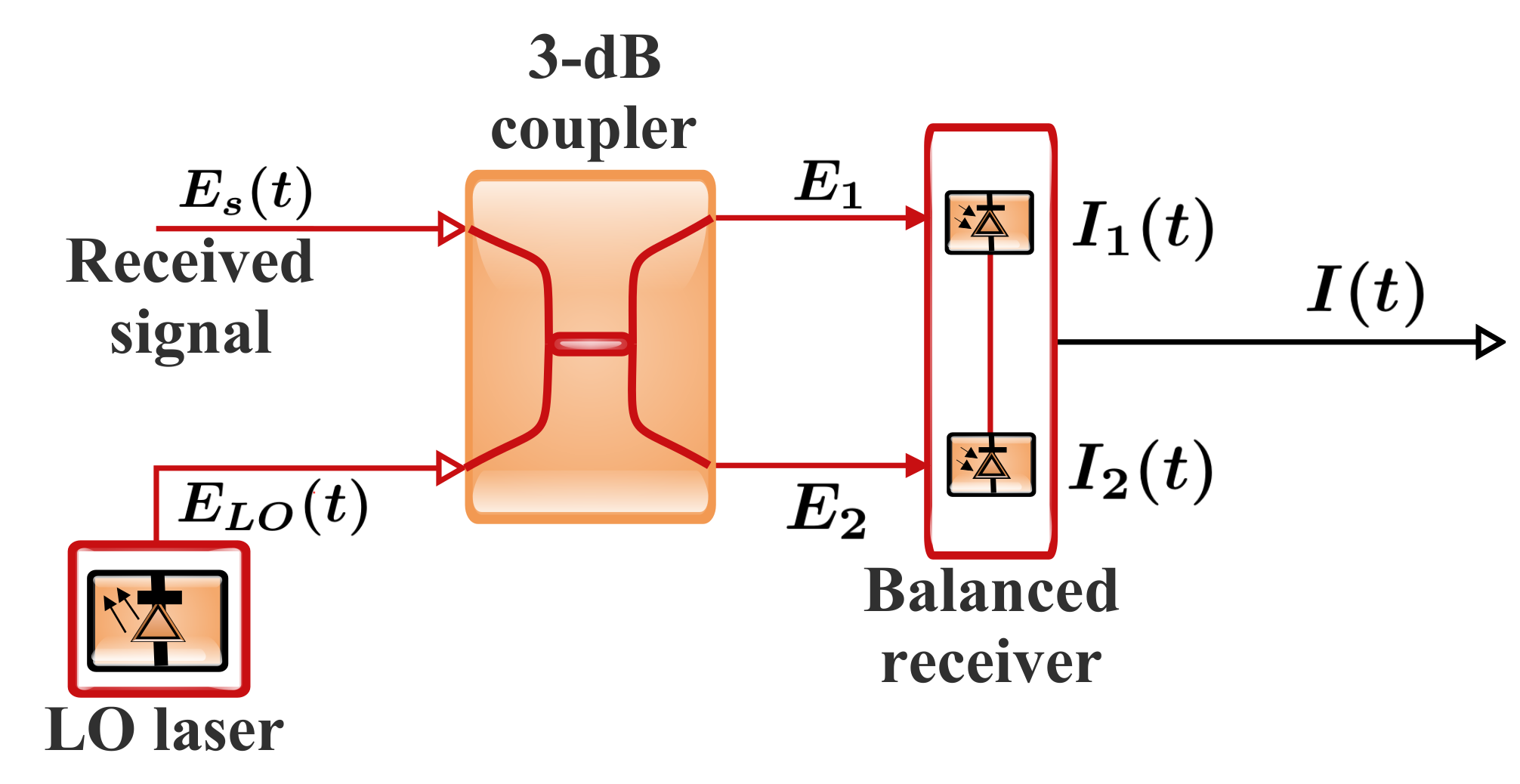
7.1.1. Optical Coherent Receiver Configurations
7.1.2. Optical Coherent Detection Principles
Heterodyne Detection
Homodyne Detection
Phase Diversity
7.2. Simplified Coherent Optical System
7.3. SCOH System Classification
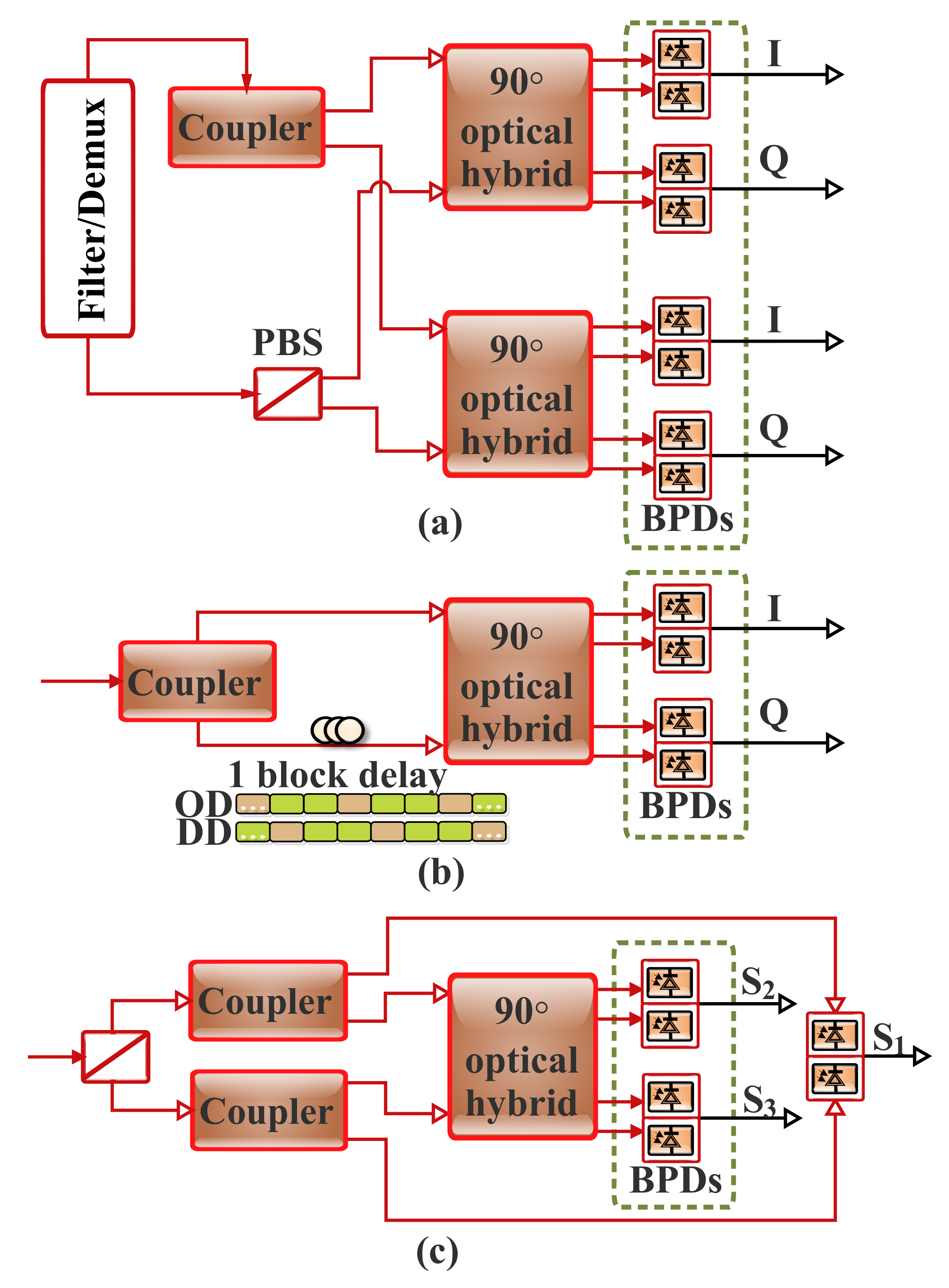
7.3.1. Direct-Detection-Based Single-Ended photodetector
7.3.2. Direct-Detection-Based Balanced Receiver
7.4. Relative Advantages of SCOH Schemes
- There is a significant simplification in the optical hardware, mainly for the optical frontend of the receiver;
- The dual-polarized receiver is highly important in the COH system to enable 2 × 2 MIMO polarization recovery. On the other hand, single-polarization is one of the suitable options in the SCOH for the polarization alignment for the signal and the carrier at the transmitter;
- The required DSP by the receiver is simplified (e.g., no need for the execution of sophisticated carrier recovery);
- The SCOH can be implemented uncooled, while this is challenging in the COH system. The cooling circuitry makes the COH system power-consuming and bulky;
- As an ultimate consequence of the previous itemized advantages, the SCOH-based scheme provides a cost-effective solution compared with the full COH scheme for short- and medium-reach applications.
- The received signal in the SCOH is a linear replica of the transmitted one based on the linear channel that facilitates optical field modulation and detection;
- The copropagated carrier facilitates phase diversity realization and helps increase the receiver sensitivity;
- Since the carrier and the signal are generated through the same laser source, there is considerable assurance that the phases between them are coherent with each other at the transmitter. Consequently, the system’s vulnerability to the laser phase noise is inherently mitigated in the SCOH system;
- A single-carrier IM-DD system is susceptible to ISI and has a transmission distance limitation. These issues can be addressed with the implementation of the SCOH system;
- The SCOH offers a 2D direct detection receiver that helps expand the optical spectrum efficiency. Furthermore, the RF bandwidth utilization ratio at the receiver can reach up to 100% with the DSB modulation;
- The supported optical field modulation in the SCOH system facilitates the DWDM and superchannel implementation.
8. SCOH Transceiver Structures
8.1. Optical Field Representation
8.1.1. Jones Space Representation
8.1.2. Stokes Space Representation
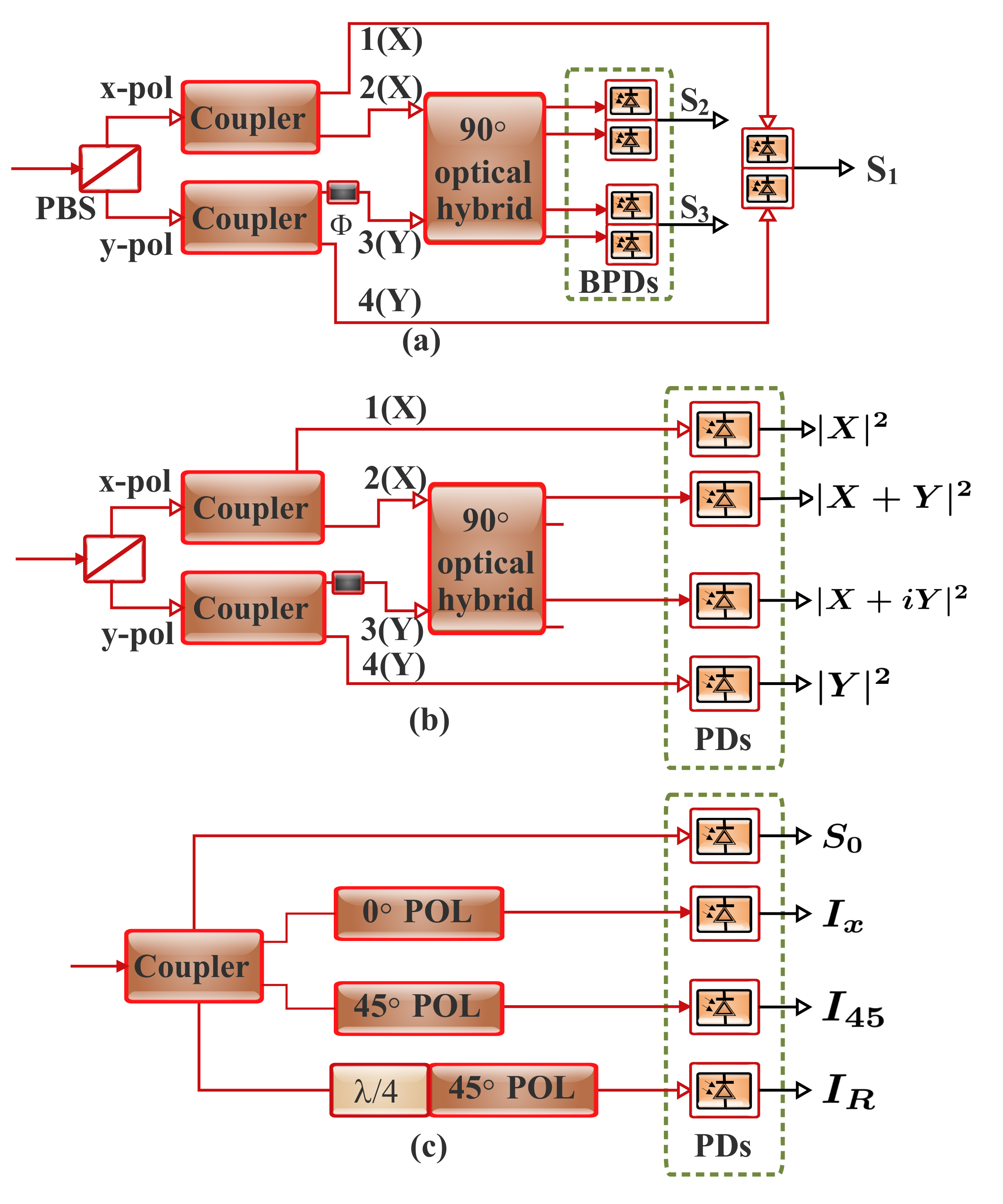
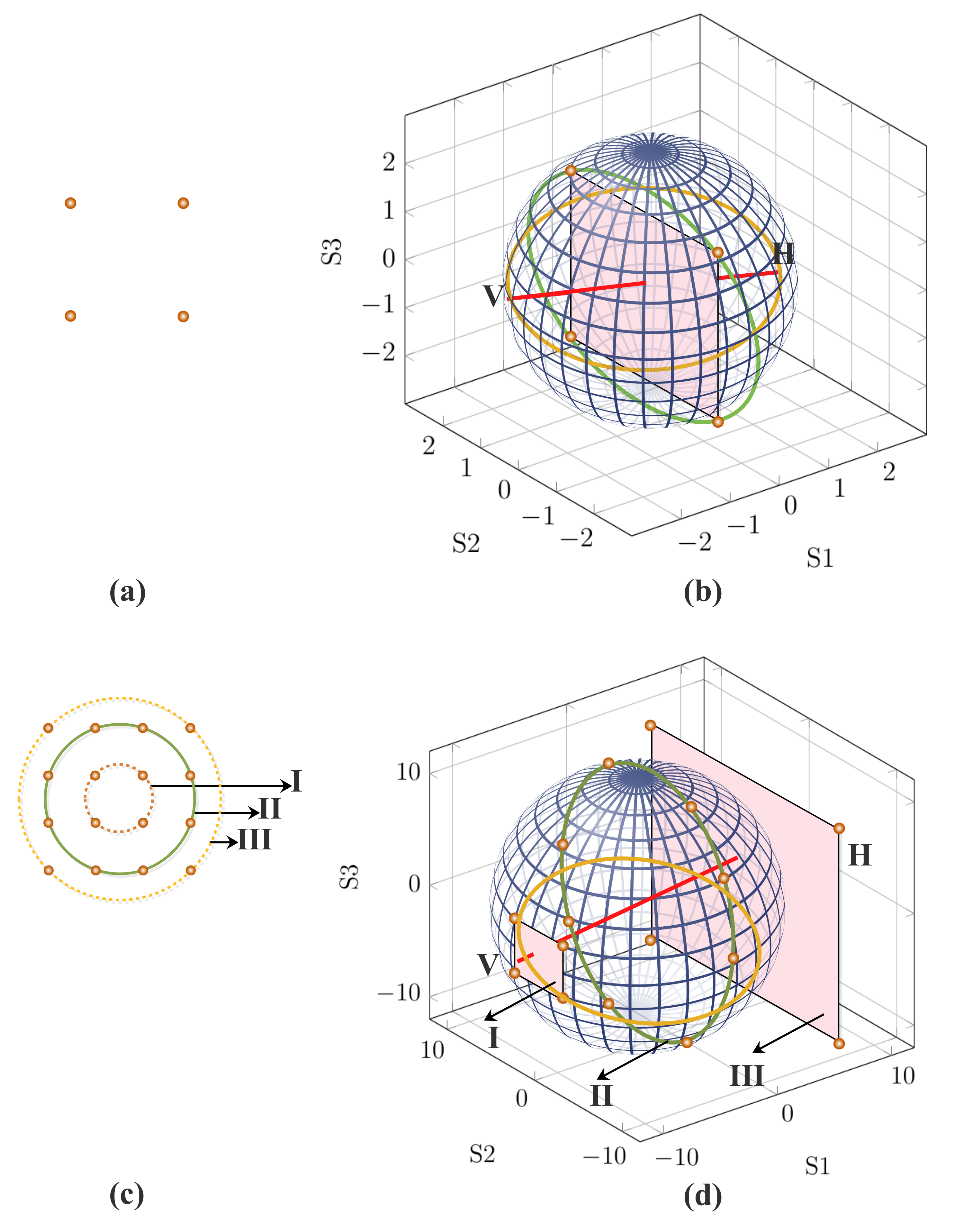
9. Stokes Space Polarization and Field Recovery Principle
9.1. Polarization Recovery Techniques in the Direct Detection Stokes Vector Receiver
9.1.1. Adaptive MIMO Equalization
9.1.2. Training-Assisted Polarization Characterization
9.1.3. Stoke Space Signal-Distribution-Based Polarization Demultiplexing
9.1.4. Analog Polarization Identification
9.2. Stokes Space Field Recovery
9.2.1. 1D Direct Detection-Based Field Recovery
9.2.2. 2D Direct-Detection-Based Field Recovery
Self-Coherent Stokes Space Modulation
Polarization Division Multiplexing Single-Sideband Modulations
9.2.3. 3D Direct-Detection-Based Field Recovery
- The intensity can be recovered, and subsequently, the field X can be retrieved from the intensity information using 1D field recovery;
- Furthermore, the field can then be retrieved.
- The polarization recovery demands field recovery in the Jones space;
- The gapless SSB-FR implementation demands a specified CSPR threshold;
- Furthermore, in a condition whereby the polarization states are arbitrary, it will be highly challenging to guarantee the CSPR beyond the threshold for the entire MIMO dimensions without the polarization recovery.
10. Experimental Implementations
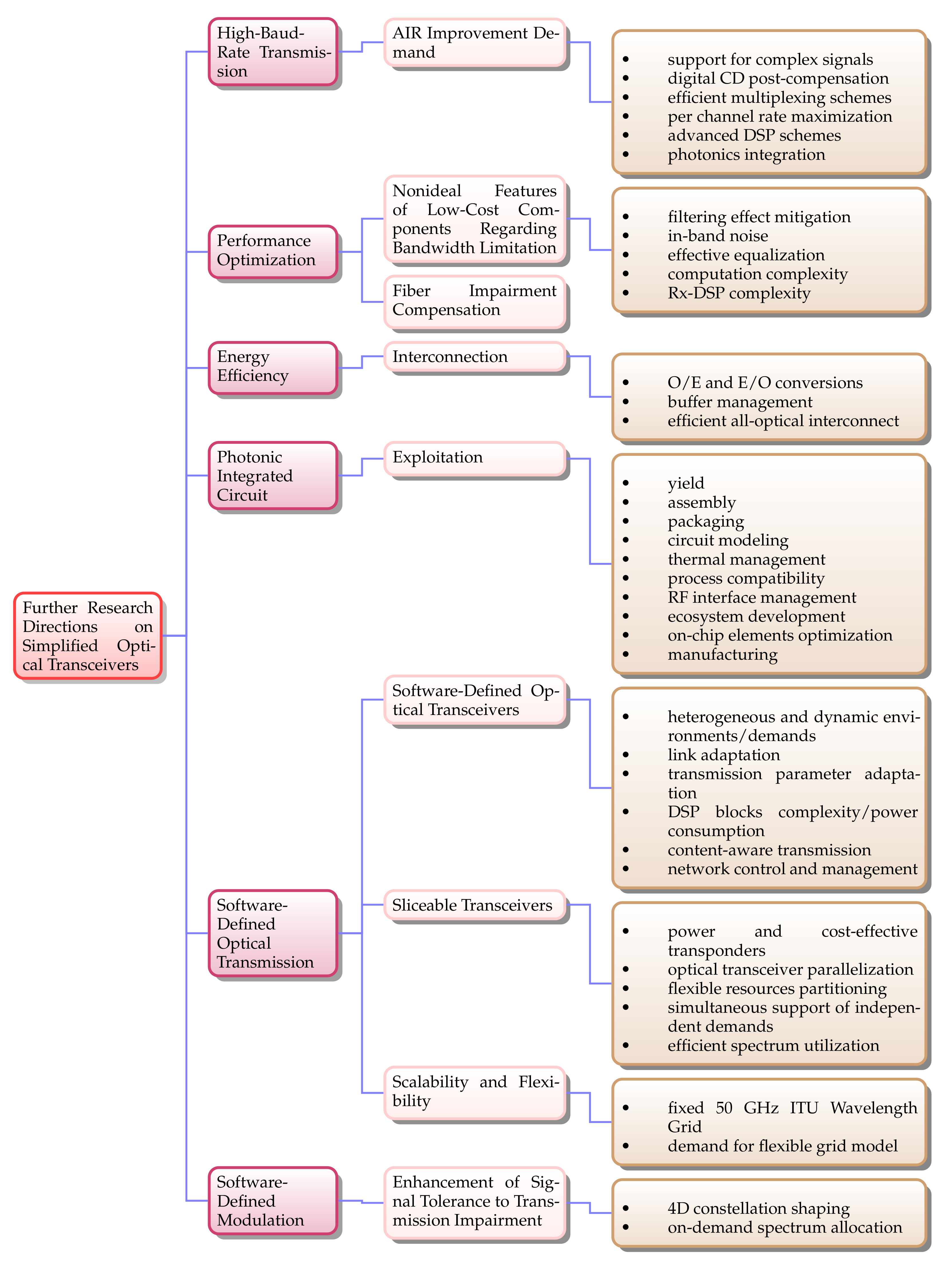
11. Further Research Directions and Future Considerations
11.1. Advancement towards High-Baud-Rate Transmission
11.2. Performance Optimization Issues of Short-Reach Transceivers
11.3. Energy-Efficient Interconnection
11.4. Photonic Integrated Circuit Exploitation
11.5. Software-Defined Optical Transmission
11.5.1. Software-Defined Optical Transceivers
11.5.2. Sliceable Transceivers
11.6. Software-Defined Modulation
12. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alimi, I.A.; Teixeira, A.L.; Monteiro, P.P. Toward an Efficient C-RAN Optical Fronthaul for the Future Networks: A Tutorial on Technologies, Requirements, Challenges, and Solutions. IEEE Commun. Surv. Tutor. 2018, 20, 708–769. [Google Scholar] [CrossRef]
- Muga, N.J.; Patel, R.K.; Alimi, I.; Silva, N.A.; Pinto, A.N. Self-coherent optical detection for access and metro networks. In Proceedings of the 2019 International Conference on Transparent Optical Networks ICTON, Angers, France, 9–13 July 2019; pp. 1–4. [Google Scholar]
- Zhu, Y.; Yi, L.; Yang, B.; Huang, X.; Wey, J.S.; Ma, Z.; Hu, W. Comparative study of cost-effective coherent and direct detection schemes for 100 Gb/s/λ PON. IEEE/OSA J. Opt. Commun. Netw. 2020, 12, D36–D47. [Google Scholar] [CrossRef]
- Alimi, I.A.; Abdalla, A.M.; Olapade Mufutau, A.; Pereira Guiomar, F.; Otung, I.; Rodriguez, J.; Pereira Monteiro, P.; Teixeira, A.L. Energy Efficiency in the Cloud Radio Access Network (C-RAN) for 5G Mobile Networks. In Optical and Wireless Convergence for 5G Networks; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2019; Chapter 11; pp. 225–248. [Google Scholar] [CrossRef]
- Alimi, I.; Shahpari, A.; Sousa, A.; Ferreira, R.; Monteiro, P.; Teixeira, A. Challenges and Opportunities of Optical Wireless Communication Technologies. In Optical Communication Technology; Pinho, P., Ed.; IntechOpen: Rijeka, Croatia, 2017; Chapter 2. [Google Scholar] [CrossRef] [Green Version]
- Balanici, M.; Pachnicke, S. Hybrid electro-optical intra-data center networks tailored for different traffic classes. IEEE/OSA J. Opt. Commun. Netw. 2018, 10, 889–901. [Google Scholar] [CrossRef]
- Erkılınç, M.S.; Lavery, D.; Shi, K.; Thomsen, B.C.; Killey, R.I.; Savory, S.J.; Bayvel, P. Comparison of Low Complexity Coherent Receivers for UDWDM-PONs (λ-to-the-User). J. Light. Technol. 2018, 36, 3453–3464. [Google Scholar] [CrossRef]
- Che, D.; Li, A.; Chen, X.; Hu, Q.; Wang, Y.; Shieh, W. Stokes vector direct detection for short-reach optical communication. Opt. Lett. 2014, 39, 3110–3113. [Google Scholar] [CrossRef] [PubMed]
- Che, D.; Chen, X.; Li, A.; Hu, Q.; Wang, Y.; Shieh, W. Optical Direct Detection for 100 G Short Reach Applications. In Proceedings of the 2014 Asia Communications and Photonics Conference (ACP), Shanghai, China, 11–14 November 2014; pp. 1–3. [Google Scholar]
- Kikuchi, K. Fundamentals of Coherent Optical Fiber Communications. J. Light. Technol. 2016, 34, 157–179. [Google Scholar] [CrossRef]
- Che, D.; Shieh, W. Polarization Demultiplexing for Stokes Vector Direct Detection. J. Light. Technol. 2016, 34, 754–760. [Google Scholar] [CrossRef]
- Che, D.; Hu, Q.; Shieh, W. Linearization of Direct Detection Optical Channels Using Self-Coherent Subsystems. J. Light. Technol. 2016, 34, 516–524. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Optical Field Recovery in Stokes Space. J. Light. Technol. 2019, 37, 451–460. [Google Scholar] [CrossRef]
- Morsy-Osman, M.; Plant, D.V. A Comparative Study of Technology Options for Next Generation Intra- and Inter-datacenter Interconnects. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Altabas, J.A.; Suhr, L.F.; Valdecasa, G.S.; Lazaro, J.A.; Garces, I.; Jensen, J.B.; Clausen, A.T. 25 Gbps Quasicoherent Receiver for Beyond NG-PON2 Access Networks. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Wei, J.; Cheng, Q.; Penty, R.V.; White, I.H.; Cunningham, D.G. 400 Gigabit Ethernet using advanced modulation formats: Performance, complexity, and power dissipation. IEEE Commun. Mag. 2015, 53, 182–189. [Google Scholar] [CrossRef]
- Chagnon, M. Optical Communications for Short Reach. J. Light. Technol. 2019, 37, 1779–1797. [Google Scholar] [CrossRef]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Kramers–Kronig coherent receiver. Optica 2016, 3, 1220–1227. [Google Scholar] [CrossRef]
- Chen, X.; Antonelli, C.; Chandrasekhar, S.; Raybon, G.; Mecozzi, A.; Shtaif, M.; Winzer, P. Kramers–Kronig Receivers for 100-km Datacenter Interconnects. J. Light. Technol. 2018, 36, 79–89. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Maximizing the spectral efficiency of Stokes vector receiver with optical field recovery. Opt. Express 2018, 26, 28976–28981. [Google Scholar] [CrossRef] [PubMed]
- Füllner, C.; Adib, M.M.H.; Wolf, S.; Kemal, J.N.; Freude, W.; Koos, C.; Randel, S. Complexity Analysis of the Kramers–Kronig Receiver. J. Light. Technol. 2019, 37, 4295–4307. [Google Scholar] [CrossRef]
- Li, Z.; Sezer Erkılınç, M.; Shi, K.; Sillekens, E.; Galdino, L.; Xu, T.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. Digital Linearization of Direct-Detection Transceivers for Spectrally Efficient 100 Gb/s/λ WDM Metro Networking. J. Light. Technol. 2018, 36, 27–36. [Google Scholar] [CrossRef]
- Che, D.; Li, A.; Chen, X.; Hu, Q.; Wang, Y.; Shieh, W. 160-Gb/s stokes vector direct detection for short reach optical communication. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Che, D.; Li, A.; Chen, X.; Hu, Q.; Wang, Y.; Shieh, W. Stokes Vector Direct Detection for Linear Complex Optical Channels. J. Light. Technol. 2015, 33, 678–684. [Google Scholar] [CrossRef]
- Morsy-Osman, M.; Chagnon, M.; Plant, D.V. Four-Dimensional Modulation and Stokes Direct Detection of Polarization Division Multiplexed Intensities, Inter Polarization Phase and Inter Polarization Differential Phase. J. Light. Technol. 2016, 34, 1585–1592. [Google Scholar] [CrossRef]
- Hoang, T.; Sowailem, M.; Zhuge, Q.; Osman, M.; Samani, A.; Paquet, C.; Paquet, S.; Woods, I.; Plant, D. Enabling High-Capacity Long-Reach Direct Detection Transmission With QAM-PAM Stokes Vector Modulation. J. Light. Technol. 2018, 36, 460–467. [Google Scholar] [CrossRef]
- Che, D.; Yuan, F.; Shieh, W. 200-Gb/s polarization-multiplexed DMT using stokes vector receiver with frequency-domain MIMO. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Presi, M.; Cossu, G.; Contestabile, G.; Ciaramella, E.; Antonelli, C.; Mecozzi, A.; Shtaif, M. Transmission in 125-km SMF with 3.9 bit/s/Hz Spectral Efficiency Using a Single-drive MZM and a Direct-detection Kramers–Kronig Receiver without Optical CD Compensation. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Li, Z.; Erkılınç, M.S.; Shi, K.; Sillekens, E.; Galdino, L.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. SSBI Mitigation and the Kramers–Kronig Scheme in Single-Sideband Direct-Detection Transmission With Receiver-Based Electronic Dispersion Compensation. J. Light. Technol. 2017, 35, 1887–1893. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Erkilinç, M.S.; Shi, K.; Sillekens, E.; Galdino, L.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. Joint Optimisation of Resampling Rate and Carrier-to-Signal Power Ratio in Direct-Detection Kramers–Kronig Receivers. In Proceedings of the 2017 European Conference on Optical Communication (ECOC), Gothenburg, Sweden, 17–21 September 2017; pp. 1–3. [Google Scholar] [CrossRef] [Green Version]
- Randel, S.; Pilori, D.; Chandrasekhar, S.; Raybon, G.; Winzer, P. 100-Gb/s discrete-multitone transmission over 80-km SSMF using single-sideband modulation with novel interference-cancellation scheme. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Altabas, J.A.; Izquierdo, D.; Lazaro, J.A.; Garces, I. Cost-Effective Transceiver Based on an RSOA and a VCSEL for Flexible uDWDM Networks. IEEE Photonics Technol. Lett. 2016, 28, 1111–1114. [Google Scholar] [CrossRef]
- Morsy-Osman, M.; Chagnon, M.; Poulin, M.; Lessard, S.; Plant, D.V. 1λ× 224 Gb/s 10 km transmission of polarization division multiplexed PAM-4 signals using 1.3 μm SiP intensity modulator and a direct-detection MIMO-based receiver. In Proceedings of the 2014 The European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Chagnon, M.; Lessard, S.; Plant, D.V. 336 Gb/s in Direct Detection Below KP4 FEC Threshold for Intra Data Center Applications. IEEE Photonics Technol. Lett. 2016, 28, 2233–2236. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Huo, J.; Yu, C.; Lu, C.; Lau, A.P.T. Digital Signal Processing for Short-Reach Optical Communications: A Review of Current Technologies and Future Trends. J. Light. Technol. 2018, 36, 377–400. [Google Scholar] [CrossRef]
- Rasmussen, J.C.; Takahara, T.; Tanaka, T.; Kai, Y.; Nishihara, M.; Drenski, T.; Li, L.; Yan, W.; Tao, Z. Digital signal processing for short reach optical links. In Proceedings of the 2014 The European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Hoang, T.; Sowailem, M.; Osman, M.; Paquet, C.; Paquet, S.; Woods, I.; Zhuge, Q.; Plant, D.V. 280-Gb/s 320-km transmission of polarization division multiplexed QAM-PAM with stokes vector receiver. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Shieh, W.; Che, D. Optical Field Recovery via Stokes Vector Direct Detection. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Li, A.; Che, D.; Chen, V.; Shieh, W. Spectrally efficient optical transmission based on Stokes vector direct detection. Opt. Express 2014, 22, 15662–15667. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Li, A.; Che, D.; Hu, Q.; Wang, Y.; He, J.; Shieh, W. Block-wise phase switching for double-sideband direct detected optical OFDM signals. Opt. Express 2013, 21, 13436–13441. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Li, Z.; Wen, Y.; Peng, W.; Cui, Y.; Bai, Y. 192-Gb/s 160-km transmission of carrier-assisted dual- polarization signal with Stokes vector direct detection. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition (OFC), Anaheim, CA, USA, 20–24 March 2016; pp. 1–3. [Google Scholar]
- Pang, X.; Ozolins, O.; Lin, R.; Zhang, L.; Udalcovs, A.; Xue, L.; Schatz, R.; Westergren, U.; Xiao, S.; Hu, W.; et al. 200 Gbps/Lane IM/DD Technologies for Short Reach Optical Interconnects. J. Light. Technol. 2020, 38, 492–503. [Google Scholar] [CrossRef] [Green Version]
- Mecozzi, A.; Antonelli, C.; Shtaif, M. Kramers–Kronig receivers. Adv. Opt. Photonics 2019, 11, 480–517. [Google Scholar] [CrossRef]
- Bo, T.; Kim, H. Toward Practical Kramers–Kronig Receiver: Resampling, Performance, and Implementation. J. Light. Technol. 2019, 37, 461–469. [Google Scholar] [CrossRef]
- Bo, T.; Kim, H. Kramers–Kronig Receiver Without Digital Upsampling. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Bo, T.; Kim, H. Kramers–Kronig receiver operable without digital upsampling. Opt. Express 2018, 26, 13810–13818. [Google Scholar] [CrossRef]
- Kahn, J.M.; Ho, K. Spectral efficiency limits and modulation/detection techniques for DWDM systems. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 259–272. [Google Scholar] [CrossRef] [Green Version]
- An, S.; Zhu, Q.; Li, J.; Su, Y. Accurate Field Reconstruction at Low CSPR Condition Based on a Modified KK Receiver with Direct Detection. J. Light. Technol. 2019, 1. [Google Scholar] [CrossRef]
- Blech, L.; Eldar, Y.; Antonelli, C.; Mecozzi, A.; Shtaif, M. The Enhanced Kramers Kronig Receiver. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Lyu, M.; Shi, W.; Rusch, L.A. SiP Alternative to Enhanced KK for OFDM. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Sun, C.; Che, D.; Ji, H.; Shieh, W. Towards Low Carrier-to-Signal Power Ratio for Kramers–Kronig Receiver. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- An, S.; Zhu, Q.; Li, J.; Su, Y. Modified KK Receiver with Accurate Field Reconstruction at Low CSPR Condition. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Zhou, X.; Huo, J.; Zhong, K.; Khan, F.N.; Gui, T.; Zhang, H.; Tu, J.; Yuan, J.; Long, K.; Yu, C.; et al. Single Channel 50 Gbit/s Transmission Over 40 km SSMF Without Optical Amplification and In-Line Dispersion Compensation Using a Single-End PD-Based PDM-SSB-DMT System. IEEE Photonics J. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Zhu, Y.; Jiang, M.; Zhang, F. Direct detection of polarization multiplexed single sideband signals with orthogonal offset carriers. Opt. Express 2018, 26, 15887–15898. [Google Scholar] [CrossRef]
- Lu, D.; Zhou, X.; Huo, J.; Gao, J.; Yang, Y.; He, K.; Yuan, J.; Long, K.; Yu, C.; Lau, A.P.T.; et al. Theoretical CSPR Analysis and Performance Comparison for Four Single-Sideband Modulation Schemes With Kramers–Kronig Receiver. IEEE Access 2019, 7, 166257–166267. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.; Chen, C.; Jin, W.; Zhong, X.; Qiu, K. Digital chromatic dispersion pre-management for SSB modulation direct-detection optical transmission systems. Opt. Commun. 2018, 427, 551–556. [Google Scholar] [CrossRef]
- Le, S.T.; Schuh, K.; Dischler, R.; Buchali, F.; Schmalen, L.; Buelow, H. Beyond 400 Gb/s Direct Detection over 80km for Data Center Interconnect Applications. J. Light. Technol. 2019, 1. [Google Scholar] [CrossRef]
- Zou, K.; Zhu, Y.; Zhang, F.; Chen, Z. Spectrally efficient terabit optical transmission with Nyquist 64-QAM half-cycle subcarrier modulation and direct detection. Opt. Lett. 2016, 41, 2767–2770. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Erkilinc, M.S.; Maher, R.; Galdino, L.; Shi, K.; Thomsen, B.C.; Bayvel, B.; Killey, R.I. Reach Enhancement for WDM Direct-Detection Subcarrier Modulation using Low-Complexity Two-Stage Signal-Signal Beat Interference Cancellation. In Proceedings of the ECOC 2016, 42nd European Conference on Optical Communication, Dusseldorf, Germany, 18–22 September 2016; pp. 1–3. [Google Scholar]
- Cano, I.N.; Lerin, A.; Polo, V.; Prat, J. Direct Phase Modulation DFBs for Cost-Effective ONU Transmitter in udWDM PONs. IEEE Photonics Technol. Lett. 2014, 26, 973–975. [Google Scholar] [CrossRef]
- Li, Z.; Erkılınç, M.S.; Shi, K.; Sillekens, E.; Galdino, L.; Xu, T.; Thomsen, B.C.; Bayvel, P.; Killey, R.I. Spectrally Efficient 168 Gb/s/λ WDM 64-QAM Single-Sideband Nyquist-Subcarrier Modulation With Kramers–Kronig Direct-Detection Receivers. J. Light. Technol. 2018, 36, 1340–1346. [Google Scholar] [CrossRef]
- Winterling, P. 100 Gigabit Ethernet—Fundamentals, Trends, and Measurement Requirements; White Paper; Viavi Solutions, Inc.: San Jose, CA, USA, 2015. [Google Scholar]
- Morsy-Osman, M.; Chagnon, M.; Poulin, M.; Lessard, S.; Plant, D.V. 224-Gb/s 10-km Transmission of PDM PAM-4 at 1.3 μm Using a Single Intensity-Modulated Laser and a Direct-Detection MIMO DSP-Based Receiver. J. Light. Technol. 2015, 33, 1417–1424. [Google Scholar] [CrossRef]
- Maniloff, E.; Gareau, S.; Moyer, M. 400 G and Beyond: Coherent Evolution to High-Capacity Inter Data Center Links. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Winzer, P.J. Beyond 100 G Ethernet. IEEE Commun. Mag. 2010, 48, 26–30. [Google Scholar] [CrossRef]
- Vernekar, A. Understanding 10G to 400 G Ethernet Speeds, Transceivers, and Selecting the Correct Fiber Optic Connectivity for Your Data Center; White Paper; AFL Hyperscale: Milton Keynes, UK, 2020. [Google Scholar]
- Cisco MDS 9000 Family Pluggable Transceivers; Data Sheet; Cisco: San Jose, CA, USA, 2017.
- Nokia. Mobile Transport Convergence Using Deterministic Time-Sensitive Networks. 2019. Available online: https://onestore.nokia.com/asset/206838 (accessed on 15 January 2021).
- Cisco. The Importance of Industrial Temperature Optics for Reliable Network Connectivity; White Paper; Cisco: San Jose, CA, USA, 2021. [Google Scholar]
- FiberStamp. Optical Transceivers Solution for 5G Fronthaul/Backhaul Bearer Network; Data Sheet; FiberStamp: Taiwan, China, 2020. [Google Scholar]
- FS. 400 G QSFP-DD; Data Sheet; FS: New Castle, DE, USA, 2020. [Google Scholar]
- Dayarathna, M.; Wen, Y.; Fan, R. Data Center Energy Consumption Modeling: A Survey. IEEE Commun. Surv. Tutorials 2016, 18, 732–794. [Google Scholar] [CrossRef]
- What Is a Data Center; White Paper; Cisco: San Jose, CA, USA, 2019.
- Kachris, C.; Kanonakis, K.; Tomkos, I. Optical interconnection networks in data centers: Recent trends and future challenges. IEEE Commun. Mag. 2013, 51, 39–45. [Google Scholar] [CrossRef]
- Ma, L.; Su, W.; Li, X.; Wu, B.; Jiang, X. Heterogeneous data backup against early warning disasters in geo-distributed data center networks. IEEE/OSA J. Opt. Commun. Netw. 2018, 10, 376–385. [Google Scholar] [CrossRef]
- Zhong, K.; Zhou, X.; Wang, Y.; Yu, C.; Lau, A.P.T.; Lu, C. Recent Advances for High Speed Data Center Inter-Connects. In Proceedings of the 2016 Asia Communications and Photonics Conference (ACP), Wuhan, China, 2–5 November 2016; pp. 1–3. [Google Scholar]
- Sun, L.; Du, J.; He, Z. Multiband Three-Dimensional Carrierless Amplitude Phase Modulation for Short Reach Optical Communications. J. Light. Technol. 2016, 34, 3103–3109. [Google Scholar] [CrossRef]
- Shieh, W.; Djordjevic, I. Chapter 11—OFDM Applications in Access Optical Networks. In OFDM for Optical Communications; Shieh, W., Djordjevic, I., Eds.; Academic Press: Oxford, UK, 2010; pp. 385–412. [Google Scholar] [CrossRef]
- Alimi, I.A. Demonstration of Effectiveness of OFDM for Mobile Communication Systems. Am. J. Mob. Syst. Appl. Serv. 2015, 1, 35–45. [Google Scholar]
- Alimi, I.A.; Popoola, J.J.; Akingbade, K.F.; Kolawole, M.O. Interference Management in MIMO-OFDM-Based Emerging Wireless Systems. Am. J. Inf. Sci. Comput. Eng. 2015, 1, 1–9. [Google Scholar]
- Che, D.; Shieh, W. Squeezing out the last few bits from band-limited channels with entropy loading. Opt. Express 2019, 27, 9321–9329. [Google Scholar] [CrossRef]
- Yekani, A.; Amiralizadeh, S.; Rusch, L.A. Analytical Study of Optical SSB-DMT With IMDD. J. Light. Technol. 2018, 36, 666–674. [Google Scholar] [CrossRef]
- Zhang, L.; Zuo, T.; Mao, Y.; Zhang, Q.; Zhou, E.; Liu, G.N.; Xu, X. Beyond 100-Gb/s Transmission Over 80-km SMF Using Direct-Detection SSB-DMT at C-Band. J. Light. Technol. 2016, 34, 723–729. [Google Scholar] [CrossRef]
- Shu, L.; Li, J.; Wan, Z.; Gao, F.; Fu, S.; Li, X.; Yang, Q.; Xu, K. Single-Lane 112-Gbit/s SSB-PAM4 Transmission With Dual-Drive MZM and Kramers–Kronig Detection Over 80-km SSMF. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Wan, Z.; Li, J.; Shu, L.; Fu, S.; Fan, Y.; Yin, F.; Zhou, Y.; Dai, Y.; Xu, K. 64-Gb/s SSB-PAM4 Transmission Over 120-km Dispersion-Uncompensated SSMF With Blind Nonlinear Equalization, Adaptive Noise-Whitening Postfilter and MLSD. J. Light. Technol. 2017, 35, 5193–5200. [Google Scholar] [CrossRef]
- Muller, M.; Hofmann, W.; Grundl, T.; Horn, M.; Wolf, P.; Nagel, R.D.; Ronneberg, E.; Bohm, G.; Bimberg, D.; Amann, M. 1550-nm High-Speed Short-Cavity VCSELs. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1158–1166. [Google Scholar] [CrossRef]
- Kapon, E.; Sirbu, A. Long-wavelength VCSELs: Power-efficient answer. Nat. Photonics 2009, 3, 27–29. [Google Scholar] [CrossRef]
- Xie, C.; Spiga, S.; Dong, P.; Winzer, P.; Gnauck, A.; Gréus, C.; Ortsiefer, M.; Neumeyr, C.; Müller, M.; Amann, M. Generation and transmission of 100-Gb/s PDM 4-PAM using directly modulated VCSELs and coherent detection. In Proceedings of the OFC 2014, San Francisco, CA, USA, 9–13 March 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Moser, P.; Lott, J.A.; Wolf, P.; Larisch, G.; Li, H.; Bimberg, D. Error-free 46 Gbit/s operation of oxide-confined 980 nm VCSELs at 85 °C. Electron. Lett. 2014, 50, 1369–1371. [Google Scholar] [CrossRef]
- Chang, Y.; Coldren, L.A. Efficient, High-Data-Rate, Tapered Oxide-Aperture Vertical-Cavity Surface-Emitting Lasers. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 704–715. [Google Scholar] [CrossRef]
- Spiga, S.; Soenen, W.; Andrejew, A.; Schoke, D.M.; Yin, X.; Bauwelinck, J.; Boehm, G.; Amann, M. Single-Mode High-Speed 1.5-μm VCSELs. J. Light. Technol. 2017, 35, 727–733. [Google Scholar] [CrossRef]
- Zhu, N.H.; Shi, Z.; Zhang, Z.K.; Zhang, Y.M.; Zou, C.W.; Zhao, Z.P.; Liu, Y.; Li, W.; Li, M. Directly Modulated Semiconductor Lasers. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–19. [Google Scholar] [CrossRef]
- Xue, L.; Yi, L.; Ji, H.; Li, P.; Hu, W. Symmetric 100-Gb/s TWDM-PON in O-Band Based on 10G-Class Optical Devices Enabled by Dispersion-Supported Equalization. J. Light. Technol. 2018, 36, 580–586. [Google Scholar] [CrossRef]
- Jacques, M.; Samani, A.; Patel, D.; El-Fiky, E.; Morsy-Osman, M.; Hoang, T.; Saber, M.G.; Xu, L.; Sonkoly, J.; Ayliffe, M.; et al. Modulator material impact on chirp, DSP, and performance in coherent digital links: Comparison of the lithium niobate, indium phosphide, and silicon platforms. Opt. Express 2018, 26, 22471–22490. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Stern, B.; Lipson, M.; Lončar, M. Nanophotonic lithium niobate electro-optic modulators. Opt. Express 2018, 26, 1547–1555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, D.; Samani, A.; Veerasubramanian, V.; Ghosh, S.; Plant, D.V. Silicon Photonic Segmented Modulator-Based Electro-Optic DAC for 100 Gb/s PAM-4 Generation. IEEE Photonics Technol. Lett. 2015, 27, 2433–2436. [Google Scholar] [CrossRef]
- Samani, A.; Patel, D.; Chagnon, M.; El-Fiky, E.; Li, R.; Jacques, M.; Abadía, N.; Veerasubramanian, V.; Plant, D.V. Experimental parametric study of 128 Gb/s PAM-4 transmission system using a multi-electrode silicon photonic Mach Zehnder modulator. Opt. Express 2017, 25, 13252–13262. [Google Scholar] [CrossRef] [PubMed]
- Cong, G.; Ohno, M.; Maegami, Y.; Okano, M.; Yamada, K. Silicon traveling-wave Mach–Zehnder modulator under distributed-bias driving. Opt. Lett. 2018, 43, 403–406. [Google Scholar] [CrossRef] [PubMed]
- Weigel, P.O.; Zhao, J.; Fang, K.; Al-Rubaye, H.; Trotter, D.; Hood, D.; Mudrick, J.; Dallo, C.; Pomerene, A.T.; Starbuck, A.L.; et al. Bonded thin film lithium niobate modulator on a silicon photonics platform exceeding 100 GHz 3-dB electrical modulation bandwidth. Opt. Express 2018, 26, 23728–23739. [Google Scholar] [CrossRef] [Green Version]
- Kimura, T. EML vs DML for Datacenter and Client Side Transceivers; Neophotonics Blog; NeoPhotonics: San Jose, CA, USA, 2015. [Google Scholar]
- Hasebe, K.; Matsuo, S.; Sanjoh, H.; Ohki, A.; Kakitsuka, T.; Shibata, Y. Directly frequency modulated DFB laser integrated with EA modulator for extended transmission reach. In Proceedings of the 36th European Conference and Exhibition on Optical Communication, Torino, Italy, 19–23 September 2010; pp. 1–3. [Google Scholar] [CrossRef]
- Verplaetse, M.; Lin, R.; Van Kerrebrouck, J.; Ozolins, O.; De Keulenaer, T.; Pang, X.; Pierco, R.; Vaernewyck, R.; Vyncke, A.; Schatz, R.; et al. Real-Time 100 Gb/s Transmission Using Three-Level Electrical Duobinary Modulation for Short-Reach Optical Interconnects. J. Light. Technol. 2017, 35, 1313–1319. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, J.; Chien, H. EML-based IM/DD 400 G (4 × 112.5-Gbit/s) PAM-4 over 80 km SSMF based on linear pre-equalization and nonlinear LUT predistortion for inter-DCI applications. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Yao, X.S.; Maleki, L. Optoelectronic microwave oscillator. J. Opt. Soc. Am. B 1996, 13, 1725–1735. [Google Scholar] [CrossRef]
- Hao, T.; Liu, Y.; Tang, J.; Cen, Q.; Li, W.; Zhu, N.; Dai, Y.; Capmany, J.; Yao, J.; Li, M. Recent advances in optoelectronic oscillators. Adv. Photonics 2020, 2, 1–21. [Google Scholar] [CrossRef]
- 3Coptics. Optical Transceivers For 5G Networks. 2020. Available online: https://www.3coptics.com/News/9.html (accessed on 5 August 2021).
- Peng, W.R.; Wu, X.; Feng, K.M.; Arbab, V.R.; Shamee, B.; Yang, J.Y.; Christen, L.C.; Willner, A.E.; Chi, S. Spectrally efficient direct-detected OFDM transmission employing an iterative estimation and cancellation technique. Opt. Express 2009, 17, 9099–9111. [Google Scholar] [CrossRef] [Green Version]
- Schuster, M.; Randel, S.; Bunge, C.A.; Lee, S.C.J.; Breyer, F.; Spinnler, B.; Petermann, K. Spectrally Efficient Compatible Single-Sideband Modulation for OFDM Transmission With Direct Detection. IEEE Photonics Technol. Lett. 2008, 20, 670–672. [Google Scholar] [CrossRef]
- Zhu, Y.; Zou, K.; Ruan, X.; Zhang, F. Single Carrier 400 G Transmission With Single-Ended Heterodyne Detection. IEEE Photonics Technol. Lett. 2017, 29, 1788–1791. [Google Scholar] [CrossRef]
- Peng, W.; Morita, I.; Tanaka, H. Enabling high capacity direct-detection optical OFDM transmissions using beat interference cancellation receiver. In Proceedings of the 36th European Conference and Exhibition on Optical Communication, Torino, Italy, 19–23 September 2010; pp. 1–3. [Google Scholar] [CrossRef]
- Al-Qadi, M.; Vedala, G.; O’Sullivan, M.; Xie, C.; Hui, R. QD-MLL-Based Single-Sideband Superchannel Generation Scheme With Kramers–Kronig Direct Detection Receivers. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Roberts, K. Electronic Dispersion Compensation Beyond 10 Gb/s. In Proceedings of the 2007 Digest of the IEEE/LEOS Summer Topical Meetings, Portland, OR, USA, 23–25 July 2007; pp. 9–10. [Google Scholar] [CrossRef]
- Bulow, H.; Buchali, F.; Klekamp, A. Electronic Dispersion Compensation. J. Light. Technol. 2008, 26, 158–167. [Google Scholar] [CrossRef]
- Singer, A.C.; Shanbhag, N.R.; Bae, H. Electronic dispersion compensation. IEEE Signal Process. Mag. 2008, 25, 110–130. [Google Scholar] [CrossRef]
- Bulow, H. Tutorial Electronic Dispersion Compensation. In Proceedings of the OFC/NFOEC 2007—2007 Conference on Optical Fiber Communication and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 25–29 March 2007; pp. 1–25. [Google Scholar] [CrossRef]
- Savory, S.J.; Gavioli, G.; Killey, R.I.; Bayvel, P. Electronic compensation of chromatic dispersion using a digital coherent receiver. Opt. Express 2007, 15, 2120–2126. [Google Scholar] [CrossRef] [PubMed]
- Killey, R.I.; Watts, P.M.; Mikhailov, V.; Glick, M.; Bayvel, P. Electronic dispersion compensation by signal predistortion using digital Processing and a dual-drive Mach-Zehnder Modulator. IEEE Photonics Technol. Lett. 2005, 17, 714–716. [Google Scholar] [CrossRef]
- Peng, W.; Zhang, B.; Feng, K.; Wu, X.; Willner, A.E.; Chi, S. Spectrally Efficient Direct-Detected OFDM Transmission Incorporating a Tunable Frequency Gap and an Iterative Detection Techniques. J. Light. Technol. 2009, 27, 5723–5735. [Google Scholar] [CrossRef]
- Patel, R.K.; Alimi, I.; Muga, N.J.; Pinto, A.N. Optical Signal Phase Retrieval with Low Complexity DC-Value Method. J. Light. Technol. 2020, 38, 4205–4212. [Google Scholar] [CrossRef]
- Patel, R.K.; Guiomar, F.P.; Fernandes, M.A.; Alimi, I.A.; Monteiro, P.P.; Muga, N.J.; Pinto, A.N. Virtual Carrier Assisted Self-Coherent Detection Employing DC-Value Method. In Proceedings of the OSA Optical Fiber Communications—OFC, Washington, DC, USA, 6–11 June 2021. [Google Scholar]
- Chen, X.; Chandrasekhar, S.; Olsson, S.; Adamiecki, A.; Winzer, P. Impact of O/E Front-End Frequency Response on Kramers–Kronig Receivers and its Compensation. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Ohlendorf, S.; Joy, R.; Pachnicke, S.; Rosenkranz, W. Flexible PAM in DWDM Transmission with Kramers–Kronig DSP. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Schuh, K.; Le, S.T. 180 Gb/s 64QAM Transmission Over 480 km Using a DFB Laser and a Kramers–Kronig Receiver. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–25 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Le, S.T.; Schuh, K.; Nguyen Tan, H. A Closed-Form Expression for Direct Detection Transmission Systems With Kramers–Kronig Receiver. IEEE Photonics Technol. Lett. 2018, 30, 2048–2051. [Google Scholar] [CrossRef]
- Sun, C.; Che, D.; Shieh, W. Comparison of Chromatic Dispersion Sensitivity between Kramers–Kronig and SSBI Iterative Cancellation Receiver. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Sun, C.; Che, D.; Schmid, R.; Shieh, W. Polarization Mode Dispersion Impacts on Kramers–Kronig Receiver. In Proceedings of the 2018 23rd Opto-Electronics and Communications Conference (OECC), Jeju Island, Korea, 2–6 July 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Bo, T.; Kim, H. Performance Analysis of Kramers–Kronig Receiver in the Presence of IQ Imbalance. IEEE Photonics Technol. Lett. 2018, 30, 2171–2174. [Google Scholar] [CrossRef]
- Chagnon, M.; Osman, M.; Patel, D.; Veerasubramanian, V.; Samani, A.; Plant, D.V. 1λ,6 bits/symbol, 280 and 350 Gb/s direct detection transceiver using intensity modulation, polarization multiplexing, and inter-polarization phase modulation. In Proceedings of the 2015 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 22–26 March 2015; pp. 1–3. [Google Scholar]
- Gui, T.; Wang, X.; Tang, M.; Yu, Y.; Lu, Y.; Li, L. Real-Time Demonstration of 600 Gb/s DP-64QAM Self-Homodyne Coherent Bi-Direction Transmission with Un-Cooled DFB Laser. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Sowailem, M.Y.S.; El-Fiky, E.; Morsy-Osman, M.; Zhuge, Q.; Hoang, T.M.; Paquet, S.; Paquet, C.; Woods, I.; Liboiron-Ladouceur, O.; Plant, D.V. Self-homodyne system for next generation intra-datacenter optical interconnects. Opt. Express 2017, 25, 27834–27844. [Google Scholar] [CrossRef]
- Che, D.; Chandrasekhar, S.; Chen, X.; Raybon, G.; Winzer, P.; Sun, C.; Shieh, W. Single-Channel Direct Detection Reception Beyond 1 Tb/s. In Proceedings of the 2019 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Savory, S.J. Digital Coherent Optical Receivers: Algorithms and Subsystems. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1164–1179. [Google Scholar] [CrossRef]
- Ip, E.; Lau, A.P.T.; Barros, D.J.F.; Kahn, J.M. Coherent detection in optical fiber systems. Opt. Express 2008, 16, 753–791. [Google Scholar] [CrossRef]
- Kazovsky, L.G. Phase- and polarization-diversity coherent optical techniques. J. Light. Technol. 1989, 7, 279–292. [Google Scholar] [CrossRef]
- Roudas, I. Coherent Optical Communication Systems. In WDM Systems and Networks: Modeling, Simulation, Design and Engineering; Antoniades, N.N., Ellinas, G., Roudas, I., Eds.; Springer: New York, NY, USA, 2012; pp. 373–417. [Google Scholar] [CrossRef]
- Lee, S.; Willner, A. Optical Communication Systems. Basic Concepts. In Encyclopedia of Modern Optics; Guenther, R.D., Ed.; Elsevier: Oxford, UK, 2005; pp. 376–387. [Google Scholar] [CrossRef]
- Westbrook, P.; Eggleton, B. Fiber Gratings. In Encyclopedia of Modern Optics; Guenther, R.D., Ed.; Elsevier: Oxford, UK, 2005; pp. 501–513. [Google Scholar] [CrossRef]
- Schmidt, B.J.C.; Zan, Z.; Du, L.B.; Lowery, A.J. 120 Gbit/s Over 500-km Using Single-Band Polarization-Multiplexed Self-Coherent Optical OFDM. J. Light. Technol. 2010, 28, 328–335. [Google Scholar] [CrossRef]
- Kahn, J.M. Modulation and Detection Techniques for Optical Communication Systems. In Proceedings of the Optical Amplifiers and Their Applications/Coherent Optical Technologies and Applications, Whistler, BC, Canada, 25–28 June 2006; p. CThC1. [Google Scholar] [CrossRef] [Green Version]
- Chagnon, M.; Morsy-Osman, M.; Patel, D.; Veerasubramanian, V.; Samani, A.; Plant, D. Digital Signal Processing for Dual-Polarization Intensity and Interpolarization Phase Modulation Formats Using Stokes Detection. J. Light. Technol. 2016, 34, 188–195. [Google Scholar] [CrossRef]
- Ziaie, S.; Guiomar, F.P.; Muga, N.J.; Nespola, A.; Bosco, G.B.; Carena, A.C.; Pinto, A.N. Adaptive Stokes-Based Polarization Demultiplexing for Long-Haul Multi-Subcarrier Systems. IEEE Photonics Technol. Lett. 2019, 31, 759–762. [Google Scholar] [CrossRef]
- Morsy-Osman, M.; Alam, M.S.; Shahriar, K.A.; Lessard, S.; Plant, D.V. Optimum Three-Dimensional Constellations for Stokes Vector Direct Detect Receivers. IEEE Photonics Technol. Lett. 2019, 31, 587–590. [Google Scholar] [CrossRef]
- Sowailem, M.Y.S.; Hoang, T.M.; Morsy-Osman, M.; Chagnon, M.; Qiu, M.; Paquet, S.; Paquet, C.; Woods, I.; Liboiron-Ladouceur, O.; Plant, D.V. Impact of Chromatic Dispersion Compensation in Single Carrier Two-Dimensional Stokes Vector Direct Detection System. IEEE Photonics J. 2017, 9, 1–10. [Google Scholar] [CrossRef]
- Chagnon, M.; Plant, D.V. 504 and 462 Gb/s direct detect transceiver for single carrier short-reach data center applications. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Sowailem, M.Y.S.; Hoang, T.M.; Chagnon, M.; Morsy-Osman, M.; Qiu, M.; Paquet, S.; Paquet, C.; Woods, I.; Liboiron-Ladouceur, O.; Plant, D.V. 100 G and 200 G single carrier transmission over 2880 and 320 km using an InP IQ modulator and Stokes vector receiver. Opt. Express 2016, 24, 30485–30493. [Google Scholar] [CrossRef]
- Savory, S.J. Digital filters for coherent optical receivers. Opt. Express 2008, 16, 804–817. [Google Scholar] [CrossRef]
- Muga, N.J.; Pinto, A.N. Extended Kalman Filter vs. Geometrical Approach for Stokes Space Based Polarization Demultiplexing. J. Light. Technol. 2015, 33, 4826–4833. [Google Scholar] [CrossRef]
- Muga, N.J.; Pinto, A.N. Adaptive 3D Stokes Space-Based Polarization Demultiplexing Algorithm. J. Light. Technol. 2014, 32, 3290–3298. [Google Scholar] [CrossRef]
- Muga, N.J.; Pinto, A.N. Digital PDL Compensation in 3D Stokes Space. J. Light. Technol. 2013, 31, 2122–2130. [Google Scholar] [CrossRef]
- Che, D.; Sun, C.; Shieh, W. Analog Polarization Identification for Asymmetric Polarization Modulations in Stokes Space. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Rome, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Li, A.; Chowdhury, S.; Wen, Y.; Peng, W.; Cui, Y.; Bai, Y. 112Gb/s Self-Heterodyne Stokes Vector Detection with Compact Receiver for Short Reach Optical Communications. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Che, D.; Li, A.; Shieh, W. Blind polarization de-multiplexing for stokes vector direct detection. In Proceedings of the 2015 European Conference on Optical Communication (ECOC), Valencia, Spain, 27 September–1 October 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Che, D.; Hu, Q.Y.; Chen, X.; Li, A.; Shieh, W. 1-Tb/s Stokes Vector Direct Detection over 480-km SSMF Transmission. In Proceedings of the OptoElectronics and Communication Conference (OECC) and Australian Conference on Optical Fibre Technology (ACT), Melbourne, VIC, Australia, 6–10 July 2014; Available online: https://www.semanticscholar.org/paper/1-Tb-%2F-s-Stokes-Vector-Direct-Detection-over-480-km-Che-Hu/1326d343159a7c4d7b1936daafe0bc4b901236cf (accessed on 8 August 2021).
- Dong, P.; Chen, X.; Kim, K.; Chandrasekhar, S.; Chen, Y.K.; Sinsky, J.H. 128-Gb/s 100-km transmission with direct detection using silicon photonic Stokes vector receiver and I/Q modulator. Opt. Express 2016, 24, 14208–14214. [Google Scholar] [CrossRef]
- Hoang, T.M.; Zhuge, Q.; Xing, Z.; Sowailem, M.; Morsy-Osman, M.; Plant, D.V. Single Wavelength 480 Gb/s Direct Detection Transmission Over 80 km SSMF Enabled by Stokes Vector Receiver and Reduced-Complexity SSBI Cancellation. In Proceedings of the 2018 Optical Fiber Communications Conference and Exposition (OFC), San Diego, CA, USA, 11–15 March 2018; pp. 1–3. [Google Scholar]
- Li, A.; Peng, W.; Kan, C.; Zhu, Y.; Li, Z.; Chowdhury, S.; Cui, Y.; Bai, Y. H-V plane projection based polarization recovery and probabilistic shaping for stokes vector direct detection. In Proceedings of the 2017 Optical Fiber Communications Conference and Exhibition (OFC), Los Angeles, CA, USA, 19–23 March 2017; pp. 1–3. [Google Scholar]
- Kong, D.; Porto Da Silva, E.; Sasaki, Y.; Aikawa, K.; Da Ros, F.; Galili, M.; Morioka, T.; Oxenløwe, L.K.; Hu, H. Kramers–Kronig Detection with Adaptive Rates for 909.5 Tbit/s Dense SDM and WDM Data Channels. In Proceedings of the 2018 European Conference on Optical Communication (ECOC), Roma, Italy, 23–27 September 2018; pp. 1–3. [Google Scholar] [CrossRef] [Green Version]
- Lorences-Riesgo, A.; Guiomar, F.P.; Sousa, A.N.; Teixeira, A.; Muga, N.J.; Medeiros, M.C.R.; Monteiro, P.P. 200 G Outdoor Free-Space-Optics Link Using a Single-Photodiode Receiver. J. Light. Technol. 2020, 38, 394–400. [Google Scholar] [CrossRef]
- Shu, L.; Li, J.; Wan, Z.; Yu, Z.; Li, X.; Luo, M.; Fu, S.; Xu, K. Single-photodiode 112-Gbit/s 16-QAM transmission over 960-km SSMF enabled by Kramers–Kronig detection and sparse I/Q Volterra filter. Opt. Express 2018, 26, 24564–24576. [Google Scholar] [CrossRef]
- Sun, C.; Che, D.; Ji, H.; Shieh, W. Study of Chromatic Dispersion Impacts on Kramers–Kronig and SSBI Iterative Cancellation Receiver. IEEE Photonics Technol. Lett. 2019, 31, 303–306. [Google Scholar] [CrossRef]
- Morero, D.A.; Castrillón, M.A.; Aguirre, A.; Hueda, M.R.; Agazzi, O.E. Design Tradeoffs and Challenges in Practical Coherent Optical Transceiver Implementations. J. Light. Technol. 2016, 34, 121–136. [Google Scholar] [CrossRef]
- Liu, X.; Chandrasekhar, S.; Winzer, P.J. Digital Signal Processing Techniques Enabling Multi-Tbs Superchannel Transmission: An overview of recent advances in DSP-enabled superchannels. IEEE Signal Process. Mag. 2014, 31, 16–24. [Google Scholar] [CrossRef]
- Shieh, W.; Sun, C.; Ji, H. Carrier-assisted differential detection. Light. Sci. Appl. 2020, 9, 1. [Google Scholar] [CrossRef] [Green Version]
- Ji, T.; Sun, C.; Ji, H.; Xu, Z.; Shieh, W. Field Recovery at Low CSPR Using Interleaved Carrier Assisted Differential Detection. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Zhou, X.; Huo, J.; Yu, B.; Guo, C.; Yu, C.; Tao Lau, A.P.; Lu, C. Advanced signal processing techniques for direct detected short reach systems. In Proceedings of the 2018 23rd Opto-Electronics and Communications Conference (OECC), Jeju Island, Korea, 2–6 July 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Osaki, S.; Nakao, M.; Ishihara, T.; Sugiura, S. Differentially Modulated Spectrally Efficient Frequency-Division Multiplexing. IEEE Signal Process. Lett. 2019, 26, 1046–1050. [Google Scholar] [CrossRef]
- Nakao, M.; Sugiura, S. Spectrally Efficient Frequency Division Multiplexing With Index-Modulated Non-Orthogonal Subcarriers. IEEE Wirel. Commun. Lett. 2019, 8, 233–236. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Manton, J.H.; Shieh, W. Computational Complexity Analysis of Neural Network-Based Nonlinear Equalization for Short Reach Direct Detection Systems. In Proceedings of the 2019 Asia Communications and Photonics Conference (ACP), Chengdu, China, 2–5 November 2019; pp. 1–3. [Google Scholar]
- Wan, Z.; Li, J.; Shu, L.; Luo, M.; Li, X.; Fu, S.; Xu, K. Nonlinear equalization based on pruned artificial neural networks for 112-Gb/s SSB-PAM4 transmission over 80-km SSMF. Opt. Express 2018, 26, 10631–10642. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Le, S.T.; Aldaya, I.; Wei, J.L.; McCarthy, M.; Doran, N.J.; Eggleton, B.J. Experimental Comparison of Artificial Neural Network and Volterra based Nonlinear Equalization for CO-OFDM. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–22 March 2016; p. W3A.4. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, C.; Ji, T.; Ji, H.; Shieh, W. Transfer Learning Aided Neural Networks for Nonlinear Equalization in Short-Reach Direct Detection Systems. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Amado, S.B.; Guiomar, F.P.; Muga, N.J.; Ferreira, R.; Reis, J.; Rossi, S.M.R.; Chiuchiarelli, A.C.; Oliveira, J.R.F.O.; Teixeira, A.; Pinto, A.N. Low Complexity Advanced DBP Techniques for Ultra-Long-Haul 400 G Transmission Systems (Invited). J. Light. Technol. 2016, 34, 1793–1799. [Google Scholar] [CrossRef]
- Altabas, J.A.; Izquierdo, D.; Clemente, J.; Sarmiento, S.; Valdecasa, G.S.; Squartecchia, M.; Suhr, L.F.; Gallardo, O.; Lopez, A.; Losada, M.A.; et al. Advanced Technologies for Coherent Access Networks. In Proceedings of the 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Ben Yoo, S.J. Heterogeneous 2D and 3D photonic integrated circuits. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8 August–11 September 2016; p. 1613. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.J.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, s12–s20. [Google Scholar] [CrossRef]
- Ou, Y.; Yan, S.; Hammad, A.; Guo, B.; Peng, S.; Nejabati, R.; Simeonidou, D. Demonstration of Virtualizeable and Software-Defined Optical Transceiver. J. Light. Technol. 2016, 34, 1916–1924. [Google Scholar] [CrossRef]
- Ou, Y.; Davis, M.; Aguado, A.; Meng, F.; Nejabati, R.; Simeonidou, D. Optical Network Virtualisation Using Multitechnology Monitoring and SDN-Enabled Optical Transceiver. J. Light. Technol. 2018, 36, 1890–1898. [Google Scholar] [CrossRef] [Green Version]
- Hillerkuss, D.; Leuthold, J. Software-Defined Transceivers in Dynamic Access Networks. J. Light. Technol. 2016, 34, 792–797. [Google Scholar] [CrossRef] [Green Version]
- Cvijetic, N. Software-defined optical access networks for multiple broadband access solutions. In Proceedings of the 18th OptoElectronics and Communications Conference Held Jointly with 2013 International Conference on Photonics in Switching (OECC/PS), Kyoto, Japan, 30 June–4 July 2013; pp. 1–2. [Google Scholar]
- Jinno, M.; Kozicki, B.; Takara, H.; Watanabe, A.; Sone, Y.; Tanaka, T.; Hirano, A. Distance-adaptive spectrum resource allocation in spectrum-sliced elastic optical path network [Topics in Optical Communications]. IEEE Commun. Mag. 2010, 48, 138–145. [Google Scholar] [CrossRef]
- Sambo, N.; Castoldi, P.; D’Errico, A.; Riccardi, E.; Pagano, A.; Moreolo, M.S.; Fàbrega, J.M.; Rafique, D.; Napoli, A.; Frigerio, S.; et al. Next generation sliceable bandwidth variable transponders. IEEE Commun. Mag. 2015, 53, 163–171. [Google Scholar] [CrossRef]
- Moreolo, M.S.; Fabrega, J.M.; Nadal, L.; Martínez, R.; Casellas, R.; Vílchez, J.; Muñoz, R.; Vilalta, R.; Gatto, A.; Parolari, P.; et al. Experimental Assessment of a Programmable VCSEL-Based Photonic System Architecture over a Multi-Hop Path with 19-Core MCF for Future Agile Tb/s Metro Networks. In Proceedings of the 2020 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
- Boffi, P.; Parolari, P.; Gatto, A.; Rapisarda, M.; Svaluto Moreolo, M.; Nadal, L.; Fabrega, J.; Calabretta, N.; Stabile, R.; Tessema, N.; et al. Multi-Tb/s Sustainable MAN Scenario Enabled by VCSEL-Based Innovative Technological Solutions; Metro and Data Center Optical Networks and Short-Reach Links III; International Society for Optics and Photonics SPIE: Bellingham, WA, USA, 2020. [Google Scholar] [CrossRef]
- Fabrega, J.M.; Svaluto Moreolo, M.; Nadal, L.; Martínez, R.; Neumeyr, C.; Gatto, A.; Parolari, P.; Rapisarda, M.; Boffi, P. Programmable transmission systems using coherent detection enabling multi-Tb/s interfaces for IT-communications convergence in optical networks. In Metro and Data Center Optical Networks and Short-Reach Links III; Society of Photo-Optical Instrumentation Engineers (SPIE): Bellingham, WA, USA, 2020; Volume 11308, p. 113080D. [Google Scholar] [CrossRef]
- Zervos, C.; Spyropoulou, M.; Kanakis, I.; Lazarou, I.; Velthaus, K.O.; Rouvalis, E.; Torfs, G.; Goodbar, E.; Santos, R.; Tessema, N.M.; et al. A new generation of high-speed electro-optical transceivers and flexible bandwidth wavelength selective switches for coherent DCI: The QAMeleon project approach. Opt. Interconnects 2019, 10924, 109240E:1–109240E:18. [Google Scholar]
- Jinno, M.; Takara, H.; Sone, Y.; Yonenaga, K.; Hirano, A. Multiflow optical transponder for efficient multilayer optical networking. IEEE Commun. Mag. 2012, 50, 56–65. [Google Scholar] [CrossRef]
- Bosco, G. Advanced Modulation Techniques for Flexible Optical Transceivers: The Rate/Reach Tradeoff. J. Light. Technol. 2019, 37, 36–49. [Google Scholar] [CrossRef]
- Yoshimoto, N.; Kani, J.; Kim, S.; Iiyama, N.; Terada, J. DSP-based optical access approaches for enhancing NG-PON2 systems. IEEE Commun. Mag. 2013, 51, 58–64. [Google Scholar] [CrossRef]
- Yan, W.; Tanaka, T.; Liu, B.; Nishihara, M.; Li, L.; Takahara, T.; Tao, Z.; Rasmussen, J.C.; Drenski, T. 100 Gb/s optical IM-DD transmission with 10G-class devices enabled by 65 GSamples/s CMOS DAC core. In Proceedings of the 2013 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), Anaheim, CA, USA, 17–21 March 2013; pp. 1–3. [Google Scholar]
- Svaluto Moreolo, M.; Fabrega, J.M.; Nadal, L.; Martínez, R.; Casellas, R. Synergy of Photonic Technologies and Software-Defined Networking in the Hyperconnectivity Era. J. Light. Technol. 2019, 37, 3902–3910. [Google Scholar] [CrossRef]







| Speed | Nomenclature | Standard | Medium | Form Factor | Interface | Reach |
|---|---|---|---|---|---|---|
| 10 GbE (10 Gb/s) | 10 GBASE-SR | 802.3ae-2002 (CL49/52) | Multimode Fiber (@850 nm) | SFP+ XENPAK X2 XPAK XFP | LC Duplex SC Duplex | OM1—33 m OM2—82 m OM3—300 m OM4—400 m |
| 10 GBASE-LR | Single-mode Fiber (@1310 nm) | SFP+ XENPAK X2 XPAK XFP | LC Duplex SC Duplex | OS2—10 km | ||
| 10 GBASE-ER | Single-mode Fiber (@1550 nm) | SFP+ XENPAK X2 XFP | LC Duplex SC Duplex | OS2—40 km | ||
| 25 GbE (25 Gb/s) | 25 GBASE-SR | 802.3by-2016 (CL112) | Multi-mode Fiber (@850 nm) | SFP28 | LC Duplex | OM3—70 m OM4—100 m |
| 25 GBASE-LR | 802.3cc-2017 (CL114) | Single-mode Fiber (@1310 nm) | OS2—10 km | |||
| 25 GBASE-ER | 802.3cc-2017 (CL114) | Single-mode Fiber (@1550 nm) | OS2—40 km | |||
| 40 GbE (40 Gb/s) | 40 GBASE-SR4 | 802.3ba-2010 (CL82/86) | Multimode Fiber (@850 nm) | CFP QSFP+ | MPO | OM3—100 m OM4—150 m |
| 40 GBASE-LR4 | 802.3ba-2010 (CL82/87) | Single-mode Fiber (WDM) | CFP QSFP+ | LC Duplex | OS2—10 km | |
| 40 GBASE-ER4 | 802.3bm-2015 (CL82/87) | Single-mode Fiber (WDM) | QSFP+ | LC Duplex | OS2—40 km | |
| 100 GbE (100 Gb/s) | 100 GBASE-SR10 | 802.3ba-2010 (CL82/86) | Multimode Fiber (@850 nm) | CXP CFP CFP2 CFP4 CPAK | MPO (2 × 12) | OM3—100 m OM4—150 m |
| 100 GBASE-PSM4 | Proprietary (non-IEEE) (January 2014) | Single-mode Fiber (@1310 nm) | QSFP28 CFP4 | MPO 12 | OS2—500 m | |
| 100 GBASE-CWDM4 | Proprietary (non-IEEE) (March 2014) | Single-mode Fiber (WDM) | QSFP28 CFP2 CFP4 | LC Duplex | OS2—2 km | |
| 100 GBASE-SR2-BiDi (Bi-directional) | proprietary (non-IEEE) | Multimode Fiber (@850 nm @900 nm) (WDM) | QSFP28 | LC Duplex | OM3—70 m OM4—100 m | |
| Proprietary (non-IEEE) (June 2016) | Wide-Band Multimode Fiber (SWDM) | SFP | LC Duplex | OM5—150 m | ||
| 100 GBASE-LR4 | 802.3ba-2010 (CL88) | Single-mode Fiber (WDM) | QSFP28 CFP CFP2 CFP4 CPAK | LC Duplex SC Duplex | OS2—10 km | |
| 100 GBASE-SR4 | 802.3bm-2015 (CL95) | Multimode Fiber (@850 nm) | QSFP28 CFP2 CFP4 CPAK | MPO 12 | OM3—70 m OM4—100 m | |
| 100 GBASE-ER4 | 802.3ba-2010 (CL88) | Single-mode Fiber (WDM) | QSFP28 CFP CFP2 | LC Duplex SC Duplex | OS2—40 km | |
| 400 GbE (400 Gb/s) | 400 GBASE-SR8 | 802.3cm | Multimode Fiber (@850 nm) | OSFP QSFP-DD | MPO (16) MPO (2 × 12) | OM3—70 m OM4—100 m OM5—100 m |
| 400 GBASE-DR4 | 802.3bs | Single-mode Fiber (WDM) | CFP8 OSFP QSFP-DD | MPO 12 SN Connector | OS2—500 m | |
| 400 GBASE-FR4 | 802.3cu | Single-mode Fiber (WDM) | CFP8 OSFP QSFP-DD | LC Duplex | OS2—2 km | |
| 400 GBASE-2FR4 (2 × 200 G-FR4) | 802.3bs | Single-mode Fiber (WDM) | OSFP QSFP-DD | CS Connector | OS2—2 km |
| Range | Power Consumption | Temperature Range | Applications | Standard | |
|---|---|---|---|---|---|
| 25 G/100 G transceivers for 5G mobile FH networks | |||||
| 25 GE/eCPRI SFP28 | 10 km | <1.5 W | I-Temp | 25 GBASE-LR Ethernet CPRI Option 10 | SFP28 MSA IEEE 802.3by 25 GBASE-LR |
| 1.8 W | CPRI Option 10 25 G Ethernet | ||||
| <3.5 W | CPRI Option 10 | SFP28 MSA, 25 G Ethernet CPRI/eCPRI specifications | |||
| 300 m | <1 W | 5G eCPRI SFP28 SR 25 GBASE-SR SFP28 25 G Ethernet | SFP28 MSA IEEE 802.3by 25 GBASE-SR | ||
| 100 m | 5G eCPRI SFP28 SR | ||||
| 100 GE/eCPRI QSFP28 4WDM-10 | 10 km | <4 W | Data Center Interconnect 100 G 4WDM-10 10 km reach 100 G CWDM4 applications InfiniBand EDR interconnects Enterprise networking | QSFP28 MSA 4WDM-10 MSA InfiniBand EDR | |
| 100 GE/eCPRI QSFP28 | 100 m | <2 W | 5G FH Network | QSFP28 MSA IEEE 802.3bm 100 GBASE-SR4 | |
| 100 G/200 G/400 G transceivers for 5G midhaul/backhaul networks | |||||
| 100 G QSFP28 4WDM-10 | 10 km | <4 W | I-Temp | Data Center Interconnect 100 G 4WDM-10 10 km reach 100 G CWDM4 applications InfiniBand EDR interconnects Enterprise networking | QSFP28 MSA 4WDM-10 MSA InfiniBand EDR |
| 100 G QSFP28 LR4 | <3.5W | C-Temp | Data Center Network Optical Transport Network (OTN) | QSFP28 MSA IEEE 802.3ba 100 GBASE-LR4 | |
| 100 G QSFP28 ELR4 | 20 km | IEEE 802.3ba 100 GBASE-LR4 OTN OTU4 and 100 GE | |||
| 100 GE/OTU4 QSFP28 ER4 Lite | 40 km | <3.8 W | IEEE 802.3ba 100 GBASE-ER4 links Client-side 100 G interconnections OTN OTU4 | QSFP28 MSA IEEE 802.3ba 100 GBASE-ER4 Lite OTN OTU4 | |
| 200 G QSFP56 FR4 | 2 km | <7.0 W | IEEE 802.3bs 200 GBASE-FR4 Ethernet 5G Backhaul Data center | QSFP56 MSA IEEE 802.3bs 200 GBASE-FR4 | |
| 200 G QSFP56 LR4 | 10 km | <7.5 W | IEEE 802.3bs 200 GBASE-LR4 Ethernet Data center | QSFP56 MSA IEEE 802.3bs 200 GBASE-LR4 | |
| 400 G-QSFPDD-ER8 | 40 km | <14 W | 400 GBASE Ethernet Data center Telecom | QSFP-DD MSA | |
| 400 G-QSFPDD-LR8 | 10 km | <14 W | Data center 400 G Ethernet | ||
| 400 G-QSFPDD-SR8 | 100 m | <10 W | |||
| QDD-400 G-DR4-S | 500 m | <10 W | Data Center 400 G Ethernet 400 G to 100 G Breakout | Compliant to QSFP-DD MSA Common Management Specification (CMIS) Rev 4.0 IEEE Std 802.3-2018 IEEE Standard for Ethernet IEEE802.3bs 400 GAUI-8 Annex 120E | |
| QDD-400 G-FR4-S | 2 km | <12 W | Data Center 400 G Ethernet | QSFP-DD MSA | |
| Data Rate | Form Type | Transmission Distance | Wavelength | Modulation Format | Transmitter and Receiver |
|---|---|---|---|---|---|
| 25 G/100 G transceivers for 5G mobile FH networks | |||||
| 25 Gbit/s | SFP28 | 70∼100 m | 850 nm | NRZ | VCSEL + PIN |
| 300 m | 1310 nm | FP/DFB + PIN | |||
| 10 km | DFB + PIN | ||||
| SFP28 BiDi | 10/15/20 km | 1270/1330 nm | NRZ/PAM4 | DFB + PIN/APD | |
| SFP28 | 10 km | CWDM | NRZ | DFB + PIN | |
| Tunable SFP28 | 10/20 km | DWDM | EML + PIN | ||
| 100 Gbit/s | QSFP28 | 70∼100 m | 850 nm | VCSELs + PINs | |
| 10 km | 4WDM-10 | DFBs + PINs | |||
| 1310 nm | PAM4/DMT | EML + PIN | |||
| QSFP28 BiDi | CWDM4 | NRZ | DFBs + PINs | ||
| 25 G/50 G/100 G/200 G/400 G transceivers for 5G midhaul/backhaul networks | |||||
| 25 Gbit/s | SFP28 | 40 km | 1310 nm | NRZ | EML + APD |
| 50 Gbit/s | QSFP28/SFP56 | 10 km | PAM4 | EML/DFB + PIN | |
| QSFP28 BiDi | 1270/1330 nm | EML/DFB + PIN | |||
| QSFP28/SFP56 | 40 km | 1330 nm | EML + APD | ||
| QSFP28 BiDi | 1295.56/1309.14 nm | EML + APD | |||
| 100 Gbit/s | QSFP28 | 10 km | CWDM/LWDM | NRZ | DFBs/EMLs + PINs |
| 40 km | LWDM | EMLs + APDs | |||
| 10/20 km | DWDM | PAM4/DMT | EMLs + PINs | ||
| 100/200/400 Gbit/s | CFP2-DCO | 80∼120 km | PM QPSK/8-QAM/16-QAM | IC-TROSA + ITLA | |
| 200/400 Gbit/s | OSFP/QSFP-DD | 2/10 km | LWDM | PAM4 | EMLs + PINs |
| Generation Classification | Adopted Technique | Modulator Bias Point | Transmitted Signal | Approach | Advantages | Disadvantages | Reference |
|---|---|---|---|---|---|---|---|
| Bias-induced carrier-generation scheme | SSB subcarrier modulation with | off null | SSB |
|
| [53,54,55,56] | |
| SSB subcarrier modulation with DDMZM | - | SSB | DDMZM |
|
| [54,55,56] | |
| Carrier-assisted generation scheme | Optical carrier-assisted SSB | null | DSB | optical carrier |
|
| [54,55,56,109] |
| Virtual carrier-assisted SSB | null | DSB | digital carrier |
|
| [53,54,55,56] |
| Technique | Advantages | Disadvantages | Reference |
|---|---|---|---|
| Single-Stage Linearization Filter |
|
| [22,29,31] |
| Two-Stage Linearization Filter |
|
| [29] |
| Iterative Linearization Filter |
|
| [29,50,57,58,118] |
| SSBN Estimation and Cancellation |
|
| [29,59] |
| Kramers–Kronig |
|
| [29,45,46,50,55] |
| Reference | Related Effect | Adopted Technique | Advantages | Tradeoff |
|---|---|---|---|---|
| Digital upsampling | ||||
| [18] |
| DSP algorithm without digital upsampling |
|
|
| [21] | modified Hilbert filter in the digital domain |
|
| |
| [45,46] | approximated functions |
|
| |
| [44] | approximated functions and exponential function elimination |
|
| |
| [43] | DSP algorithm without digital upsampling |
|
| |
| High CSPR | ||||
| [49] |
| flexible adaptive dispersion compensation |
|
|
| [50] | hardware SSBN cancellation |
|
| |
| [51] | enhanced SSBN mitigation algorithm |
|
| |
| [52] | employs an exponential operation |
|
| |
| [48] | employs an exponential operation |
|
| |
| Technique | IM/DD | / DD-KK or DD-IC | DP-IM/ >DD DP-IM or SVR | PolMux / SVR | offsetC/ DD | DP-IM-IPM/ SVR | PolMux- -IM/ SVR | DP-COH | RLOD | Reference |
|---|---|---|---|---|---|---|---|---|---|---|
| Tx scheme | IM | DP-IM | PolMux | DP-IM- IPM | PolMux- -IM | DP | [12,13,14,33,34,37,129] | |||
| Rx scheme | DD | DD-KK DD-IC | DD DP-IM SVR | SVR | DD | SVR | COH | [12,13,14,33,34,37,129] | ||
| DoF | 1 | 2 | 3 | 4 | [12,13,14,38,129,131] | |||||
| Modulator | 1 IM | 1 1 OFS | 2 IM | 2 | 1 1 OFS | 2 IM 1 PM | 1 IM 1 | 2 | [12,13,129] | |
| OSE relative to DP-COH (%) | 25 | 50 | 25 | 75 | 100 | [12,13,14,129] | ||||
| Detector | 1D PD | 3D SVR | 1D PD | 3D SVR | 4D Co-Rx | [12,13,129] | ||||
| Min. Rx RF bandwidth at Gbaud | R | 2R | [12,13,14,129] | |||||||
| Supports digital CD at Rx | No | Yes | No | Yes | No | Yes | [7,14,37,129] | |||
| Typical Rx DSP |
|
|
|
|
|
|
| [7,14,21,37,44,45,46,129] | ||
| Cost |  |  |  |  | [21,37,38,44,45,129,131] | |||||
| Complexity |  |  |  |  | [7,14,21,37,44,45] | |||||
| Data rate |  |  |  |  | [12,13,14,21,131] | |||||
| Distance |  |  |  |  | [12,21,34,38] | |||||
 : low;
: low;  : medium;
: medium;  : high. Note: It is noteworthy that the groupings do not signify a mutually exclusive classification and depend on the adopted techniques.
: high. Note: It is noteworthy that the groupings do not signify a mutually exclusive classification and depend on the adopted techniques.| Detection Schemes | ||||
|---|---|---|---|---|
| Feature | Coherent | Self-Coherent | IM-DD | Reference |
| Maximum DoFs per polarization | 2 | 2 | 1 | [12,13,47,139] |
| Adopted method | Heterodyne or homodyne | Heterodyne or homodyne | Direct | [10,11,12,13,107] |
| Modulation parameters | I and Q or amplitude and phase | I and Q or amplitude and phase | Intensity | [10,11,12,13,107] |
| Polarization sensitivity | ⬤ | ◐ | ◯ | [10,11,12,13,107] |
| Carrier phase sensitivity | ⬤ | ◐ | ◯ | [10,11,12,107] |
| Electrical filter usage for selecting the WDM channel | ⬤ | ◐ | ◯ | [11,13,47,107,139] |
| CD is a linear distortion (offers more effective CD) | ⬤ | ◐ | ◯ | [11,12,13,47,107,139] |
| Requirement of LO laser at Rx | ⬤ | ◐ | ◯ | [12,13,47,107,139] |
| Requirement of polarization control or diversity at Rx | ⬤ | ◐ | ◯ | [11,12,13,47,139] |
| DSP complexity | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Implementation cost | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Footprint | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Power consumption | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Spectral efficiency | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Reach | ⬤ | ◐ | ◯ | [11,12,13,107] |
| Structures | Exploited DoFs (Highlighted) | Features | Reference |
|---|---|---|---|
| Dual-Polarized IM |
| [26,63] | |
| Dual-Polarized IM-PM |
| [26,144] | |
| Single-Polarization Complex Modulation |
| [26,145] | |
| Dual-Polarized Complex Modulation |
| [26,41] |
| DoF | Scheme | IQM | OFS | Rx | CSPR (dB) | Baud- Rate (Gbaud) | OSE | ESE | Merit | Demerit | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1D | DD | 1 | 1 | 1D PD | 10 | 25 | 4 | 4 |
|
| [11,12,107] |
| 2D | SCOH SSM | 1 | - | 3D SVR | 0 | 25 | 4 | 8 |
|
| [9,11] |
| 3D | PDM-SSB | 2 | 1 | 3D SVR | 10 | 12.5 | 8 | 8 |
|
| |
| CA-DP SV-DD | 3 | 2 | 3D SVR | 10 | 8.3 | 6 | 12 |
|
| [11,41] | |
| SS-FM | 3 | 2 | 3D SVR | 10 | 16.7 | 6 | 12 |
|
| [8,11,13] | |
| 4D | PDM DSB | 2 | - | 4D Co-Rx | - | 12.5 | 8 | 16 |
|
| [11,13,107] |
| RLOD | 2 | (·) | 4D Co-Rx | - | 12.5 | 8 | 16 |
|
| [129,130] |
| Experiment | Distance (km) | Data Rate Gb/s | Scheme Employed | QAM Modulation | FFT Size | Subcarriers | Cyclic Prefix (CP) | Symbol Length | AWG/DAC Operation (GSa/s) | Pre-FEC (20%) ESE (bits/s/Hz) | Post-FEC ESE (Bits/s/Hz) | RTO Rate (GSa/s) | Net/Aggregate OSE/ISD (b/s/Hz) | CSPR (dB) | Optimum Launch Power (dBm) | Reference |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stokes Vector Direct-Detection (SV-DD)-Based Schemes | ||||||||||||||||
| 1 | 160 | 160 | OFDM | 16 | 4096 | 2184 | 128 | 384 | 25 | 7.76 | 6.46 | 50 | - | 0 | 4 | |
| 2 | 160 | 80/160 | OFDM | 64/16 | 4096 | 2184 | 128 | 384 | 25 | 11.64/7.76 | 9.71/6.46 | 50 | - | 0 | 0-4 | [24] |
| 3 | 160 | 80 | OFDM | 64 | 4096 | 2184 | 128 | 384 | 25 | 11.64 | 9.71 | 50 | - | 0 | 4 | [11] |
| 4 | 160 | 40/20 | PDM | 16/4 | - | - | - | - | 10 | - | - | 50 | - | 0 | - | [152] |
| 5 | 160 | 80 | OFDM | 64 | 4096 | 2184 | 128 | 384 | 25 | 11.64 | 9.71 | 50 | - | 0 | 4 | [8] |
| 6 | 160 | 62.5 | OFDM | 32 | 4096 | 2184 | 128 | 384 | 25 | - | 9.34 | 50 | - | 0 | 4 | [39] |
| 7 | (·) | (·) | (·) | - | - | - | - | - | 64 | - | - | 80 | - | (·) | (·) | [145] |
| 8 | 480 | 1000 | OFDM | 16 | 4096 | 2184 | 128 | 384 | 10 | 7.76 | 6.47 | 50 | - | 0 | 8 | [153] |
| 9 | 100 | 128 | - | 16 | - | - | - | - | 88 | - | - | 40 | - | - | 6 | [154] |
| 10 | 80 | 480 | PDM | 16 | - | - | - | - | 88 | - | - | 160 | - | - | 8 | [155] |
| 11 | (·) | (·) | PDM-PAM-4 | - | - | - | - | - | 70 | - | - | 80 | - | - | - | [63] |
| 12 | 80 | 112 | 16 | - | - | - | - | 80 | - | - | 80 | - | 0 | - | [151] | |
| 13 | 20 | 280/350 | DP-x a | - | - | - | - | - | 70 | - | - | 80 | - | - | - | [128] |
| 14 | 0.5 | 504 | DP-x a | - | - | - | - | - | 84 | - | - | 160 | - | - | - | [144] |
| 15 | 80 | 480 | POL-x b | - | 800 | 600 | - | - | 80 | - | - | 160 | - | 9 | 8 | [13] |
| 16 | 320/80 | 280/336 | 16-QAM-PAM2/4 | - | 800 | 600 | - | - | 80 | - | - | 160 | - | - | - | [26] |
| 17 | 1 | 200 | PDM-DMT | 16 | 512 | 320 | - | - | 80 | - | - | - | - | - | - | [27] |
| 18 | 10 | 320 | (·) | - | - | - | - | - | 64 | - | - | 80 | - | - | - | [25] |
| 19 | 20 | 360 | (·) | - | - | - | - | - | 64 | - | - | 80 | - | - | - | [25] |
| 20 | 160 | 192 | OFDM | 16 | 1024 | 512 | 64 | - | 64 | - | - | 80 | - | - | 3 | [41] |
| 21 | 20 | 176 | OFDM | 64 | 1024 | 512 | 16 | 500 | 88 | - | - | 80 | - | - | - | [156] |
| 22 | 260 | 446 | - | 64 | - | - | - | - | - | 16.5 | 13.9 | 80 | - | 6.3 | 7 | [20] |
| 23 | 100 | (·) | OFDM | 64 | - | - | - | - | - | - | - | 256 | - | 7.3 | 11 | [131] |
| 24 | (5/40) | 600/400 | - | 64/16 | - | - | - | - | - | - | - | - | - | - | - | [129] |
| Kramers–Kronig (KK)-Based Schemes | ||||||||||||||||
| 25 | 100 | 240 | WDM-PDM | 32 | - | - | - | - | 88 | - | - | 62 | 5.3 | 9 | 2 | [19] |
| 26 | 125 | 59 | DMT | 16 | 512 | 128 | - | - | 60 | - | - | 80 | 3.9 | 8 | 9 | [28] |
| 27 | 100 | 220/240 e | DMT/WDM | 16/32 | 1024 | 768 | - | - | - | - | - | 63 | - | 7.5/9 | 9/8 | [19] |
| 28 | 240 | 112 | WDM | 16 | - | - | - | - | 92 | - | - | 63 | 2.8/3.18 | 11 | 2.5 | [22] |
| 29 | 80 | 100 | SSB-DMT | 32 | 512 | 224 | - | 72 | - | - | 160 | - | - | 9 | [31] | |
| 30 | 300 | 267 | - | 16 | - | - | - | 72 | - | - | 256 | - | (·) | (·) | [21] | |
| 31 | 7.9 | (·) | SDM-WDM | (·) | - | - | - | 64 | - | - | 160 | 184.42 | 8 | 8 | [157] | |
| 32 | (·) | (·) | - | (·) | - | - | - | 64 | - | - | 200 | - | 10.5 | 15 | [158] | |
| 33 | 80 | 112 | OFDM | 16 | 1024 | 448 | 576 | - | 64 | - | - | 80 | - | 10 | 7 | [46] |
| 34 | 100 | 218 | DMT j | 16 | 1024 | 768 | - | - | 80 | - | - | 63 | - | 7.5 | 9 | [19] |
| 35 | (·) | (·) | WDM | 16 | - | - | - | - | 92 | - | - | 160 | 5.71 | 12 | 1/6 | [109] |
| 36 | 80 | 168 | WDM | 64 | - | - | - | - | 92 | - | - | 80 | 4.61/4.54 | 12 | 2 | [61] |
| 37 | 960 | 112 | PAM4 | 16 | - | - | - | - | 65 | - | - | 160 | - | 12 | 5 | [159] |
| 38 | 160 | 80 | OFDM | - | 4096 | 2176 | 136 | - | 80 | - | - | 160 | - | 8 | - | [160] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimi, I.; Patel, R.; Silva, N.; Sun, C.; Ji, H.; Shieh, W.; Pinto, A.; Muga, N. A Review of Self-Coherent Optical Transceivers: Fundamental Issues, Recent Advances, and Research Directions. Appl. Sci. 2021, 11, 7554. https://doi.org/10.3390/app11167554
Alimi I, Patel R, Silva N, Sun C, Ji H, Shieh W, Pinto A, Muga N. A Review of Self-Coherent Optical Transceivers: Fundamental Issues, Recent Advances, and Research Directions. Applied Sciences. 2021; 11(16):7554. https://doi.org/10.3390/app11167554
Chicago/Turabian StyleAlimi, Isiaka, Romil Patel, Nuno Silva, Chuanbowen Sun, Honglin Ji, William Shieh, Armando Pinto, and Nelson Muga. 2021. "A Review of Self-Coherent Optical Transceivers: Fundamental Issues, Recent Advances, and Research Directions" Applied Sciences 11, no. 16: 7554. https://doi.org/10.3390/app11167554
APA StyleAlimi, I., Patel, R., Silva, N., Sun, C., Ji, H., Shieh, W., Pinto, A., & Muga, N. (2021). A Review of Self-Coherent Optical Transceivers: Fundamental Issues, Recent Advances, and Research Directions. Applied Sciences, 11(16), 7554. https://doi.org/10.3390/app11167554









