Experimental Study on the Ventilation Resistance Characteristics of Paddy Grain Layer Modelled with Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Apparatus
2.3. Experimental Design
2.3.1. RSM Design
2.3.2. Model Validation
2.3.3. RSM Model Validation Metrics
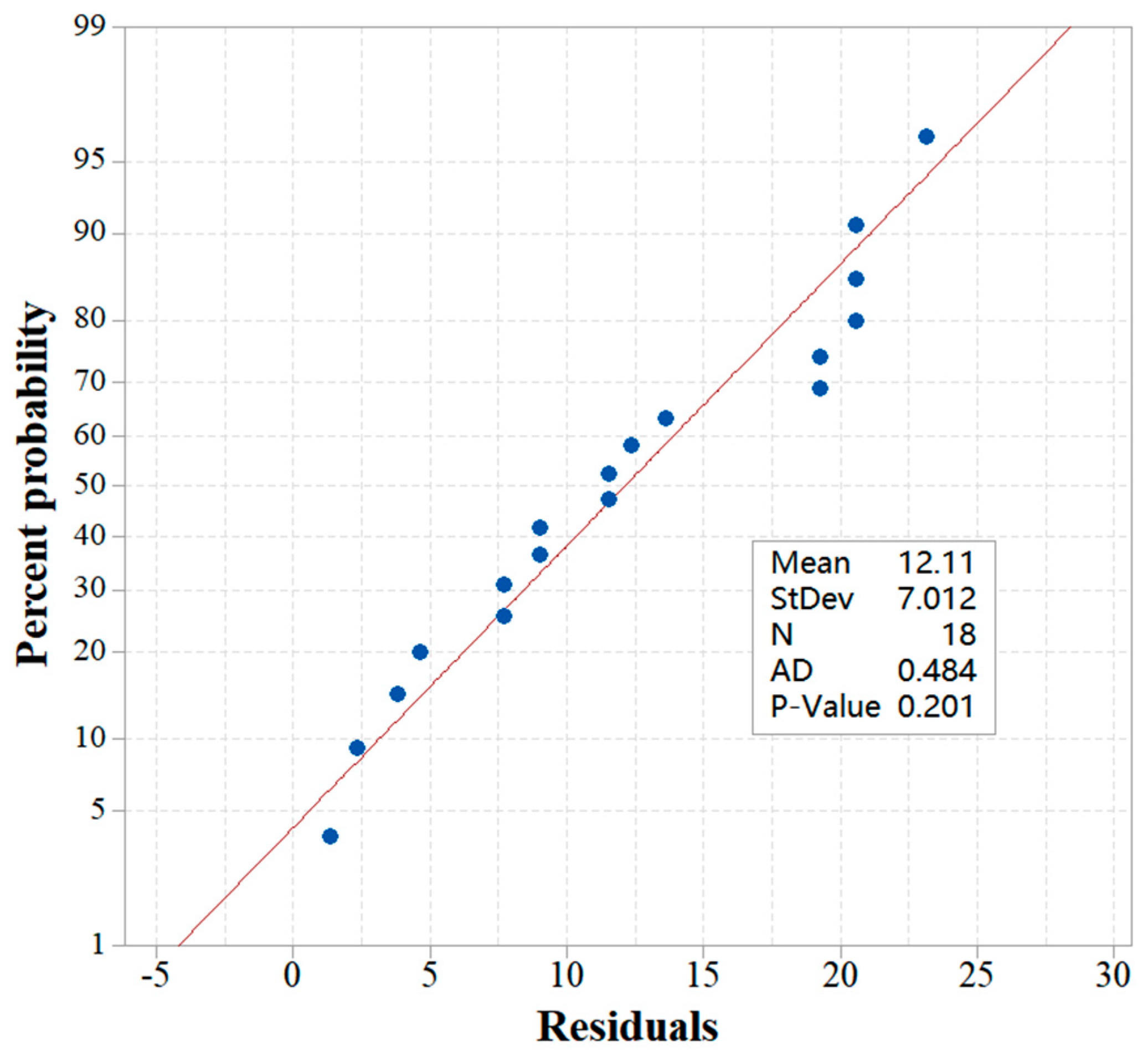
2.3.4. ANOVA Validation: Anderson-Darling (AD) Test for Normality
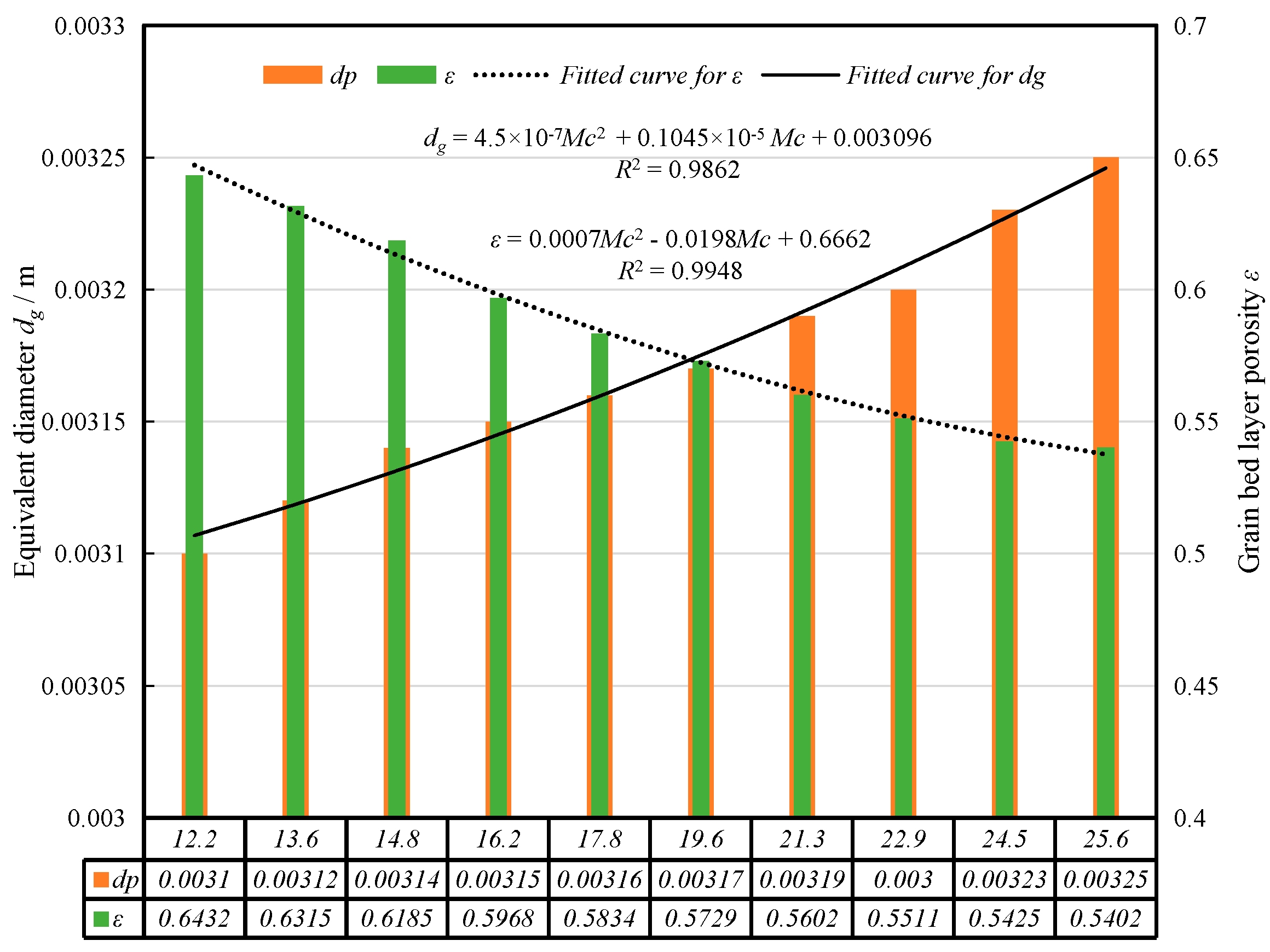
2.3.5. Single Factor Experiments
2.4. Ergun Model
3. Results
3.1. ANOVA Analysis
3.2. Anderson-Darling Normality Test Results
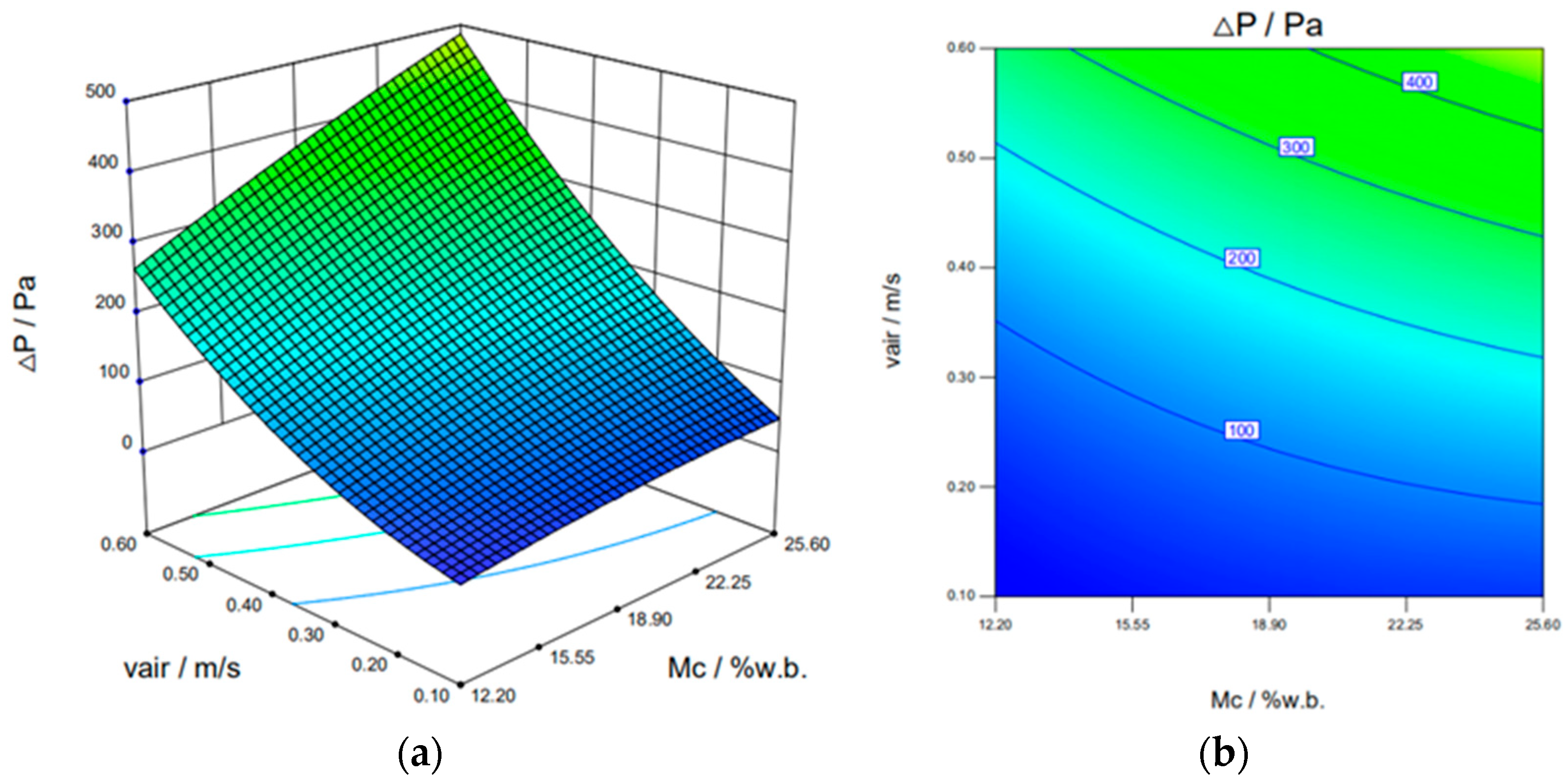
3.3. The Interactions of the Independent Variables on the Pressure Drop
3.4. The Comparison of the Δp Model Developed by RSM and Ergun Model
3.4.1. The Comparison of the Δp in the RSM Experiments
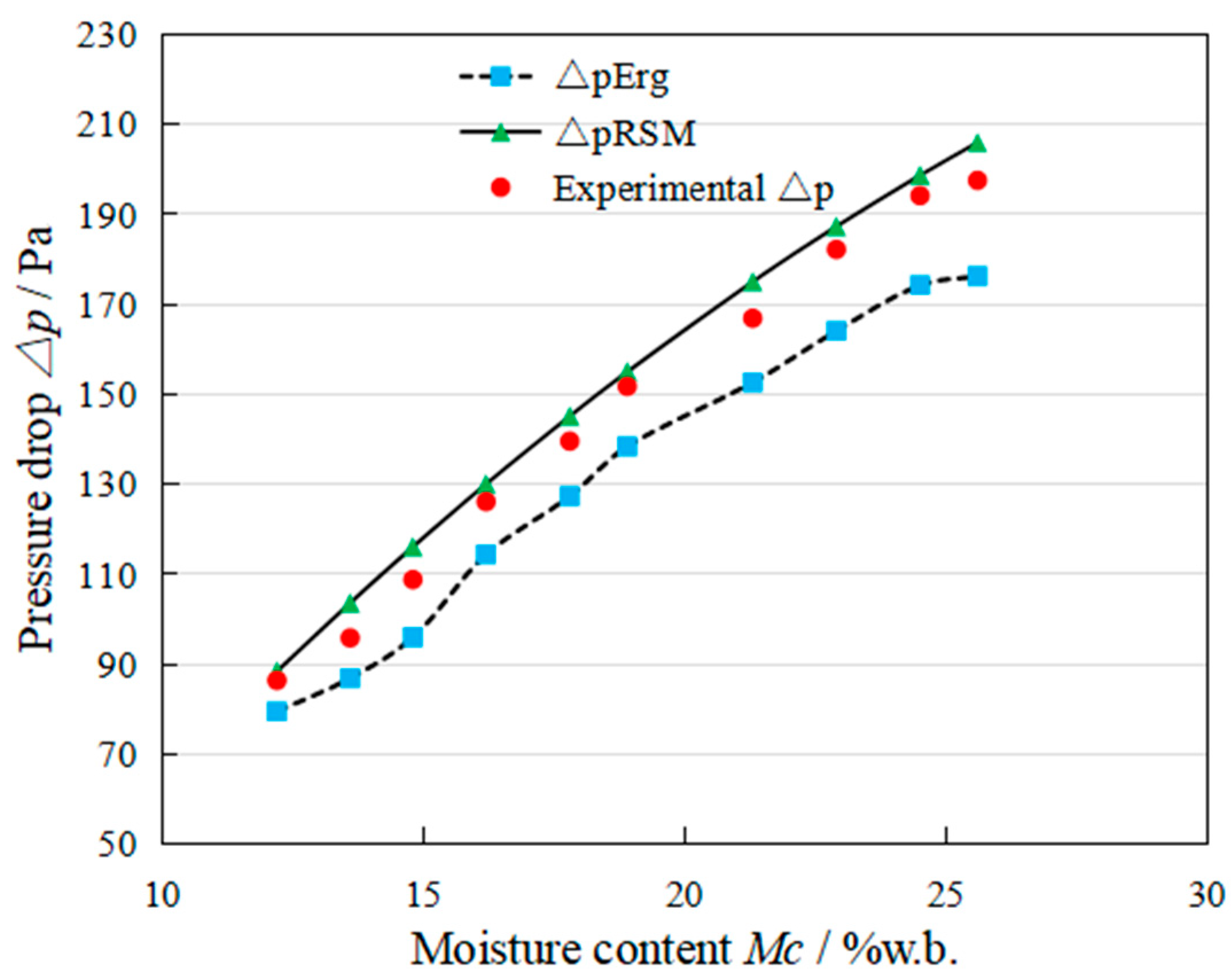
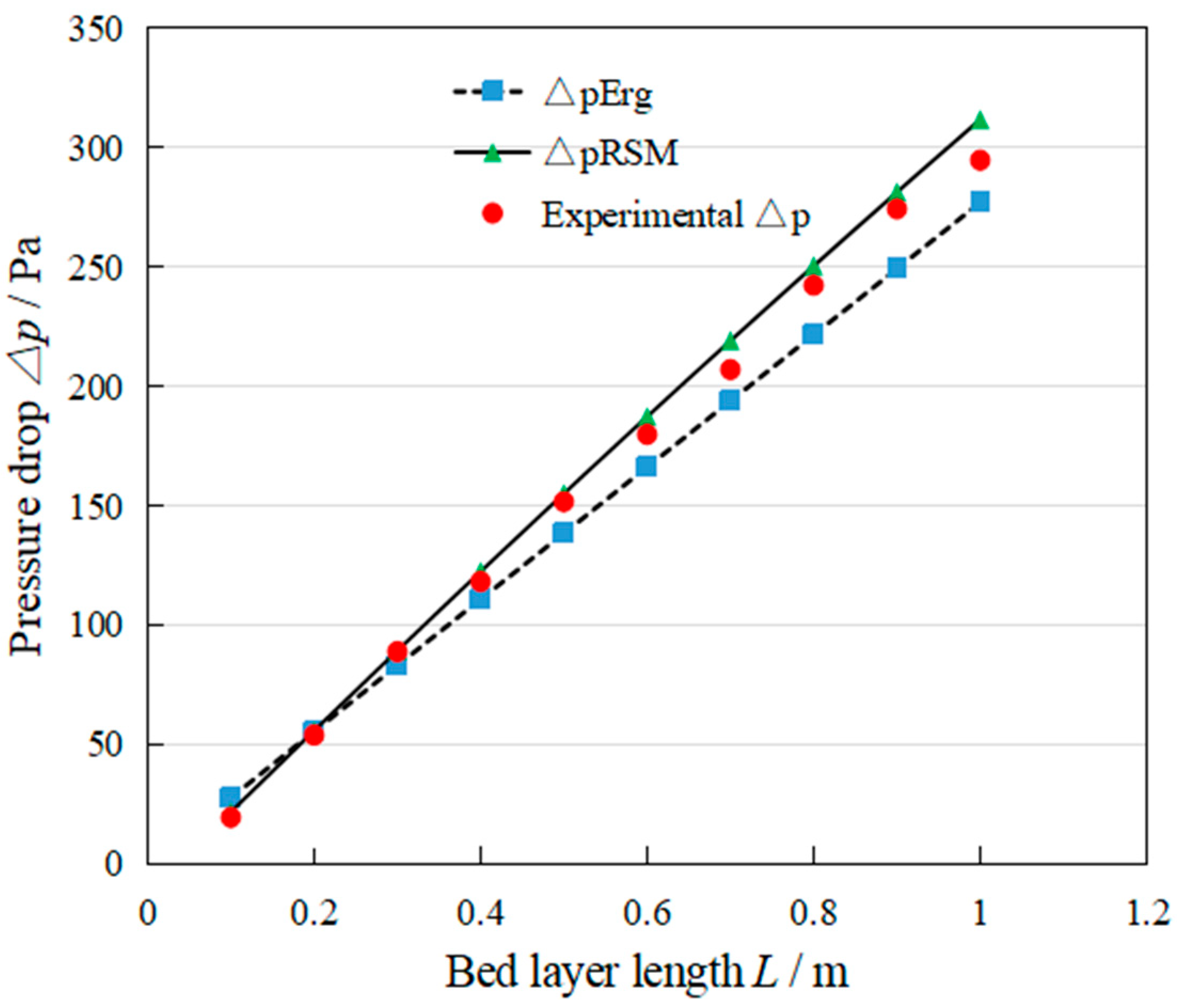
3.4.2. The Single Factor Analysis of the Δp
4. Conclusions
- (1)
- The relations among the Mc, ε, and dg were revealed and the mathematical expressions were also given in the present work.
- (2)
- The Δp increases with the increase of Mc, vair, and L and the contributors to the Δp, in ascending order of significance, are as follows: Mc < L < vair.
- (3)
- The interaction analysis indicates that the interactions of the vair and L has the most significant influence on the Δp, and the match principle between the vair and L should be firstly considered when optimizing the drying process.
- (4)
- A second-order polynomial Δp model based on the RSM was obtained, and its fitting performance was verified to be better than that of the traditional Ergun model by evaluating the R2, MSE, MAE, and RMSE.
- (5)
- The developed Δp model based on the RSM shows a better fitting performance than the Ergun model when the vair ≥ 0.2 m/s, while the Ergun model shows better when the vair is under 0.2 m/s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mujumdar, A.S. Handbook of Industrial Drying, 3rd ed.; Taylor & Francis Group: Abingdon, UK; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar] [CrossRef]
- Li, C. Theoretical analysis of exergy transfer and conversion in grain drying process. Trans. Chin. Soc. Agric. Eng. 2018, 34, 1–8. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Ma, X. Experimental study on ventilation resistance of paddy. Guangdong Agric. Sci. 2012, 39, 191–193. [Google Scholar] [CrossRef]
- Chu, J.C.; Teng, J.T.; Xu, T.T.; Huang, S.; Jin, S.; Yu, X.F. Characterization of frictional pressure drop of liquid flow through curved rectangular microchannels. Exp. Therm. Fluid Sci. 2012, 38, 171–183. [Google Scholar] [CrossRef]
- Norouzi, A.M.; Siavashi, M.; Soheili, A.R.; Oskouei, M.H.K. Experimental investigation of effects of grain size, inlet pressure and flow rate of air and argon on pressure drop through a packed bed of granular activated carbon. Int. Commun. Heat Mass Transf. 2018, 96, 20–26. [Google Scholar] [CrossRef]
- Spieler, O.; Alidibirov, M.; Dingwell, D.B. Grain-size characteristics of experimental pyroclasts of 1980 mount st. helens cryptodome dacite: Effects of pressure drop and temperature. Bull. Volcanol. 2003, 65, 90–104. [Google Scholar] [CrossRef]
- Yue, R.; Zhang, Q. A pore-scale model for predicting resistance to airflow in bulk grain. Biosyst. Eng. 2017, 155, 142–151. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Jackson, C.Y. Resistance to airflow of grain sorghum. Trans. ASAE 1988, 31, 1237–1240. [Google Scholar] [CrossRef]
- Li, Q.T.; Hu, T.Q.; Yu, Z.; Yang, Y.Q.; Fang, Y.L. Experimental study of fluid drag in granary ventilation. J. Hydrodyn. (Ser. A) 2006, 21, 473–478. [Google Scholar]
- Zhang, Y.; Li, C.; Ma, X.; Li, J.; Zou, X.; Wang, R. Experiment and Numerical Simulation of Layer Resistance Parameters in Dryer. Trans. Chin. Soc. Agric. Mach. 2014, 45, 216–221. [Google Scholar] [CrossRef]
- Li, B.; Peng, G.; Luo, C.; Qiu, G.; Yang, L. Optimization of rapeseed vacuum drying technology parameter by response surface methodology. Food Ferment. Ind. 2016, 42, 105–110. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Chen, G.; Yue, W.; Liang, Q.; Wu, Q. Optimisation of ultrasound assisted extraction of phenolic compounds from sparganii rhizoma with response surface methodology. Ultrason. Sonochem. 2013, 20, 846–854. [Google Scholar] [CrossRef]
- Zeng, Z.; Chen, M.; Wang, X.; Wu, W.; Zheng, Z.; Hu, Z.; Ma, B. Modeling and Optimization for Konjac Vacuum Drying Based on Response Surface Methodology (RSM) and Artificial Neural Network (ANN). Processes 2020, 8, 1430. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Wang, J.; Zhang, C.; Sun, L.; Qi, W. Optimization design of fertilizer-guiding mechanism for orchard ditching and fertilizing machin. J. Chin. Agric. Mech. 2017, 38, 45–53. [Google Scholar] [CrossRef]
- Kowalczyk, P.; Ligas, B.; Skrzypczak, D.; Mikula, K.; Chojnacka, K. Biosorption as a method of biowaste valorization to feed additives: Rsm optimization. Environ. Pollut. 2020, 268, 115937. [Google Scholar] [CrossRef] [PubMed]
- Sander, A.; Kardum, J.P.; Skansi, D. Transport properties in drying of solids. Chem. Biochem. Eng. Q. 2000, 15, 131–137. [Google Scholar] [CrossRef]
- Brzinski, T.A., III; Mayor, P.; Durian, D.J. Depth-dependent resistance of granular media to vertical penetration. Phys. Rev. Lett. 2013, 111, 168002. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Luo, X.; Li, C. Study on optimal ratio of air flux to grain mass for rough rice drying. Trans. Chin. Soc. Agric. Mach. 2007, 38, 122–125. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, L.; Xing, X.; Yan, M.; Guo, X.; Yang, B.; Wang, Q.; Kuang, H. Chemometrics coupled with UPLC-MS/MS for simultaneous analysis of markers in the raw and processed Fructus Xanthii, and application to optimization of processing method by BBD design. Phytomedicine 2018, 57, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.K.; Sehgal, V.K.; Arora, S. Optimization of drying process parameters for cauliflower drying. J. Food Sci. Technol. 2013, 5, 62–69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mhe, A.; Mhh, A.; Shr, B. Multi-objective particle swarm optimization of thermal conductivity and dynamic viscosity of magnetic nanodiamond-cobalt oxide dispersed in ethylene glycolusing RSM. Int. Commun. Heat Mass Transf. 2020, 117, 104760. [Google Scholar] [CrossRef]
- Aflaki, S.; Memarzadeh, M. Using two-way anova and hypothesis test in evaluating crumb rubber modification (crm) agitation effects on theological properties of bitumen. Constr. Build. Mater. 2011, 25, 2094–2106. [Google Scholar] [CrossRef]
- Cdd, A.; Yntn, A.; Dlt, B.; Quan, N.; Dcnb, C.; Long, G. Extraction conditions of polyphenol, flavonoid compounds with antioxidant activity from veronia amygdalina del. leaves: Modeling and optimization of the process using the response surface methodology rsm. Mater. Today: Proc. 2019, 18, 4004–4010. [Google Scholar] [CrossRef]
- Chokphoemphun, S.; Chokphoemphun, S. Moisture content prediction of paddy drying in a fluidized-bed drier with a vortex flow generator using an artificial neural network. Appl. Therm. Eng. 2018, 145, 630–636. [Google Scholar] [CrossRef]
- Konwarh, R.; Misra, M.; Mohanty, A.K.; Karak, N. Diameter-tuning of electrospun cellulose acetate fibers: A Box–Behnken design (BBD) study. Carbohydr. Polym. 2013, 92, 1100–1106. [Google Scholar] [CrossRef] [PubMed]
- Myer, R.H.; Montogomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiment, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2002; pp. 343–350. [Google Scholar]
- Box, G.E.P.; Draper, N.R. Empirical Model Building and Response Surfaces; John Wiley & Sons: New York, NY, USA, 1987; pp. 205–477. [Google Scholar]
- Huang, W.; Luo, Z.; Zhuang, H. Pressure drop calculation model of air dense-medium fluidized bed. Coal Eng. 2014, 46, 117–119. [Google Scholar] [CrossRef]
- Vicente, P.G.; Garcia, A.; Viedma, A. Mixed convection heat transfer and isothermal pressure drop in corrugated tubes for laminar and transition flow. Int. Commun. Heat Mass Transf. 2004, 31, 651–662. [Google Scholar] [CrossRef]
- Sieder, E.N.; Tate, G.E. Heat transfer and pressure drop of liquids in tubes. Ind. Eng. Chem. 1936, 28, 1429–1435. [Google Scholar] [CrossRef]
- Sarker, M.S.H.; Ibrahim, M.N.; Aziz, N.A. Energy and rice quality aspects during drying of freshly harvested paddy with industrial inclined bed dryer. Energy Convers. Manag. 2014, 77, 389–395. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Li, T.; Zeng, Z.; Ou, W.; Li, C. Exergetic, Energetic, and Quality Performance Evaluation of Paddy Drying in a Novel Industrial Multi-Field Synergistic Dryer. Energies 2019, 12, 4588. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Fang, Z.; Mai, Z. Design and Test on Porosimeter for Particle Material. Trans. Chin. Soc. Agric. Mach. 2014, 45, 200–206. [Google Scholar] [CrossRef]
- Li, T.; Li, C.; Li, C.; Xu, F.; Fang, Z. Porosity of flowing rice layer: Experiments and numerical simulation. Biosyst. Eng. 2019, 179, 1–12. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Mandegari, M.; Tabatabaei, M.; Farzad, S.; Soufiyan, M.M.; Görgens, J.F. Exergy analysis of a lignocellulosic-based biorefinery annexed to a sugarcane mill for simultaneous lactic acid and electricity production. Energy 2018, 149, 623–638. [Google Scholar] [CrossRef]
- Erbay, Z.; Icier, F. Optimization of hot air drying of olive leaves using response surface methodology. J. Food Eng. 2009, 91, 533–541. [Google Scholar] [CrossRef]
- Dalvand, M.J.; Mohtasebi, S.S.; Rafiee, S. Modeling of electrohydrodynamic drying process using response surface methodology. Food Sci. Nutr. 2014, 2, 200–209. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Mai, Z.; Fang, Z. Analytical study of grain moisture binding energy and hot air drying dynamics. Trans. Chin. Soc. Agric. Eng. 2014, 30, 236–242. [Google Scholar] [CrossRef]
- Rocha, J.C.D.; Pohndorf, R.S.; Meneghetti, V.L.; de Oliveira, M.; Elias, M.C. Effects of mass compaction on airflow resistance through paddy rice grains. Biosyst. Eng. 2020, 194, 39. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Yu, Z. Experimental Study of Grain Physics and Grain Bulk Resistance. Res. Explor. Lab. 2008, 27, 32–34. [Google Scholar] [CrossRef]
- Bazmi, M.; Hashemabadi, S.H.; Bayat, M. Modification of ergun equation for application in trickle bed reactors randomly packed with trilobe particles using computational fluid dynamics technique. Korean J. Chem. Eng. 2011, 28, 1340–1346. [Google Scholar] [CrossRef]
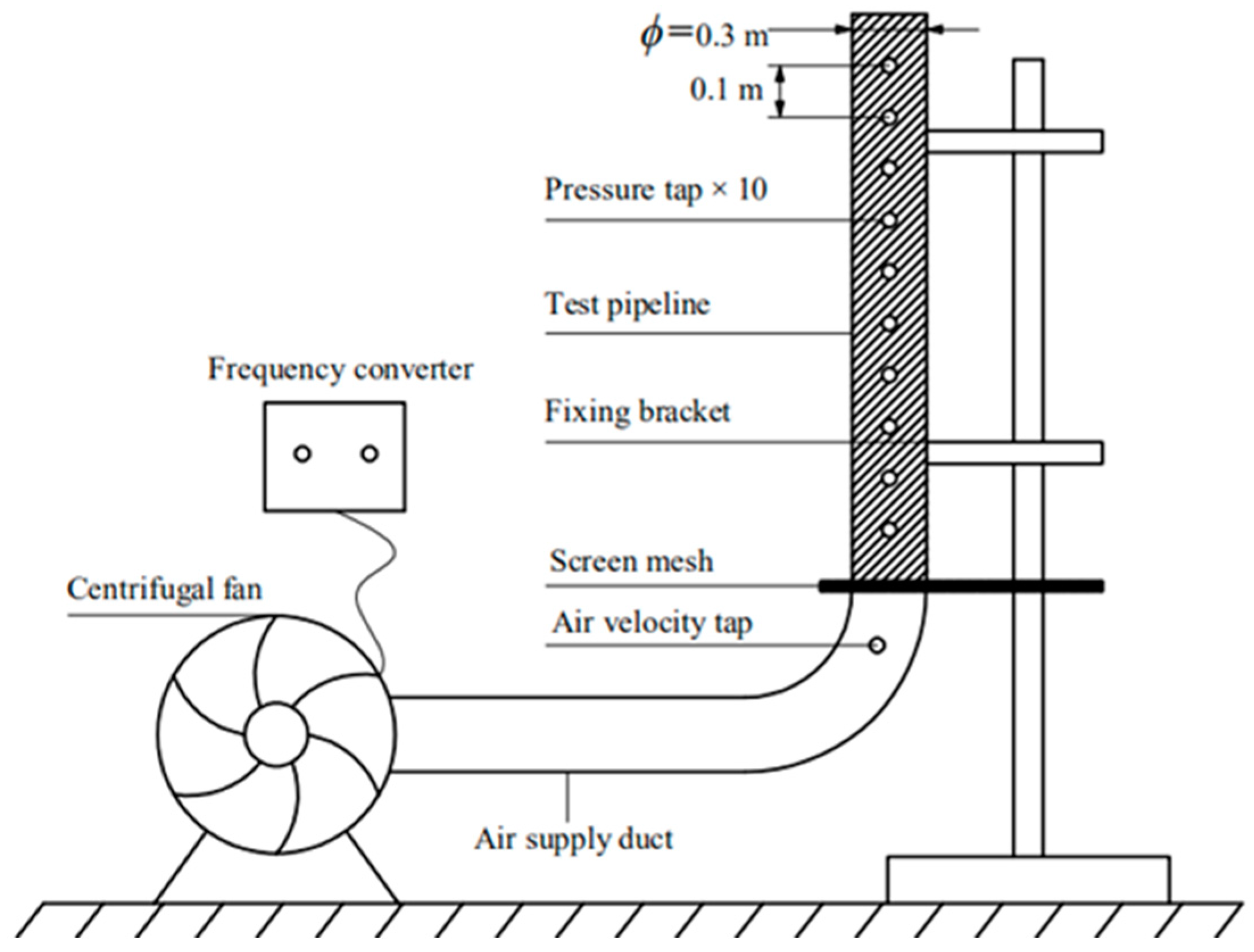



| Instruments | Type | Range/Value | Precision |
|---|---|---|---|
| Frequency converter | Delta VFD002M43B | 2.2 kW | - |
| Centrifugal fan | XYFL-170 | 2.2 kW | - |
| Air supply duct | Round plastic pipe | ϕ = 300 mm | - |
| Screen mesh | Stainless steel screen | 2 × 2 mm | - |
| Anemometer | SUMMIT-565 | 0.1–20 m/s | 0.1 m/s |
| Digital pressure gauge | DP2000-5 | 0–1000 Pa | 1 Pa |
| Electronic digital calliper | MNT-150 | 0–200 mm | 0.02 mm |
| Independent Variables | Code Levels | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Natural Levels | |||
| Mc (%w.b.) | 12.2 | 18.9 | 25.6 |
| vair (m/s) | 0.10 | 0.35 | 0.60 |
| L (m) | 0.10 | 0.55 | 1.0 |
| Standard | Run | Independent Variables | Response | ||
|---|---|---|---|---|---|
| Mc (%w.b.) | vair (m/s) | L (m) | Δp (Pa) | ||
| 12 | 1 | 18.90 | 0.60 | 1.00 | 689.56 |
| 15 | 2 | 18.90 | 0.35 | 0.55 | 194.26 |
| 3 | 3 | 12.20 | 0.60 | 0.55 | 255.21 |
| 1 | 4 | 18.90 | 0.60 | 0.10 | 83.13 |
| 1 | 5 | 12.20 | 0.10 | 0.55 | 1375 |
| 2 | 6 | 25.60 | 0.10 | 0.55 | 60.58 |
| 4 | 7 | 25.60 | 0.60 | 0.55 | 485.12 |
| 11 | 8 | 18.90 | 0.10 | 1.00 | 42.52 |
| 14 | 9 | 18.90 | 0.35 | 0.55 | 167.28 |
| 7 | 10 | 12.20 | 0.35 | 1.00 | 182.54 |
| 9 | 11 | 18.90 | 0.10 | 0.10 | 12.62 |
| 16 | 12 | 18.90 | 0.35 | 0.55 | 158.76 |
| 5 | 13 | 12.20 | 0.35 | 0.10 | 17.11 |
| 6 | 14 | 25.60 | 0.35 | 0.10 | 38.82 |
| 17 | 15 | 18.90 | 0.35 | 0.55 | 168.76 |
| 13 | 16 | 18.90 | 0.35 | 0.55 | 166.46 |
| 8 | 17 | 25.60 | 0.35 | 1.00 | 396.69 |
| Level | Single Factor Test 1 | Single Factor Test 2 | Single Factor Test 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mc (%w.b.) | vair (m/s) | L (m) | Mc (%w.b.) | vair (m/s) | L (m) | Mc (%w.b.) | vair (m/s) | L (m) | |
| 1 | 12.2 | 0.35 | 0.5 | 18.9 | 0.1 | 0.5 | 18.9 | 0.35 | 0.1 |
| 2 | 13.6 | 0.15 | 0.2 | ||||||
| 3 | 14.8 | 0.2 | 0.3 | ||||||
| 4 | 16.2 | 0.25 | 0.4 | ||||||
| 5 | 17.8 | 0.3 | 0.5 | ||||||
| 6 | 18.9 | 0.35 | 0.6 | ||||||
| 7 | 21.3 | 0.4 | 0.7 | ||||||
| 8 | 22.9 | 0.45 | 0.8 | ||||||
| 9 | 24.5 | 0.5 | 0.9 | ||||||
| 10 | 25.6 | 0.6 | 1.0 | ||||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5.480 × 105 | 9 | 60,885.15 | 148.56 | <0.0001 ** |
| Mc | 32,848.69 | 1 | 32,848.69 | 80.15 | <0.0001 ** |
| vair | 2.393 × 105 | 1 | 2.393 × 105 | 583.84 | <0.0001 ** |
| L | 1.681 × 105 | 1 | 1.681 × 105 | 410.13 | <0.0001 ** |
| Mc · vair | 8379.57 | 1 | 8379.57 | 20.45 | 0.0027 ** |
| Mc · L | 9255.40 | 1 | 9255.40 | 22.58 | 0.0021 ** |
| vair · L | 83,096.71 | 1 | 83,096.71 | 202.76 | <0.0001 ** |
| Mc 2 | 256.14 | 1 | 256.14 | 0.62 | 0.4551 |
| vair 2 | 6858.82 | 1 | 6858.62 | 16.74 | 0.0046 ** |
| L 2 | 85.53 | 1 | 85.53 | 0.21 | 0.6616 |
| Residual | 2868.84 | 7 | 409.83 | ||
| Lack of Fit | 2138.59 | 3 | 712.86 | 3.90 | 0.1106 (NS) |
| Pure Error | 730.26 | 4 | 182.56 | ||
| Std. Dev | 20.24 | ||||
| Mean | 184.31 | ||||
| R2 | 0.9948 | ||||
| Adj R2 | 0.9881 | ||||
| Pred R2 | 0.9358 | ||||
| Adep Pre | 43.223 | ||||
| C.V.% | 10.98 | ||||
| PRESS | 35,358.41 | ||||
| Statistical Indexes | RSM Model | Ergun Model |
|---|---|---|
| Δ pRSM | Δ pEur | |
| Determination coefficient (R2) | 0.9948 | 0.9868 |
| Mean-square error (MSE) | 10.9021 | 15.7041 |
| Mean absolute error (MAE) | 2868.9372 | 7292.4115 |
| Root-mean-square error(RMSE) | 12.9908 | 20.7115 |
| Statistical Indexes | RSM Model | Ergun Model | ||||
|---|---|---|---|---|---|---|
| ΔpMc | Δpvair | ΔpL | ΔpMc | Δpvair | ΔpL | |
| Determination coefficient (R2) | 0.9755 | 0.9909 | 0.9918 | 0.8539 | 0.9846 | 0.9737 |
| Mean-square error (MSE) | 35.9195 | 89.4276 | 64.5378 | 213.7543 | 151.9289 | 206.1363 |
| Mean absolute error (MAE) | 5.6094 | 8.4528 | 6.3943 | 13.9521 | 10.1731 | 12.6444 |
| Root-mean-square error(RMSE) | 5.9933 | 9.4566 | 8.0335 | 14.6203 | 12.3259 | 14.3574 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Han, C.; Wu, W.; Xu, J.; Zeng, Z.; Tang, T.; Zheng, Z.; Huang, T. Experimental Study on the Ventilation Resistance Characteristics of Paddy Grain Layer Modelled with Response Surface Methodology. Appl. Sci. 2021, 11, 7826. https://doi.org/10.3390/app11177826
Wang X, Han C, Wu W, Xu J, Zeng Z, Tang T, Zheng Z, Huang T. Experimental Study on the Ventilation Resistance Characteristics of Paddy Grain Layer Modelled with Response Surface Methodology. Applied Sciences. 2021; 11(17):7826. https://doi.org/10.3390/app11177826
Chicago/Turabian StyleWang, Xiaoming, Chongyang Han, Weibin Wu, Jian Xu, Zhiheng Zeng, Ting Tang, Zefeng Zheng, and Tao Huang. 2021. "Experimental Study on the Ventilation Resistance Characteristics of Paddy Grain Layer Modelled with Response Surface Methodology" Applied Sciences 11, no. 17: 7826. https://doi.org/10.3390/app11177826
APA StyleWang, X., Han, C., Wu, W., Xu, J., Zeng, Z., Tang, T., Zheng, Z., & Huang, T. (2021). Experimental Study on the Ventilation Resistance Characteristics of Paddy Grain Layer Modelled with Response Surface Methodology. Applied Sciences, 11(17), 7826. https://doi.org/10.3390/app11177826







