Abstract Rotations for Uniform Adaptive Control and Soft Modeling of Mechanical Devices
Abstract
:1. Introduction
- 1.
- For the free system, the two dimensional vectors and were augmented to three-dimensional ones of identical Frobenius norms and exactly as it was performed in the rotations-based abstract deformations applied in [29]. In the case of the controlled model the three-dimensional vectors and were similarly augmented to produce the four dimensional ones of identical norms as and in which and were the “dummy components” without any physical interpretation. Their role was to guarantee equal norms.
- 2.
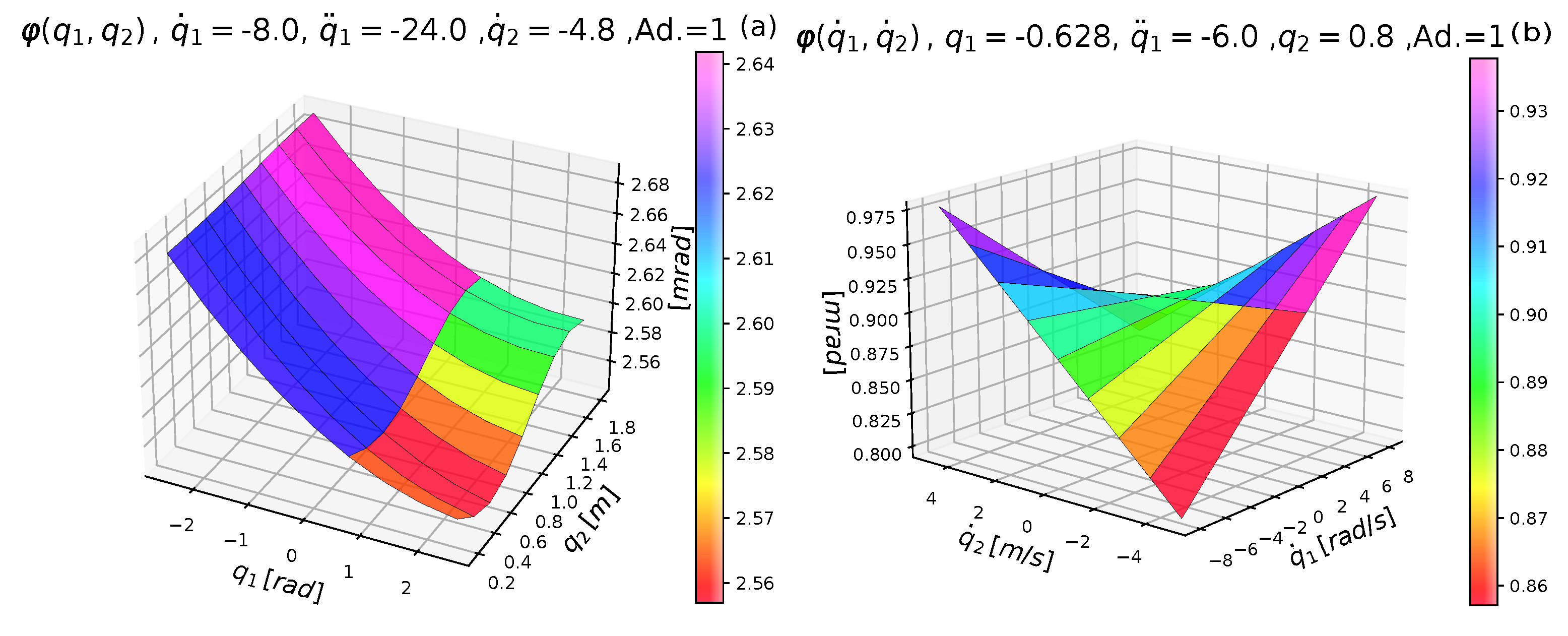
- Coarse resolution grids were introduced in for the values, and in for the values. In the center points of the grids, the appropriate and Q values were computed from the available exact model of the van der Pol oscillator. Following that, the abstract rotations defined in (7) were calculated that rotated into , and transformed into , respectively. Each grid cell was associated with a “neuron” that had the “activation function”. It executed the rotations according to (7), and had the following parameters:
- Its cell-limits as , for the free motion, and , , for the controlled system, respectively;
- The orthogonal unit vectors and of which the generator of the rotation in (7) can be computed, and the angle of the necessary rotation, .
- 3.
- These neurons were arranged in a single layer in which each neuron obtained its input value for the “teaching process” as for the free system, and for the dynamic model. If the input signal belonged to the “range of competence” of the given neuron, , , and were computed. During the “normal operation” the neuron used the input for the free system modeling as and for “the use for control mode”. If the input data belonged to its range of competence, it computed , computed the rotated vector for the free system, and for the control application, and as its output, it provided the first component of the rotated vector that corresponded to the modeled value of and Q, respectively.
- 4.
- The last layer of the novel neural structure consisted of a single neuron that summarized the calculated outputs. Since the cells’ limits were determined in a way that the model had only disjoint cells, the output of the summarizing layer was the result of the “soft model”.
- 5.
- To reduce the effects of the jumps in the control signal at the cell boundaries, the really applied generalized force was smoothed by the tracking rule based on a positive constant in (8)that, for a stationary “driving term" , has the stationary solution , furthermore, for time-varying , two different solutions of (8), i.e., and , can differ from each other by that satisfies the differential equation , that is, the differences can stem from the initial conditions and converge to 0 as . Consequently, the smoothed signal tracks well the actual if the variation of which is not significant during the time-interval of duration , and “smooths well” the signals that have faster variation.
- 6.
- The data representation made it possible to apply real-time modification (“step-by-step learning”) of the neuron’s previously learned parameters as the unit vectors , and were refreshed according to a learning rule determined by the parameter asIt must be noted that even if and were orthogonal to each other, the new unit vectors and will not be exactly orthogonal ones. Consequently, the new skew symmetric matrix can generate rotations in the form , but, because , instead of (7) we can state only thati.e., by maintaining the right-hand side of (10) that is easy to compute, instead of exact rotations, linear transformations can be used that are good approximations of rotations.
- 1.
- The controlled system is an underactuated two degree of freedom construction in which the directly controlled subsystem is dynamically coupled with a non-controllable one acting as “parasite dynamics”.
- 2.
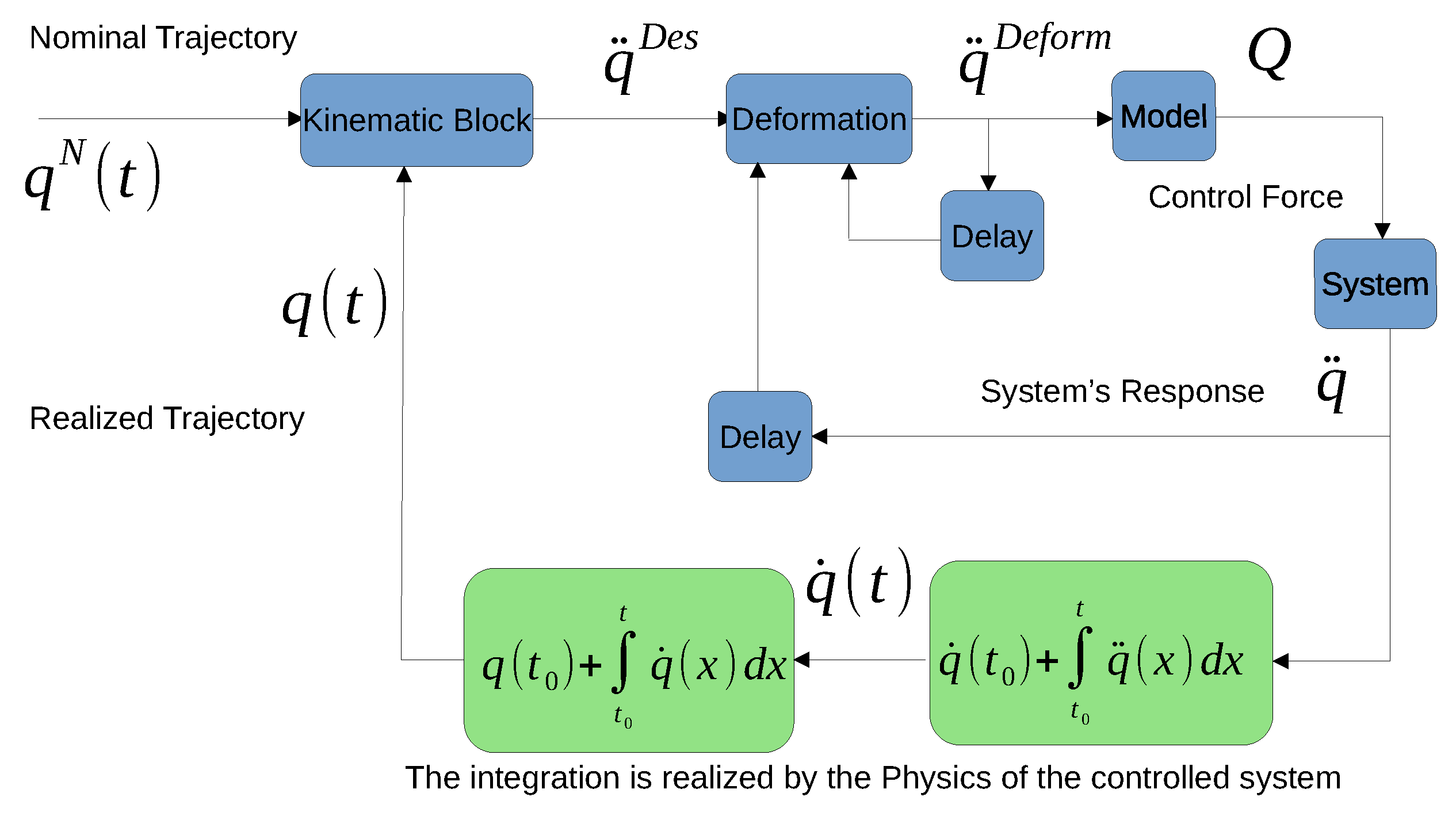
- Instead of the simple CTC control and its robust variable structure/sliding mode-based correction (e.g., [88,89,90]), the “fixed point iteration-based adaptive control scheme” depicted in Figure 1 is applied to compensate the effects of the imprecisions of the coarse grid-based model with the application of the rotations-based adaptive controller announced in [29].
- 3.
- The effects of the measurement noises are investigated and reduced by a smoothing technique that is similar to the solution published in [91].
- 4.
- The computation time of the controller was measured for the hardware and software environment that was used in the simulations.
2. The Dynamic Model of the Controlled System
3. The Rotational Neural Model Structure Tailored to the Controlled System
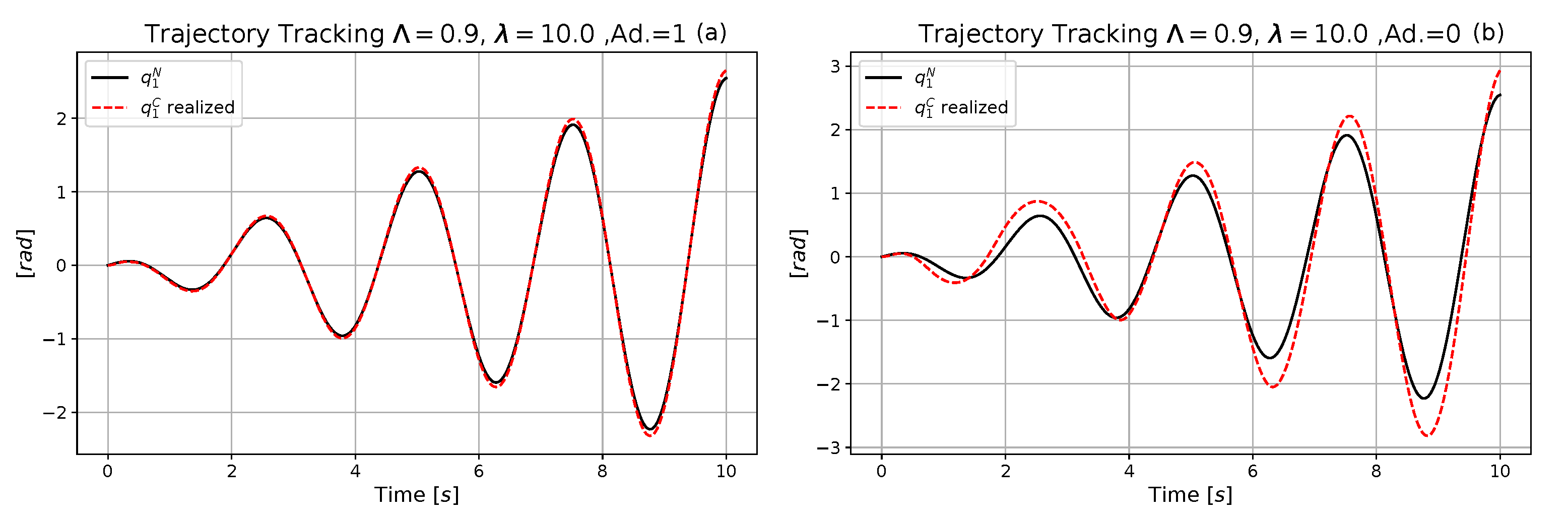
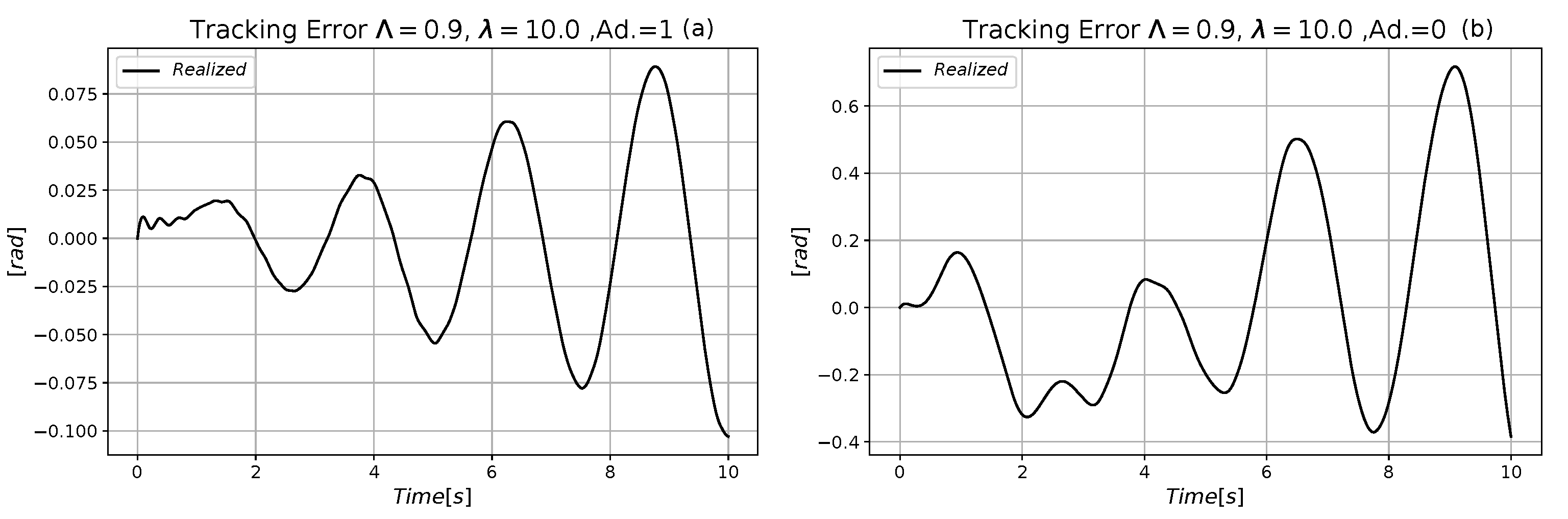
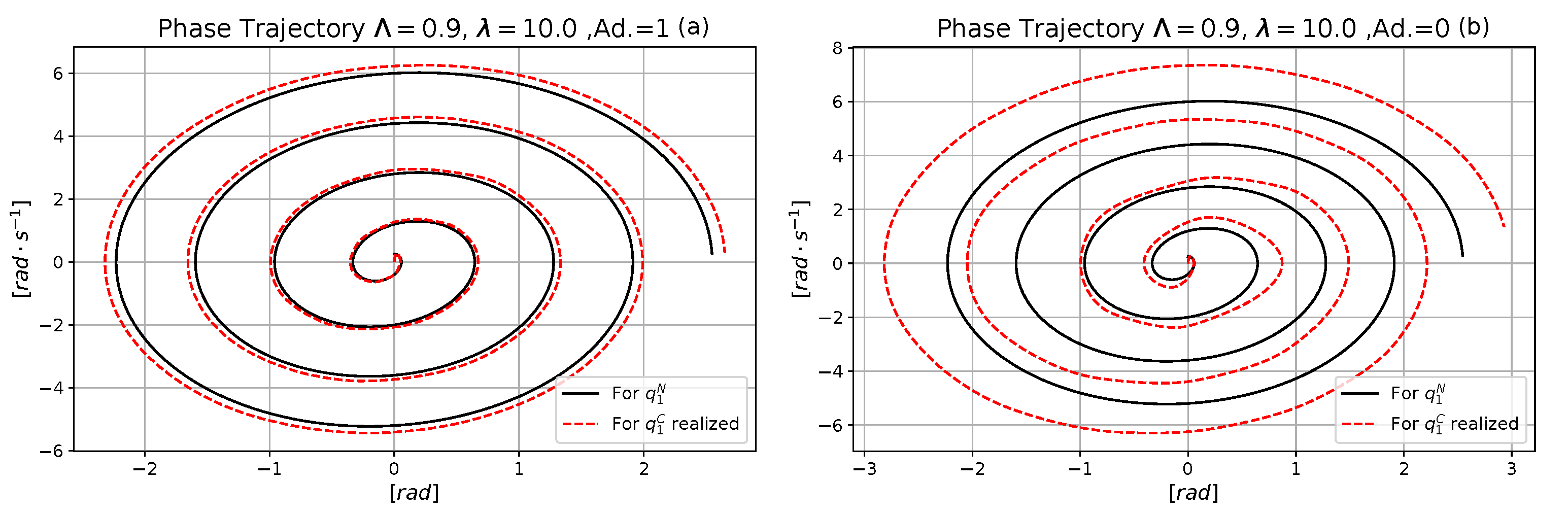
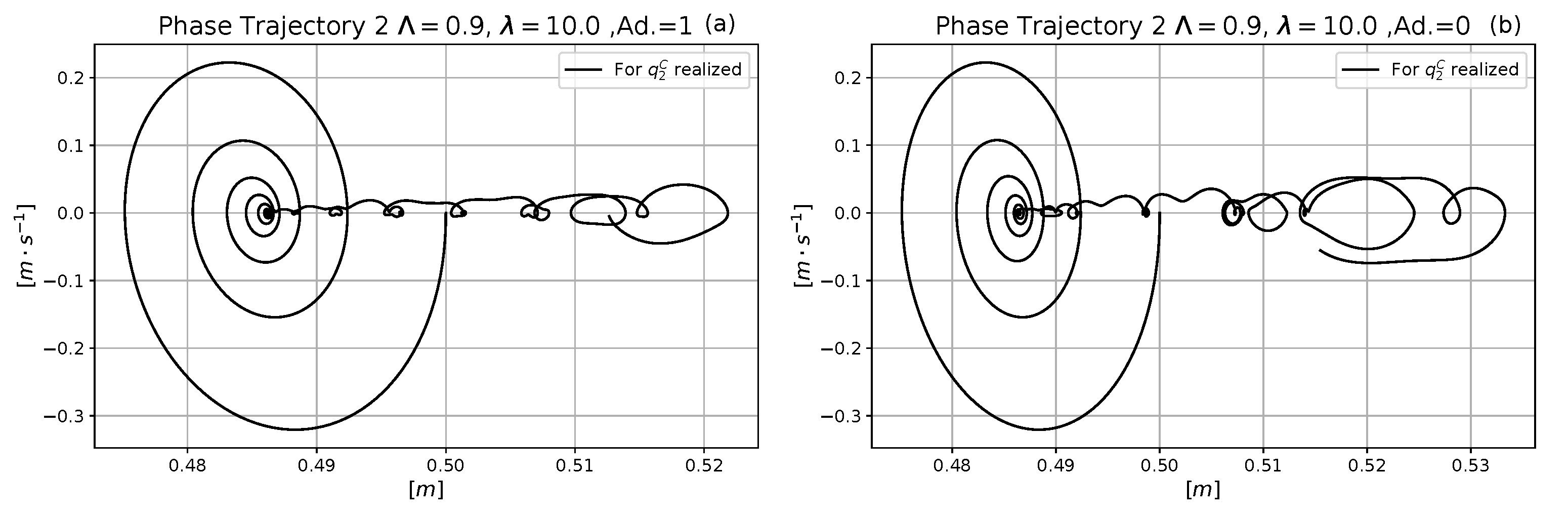
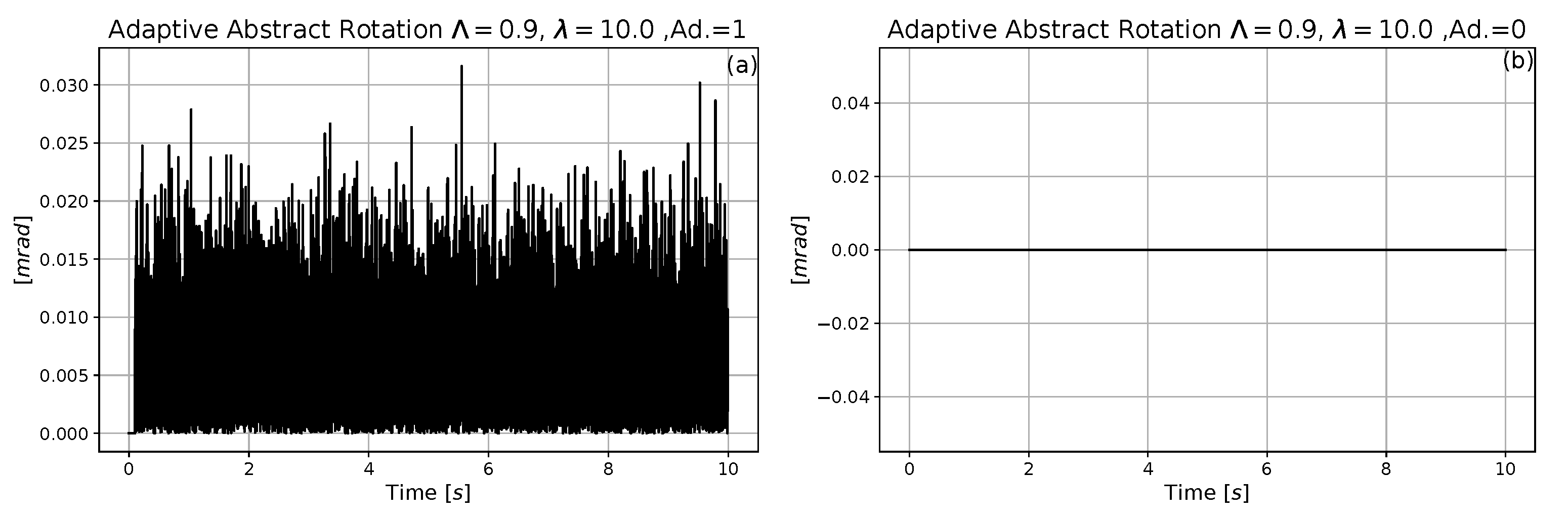
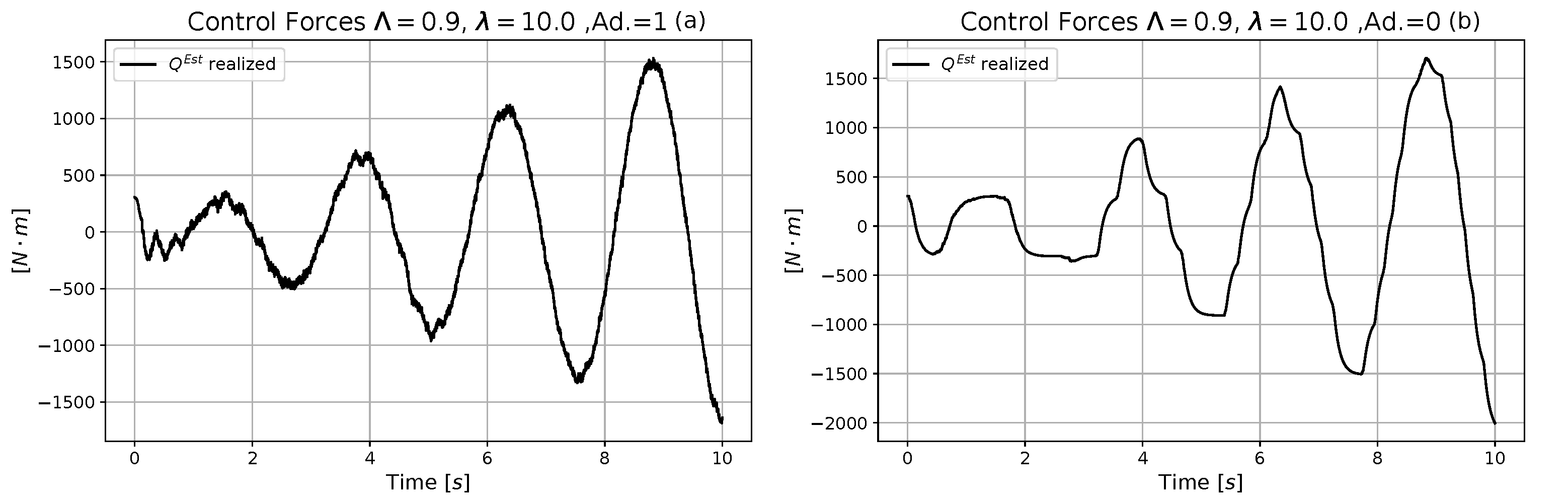
4. Simulation Results
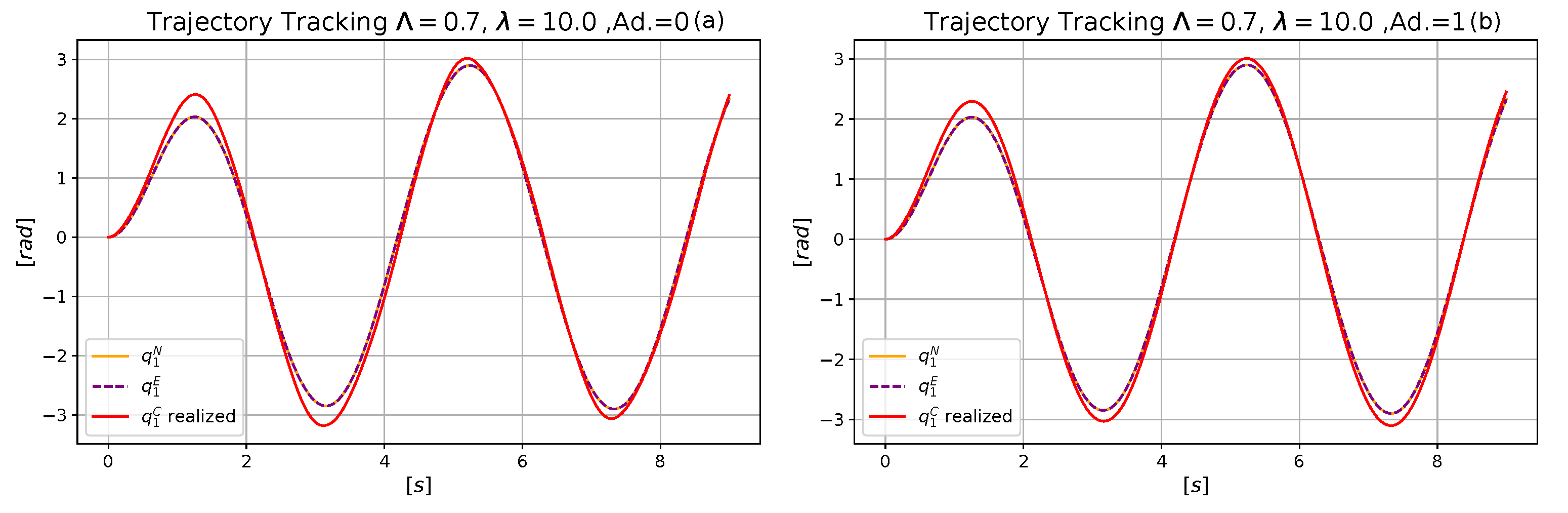
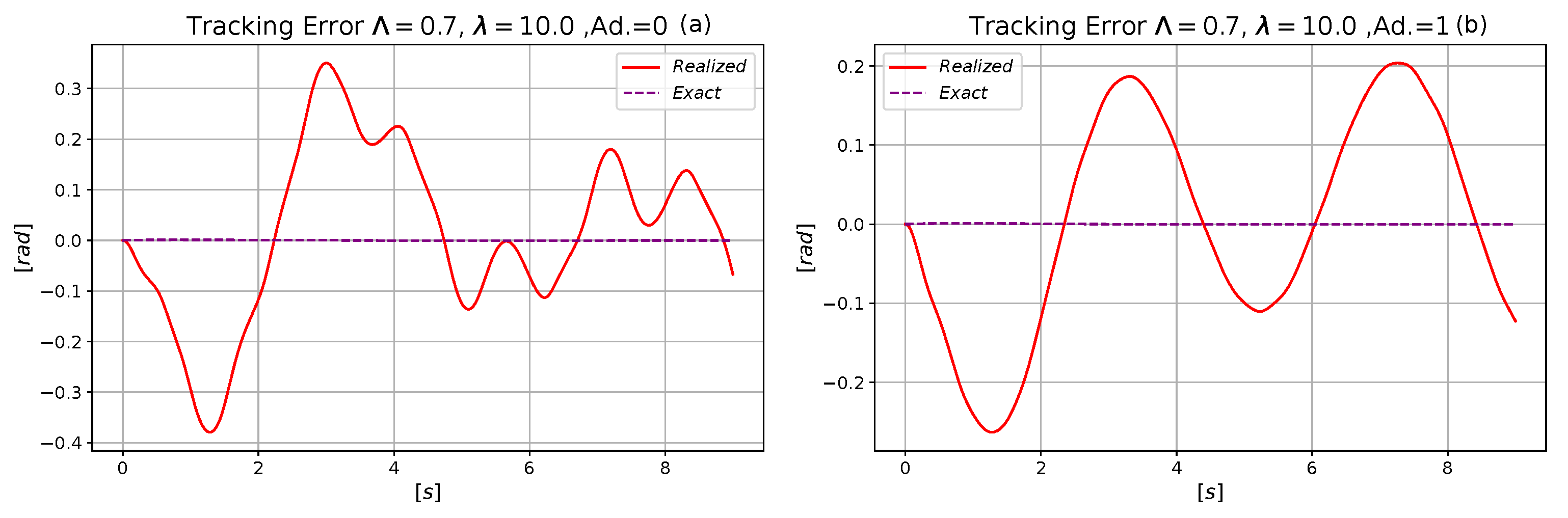
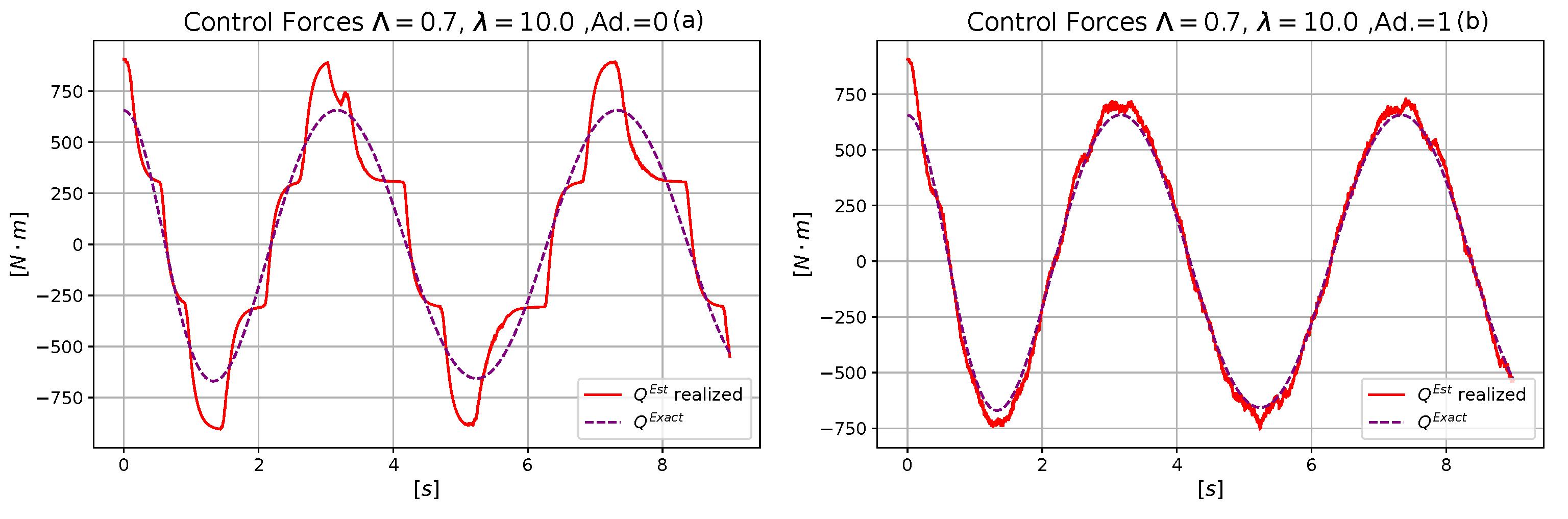
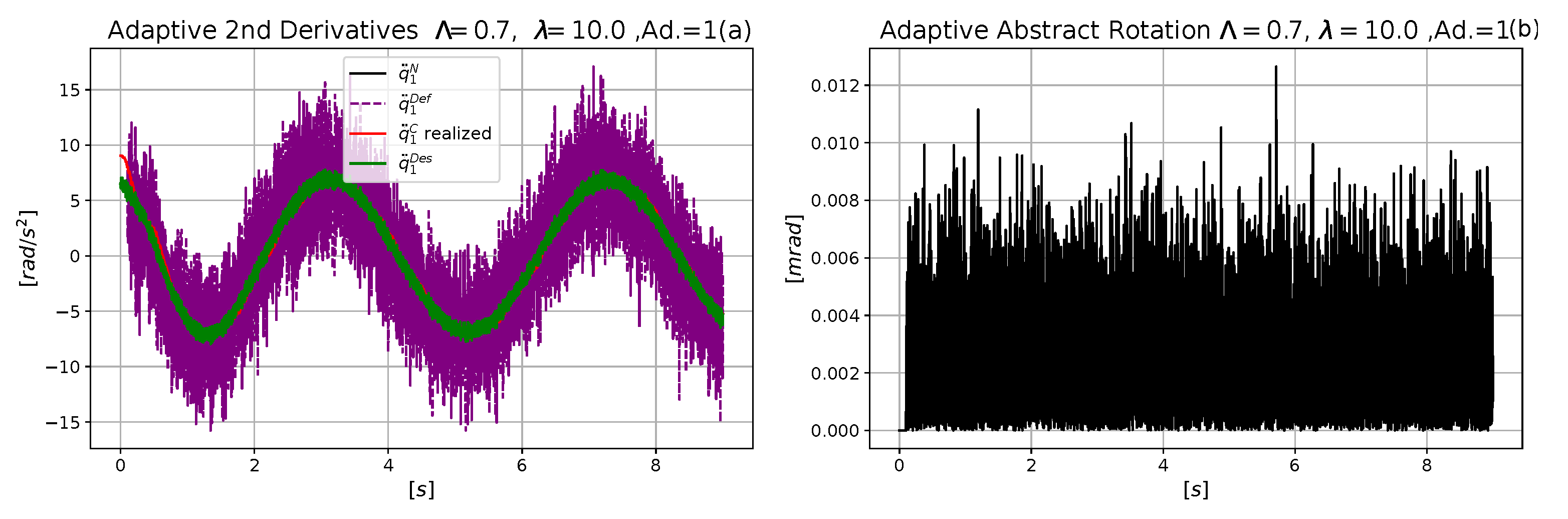
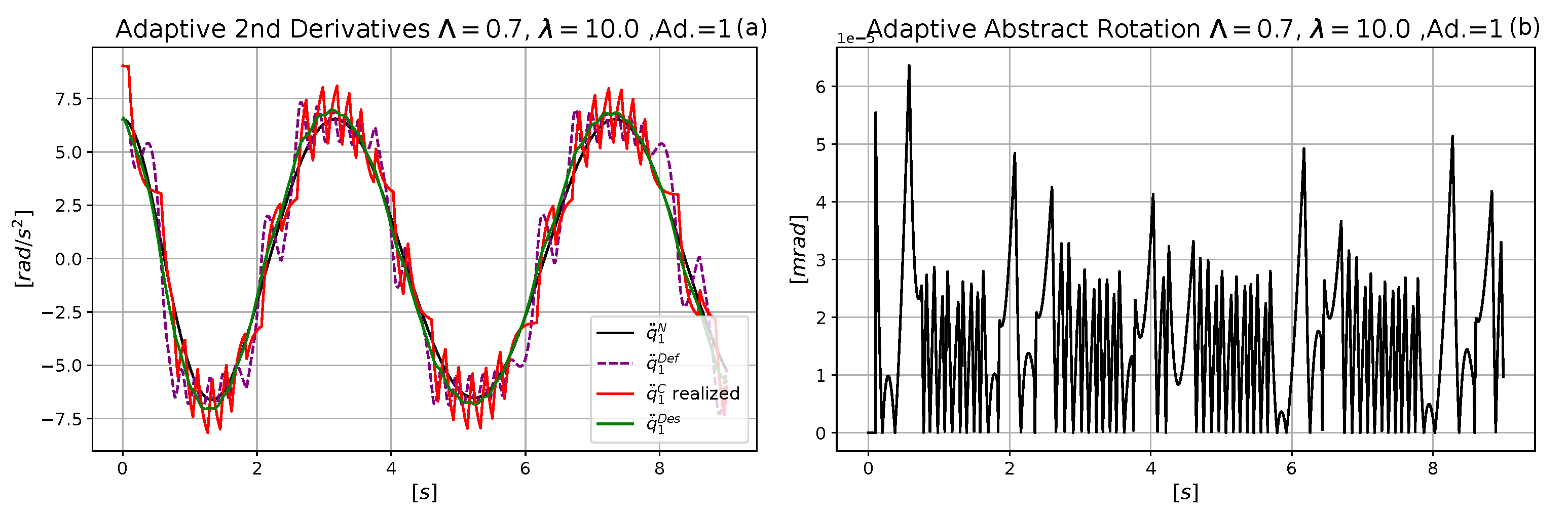
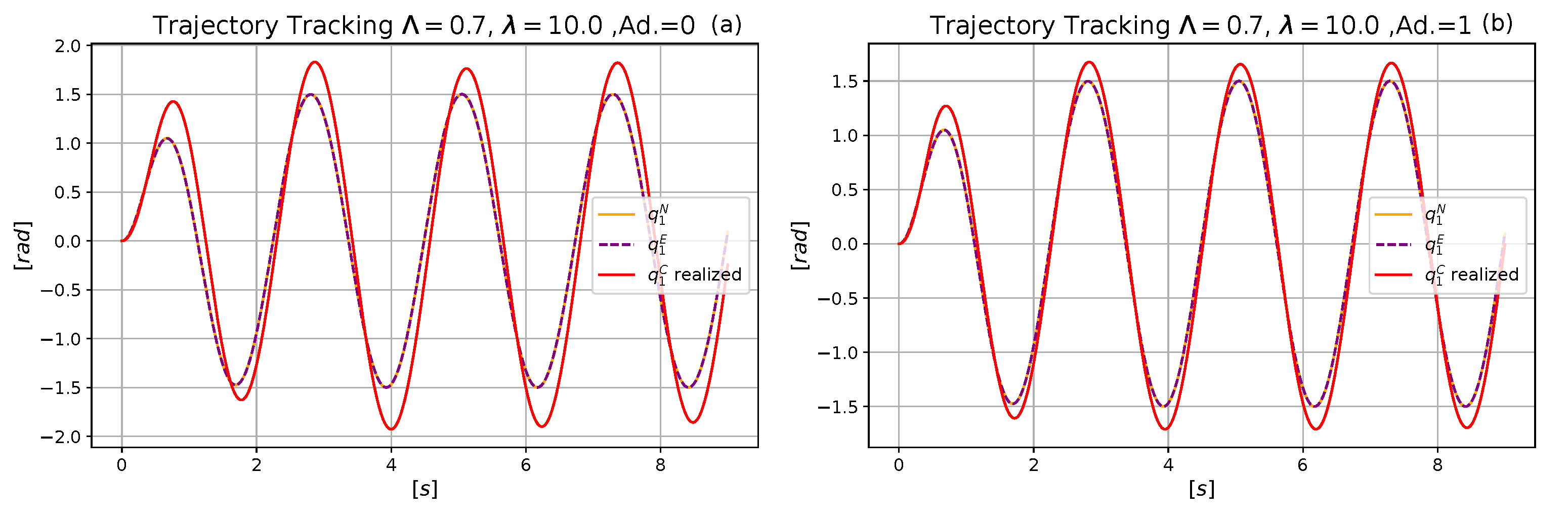
4.1. Comparative Analysis of the Performances of the Neural and the Exact Models
4.2. Estimation of the Computational Time of the Operations in the Control Cycles
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Bellman, R. Dynamic Programming and a new formalism in the calculus of variations. Proc. Natl. Acad. Sci. USA 1954, 40, 231–235. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R. Dynamic Programming; Princeton Univ. Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Lagrange, J.; Binet, J.; Garnier, J. Mécanique Analytique (Analytical Mechanics); Binet, J.P.M., Garnier, J.G., Eds.; Ve Courcier: Paris, France, 1811. [Google Scholar]
- Richalet, J.; Rault, A.; Testud, J.; Papon, J. Model predictive heuristic control: Applications to industrial processes. Automatica 1978, 14, 413–428. [Google Scholar] [CrossRef]
- Moldoványi, N. Model Predictive Control of Crystallisers. Ph.D. Thesis, Department of Process Engineering, University of Pannonia, Veszprém, Hungary, 2012. [Google Scholar]
- Pinsker, J.E.; Lee, J.B.; Dassau, E.; Seborg, D.E.; Bradley, P.K.; Gondhalekar, R.; Bevier, W.C.; Huyett, L.; Zisser, H.C.; Doyle, F.J. Randomized Crossover Comparison of Personalized MPC and PID Control Algorithms for the Artificial Pancreas. Diabetes Care 2016, 39, 1135–1142. [Google Scholar] [CrossRef] [Green Version]
- Bellemans, T.; Schutter, B.D.; Moor, B.D. Anticipative model predictive control for ramp metering in freeway networks. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4007–4082. [Google Scholar]
- Muthukumar, N.; Srinivasan, S.; Ramkumar, K.; Kannan, K.; Balas, V. Adaptive Model Predictive Controller for Web Transport Systems. Acta Polytech. Hung. 2016, 13, 181–194. [Google Scholar]
- Reda, A.; Bouzid, A.; Vásárhelyi, J. Model Predictive Control for Automated Vehicle Steering. Acta Polytech. Hung. 2020, 17, 163–182. [Google Scholar] [CrossRef]
- Armstrong, B.; Khatib, O.; Burdick, J. The Explicit Dynamic Model and Internal Parameters of the PUMA 560 Arm. In Proceedings of the 1986 IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 7–10 April 1986; pp. 510–518. [Google Scholar]
- Sciavicco, L.; Siciliano, B. Modeling and Control of Robot Manipulators; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Khalil, W.; Dombre, E. Modeling, Identification & Control of Robots; Hermes Penton Science: London, UK, 2002. [Google Scholar]
- Corke, P.; Armstrong-Helouvry, B. A Search for Consensus Among Model Parameters Reported for the PUMA 560 Robot. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 1608–1613. [Google Scholar]
- Márton, L.; Lantos, B. Identification and Model-based Compensation of Striebeck Friction. Acta Polytech. Hung. 2006, 3, 45–58. [Google Scholar]
- Canudas de Wit, C.; Olsson, H.; Åström, K.; Linschinsky, P. Dynamic friction models and control design. In Proceedings of the 1993 American Control Conference, San Francisco, CA, USA, 2–4 June 1993; Volume 40, pp. 1920–1926. [Google Scholar]
- Lyapunov, A. A General Task about the Stability of Motion. Ph.D. Thesis, University of Kazan, Tatarstan, Russia, 1892. (In Russian). [Google Scholar]
- Lyapunov, A. Stability of Motion; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall International, Inc.: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Nguyen, C.; Antrazi, S.; Zhou, Z.L.; Campbell, C., Jr. Adaptive Control of a Stewart Platform-based Manipulator. J. Robot. Syst. 1993, 10, 657–687. [Google Scholar] [CrossRef]
- Gahinet, P.; Apkarian, P.; Chilali, M. Affine parameter-dependent Lyapunov functions for real parametric uncertainty. IEEE Trans. Autom. Control 1994, 41, 436–442. [Google Scholar] [CrossRef]
- Tar, J.; Bitó, J.; Nádai, L.; Tenreiro Machado, J. Robust Fixed Point Transformations in Adaptive Control Using Local Basin of Attraction. Acta Polytech. Hung. 2009, 6, 21–37. [Google Scholar]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A. Novel Generation of Fixed Point Transformation for the Adaptive Control of a Nonlinear Neuron Model. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 10–13 October 2015; pp. 987–992. [Google Scholar]
- Dineva, A.; Tar, J.; Várkonyi-Kóczy, A.; Piuri, V. Generalization of a Sigmoid Generated Fixed Point Transformation from SISO to MIMO Systems. In Proceedings of the IEEE 19th International Conference on Intelligent Engineering Systems, Bratislava, Slovakia, 3–5 September 2015; pp. 135–140. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (About the Operations in the Abstract Sets and Their Application to Integral Equations). Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Dineva, A. Non-Conventional Data Representation and Control. Ph.D. Thesis, Óbuda University, Budapest, Hungary, 2016. [Google Scholar]
- Tar, J.; Bitó, J.; Rudas, I. Replacement of Lyapunov’s Direct Method in Model Reference Adaptive Control with Robust Fixed Point Transformations. In Proceedings of the 2010 IEEE 14th International Conference on Intelligent Engineering Systems, Las Palmas, Spain, 5–7 May 2010; pp. 231–235. [Google Scholar]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. Revisiting Lyapunov’s Technique in the Fixed Point Transformation-based Adaptive Control. In Proceedings of the 22nd IEEE International Conference on Intelligent Engineering Systems, Las Palmas de Gran Canaria, Spain, 21–23 June 2018; pp. 329–334. [Google Scholar]
- Csanádi, B.; Tar, J.; Bitó, J. Novel Model Reference Adaptive Control Designed by a Lyapunov Function that is Kept at Low Value by Fixed Point Iteration. In Topics in Intelligent Engineering and Informatics 14, Recent Advances in Intelligent Engineering Volume Dedicated to Imre J. Rudas’ Seventieth Birthday; Kovács, L., Haidegger, T., Szakál, A., Eds.; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 129–138. [Google Scholar]
- Csanádi, B.; Galambos, P.; Tar, J.; Györök, G.; Serester, A. A Novel, Abstract Rotation-based Fixed Point Transformation in Adaptive Control. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC2018), Miyazaki, Japan, 7–10 October 2018; pp. 2577–2582. [Google Scholar]
- Rodrigues, O. Des lois géometriques qui regissent les déplacements d’ un systéme solide dans l’ espace, et de la variation des coordonnées provenant de ces déplacement considérées indépendent des causes qui peuvent les produire (Geometric laws which govern the displacements of a solid system in space: And the variation of the coordinates coming from these displacements considered independently of the causes which can produce them). J. Math. Pures Appl. 1840, 5, 380–440. [Google Scholar]
- Weierstraß, K. Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen (On single variable continuous functions that nowhere are differentiable). In Königlich Preussichen Akademie der Wissenschaften, Mathematische Werke von Karl Weierstrass; Mayer & Mueller: Berlin, Germany, 1895; Volume 2, pp. 71–74. [Google Scholar]
- Weierstraß, K. Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen einer reellen Veränderlichen (About the analytical representability of so-called arbitrary functions of a real variable). In Sitzungsberichte der Akademie zu Berlin (Inaugural Lecture at the Academy of Berlin, 1885); Mathematische Werke von Karl Weierstrass, Mayer & Müller: Berlin, Germany, 1903; Volume 3, pp. 633–639, 789–805. [Google Scholar]
- Stone, M. A generalized Weierstrass approximation theorem. Math. Mag. 1948, 21, 237–254. [Google Scholar] [CrossRef]
- Hilbert, D. Mathematical Problems. Bull. Am. Math. Soc. 1902, 8, 437–479. [Google Scholar] [CrossRef] [Green Version]
- Volterra, V. Theory of Functionals and of Integrals and Integro-Differential Equations (Reprinted Translation of the Original Work in Spanish Issued in Madrid in 1927); Dover Publications: New York, NY, USA, 1959. [Google Scholar]
- Zoumpourlis, G.; Doumanoglou, A.; Vretos, N.; Daras, P. Non-linear Convolution Filters for CNN-based Learning. In Proceedings of the International Conference in Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar] [CrossRef] [Green Version]
- Arnold, V. On functions of Three Variables. Dokl. Akad. Nauk. SSSR 1957, 114, 679–681. (In Russian) [Google Scholar]
- Kolmogorov, A. On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition. Dokl. Akad. Nauk. SSSR 1957, 114, 953–956. (In Russian) [Google Scholar]
- Sprecher, D. On the Structure of Continuous Functions of Several Variables. Trans. Amer. Math. Soc. 1965, 115, 340–355. [Google Scholar] [CrossRef]
- Lorentz, G. Approximation of Functions; Holt, Reinhard and Winston: New York, NY, USA, 1965. [Google Scholar]
- Lorentz, G. Mathematical Developments Arising from Hilbert’s Problems; Browder, F., Ed.; American Mathematical Society: Providence, RI, USA, 1976; Volume 2, pp. 419–430. [Google Scholar]
- Blum, E.; Li, L. Approximation Theory and Feedforward Networks. Neural Netw. 1991, 4, 511–515. [Google Scholar] [CrossRef]
- Kůrková, V. Kolmogorov’s Theorem and Multilayer Neural Networks. Neural Netw. 1992, 5, 501–506. [Google Scholar] [CrossRef]
- Le Cun, Y.; Boser, B.; Denker, J.; Howard, R.; Habbard, W.; Jackel, L.; Henderson, D. Advances in Neural Information Processing Systems 2. Chapter Handwritten Digit Recognition with a Backpropagation Network; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1990; pp. 396–404. [Google Scholar]
- Kumar, R.; Banerjee, A.; Vemuri, B. Volterrafaces: Discriminant analysis using Volterra kernels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, FL, USA, 20–25 June 2009; pp. 150–155. [Google Scholar]
- Kohonen, T. Self-Organized Formation of Topologically Correct Feature Maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Hopfield, J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elman, J. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Liang, M.; Hu, X. Recurrent convolutional neural network for object recognition. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3367–3375. [Google Scholar]
- Zadeh, L. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Mohammadzadeh, A.; Sabzalian, M.; Zhang, W. An interval type-3 fuzzy system and a new online fractional-order learning algorithm: Theory and practice. IEEE Trans. Fuzzy Syst. 2019, 28, 1940–1950. [Google Scholar] [CrossRef]
- Kosko, B. Fuzzy Systems as Universal Approximators. IEEE Trans. Comput. 1992, 43, 1153–1162. [Google Scholar]
- Castro, J. Fuzzy Logic Controllers are Universal Approximators. IEEE Trans. SMC 1995, 25, 629–635. [Google Scholar] [CrossRef]
- Wang, L.X.; Mendel, J. Fuzzy Basis Functions, Universal Approximation and Orthogonal Least Squares Learning. IEEE Trans. Neural Netw. 1992, 3, 807–814. [Google Scholar] [CrossRef] [Green Version]
- Andoga, R.; Főző, L. Near Magnetic Field of a Small Turbojet Engine. Acta Phys. Pol. 2017, 131, 1117–1119. [Google Scholar] [CrossRef]
- Nyulászi, L.; Andoga, R.; Butka, P.; Főző, L.; Kovacs, R.; Moravec, T. Fault Detection and Isolation of an Aircraft Turbojet Engine Using a Multi-Sensor Network and Multiple Model Approach. Acta Polytech. Hung. 2018, 15, 189–209. [Google Scholar]
- Andoga, R.; Főző, L.; Schrötter, M.; Češkovič, M.; Szabo, S.; Bréda, R.; Schreiner, M. Intelligent Thermal Imaging-Based Diagnostics of Turbojet Engines. Appl. Sci. 2019, 9, 2253. [Google Scholar] [CrossRef] [Green Version]
- Andoga, R.; Főző, L.; Madarász, L.; Považan, J.; Judičák, J. Basic approaches in adaptive control system design for small turbo-compressor engines. In Proceedings of the IEEE 18th International Conference on Intelligent Engineering Systems (INES 2014), Tihany, Hungary, 3–5 July 2014; pp. 95–99. [Google Scholar]
- Főző, L.; Andoga, R.; Kovács, L.; Schreiner, M.; Beneda, K.; Savka, J.; Soušek, R. Virtual Design of Advanced Control Algorithms for Small Turbojet Engines. Acta Polytech. Hung. 2019, 16, 101–117. [Google Scholar] [CrossRef]
- Magoulas, G.; Vrahatis, N.; Androulakis, G. Effective Backpropagation Training with Variable Stepsize. Neural Netw. 1997, 10, 69–82. [Google Scholar] [CrossRef]
- Kinnenbrock, W. Accelerating the Standard Backpropagation Method Using a Genetic Approach. Neurocomputing 1994, 6, 583–588. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Moscato, P. On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms. Caltech Concurrent Computation Program, Report 826; Caltech: Pasadena, CA, USA, 1989. [Google Scholar]
- Földesi, P.; Botzheim, J.; Kóczy, L. Eugenic bacterial memetic algorithm for fuzzy road transport traveling salesman problem. Int. J. Innov. Comput. 2009, 7, 2775–2798. [Google Scholar]
- Botzheim, J.; Toda, Y.; Kubota, N. Bacterial memetic algorithm for offline path planning of mobile robots. Memetic Comput. 2012, 4, 73–86. [Google Scholar] [CrossRef]
- Botzheim, J.; Toda, Y.; Kubota, N. Bacterial memetic algorithm for simultaneous optimization of path planning and flow shop scheduling problems. Artif. Life Robot. 2012, 17, 107–112. [Google Scholar] [CrossRef]
- Nelder, J.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Lagarias, J.; Reeds, J.; Wright, M.; Wright, P. Convergence properties of the Nelder-Mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Galántai, A. A convergence analysis of the Nelder-Mead simplex method. Acta Polytech. Hung. 2021, 18, 93–105. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Solteiro Pires, E.; Tenreiro Machado, J.; de Moura Oliveira, P. Dynamic Shannon Performance in a Multiobjective Particle Swarm Optimization. Entropy 2019, 21, 827. [Google Scholar] [CrossRef] [Green Version]
- Moser, B. Sugeno Controllers with a Bounded Number of Rules are Nowhere Dense. Int. J. Gen. Syst. 1999, 28, 269–277. [Google Scholar] [CrossRef]
- Tikk, D. On Nowhere Denseness of Certain Fuzzy Controllers Containing Prerestricted Number of Rules. Tatra Mt. Math. Publ. 1999, 16, 369–377. [Google Scholar]
- Klement, E.; Kóczy, L.; Moser, B. Are fuzzy systems universal approximators? Int. J. Gen. Syst. 1999, 28, 259–282. [Google Scholar] [CrossRef]
- Baranyi, P.; Szeidl, L.; Várlaki, P.; Yam, Y. Definition of the HOSVD-based canonical form of polytopic dynamic models. In Proceedings of the 3rd International Conference on Mechatronics (ICM 2006), Budapest, Hungary, 3–5 July 2006; pp. 660–665. [Google Scholar]
- Baranyi, P.; Szeidl, L.; Várlaki, P.; Yam, Y. Numerical reconstruction of the HOSVD-based canonical form of polytopic dynamic models. In Proceedings of the 10th International Conference on Intelligent Engineering Systems, London, UK, 26–28 June 2006; pp. 196–201. [Google Scholar]
- Golub, G.; Kahan, W. Calculating the singular values and pseudoinverse of a matrix. SIAM J. Numer. Anal. 1965, 2, 205–224. [Google Scholar]
- Lathauwer, L.; Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef] [Green Version]
- Tikk, D.; Baranyi, P.; Patton, R.; Rudas, I.; Tar, J. Design Methodology of Tensor Product Based Control Models via HOSVD LMIs. In Proceedings of the 2002 IEEE International Conference on Industrial Technology, IEEE ICIT ’02, Bankok, Thailand, 11–14 December 2002; pp. 1290–1295. [Google Scholar]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control Theory; SIAM Books: Philadelphia, PA, USA, 1994. [Google Scholar]
- Gahinet, P.; Nemirovskii, A.; Laub, A.; Chilali, M. The LMI Control Toolbox. In Proceedings of the 1994 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 3, pp. 2038–2041. [Google Scholar] [CrossRef]
- Colaneri, P. Analysis and Control of Linear Switched Systems (Lecture Notes); Politecnico Di Milano: Milan, Italy, 2009. [Google Scholar]
- Li, Q.K.; Zhao, J.; Dimirovski, G.M. Tracking control for switched time-varying delay systems with stabilizable and unstabilizable subsystems. Nonlinear Anal. Hybrid Syst. 2009, 3, 133–142. [Google Scholar] [CrossRef]
- Horváth, Z.; Edelmayer, A. Robust Model-Based Detection of Faults in the Air Path of Diesel Engines. Acta Univ. Sapientiae Electr. Mech. Eng. 2015, 7, 5–22. [Google Scholar]
- Eigner, G.; Tar, J.; Rudas, I.; Kovács, L. LPV-based quality interpretations on modeling and control of diabetes. Acta Polytech. Hung. 2016, 13, 171–190. [Google Scholar] [CrossRef]
- Redjimi, H.; Tar, J.K. A Simple Soft Computing Structure for Modeling and Control. Machines 2021, 9, 168. [Google Scholar] [CrossRef]
- van der Pol, B. Forced oscillations in a circuit with non-linear resistance (reception with reactive triode). Lond. Edinb. Dublin Philos. Mag. J. Sci. 1927, 7, 65–80. [Google Scholar] [CrossRef]
- Emelyanov, S.; Korovin, S.; Levantovsky, L. Higher Order Sliding Regimes in the Binary Control Systems. Sov. Phys. 1986, 31, 291–293. [Google Scholar]
- Utkin, V. Sliding Modes in Optimization and Control Problems; Springer: New York, NY, USA, 1992. [Google Scholar]
- Levant, A. Arbitrary-order Sliding Modes with Finite Time Convergence. In Theory and Practice of Control and Systems, Proceedings of the 6th IEEE Mediterranean Conference on Control and Systems, Sardinia, Italy, 9–11 June 1998; Tornambe, A., Perdon, A.M., Eds.; World Scientific, 1999; pp. 349–354. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.6.7836&rep=rep1&type=pdf (accessed on 24 August 2021).
- Lantos, B.; Bodó, Z. High Level Kinematic and Low Level Nonlinear Dynamic Control of Unmanned Ground Vehicles. Acta Polytech. Hung. 2019, 16, 97–117. [Google Scholar]
- de Oliveira, E.C.; Tenreiro Machado, J.A. A Review of Definitions for Fractional Derivatives and Integral. Math. Probl. Eng. 2014, 2014, 6. [Google Scholar] [CrossRef] [Green Version]
- Folea, S.; De Keyser, R.; Birs, I.R.; Muresan, C.I.; Ionescu, C. Discrete-Time Implementation and Experimental Validation of a Fractional Order PD Controller for Vibration Suppression in Airplane Wings. Acta Polytech. Hung. 2017, 14, 191–206. [Google Scholar]
- Tar, J.; Bitó, J.; Kovács, L.; Faitli, T. Fractional Order PID-Type Feedback in Fixed Point Transformation-Based Adaptive Control of the FitzHugh-Nagumo Neuron Model with Time-Delay. In Proceedings of the 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; IFAC: New York, NY, USA, 2018; pp. 906–911. [Google Scholar]
- Varga, A.; Eigner, G.; Rudas, I.; Tar, J. Experimental and Simulation-Based Performance Analysis of a Computed Torque Control (CTC) Method Running on a Double Rotor Aeromechanical Testbed. Electronics 2021, 10, 1745. [Google Scholar] [CrossRef]




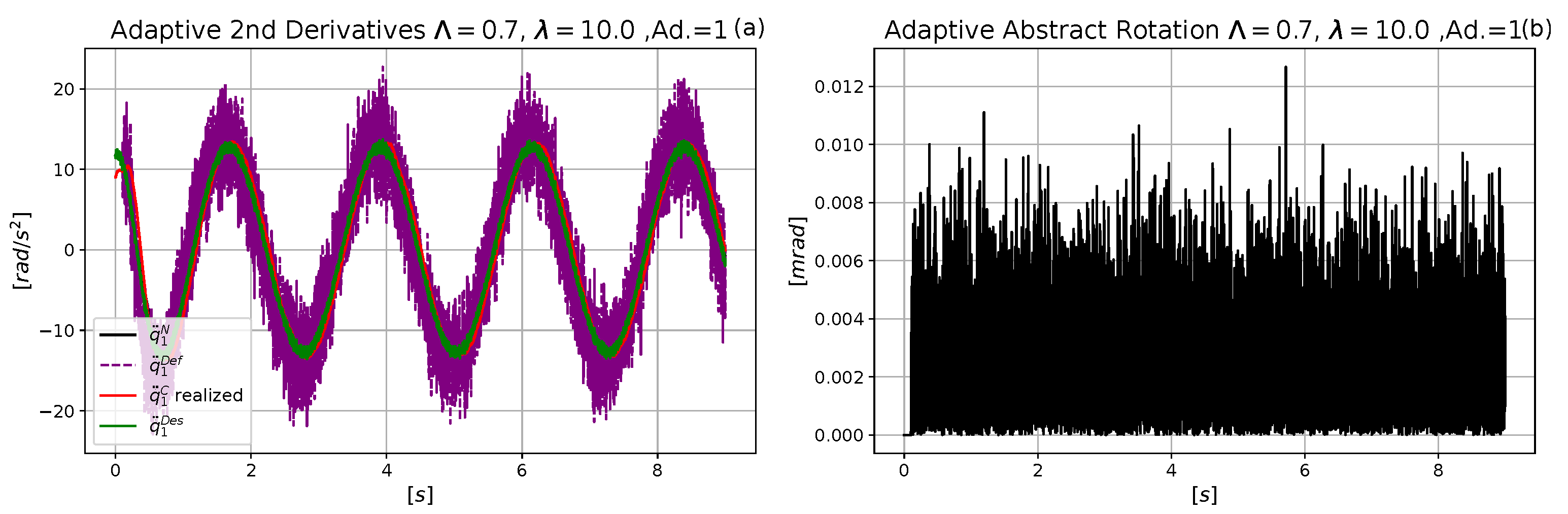

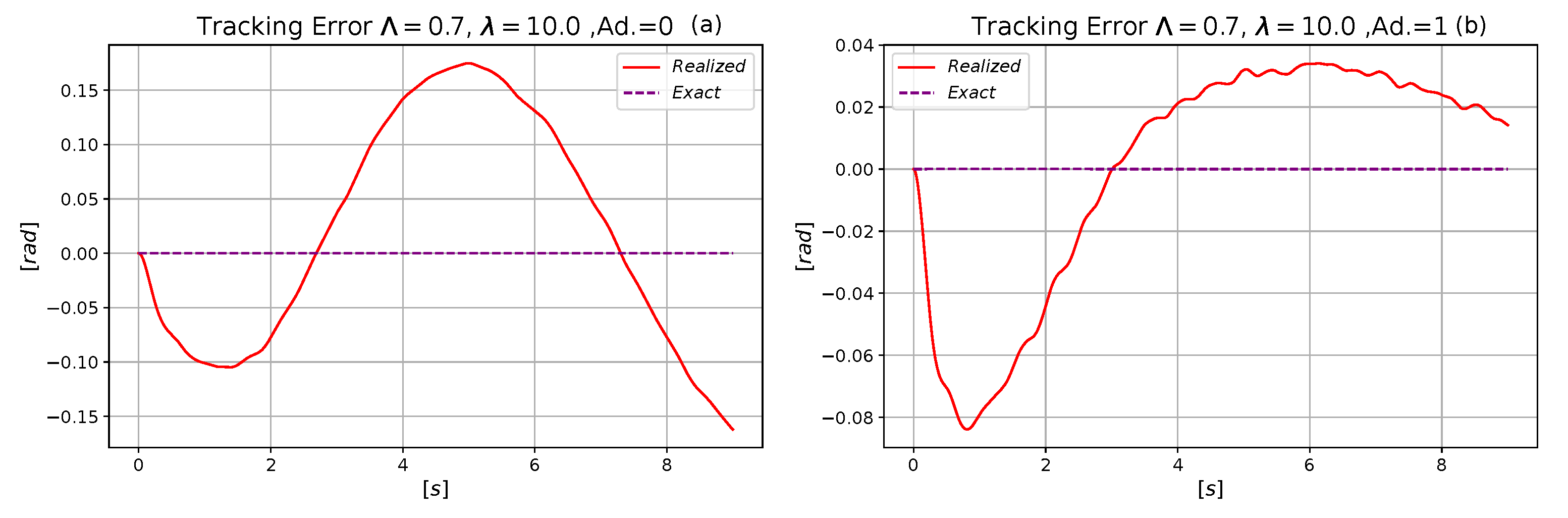
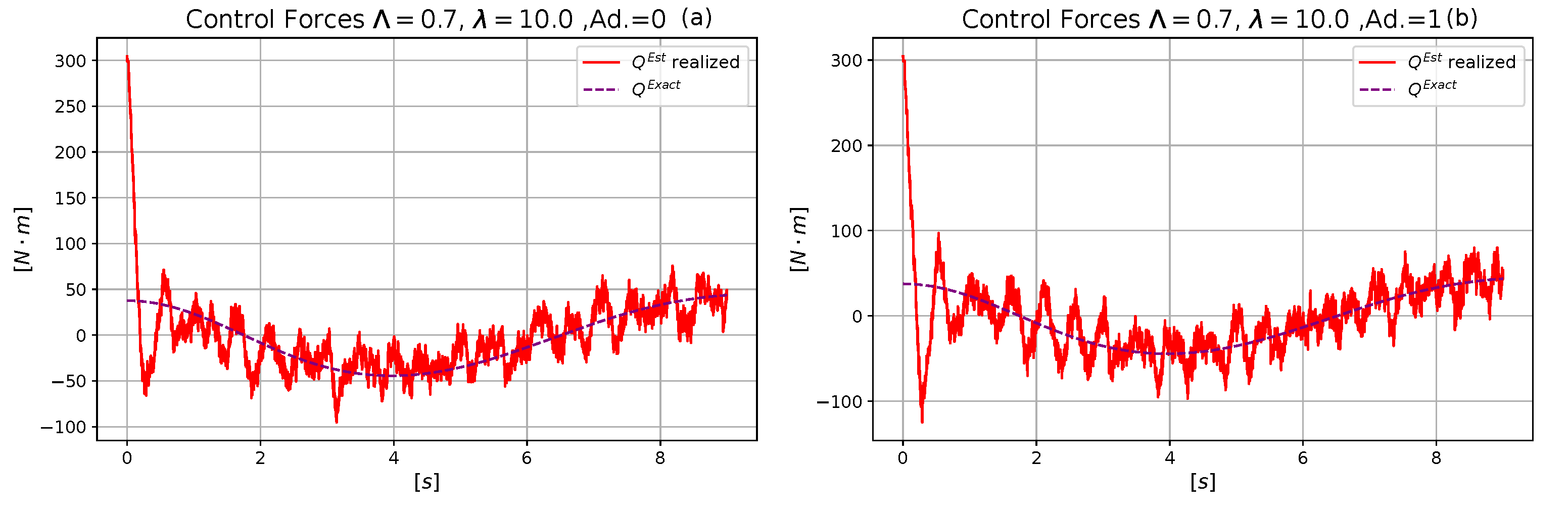

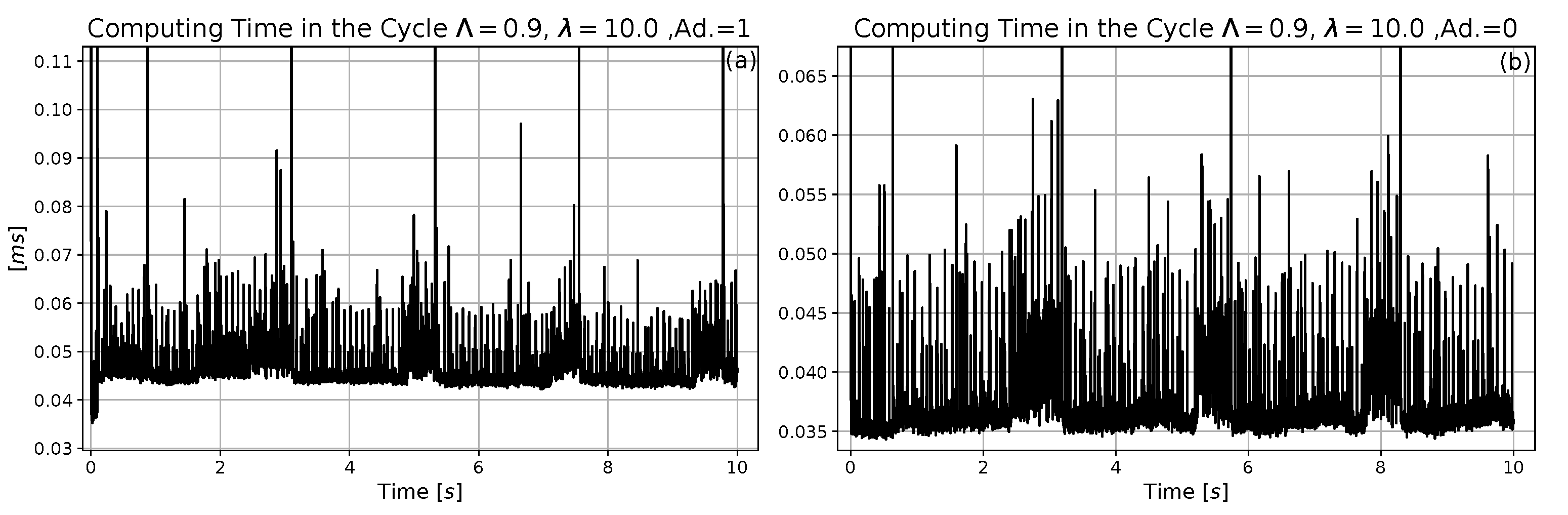

| Parameter | Measurement Unit | Numerical Value |
|---|---|---|
| Inertia momentum of the wheel | ||
| Inertia of the mass-point m | ||
| Spring constant k | ||
| Spoke length r | ||
| Gravitational acceleration g | ||
| Damping constant along the spoke d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bitó, J.F.; Rudas, I.J.; Tar, J.K.; Varga, Á. Abstract Rotations for Uniform Adaptive Control and Soft Modeling of Mechanical Devices. Appl. Sci. 2021, 11, 7939. https://doi.org/10.3390/app11177939
Bitó JF, Rudas IJ, Tar JK, Varga Á. Abstract Rotations for Uniform Adaptive Control and Soft Modeling of Mechanical Devices. Applied Sciences. 2021; 11(17):7939. https://doi.org/10.3390/app11177939
Chicago/Turabian StyleBitó, János F., Imre J. Rudas, József K. Tar, and Árpád Varga. 2021. "Abstract Rotations for Uniform Adaptive Control and Soft Modeling of Mechanical Devices" Applied Sciences 11, no. 17: 7939. https://doi.org/10.3390/app11177939
APA StyleBitó, J. F., Rudas, I. J., Tar, J. K., & Varga, Á. (2021). Abstract Rotations for Uniform Adaptive Control and Soft Modeling of Mechanical Devices. Applied Sciences, 11(17), 7939. https://doi.org/10.3390/app11177939







