Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance
Abstract
:1. Introduction
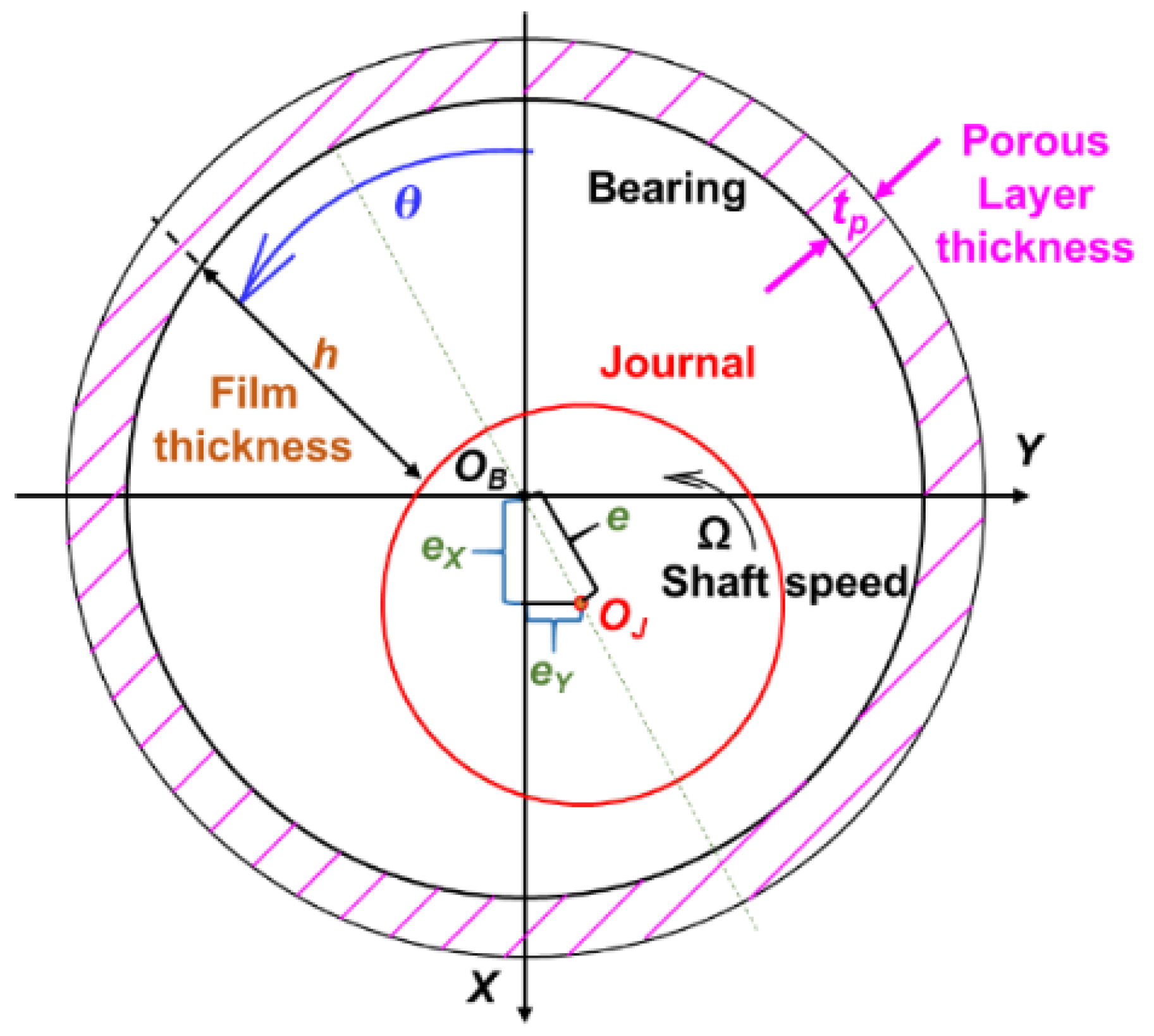
2. The Governing Equations for a PGB and Derived Operating Parameters
3. An Appraisal of the Past Literature
4. A Close Form Solution to the Flow and Dynamic Force Coefficients in a PGB
5. PGB Aerostatic Operation
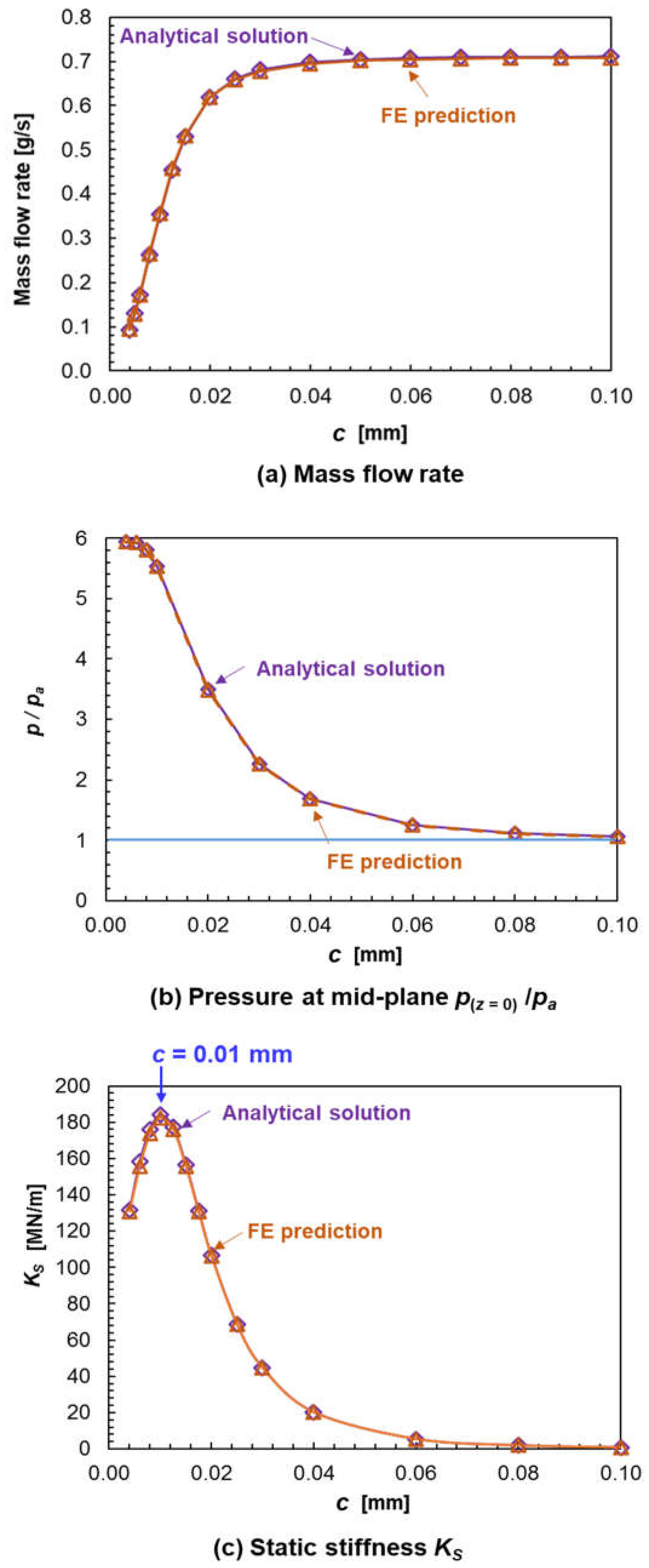
6. Experimental Estimation of Porous Material Permeability Coefficient (κ)
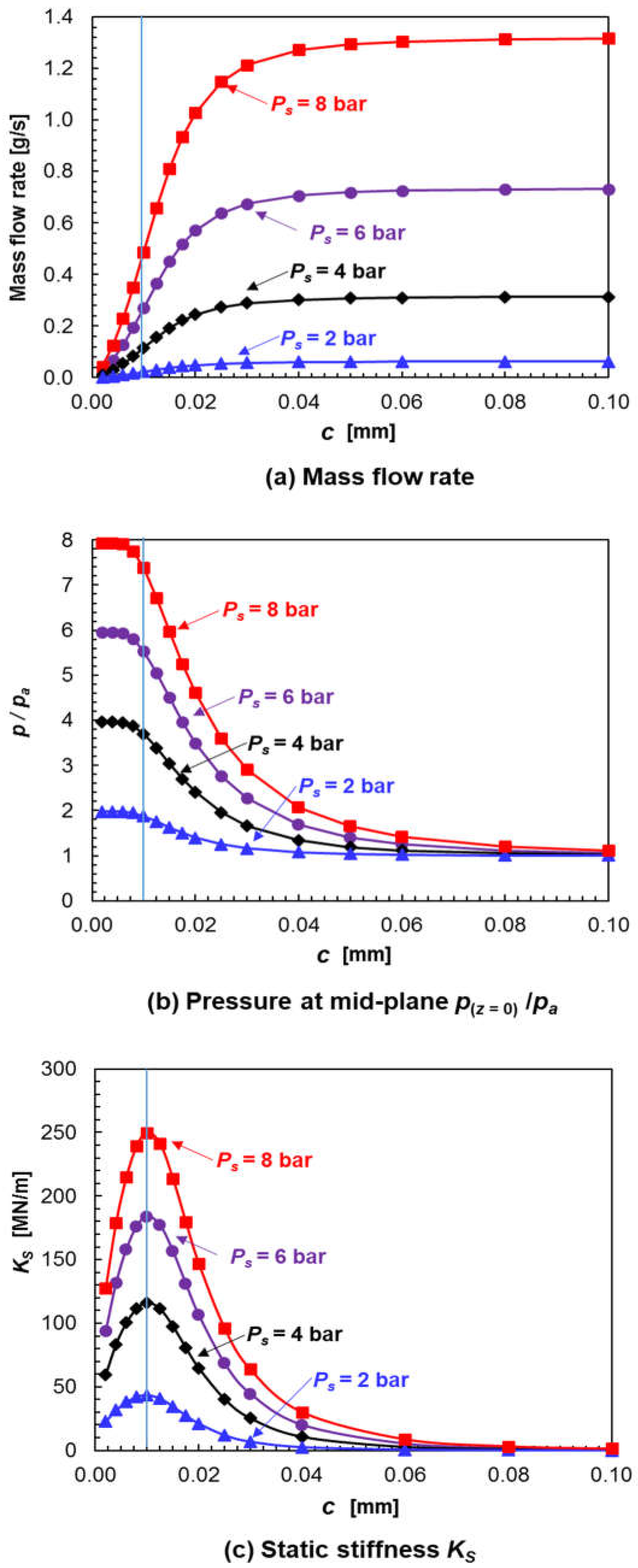
7. PGB Mass Flow Rate, Peak Pressure, and Aerostatic Stiffness vs. Clearance
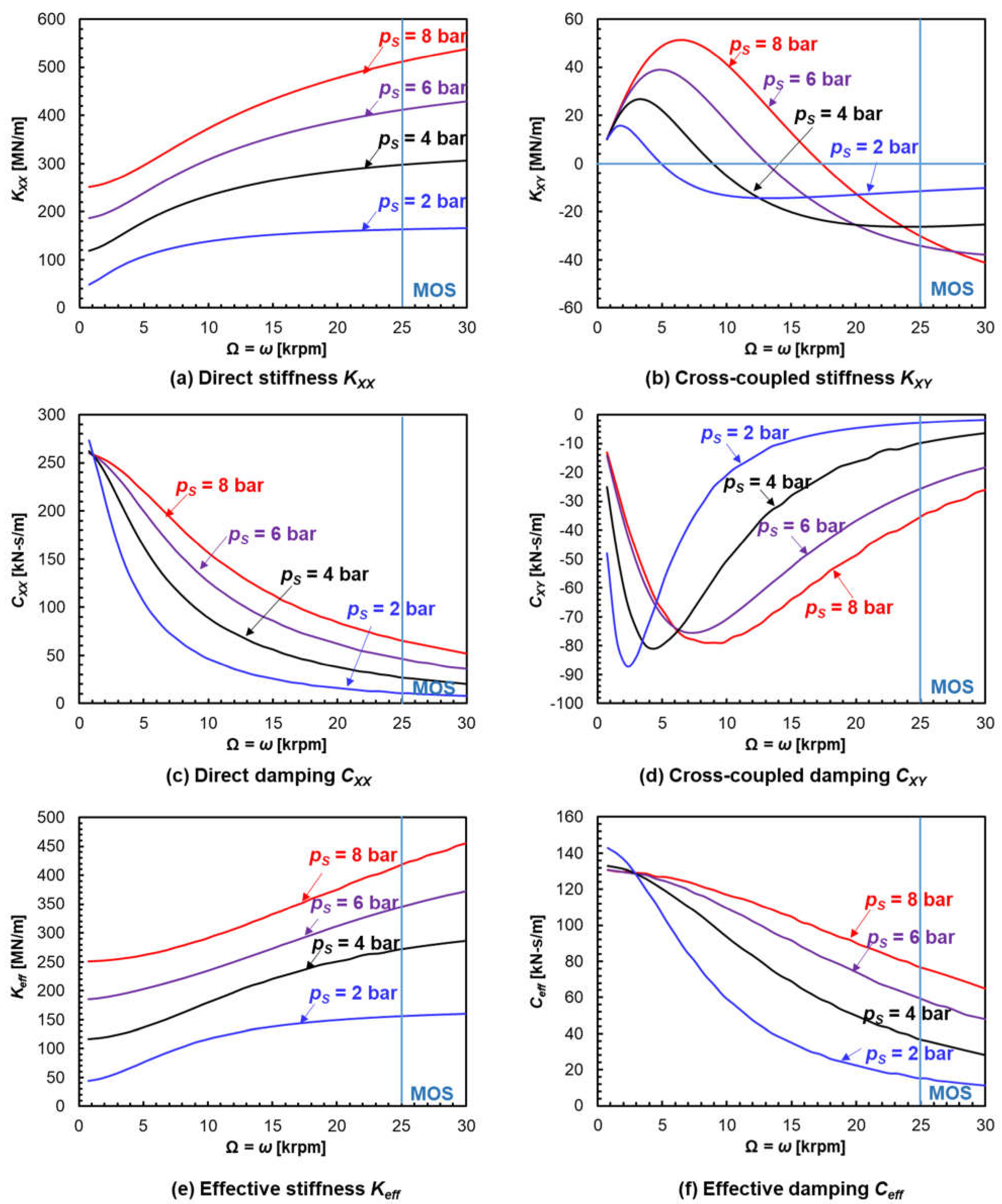
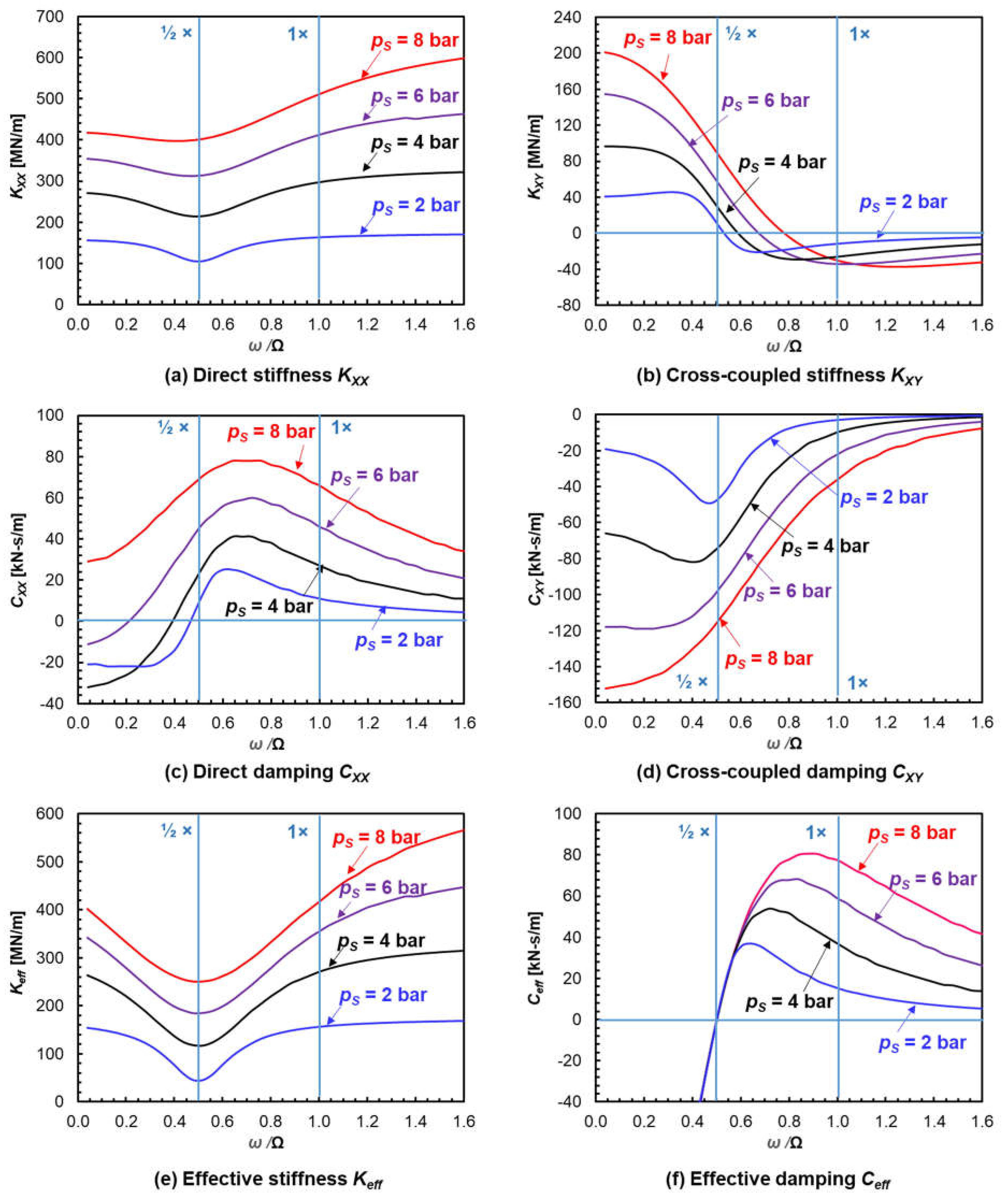
8. PGB Force Coefficients vs. Rotor Speed (Synchronous Frequency Condition)
9. PGB Force Coefficients vs. Excitation Frequency
10. Stability of PGB
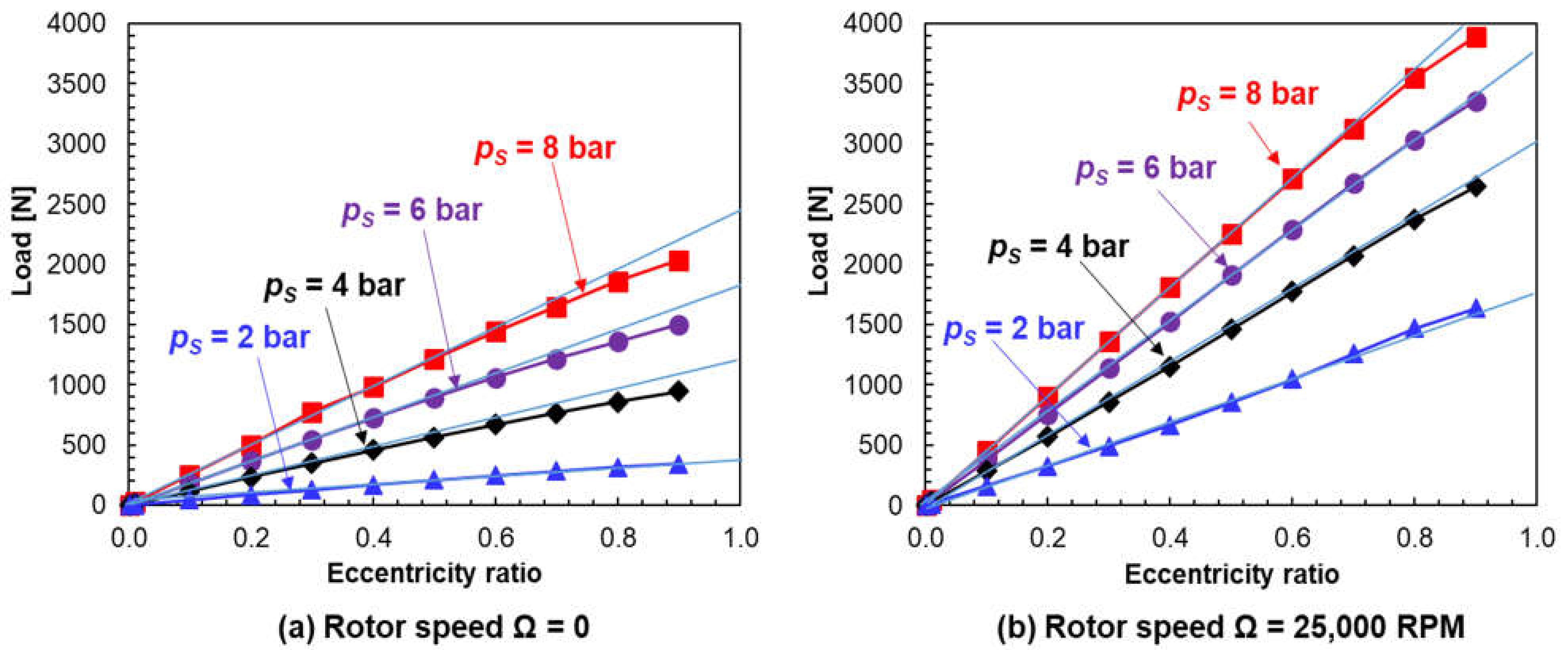
11. PGB Load Capacity and Attitude Angle
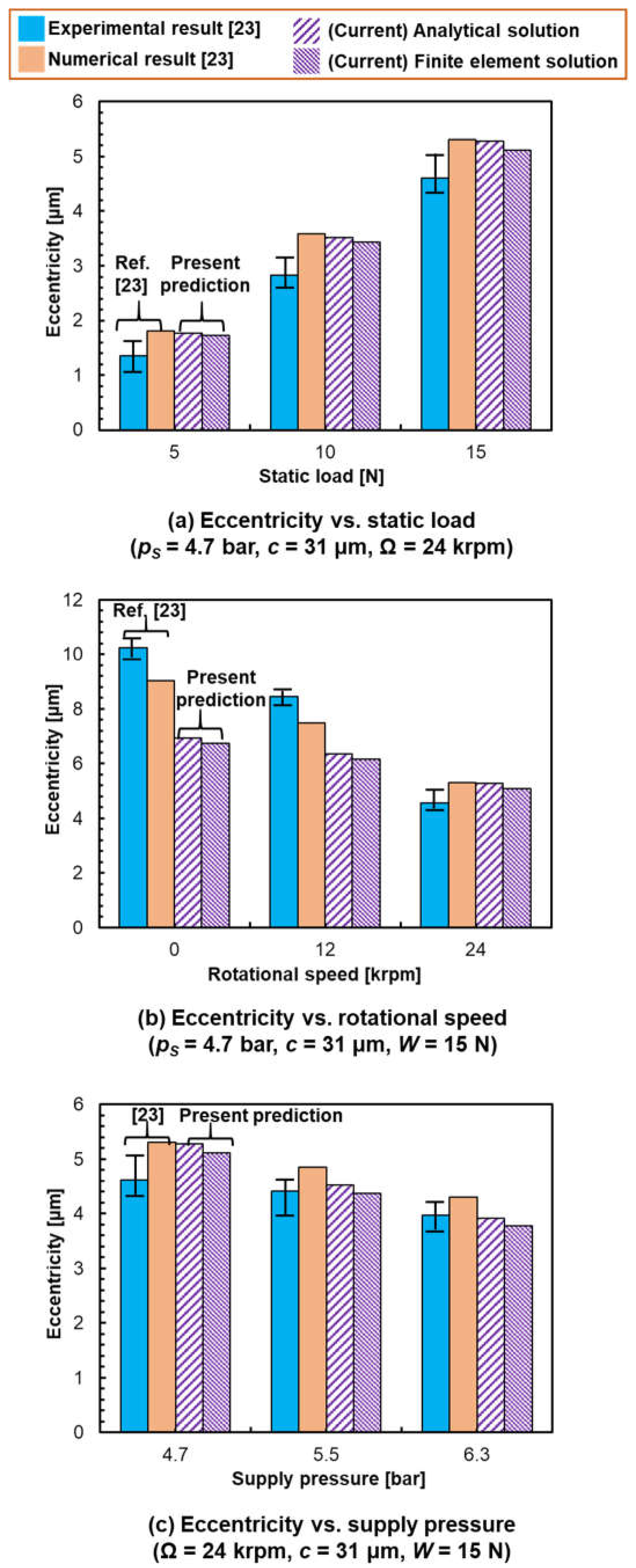
12. An Example of Validation for the Static Performance of a PGB
13. Conclusions
- For a given external pressure, the supplied flow rate increases quickly as the bearing clearance enlarges and ultimately reaches a flow limit.
- There is a narrow clearance region that ensures the maximum centering stiffness for a PGB. Selecting the appropriate clearance is necessary and rather difficult to achieve when also considering manufacturing costs and devising procedures for easy installation.
- The load capacity of a PGB under aerostatic conditions is a fraction of the imposed pressure difference and the bearing projected area (L × D). The bearing load is proportional to the static eccentricity.
- Under aerodynamic conditions, i.e., operation with shaft speed, the PGB load capacity still remains proportional to shaft eccentricity and can be much larger than the aerostatic load. That is, shaft speed shear flow effects increase the PGB load capacity.
- For operation as the shaft speed varies from low (start-up) to the mean operating speed (MOS = Ω*) and above, the PGB bearing shows synchronous excitation (ω = Ω) force coefficients that increase in magnitude as pS increases. Most importantly, as the shaft speed increases, Keff increases (hardens) while Ceff decreases rapidly.
- For operation at a constant (high) speed, the bearing effective stiffness (Keff) decreases at low whirl frequencies, reaches a dip or minimum at ½ whirl frequency operation (ω = ½ Ω), and then increases (hardens) as the frequency approaches synchronous speed (ω → Ω) and surpasses it. The bearing effective damping coefficient Ceff < 0 at low frequencies and equals zero at ω = ½ Ω. For larger ω, Ceff > 0 and reaches a peak at a certain frequency; the larger the external pressure pS, the higher the frequency at which Ceff is a maximum. For larger frequencies (ω >> Ω), Ceff → 0.
- Note a PGB operating with shaft rotation (hybrid mode) has the same stability restriction as a plain cylindrical hydrodynamic bearing, i.e., a 50% whirl frequency ratio. However, a rigid rotor–PGB system natural frequency is rather large, since the bearing centering stiffness grows with both external pressurization and shaft speed. Hence, the threshold speed of instability, equal to two times the system natural frequency, can be tailored to exceed the system operating speed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| c | Bearing radial clearance (m) |
| cκ | (12 κ tp)1/3. Equivalent clearance for layer of porous material (m) |
| Ceff | Ceff = (CXX − KXY/ω). Effective damping coefficient (N-s/m) |
| CXX, CYY | Direct damping coefficients (N-s/m) |
| CXY, CYX | Cross-coupled damping coefficients (N-s/m) |
| D | 2R. Rotor diameter (m) |
| e | Journal eccentricity (m) |
| (eX, eY) | Components of journal eccentricity (m), |
| (FX, FY) | Bearing reaction force components along X and Y directions (N) |
| He | Equivalent complex stiffness at threshold speed of instability (N/m) |
| HXX, HYY | Direct complex stiffness coefficients (N/m) |
| HXY, HYX | Cross coupled complex stiffness coefficients (N/m) |
| h | Film thickness (m) |
| KS | PGB aerostatic (zero frequency) stiffness coefficient (N/m) |
| Keff | Keff = KXX + CXY ·ω. Effective stiffness coefficient (N/m) |
| KΩ | . PGB hybrid (zero frequency) stiffness coefficient (N/m) |
| KXX, KYY | Direct stiffness coefficients (MN/m) |
| KXY, KYX | Cross-coupled stiffness coefficients (MN/m) |
| L | Bearing axial length (m) |
| Mr | Mass of point rotor (kg) |
| Mcr | Mcr = Keff/. Rotor critical mass (kg) |
| Mass flow rate through a porous gas bearing (kg/s) | |
| Maximum mass flow rate for a porous gas bearing as c → ꝏ (kg/s) | |
| p | Absolute pressure (bar) |
| pS, pa | Supply and ambient absolute pressures (bar) |
| Rg | Gas constant (J/(kg K)) |
| T | Supply/ambient temperature (K) |
| To | Drag torque (Nm). Power loss = (To Ω) |
| tp | Porous layer radial thickness (m) |
| W | Applied load (N) |
| W* | ((pS − pa) L D). Nominal load for aerostatic operation |
| x = Rθ, z | Coordinate system on bearing surface |
| X, Y | Cartesian coordinate system |
| β | Attitude angle (deg) |
| Λκ = γ2 | . PGB feed flow parameter |
| ΛΩ | . PGB speed number, |
| Λω | . PGB frequency number. |
| κ | Permeability coefficient for the porous material (m2) |
| μ | Gas absolute viscosity (Pa-s) |
| ρ | p/(RgT). Gas density (kg/m3) |
| θ | Circumferential coordinate (-) |
| ω | Whirl frequency (rad/s) |
| = ωn = ½ ΩT. Whirl frequency = natural frequency at threshold speed of instability (rad/s) | |
| Ω | Rotor speed (rad/s) |
| ΩT | Threshold speed of rotor stability (rad/s) |
| Abbreviations | |
| FE | Finite element |
| FD | Finite difference |
| LPM | Liter per minute |
| MOS | Mean operating speed |
| PGB | Porous gas bearing |
| SSV | Subsynchronous whirl vibration |
References
- San Andrés, L. Modern Lubrication Theory, Notes 15: Gas Bearings for Oil-Free MTM; Texas A&M University Digital Libraries: College Station, TX, USA, 2020; Available online: http://oaktrust.library.tamu.edu/handle/1969.1/93197 (accessed on 27 June 2021).
- San Andrés, L.; Yang, J.; McGowan, R. Measurements of Static and Dynamic Load Performance of a 102 mm Carbon-Graphite Porous Surface Tilting-Pad Gas Journal Bearing. ASME J. Eng. Gas Turbines Power 2021. in print. [Google Scholar] [CrossRef]
- New Way Air Bearings. Air Bearing Application and Design Guide. Revision E. January 2006. Available online: https://www.newwayairbearings.com/sites/default/files/new_way_application_and_design_guide_%20Rev_E_2006-01-18.pdf (accessed on 27 June 2021).
- San Andrés, L.; Yang, J.; Devitt, A. About Tilting Pad Carbon-Graphite Porous Gas Bearings: Measurements in a Rotordynamic Test Rig and Predictions. Tribol. Trans. 2021. in print. [Google Scholar] [CrossRef]
- Gargiulo, E., Jr. Porous Wall Gas Lubricated Journal Bearings: Theoretical Investigation. ASME J. Lubr. Tech. 1979, 101, 458–465. [Google Scholar] [CrossRef]
- Sneck, H.; Yen, K. The Externally Pressurized, Porous Wall, Gas Lubricated Journal Bearing. ASLE Trans. 1964, 7, 288–298. [Google Scholar] [CrossRef]
- Sneck, H.; Elwell, R. The Externally Pressurized, Porous Wall, Gas Lubricated Journal Bearing. ASLE Trans. 1965, 8, 339–345. [Google Scholar] [CrossRef]
- Sneck, H.; Yen, K. The Externally Pressurized, Porous Wall, Gas Lubricated Journal Bearing. ASLE Trans. 1967, 10, 339–347. [Google Scholar] [CrossRef]
- Kwan, Y.P.B.; Corbett, J. Porous Aerostatic Bearings—An Updated Review. Wear 1998, 222, 69–73. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Permeability and Inertial Coefficients of Porous Media for Air Bearing Feeding Systems. ASME J. Tribol. 2007, 129, 705–711. [Google Scholar] [CrossRef]
- Mori, H.; Yabe, H.; Yamakage, H.; Furukawa, J. Theoretical Analysis of Externally Pressurized Porous Journal Gas Bearings (1st Report). Bull JSME 1968, 11, 527–535. [Google Scholar] [CrossRef] [Green Version]
- Mori, H.; Yabe, H.; Yamakage, H. Theoretical Analysis of Externally Pressurized Porous Journal Gas Bearings (2nd Report, Journal Bearing with Solid Sleeves). Bull. JSME 1968, 11, 1512–1518. [Google Scholar] [CrossRef] [Green Version]
- Rao, N.S.; Majumdar, B.C. Dynamic Stiffness and Damping Coefficients of Aerostatic, Porous, Journal Gas Bearings. J. Mech. Eng. Sci. 1978, 20, 291–296. [Google Scholar] [CrossRef]
- Hwang, P. Pneumatic Hammer. Encyclopedia of Tribology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 2545–2548. [Google Scholar]
- Lund, J.W. Calculation of Stiffness and Damping Properties of Gas Bearings. ASME J. Lubr. Tech. 1968, 90, 793–804. [Google Scholar] [CrossRef]
- Gargiulo, E., Jr. Porous Wall Gas Lubricated Journal Bearings: Experimental Investigation. ASME J. Lubr. Tech. 1979, 101, 466–473. [Google Scholar] [CrossRef]
- Miyatake, M.; Yoshimoto, S.; Sato, J. Whirling Instability of a Rotor Supported by Aerostatic Porous Journal Bearings with a Surface-Restricted Layer. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 95–103. [Google Scholar] [CrossRef]
- Otsu, Y.; Miyatake, M.; Yoshimoto, S. Dynamic Characteristics of Aerostatic Porous Journal Bearings with a Surface-Restricted Layer. ASME J. Tribol. 2011, 133, 011701. [Google Scholar] [CrossRef]
- San Andrés, L.; Jeung, S.-H.; Rohmer, M.; Devitt, D. Experimental Assessment of Drag and Rotordynamic Response for A Porous Type Gas Bearing. In Proceedings of the Extended Abstract, STLE Annual Meeting, Dallas, TX, USA, 17–21 May 2015; pp. 17–21. [Google Scholar]
- San Andrés, L.; Cable, A.T.; Zheng, Y.; De Santiago, O.; Devitt, D. Assessment of Porous Type Gas Bearings: Measurements of Bearing Performance and Rotor Vibrations. In Proceedings of the ASME Turbo Expo 2016: Turbine Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. ASME Paper GT2016-57876. [Google Scholar]
- Feng, K.; Wu, Y.; Liu, W.; Zhao, X.; Li, W. Theoretical Investigation on Porous Tilting Pad Bearings Considering Tilting Pad Motion and Porous Material Restriction. Precis. Eng. 2018, 53, 26–37. [Google Scholar] [CrossRef]
- Liu, W.; Feng, K.; Huo, Y.; Guo, Z. Measurements of the Rotordynamic Response of a Rotor Supported on Porous Type Gas Bearing. ASME J. Eng. Gas Turbines Power 2018, 140, 102501. [Google Scholar] [CrossRef]
- Li, W.; Wang, S.; Zhao, K.; Feng, K.; Hou, W. Numerical and Experimental Investigation on the Performance of Hybrid Porous Gas Journal Bearings. Lubr. Sci. 2020, 33, 60–68. [Google Scholar] [CrossRef]
- Bohle, M. Numerical Investigation of the Flow in Hydrostatic Journal Bearings with Porous Materials. In Proceedings of the ASME 2018 5th Joint US-European Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 15–20 July 2018. paper No. FEDSM 2018-83437. [Google Scholar]
- Lawrence, T.; Kemple, M. Numerical Method for Studying Bearing Gap Pressure Wave Development and Subsequent Performance Mapping of Externally Pressurized Gas Journal Bearings. In Proceedings of the ASME-JSME-KSME 8th Joint Fluids Engineering Conference, San Francisco, CA, USA, 28 July–1 August 2019. Paper No. AJKFluids 2019-4732. [Google Scholar]
- San Andrés, L. Hybrid Flexure Pivot-Tilting Pad Gas Bearings: Analysis and Experimental Validation. ASME J. Tribol. 2006, 128, 551–558. [Google Scholar] [CrossRef]
- NewWay® Air Bearings. Specification Sheet for Porous MediaTM Air Bushing, 3.00 Inch Inside Diameter. Part No. 3307501. Available online: https://www.newwayairbearings.com/catalog/product/air-bushings-english-3-00-inch-id/ (accessed on 27 June 2021).
- Feng, K. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha, China. Personal communication, 2021. [Google Scholar]


| Bearing Length, L = 1.17 D | 88.8 mm (3.5 inch) |
| inner diameter, D | 76.2 mm (3.0 inch) |
| outer diameter, Dout | 99.5 mm (3.9 inch) |
| Carbon-graphite permeability, κ | 8.2 × 10−16 m2 |
| Porous layer radial thickness, tp | 2.71 mm (0.11 inch) |
| Equivalent clearance for porous layer, cκ | 3 μm |
| Supply pressure, pS | 2–8 bar |
| Exit pressure, pa | 1 bar |
| Temperature, T | 294 K |
| Air density at (pa, T), ρa | 1.2 kg/m3 |
| viscosity at (pS, T), μ | 18.3 × 10−6 Pa-s |
| gas constant, Rg | 287.05 J/(kg·K) |
| Parameters | For c = 0.010 mm |
| Feed flow parameter | Λκ= = 5.3 |
| At pS = 6 bar, and Ω = ω = 22,618 rad/s (25 krpm) | |
| Speed and frequency numbers | ΛΩ= = 7, Λω= = 14 |
| Pressure | Aerostatic (Ω = 0) | Hybrid | Ω = 25 krpm | Attitude Angle | Critical Mass | ||
|---|---|---|---|---|---|---|---|
| pS | KS | KXX | KXY | KΩ | β | KΩKS | Mcr |
| Bar | MN/m | MN/m | MN/m | MN/m | degrees | kg | |
| 2 bar | 43 | 156 | 41 | 162 | 14.6 | 3.76 | 26.2 |
| 4 bar | 116 | 271 | 96 | 288 | 19.6 | 2.48 | 68.8 |
| 6 bar | 184 | 354 | 155 | 387 | 23.6 | 2.10 | 107.7 |
| 8 bar | 250 | 418 | 201 | 464 | 25.7 | 1.85 | 146.1 |
| KXY = 0 |
| Bearing Length, L | 57 mm |
| Inner diameter, D | 25 mm (*) |
| Radial clearance, c | 16 μm, 31 μm |
| Porous layer radial thickness, tp | 2.5 mm |
| permeability coefficient, κ | 1.0 × 10−15 m2 |
| Equivalent clearance porous layer, cκ | 3.1 μm |
| Supply pressure, pS | 4–6 bar (*) |
| Exit pressure, pa | 1 bar |
| Ambient temperature, T | 293 K |
| Air density at (pa, T), ρa | 1.2 kg/m3 |
| viscosity at (pa, T), μ | 18.5 × 10−6 Pa-s |
| Parameters | For c = 0.031 mm, pS = 4.7 bar, and Ω = 2513 rad/s (24 krpm) |
| Feed flow parameter | Λκ = 0.025 |
| Speed number | ΛΩ = 0.097 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés, L.S.; Yang, J.; Devitt, A. Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance. Appl. Sci. 2021, 11, 7949. https://doi.org/10.3390/app11177949
Andrés LS, Yang J, Devitt A. Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance. Applied Sciences. 2021; 11(17):7949. https://doi.org/10.3390/app11177949
Chicago/Turabian StyleAndrés, Luis San, Jing Yang, and Andrew Devitt. 2021. "Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance" Applied Sciences 11, no. 17: 7949. https://doi.org/10.3390/app11177949
APA StyleAndrés, L. S., Yang, J., & Devitt, A. (2021). Porous Gas Journal Bearings: An Exact Solution Revisited and Force Coefficients for Stable Rotordynamic Performance. Applied Sciences, 11(17), 7949. https://doi.org/10.3390/app11177949







