Optimization of Neural Network-Based Self-Tuning PID Controllers for Second Order Mechanical Systems
Abstract
:1. Introduction
2. Methods
2.1. Simulator for PID Control
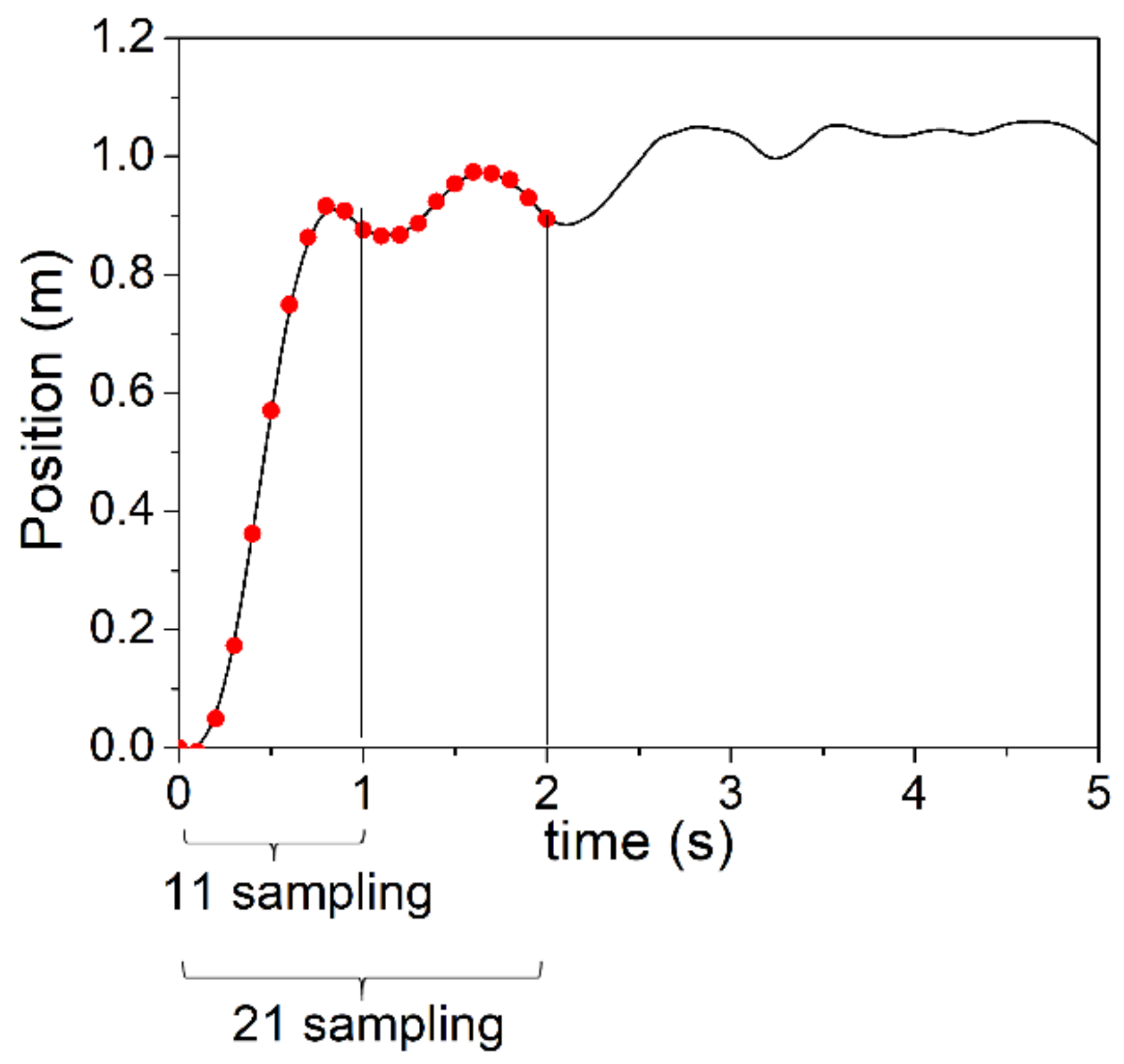
2.2. Data Acquisition for Learning and Testing
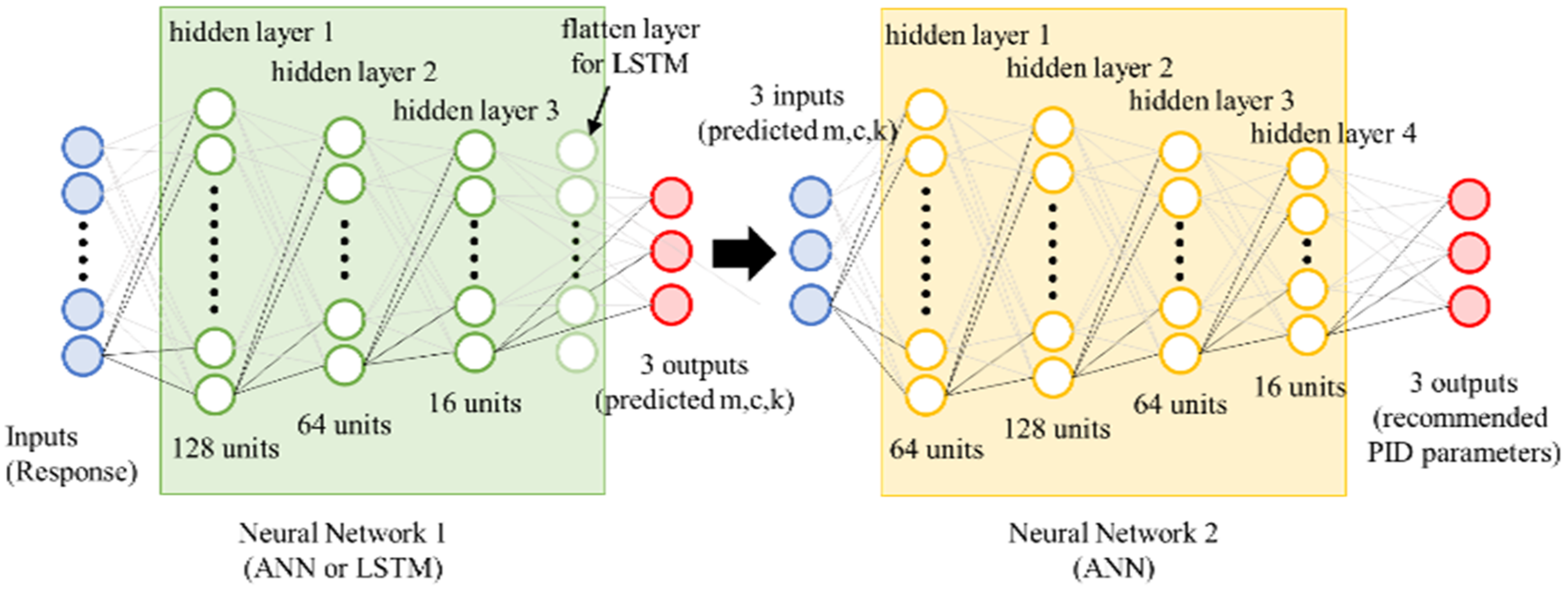
2.3. Learning Process
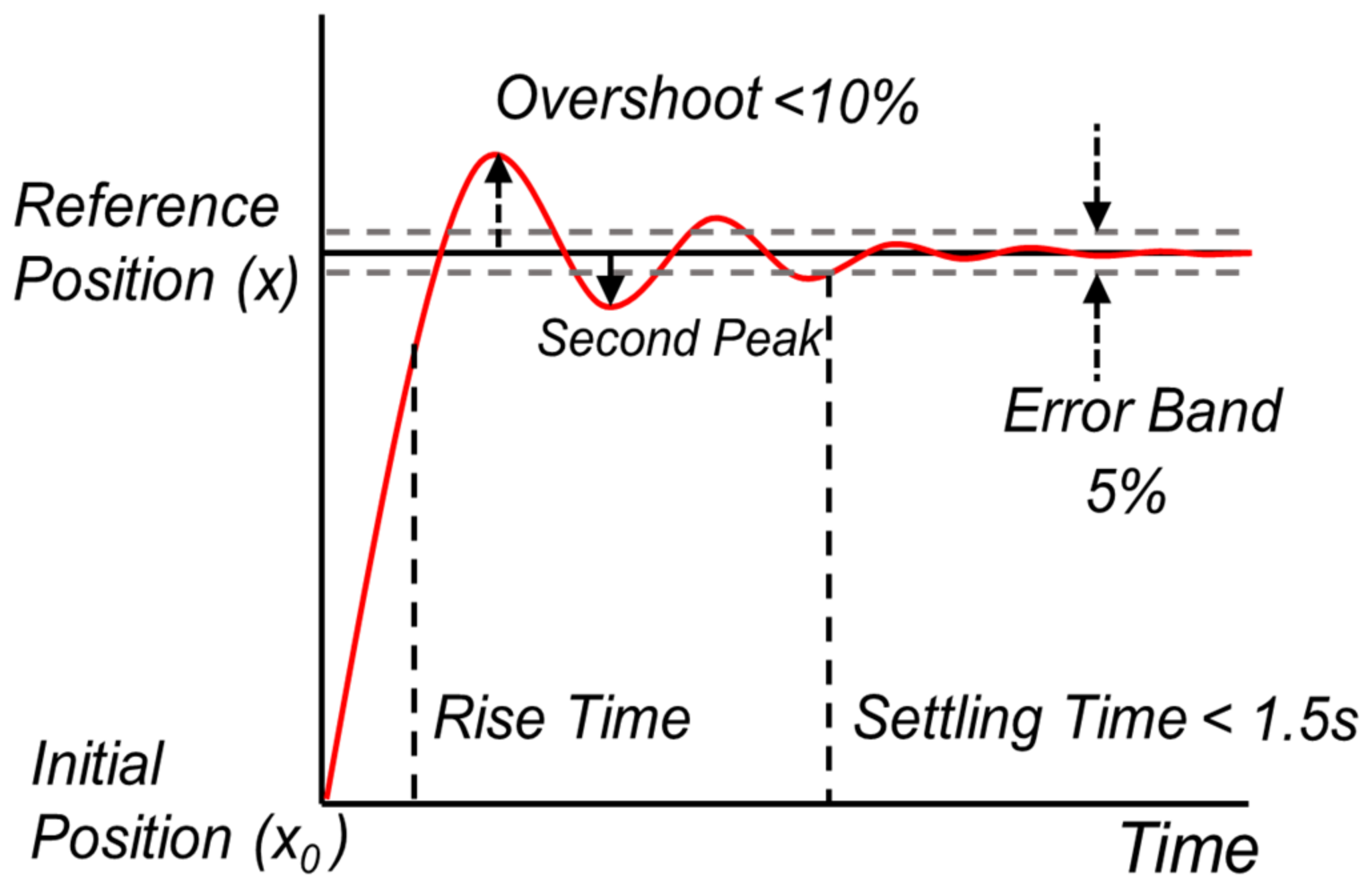
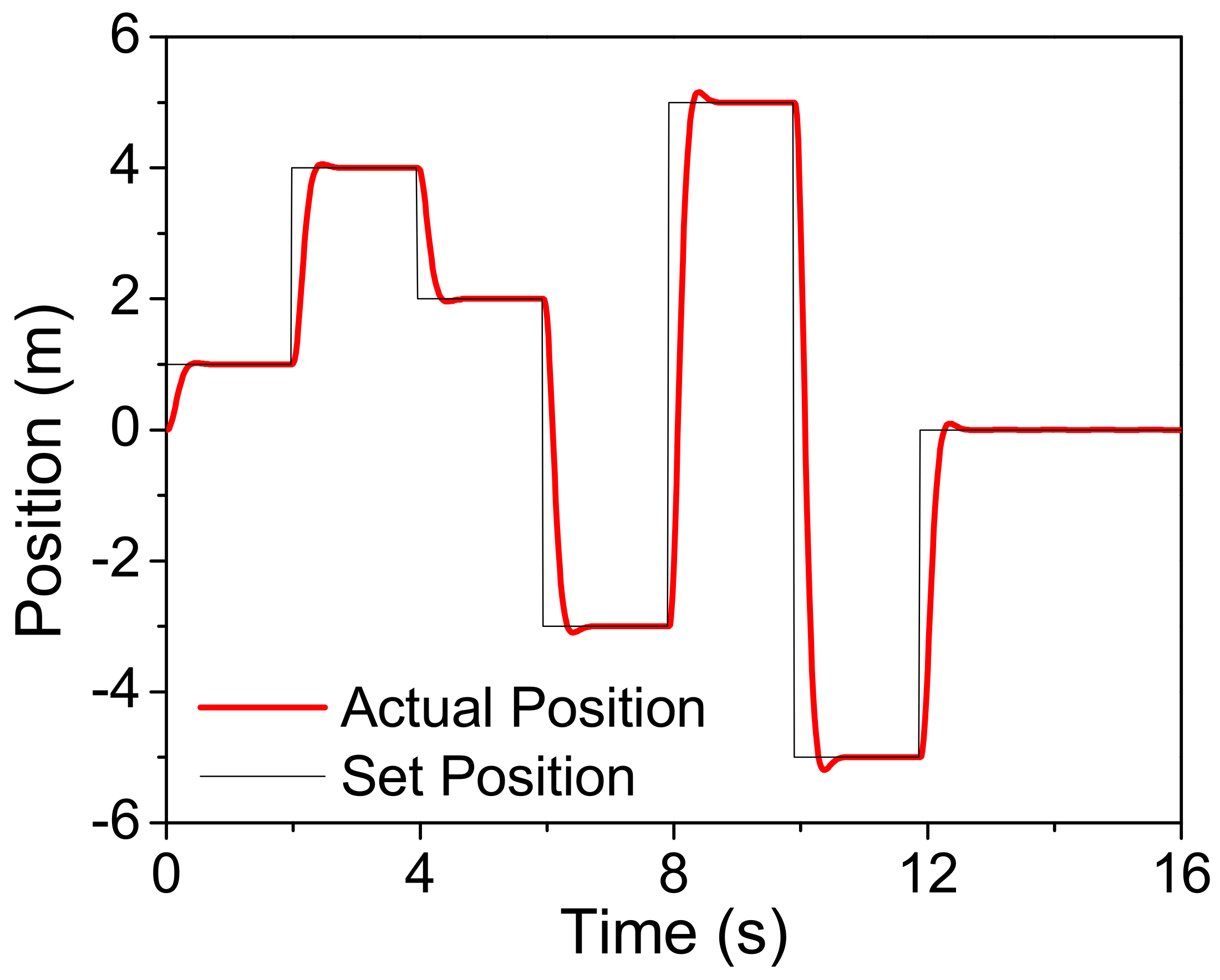
2.4. Inference and Performance Evaluation
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bennett, S. A Brief History of Automatic Control. IEEE Control Syst. Mag. 1996, 16, 17–25. [Google Scholar] [CrossRef]
- Bennett, S. Development of the PID Controller. IEEE Control Syst. Mag. 1993, 13, 58–62. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID Control System Analysis, Design, and Technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, J.G.; Nichols, N.B. Optimum Settings for Automatic Controllers. J. Dyn. Syst. Meas. Control Trans. ASME 1993, 115, 220–222. [Google Scholar] [CrossRef]
- Cohen, G.H.; Coon, G.A. Theoretical Consideration of Retarded Control. Trans. ASME 1953, 75, 827–834. [Google Scholar]
- Chien, K.L.; Hrons, J.A.; Reswick, J.B. On the Automatic Control of Generalized Passive Systems. Trans. Am. Soc. Mech. Eng. 1972, 74, 175–185. [Google Scholar]
- Åström, K.J.; Hägglund, T.; Hang, C.C.; Ho, W.K. Automatic Tuning and Adaptation for PID Controllers—A Survey. IFAC Proc. Vol. 1992, 25, 371–376. [Google Scholar] [CrossRef]
- Luyben, W.L. Tuning Proportional-Integral-Derivative Controllers for Integrator/Deadtime Processes. Ind. Eng. Chem. Res. 1996, 35, 3480–3483. [Google Scholar] [CrossRef]
- Maiti, D.; Acharya, A.; Chakraborty, M.; Konar, A.; Janarthanan, R. Tuning Pid and Piλdδ Controllers Using the Integral Time Absolute Error Criterion. In Proceedings of the 2008 4th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 12–14 December 2008; pp. 457–462. [Google Scholar]
- Foley, M.W.; Julien, R.H.; Copeland, B.R. A Comparison of PID Controller Tuning Methods. Can. J. Chem. Eng. 2005, 83, 712–722. [Google Scholar] [CrossRef]
- Portillo, J.; Marcos, M.; Orive, D.; López, F.; Pérez, F. PID_ATC: A Real-Time Tool for PID Control and Auto-Tuning. IFAC Proc. Vol. 1998, 31, 41–46. [Google Scholar] [CrossRef]
- Starr, K.D.; Petersen, H.; Bauer, M. Control Loop Performance Monitoring—ABB’s Experience over Two Decades. Proc. IFAC-PapersOnLine 2016, 49, 526–532. [Google Scholar] [CrossRef]
- Sutikno, J.P.; Chin, S.Y.; Abdul Aziz, B.B.; Mamat, R. Experimental Implementation of the Mp-GM (Maximum Peak—Gain Margin) Tuning Method: A Tuning Method for 2DOF-IMC under Uncertainty Process. In Proceedings of the 2012 International Conference on Systems and Informatics, Yantai, China, 19–20 May 2012; pp. 414–418. [Google Scholar]
- Sukede, A.K.; Arora, J. Auto Tuning of PID Controller. In Proceedings of the 2015 International Conference on Industrial Instrumentation and Control, Pune, India, 28–30 May 2015; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 6 July 2015; pp. 1459–1462. [Google Scholar]
- Versteeg, H.J.; Jansma, H.J.; Turner, K. Evaluation of Commercially Available Adaptive Controllers. Journal A 1986, 27, 120–126. [Google Scholar]
- Berner, J.; Soltesz, K.; Hägglund, T.; Åström, K.J. An Experimental Comparison of PID Autotuners. Control Eng. Pract. 2018, 73, 124–133. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Gouda, M.M.; Danaher, S.; Underwood, C.P. Fuzzy Logic Control Versus Conventional PID Control for Controlling Indoor Temperature of a Building Space. IFAC Proc. Vol. 2000, 33, 249–254. [Google Scholar] [CrossRef]
- Tang, K.S.; Man, K.F.; Chen, G.; Kwong, S. An Optimal Fuzzy PID Controller. IEEE Trans. Ind. Electron. 2001, 48, 757–765. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Oh, S.J. A Fuzzy PID Controller for Nonlinear and Uncertain Systems. Soft Comput. 2000, 4, 123–129. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Singh, M.; Chandra, A. Application of Adaptive Network-Based Fuzzy Inference System for Sensorless Control of PMSG-Based Wind Turbine with Nonlinear-Load-Compensation Capabilities. IEEE Trans. Power Electron. 2011, 26, 165–175. [Google Scholar] [CrossRef]
- Chang, F.J.; Chang, Y.T. Adaptive Neuro-Fuzzy Inference System for Prediction of Water Level in Reservoir. Adv. Water Resour. 2006, 29, 1–10. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Sun, L.; Xue, W.; Li, D.; Zhu, H.; Su, Z. gang Quantitative Tuning of Active Disturbance Rejection Controller for FOPDT Model with Application to Power Plant Control. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Hu, K.; Lee, K.Y.; Pan, F. On Tuning and Practical Implementation of Active Disturbance Rejection Controller: A Case Study from a Regenerative Heater in a 1000 MW Power Plant. Ind. Eng. Chem. Res. 2016, 55, 6686–6695. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Saleh Alshandoli, A.F. On Replacing a PID Controller with Neural Network Controller for Segway. In Proceedings of the 2020 International Conference on Electrical Engineering, Yogyakarta, Indonesia, 1–2 October 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 25 September 2020. [Google Scholar]
- Cheon, K.; Kim, J.; Hamadache, M.; Lee, D. On Replacing PID Controller with Deep Learning Controller for DC Motor System. J. Autom. Control Eng. 2015, 3, 452–456. [Google Scholar] [CrossRef]
- Salloom, T.; Yu, X.; He, W.; Kaynak, O. Adaptive Neural Network Control of Underwater Robotic Manipulators Tuned by a Genetic Algorithm. J. Intell. Robot. Syst. Theory Appl. 2020, 97, 657–672. [Google Scholar] [CrossRef]
- Jung, S.; Kim, S.S. Control Experiment of a Wheel-Driven Mobile Inverted Pendulum Using Neural Network. IEEE Trans. Control Syst. Technol. 2008, 16, 297–303. [Google Scholar] [CrossRef]
- Wang, X.-S.; Cheng, Y.-H.; Sun, W. A Proposal of Adaptive PID Controller Based on Reinforcement Learning. J. China Univ. Min. Technol. 2007, 17, 40–44. [Google Scholar] [CrossRef]
- Shipman, W.J.; Coetzee, L.C. Reinforcement Learning and Deep Neural Networks for PI Controller Tuning. Proc. IFAC-PapersOnLine 2019, 52, 111–116. [Google Scholar] [CrossRef]
- Arzaghi-Haris, D. Adaptive PID Controller Based on Reinforcement Learning for Wind Turbine Control. In Proceedings of the 6th WSEAS International Conference on Environment, Ecosystems and Development, Timisoara, Romania, 21–23 October 2010; p. 7. [Google Scholar]
- Sun, Q.; Du, C.; Duan, Y.; Ren, H.; Li, H. Design and Application of Adaptive PID Controller Based on Asynchronous Advantage Actor–Critic Learning Method. Wirel. Netw. 2019, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Isaksson, A.J.; Graebe, S.F. Model Reduction for PID Design. IFAC Proc. Vol. 1993, 26, 467–472. [Google Scholar] [CrossRef]
- Davison, E.J. A Method for Simplifying Linear Dynamic Systems. IEEE Trans. Autom. Control 1966, 11, 93–101. [Google Scholar] [CrossRef]
- Shamash, Y. Model Reduction Using the Routh Stability Criterion and the Pade Approximation Technique. Int. J. Control 1975, 21, 475–484. [Google Scholar] [CrossRef]
- Skogestad, S. Simple Analytic Rules for Model Reduction and PID Controller Tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef] [Green Version]
- Deniz, F.N.; Alagoz, B.B.; Tan, N. PID Controller Design Based on Second Order Model Approximation by Using Stability Boundary Locus Fitting. In Proceedings of the ELECO 2015—9th International Conference on Electrical and Electronics Engineering, Bursa, Turkey, 26–28 November 2015; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 28 January 2016; pp. 827–831. [Google Scholar]
- Sahib, M.A.; Ahmed, B.S. A New Multiobjective Performance Criterion Used in PID Tuning Optimization Algorithms. J. Adv. Res. 2016, 7, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Micev, M.; Ćalasan, M.; Ali, Z.M.; Hasanien, H.M.; Abdel Aleem, S.H.E. Optimal Design of Automatic Voltage Regulation Controller Using Hybrid Simulated Annealing—Manta Ray Foraging Optimization Algorithm. Ain. Shams Eng. J. 2021, 12, 641–657. [Google Scholar] [CrossRef]
- Kurokawa, R.; Sato, T.; Vilanova, R.; Konishi, Y. Design of Optimal PID Control with a Sensitivity Function for Resonance Phenomenon-Involved Second-Order Plus Dead-Time System. J. Frankl. Inst. 2020, 357, 4187–4211. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.; Atherton, D.P. Linear Feedback Control: Analysis and Design with MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007. [Google Scholar]




| Method | Type of Network | Number of Sampling Data (N) | Response Characteristic (RC) |
|---|---|---|---|
| A-21-RC | ANN | 21 | Included |
| A-11-RC | ANN | 11 | Included |
| A-21 | ANN | 21 | Excluded |
| A-11 | ANN | 11 | Excluded |
| L-21-RC | LSTM | 21 | Included |
| L-11-RC | LSTM | 11 | Included |
| L-21 | LSTM | 21 | Excluded |
| L-11 | LSTM | 11 | Excluded |
| Method | Relative Error (%) | |||
|---|---|---|---|---|
| Mass | Spring | Damper | Average | |
| A-21-RC | 4.37 | 9.90 | 29.3 | 14.5 |
| A-11-RC | 4.07 | 12.2 | 36.8 | 17.6 |
| A-21 | 32.5 | 30.0 | 26.6 | 29.7 |
| A-11 | 34.3 | 52.3 | 26.1 | 37.6 |
| L-21-RC | 5.81 | 13.4 | 26.5 | 15.2 |
| L-11-RC | 6.50 | 25.0 | 15.3 | 15.6 |
| L-21 | 15.3 | 17.9 | 17.6 | 16.9 |
| L-11 | 10.0 | 25.7 | 34.6 | 23.3 |
| Method | Number of Successful Cases (Total 1000 Cases) | Average Number of Tuning Attempts to Achieve Success |
|---|---|---|
| A-21-RC | 985 | 1.047 |
| A-11-RC | 991 | 1.115 |
| A-21 | 738 | 1.344 |
| A-11 | 552 | 1.001 |
| L-21-RC | 982 | 1.085 |
| L-11-RC | 979 | 1.048 |
| L-21 | 992 | 1.004 |
| L-11 | 992 | 1.571 |
| Method | Number of Trained Data | |||||
|---|---|---|---|---|---|---|
| 10 Million | 10,000 | 1000 | ||||
| # of Succ. | # of Tune. | # of Succ. | # of Tune. | # of Succ. | # of Tune | |
| L-21-RC | 982 | 1.185 | 983 | 1.265 | 963 | 2.478 |
| L-11-RC | 979 | 1.048 | 913 | 1.685 | 964 | 2.621 |
| L-11 | 992 | 1.571 | 982 | 1.864 | 929 | 2.940 |
| Method with Noise | Number of Successful Tuning Attempts (Total 1000) | Average Number of Tuning Attempts to Success |
|---|---|---|
| L-21-RC | 974 | 2.82546 |
| L-21-RC-1000 | 934 | 3.15096 |
| L-11 | 996 | 1.85241 |
| L-11-1000 | 944 | 3.29131 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.-S.; Jang, D.-W. Optimization of Neural Network-Based Self-Tuning PID Controllers for Second Order Mechanical Systems. Appl. Sci. 2021, 11, 8002. https://doi.org/10.3390/app11178002
Lee Y-S, Jang D-W. Optimization of Neural Network-Based Self-Tuning PID Controllers for Second Order Mechanical Systems. Applied Sciences. 2021; 11(17):8002. https://doi.org/10.3390/app11178002
Chicago/Turabian StyleLee, Yong-Seok, and Dong-Won Jang. 2021. "Optimization of Neural Network-Based Self-Tuning PID Controllers for Second Order Mechanical Systems" Applied Sciences 11, no. 17: 8002. https://doi.org/10.3390/app11178002
APA StyleLee, Y.-S., & Jang, D.-W. (2021). Optimization of Neural Network-Based Self-Tuning PID Controllers for Second Order Mechanical Systems. Applied Sciences, 11(17), 8002. https://doi.org/10.3390/app11178002





