Vehicle Interior Noise Prediction Based on Elman Neural Network
Abstract
:1. Introduction
2. Establish a Finite Element Model
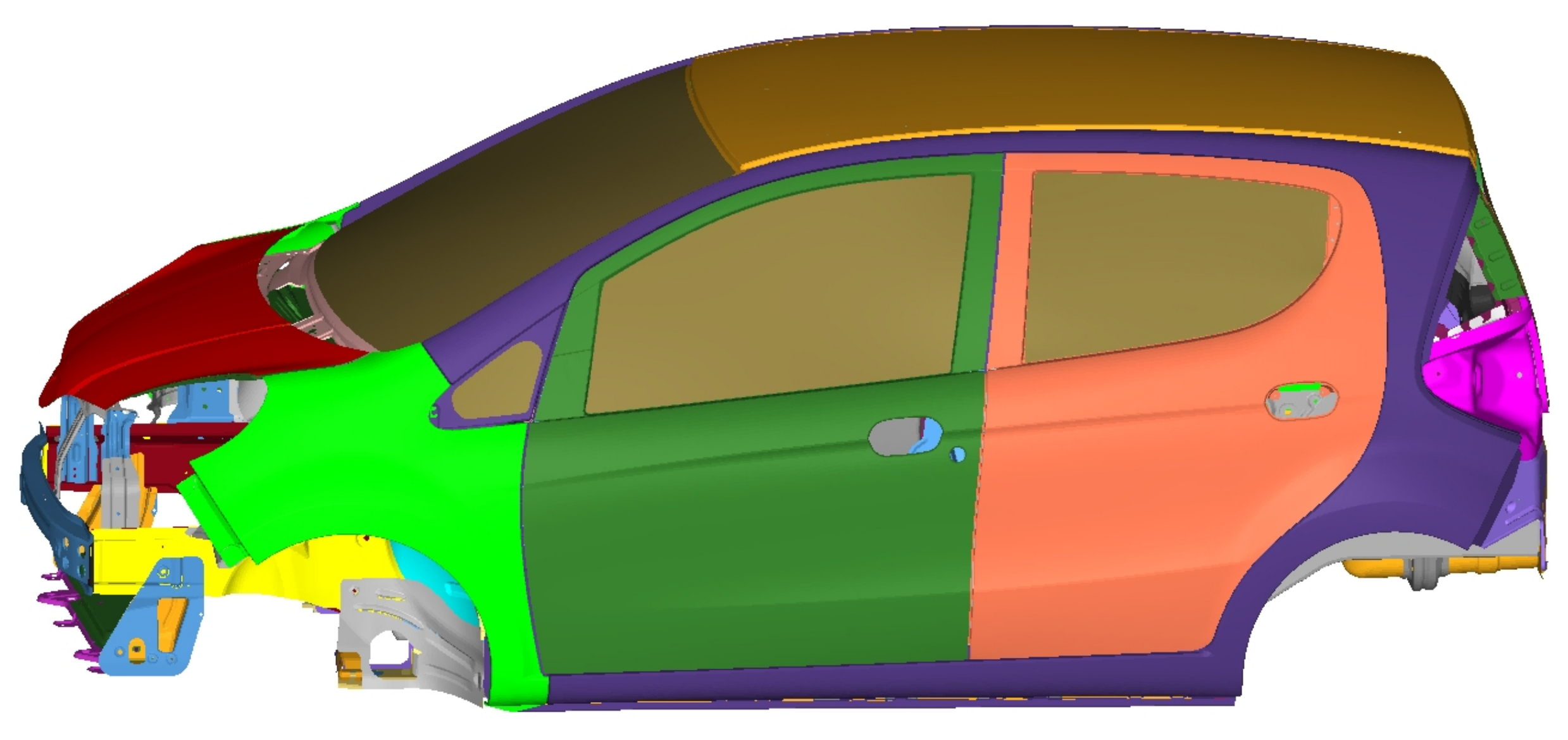
2.1. Vehicle Body Finite Element Model
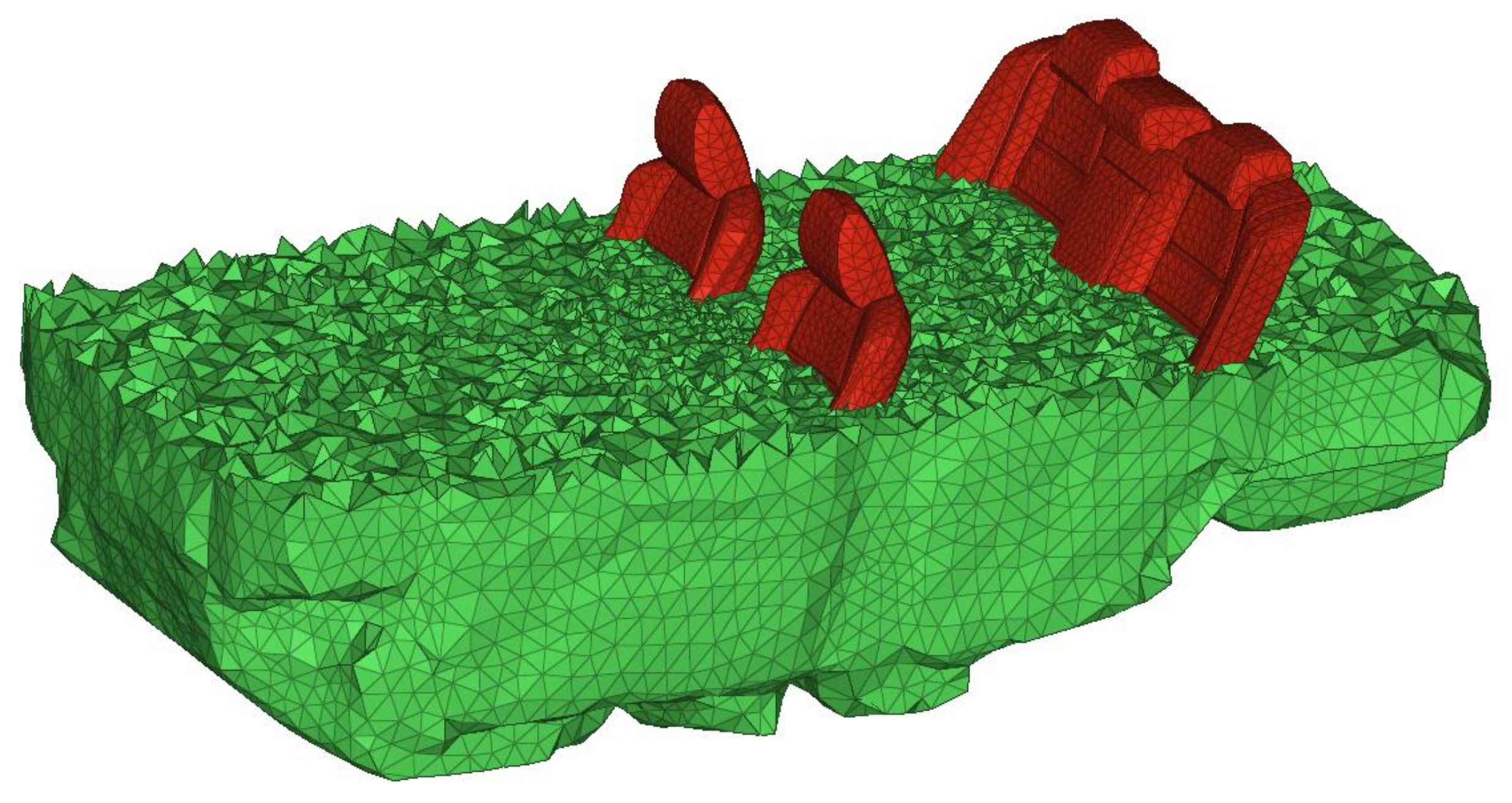
2.2. Acoustic-Structure Coupling Model
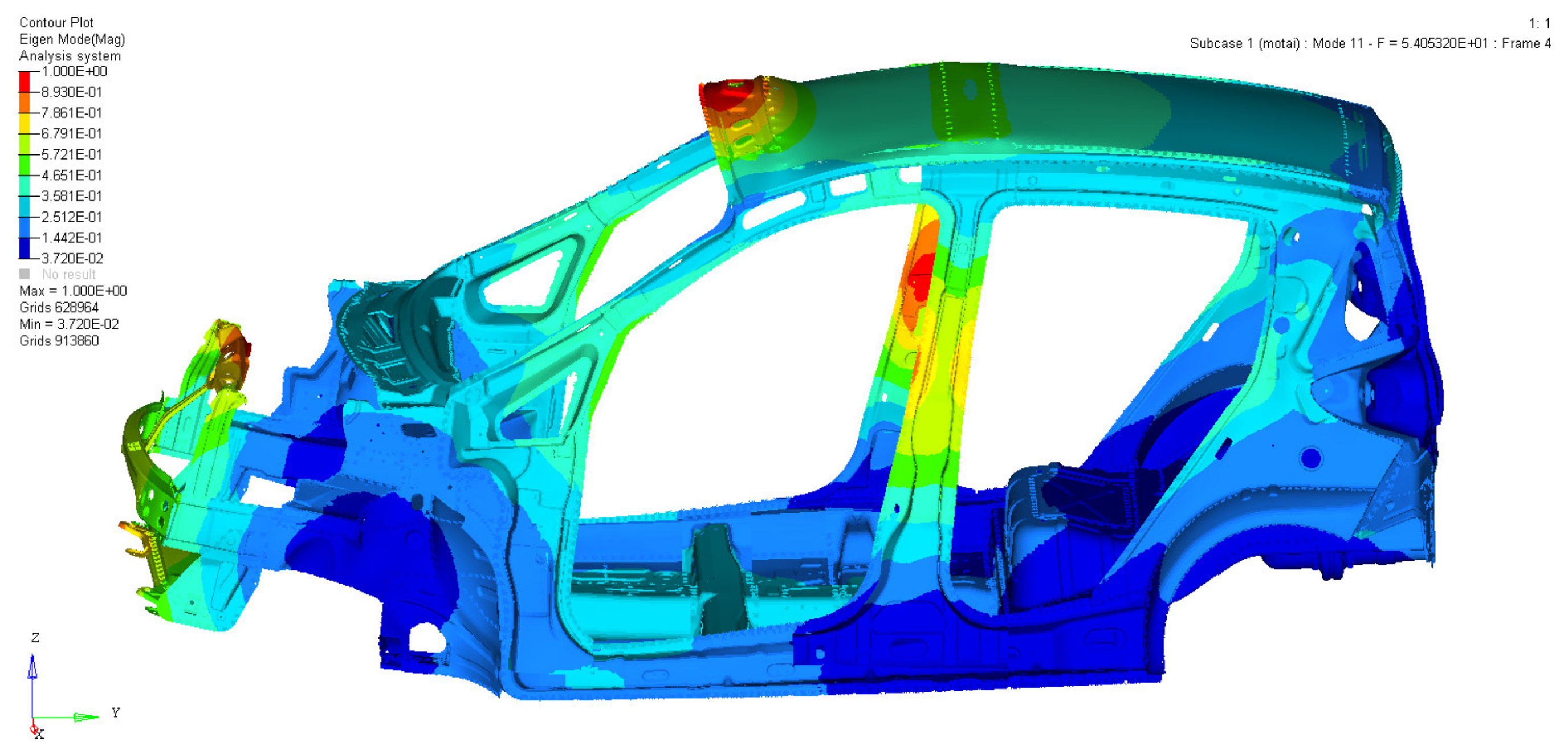
2.3. Modal Analysis
3. Side Impact Simulation Analysis
3.1. Side Impact Simulation Model
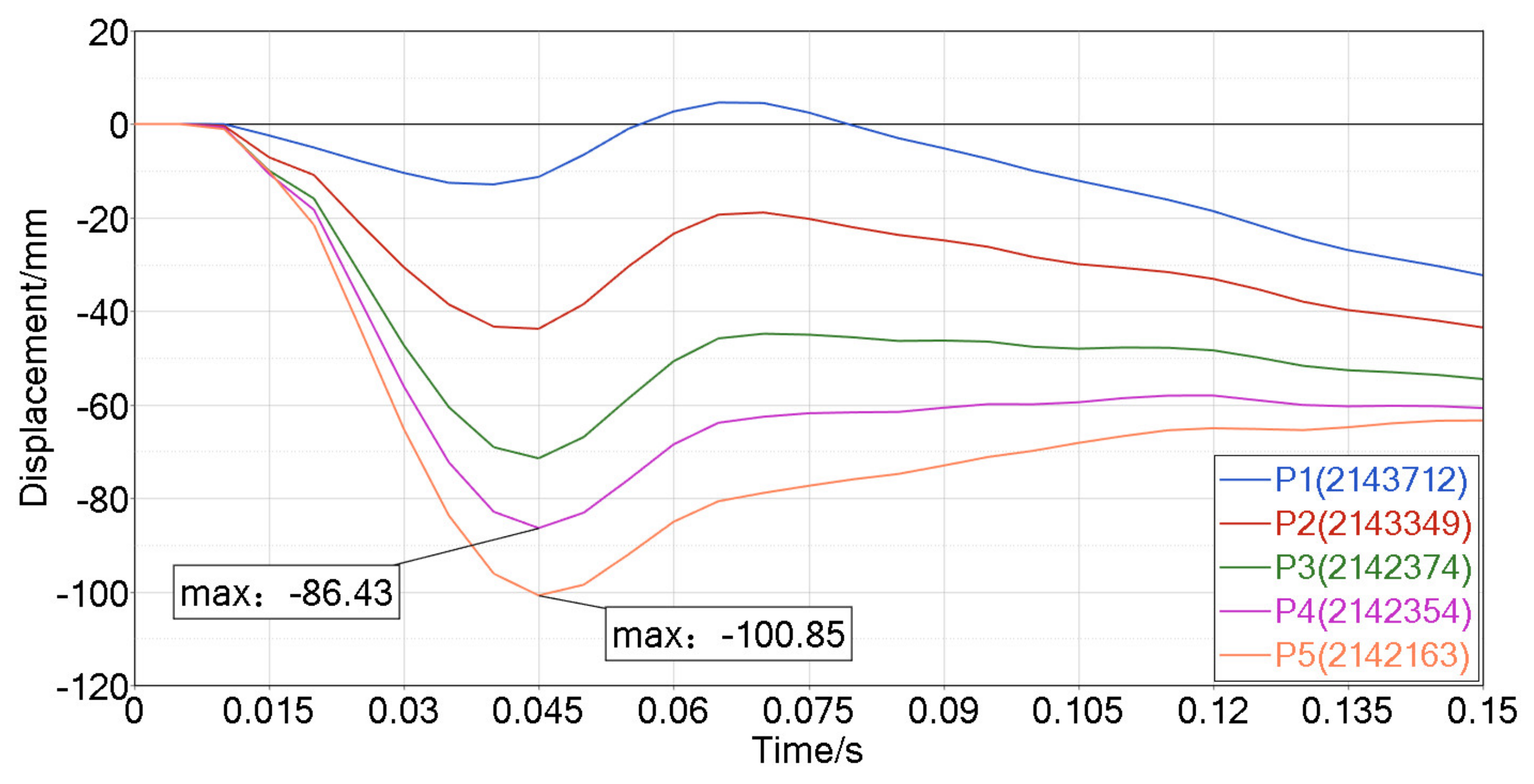
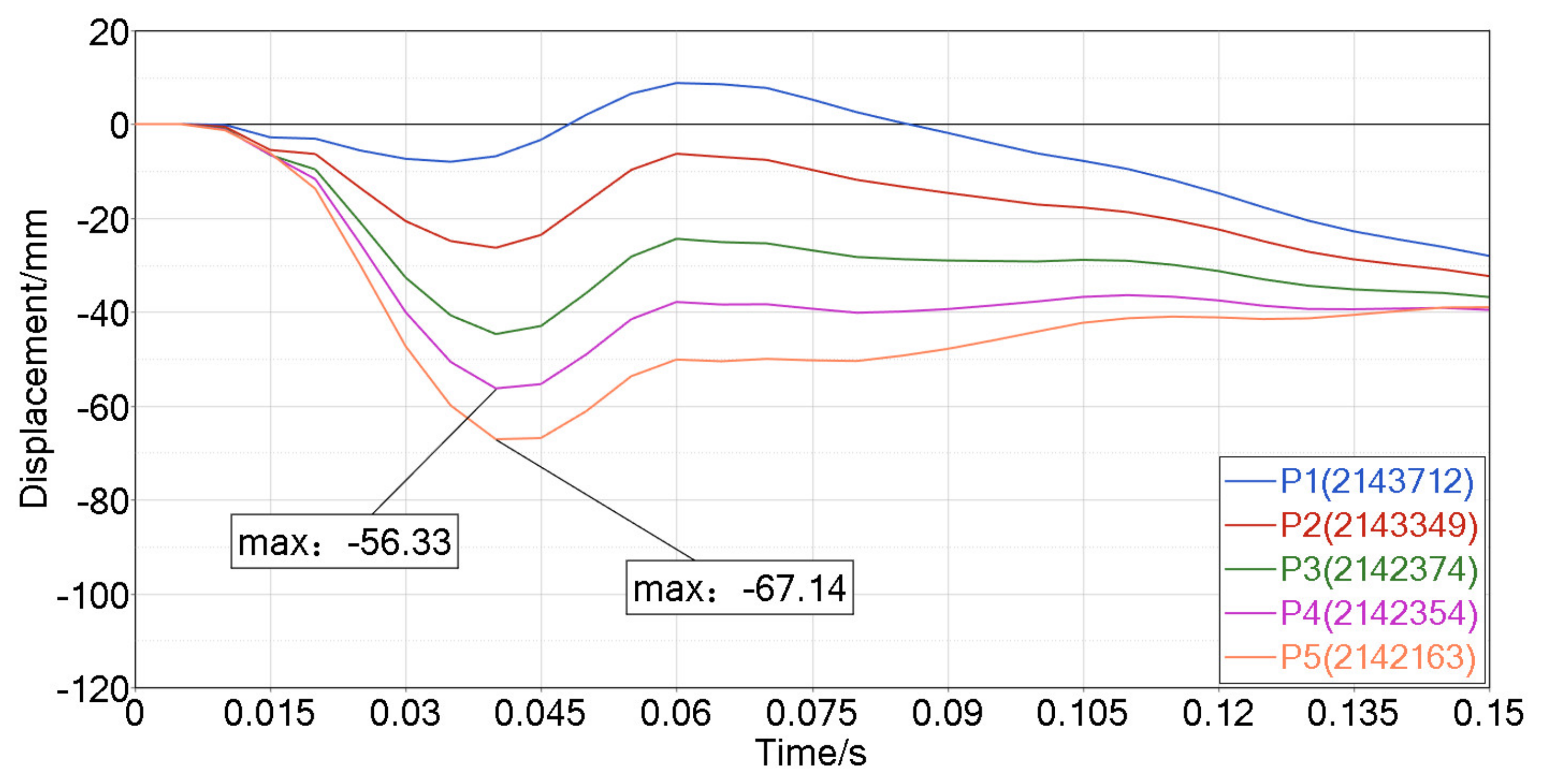
3.2. Side Impact Analysis Results
4. NVH Simulation Analysis
4.1. Working Condition Setting
4.2. Vibration and Noise Theory
5. Prediction and Optimization of Noise in the Vehicle
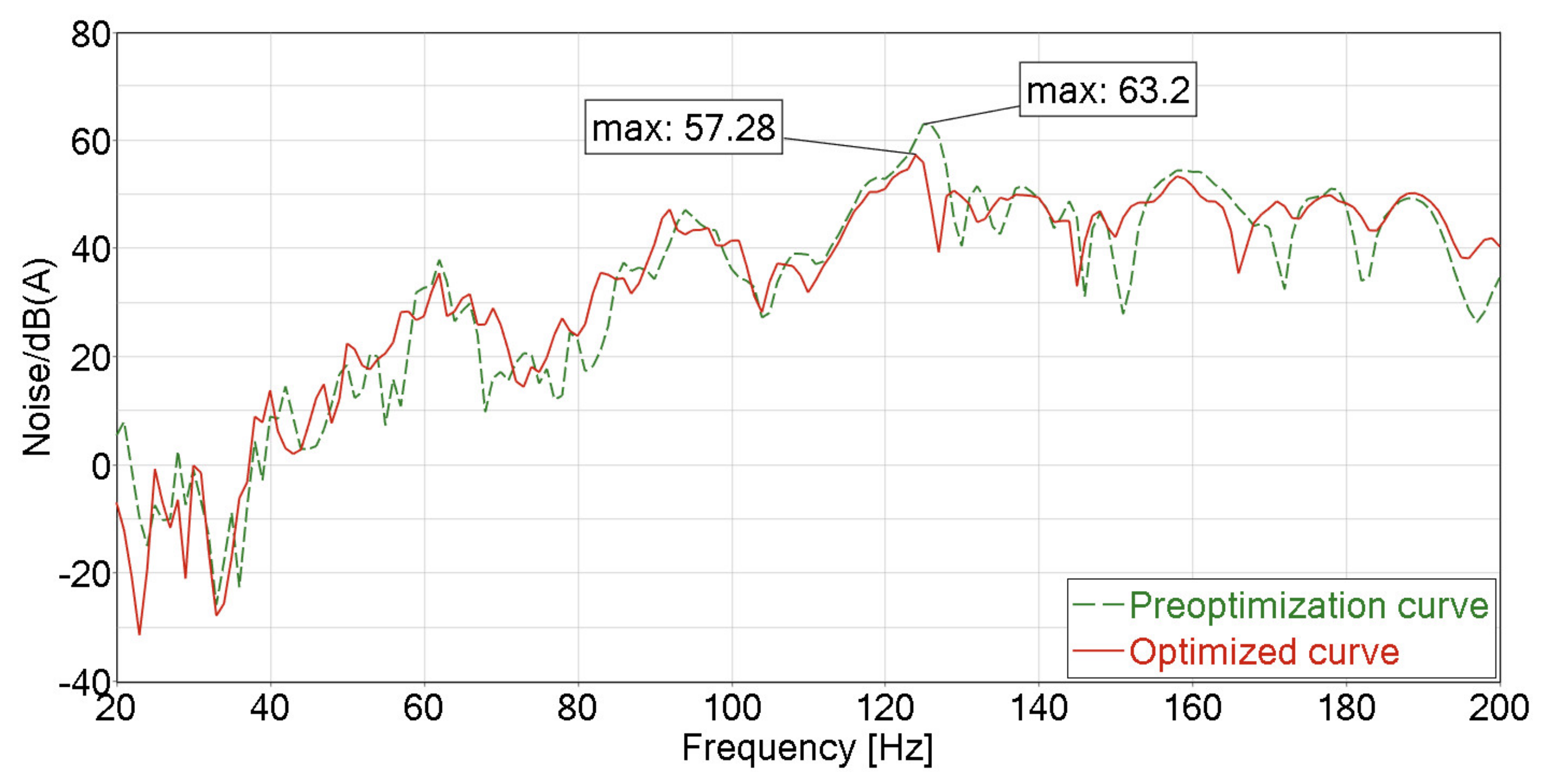
5.1. Acoustic Sensitivity Analysis of Panels
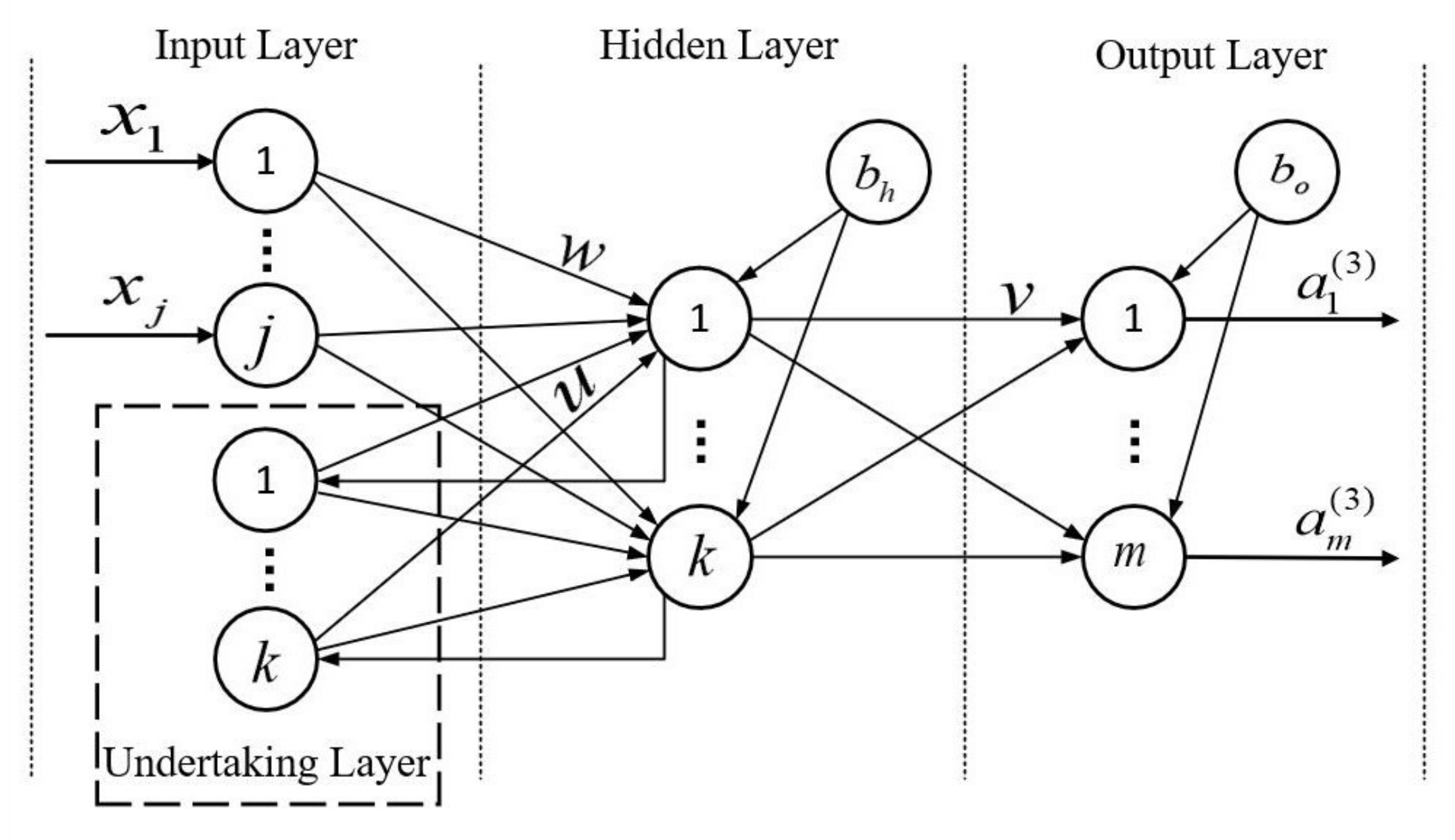
5.2. Elman Neural Network
5.3. Prediction of Noise Value in the Vehicle
5.3.1. Experimental Design
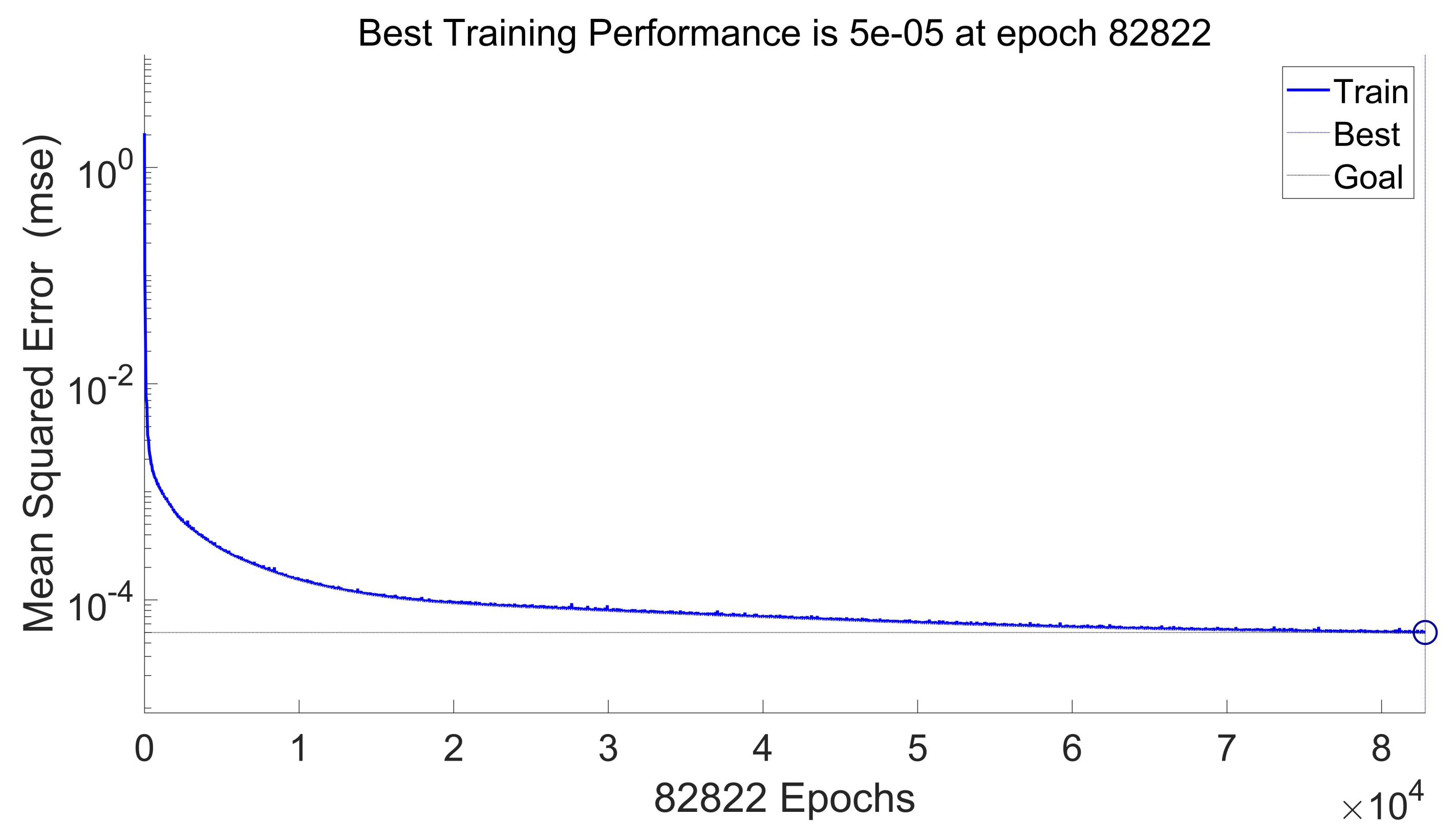
5.3.2. Algorithm Structure
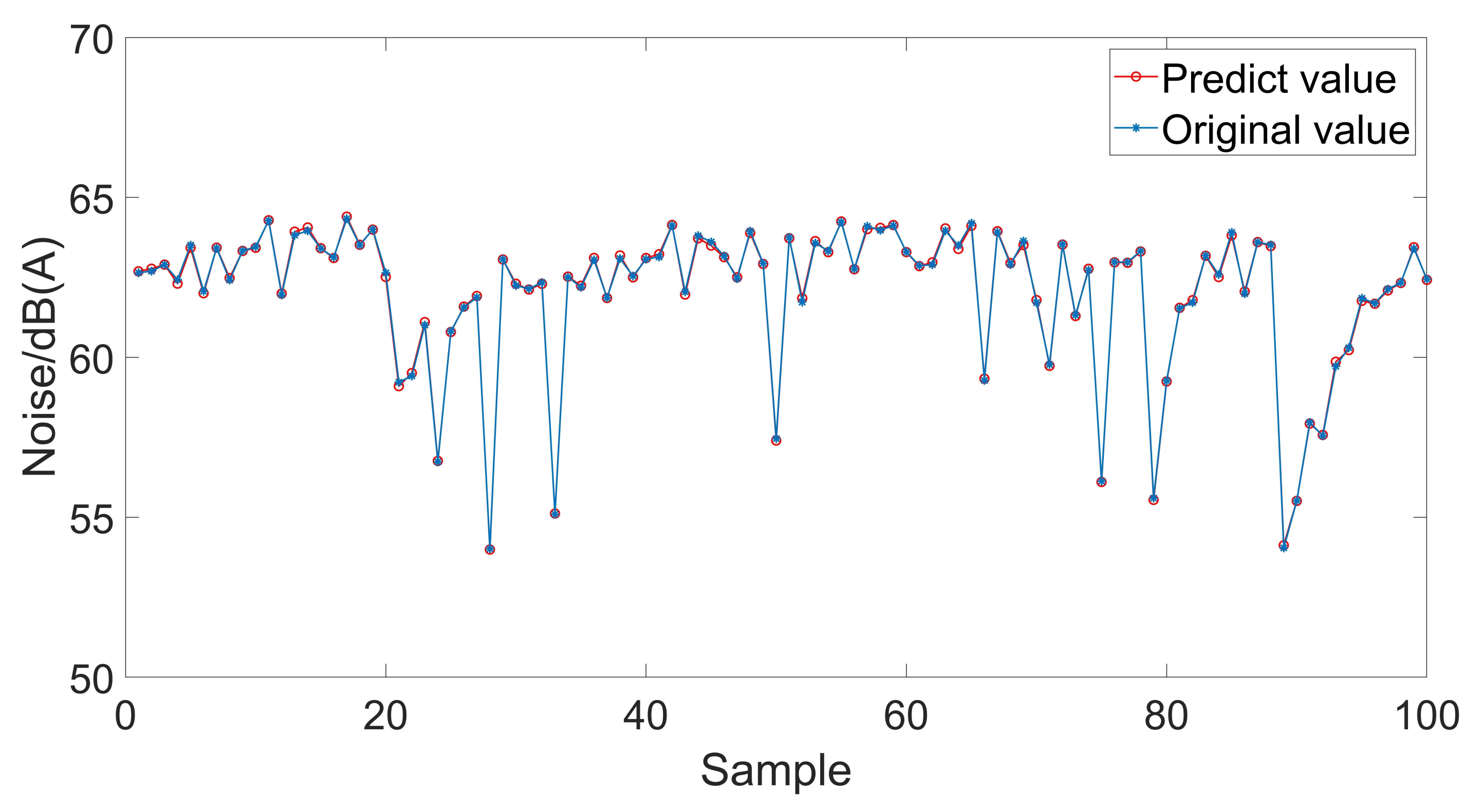
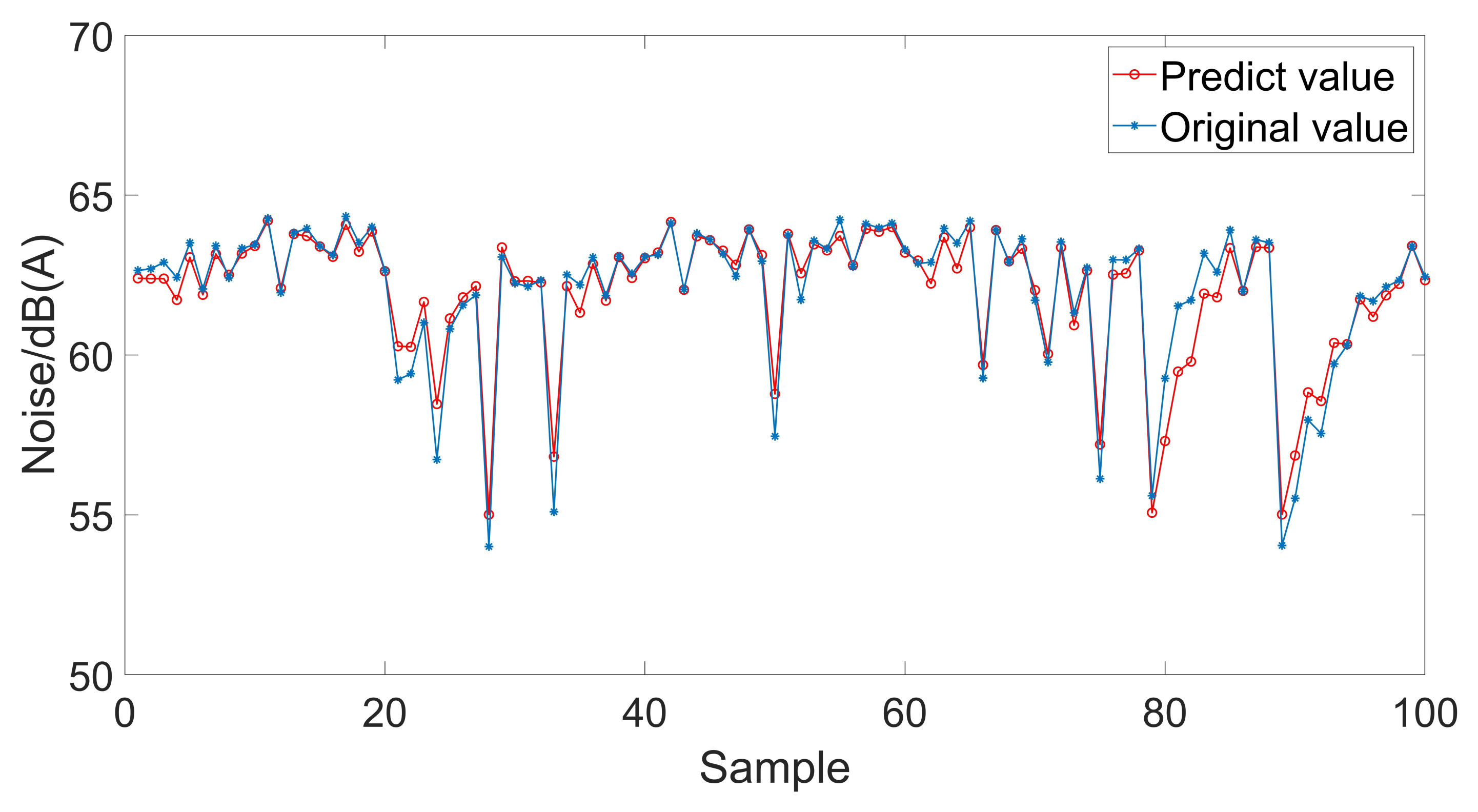
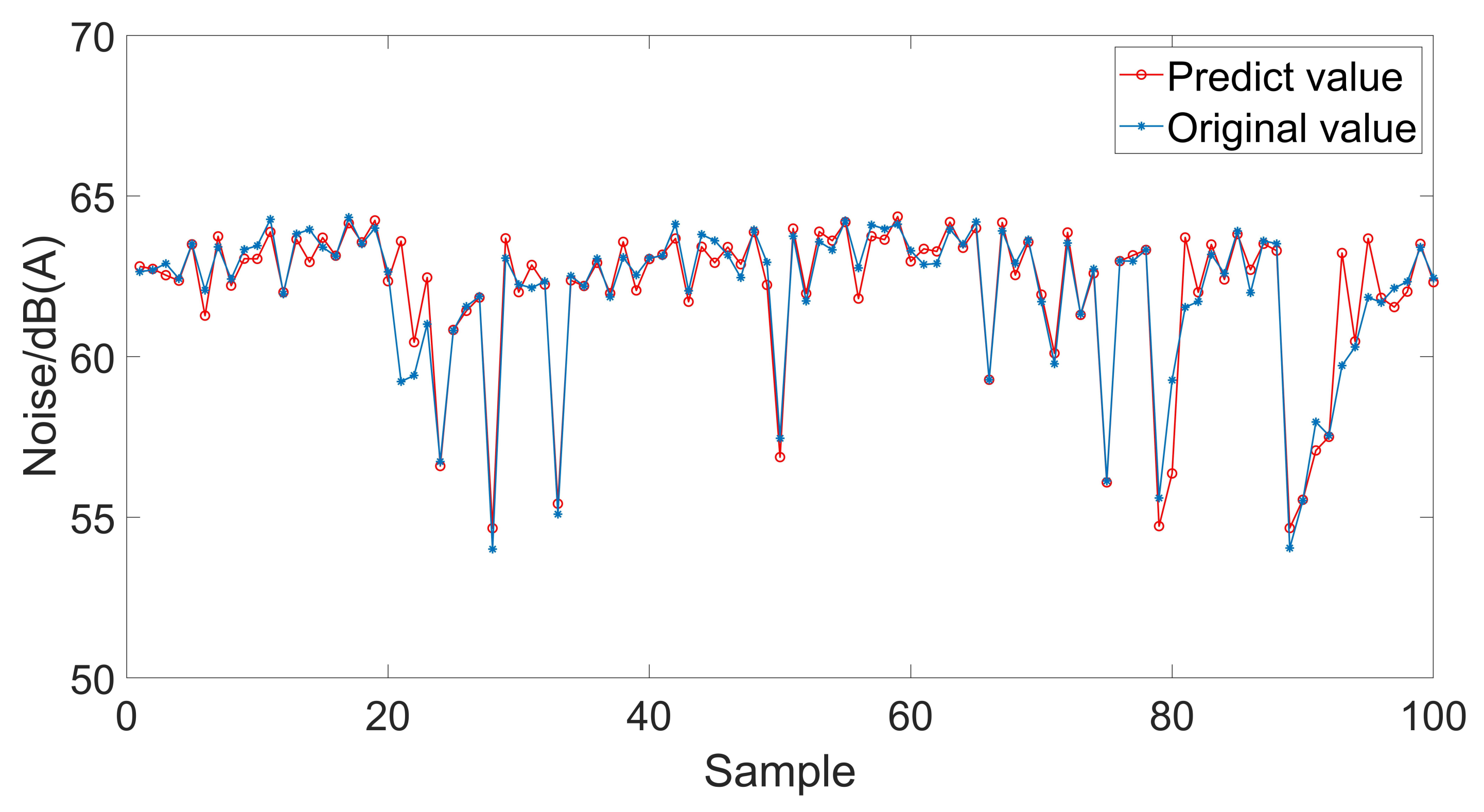
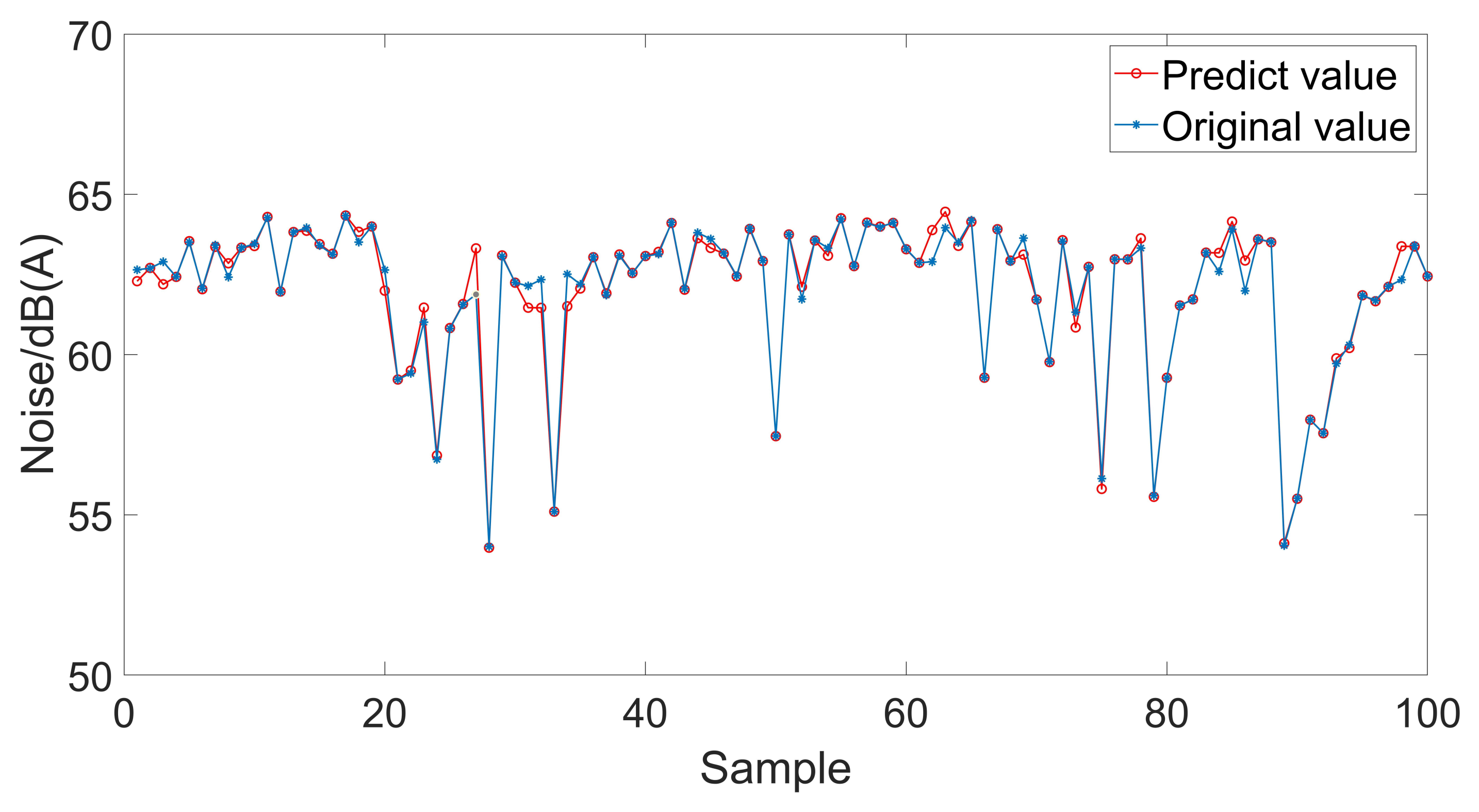
6. Analysis of Prediction Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, S.; Mohanty, A.R. HVAC noise control using natural materials to improve vehicle interior sound quality. Appl. Acoust. 2018, 140, 100–109. [Google Scholar] [CrossRef]
- Ye, S.G.; Zhang, J.H.; Xu, B. Noise Reduction of an Axial Piston Pump by Valve Plate Optimization. Chin. J. Mech. Eng. 2018, 31, 57. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.X.; Tang, B.; Zhao, Y. Active control of structures and sound radiation modes and its application in vehicles. J. Low Frequency Noise Vib. Act. Control 2016, 35, 291–302. [Google Scholar] [CrossRef] [Green Version]
- Guo, R.; Qiu, S.; Yu, Q.L.; Zhou, H.; Zhang, L.J. Transfer path analysis and control of vehicle structure-borne noise induced by the powertrain. Proc. Inst. Mech. Eng. Part D 2012, 226, 1000–1109. [Google Scholar] [CrossRef]
- Bao, G.Z.; Shao, G.S.; Xia, Z.W.; Den, J.H. Identification and contribution analysis of vehicle interior noise based on acoustic array technology. Adv. Mech. Eng. 2017, 9, 1687814017730031. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.M.; Wang, L.H.; Song, J.Q.; Wang, D.F.; Chen, J. Interior High Frequency Noise Analysis of Heavy Vehicle Cab and Multi-Objective Optimization with Statistical Energy Analysis Method. Fluct. Noise Lett. 2017, 16, 1750017. [Google Scholar] [CrossRef]
- Huang, H.B.; Huang, X.R.; Yang, M.L.; Lim, T.C.; Ding, W.P. Identification of vehicle interior noise sources based on wavelet transform and partial coherence analysis. Mech. Syst. Signal Process. 2018, 109, 247–267. [Google Scholar] [CrossRef]
- Liao, L.Y.; Zuo, Y.Y.; Meng, H.D.; Liao, X.H. Research on the technology of noise reduction in hybrid electric vehicle with composite materials. Adv. Mech. Eng. 2018, 10, 1687814018766916. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.D.; Li, R.X.; Ding, W.P.; Croes, J.; Yang, M.L. Mechanism Study and Reduction of Minivan Interior Booming Noise during Acceleration. Shock Vib. 2019, 2019, 2190462. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.R.; Kim, H.Y.; Jeon, J.H.; Kang, Y.J. Application of global sensitivity analysis to statistical energy analysis: Vehicle model development and transmission path contribution. Appl. Acoust. 2019, 146, 368–389. [Google Scholar] [CrossRef]
- Huang, H.B.; Wu, J.H.; Huang, X.R.; Ding, W.P.; Yang, M.L. A novel interval analysis method to identify and reduce pure electric vehicle structure-borne noise. J. Sound Vib. 2020, 475, 115258. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, L.J.; Zhao, J.; Zhou, H. Interior structure-borne noise reduction by controlling the automotive body panel vibration. Proc. Inst. Mech. Eng. Part D 2012, 226, 943–956. [Google Scholar] [CrossRef]
- Wang, Y.L.; Qin, X.P.; Lu, L.; Liu, H.M.; Huang, J.J. The noise control of minicar body in white based on acoustic panel participation method. J. Vibroeng. 2016, 18, 1332–1345. [Google Scholar]
- Tian, W.Y.; Yao, L.Y.; Li, L. A Coupled Smoothed Finite Element-Boundary Element Method for Structural-Acoustic Analysis of Shell. Arch. Acoust. 2017, 42, 49–59. [Google Scholar] [CrossRef]
- Wang, Y.L.; Lu, C.H.; Qin, X.P.; Huang, S.; Tan, X.D.; Sun, Y. Control of structure-borne noise for a vehicle body by using power flow analysis and acoustic path participation method. Appl. Acoust. 2020, 157, 106981. [Google Scholar] [CrossRef]
- Wu, X.D.; Kong, Y.; Zuo, S.G.; Liu, P.X. Research on multi-band structural noise reduction of vehicle body based on two-degree-of-freedom locally resonant phononic crystal. Appl. Acoust. 2021, 179, 108073. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, Y.T.; Liu, X.D.; Shan, Y.C.; Hu, X.J. Analysis of Tire Acoustic Cavity Resonance Energy Transmission Characteristics in Wheels Based on Power Flow Method. Appl. Sci. 2021, 11, 3979. [Google Scholar] [CrossRef]
- Hu, X.J.; Liu, X.D.; Shan, Y.C.; He, T. Simulation and Experimental Validation of Sound Field in a Rotating Tire Cavity Arising from Acoustic Cavity Resonance. Appl. Sci. 2021, 11, 1121. [Google Scholar] [CrossRef]
- Kim, Y.D.; Jeong, J.E.; Park, J.S.; Yang, I.H.; Park, T.S.; Muhamad, P.B.; Choi, D.H.; Oh, J.E. Optimization of the lower arm of a vehicle suspension system for road noise reduction by sensitivity analysis. Mech. Mach. Theory 2013, 69, 278–302. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhang, Y.B.; Huang, C.X.; Liu, X. Low-noise structure optimization of a heavy commercial vehicle cab based on approximation model. J. Low Freq. Noise Vib. Act. Control 2018, 37, 987–1002. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Qiu, N.N.; Zang, L.B.; Wei, C.Y.; Li, G.X.; Li, L. Investigation into transmission radiated noise during the acceleration of electric buses based on response surface methodology. Int. J. Vehicle Des. 2020, 82, 205–223. [Google Scholar] [CrossRef]
- Guo, Z.H.; Jie, W.; Lu, H.Y.; Wang, J.-Z. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl.-Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Jeong, U.C.; Kim, J.S.; Kim, Y.D.; Oh, J.E. Noise reduction of the automobile multi-mode muffler using differential gap control and neural network control. Proc. Inst. Mech. Eng. Part D 2016, 230, 928–941. [Google Scholar] [CrossRef]
- Ma, C.G.; Chen, C.Y.; Liu, Q.H.; Gao, H.B.; Li, Q.; Gao, H.; Shen, Y. Sound Quality Evaluation of the Interior Noise of Pure Electric Vehicle Based on Neural Network Model. IEEE Trans. Ind. Electron. 2017, 64, 9442–9450. [Google Scholar] [CrossRef]
- Huang, X.R.; Huang, H.B.; Wu, J.H.; Yang, M.L.; Ding, W.P. Sound quality prediction and improving of vehicle interior noise based on deep convolutional neural networks. Expert Syst. Appl. 2020, 160, 113657. [Google Scholar] [CrossRef]
- Wang, Y.S.; Guo, H.; Feng, T.P.; Ju, J.; Wang, X.L. Acoustic behavior prediction for low-frequency sound quality based on finite element method and artificial neural network. Appl. Acoust. 2017, 122, 62–71. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Zhou, J.Y.; Xie, Y.Z. Virtual reality of interior noises of vehicles based on boundary element and neural networks. Neural Comput. Appl. 2018, 29, 1281–1291. [Google Scholar] [CrossRef]
- Peng, J.S.; Xu, L.; Shao, Y.M. Research on the virtual reality of vibration characteristics in vehicle cabin based on neural networks. Neural Comput. Appl. 2018, 29, 1225–1232. [Google Scholar] [CrossRef]
- Qian, K.; Hou, Z.C.; Sun, D.K. Sound Quality Estimation of Electric Vehicles Based on GA-BP Artificial Neural Networks. Appl. Sci. 2020, 10, 5567. [Google Scholar] [CrossRef]
- Liang, Y.; Qiu, L.; Zhu, J.; Pan, J. A digester temperature prediction model based on the elman neural network. Appl. Eng. Agric. 2017, 33, 143–148. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, Z.P.; Zhang, L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019, 174, 33–44. [Google Scholar] [CrossRef]
- Abdelhafez, E.; Hamdan, M. Correlation between weather and COVID-19 Pandemic in Jordan. Fresenius Environ. Bull. 2021, 30, 4893–4900. [Google Scholar]
- Li, X.M.; Han, Z.W.; Zhao, T.Y.; Zhang, J.L.; Xue, D. Modeling for indoor temperature prediction based on time-delay and Elman neural network in air conditioning system. J. Build. Eng. 2021, 33, 101854. [Google Scholar] [CrossRef]
- Guo, Z.Q.; Wu, H.X.; Zhao, W.Z.; Wang, C.Y. Coordinated control strategy for vehicle electro-hydraulic compound steering system. Proc. Inst. Mech. Eng. Part D 2021, 235, 732–743. [Google Scholar] [CrossRef]
- Ozturk, I.; Kaya, N.; Ozturk, F. Design of vehicle parts under impact loading using a multi-objective design approach. Mater. Test. 2018, 60, 501–509. [Google Scholar] [CrossRef]
- Lee, Y.; Han, Y.H.; Park, S.O.; Park, G.J. Vehicle crash optimization considering a roof crush test and a side impact test. Proc. Inst. Mech. Eng. Part D 2019, 233, 2455–2466. [Google Scholar] [CrossRef]
- Wu, H.Q.; Kuang, S.J.; Hou, H.B. Research on Application of Electric Vehicle Collision Based on Reliability Optimization Design Method. Int. J. Comput. Methods 2019, 16, 1950034. [Google Scholar] [CrossRef]
- Rashid, A.S.Y.; Ramli, R.; Haris, S.M.; Alias, A. Improving the Dynamic Characteristics of Body-in-White Structure Using Structural Optimization. Sci. World J. 2014, 2014, 190214. [Google Scholar] [CrossRef]
- Qu, X.J.; Liang, H.L.; Zhang, B.C.; Cui, X.Y. Numerical optimization of vehicle noises in multi-peak frequency points based on hybrid genetic algorithm and simulated annealing. J. Vibroeng. 2016, 18, 2613–2625. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, S.A.; Xiao, S.H.; Du, S.Z.; Zhang, Y.; Lu, C.H. Full Vehicle Vibration and Noise Analysis Based on Substructure Power Flow. Shock Vib. 2017, 2017, 8725346. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Lu, C.H.; Liu, Z.E.; Shen, C.R.; Sun, Y.; Sun, M.L. Structural Modal Analysis and Optimization of SUV Door Based on Response Surface Method. Shock Vib. 2020, 2020, 9362434. [Google Scholar] [CrossRef]
- Wang, Y.S.; Shen, G.Q.; Guo, H.; Tang, X.L.; Hamade, T. Roughness modelling based on human auditory perception for sound quality evaluation of vehicle interior noise. J. Sound Vib. 2013, 332, 3893–3904. [Google Scholar] [CrossRef]
- Jin, X.X.; Zhang, L.J.; Jiang, H. Automobile Vibration Analysis; Tongji University Press: Shanghai, China, 2002; pp. 46–56. [Google Scholar]
- Yu, S.W. Case Analysis and Application of MATLAB Optimization Algorithm; Tsinghua University Press: Beijing, China, 2015; pp. 64–68. [Google Scholar]
- Kayaalp, K.; Metlek, S.; Ekici, S.; Sohret, Y. Developing a model for prediction of the combustion performance and emissions of a turboprop engine using the long short-term memory method. Fuel 2021, 302, 121202. [Google Scholar] [CrossRef]



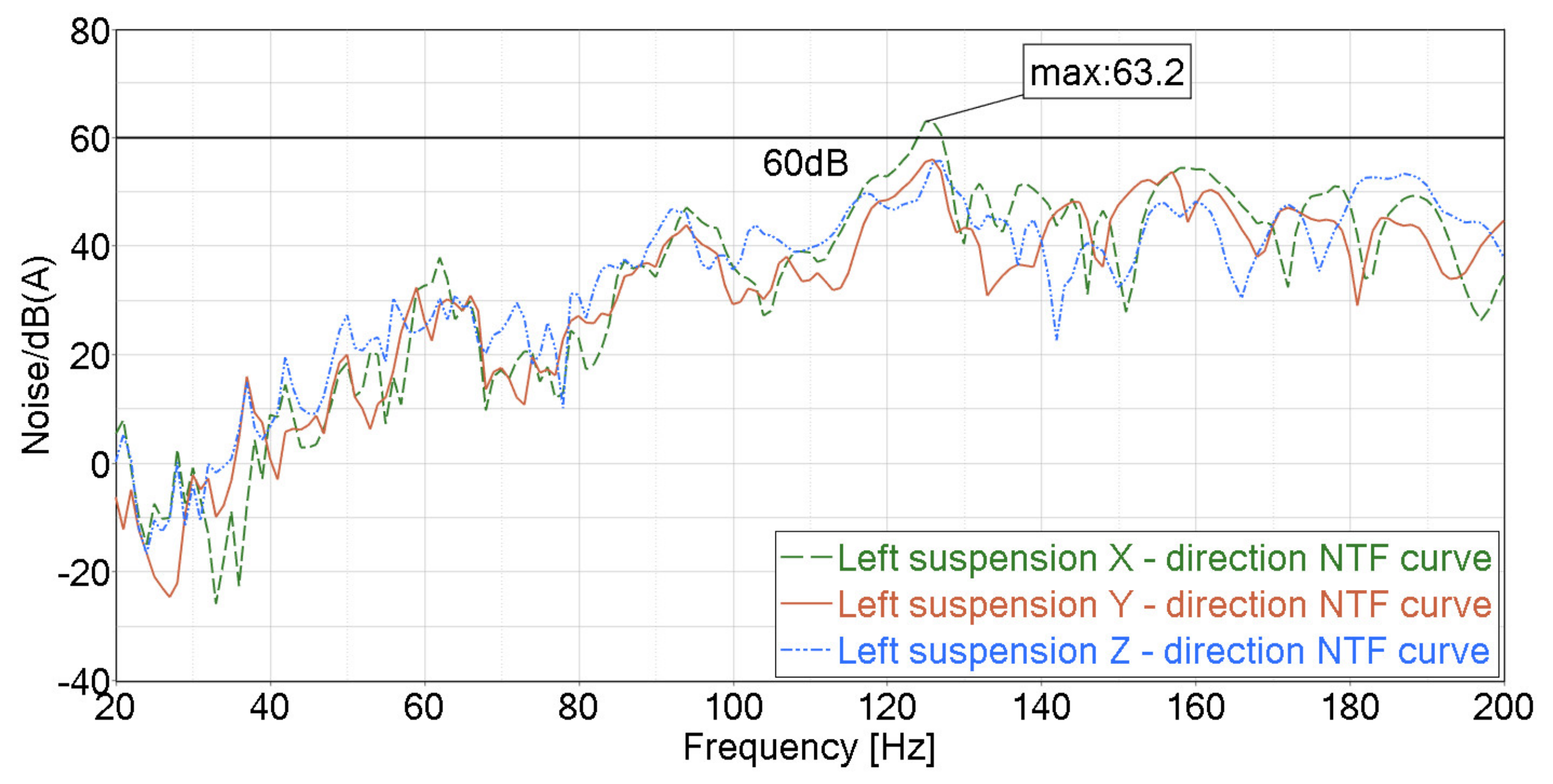
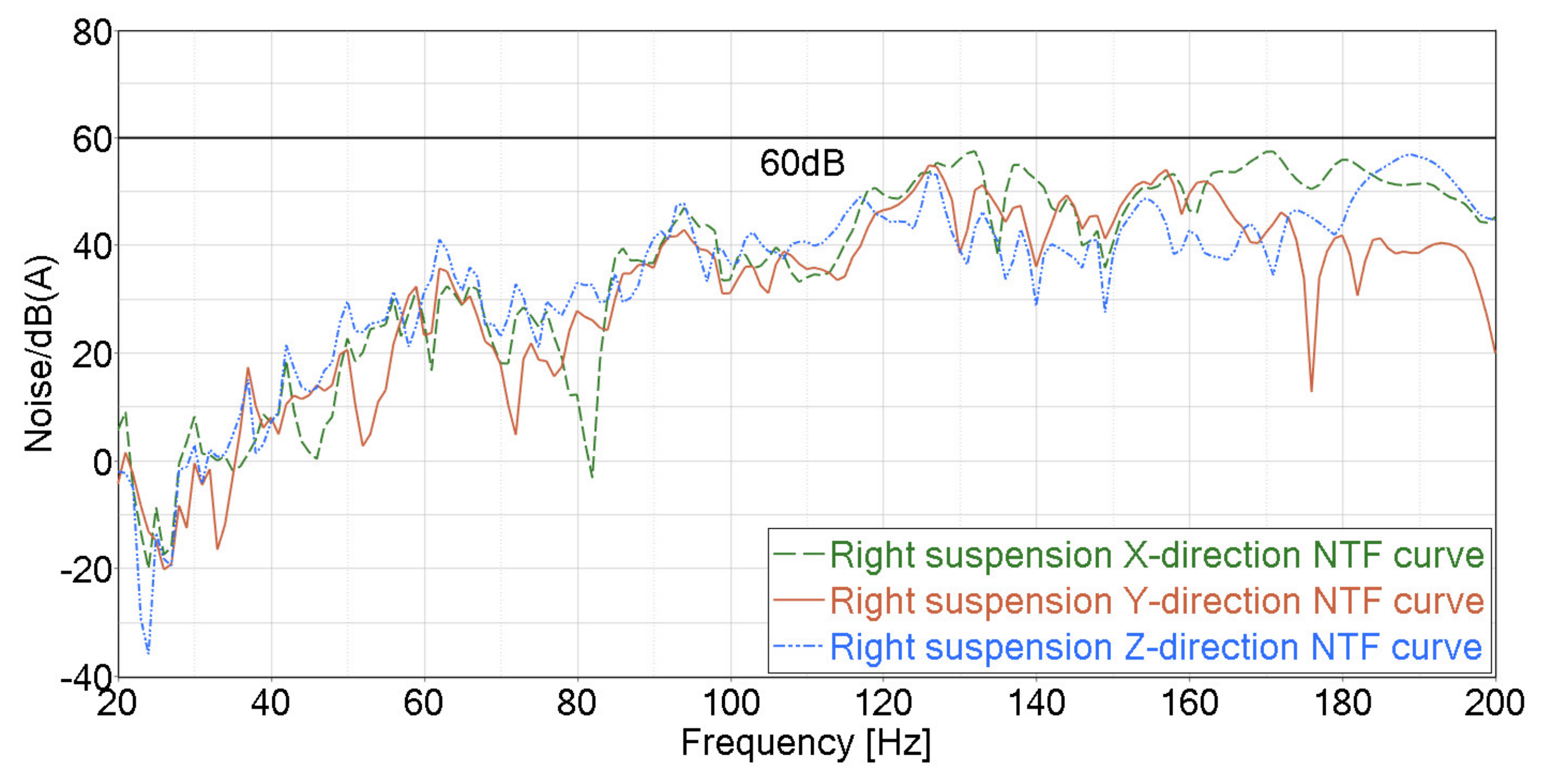
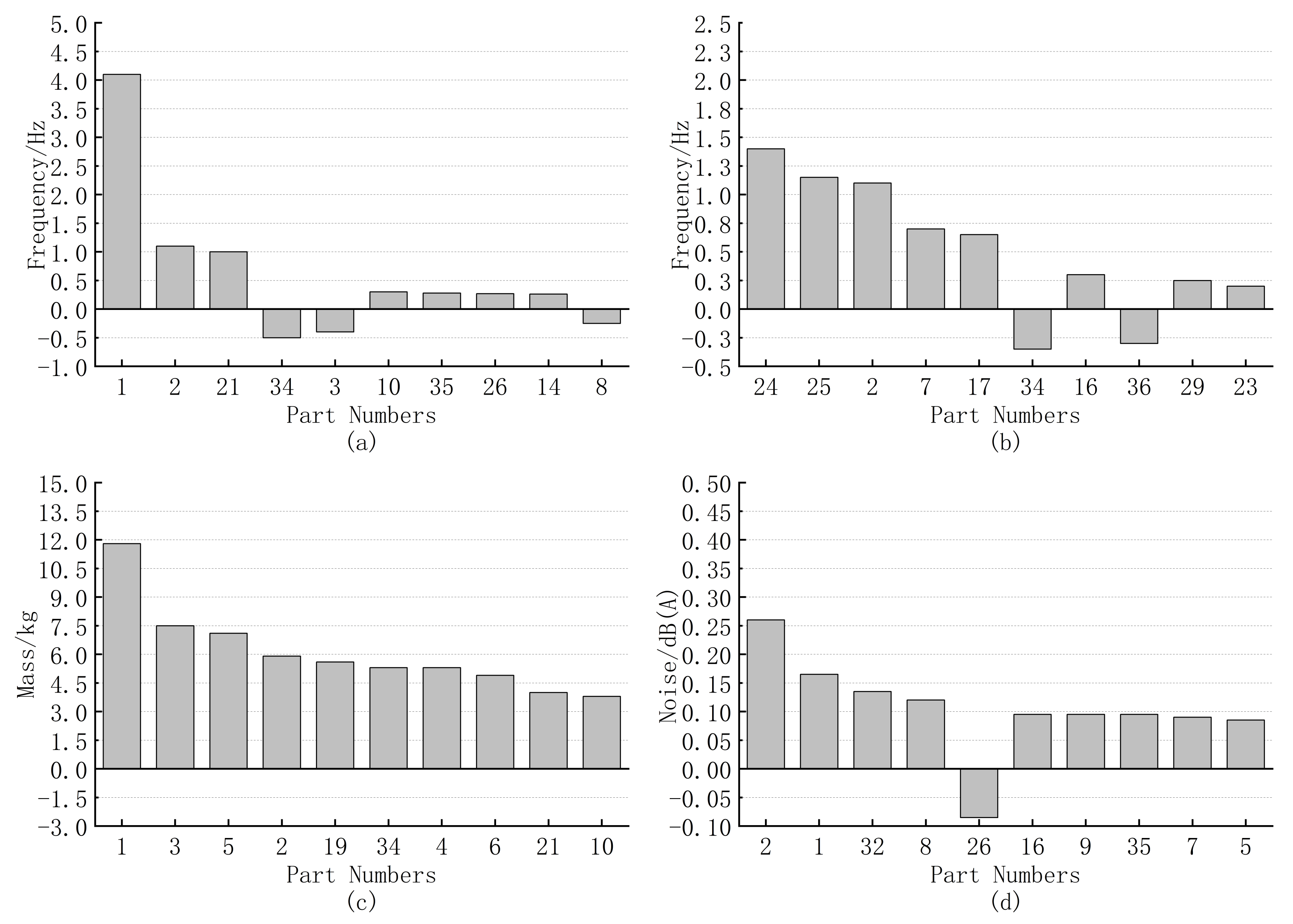
| Modal Frequency Order | Frequency/Hz | Modal Shape |
|---|---|---|
| First order | 27.04 | Transverse local modal at the front of the roof |
| Second order | 38.60 | First-order torsional modal |
| Third order | 45.66 | Lateral local modal of water tank bracket |
| Fourth order | 50.26 | Vertical local modal at the front of the roof |
| Fifth order | 54.05 | First-order bending modal |
| Sixth order | 59.92 | C-pillar lateral local modal |
| Seventh order | 67.20 | Vertical local modal at the front of the roof |
| Eighth order | 67.69 | B-pillar local modal |
| Modal Shape | Frequency/Hz |
|---|---|
| Local modal of front windshield | 44.33 |
| Rear door local modal | 50.16 |
| Local modal of front window | 54.45 |
| Local modal of trunk glass | 55.32 |
| Front door local modal | 58.71 |
| Local modal of rear window | 74.26 |
| Variable Name | Initial Value/mm | Variable Interval/mm |
|---|---|---|
| Side wall | 0.9 | [0.7, 1.1] |
| B-pillar inner panel | 1.0 | [0.8, 1.2] |
| C-pillar inner panel | 1.0 | [0.8, 1.2] |
| Middle bottom panel | 1.6 | [1.3, 1.9] |
| Rear bottom panel | 1.6 | [1.3, 1.9] |
| Taillight inner panel | 0.8 | [0.6, 1.0] |
| A-pillar inner panel | 2.0 | [1.7, 2.3] |
| Roof | 1.0 | [0.8, 1.2] |
| Arithmetic | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|
| Elman | 0.004056 | 0.063685 | 0.047954 | 0.000772 |
| GRNN | 0.382991 | 0.618863 | 0.401589 | 0.006679 |
| BP | 0.636089 | 0.797552 | 0.433544 | 0.007105 |
| GA-BP | 0.105924 | 0.325459 | 0.159235 | 0.002559 |
| Prediction Object | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|
| Body mass | ||||
| First-order torsion modal | ||||
| First-order bending modal | ||||
| P4 maximum intrusion | ||||
| P5 maximum intrusion |
| Object | ENN Prediction | FEA | Error (%) |
|---|---|---|---|
| Maximum sound pressure level/db (A) | 57.52 | 57.28 | 0.41 |
| Body mass/kg | 362.8 | 363.7 | 0.25 |
| First-order torsion modal/Hz | 38.71 | 38.85 | 0.36 |
| First-order bending modal/Hz | 54.70 | 54.34 | 0.66 |
| P4 maximum intrusion/mm | 55.04 | 56.33 | 2.29 |
| P5 maximum intrusion/mm | 68.95 | 67.14 | 2.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhou, W.; Liu, J.; Zhang, X.; Pan, F.; Yang, H.; Li, M.; Luo, D. Vehicle Interior Noise Prediction Based on Elman Neural Network. Appl. Sci. 2021, 11, 8029. https://doi.org/10.3390/app11178029
Li M, Zhou W, Liu J, Zhang X, Pan F, Yang H, Li M, Luo D. Vehicle Interior Noise Prediction Based on Elman Neural Network. Applied Sciences. 2021; 11(17):8029. https://doi.org/10.3390/app11178029
Chicago/Turabian StyleLi, Min, Wei Zhou, Jiang Liu, Xilong Zhang, Fuquan Pan, Huan Yang, Mengshan Li, and Dijia Luo. 2021. "Vehicle Interior Noise Prediction Based on Elman Neural Network" Applied Sciences 11, no. 17: 8029. https://doi.org/10.3390/app11178029






