Abstract
The short encapsulation pull-out test (SEPT) is extensively used in rockbolting research or engineering. The field SEPT is time-consuming and labor-intensive, and its result is only applicable to the tested in situ. The laboratory SEPT is usually employed in theoretical rockbolting research due to its easily controlled variables. However, the design of laboratory SEPT is quite different, as there is no standard testing method, resulting in the applicability and limitations of each study not being clear. Accordingly, the aim of this paper is to bridge the gap between laboratory SEPT research and field application. On the basis of thick-walled cylinder theory, a mechanical model of a rock bolt subjected to axial load was established under consideration of the deformational behavior of confining materials around the bolt. Plane stress analysis was introduced to derive the analytical relationship between the axial force of the bolt and the deformation of the confining materials. A new approach of laboratory SEPT sample design was established, namely, equivalent radial stiffness theory, to simulate anchorage performance in a specific in-situ geocondition. Consequently, the field SETP could be replaced by laboratory testing using properly designed bolting samples with a certain level of accuracy. In addition, the application scope of previous laboratory SEPT research could be accurately defined. Laboratory SEPT was carried out to study the anchoring performance of right spiral rebar bolts under different confining materials. Poly Vinyl Chloride (PVC) tubes with a thickness of 31 mm, #60 aluminum (Al) tubes with a thickness of 5.8 mm, and #20 steel tubes with a thickness of 5.5, 7.0 mm were used in sample preparation to simulate soft, medium, and hard surrounding rocks in the field. The anchorage performance of the bolt under different geoconditions was systematically proposed, which provides a technical approach for similar research using different anchoring materials. A negative exponential expression formulating the axial load capacity of the right spiral bolts for the full spectrum of the surrounding rocks’ strength was derived on the basis of theoretical analysis and data regression. It can be used for preliminary reinforcement design, as well as the accurate key parameter setting in the numerical calculation of roadway deformation using right spiral bolts. The theoretical prediction is highly consistent with the testing results in the literature, which confirms the validity and reliability of this research. This study contributes to the establishment of a laboratory SEPT standard in rock mechanics.
1. Introduction
Rockbolts have been used to provide ground support in mines for more than one century [1,2,3,4,5]. Rockbolts are characterized by highly effective reinforcement and simple operation, which can guarantee the rapid development of roadways, the efficient mining of working faces, and the safe operation of mines [6].
The bolting system consists of four components, namely, surrounding rocks, bolts, and internal and external fixtures [7,8]. External fixtures are trays and nuts, which connect the reinforcing elements at the roadway surface. Internal fixtures can be divided into three types on the basis of the bolt–rock coupling structure, i.e., continuous frictionally coupled (CFC), continuous mechanically coupled (CMC), and discretely mechanically or frictionally coupled (DMFC) [9], corresponding to mechanical, fully resin-grouted, and partially grouted bolts, respectively.
The reinforcing effect is based on load transfer from unstable surrounding rock to stable rock mass through the bolt. The load-transfer capacity of the bolt is one of the most important indicators of the bolting effect. Therefore, the accurate estimation of the bolting force is fundamental for reinforcement-system design and an important parameter in the numerical modeling of the deformation of underground roadways.
The pull-out test is commonly used to evaluate anchorage performance. In practice, the rockbolting failure of fully resin-grouted rockbolts is often at the rock–resin interface, the resin, or resin–bolt interface failure. The tensile failure of the bolt shank is rarely observed. Thus, the short encapsulation pull-out test (SEPT) is normally employed to evaluate anchorage performance in the laboratory and in the field. As the SEPT measures the anchorage performance of rockbolting exclusive to the deformation of the bolt shank, the design criterion in SEPT is accordingly that the peak anchorage force should be lower than the yielding load of the bolt shank [10].
The most straightforward method to measure anchorage performance is the in situ pull-out test. According to the GB/T35056-2018 standard [11], in situ pull-out testing holes should be drilled at different depths into the surrounding rock. The bolting materials, equipment, and procedure should be identical to those on-site. The anchorage length should be less than 300 mm, and the test should be conducted within 1–24 h. However, the in situ test has the following disadvantages: (1) it is extremely time-consuming and laborious; (2) the accuracy of the measurement is low due to the limitation of the instrument; (3) the variation of the testing results is largely due to the complexity of the site conditions; and (4) many variables can hardly be controlled, such as the mechanical properties of the surrounding rock and ground stress. As a result, the repeatability and university of the testing result are limited. Field testing is useful in the case of rockbolting design for a specific site, but it is inefficient for rockbolting research that focuses on the generality of the testing result.
The laboratory pull-out test is the most popular measure in rockbolting study due to its simplicity and high consistency of the data. Currently, there is no universal standard for the laboratory SEPT. Researchers often design their testing sample on the basis of the studied object and the availability of the material [12,13,14,15,16,17]. Concrete blocks or steel tubes are normally used as the confining material to simulate the surrounding rock in the field. For instance, Biumel et al. used cement specimens in investigating the influence of borehole diameter, rock joint, and rock strength on the anchoring effect, the shear- and axial-stress distribution along the bolt, the performance of the rebar and D bolts, and the anchorage-failure model [18,19,20]. By using steel-tube confinement, Jalalifar et al. studied the effect of the bolt profile, resin temperature, resin mixture, installation procedure, and cyclic loading on anchoring force [21,22,23,24,25,26,27]. All of them, either C20–C40 cement or steel tubes, were used as confining materials to prepare the bolting specimen, whereas tubes produced of other materials are scarcely reported.
However, the conclusions drawn from laboratory SEPT applied to what kind of field geoconditions are not very clear, i.e., the result of a laboratory study is inconclusive if the experiment cannot correspond to a field condition. Studies show that anchorage performance is highly related to the geoconditions of the surrounding rock [28,29,30,31,32,33]. To ensure that laboratory SEPT results represent actual anchorage performance, geoconditions insitu should be considered in the experimental design. Theory and technology must be developed to realize anchorage performance in laboratory testing to be similar to its field behavior.
On the basis of thick-walled cylinder theory, this study establishes the relationship between laboratory SEPT sample confinement with the mechanical properties of rock mass. On the basis of the equivalent radial stiffness principle, laboratory SEPT was designed using PVC, #6061 Al, and #20 steel as confining material of the specimens to simulate the different strengths of rock mass. The anchorage performance of the dextral bolt, which is one kind of the two most commonly used rock bolts in the underground coal-mine industry in China, was investigated under different field geoconditions. The relationship between the axial loading capacity of the bolt and the elastic properties of the surrounding rock was obtained via theoretical analysis, which provides a theoretical basis for anchorage-performance prediction in dextral-bolt support design and accurate parameters for related numerical modeling.
2. Materials and Methods
2.1. Equivalent Radial Stiffness Theory
Yazici and Kaiser introduced the plane strain analysis of thick-walled cylinder theory to the study of rockbolting mechanics [34]. Hyett et al. further applied this method to investigate the stress distribution of the bolt subjected to axial loading and established a framework of rockbolting in field conditions, a theoretical model, and corresponding laboratory configuration (Figure 1) [35]. For laboratory testing to reflect the real situation, a confining tube with the same radial stiffness to the surrounding rock should be selected to prepare the testing sample.
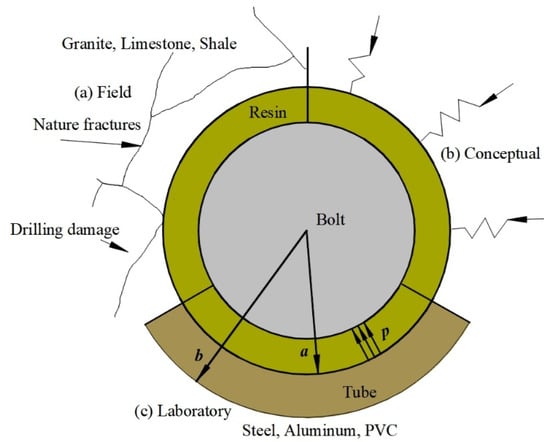
Figure 1.
Rockbolting models, modified [34].
Under plane stress analysis, according to Lame’s equation, the radial stiffness of a tube and the infinite surrounding rock can be expressed as [36]:
where
E is the elastic modulus of tube material, MPa;
is Poisson’s ratio of the tube material;
a is the inner tube diameter (borehole radius), mm;
b is the outer tube diameter, mm;
is the elastic modulus of the surrounding rock, MPa; and
is Poisson’s ratio of the surrounding rock.
For a specific mining site or roadway, the equivalent radial stiffness principle should be implemented in laboratory SEPT design, i.e.,
2.2. Equivalent Radial Stiffness Calculation
To provide an overview of the tube, the surrounding rock classification is introduced here. On the basis of integrality, the uniaxial compressive strength (UCS) of the saturated rock sample () and the self-stability time of the surrounding rock, the surrounding rock was classified into 5 categories in the underground mining industry in China, namely, (I) stable strata, (II) fair stable strata, (III) medium-stable strata, (IV) poor stable strata, and (V) unstable strata [37]. According to the magnitude of it can be roughly simplified into 3 categories: for > 60 MPa, the surrounding rock is strong; for 30 < < 60 MPa, the surrounding rock is medium-strong; and for < 30 MPa, the surrounding rock is weak [38]. According to the statistical relationship between UCS and the elastic properties of the rock, the strong, medium-strong, and weak surrounding rocks correlate to and and and and , respectively.
In China, borehole diameter was usually about 30 mm in the bolting support of a coal mine, i.e., a = 30 mm. Accordingly, by substituting the above parameters into Equation (3), the radial stiffness of the PVC (E = 4.0 GPa and v = 0.35) tube corresponds to the weak surrounding rock (Er = 1.0–3.5 GPa, vr = 0.25–0.30). The radial stiffness of the #6061 Al (E = 68.9 GPa and v = 0.33) tube corresponds to the medium-strong surrounding rock (Er = 15–50 GPa, vr = 0.20–0.25). The radial stiffness of the #20 steel (E = 206 GPa and v = 0.3) tube corresponds to the strong surrounding rock (Er = 50–140 GPa, vr = 0.15–0.20). Figure 2 illustrates the calculation results.
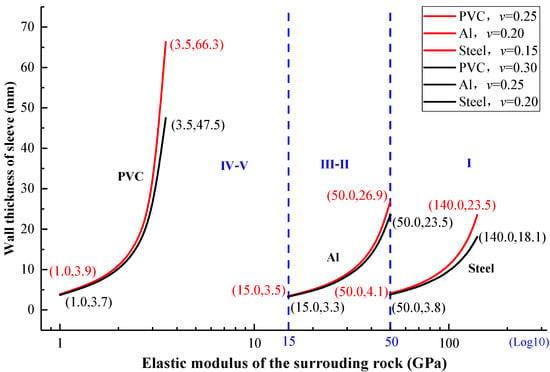
Figure 2.
Relationship between tube wall thickness and the elastic modulus of the surrounding rock (I–V corresponding to surrounding rock classification).
Figure 2 shows that, on the basis of the equivalent radial stiffness principle, tubes composed of PVC, #6061 Al, and #20 steel with proper wall thickness nearly cover the full range of the surrounding rock’s strength. Figure 2 does not give the corresponding tube materials and wall thickness of the surrounding rock with the elastic modulus of 3.5 to 15 GPa, and materials such as C20 to C40 concrete can be used to mimic the surrounding rock or used material with an elastic modulus of roughly 20 to 30 GPa. Currently, the material with an elastic modulus of roughly 20 to 30 GPa has not been found to be available, and using C20 to C40 concrete is the universal method used by many researchers. Consequently, a series of laboratory SEPT were conducted to investigate the anchorage performance of dextral bolts under different confining materials.
3. Laboratory Configuration
- (1)
- Bolt
Two kinds of dextral bolt were studied. First was the original dextral bolt commonly used in underground support. It is a dextral-threaded, nonlongitudinal imprint with a diameter of 20 mm and rib spacing of 12 mm. Second was a modified dextral bolt, which was in a rib spacing of 48 mm through polishing out three transverse ribs. Both bolts were cut to a length of 280 mm, as shown in Figure 3. Table 1 shows the geometric and mechanical parameters of the testing bolts.

Figure 3.
Dextral bolt, rib spacing 12 or 48 mm.

Table 1.
Geometric and mechanical properties of bolts.
- (2)
- Confining tubes
The tubes were composed of PVC, # 6061 Al, and # 20 steel, respectively. The geometric parameters of the tubes are shown in Figure 4. The inner wall was treated through wire cutting to 1.0 mm depth to enhance the friction between resin and the inner wall of the tube, thus that there was no slippage in the resin–tube interface over the pull-out process [39].

Figure 4.
Dimensions of confining tubes of different materials.
- (3)
- Resin anchorage agent
In this test, medium-curing-time resin produced in accordance with the MT146.1-2011 standard [40] was used as the grouting material. On the basis of uniaxial compressive and shear tests, the UCS of the resin grout was 60.9 MPa, cohesion was 19.1 MPa, and the internal friction angle was 32.3°.
- (4)
- Pull-out specimens
After the resin had been cured, the specimens were placed in an incubator at a temperature of (22 ± 1) °C for 24 h. The pretesting specimens are shown in Figure 5.

Figure 5.
Specimens for pull-out tests.
4. Results and Discussion
4.1. Experimental Results
High-strength # 40 Cr steel was used to manufacture a pulling cell to content the testing specimen. WAW-600C microcomputer-controlled electrohydraulic servo-testing machine was used to conduct the test, and loading displacement was controlled at a speed of 1 mm/s. Figure 6 illustrates the pull-out testing arrangement.

Figure 6.
Pull-out test arrangement.
Figure 7 shows the load–displacement curves of all tests. There were three pull-out specimens for each type of confining tubes. Table 2 lists the average axial anchorage load capacity and standard deviation of the axial force. It shows that, for the original dextral bolt compared with PVC tube specimens, the average peak anchorage force of the Al tube and the steel tube specimens increased by 31.5%, 78.0%, and 97.3%, respectively. For the modified dextral bolt, the peak anchorage force of the Al tube and the steel tube specimens increased by 22.5%, 89.6%, and 99.8%, respectively, compared to that of the PVC tube. The axial load capacity of the bolt thus increased with an increase in the radial stiffness of the confining materials; anchorage performance may be quite different for the same dextral bolting support system but in the different surrounding rock. Meanwhile, the experimental results also highlight the influence of rib spacing on the anchorage force. In this case, increasing the rib spacing also increases the anchorage force, as reported by experimental works [24].
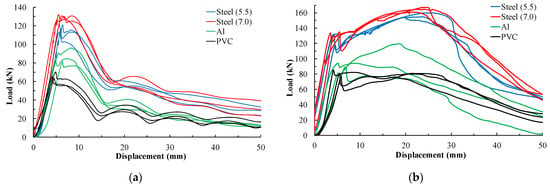
Figure 7.
Load–displacement curves. (a) Bolt with rib spacing of 12 mm; (b) bolt with rib spacing of 48 mm.

Table 2.
Pull-out test results.
4.2. Anchorage Force vs. Radial Stiffness
Using Equation (1), the radial stiffness of the tubes of PVC, Al, and steel with wall thicknesses of 5.5 and 7.5 mm used in the test could be calculated as 0.15, 1.00, 2.90, and 3.63 GPa/mm, respectively. Figure 8a,b show the relationships of the average peak anchorage force with the radial stiffness of confinement for the original and modified dextral bolting sample, respectively. Combined with Figure 2 and Equation (1), the radial stiffness of 0.85 and 2.90 GPa/mm represent the boundaries between the weak/medium-strong and medium-strong/strong surrounding rock, respectively, as indicated by the two dotted blue lines in Figure 8a,b.
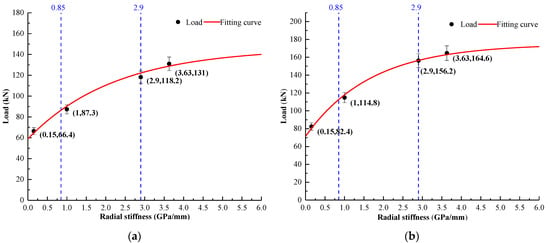
Figure 8.
Relationship between tube radial stiffness and measured peak anchorage force. (a) Bolt with rib spacing of 12 mm; (b) bolt with rib spacing of 48 mm.
To study the pattern of the bolting capacity vs confinement curves, the following negative exponential relationship was proposed for peak anchorage force and the radial stiffness of the confinement in this study:
where
is the anchorage load capacity (kN);
S is the radial stiffness of confining material (GPa/mm);
A is a constant, it is the peak anchorage force while S→+∞;
B is a constant, thus that (A−B) equals the peak anchorage force at S→0; and
C is the curvature parameter.
Using Equation (4) to fit the experimental data of the two kinds of dextral bolt, the fitting curves of the peak anchorage force and the stiffness of the confinement for original and modified dextral bolts can be expressed as the following equations, shown in Figure 8a,b, respectively.
Determinations for Equations (5) and (6) are 0.99; thus, Equation (4) is suitable to determine the relationship between peak anchorage force and stiffness of the confinement.
4.3. Validity Study of Equation (4)
This section further discusses the validity of Equation (4). In the equation, parameter A is the theoretical peak anchorage force when the radial stiffness of the confinement S→+∞, i.e., the peak axial force of a bolt anchored within an extremely rigid confining rock mass. A previous study [41] identified that rockbolting failure while subjected to the axial load can be classified into two modes: parallel shear failure and expansive slippage failure, as shown in Figure 9.
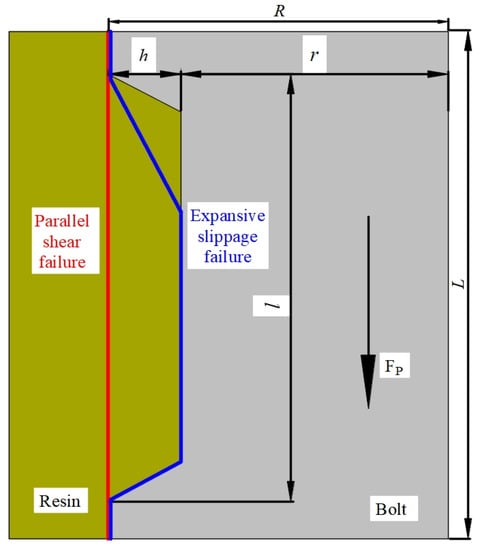
Figure 9.
Rockbolting failure modes. Red line: parallel shear failure; blue line: expansive slippage failure [41].
Parallel shear failure occurs along a cylindrical interface between bolt and resin, whereas expansive slippage failure takes place within the resin material under the transverse rib of the bolt and then slips along the axial direction while expanding in the surrounding material. Under the condition of the infinite radial stiffness of the confining tube, expansion slip failure cannot occur. In other words, anchorage failure can merely exhibit parallel shear failure. In such a situation, the axial force of the bolt equals the shear stress along the failure interface [41]:
where
is the axial load (N);
is the shear stress along the resin/bolt interface (MPa);
is the area of the resin/bolt interface (mm2);
is the shear strength of the resin of the parallel shear failure interface (MPa); and
is the area of the parallel shear failure interface (mm2).
In critical state,
where
is the cohesion of the resin–bolt interface (MPa);
p is the confining pressure when failure occurs (MPa);
is the internal friction angle of the resin–bolt interface (°);
is the resin cohesion (MPa); and
is the internal friction angle of resin (°).
According to the specimen size and dextral-bolt dimensions (Table 1 and Figure 9), ratios l/L were 64% and 91% for the original and modified dextral-threaded bolt, respectively. The outer diameter of the bolt R = 11.8 mm under both conditions. Therefore, for the bolt with a rib spacing of 12 mm, we have mm2 and mm2. For the bolt with the rib spacing of 48 mm, we have 664 mm2 and = 6750 mm2. For resin mechanical properties, = 19.1 MPa and ϕ =32.3°; for the mechanical properties resin–steel interface, we assumed and . Confining pressure p is mainly caused by the shrinkage of the resin, thus, we assumed p = 5.0 MPa [41]. Substituting these parameters into Equations (7)–(9), the theoretical kN, and kN. Compared with the experimental data of = 146.0 kN and = 174.8 kN, two theoretical values agreed well.
According to Equation (3), (A−B) is the anchorage force when radial stiffness S→0. At present, there is no commonly accepted approach to estimate the peak anchorage force in such situations. The minimal peak anchorage force should be related to bolt type and grout strength but is independent of the surrounding rock conditions. In this study, the theoretical peak anchorage force without the radial stiffness of confining material for the original dextral bolt was 58.9 kN, which can be used as a reference for subsequent study.
4.4. Failure Mode
Figure 10 shows the post-testing specimens. Two failure modes can be identified. The failure interface of the bolting specimens with a rib spacing of 12 mm was nearly a regular cylinder surface, which indicates that its predominant failure mode was a parallel shear failure. For the dextral bolt with rib spacing of 48 mm, the grout of specimens was relatively broken, and blocky grout accumulated beneath the transverse rib, suggesting that of the bolt was dominated by the expansive slippage failure. The difference between these two failure modes can be understood in the previous study [41]. In addition, it suggests that changing the rib spacing can change the failure mode and process of the anchorage system. Therefore, it may improve the bolt anchoring performance by optimizing the bolt rib spacing.

Figure 10.
Failure modes of bolt specimens with different rib spacings.
5. Conclusions
SEPT is an effective approach to study the reinforcement mechanism and bolting-support technology. To realize laboratory SEPT results reflecting site conditions, the influence of radial stiffness on reinforcement performance was studied. The following conclusions are summarized on the basis of laboratory testing and theoretical analysis.
- (1)
- On the basis of thick wall cylinder theory, an equivalent radial stiffness method was developed to establish the relationship between the confining tube in the laboratory and the elastic properties of surrounding rock (Equations (1)–(3)). Calculation results showed that the PVC tube (E = 4.0 GPa and v = 0.35) corresponds to the radial stiffness of the weak surrounding rock (Er = 1.0–3.5 GPa, vr = 0.25–0.30); Al tube (E = 68.9 GPa and v = 0.33) corresponds to the medium-strong surrounding rock (Er = 15.0–50 GPa, vr = 0.20–0.25); and the steel tube (E = 206 GPa and v = 0.3) corresponds to the strong surrounding rock (Er = 50.0–140.0 GPa, vr = 0.15–0.20). This can be used to improve the accuracy of laboratory SEPT results towards the site outcome (Figure 2).
- (2)
- Two kinds of dextral-threaded bolt were studied using the developed method of this study. PVC, Al, and steel tubes were used as confinement in laboratory SEPT, and anchorage performance was obtained under different surrounding rock strength levels (Figure 7). The results show that axial load capacity increased with the increase in radial stiffness of the confining materials. Compared with PVC tube specimens, peak axial force was nearly double when using thick steel tubes (Table 2).
- (3)
- On the basis of theoretical analysis and curve fitting, the relationship between the average peak axial force and radial stiffness of the confining materials was proposed to be a negative exponential (Equation (4)) function. A validity study was conducted, and its result showed that the proposed relationship agreed well with the theory in the literature. The developed equation could be used to determine the performance of a specific bolt under different field geoconditions and provide accurate parameters for numerical modeling.
- (4)
- Post-testing specimens showed that the failure modes of the original and modified dextral bolts were parallel shear failure and expansive slippage failure, respectively (Figure 10). As anchorage performance is determined by the load-transfer mechanism in a bolting system, which is closely related to the failure model of rockbolting, it may be practical to design and realize different anchorage effects for different field geoconditions via controlling the technology of rockbolting failures, such as with rebar-profile modification.
Author Contributions
Conceptualization, J.H. and C.C.; methodology, C.C.; software, M.Z.; validation, M.Z., C.C., T.W., and S.M.; formal analysis, M.Z.; investigation, Z.B.; resources, J.H.; writing—original draft preparation, M.Z.; writing—review and editing, J.H., and C.C.; supervision, M.Z. and C.C.; project administration, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52074145; and the Liaoning Revitalization Talents Program, grant number XLYC2002110.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, C.C. Rockbolting: Principles and Applications, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2017; pp. 1–2. [Google Scholar]
- Małkowski, P.; Niedbalski, Z.; Balarabe, T. A statistical analysis of geomechanical data and its effect on rock mass numerical modeling: A case study. Int. J. Coal Sci. Technol. 2021, 8, 312–323. [Google Scholar] [CrossRef]
- Cao, D.; Wang, A.; Ning, S.; Li, H.; Guo, A.; Chen, L.; Liu, K.; Tan, J.; Zheng, Z. Coalfield structure and structural controls on coal in China. Int. J. Coal Sci. Technol. 2020, 7, 220–239. [Google Scholar] [CrossRef]
- Mao, S. Development of coal geological information technologies in China. Int. J. Coal Sci. Technol. 2020, 7, 320–328. [Google Scholar] [CrossRef]
- Han, J.; Liang, H.; Cao, C.; Bi, Z.Q.; Zhu, Z.J. A mechanical model for sheared joints based on Mohr-Coulomb material properties. Geotech. Lett. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Kang, H.P. 60 years development and prospects of rock bolting technology for underground coal mine roadways in China. J. China Univ. Min. Techno. 2016, 45, 1071–1081. [Google Scholar]
- Li, C.C.; Stillborg, B. Analytical models for rock bolts. Int. J. Rock Mech Min. 1999, 36, 1013–1029. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Sun, Z.Y.; Li, J.Z. Experimental study on reinforcement effect of bolt support composite members on reinforced mesh. J. China Coal Soci. 2020, 45, 556–567. [Google Scholar]
- Windsor, C.R. Rock reinforcement systems. Int. J. Rock Mech Min. 1997, 34, 919–951. [Google Scholar] [CrossRef]
- Fabjanczyk, M.; Hurt, K.; Hindmarsh, D. Optimization of roof bolt performance. In Proceedings of the International Conference on Geomechanics/Ground Control in Mining and Underground Construction, Wollongong, Australia, 14–17 July 1998; Wollongong of University: Wollongong, Australia, 1998; pp. 413–424. [Google Scholar]
- People’s Republic of China Coal Industry Standards. GB/T35056-2018 Technical Specifications for Rock Bolting in Coal Mine Roadways; China National Coal Association: Beijing, China, 2018. [Google Scholar]
- Kang, H.P.; Cui, Q.L.; Hu, B.; Wu, Z.G. Analysis of anchorage properties and affecting factors of resin bolts. J. China Coal Soci. 2014, 39, 1–10. [Google Scholar]
- Chen, Y.; Li, C.C. Influences of loading condition and rock strength to the performance of rock bolts. Geotech. Test. J. 2015, 38, 208–218. [Google Scholar] [CrossRef]
- Wu, T.; Cao, C.; Han, J.; Ren, T. Effect of bolt rib spacing on load transfer mechanism. Int. J. Min. Sci. Technol. 2017, 27, 431–434. [Google Scholar]
- Xue, D.J.; Zhou, J.; Liu, Y.T.; Gao, L. On the excavation-induced stress drop in damaged coal considering a coupled yield and failure criterion. Int. J. Coal Sci. Technol. 2020, 7, 58–67. [Google Scholar] [CrossRef] [Green Version]
- Xue, D.J.; Liu, Y.T.; Zhou, H.W.; Wang, J.Q.; Liu, J.F.; Zhou, J. Fractal characterization on anisotropy and fractal reconstruction of rough surface of granite under orthogonal shear. Rock Mech Rock Eng. 2020, 53, 1225–1242. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, S.; Zhang, C.; Fang, X.Q.; Li, S. The characterization of bituminous coal microstructure and permeability by liquid nitrogen fracturing based on μCT technology. Fuel 2020, 262, 116635. [Google Scholar] [CrossRef]
- Biumel, M. Performance of grouted bolts in squeezing rock. In Proceedings of the ISRM International Symposium-EUROCK 96, International Society for Rock Mechanics and Rock Engineering, Turin, Italy, 2–5 September 1996; pp. 885–891. [Google Scholar]
- Overwin, U.; Rock, R.; Biumel, M.; Schwab, P. New development for grouted rock bolts. Int. J. Rock Mech Min. Sci. Geomech. Abstr. 1996, 33, 42–48. [Google Scholar]
- Biumel, M.; Schweiger, H.F.; Golser, H. Effect of rib geometry on the mechanical behaviour of grouted rock bolts. In Proceedings of the 23rd General Assembly of the International Tunnelling, Wien, Austria, 12–17 April 1997; pp. 6–7. [Google Scholar]
- Jalalifar, H. A New Approach in Determining the Load Transfer Mechanism in Fully Grouted Bolts. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2006. [Google Scholar]
- Aziz, N.; Jalalifar, H.; Concalves, J. Bolt surface configurations and load transfer mechanism. In Proceedings of the 7th Underground Coal Operators Conference, Wollongong, Australia, 6–7 July 2006; pp. 236–244. [Google Scholar]
- Aziz, N.; Jalalifar, H.; Remennikov, A.M.; Sinclair, S.; Green, A. Optimisation of the bolt profile configuration for load transfer enhancement. In Proceedings of the 8th Underground Coal Operators Conference, Wollongong, Australia, 14–15 February 2008; pp. 125–131. [Google Scholar]
- Wu, T.; Cao, C.; Zhao, X.Z.; Zhang, M.; Zhang, H.D.; Ma, S.W.; Han, J. Laboratory study on anchorage performance in different rib spacings of bolt. J. China Coal Soci. 2017, 42, 2545–2553. [Google Scholar]
- Ma, S.; Aziz, N.; Nemcik, J.; Mirzaghorbanali, A. The effects of installation procedure on bond characteristics of fully grouted rock bolts. Geotech. Test. J. 2016, 40, 846–857. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, N.; Yang, S.; He, F. Mechanical response of fully bonded bolts under cyclic load. Int. J. Rock Mech. Min. 2018, 109, 138–154. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, C.; Zhang, H.D.; Tran, V.; Ren, T.; Ma, S.W.; Han, J. Effect of anchoring force by adding steel aggregate in resin anchoring agent. J. China Coal Soci. 2019, 44, 1690–1697. [Google Scholar]
- Zhang, L.; Li, J.H.; Xue, J.H.; Zhang, C. Experimental studies on the changing characteristics of the gas flow capacity on bituminous coal in CO2-ECBM and N2-ECBM. Fuel 2021, 291, 120115. [Google Scholar] [CrossRef]
- Lin, J.; Ren, T.; Cheng, Y.P.; Nemcik, J.; Wang, G.D. Cyclic N2 injection for enhanced coal seam gas recovery: A laboratory study. Energy 2019, 188, 116115. [Google Scholar] [CrossRef]
- Lin, J.; Ren, T.; Wang, G.D.; Booth, P.; Nemcik, J. Experimental investigation of N2 injection to enhance gas drainage in CO2-rich low permeable seam. Fuel 2018, 215, 665–674. [Google Scholar] [CrossRef]
- Chen, B. Stress-induced trend: The clustering feature of coal mine disasters and earthquakes in China. Int. J. Coal Sci. Technol. 2020, 7, 676–692. [Google Scholar] [CrossRef]
- Wu, X.; Peng, Y.; Xu, J.; Yan, Q.; Nie, W.; Zhang, T.T. Experimental study on evolution law for particle breakage during coal and gas outburst. Int. J. Coal Sci. Technol. 2020, 7, 97–106. [Google Scholar] [CrossRef] [Green Version]
- Xue, D.J.; Lu, L.L.; Zhou, J.; Lu, L.; Liu, Y.T. Cluster modeling of the short-range correlation of acoustically emitted scattering signals. Int. J. Coal Sci. Technol. 2020, 1–15. [Google Scholar] [CrossRef]
- Yazici, S.; Kaiser, P.K. Bond strength of grouted cable bolts. Int. J. Rock Mech Min. Sci. Geomech. Abstrs. 1992, 29, 279–292. [Google Scholar] [CrossRef]
- Hyett, A.J.; Bawden, W.F.; Macsporran, G.R.; Moosavi, M. A constitutive law for bond failure of fully-grouted cable bolts using a modified hoek cell. Int. J. Rock Mech Min. Sci. Geomech. Abstrs. 1995, 32, 11–36. [Google Scholar] [CrossRef]
- Zhao, X.Z.; Zhang, H.W.; Cao, C.; Zhang, M.; Zhang, H.D.; Han, J. Optimization of bolt rib spacing and anchoring force under different conditions of surrounding rock. Rock Soil Mech 2018, 39, 1–9. [Google Scholar]
- Hou, C.J. Ground Control of Roadway, 1st ed.; China University of Mining and Technology Press: Xuzhou, China, 2013; pp. 29–33. [Google Scholar]
- Peng, S.S.; Li, H.M.; Zhou, Y. Research on Rock Stratum Control in Shendong and Zhungeer Mining Areas, 1st ed.; Science Press: Beijing, China, 2015; pp. 58–62. [Google Scholar]
- Aziz, N.; Webb, B. Study of load transfer capacity of bolts using short encapsulation push test. In Proceedings of the 22nd International Conference on Ground Control in Mining, US Mine Safety and Health Administration, Morgantown, WV, USA, 5–7 August 2003; pp. 203–207. [Google Scholar]
- People’s Republic of China Coal Industry Standards. GB/MT146.1-2011 Resin Anchor Bolts. Part. 1: Capsules; China National Coal Association: Beijing, China, 2011. [Google Scholar]
- Cao, C.; Ren, T.; Cook, C.; Cao, Y. Analytical approach in optimising selection of rebar bolts in preventing rock bolting failure. Int. J. Rock Mech Min. 2014, 72, 16–25. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).