Hemodynamic Analysis on the Anastomosis Angle in Arteriovenous Graft Using Multiphase Blood Model
Abstract
:1. Introduction
2. Materials and Methods
3. Numerical Details
3.1. Governing Equations
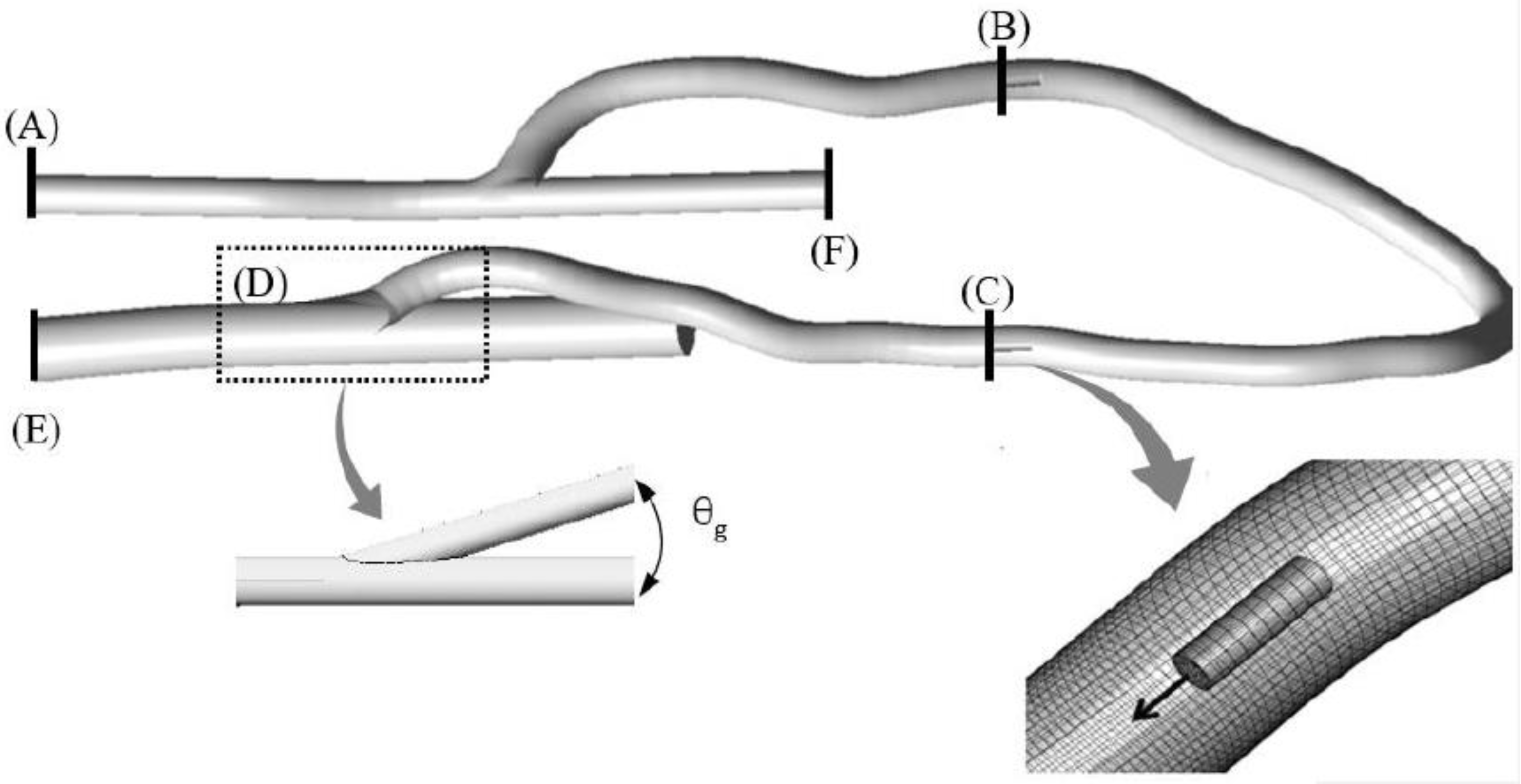
3.2. Geometry and Numerical Detail
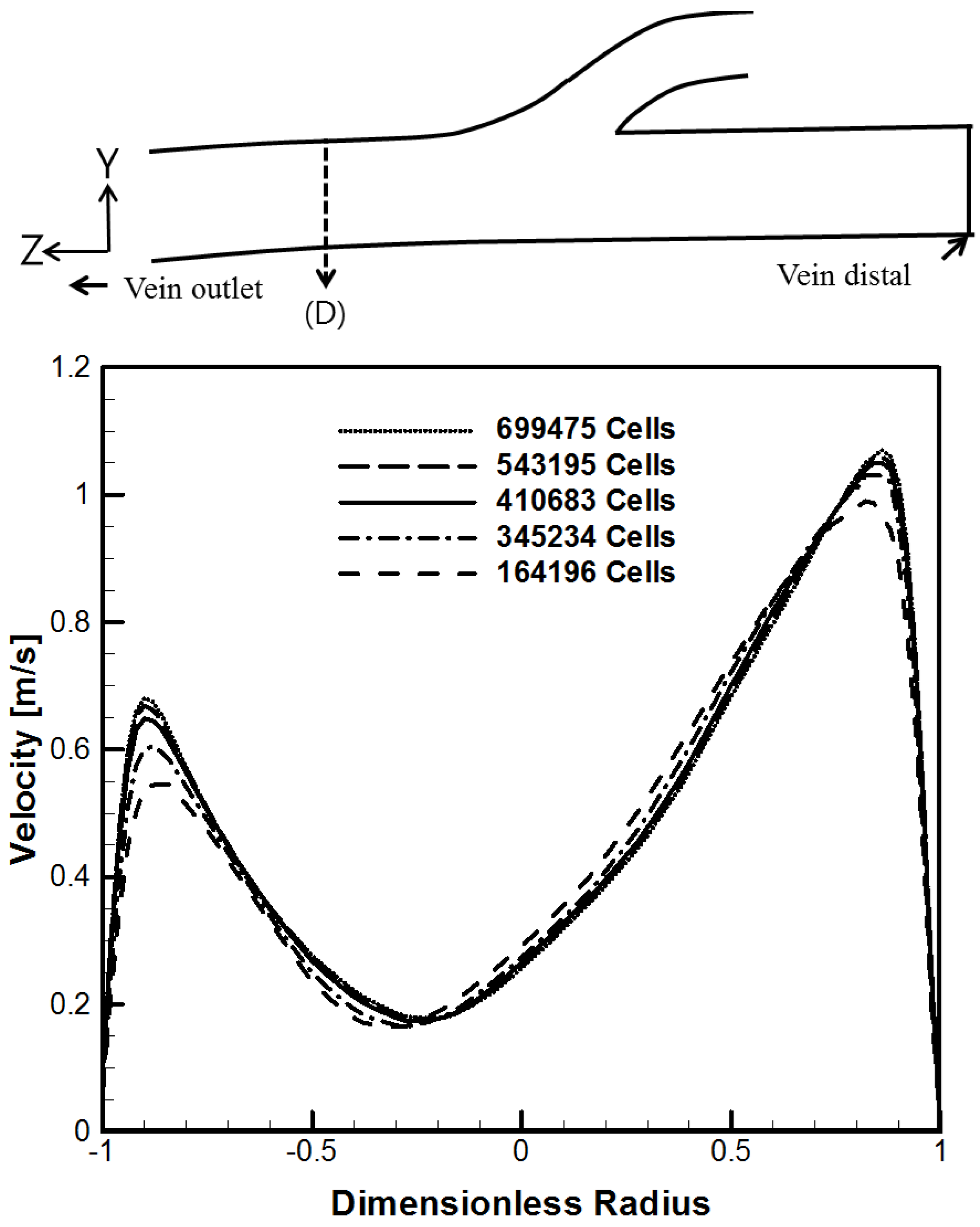
3.3. Grid Independence Test
4. Results and Discussion
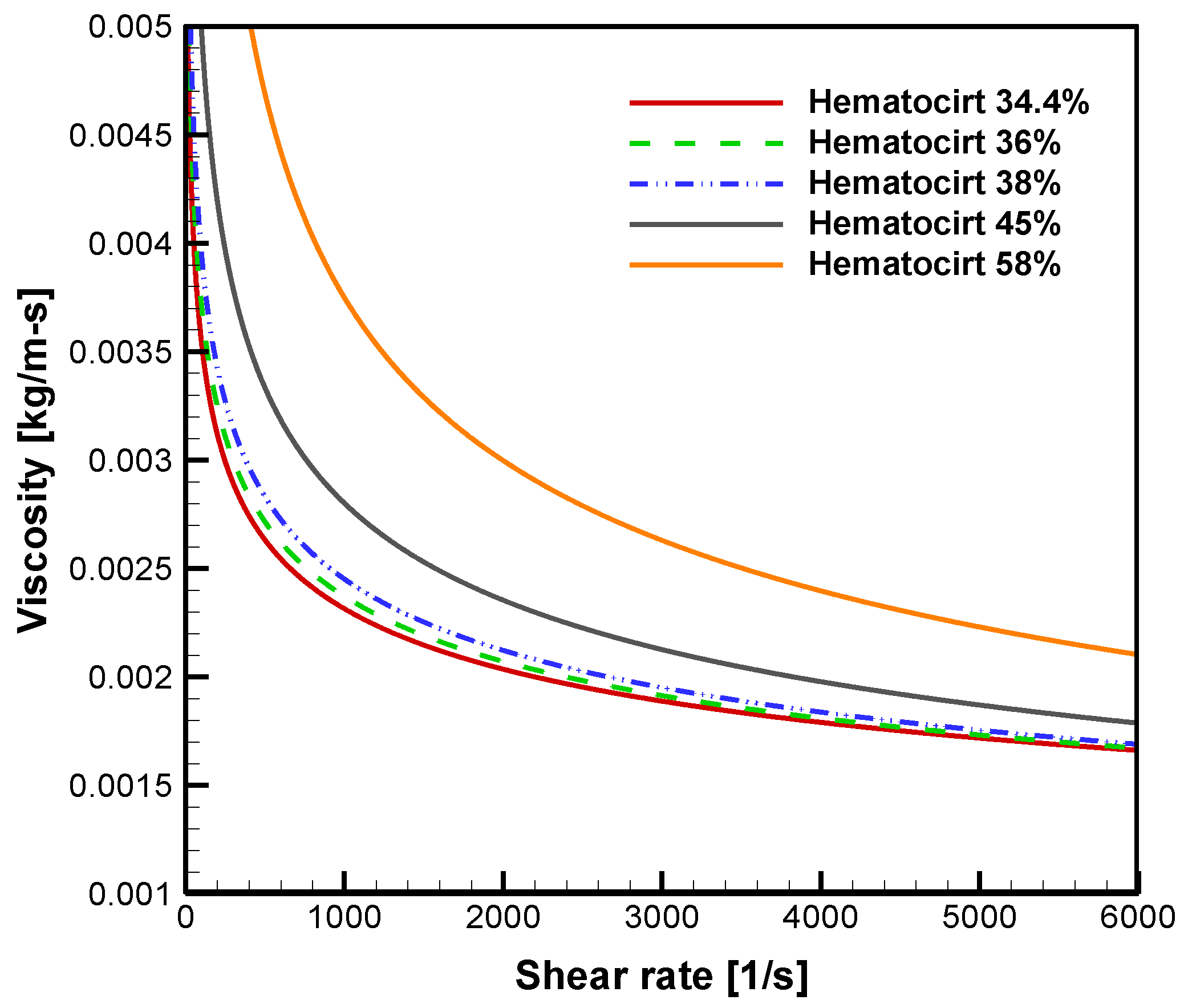
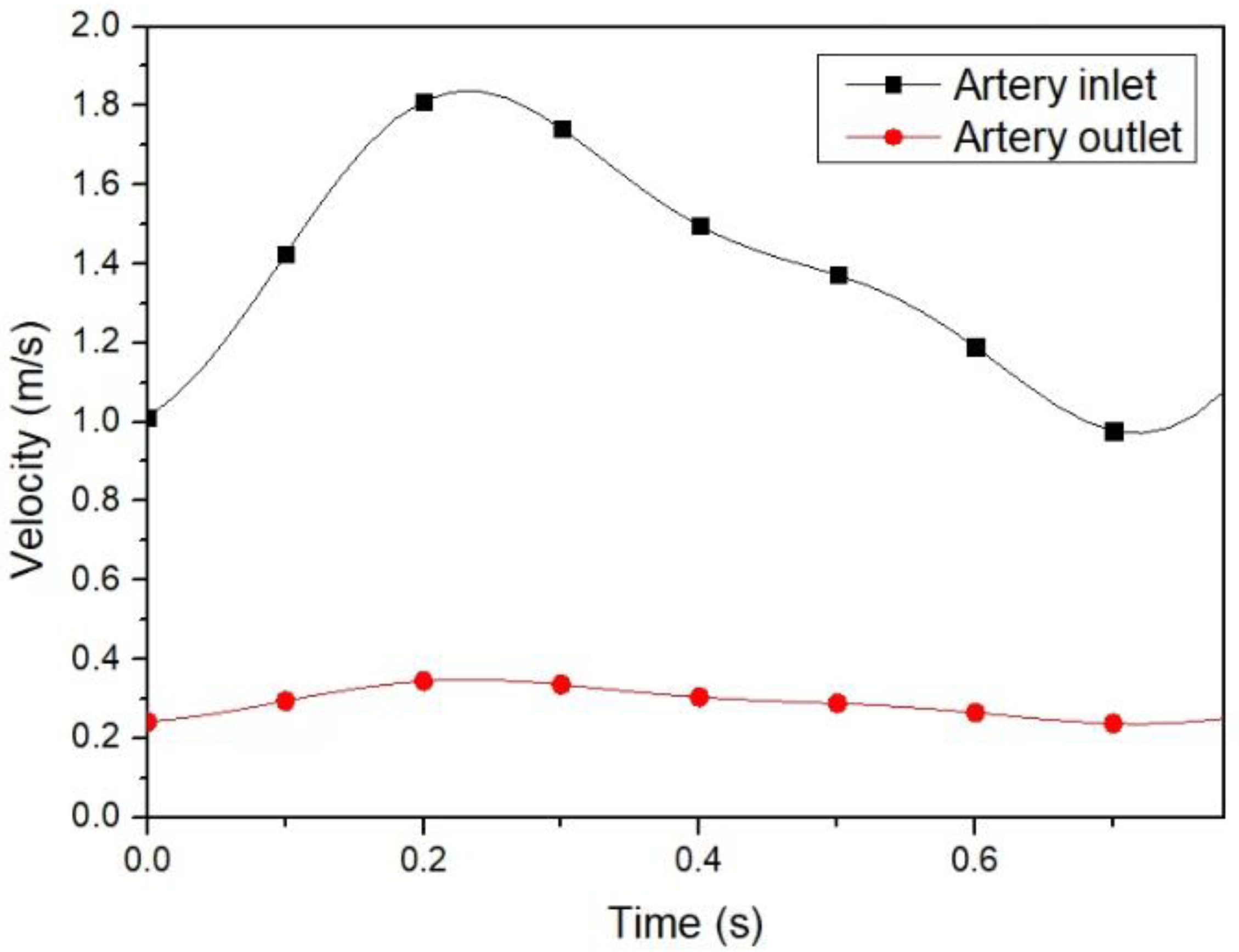
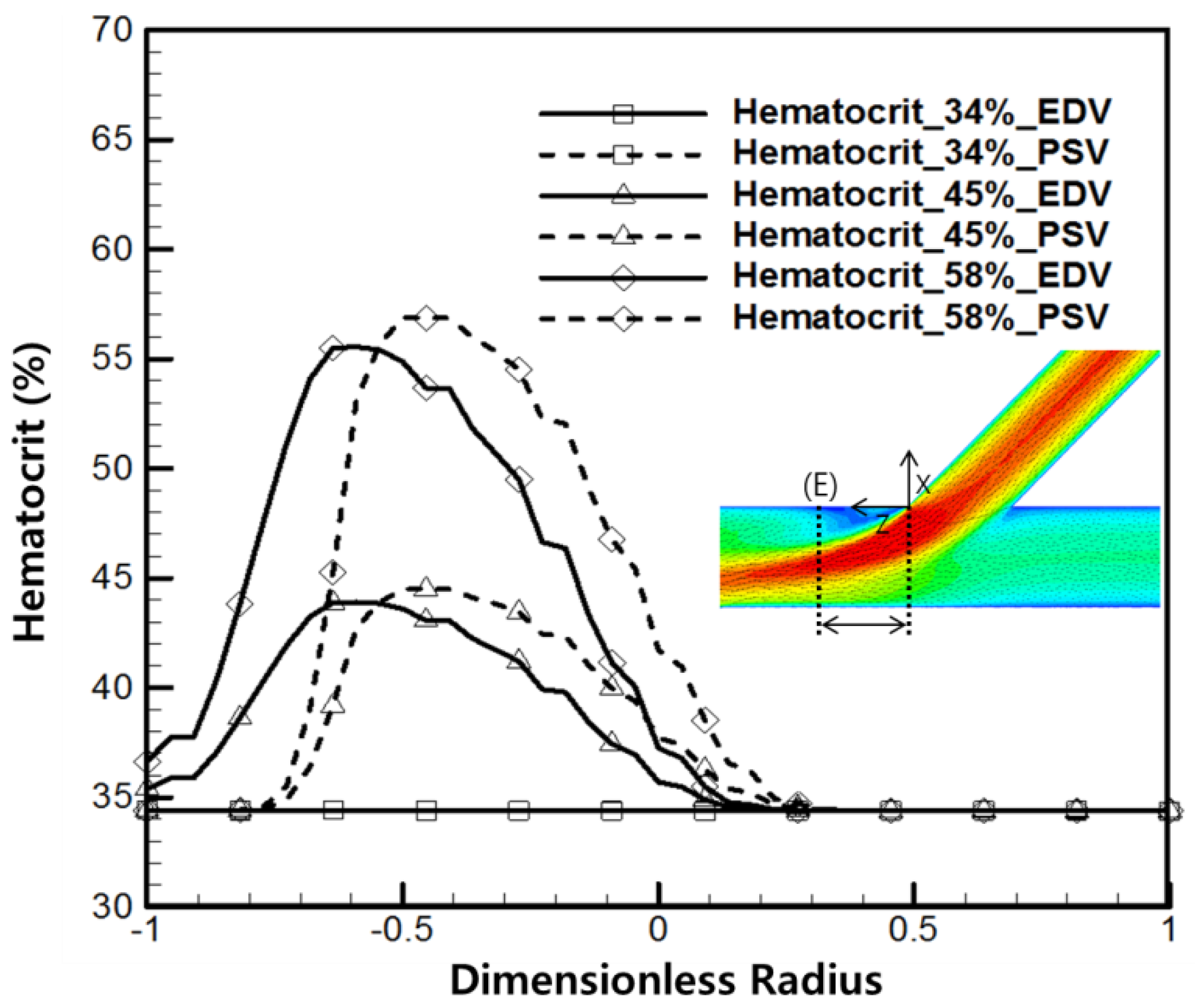
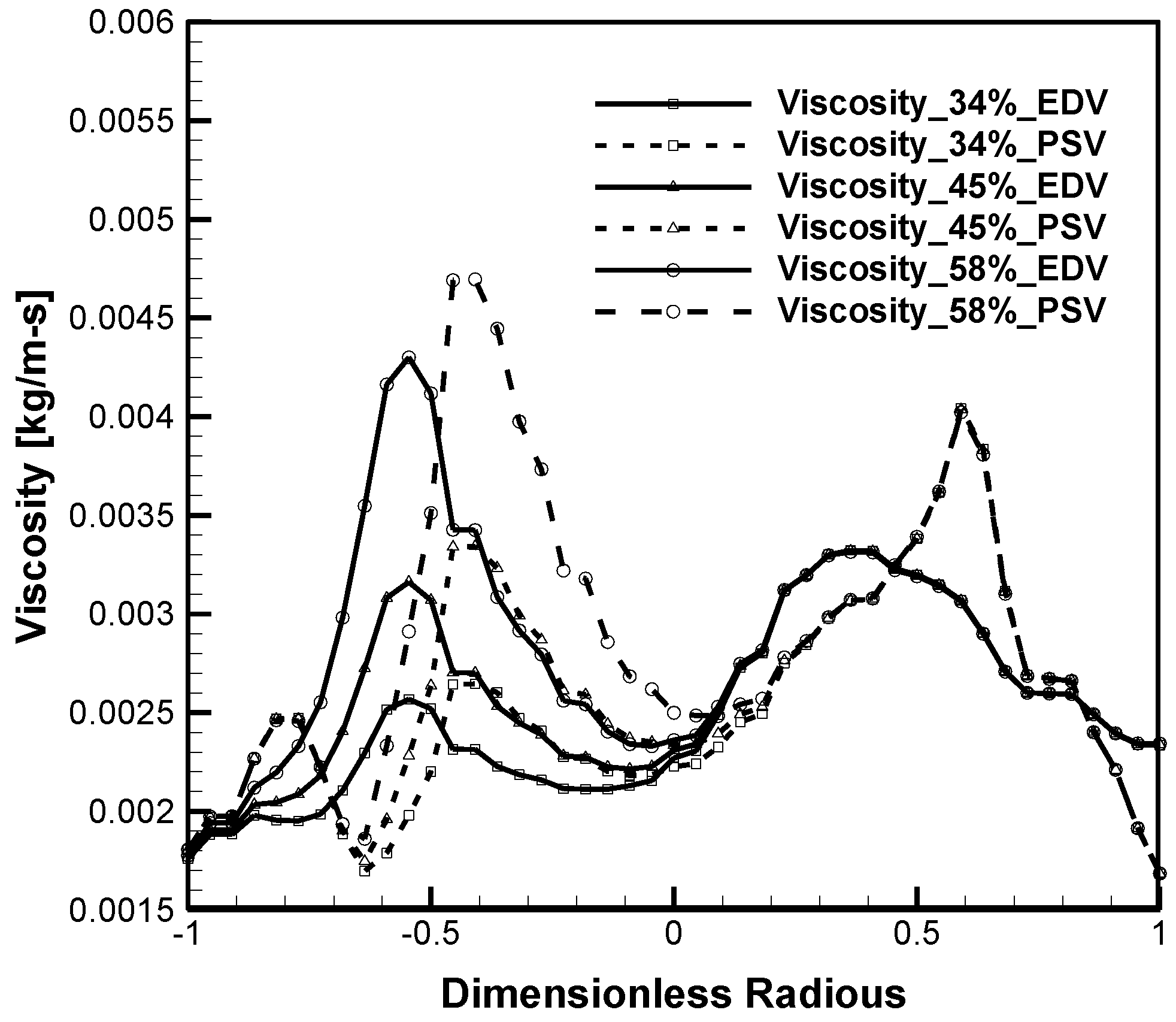
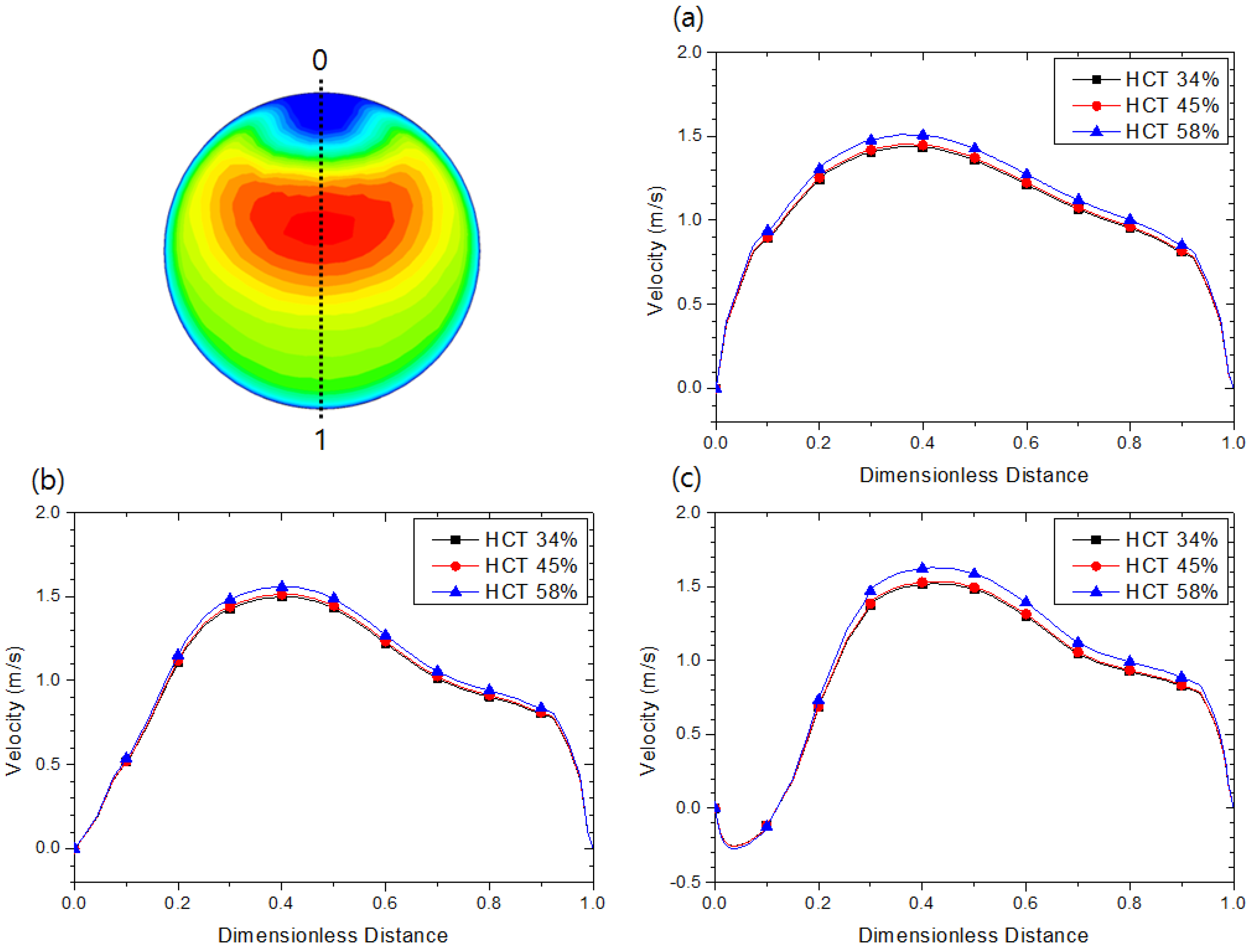
4.1. Hematocrit and Flow Analysis
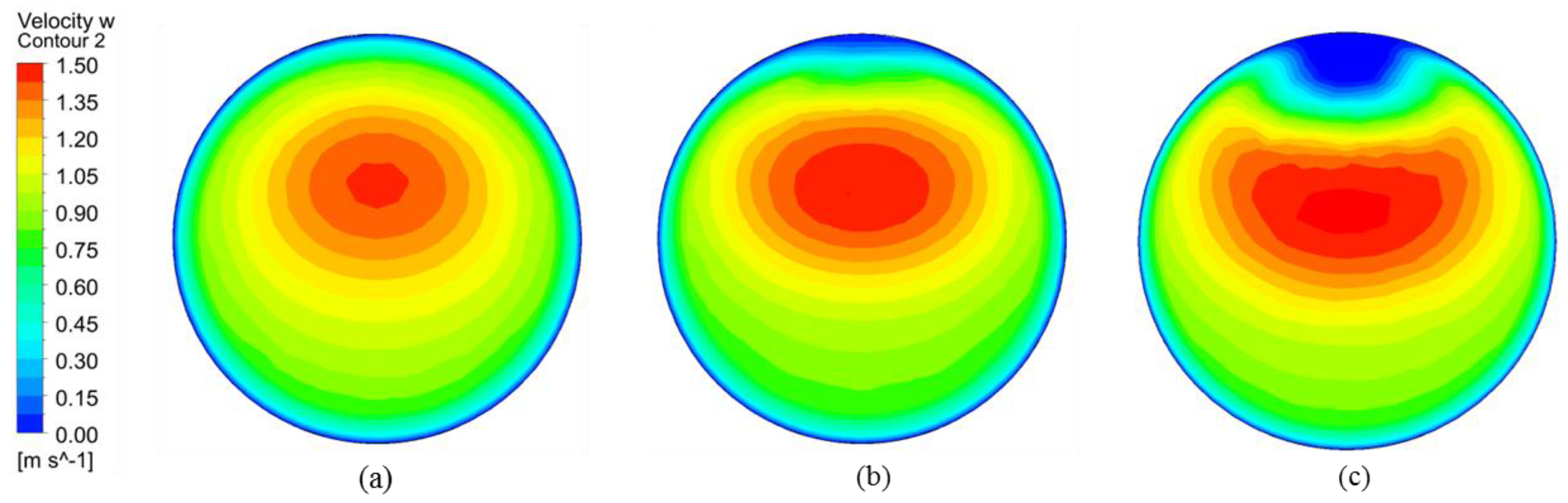
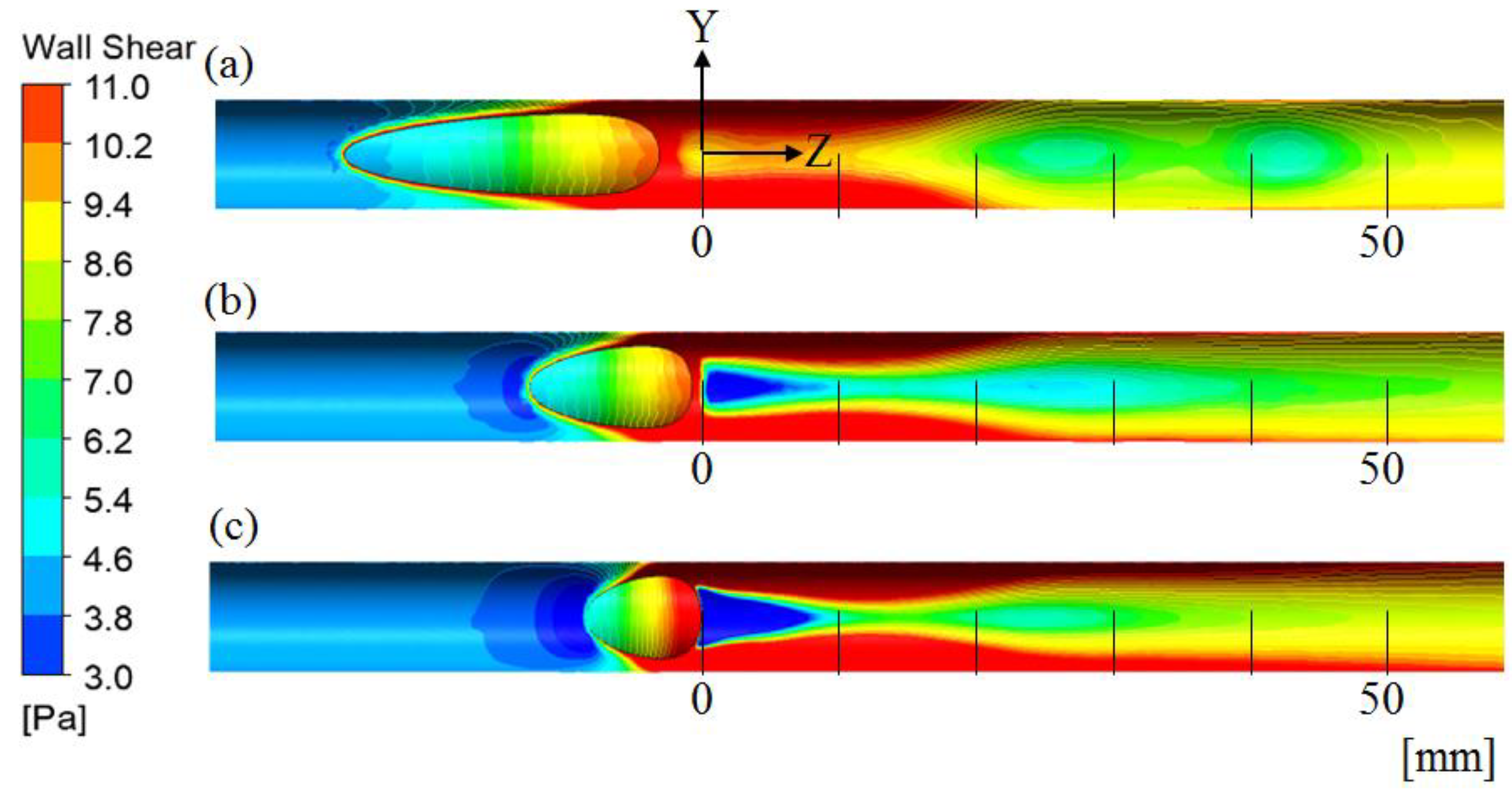
4.2. Effect of the Anastomosis Angle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Lok, C.E.; Huber, T.S.; Lee, T.; Shenoy, S.; Yevzlin, A.S.; Abreo, K.; Allon, M.; Asif, A.; Astor, B.C.; Glickman, M.H.; et al. KDOQI Clinical Practice Guideline for Vascular Access: 2019 Update. Am. J. Kidney Dis. 2020, 75 (Suppl. 2), S1–S164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riella, M.C.; Roy-Chaudhury, P. Vascular access in haemodialysis: Strengthening the Achilles’ heel. Nat. Rev. Nephrol. 2013, 9, 348. [Google Scholar] [CrossRef]
- Feldman, H.I.; Kobrin, S.; Wasserstein, A. Hemodialysis vascular access morbidity. J. Am. Soc. Nephrol. 1996, 7, 523–535. [Google Scholar] [CrossRef]
- Malovrh, M. Interventional Nephrology and Dialysis: The Role of Sonography in the Planning of Arteriovenous Fistulas for Hemodialysis. Semin. Dial. 2003, 16, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Brahmbhatt, A.; Misra, S. The biology of hemodialysis vascular access failure. Semin. Interv. Radiol. 2016, 33, 015–020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skartsis, N.; Manning, E.; Wei, Y.; Velazquez, O.C.; Liu, Z.J.; Goldschmidt-Clermont, P.J.; Salman, L.H.; Asif, A.; Vazquez-Padron, R.I. Origin of neointimal cells in arteriovenous fistulae: Bone marrow, artery, or the vein itself? Semin. Dial. 2011, 24, 242–248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kraiss, L.W.; Geary, R.L.; Mattsson, E.J.; Vergel, S.; Au, Y.P.; Clowes, A.W. Acute reductions in blood flow and shear stress induce platelet-derived growth factor-A expression in baboon prosthetic grafts. Circ. Res. 1996, 79, 45–53. [Google Scholar] [CrossRef]
- Collins, M.J.; Li, X.; Lv, W.; Yang, C.; Protack, C.D.; Muto, A.; Jadlowiec, C.C.; Shu, C.; Dardik, A. Therapeutic strategies to combat neointimal hyperplasia in vascular grafts. Expert Rev. Cardiovasc. 2012, 10, 635–647. [Google Scholar] [CrossRef]
- Staalsen, N.-H.; Ulrich, M.; Winther, J.; Pedersen, E.M.; How, T.; Nygaard, H. The anastomosis angle does change the flow fields at vascular end-to-side anastomoses in vivo. J. Vasc. Surg. 1995, 21, 460–471. [Google Scholar] [CrossRef] [Green Version]
- Nanjo, H.; Sho, E.; Komatsu, M.; Sho, M.; Zarins, C.K.; Masuda, H. Intermittent short-duration exposure to low wall shear stress induces intimal thickening in arteries exposed to chronic high shear stress. Exp. Mol. Pathol. 2006, 80, 38–45. [Google Scholar] [CrossRef]
- Misra, S.; Fu, A.A.; Misra, K.D.; Glockner, J.F.; Mukhopadhyay, D. Wall shear stress measurement using phase contrast magnetic resonance imaging with phase contrast magnetic resonance angiography in arteriovenous polytetrafluoroethylene grafts. Angiology 2009, 60, 441–447. [Google Scholar] [CrossRef] [Green Version]
- Boghosian, M.; Cassel, K.; Hammes, M.; Funaki, B.; Kim, S.; Qian, X.; Wang, X.; Dhar, P.; Hines, J. Hemodynamics in the cephalic arch of a brachiocephalic fistula. Med. Eng. Phys. 2014, 36, 822–830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carroll, G.T.; McGloughlin, T.M.; Burke, P.E.; Egan, M.; Wallis, F.; Walsh, M.T. Wall shear stresses remain elevated in mature arteriovenous fistulas: A case study. J. Biomech. Eng. 2011, 133, 021003. [Google Scholar] [CrossRef]
- Carroll, G.T.; McGloughlin, T.M.; O’Keeffe, L.M.; Callanan, A.; Walsh, M.T. Realistic Temporal Variations of Shear Stress Modulate MMP-2 and MCP-1 Expression in Arteriovenous Vascular Access. Cell. Mol. Bioeng. 2009, 2, 591–605. [Google Scholar] [CrossRef]
- McGah, P.M.; Leotta, D.F.; Beach, K.W.; Aliseda, A. Effects of wall distensibility in hemodynamic simulations of an arteriovenous fistula. Biomech. Model. Mechanobiol. 2014, 13, 679–695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGah, P.M.; Leotta, D.F.; Beach, K.W.; Eugene Zierler, R.; Aliseda, A. Incomplete restoration of homeostatic shear stress within arteriovenous fistulae. J. Biomech. Eng. 2013, 135, 011005. [Google Scholar] [CrossRef] [Green Version]
- Ene-Iordache, B.; Cattaneo, L.; Dubini, G.; Remuzzi, A. Effect of anastomosis angle on the localization of disturbed flow in ‘side-to-end’ fistulae for haemodialysis access. Nephrol. Dial. Transplant. 2013, 28, 997–1005. [Google Scholar] [CrossRef] [PubMed]
- Hakaim, A.G.; Nalbandian, M.N.; Heller, J.K.; Chowla, A.C.; Oldenburg, W.A. Improved patency of prosthetic arteriovenous grafts with an acute anastomotic angle and flow diffuser. J. Vasc. Surg. 2003, 37, 1032–1035. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, C.-Y.; Li, M.-C.; Lan, C.-W.; Lee, W.-J.; Lee, C.-J.; Wu, C.-H.; Tang, J.-M.; Niu, Y.-Y.; Lin, Y.-P.; Shiu, Y.-T.; et al. The Anastomotic Angle of Hemodialysis Arteriovenous Fistula Is Associated With Flow Disturbance at the Venous Stenosis Location on Angiography. Front. Bioeng. Biotechnol. 2020, 8, 846. [Google Scholar] [CrossRef] [PubMed]
- Tordoir, J.H.M.; Zonnebeld, N.; van Loon, M.M.; Gallieni, M.; Hollenbeck, M. Surgical and Endovascular Intervention for Dialysis Access Maturation Failure During and After Arteriovenous Fistula Surgery: Review of the Evidence. Eur. J. Vasc. Endovasc. Surg. 2018, 55, 240–248. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.; Hassanein, A. Three-phase CFD analytical modeling of blood flow. Med. Eng. Phys. 2008, 30, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Scardulla, F.; Pasta, S.; D’Acquisto, L.; Sciacca, S.; Agnese, V.; Vergara, C.; Quarteroni, A.; Clemenza, F.; Bellavia, D.; Pilato, M. Shear stress alterations in the celiac trunk of patients with a continuous-flow left ventricular assist device as shown by in-silico and in-vitro flow analyses. J. Heart Lung Transpl. 2017, 36, 906–913. [Google Scholar] [CrossRef]
- Elhanafy, A.; Elsaid, A.; Guaily, A. Numerical investigation of hematocrit variation effect on blood flow in an arterial segment with variable stenosis degree. J. Mol. Liq. 2020, 313, 113550. [Google Scholar] [CrossRef]
- Masuda, H.; Kawamura, K.; Sugiyama, T.; Kamiya, A. Effects of endothelial denudation in flow-induced arterial dilatation. Front. Med. Biol. Eng. 1993, 5, 57–62. [Google Scholar] [PubMed]
- Dobrin, P.B.; Littooy, F.N.; Endean, E.D. Mechanical factors predisposing to intimal hyperplasia and medial thickening in autogenous vein grafts. Surgery 1989, 105, 393–400. [Google Scholar] [PubMed]
- Franzoni, M.; Cattaneo, I.; Longaretti, L.; Figliuzzi, M.; Ene-Iordache, B.; Remuzzi, A. Endothelial cell activation by hemodynamic shear stress derived from arteriovenous fistula for hemodialysis access. Am. J. Physiol. Heart Circ. Physiol. 2016, 310, H49–H59. [Google Scholar] [CrossRef] [Green Version]
- Fillinger, M.F.; Reinitz, E.R.; Schwartz, R.A.; Resetarits, D.E.; Paskanik, A.M.; Bredenberg, C.E. Beneficial effects of banding on venous intimal-medial hyperplasia in arteriovenous loop grafts. Am. J. Surg. 1989, 158, 87–94. [Google Scholar] [CrossRef]
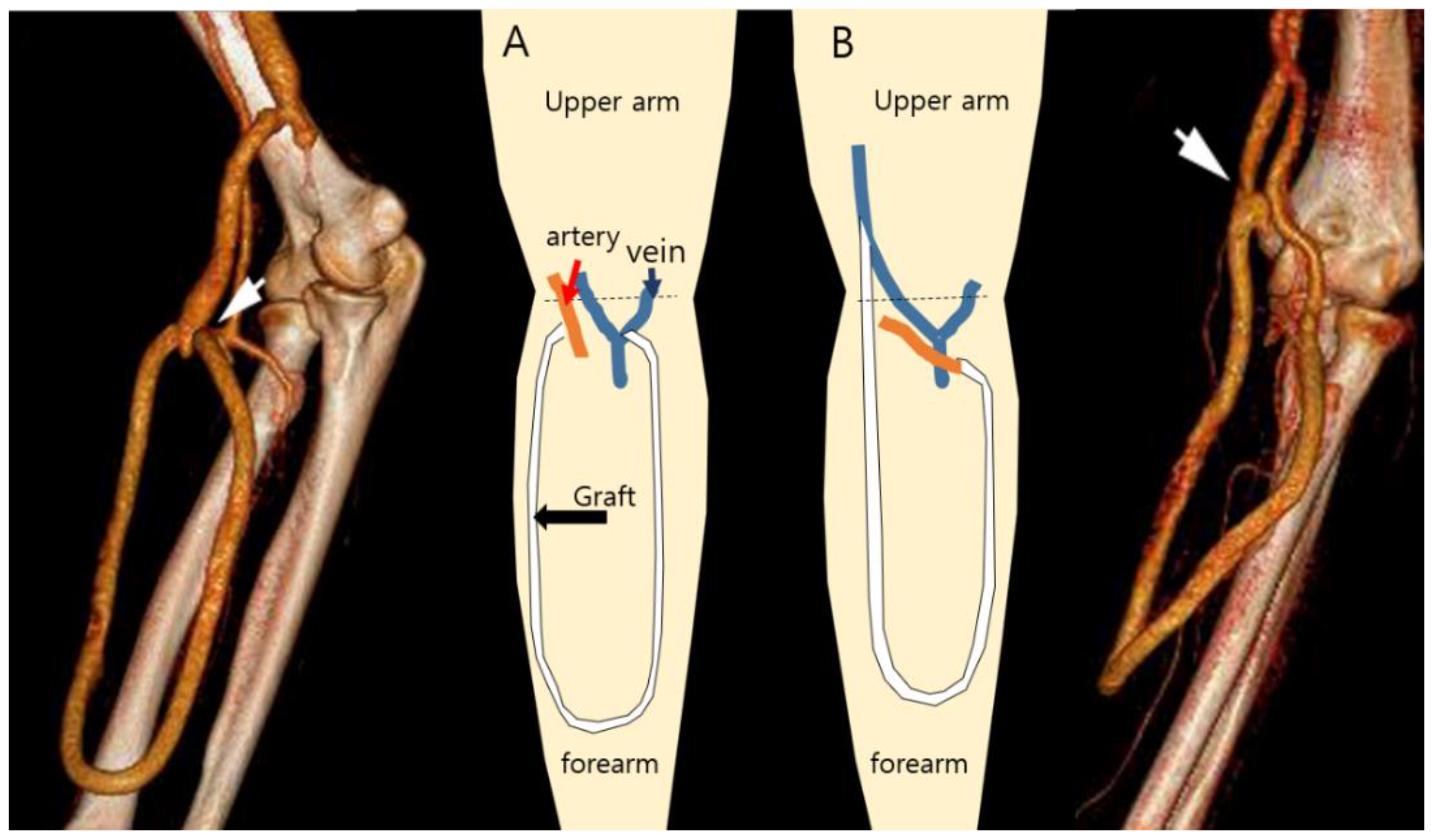

| Patient 1 | Patient 2 | Patient 3 | Patient 4 | Mean | |
|---|---|---|---|---|---|
| Graft diameter (mm) | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 |
| Vein diameter (mm) | 7.0 | 8.7 | 7.1 | 9.2 | 8.0 |
| Artery diameter (mm) | 4.0 | 3.0 | 3.9 | 4.1 | 3.75 |
| Anastomosis angle | 15 | 18 | 21 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.T.; Kim, H.; Ryou, H.S. Hemodynamic Analysis on the Anastomosis Angle in Arteriovenous Graft Using Multiphase Blood Model. Appl. Sci. 2021, 11, 8160. https://doi.org/10.3390/app11178160
Kim JT, Kim H, Ryou HS. Hemodynamic Analysis on the Anastomosis Angle in Arteriovenous Graft Using Multiphase Blood Model. Applied Sciences. 2021; 11(17):8160. https://doi.org/10.3390/app11178160
Chicago/Turabian StyleKim, Ji Tae, Hyangkyoung Kim, and Hong Sun Ryou. 2021. "Hemodynamic Analysis on the Anastomosis Angle in Arteriovenous Graft Using Multiphase Blood Model" Applied Sciences 11, no. 17: 8160. https://doi.org/10.3390/app11178160
APA StyleKim, J. T., Kim, H., & Ryou, H. S. (2021). Hemodynamic Analysis on the Anastomosis Angle in Arteriovenous Graft Using Multiphase Blood Model. Applied Sciences, 11(17), 8160. https://doi.org/10.3390/app11178160







