Portable and Highly Versatile Impedance Meter for Very Low Frequency Measurements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Principle of Operation
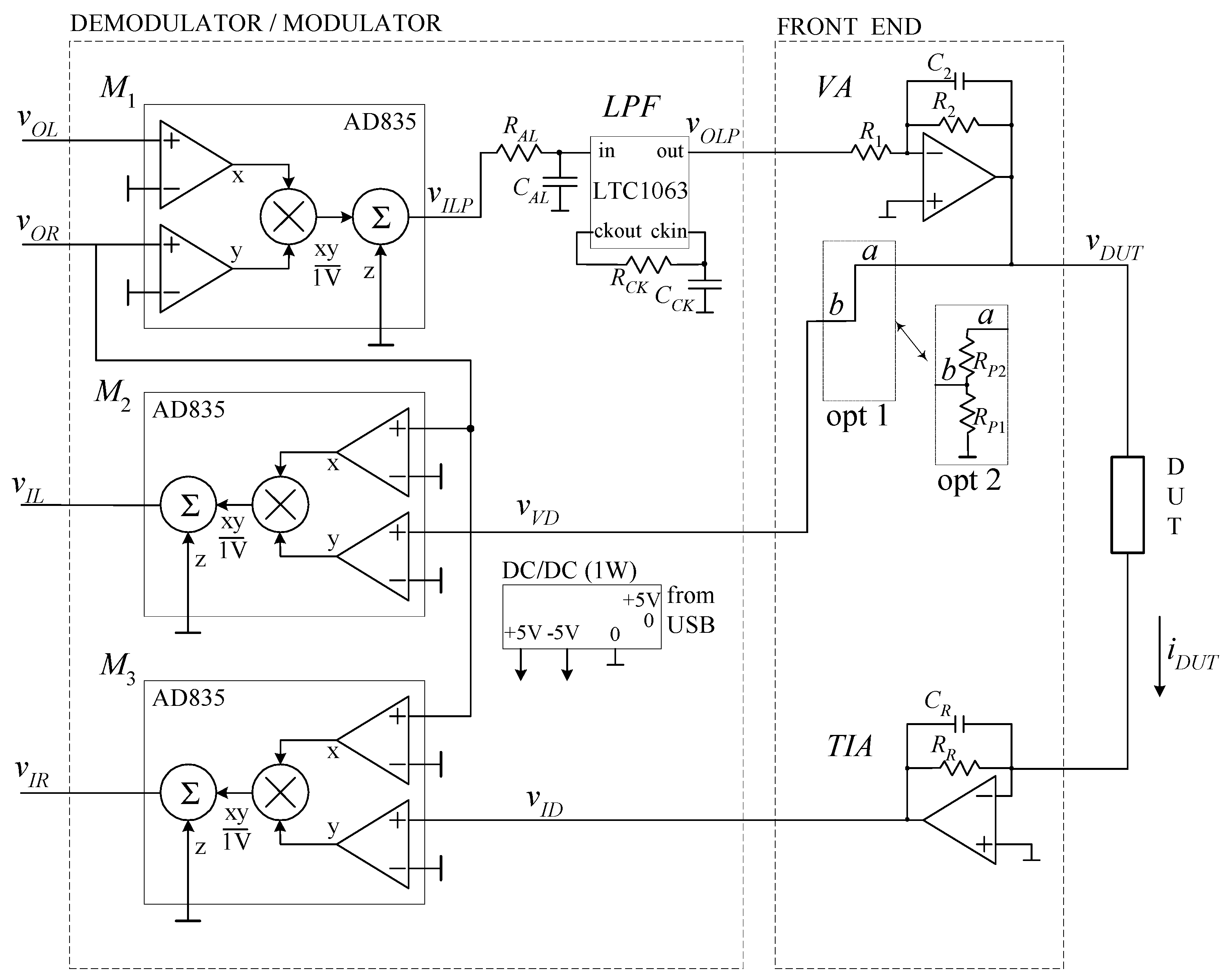
2.2. Hardware Configuration
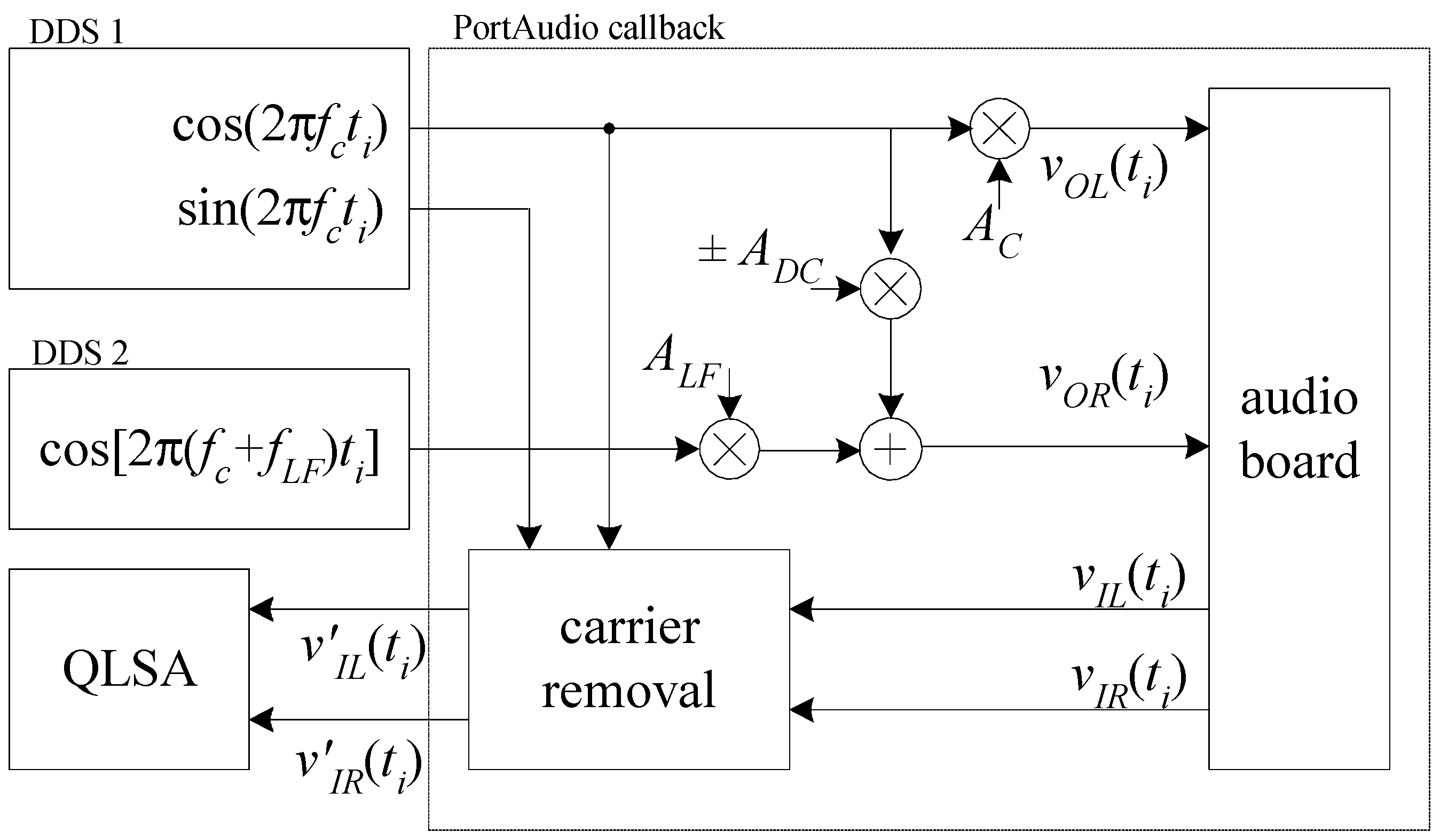
2.3. Digital Signal Elaboration Software
3. Results and Discussion
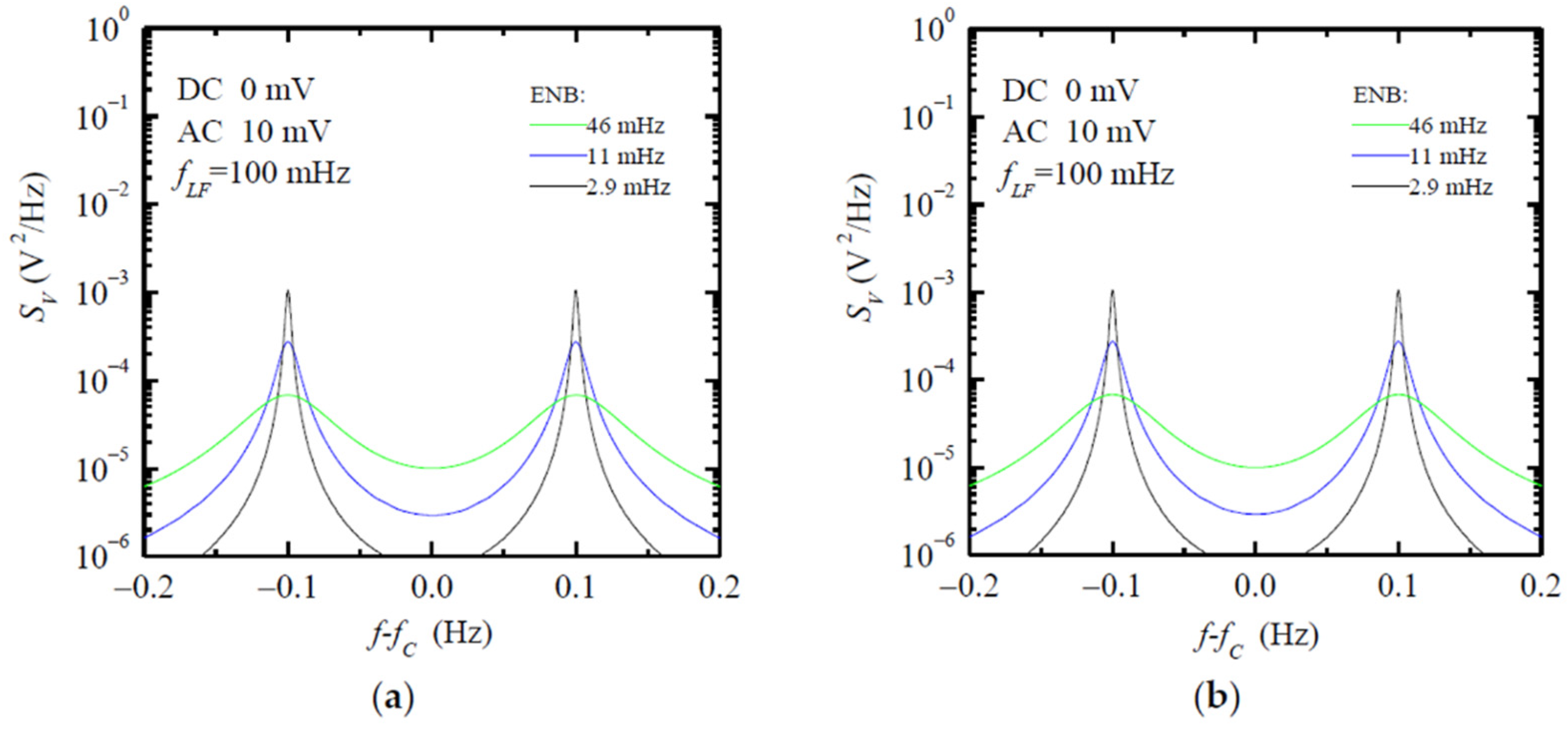
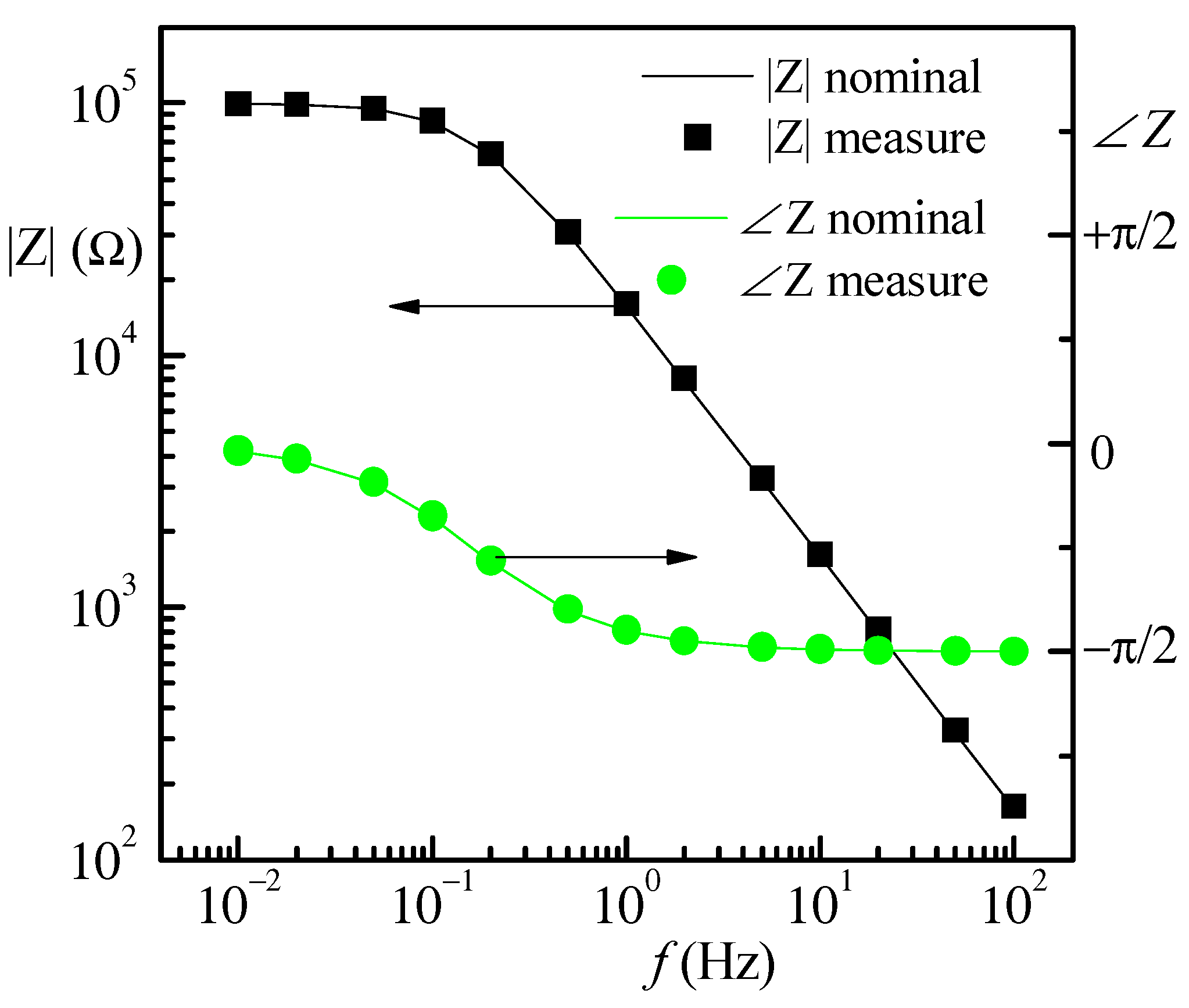
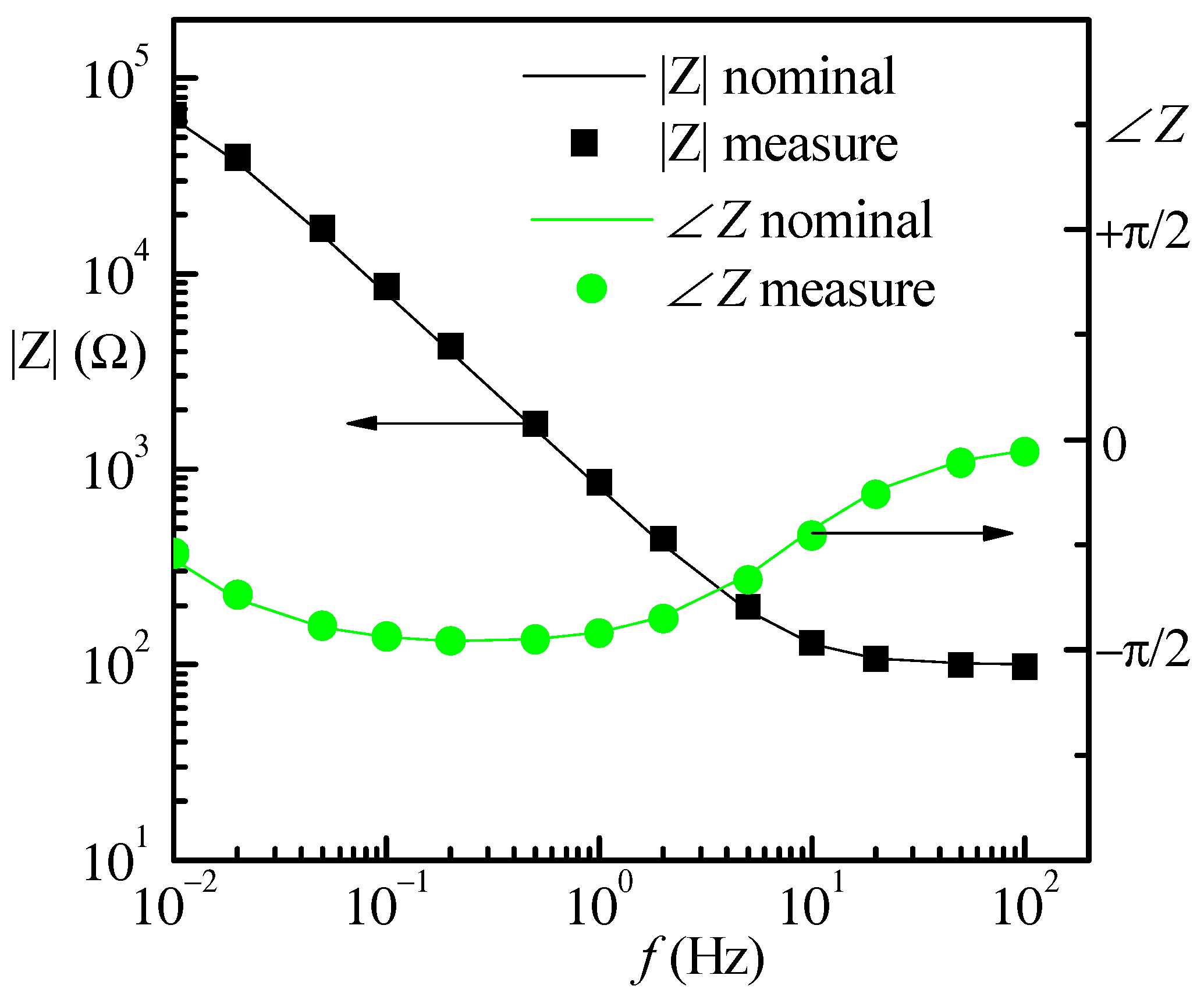
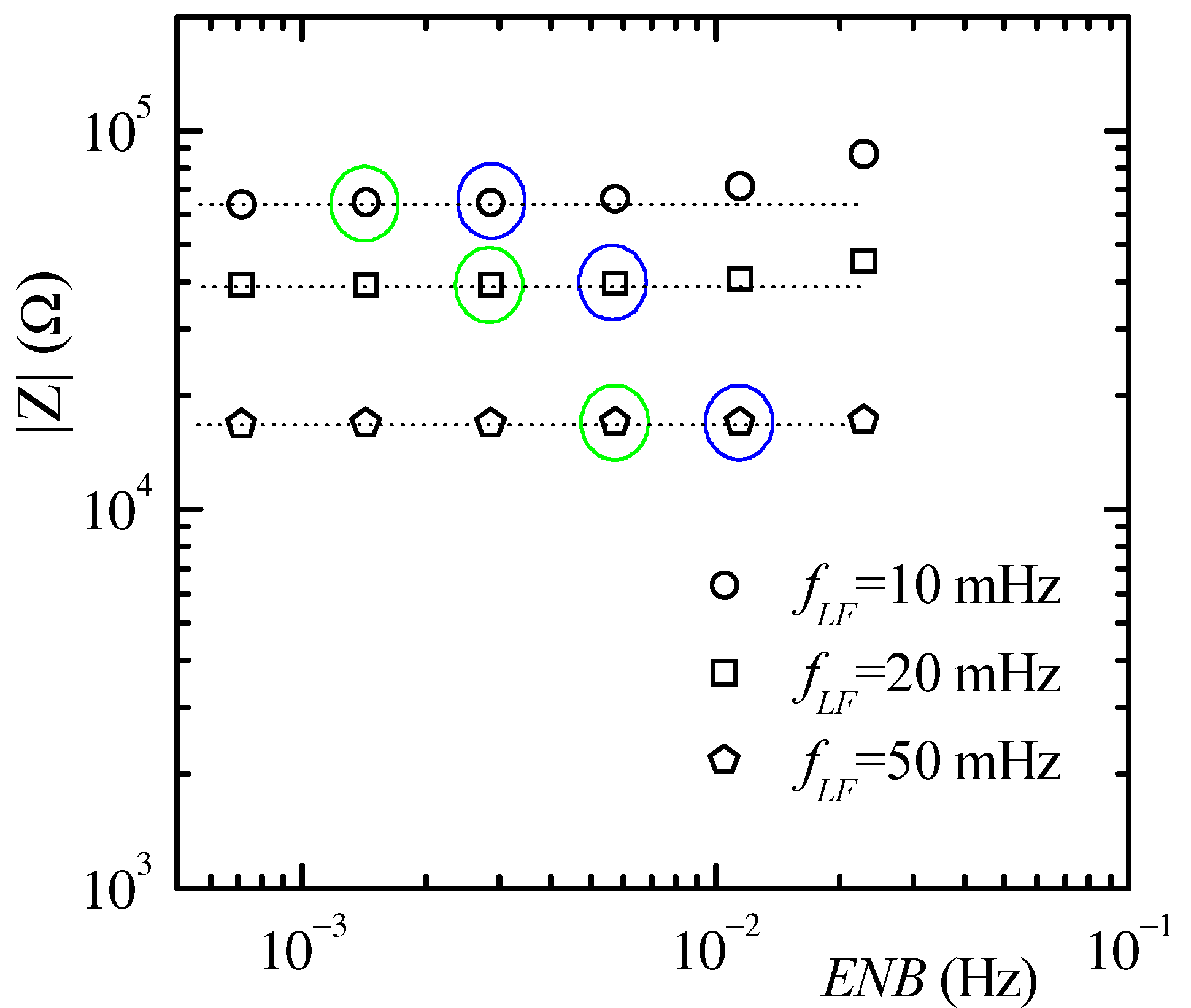
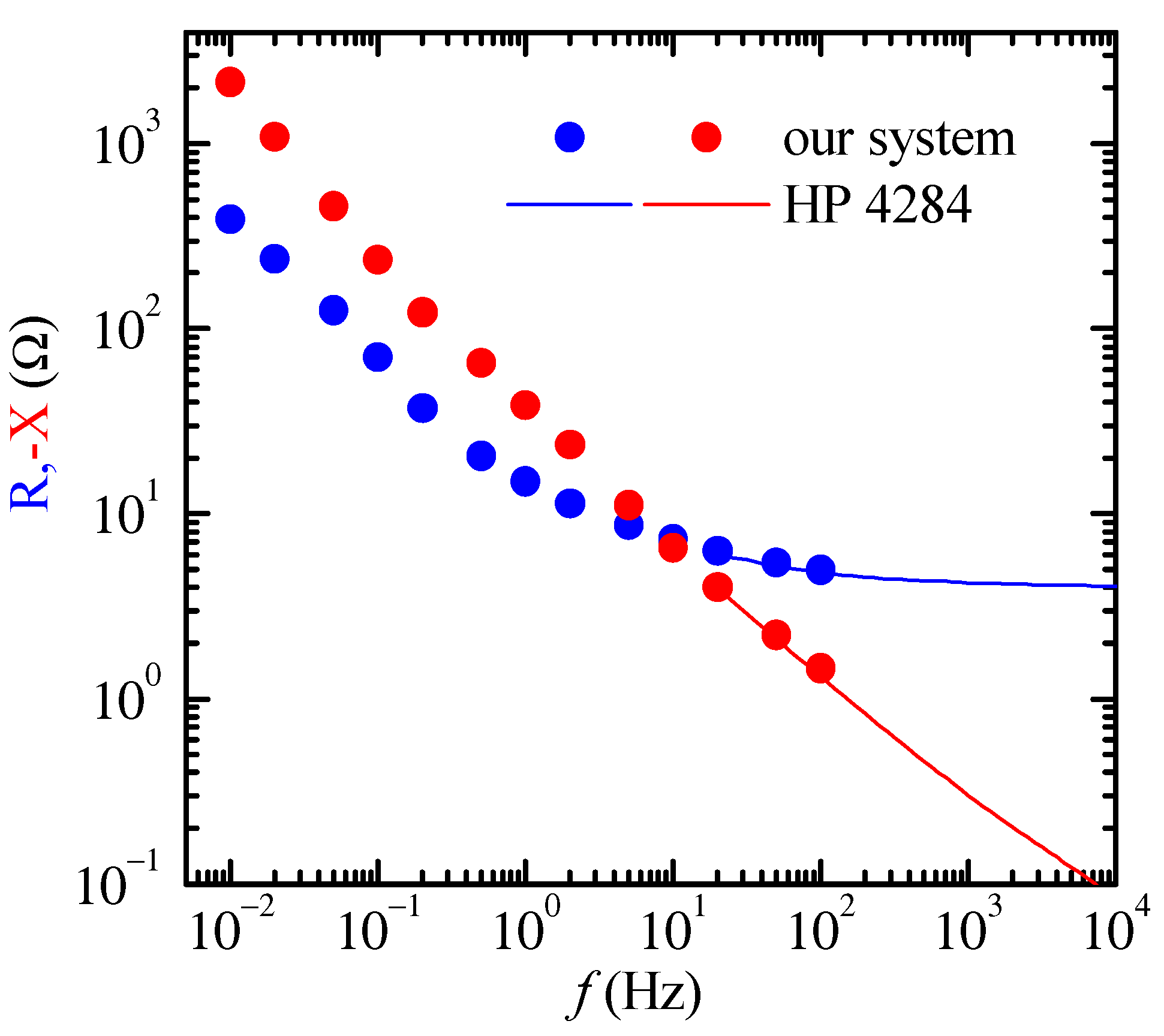
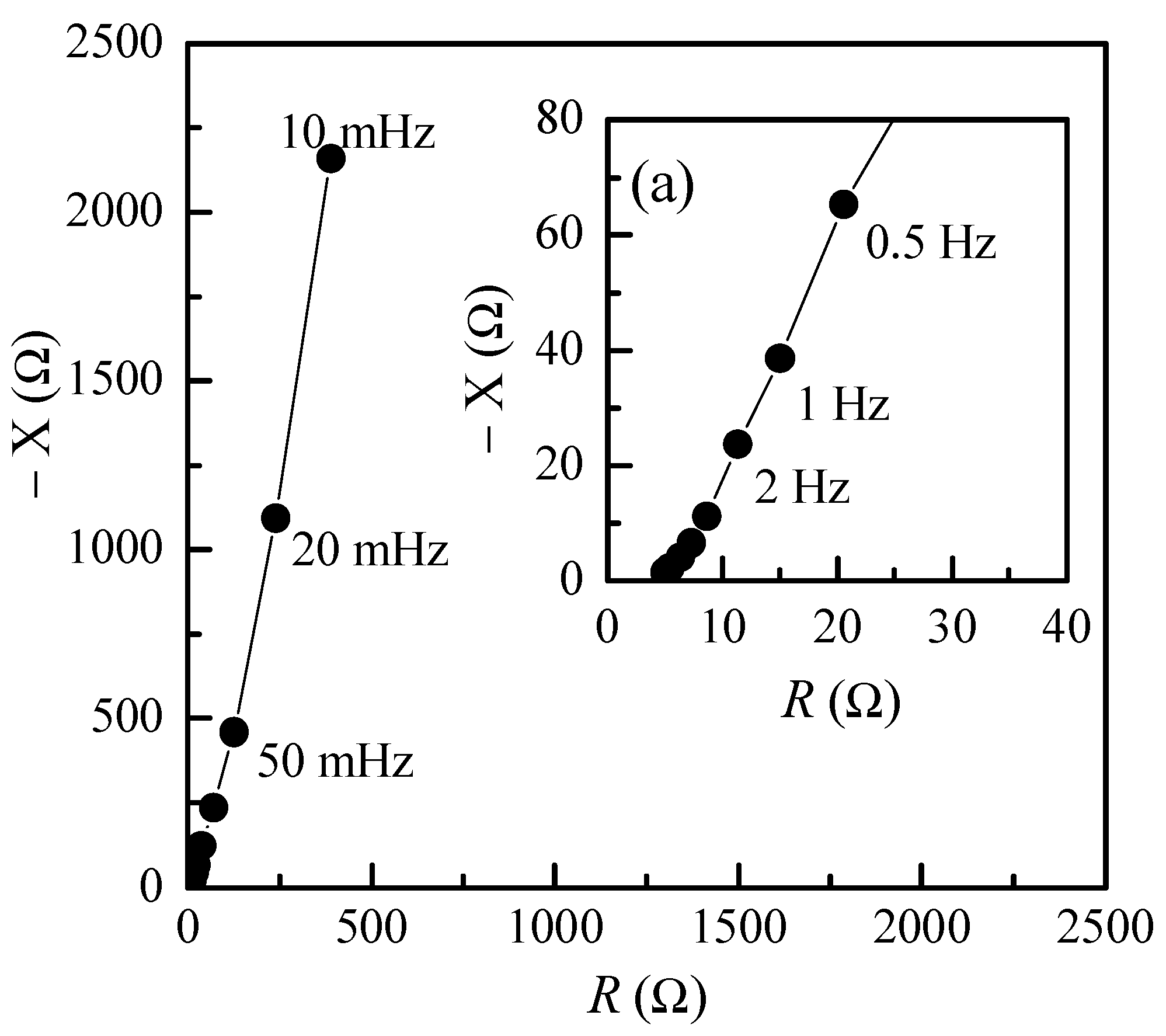
3.1. Preliminary System Testing
3.2. System Testing: An Example of Application
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Młyńczak, M.; Rosoł, M.; Spinelli, A.; Dziki, A.; Wlaźlak, E.; Surkont, G.; Krzycka, M.; Pająk, P.; Dziki, Ł.; Mik, M.; et al. Obstetric Anal Sphincter Injury Detection Using Impedance Spectroscopy with the ONIRY Probe. Appl. Sci. 2021, 11, 637. [Google Scholar] [CrossRef]
- Jin, K.; Zhao, P.; Fang, W.; Zhai, Y.; Hu, S.; Ma, H.; Li, J. An Impedance Sensor in Detection of Immunoglobulin G with Interdigitated Electrodes on Flexible Substrate. Appl. Sci. 2020, 10, 4012. [Google Scholar] [CrossRef]
- Scandurra, G.; Cardillo, E.; Giusi, G.; Ciofi, C.; Alonso, E.; Giannetti, R. Portable Knee Health Monitoring System by Impedance Spectroscopy Based on Audio-Board. Electronics 2021, 10, 460. [Google Scholar] [CrossRef]
- Arpaia, P.; Cesaro, U.; Frosolone, M.; Moccaldi, N.; Taglialatela, M. A micro-bioimpedance meter for monitoring insulin bioavailability in personalized diabetes therapy. Sci. Rep. 2020, 10, 13656. [Google Scholar] [CrossRef]
- Coates, J.; Chipperfield, A.; Clough, G. Wearable Multimodal Skin Sensing for the Diabetic Foot. Electronics 2016, 5, 45. [Google Scholar] [CrossRef] [Green Version]
- Zink, M.D.; König, F.; Weyer, S.; Willmes, K.; Leonhardt, S.; Marx, N.; Napp, A. Segmental bioelectrical impedance spec-troscopy to monitor fluid status in heart failure. Sci. Rep. 2020, 10, 3577. [Google Scholar] [CrossRef]
- Jotta, B.; Coutinho, A.B.B.; Pino, A.V.; Souza, M.N. Lactate threshold by muscle electrical impedance in professional rowers. Rev. Sci. Instrum. 2017, 88, 045105. [Google Scholar] [CrossRef]
- Morais, A.P.; Pino, A.V.; Souza, M.N. Detection of questionable occlusal carious lesions using an electrical bioimpedance method with fractional electrical model. Rev. Sci. Instrum. 2016, 87, 084305. [Google Scholar] [CrossRef]
- Vázquez-Nambo, M.; Gutiérrez-Gnecchi, J.-A.; Reyes-Archundia, E.; Yang, W.; Rodriguez-Frias, M.-A.; Olivares-Rojas, J.-C.; Lorias-Espinoza, D. Experimental Study of Electrical Properties of Pharmaceutical Materials by Electrical Impedance Spectroscopy. Appl. Sci. 2020, 10, 6576. [Google Scholar] [CrossRef]
- Maalouf, R.; Fournier-Wirth, C.; Coste, J.; Chebib, H.; Saïkali, Y.; Vittori, O.; Errachid, A.; Cloarec, J.-P.; Martelet, C.; Jaffrezic-Renault, N. Label-Free Detection of Bacteria by Electrochemical Impedance Spectroscopy: Comparison to Surface Plasmon Resonance. Anal. Chem. 2007, 79, 4879–4886. [Google Scholar] [CrossRef]
- Ruan, C.; Yang, L.; Li, Y. Immunobiosensor Chips for Detection ofEscherichiacoliO157:H7 Using Electrochemical Impedance Spectroscopy. Anal. Chem. 2002, 74, 4814–4820. [Google Scholar] [CrossRef]
- Nandakumar, V.; La Belle, J.T.; Reed, J.; Shah, M.; Cochran, D.; Joshi, L.; Alford, T.L. A methodology for rapid detection of Sal-monella typhimurium using label-free electrochemical impedance spectroscopy. Biosens. Bioelectron. 2008, 24, 1039–1042. [Google Scholar] [CrossRef]
- Naranjo-Hernández, D.; Reina-Tosina, J.; Min, M. Fundamentals, Recent Advances, and Future Challenges in Bioimpedance Devices for Healthcare Applications. J. Sens. 2019, 2019, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Bhargavan, B.; Kanmogne, G.D. Differential Mechanisms of Inflammation and Endothelial Dysfunction by HIV-1 Subtype-B and Recombinant CRF02-AG Tat Proteins on Human Brain Microvascular Endothelial Cells: Implications for Viral Neuro-pathogenesis. Mol. Neurobiol. 2018, 55, 1352–1363. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Lu, M.; Yin, W. Cellular structure analysis based on magnetic induction finite element method simulations and measurements. bioRxiv 2018. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Freeborn, T.J. Residual impedance effect on emulated bioimpedance measurements using Keysight E4990A precision impedance analyser. Measurement 2019, 134, 468–479. [Google Scholar] [CrossRef]
- Pérez, P.; Huertas, G.; Maldonado-Jacobi, A.; Martín, M.; Serrano, J.A.; Olmo, A.; Daza, P.; Yúfera, A. Sensing Cell-Culture Assays with Low-Cost Circuitry. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Huerta-Nuñez, L.F.E.; Gutierrez-Iglesias, G.; Martínez-Cuazitl, A.; Mata-Miranda, M.M.; Alvarez-Jiménez, V.D.; Sánchez-Monroy, V.; Golberg, A.; González-Díaz, C.A. A biosensor capable of identifying low quantities of breast cancer cells by electrical impedance spectroscopy. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lukaski, H.C.; Moore, M. Bioelectrical Impedance Assessment of Wound Healing. J. Diabetes Sci. Technol. 2012, 6, 209–212. [Google Scholar] [CrossRef] [Green Version]
- García, E.; Pérez, P.; Olmo, A.; Díaz, R.; Huertas, G.; Yúfera, A. Data-Analytics Modeling of Electrical Impedance Measurements for Cell Culture Monitoring. Sensors 2019, 19, 4639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Li, C.; Mei, W.; Guo, M.; Yang, Y. Equivalent circuit models for a biomembrane impedance sensor and analysis of electrochemical impedance spectra based on support vector regression Medical, Biological Engineering and Computing. Med. Biol. Eng. Comput. 2019, 57, 1515–1524. [Google Scholar] [CrossRef] [Green Version]
- Vizvari, Z.; Gyorfi, N.; Odry, A.; Sari, Z.; Klincsik, M.; Gergics, M.; Kovacs, L.; Kovacs, A.; Pal, J.; Karadi, Z.; et al. Physical Validation of a Residual Impedance Rejection Method during Ultra-Low Frequency Bio-Impedance Spectral Measurements. Sensors 2020, 20, 4686. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; De Doncker, R.W. A frequency-domain approach to dynamical modeling of electrochemical power sources. Electrochim. Acta 2002, 47, 2347–2356. [Google Scholar] [CrossRef]
- Anjum, N.; Joyal, N.; Iroegbu, J.; Li, D.; Shen, C. Humidity-modulated properties of hydrogel polymer electrolytes for flexible supercapacitors. J. Power Sources 2021, 499, 229962. [Google Scholar] [CrossRef]
- Kötz, R.; Hahn, M.; Gallay, R. Temperature behavior and impedance fundamentals of supercapacitors. J. Power Sources 2006, 154, 550–555. [Google Scholar] [CrossRef]
- Ge, Y.; Xie, X.; Roscher, J.; Holze, R.; Qu, Q. How to measure and report the capacity of electrochemical double layers, supercapacitors, and their electrode materials. J. Solid State Electrochem. 2020, 24, 3215–3230. [Google Scholar] [CrossRef]
- Scott, J.; Hasan, R. New Results for Battery Impedance at Very Low Frequencies. IEEE Access 2019, 7, 106925–106930. [Google Scholar] [CrossRef]
- Solartron: Frequency Response Analyzer 1255. Available online: https://www.ameteksi.com/-/media/ameteksi/download_links/documentations/1255b/model-1255b.pdf?revision=4412c40c-8960-4a99-8d95-7b9d29604323 (accessed on 9 July 2021).
- Novocontrol: BETA Series Analyzers. Available online: https://www.novocontrol.de/php/ana_alpha_n.php (accessed on 9 July 2021).
- Zahner: Electrochemical Workstation IM6, User Brochure. Available online: http://zahner.de/pdf/b_im6ex.pdf (accessed on 9 July 2021).
- CorrTest, CS350 Electrochemical Workstation. Available online: https://www.corrtest.com.cn/producten/dhxgcz/t1/2016/0601/379.html (accessed on 9 July 2021).
- Hioki:LCR Meter IM3533. Available online: https://www.hioki.com/global/products/lcr-meters/10-mhz/id_6065 (accessed on 9 July 2021).
- Ciofi, C.; Scandurra, G.; Giusi, G. QLSA: A software library for spectral estimation in low-frequency noise measurementap-plications. Fluct. Noise Lett. 2019, 18, 1940004. [Google Scholar] [CrossRef]
- Scandurra, G.; Giusi, G.; Ciofi, C. Accurate QTF Sensing Approach by Means of Narrow Band Spectral Estimation. J. Sens. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- AD 835 Datasheet. AD835 (Rev. E). Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD835.pdf (accessed on 19 July 2021).
- LTC 1063 Datasheet. LTC1063-DC Accurate, Clock-Tunable 5th Order Butterworth Lowpass Filter. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/1063fa.pdf (accessed on 19 July 2012).
- USB Audio Board Behringer U-PHORIA UMC202HD. Available online: https://www.behringer.com/behringer/product?modelCode=P0BJZ (accessed on 19 July 2021).
- PortAudio Libraries. Available online: www.portaudio.com (accessed on 19 July 2021).
- Tierney, J.; Rader, C.; Gold, B. A digital frequency synthesizer. IEEE Trans. Audio Electroacoust. 1971, 19, 48–57. [Google Scholar] [CrossRef]
- Jwo, D.-J.; Chang, W.-Y.; Wu, I.-H. Windowing Techniques, the Welch Method for Improvement of Power Spectrum Estimation. Comput. Mater. Contin. 2021, 67, 3983–4003. [Google Scholar] [CrossRef]
- Mirfakhrai, T.; Madden, J.D.W.; Baughman, R.H. Polymer artificial muscles. Mater. Today 2007, 10, 30–38. [Google Scholar] [CrossRef]
- Wang, H.F.; Barrett, M.; Duane, B.; Gu, J.; Zenhausern, F. Materials and processing of polymer-based electrochromic devices. Mater. Sci. Eng. B 2017, 228, 167–174. [Google Scholar] [CrossRef]
- Terán-Alcocer, Á.; Bravo-Plascencia, F.; Cevallos-Morillo, C.; Palma-Cando, A. Electrochemical Sensors Based on Conducting Polymers for the Aqueous Detection of Biologically Relevant Molecules. Nanomaterials 2021, 11, 252. [Google Scholar] [CrossRef]
- Lakard, B. Electrochemical Biosensors Based on Conducting Polymers: A Review. Appl. Sci. 2020, 10, 6614. [Google Scholar] [CrossRef]
- Hong, X.; Liu, Y.; Li, Y.; Wang, X.; Fu, J.; Wang, X. Application Progress of Polyaniline, Polypyrrole and Polythiophene in Lithium-Sulfur Batteries. Polymers 2020, 12, 331. [Google Scholar] [CrossRef] [Green Version]
- Gul, H.; Shah, A.-u.-H.A.; Bilal, S. Fabrication of Eco-Friendly Solid-State Symmetric Ultracapacitor Device Based on Co-Doped PANI/GO Composite. Polymers 2019, 11, 1315. [Google Scholar] [CrossRef] [Green Version]
- Kim, O.; Kwon, J.; Kim, S.; Xu, B.; Seo, K.; Park, C.; Do, W.; Bae, J.; Kang, S. Effect of PVP-Capped ZnO Nanoparticles with Enhanced Charge Transport on the Performance of P3HT/PCBM Polymer Solar Cells. Polymers 2019, 11, 1818. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Ma, G.; Qin, F.; Hu, L.; Luo, B.; Liu, T.; Yin, X.; Su, Z.; Zeng, Z.; Jiang, Y.; et al. High-Conductivity, Flexible and Transparent PEDOT:PSS Electrodes for High Performance Semi-Transparent Supercapacitors. Polymers 2020, 12, 450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asnawi, A.S.F.M.; Aziz, S.B.; Nofal, M.M.; Hamsan, M.H.; Brza, M.A.; Yusof, Y.M.; Abdilwahid, R.T.; Muzakir, S.K.; Kadir, M.F.Z. Glycerolized Li+ Ion Conducting Chitosan-Based Polymer Electrolyte for Energy Storage EDLC Device Applications with Relatively High Energy Density. Polymers 2020, 12, 1433. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.; Hong, W.T.; Kim, Y.E.; Choe, W.-S.; Kim, D.-H.; Kim, J.K. Metal-Organic Decomposition-Mediated Nanoparticulate Vanadium Oxide Hole Transporting Buffer Layer for Polymer Bulk-Heterojunction Solar Cells. Polymers 2020, 12, 1791. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Li, H.; Wang, Z.; Zhu, M.; Pei, Z.; Xue, Q.; Zhi, C. Nanostructured Polypyrrole as a flexible electrode material of supercapacitor. Nano Energy 2016, 22, 422–438. [Google Scholar] [CrossRef]
- Khuyen, N.Q.; Kiefer, R.; Zondaka, Z.; Anbarjafari, G.; Peikolainen, A.-L.; Otero, T.F.; Tamm, T. Multifunctionality of Polypyrrole Polyethyleneoxide Composites: Concurrent Sensing, Actuation and Energy Storage. Polymers 2020, 12, 2060. [Google Scholar] [CrossRef] [PubMed]
- Kulandaivalu, S.; Azahari, M.N.M.; Azman, N.H.N.; Sulaiman, Y. Ultrahigh specific energy of layer by layer polypyrrole/graphene oxide/multi-walled carbon nanotube| polypyrrole/manganese oxide composite for supercapacitor. J. Energy Storage 2020, 28, 101219. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liaw, B.Y.; Zhang, J. Graphical analysis of electrochemical impedance spectroscopy data in Bode and Nyquist representations. J. Power Sources 2016, 309, 82–98. [Google Scholar] [CrossRef]
- Khoh, W.-H.; Hong, J.-D. Layer-by-layer self-assembly of ultrathin multilayer films composed of magnetite/reduced graphene oxide bilayers for supercapacitor application. Colloids Surf. A 2013, 436, 104–112. [Google Scholar] [CrossRef]


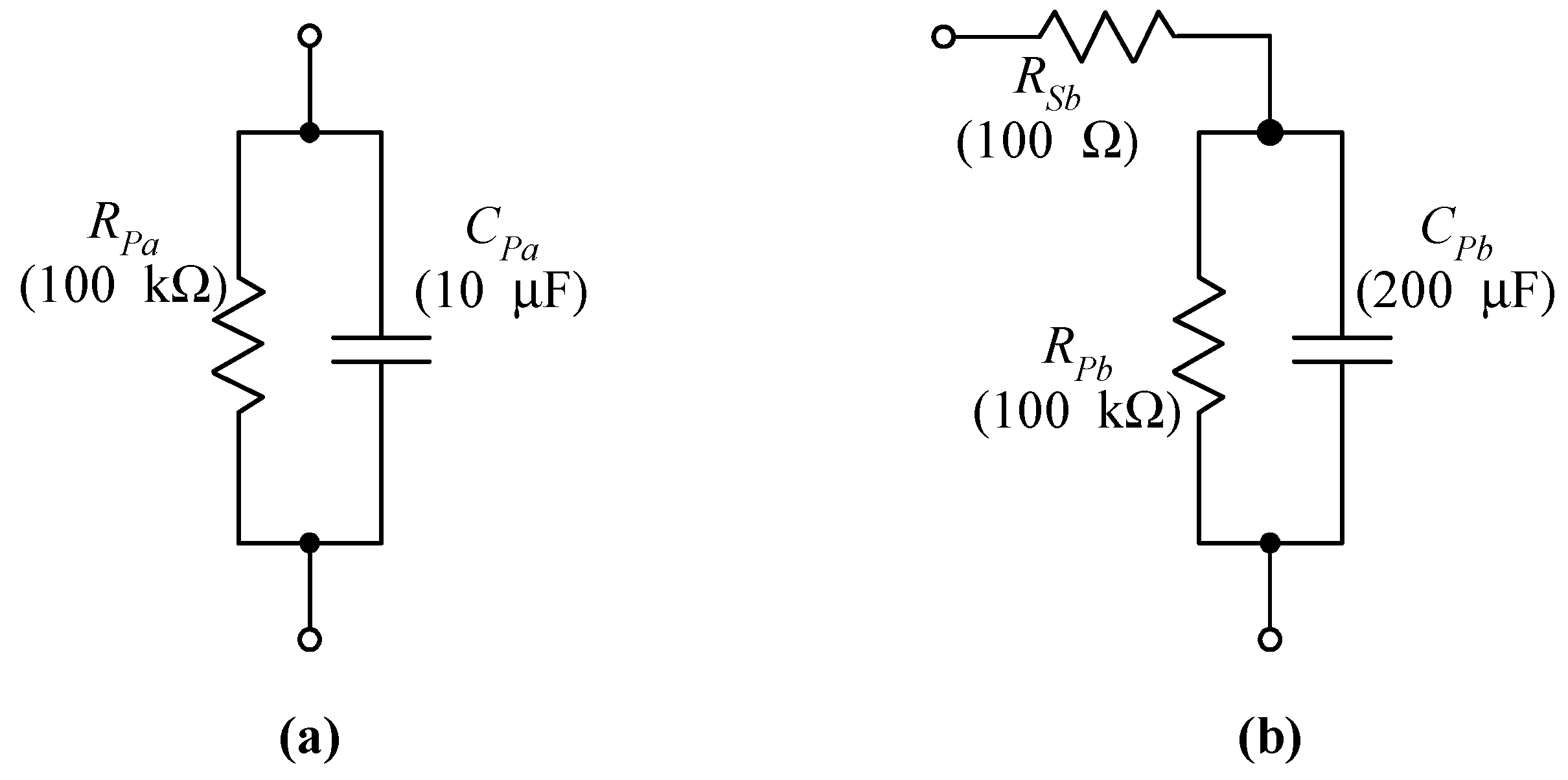


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scandurra, G.; Arena, A.; Cardillo, E.; Giusi, G.; Ciofi, C. Portable and Highly Versatile Impedance Meter for Very Low Frequency Measurements. Appl. Sci. 2021, 11, 8234. https://doi.org/10.3390/app11178234
Scandurra G, Arena A, Cardillo E, Giusi G, Ciofi C. Portable and Highly Versatile Impedance Meter for Very Low Frequency Measurements. Applied Sciences. 2021; 11(17):8234. https://doi.org/10.3390/app11178234
Chicago/Turabian StyleScandurra, Graziella, Antonella Arena, Emanuele Cardillo, Gino Giusi, and Carmine Ciofi. 2021. "Portable and Highly Versatile Impedance Meter for Very Low Frequency Measurements" Applied Sciences 11, no. 17: 8234. https://doi.org/10.3390/app11178234
APA StyleScandurra, G., Arena, A., Cardillo, E., Giusi, G., & Ciofi, C. (2021). Portable and Highly Versatile Impedance Meter for Very Low Frequency Measurements. Applied Sciences, 11(17), 8234. https://doi.org/10.3390/app11178234









