Reconstruction of Ocean Front Model Based on Sound Speed Clustering and Its Effectiveness in Ocean Acoustic Forecasting
Abstract
:1. Introduction
2. Data and Methods
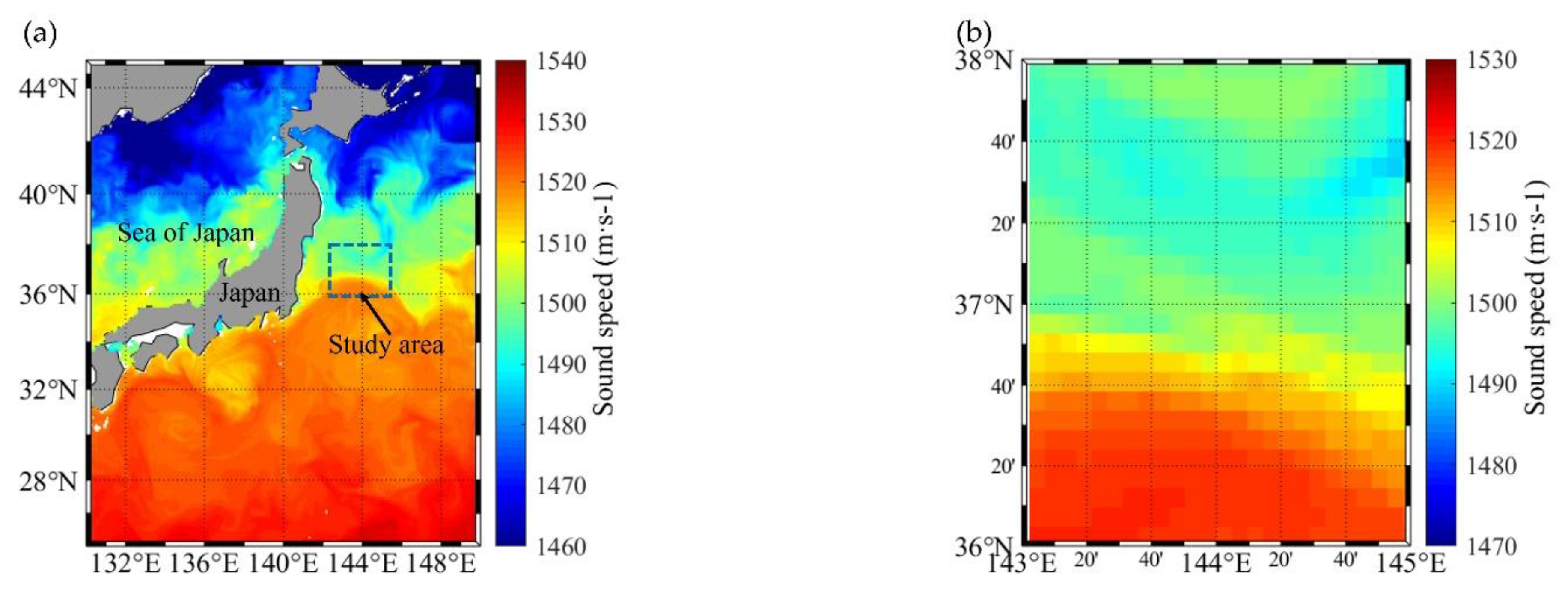
2.1. Physical Oceanography and Data Introduction
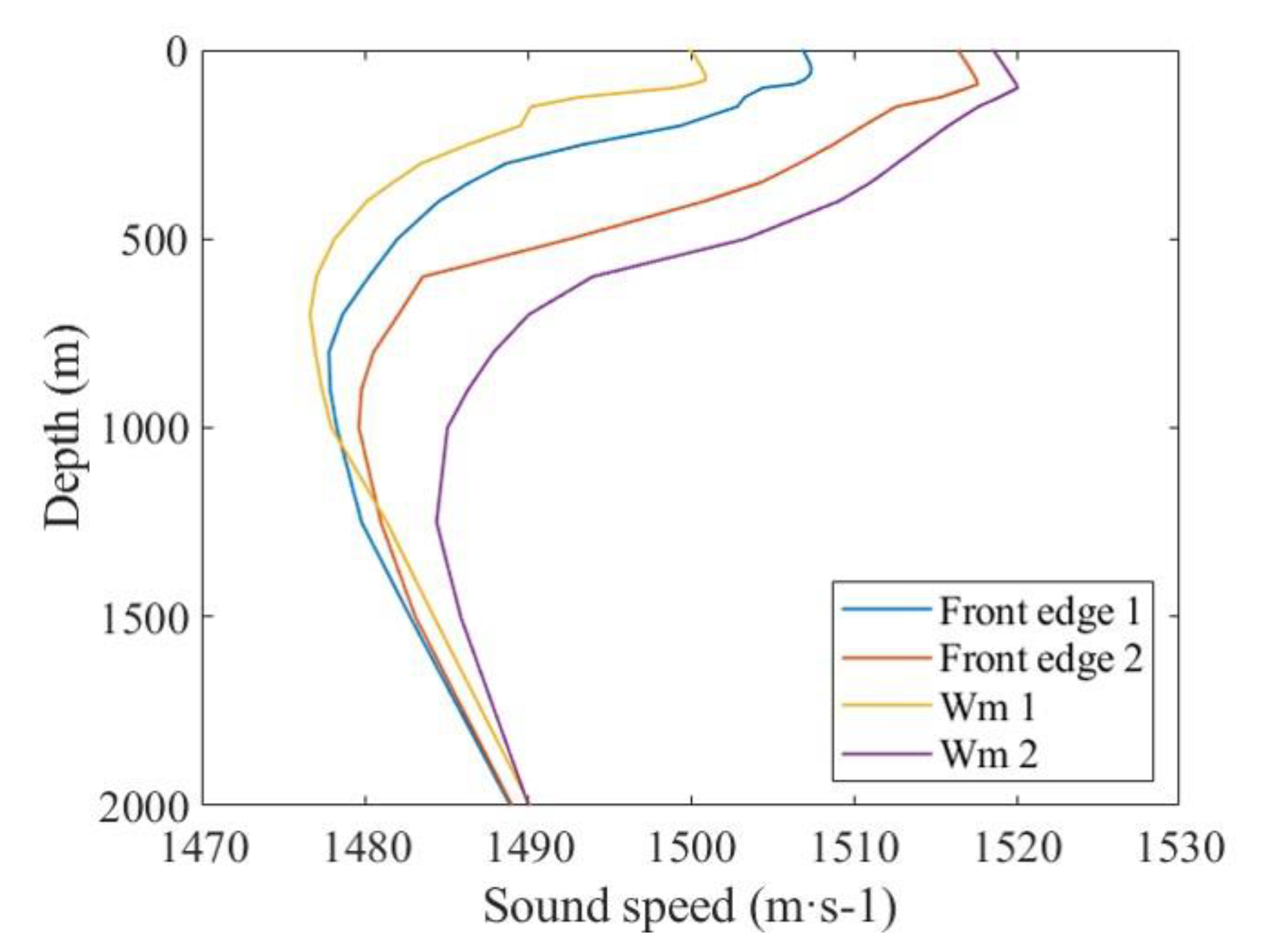
2.2. Description of Ocean Front Characteristic Model
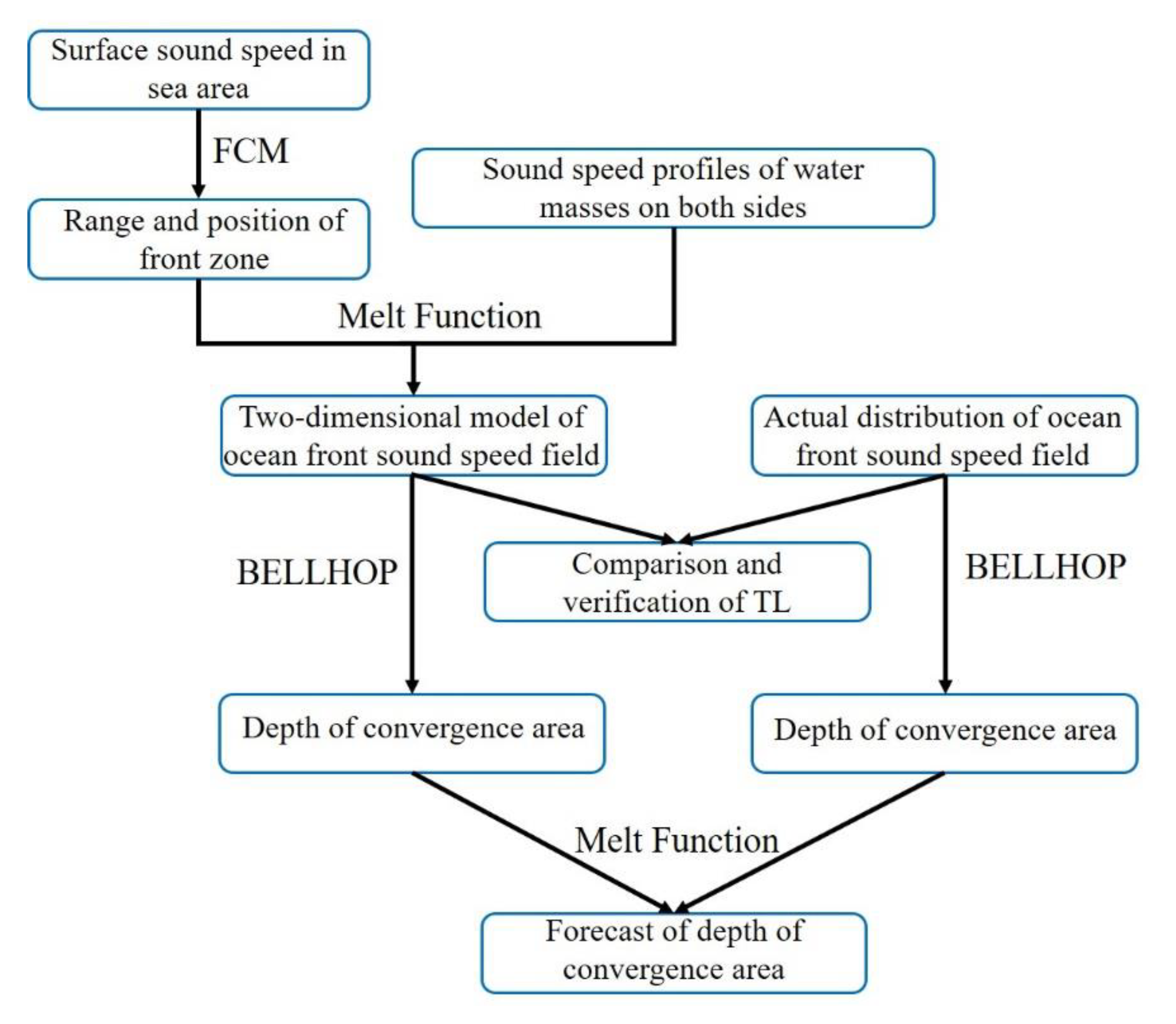
2.3. Introduction of Technical Route
3. Results and Discussion
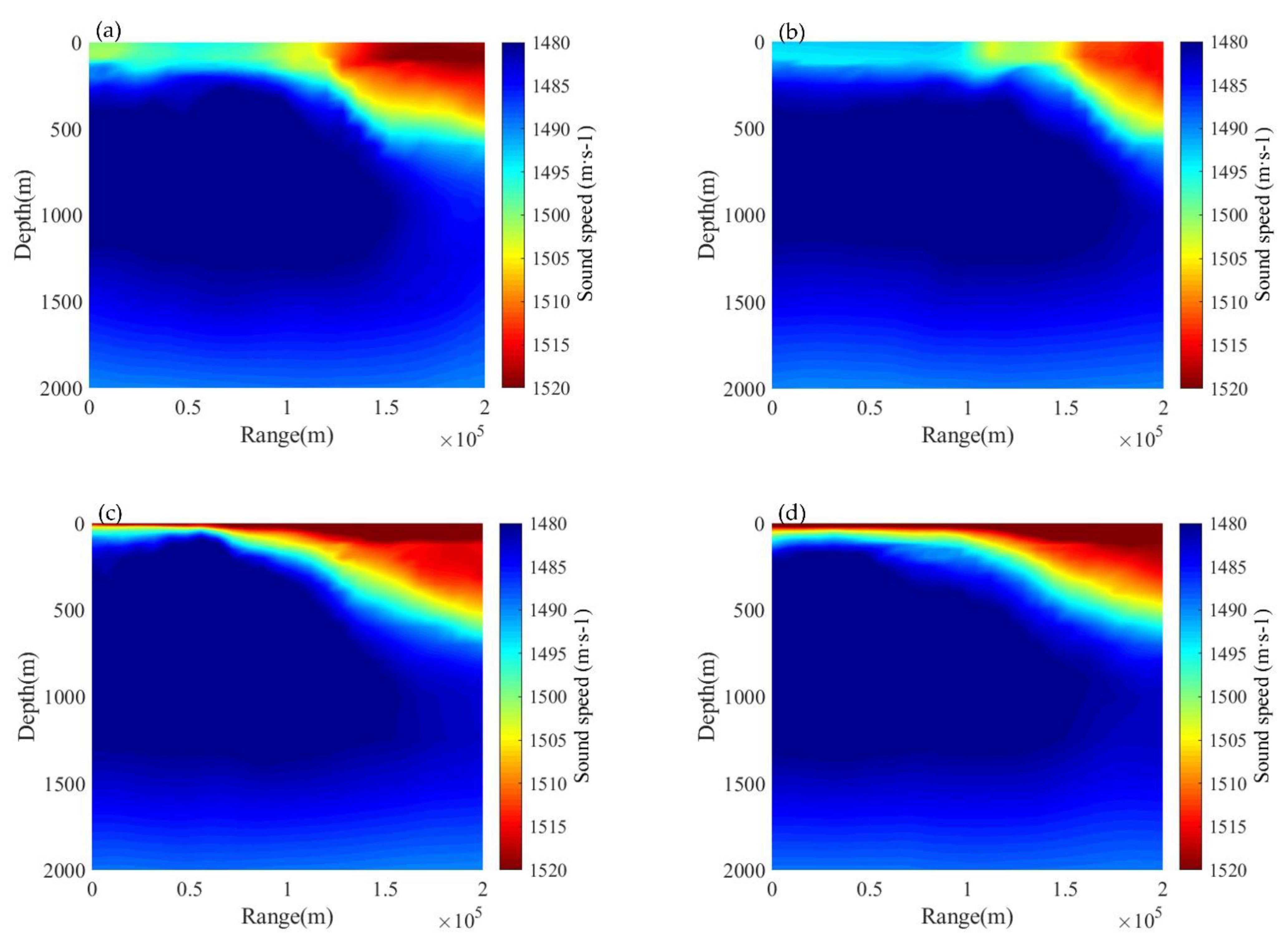
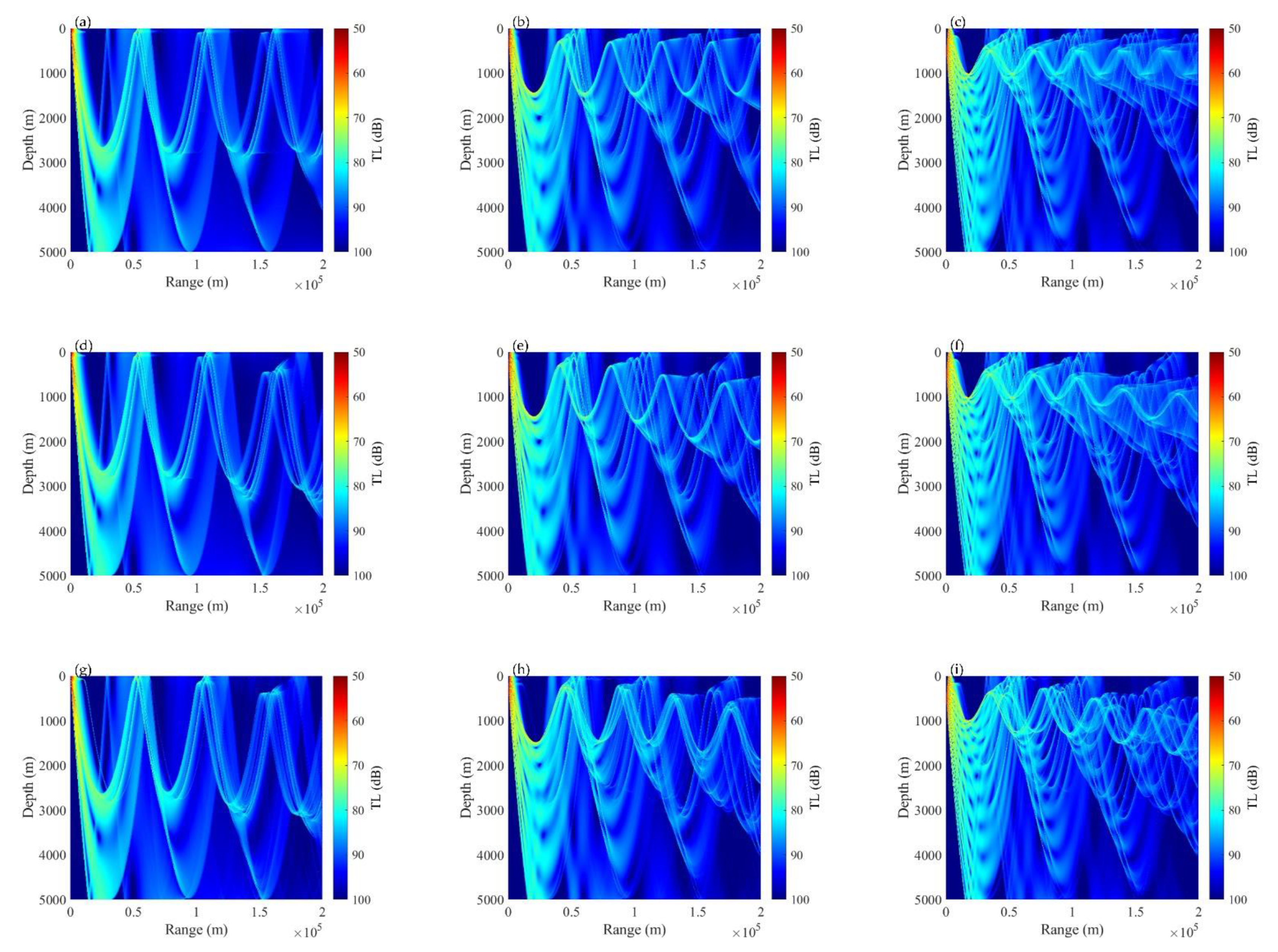
3.1. Reconstruction Results of Ocean Front Sound Speed Field Model
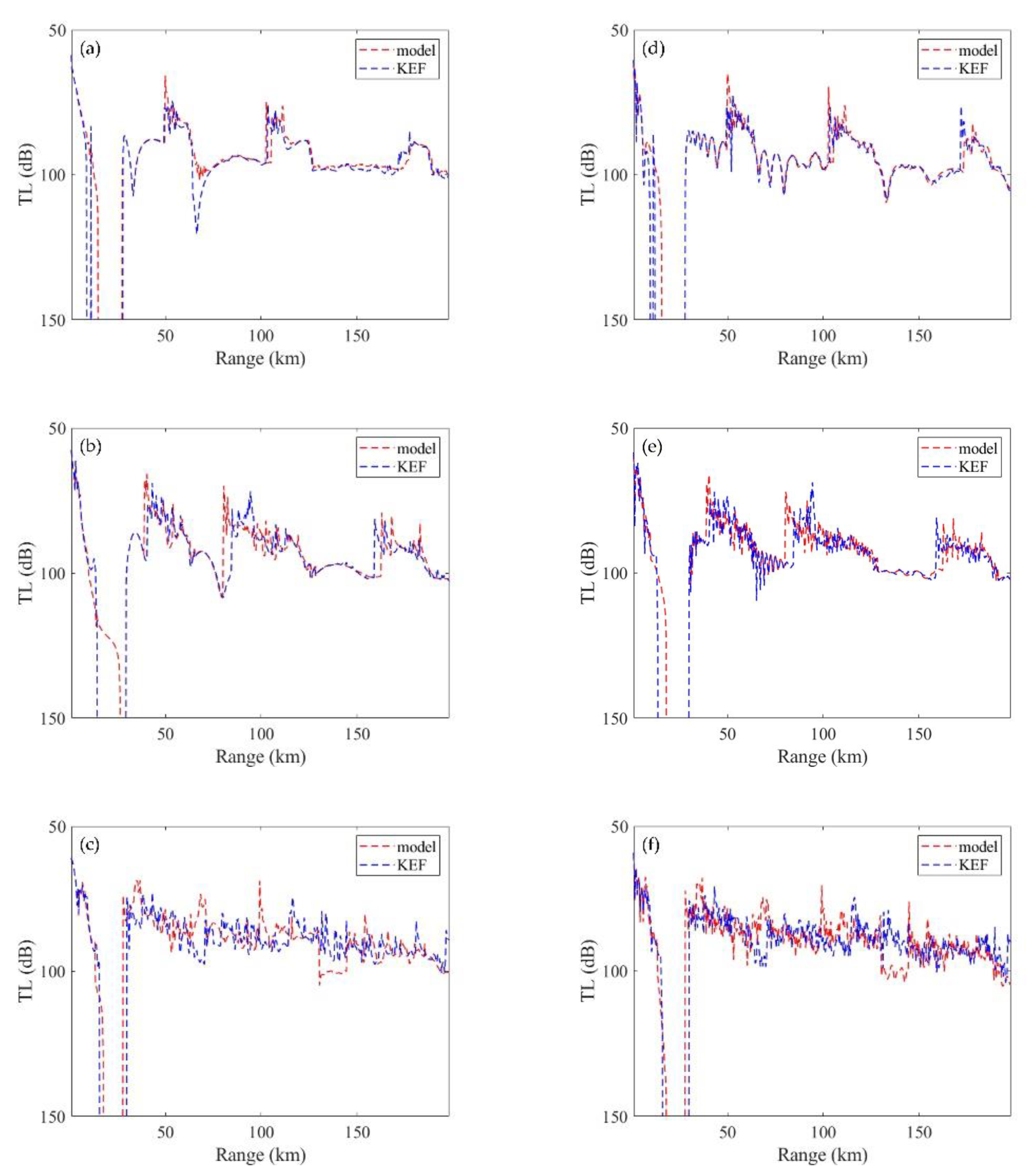
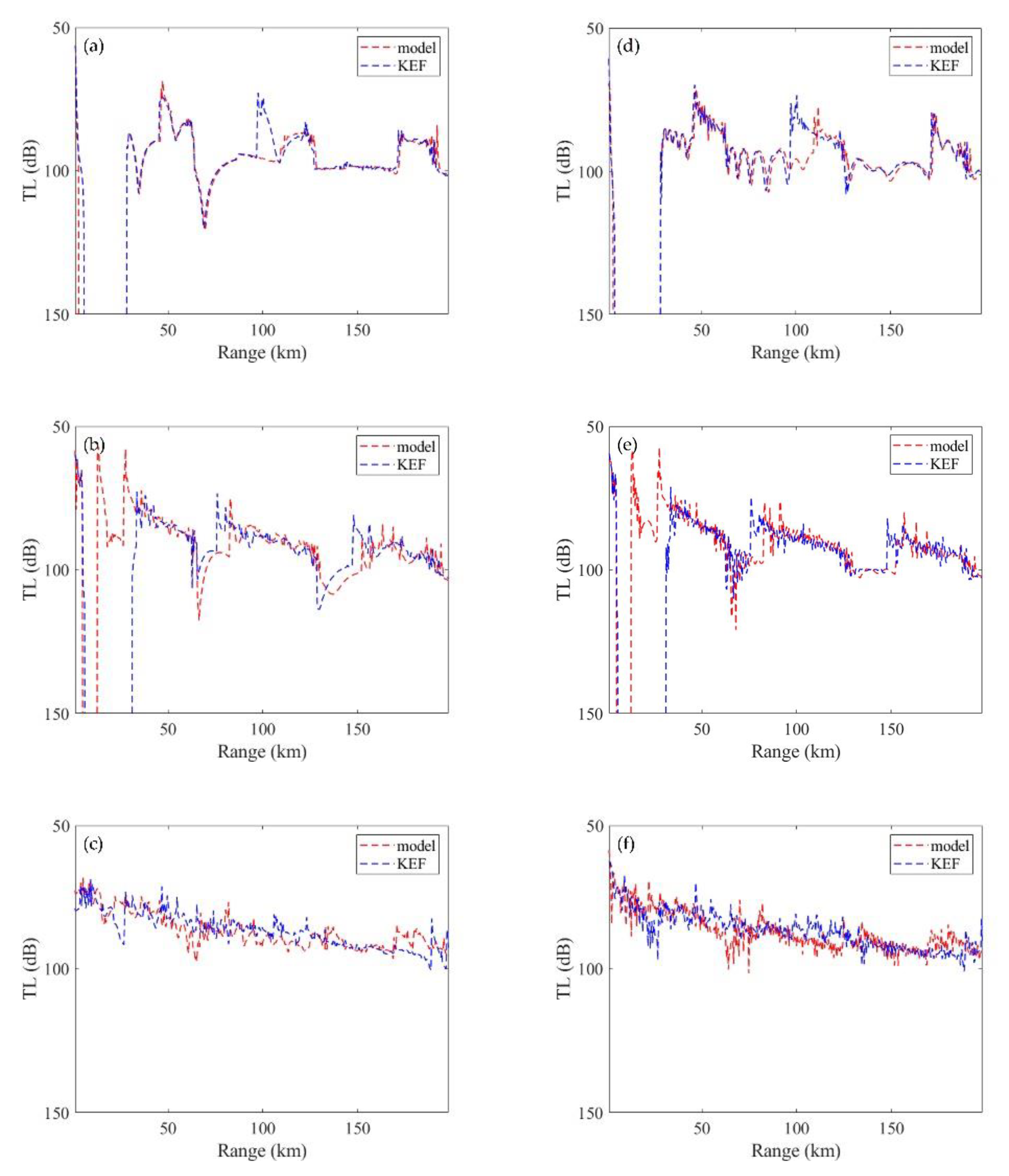
3.2. Comparison Results of TL Calculations
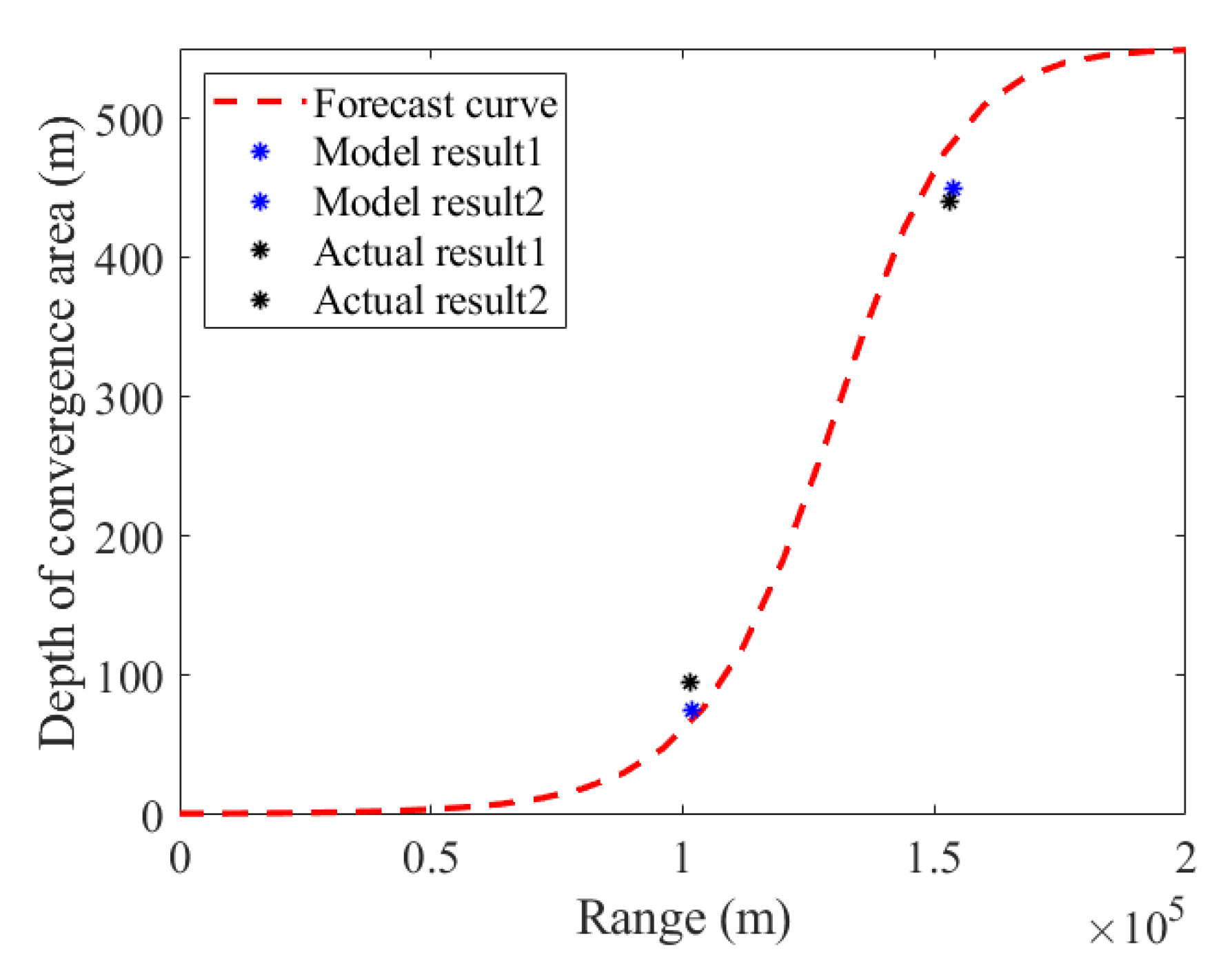
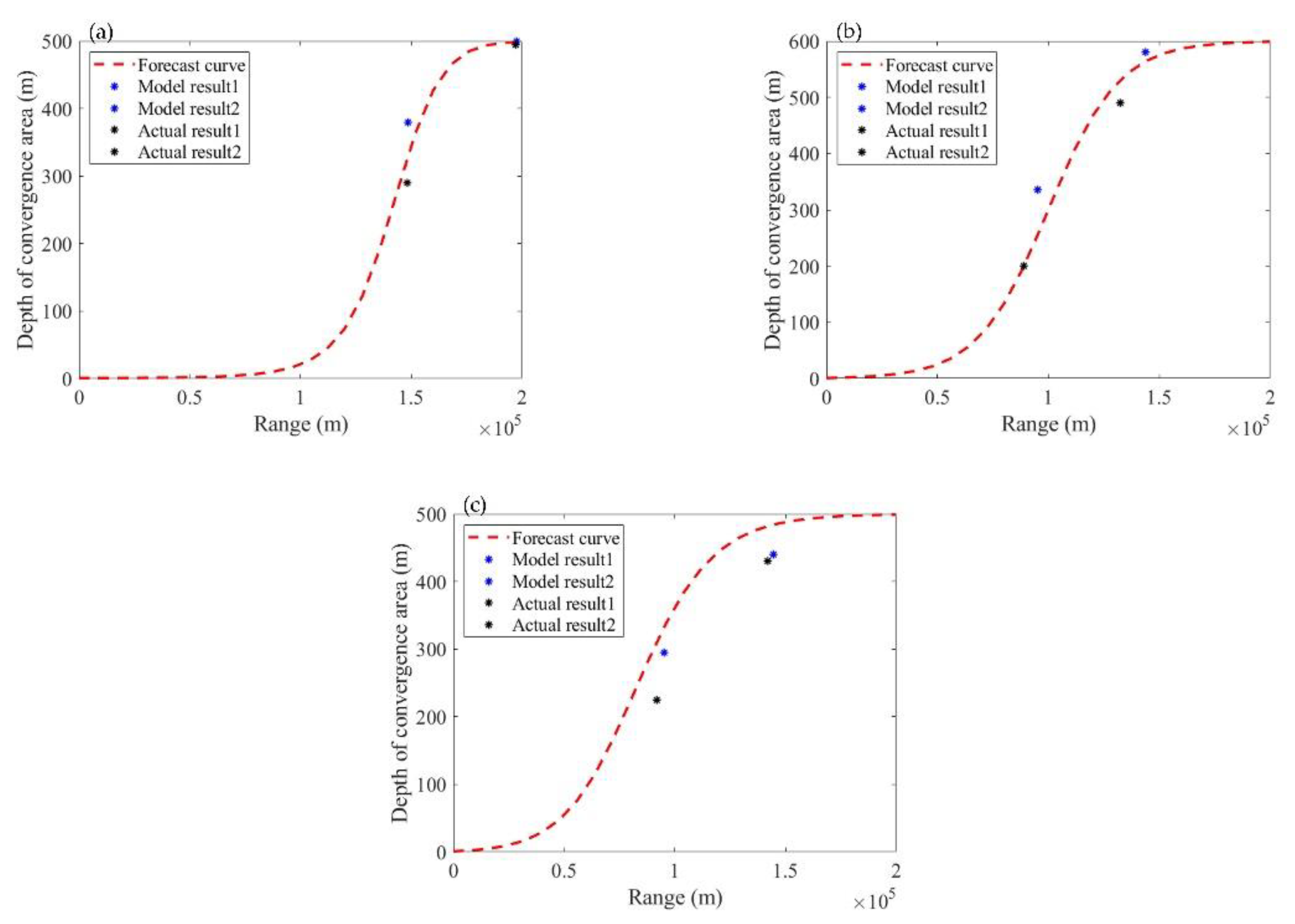
3.3. Effectiveness of Forecasting the Changes of Depth in Convergence Areas
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Belkin, I.M.; Cornillon, P.C.; Sherman, K. Fronts in large marine ecosystems. Prog. Oceanogr. 2009, 81, 223–236. [Google Scholar] [CrossRef]
- Bost, C.A.; Cotté, C.; Bailleul, F.; Cherel, Y.; Charrassin, J.B.; Guinet, C. The importance of oceanographic fronts to marine birds and mammals of the southern oceans. J Mar Syst. 2009, 78, 363–376. [Google Scholar] [CrossRef]
- Peter, C.; Wang, G. Seasonal variability of thermohaline front in the central South China Sea. J. Oceanogr. 2003, 59, 65–78. [Google Scholar] [CrossRef]
- Avijit, G.; Allan, R. Feature-oriented regional modeling of oceanic fronts. Dyn. Atmos. Ocean. 2002, 36, 201–232. [Google Scholar]
- Moore, J.K.; Abbott, M.R.; Richman, J.G. Variability in the location of the Antarctic Polar Front (90°–20°W) from satellite sea surface temperature data. J. Geophys. Res. Ocean. 1997, 102, 27825–27833. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Liang, M.A.; Zhang, C.; Bing, L.I.; Liu, H. Ocean front analysis in subdivided sea areas by using satellite remote sea surface temperature data. Ocean. Eng. 2018, 36, 108–118. [Google Scholar]
- Shapiro, G.; Chen, F.; Thain, R. The effect of ocean fronts on acoustic wave propagation in the Celtic sea. J Mar. Syst. 2014, 139, 217–226. [Google Scholar] [CrossRef]
- Mooers, C.N.K. Oceanic fronts and their effects on underwater acoustics. J. Acoust. Soc. Am. 1978, 63, S87. [Google Scholar] [CrossRef]
- Rousseau, T.H. Acoustic propagation through a model of shallow fronts in the deep ocean. J. Acoust. Soc. Am. 1982, 72, 924–936. [Google Scholar] [CrossRef]
- Ramp, S.R.; Chiu, C.S.; Bahr, F.L.; Qi, Y.; Dahl, P.H.; Miller, J.; Lynch, J.F.; Zhang, R.; Zhou, J. The shelf-edge frontal structure in the central East China Sea and its impact on low-frequency acoustic propagation. IEEE J. Ocean. Eng. 2005, 29, 1011–1031. [Google Scholar] [CrossRef]
- Rajkumar, K.V.; Yesubabu, A.; Subrahmanyam, K. Fuzzy clustering and Fuzzy C-Means partition cluster analysis and validation studies on a subset of citescore dataset. Int. J. Electr. Comput. Eng. 2019, 9, 2760–2770. [Google Scholar] [CrossRef]
- Mandelberg, M.D.; Frizzell-Makowski, L.J. Acoustic provincing of ocean basins. Ocean. 2000 MTS IEEE Conf. Exhib. 2000, 105–108. [Google Scholar] [CrossRef]
- Abiva, J.; Fabbri, T.; Raúl, V. Automatic classification of sound speed profiles using PCA and Self-Organizing Map techniques. Ocean. 2019- Marseille IEEE 2019, 1–10. [Google Scholar] [CrossRef]
- Dubberley, J.; Zingerelli, R. Fuzzy clustering of oceanographic sound speed profiles for acoustic characterization. J. Acoust. Soc. Am. 2008, 123, 3625. [Google Scholar] [CrossRef]
- Chen, C.; Yang, K.; Duan, R.; Ma, Y. Acoustic propagation analysis with a sound speed feature model in the front area of kuroshio extension. Appl. Ocean. Res. 2017, 68, 1–10. [Google Scholar] [CrossRef]
- Gangopadhyay, A.; Robinson, A.R.; Haley, P.J.; Leslie, W.G.; Yu, Z. Feature-oriented regional modeling and simulations in the Gulf of Maine and Georges Bank. Cont. Shelf Res. 2003, 23, 317–353. [Google Scholar] [CrossRef]
- Carriere, O.; Hermand, J.P. Feature-oriented acoustic tomography for coastal ocean observatories. IEEE J. Ocean. Eng. 2013, 38, 534–546. [Google Scholar] [CrossRef]
- Lin, Y.T.; Lynch, J.F. Analytical study of the horizontal ducting of sound by an oceanic front over a slope. J. Acoust. Soc. Am. 2012, 131, EL1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramp, S.R.; Schlitz, R.J.; Wright, W.R. The deep flow through the northeast channel, Gulf of Marine. J. Phys. Oceanogr. 1985, 15, 1790–1808. [Google Scholar] [CrossRef] [Green Version]
- Small, J.; Shackleford, L.; Pavey, G. Ocean feature models-their use and effectiveness in ocean acoustic forecasting. Ann. Geophys. 1997, 15, 101–112. [Google Scholar] [CrossRef]
- Kwon, Y.O.; Alexander, M.A.; Bond, N.A.; Frankignoul, C.; Lu, A.T. Role of the gulf stream and kuroshio–oyashio systems in large-scale atmosphere–ocean interaction: A review. J. Clim. 2010, 23, 3249–3281. [Google Scholar] [CrossRef]
- Xue, H.J.; Chai, F.; Pettigrew, N.; Xu, D.Y.; Shi, M.C.; Xu, J.P. Kuroshio intrusion and the circulation in the south china sea. J. Geophys. Res. Ocean. 2004, 109, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Yasuda, I.; Yoon, J.H.; Suginohara, N. Dynamics of the Kuroshio large meander. J. Oceanogr. Soc. Jpn. 1985, 41, 259–273. [Google Scholar] [CrossRef]
- Li, Y.; Kang, J.C.; Liu, C. Spatial change of salinity at Kuroshio in East China Sea with seasons. Appl. Mech. Mater. 2011, 71–78, 56–60. [Google Scholar] [CrossRef]
- Imawaki, S.; Uchida, H.; Ichikawa, H.; Fukasawa, M.; Umatani, S.I. Satellite altimeter monitoring the Kuroshio transport south of Japan. Geophys. Res. Lett. 2001, 28, 17–20. [Google Scholar] [CrossRef]
- Nonaka, M.; Xie, S.P. Covariations of sea surface temperature and wind over the Kuroshio and its extension: Evidence for ocean-to-atmosphere feedback. J. Clim. 2003, 16, 1404–1413. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hulburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Smith, L.T.; Halliwell, G.R.; Bleck, R. North Atlantic simulations with the Hybrid Coordinate Ocean Model (HYCOM): Impact of the vertical coordinate choice, reference pressure, and thermobaricity. J. Phys. Oceanogr. 2003, 33, 2504–2526. [Google Scholar] [CrossRef] [Green Version]
- Medwin, H. Speed of sound in water: A simple equation for realistic parameters. J. Acoust. Soc. Am. 1975, 58, 1318–1319. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c -means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Bezdek, J.C. A Convergence Theorem for the Fuzzy ISODATA Clustering Algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 1–8. [Google Scholar] [CrossRef]
- Arkajyoti, S.; Swagatam, D. Axiomatic generalization of the membership degree based weighting function for fuzzy C means clustering: Theoretical development and convergence analysis. Inf. Sci. 2017, 408, 129–145. [Google Scholar] [CrossRef]
- Andreeva, T.A.; Durgin, W.W.; Wojcik, S.E. Influence of internal wave fluctuations on acoustic underwater propagation. J. Acoust. Soc. Am. 2005, 117, 2548. [Google Scholar] [CrossRef]
- Ju, L.; Wang, H.; Sun, J. Effect of tidal internal wave fields on shallow water acoustic propagation. AIP Conf. Proc. 2010, 191, 1272. [Google Scholar] [CrossRef]
- Hale, F.E. Long-range sound propagation in the deep ocean. J. Acoust. Soc. Am. 1959, 31, 1572. [Google Scholar] [CrossRef] [Green Version]
- Mellberg, L.E.; Johannessen, O.M.; Connors, D.N.; Botseas, G.; Browning, D. Modeled acoustic propagation through an ice edge eddy in the east greenland sea marginal ice zone. J. Geophys. Res. Oceans. 1987, 92, C7. [Google Scholar] [CrossRef]
- Lynch, J.F.; Newhall, A.E.; Sperry, B.; Gawarkiewicz, G.; Fredricks, A.; Tyack, P.; Chiu, C.S.; Abbot, P. Spatial and temporal variations in acoustic propagation characteristics at the New England shelfbreak front. IEEE J. Ocean. Eng. 2003, 28, 129–150. [Google Scholar] [CrossRef]
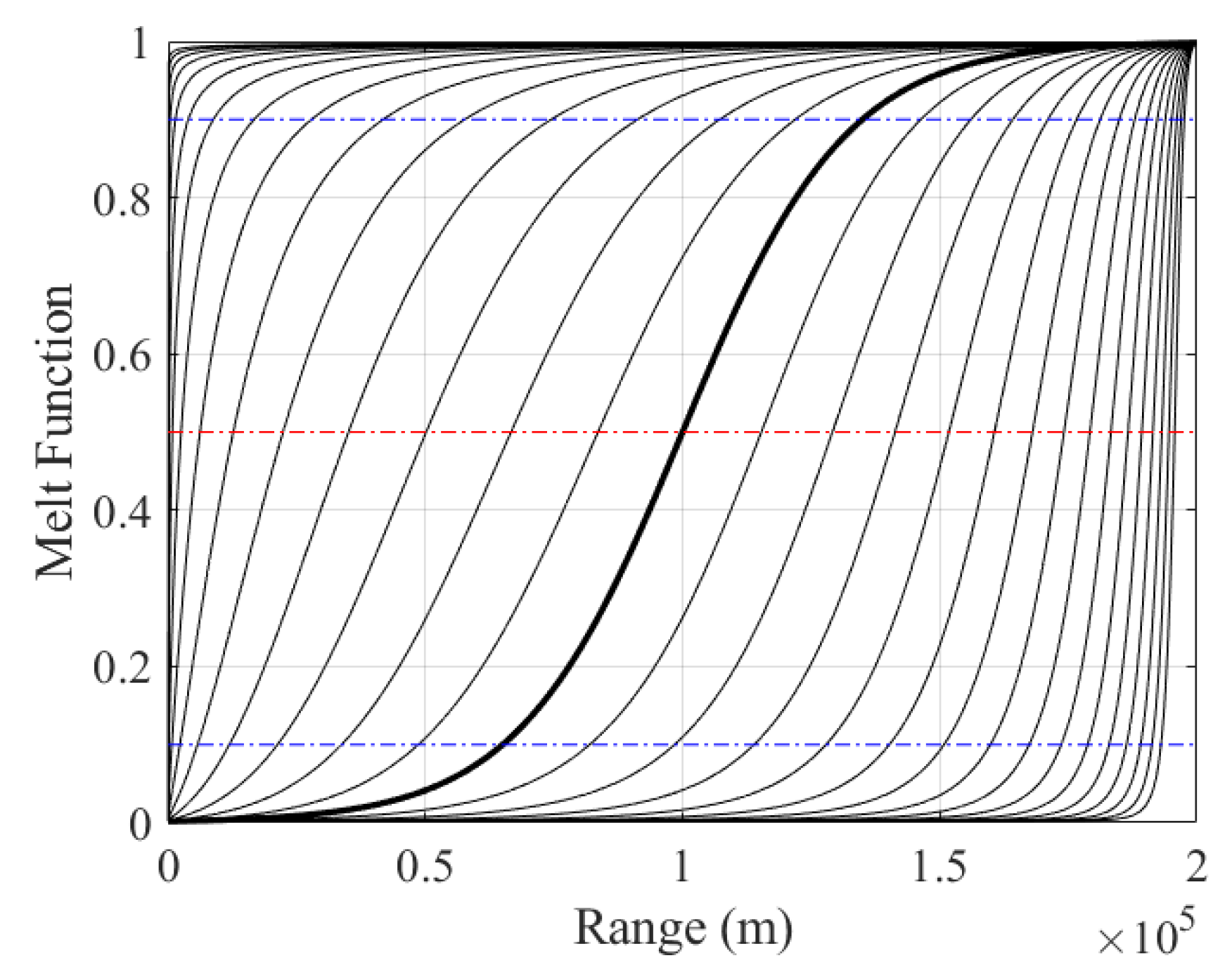
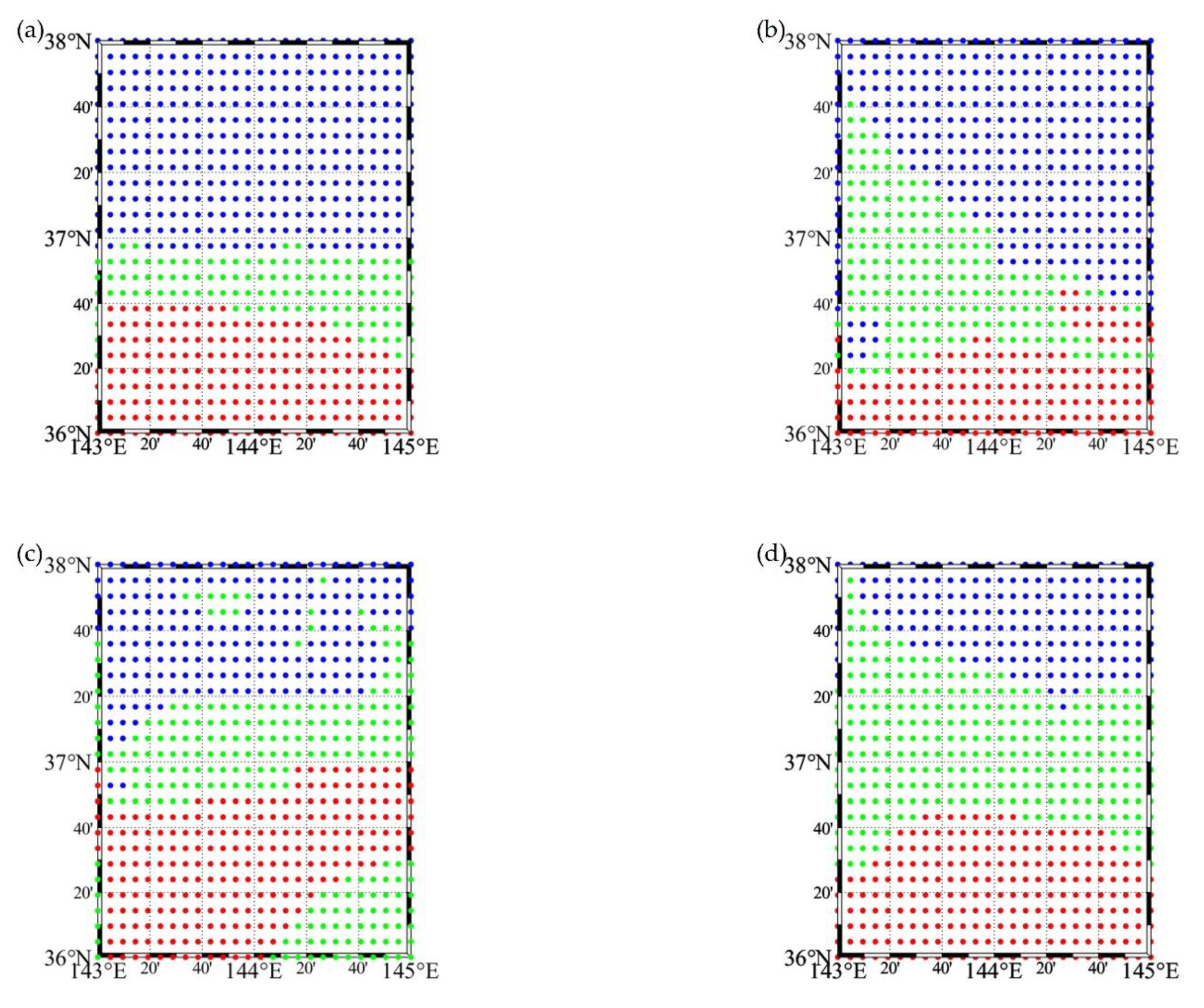
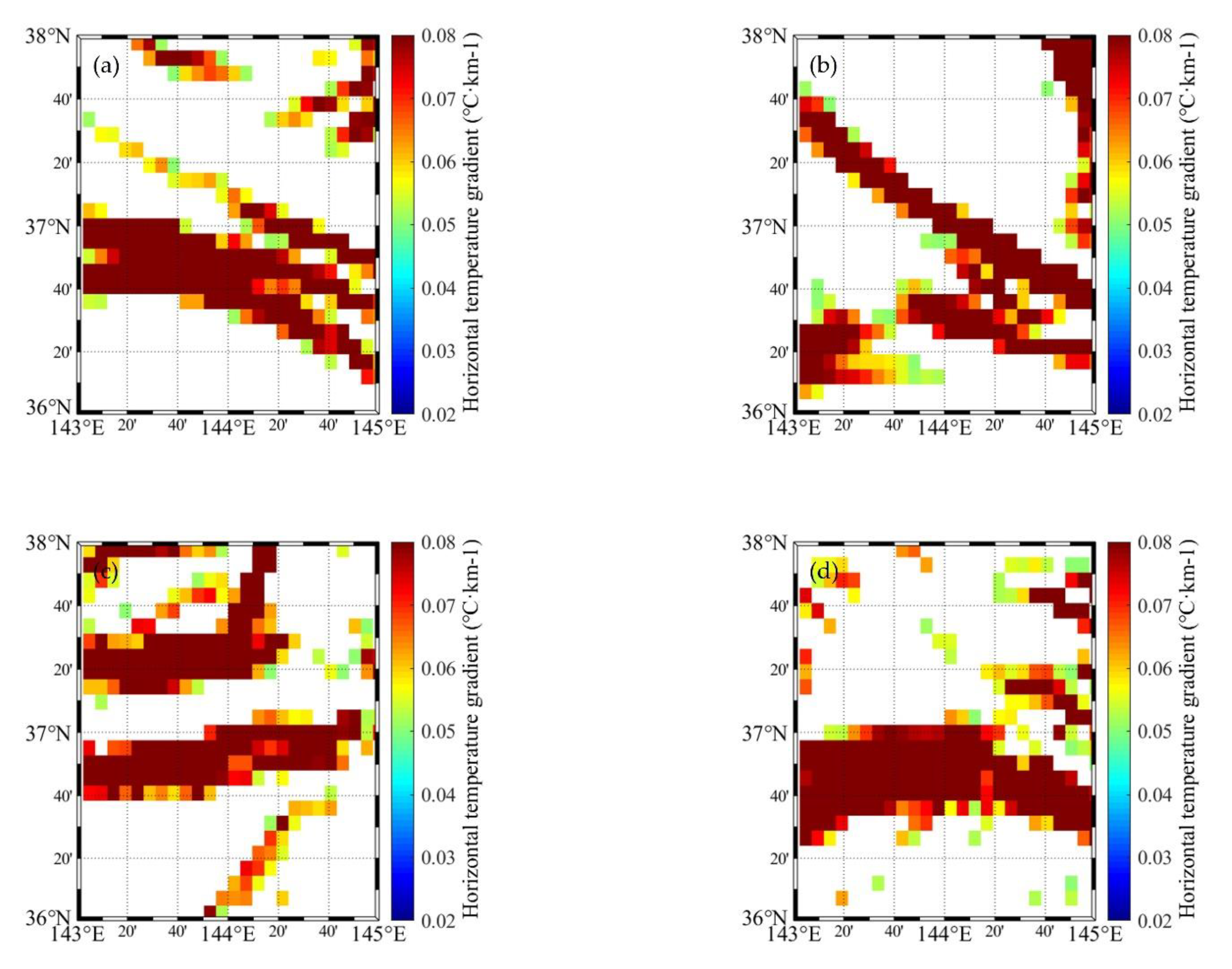



| Date | Starting Position of Frontal Zone (km) | Ending Position of Frontal Zone (km) | The Width of Frontal Zone (km) | Melt Parameter (a) |
|---|---|---|---|---|
| 0101 | 100 | 150 | 30 | 0.2 |
| 0201 | 110 | 160 | 60 | 0.3 |
| 0701 | 70 | 120 | 50 | 0 |
| 0801 | 50 | 130 | 70 | −0.1 |
| Date | SD | Frequency | Unsmoothed Results | Smoothed Results | ||
|---|---|---|---|---|---|---|
| RMSE (dB) | % Over 10 dB Difference | RMSE (dB) | % Over 10 dB Difference | |||
| 0101 | 100 m | 50 Hz | 4.0979 | 4.51 | 4.0635 | 3.09 |
| 400 Hz | 3.5768 | 3.56 | 2.2081 | 1.43 | ||
| 300 m | 50 Hz | 6.0864 | 7.84 | 5.0327 | 6.41 | |
| 400 Hz | 5.3627 | 7.13 | 4.0636 | 4.51 | ||
| 500 m | 50 Hz | 6.7936 | 13.06 | 5.9864 | 10.21 | |
| 400 Hz | 7.2301 | 16.63 | 6.0486 | 11.88 | ||
| 0201 | 100 m | 50 Hz | 3.6767 | 3.33 | 2.7750 | 2.14 |
| 400 Hz | 4.5213 | 4.75 | 4.3992 | 4.04 | ||
| 300 m | 50 Hz | 5.3600 | 9.74 | 4.7712 | 7.84 | |
| 400 Hz | 5.8099 | 12.11 | 4.8880 | 10.93 | ||
| 500 m | 50 Hz | 5.2164 | 5.70 | 4.0808 | 1.90 | |
| 400 Hz | 5.3095 | 6.65 | 3.8610 | 2.61 | ||
| 0701 | 100 m | 50 Hz | 6.4535 | 11.96 | 5.9976 | 10.53 |
| 400 Hz | 4.6909 | 5.26 | 4.2114 | 3.59 | ||
| 300 m | 50 Hz | 5.2250 | 6.46 | 4.4719 | 3.83 | |
| 400 Hz | 5.4706 | 8.37 | 3.9669 | 5.02 | ||
| 500 m | 50 Hz | 5.8910 | 13.64 | 5.2886 | 11.72 | |
| 400 Hz | 5.7010 | 8.61 | 4.8033 | 5.02 | ||
| 0801 | 100 m | 50 Hz | 4.2503 | 5.50 | 3.8117 | 4.55 |
| 400 Hz | 4.9431 | 7.18 | 4.7813 | 6.46 | ||
| 300 m | 50 Hz | 5.8038 | 9.81 | 4.9057 | 7.18 | |
| 400 Hz | 5.4635 | 9.81 | 3.7415 | 6.46 | ||
| 500 m | 50 Hz | 4.4016 | 1.91 | 3.8120 | 1.20 | |
| 400 Hz | 4.8585 | 3.83 | 3.8297 | 1.20 | ||
| Season | Frequency | Unsmoothed Results RMSE (dB) | Smoothed Results RMSE (dB) |
|---|---|---|---|
| Winter | 50 Hz | 5.2052 | 4.4518 |
| 400 Hz | 5.3020 | 4.2448 | |
| Summer | 50 Hz | 5.3399 | 4.6469 |
| 400 Hz | 5.1879 | 4.2224 |
| Season | SD | Unsmoothed Results RMSE (dB) | Smoothed Results RMSE (dB) |
|---|---|---|---|
| Winter | 100 m | 3.9682 | 3.3615 |
| 300 m | 5.6548 | 4.6889 | |
| 500 m | 6.1374 | 4.9942 | |
| Summer | 100 m | 5.0845 | 4.7005 |
| 300 m | 5.4907 | 4.2715 | |
| 500 m | 5.2130 | 4.4184 |
| Date | SD | Convergence Area 1 | Convergence Area 2 | ||||
|---|---|---|---|---|---|---|---|
| Forecast | Model | Actual | Forecast | Model | Actual | ||
| 0101 | 100 m | 68 | 75 | 95 | 484 | 450 | 440 |
| 300 m | 402 | 465 | 435 | 733 | 710 | 700 | |
| 500 m | 739 | 755 | 500 | 943 | 925 | 800 | |
| 0201 | 100 m | 332 | 380 | 290 | 499 | 500 | 495 |
| 300 m | 326 | 375 | 320 | 676 | 690 | 620 | |
| 500 m | none | none | none | none | none | none | |
| 0701 | 100 m | 255 | 335 | 200 | 564 | 580 | 490 |
| 300 m | 698 | 670 | 545 | 790 | 795 | 755 | |
| 500 m | 959 | 945 | none | 996 | 965 | none | |
| 0801 | 100 m | 332 | 295 | 225 | 484 | 440 | 430 |
| 300 m | 637 | 635 | 580 | 691 | 680 | 670 | |
| 500 m | none | none | none | none | none | none | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, W.; Chen, W.; Chen, Y.; Ma, L.; Meng, Z. Reconstruction of Ocean Front Model Based on Sound Speed Clustering and Its Effectiveness in Ocean Acoustic Forecasting. Appl. Sci. 2021, 11, 8461. https://doi.org/10.3390/app11188461
Liu Y, Chen W, Chen W, Chen Y, Ma L, Meng Z. Reconstruction of Ocean Front Model Based on Sound Speed Clustering and Its Effectiveness in Ocean Acoustic Forecasting. Applied Sciences. 2021; 11(18):8461. https://doi.org/10.3390/app11188461
Chicago/Turabian StyleLiu, Yuyao, Wei Chen, Wen Chen, Yu Chen, Lina Ma, and Zhou Meng. 2021. "Reconstruction of Ocean Front Model Based on Sound Speed Clustering and Its Effectiveness in Ocean Acoustic Forecasting" Applied Sciences 11, no. 18: 8461. https://doi.org/10.3390/app11188461
APA StyleLiu, Y., Chen, W., Chen, W., Chen, Y., Ma, L., & Meng, Z. (2021). Reconstruction of Ocean Front Model Based on Sound Speed Clustering and Its Effectiveness in Ocean Acoustic Forecasting. Applied Sciences, 11(18), 8461. https://doi.org/10.3390/app11188461






