Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method
Abstract
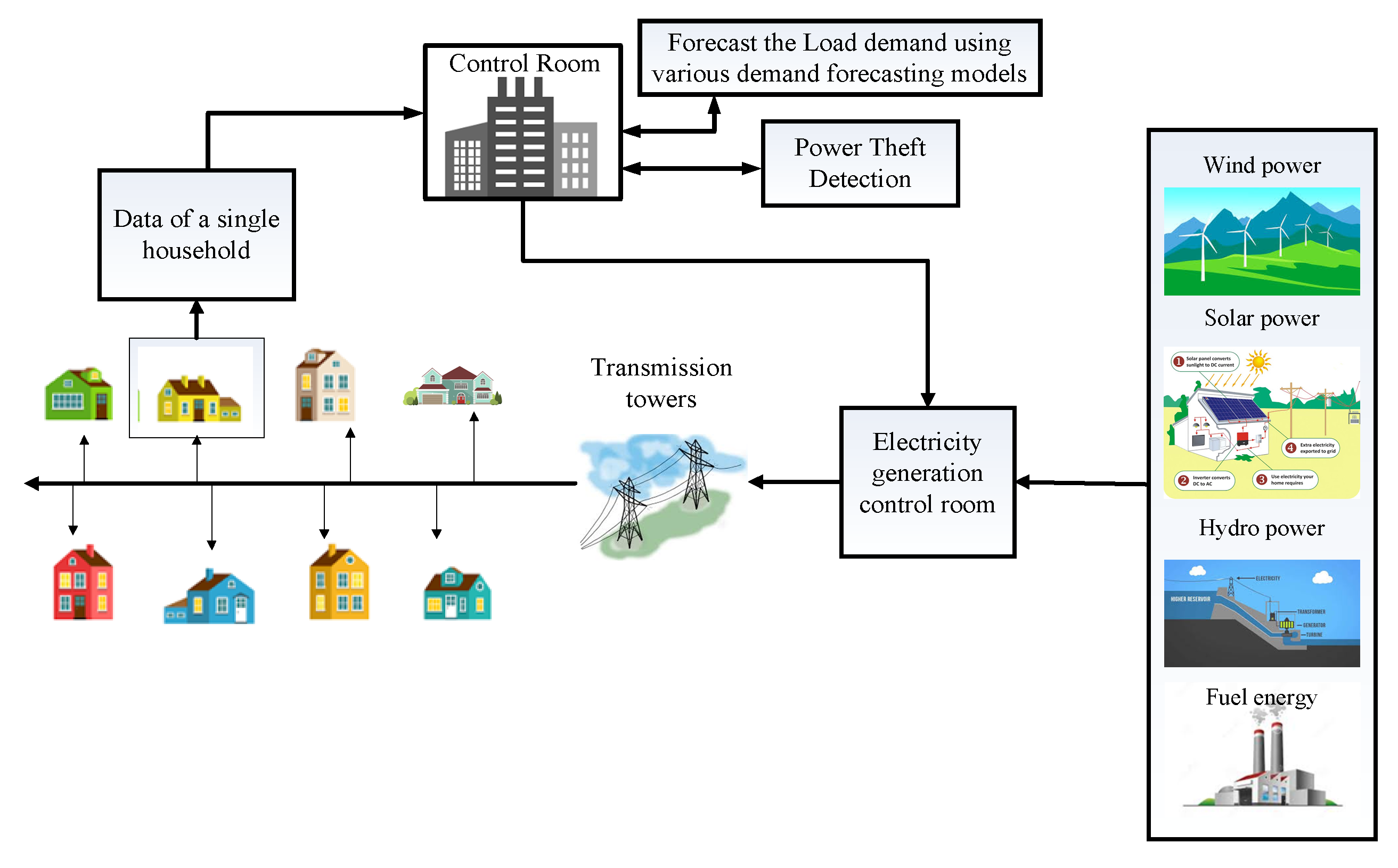
:1. Introduction
2. Related Works
3. Demand Forecasting Models and Power Theft Detection Strategy
3.1. ARIMA Model
- Step 1:
- Collection of dataset: Forecasting is always triggered by a set of values.
- Step 2:
- Observation of series: The obtained series of data are plotted, and the pattern of series is observed. The underlying characteristics, such as trend, seasonality, and noise, are identified. Various break points and elevated points of the series are also observed. This is a crucial part of TSA, wherein the data, with respect to its time series, is thoroughly analyzed; various statistical components of the series are discovered.
- Step 3:
- Stationarity: When the statistical properties of a series, such as mean, variance, autocorrelation, etc., are constant over time, then such a time series is stationary. The augmented Dickey–Fuller (ADF) test is the test for stationarity, where the time series must have a ‘H’ parameter less than 0.05 to be stationary [28].
- Step 4:
- Extraction of the optimal model parameters: This can be done by identifying the Autocorrelation function (ACF) and partial autocorrelation function (PACF) plots. The autocorrelation function is the plot of autocorrelation of a time series by lag; partial autocorrelation is the relationship among the prior time observations of time series. In this step, all the parameters are checked, and the most appropriate models are selected.
- Step 5:
- Fitting Model: Optimal model parameters are followed by the ARIMA model, which is fit to learn the series pattern. ARIMA(7,1,6) is the prediction model.
- Step 6:
- Prediction: After fitting the model, the event is predicted. In the present research paper, the predicted test data is obtained and compared with the original dataset.
- Step 7:
- Determination of accuracy: Finally, the various erroneous parameters are considered to determine the efficiency of the model. Various error parameters are tabulated in the results section. Generally, a time series data is a combination of seasonality , trend , and noise components, which can be determined as , known as an additive model. This additive model does not show good performance for the household electricity consumption data prediction due to its dependence on seasonality.
3.2. Support Vector Regression Forecasting Model
- Step 1:
- Create Testing and training datasets with the train_test_split function. Here, we divided it into 70% training dataset, 30% testing dataset.
- Step 2:
- Build the support vector regression model using SVR function for RBF kernel with appropriate parameters for the training dataset.
- Step 3:
- Forecast the consumption values for the testing dataset.
- Step 4:
- Plot the actual and forecasted values of the testing dataset.
- Step 5:
- Calculate MSE, MAE, and RMSE.
3.3. Linear Regression Forecasting Model
- Step 1:
- Create testing and training datasets with the train_test_split function. Here, we divided it into 70% training dataset, 30% testing dataset.
- Step 2:
- Build the linear regression model using a linear regression function with appropriate parameters for the training dataset.
- Step 3:
- Forecast the consumption values for the testing dataset.
- Step 4:
- Plot the actual and forecasted values of the testing dataset.
- Step 5:
- Calculate MSE, MAE, and RMSE.
3.4. Long Short Term Memory Model
- Step 1:
- Create testing and training datasets with the train _test_split function. Here, we divided it into 70% training dataset, 30% testing dataset.
- Step 2:
- Build the linear regression model using long short term memory model with predefined parameters for the training dataset.
- Step 3:
- Forecast the consumption values for the testing dataset.
- Step 4:
- Plot the actual and forecasted values of the testing dataset.
- Step 5:
- Calculate MSE, MAE, and RMSE.
3.5. Recurrent Neural Networks Model
3.6. Proposed RNN-GBRT Hybrid Model
3.7. Power Theft Detection Algorithm
4. Implementation of Energy Forecasting and Power Theft Detection Models
4.1. Comparative Analysis Based on Error Indices Calculations
4.2. Power Theft Detection Results Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sadorsky, P. Renewable energy consumption and income in emerging economies. Energy Policy 2009, 37, 4021–4028. [Google Scholar] [CrossRef]
- Zou, C.; Zhao, Q.; Zhang, G.; Xiong, B. Energy revolution: From a fossil energy era to a new energy era. Nat. Gas Ind. B 2016, 3, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wen, Y. The Making of an Economic Superpower-Unlocking China’s Secret of Rapid Industrialization; World Scientific: Singapore, 2015; pp. 1–180. [Google Scholar]
- Ghosh, S.; Manna, D.; Chatterjee, A.; Chatterjee, D. Remote Appliance Load Monitoring and Identification in a Modern Residential System With Smart Meter Data. IEEE Sens. J. 2021, 21, 5082–5090. [Google Scholar] [CrossRef]
- Chakraborty, S.; Das, S. Application of Smart Meters in High Impedance Fault Detection on Distribution Systems. IEEE Trans. Smart Grid 2019, 10, 3465–3473. [Google Scholar] [CrossRef]
- Haben, S.; Singleton, C.; Grindrod, P. Analysis and clustering of residential customers’ energy behavioral demand using smart meter data. IEEE Trans. Smart Grid 2016, 7, 136–144. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef] [Green Version]
- Tom, R.J.; Sankaranarayanan, S. IoT based SCADA Integrated with Fog for Power Distribution Automation. In Proceedings of the 12th Iberian Conference on Information Systems and Technologies, Lisbon, Portugal, 21–24 June 2017; pp. 1772–1775. [Google Scholar]
- Sankar, V.J.; Hareesh, V.; Nair, M.G. Integration of Demand Response with Prioritized Load Optimization for Multiple Homes. In Proceedings of the 2017 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017; pp. 1–6. [Google Scholar]
- Cerquitelli, T.; Chicco, G.; Di Corso, E.; Ventura, F.; Montesano, G.; Del Pizzo, A.; González, A.M.; Sobrino, E.M. Discovering Electricity Consumption over Time for Residential Consumers through Cluster Analysis. In Proceedings of the International Conference on Development and Application Systems, Suceava, Romania, 24–26 May 2018; pp. 164–169. [Google Scholar]
- Wang, C.-K.; Lee, C.-M.; Hong, Y.-R.; Cheng, K. Assessment of Energy Transition Policy in Taiwan—A View of Sustainable Development Perspectives. Energies 2021, 14, 4402. [Google Scholar] [CrossRef]
- Vink, K.; Ankyu, E.; Kikuchi, Y. Long-Term Forecasting Potential of Photo-Voltaic Electricity Generation and Demand Using R. Appl. Sci. 2020, 10, 4462. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Singh, A.K.; Khatoon, S. An Overview of Electricity Demand Forecasting Techniques. In Proceedings of the 2012 Emerging Trends in Electrical, Instrumentation and Communication Engineering Conference, Uttar Pradesh, India, 6–7 April 2012. [Google Scholar]
- Cecati, C.; Kolbusz, J.; Różycki, P.; Siano, P.; Wilamowski, B.M. A novel rbf training algorithm for short-term electric load forecasting and comparative studies. IEEE Trans. Ind. Electron. 2015, 62, 6519–6529. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Hill, D.J.; Luo, F.; Xu, Y. Short-term residential load forecasting based on resident behaviour learning. IEEE Trans. Power Syst. 2018, 33, 1087–1088. [Google Scholar] [CrossRef]
- Song, K.B.; Baek, Y.S.; Hong, D.H.; Jang, G. Short-term load forecasting for the holidays using fuzzy linear regression method. IEEE Trans. Power Syst. 2005, 20, 96–101. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A Strategy for Short-Term Load Forecasting by Support Vector Regression Machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 498–505. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Leon-Garcia, A. Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 2010, 1, 120–133. [Google Scholar] [CrossRef]
- Ugurlu, U.; Oksuz, I.; Tas, O. Electrical price forecasting using recurrent neural networks. Energy 2018, 11, 1255. [Google Scholar]
- Taylor, J.W.; McSharry, P.E. Short-term load forecasting methods: An evaluation based on European data. IEEE Trans. Power Syst. 2007, 22, 2213–2219. [Google Scholar] [CrossRef] [Green Version]
- Ullah, F.U.M.; Ullah, A.; Haq, I.U.; Rho, S.; Baik, S.W. Short-term prediction of residential power energy consumption via CNN and multi-layer bi-directional LSTM networks. IEEE Access 2020, 8, 123369–123380. [Google Scholar] [CrossRef]
- Manowska, A. Using the LSTM Network to Forecast the Demand for Electricity in Poland. Appl. Sci. 2020, 10, 8455. [Google Scholar] [CrossRef]
- Son, N.; Yang, S.; Na, J. Deep Neural Network and Long Short-Term Memory for Electric Power Load Forecasting. Appl. Sci. 2020, 10, 6489. [Google Scholar] [CrossRef]
- Le Cam, M.; Daoud, A.; Zmeureanu, R. Forecasting electric demand of supply fan using data mining techniques. Energy 2016, 101, 541–557. [Google Scholar] [CrossRef]
- Yu, S.-W.; Zhu, K.-J. A hybrid procedure for energy demand forecasting in China. Energy 2012, 37, 396–404. [Google Scholar] [CrossRef]
- Cardoso, C.A.V.; Cruz, G.L. Forecasting Natural Gas Consumption using ARIMA Models and Artificial Neural Networks. IEEE Lat. Am. Trans. 2016, 14, 2233–2238. [Google Scholar] [CrossRef]
- Bissing, D.; Klein, M.T.; Chinnathambi, R.A.; Selvaraj, D.F.; Ranganathan, P. A Hybrid Regression Model for Day-Ahead Energy Price Forecasting. IEEE Access 2019, 7, 36833–36842. [Google Scholar] [CrossRef]
- Jagait, R.K.; Fekri, M.N.; Grolinger, K.; Mir, S. Load Forecasting Under Concept Drift: Online Ensemble Learning With Recurrent Neural Network and ARIMA. IEEE Access 2021, 9, 98992–99008. [Google Scholar] [CrossRef]
- Nie, P.; Roccotelli, M.; Fanti, M.P.; Ming, Z.; Li, Z. Prediction of home energy consumption based on gradient boosting regression tree. Energy Rep. 2021, 7, 1246–1255. [Google Scholar] [CrossRef]
- Glauner, P.; Boechat, A.; Dolberg, L.; State, R.; Bettinger, F.; Rangoni, Y.; Duarte, D. Large-scale detection of non-technical losses in imbalanced data sets. Presented at the Innovative Smart Grid Technologies Conference (ISGT), 2016 IEEE Power & Energy Society, Minneapolis, MN, USA, 6–9 September 2016; pp. 1–5. [Google Scholar]
- Glauner, P.; Meira, J.A.; Valtchev, P.; State, R.; Bettinger, F. The Challenge of Non-Technical Loss Detection Using Artificial Intelligence: A Survey. Int. J. Comput. Intell. Syst. 2017, 10, 760–775. [Google Scholar] [CrossRef] [Green Version]
- Depuru, S.S.S.R.; Wang, L.; Devabhaktuni, V. Electricity theft: Overview, issues, prevention and a smart meter based approach to control theft. Energy Policy 2011, 39, 1007–1015. [Google Scholar] [CrossRef]
- Richardson, C.; Race, N.; Smith, P. A privacy preserving approach to energy theft detection in smart grids. In Proceedings of the 2016 IEEE International Smart Cities Conference, Trento, Italy, 12 September 2016. [Google Scholar]
- Salinas, S.A.; Li, P. Privacy-preserving energy theft detection in microgrids: A state estimation approach. IEEE Trans. Power Syst. 2016, 31, 883–894. [Google Scholar] [CrossRef]
- Luan, W.; Wang, G.; Yu, Y.; Lin, J.; Zhang, W.; Liu, Q. Energy theft detection via integrated distribution state estimation based on AMI and SCADA measurements. In Proceedings of the International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Changsha, China, 26–29 November 2015; pp. 751–756. [Google Scholar]
- Su, C.L.; Lee, W.H.; Wen, C.K. Electricity theft detection in low voltage networks with smart meters using state estimation. In Proceedings of the IEEE International Conference on Industrial Technology, Taipei, Taiwan, 14–17 March 2016; pp. 493–498. [Google Scholar]
- Huang, S.C.; Lo, Y.L.; Lu, C.N. Non-technical loss detection using state estimation and analysis of variance. IEEE Trans. Power Syst. 2013, 28, 2959–2966. [Google Scholar] [CrossRef]
- Maurya, A.; Akyurek, A.S.; Aksanli, B.; Rosing, T.S. Rosing, Time series clustering for data analysis in Smart Grid. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications, Sydney, Australia, 6–9 November 2016; pp. 606–611. [Google Scholar]
- Fanti, M.P.; Mangini, A.M.; Roccotelli, M.; Nolich, M.; Ukovich, W. Modeling Virtual Sensors for Electric Vehicles Charge Services. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 3853–3858. [Google Scholar]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dash, S.K.; Roccotelli, M.; Khansama, R.R.; Fanti, M.P.; Mangini, A.M. Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method. Appl. Sci. 2021, 11, 8612. https://doi.org/10.3390/app11188612
Dash SK, Roccotelli M, Khansama RR, Fanti MP, Mangini AM. Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method. Applied Sciences. 2021; 11(18):8612. https://doi.org/10.3390/app11188612
Chicago/Turabian StyleDash, Santanu Kumar, Michele Roccotelli, Rasmi Ranjan Khansama, Maria Pia Fanti, and Agostino Marcello Mangini. 2021. "Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method" Applied Sciences 11, no. 18: 8612. https://doi.org/10.3390/app11188612
APA StyleDash, S. K., Roccotelli, M., Khansama, R. R., Fanti, M. P., & Mangini, A. M. (2021). Long Term Household Electricity Demand Forecasting Based on RNN-GBRT Model and a Novel Energy Theft Detection Method. Applied Sciences, 11(18), 8612. https://doi.org/10.3390/app11188612






