Solid-State Transformation of an Additive Manufactured Inconel 625 Alloy at 700 °C
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Fabrication and Sample Preparation
2.2. Ex Situ Scanning Electron Microscopy (SEM)
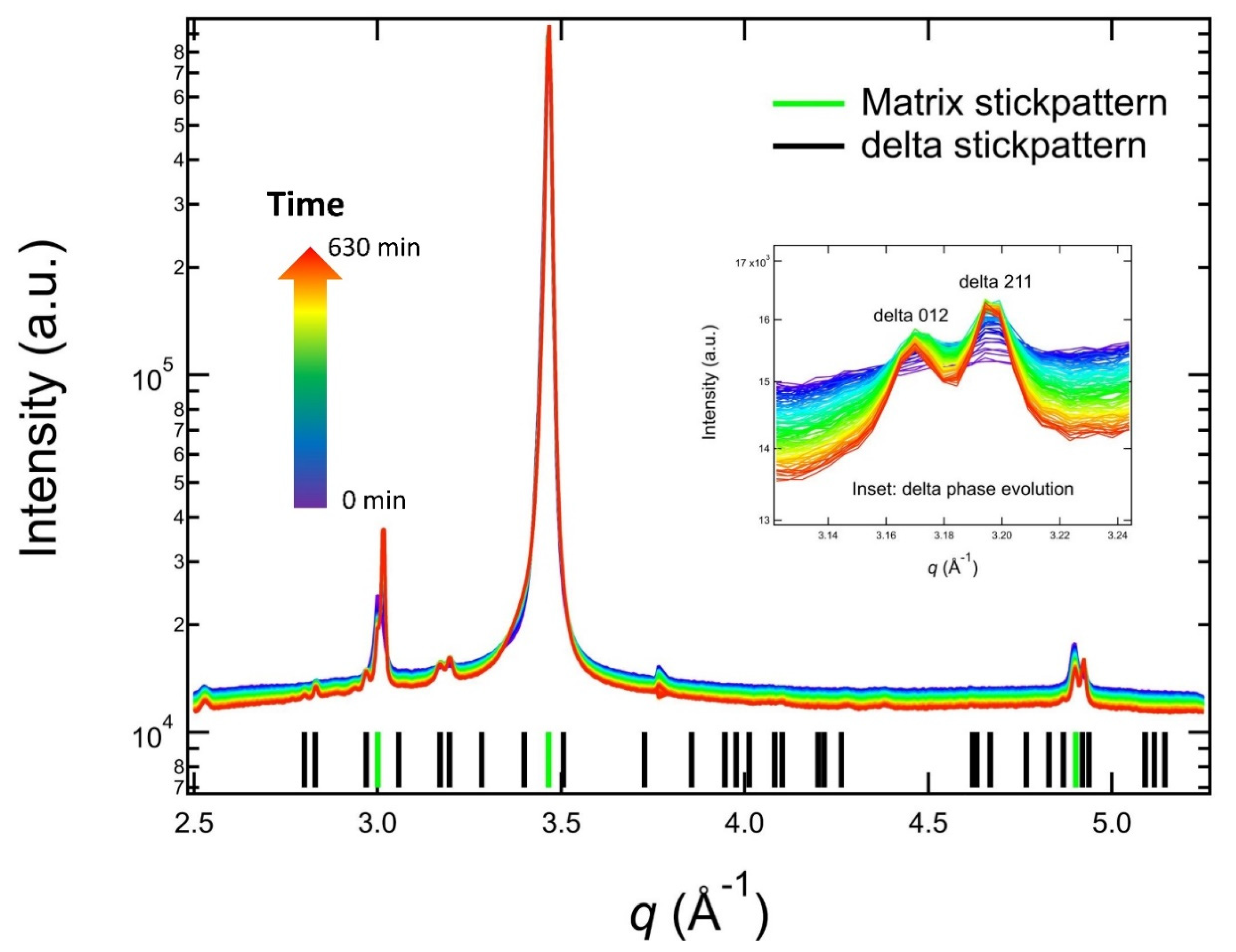
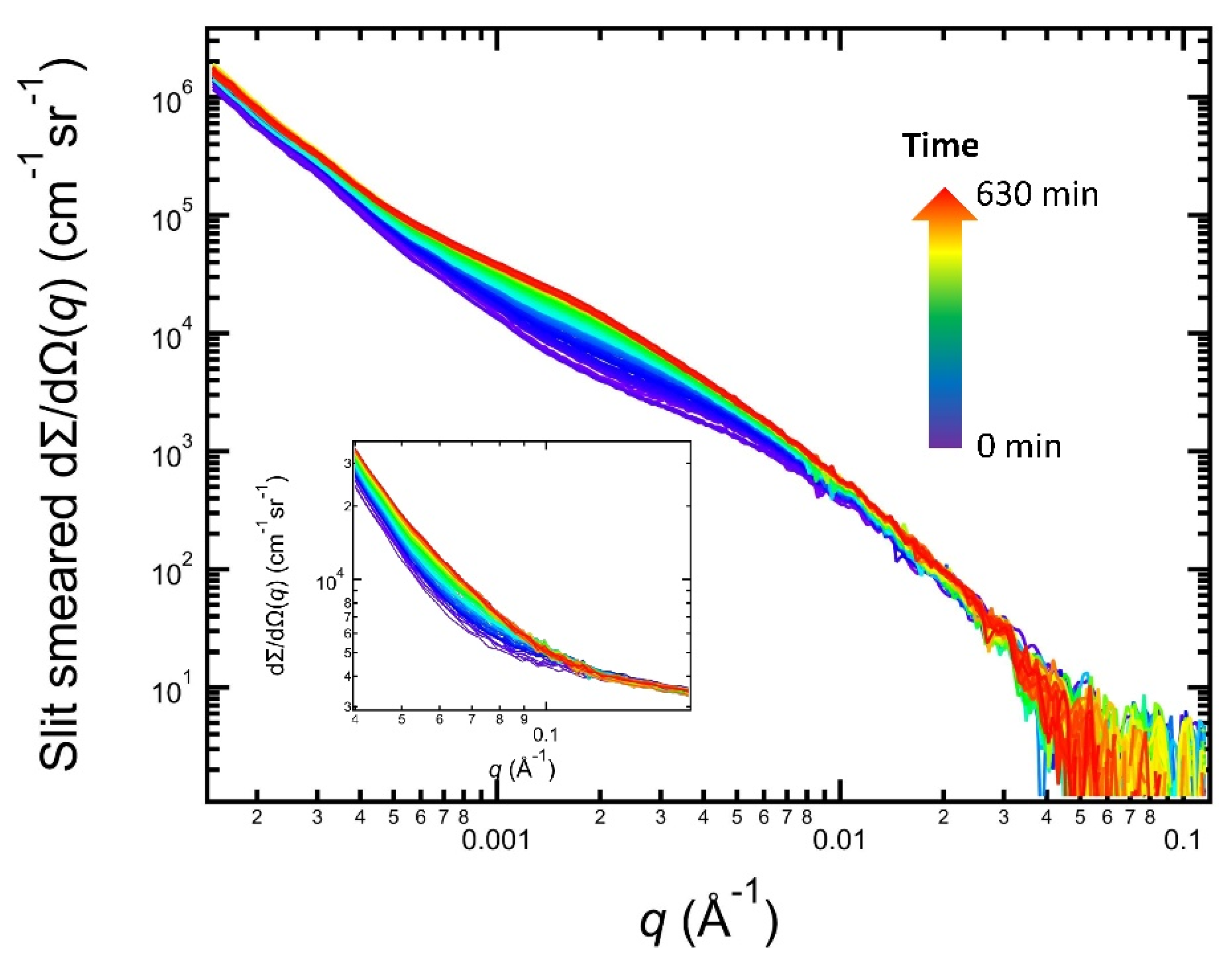
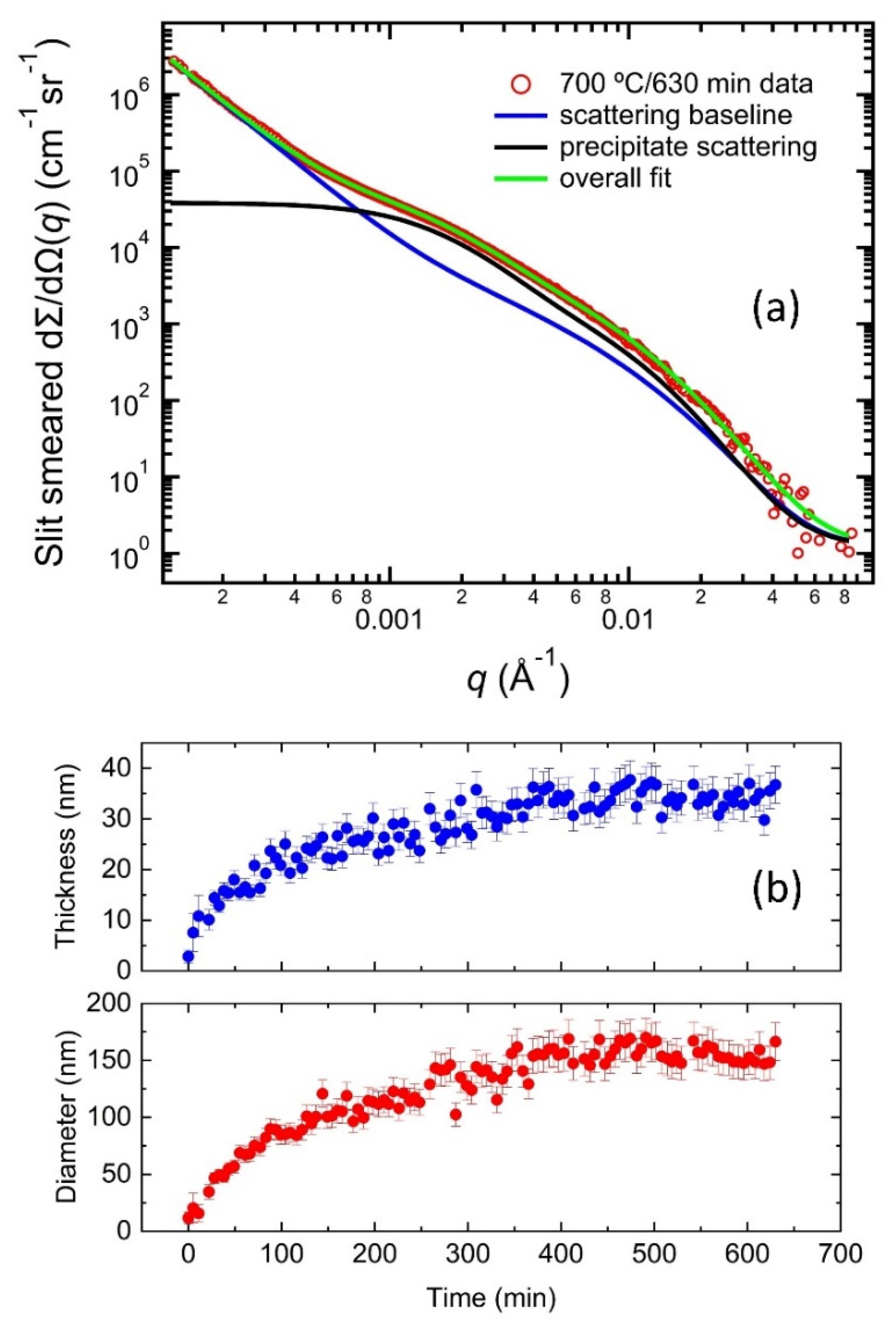
2.3. In Situ Synchrotron Small Angle X-ray Scattering and X-ray Diffraction
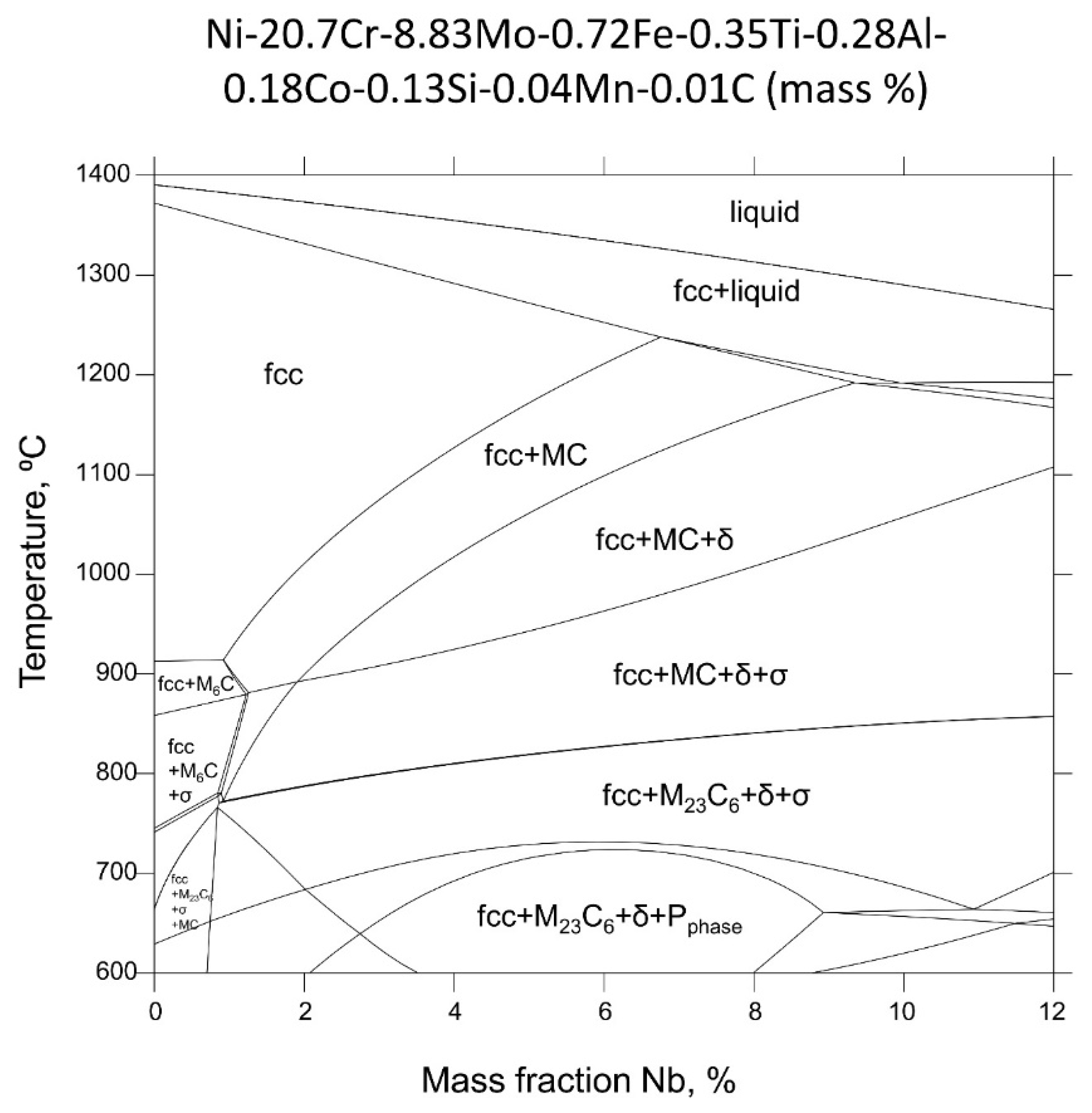
2.4. Thermodynamic Calculations
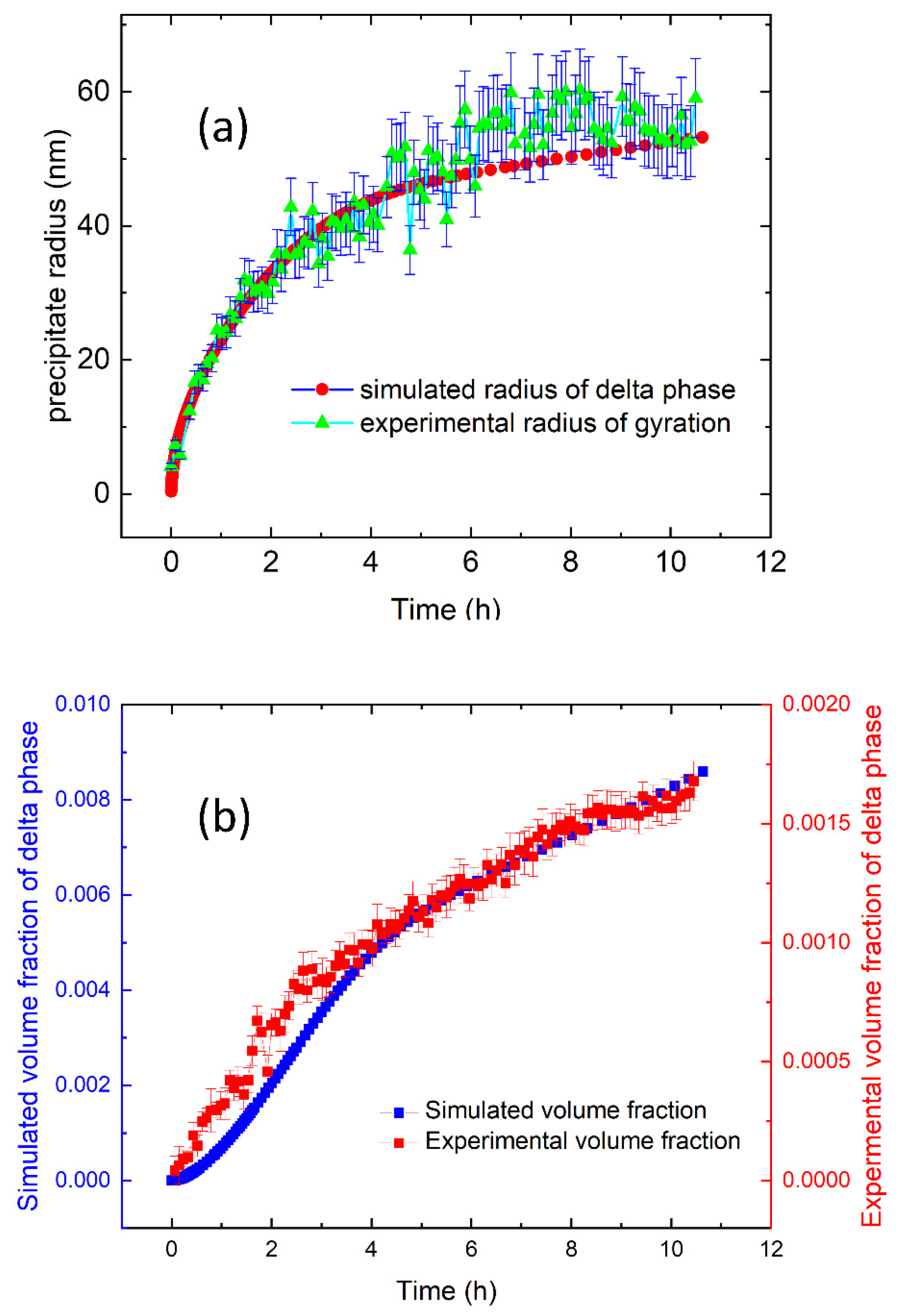
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Disclaimer
References
- Floreen, S.; Fuchs, G.E.; Yang, W.J. The metallurgy of alloy 625. Superalloys 1994, 718, 13–37. [Google Scholar]
- Yangfan, W.; Xizhang, C.; Chuanchu, S. Microstructure and mechanical properties of Inconel 625 fabricated by wire-arc additive manufacturing. Surf. Coatings Technol. 2019, 374, 116–123. [Google Scholar] [CrossRef]
- Gonzalez, J.; Mireles, J.; Stafford, S.; Perez, M.; Terrazas, C.; Wicker, R. Characterization of Inconel 625 fabricated using powder-bed-based additive manufacturing technologies. J. Mater. Process. Technol. 2019, 264, 200–210. [Google Scholar] [CrossRef]
- Pleass, C.; Jothi, S. Influence of powder characteristics and additive manufacturing process parameters on the microstructure and mechanical behaviour of Inconel 625 fabricated by Selective Laser Melting. Addit. Manuf. 2018, 24, 419–431. [Google Scholar] [CrossRef]
- Rivera, O.; Allison, P.; Jordon, J.; Rodriguez, O.; Brewer, L.; McClelland, Z.; Whittington, W.; Francis, D.; Su, J.; Martens, R.; et al. Microstructures and mechanical behavior of Inconel 625 fabricated by solid-state additive manufacturing. Mater. Sci. Eng. A 2017, 694, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A. Residual stress mapping in Inconel 625 fabricated through additive manufacturing: Method for neutron diffraction measurements to validate thermomechanical model predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef] [Green Version]
- List, F.; Dehoff, R.; Lowe, L.; Sames, W. Properties of Inconel 625 mesh structures grown by electron beam additive manufacturing. Mater. Sci. Eng. A 2014, 615, 191–197. [Google Scholar] [CrossRef] [Green Version]
- Martin, J.H.; Yahata, B.D.; Hundley, J.M.; Mayer, J.; Schaedler, T.A.; Pollock, T.M. 3D printing of high-strength aluminium alloys. Nature 2017, 549, 365–369. [Google Scholar] [CrossRef] [PubMed]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Lass, E.A.; Stoudt, M.R.; Williams, M.E.; Katz, M.B.; Levine, L.E.; Phan, T.Q.; Gnaeupel-Herold, T.H.; Ng, D.S. Formation of the Ni3Nb δ-Phase in Stress-Relieved Inconel 625 Produced via Laser Powder-Bed Fusion Additive Manufacturing. Met. Mater. Trans. A 2017, 48, 5547–5558. [Google Scholar] [CrossRef] [Green Version]
- Megahed, M.; Mindt, H.-W.; N’Dri, N.; Duan, H.; Desmaison, O. Metal additive-manufacturing process and residual stress modeling. Integr. Mater. Manuf. Innov. 2016, 5, 61–93. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Liu, Z.; Fang, X.; Guo, Y. Residual Stress in Metal Additive Manufacturing. Procedia CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Sun, L.; Ren, X.; He, J.; Zhang, Z. Numerical investigation of a novel pattern for reducing residual stress in metal additive manufacturing. J. Mater. Sci. Technol. 2021, 67, 11–22. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.-C. Influence of scanning length and energy input on residual stress reduction in metal additive manufacturing: Numerical and experimental studies. J. Manuf. Process. 2020, 49, 247–259. [Google Scholar] [CrossRef]
- Papadakis, L.; Chantzis, D.; Salonitis, K. On the energy efficiency of pre-heating methods in SLM/SLS processes. Int. J. Adv. Manuf. Technol. 2018, 95, 1325–1338. [Google Scholar] [CrossRef]
- Ghosh, S.; Ma, L.; Ofori-Opoku, N.; Guyer, J.E. On the primary spacing and microsegregation of cellular dendrites in laser deposited Ni–Nb alloys. Model. Simul. Mater. Sci. Eng. 2017, 25, 065002. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P.W.; Ji, Y.; Liu, Y.; Horstemeyer, M.H.; Chen, L. Investigation on Microsegregation of IN718 Alloy During Additive Manufacturing via Integrated Phase-Field and Finite-Element Modeling. J. Mater. Eng. Perform. 2019, 28, 657–665. [Google Scholar] [CrossRef]
- Flemings, M.C. Our Understanding of Macrosegregation. Past and Present. ISIJ Int. 2000, 40, 833–841. [Google Scholar] [CrossRef]
- Keller, T.; Lindwall, G.; Ghosh, S.; Ma, L.; Lane, B.M.; Zhang, F.; Kattner, U.R.; Lass, E.A.; Heigel, J.C.; Idell, Y. Application of finite element, phase-field, and calphad-based methods to additive manufacturing of ni-based superalloys. Acta Mater. 2017, 139, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.C.; Miranda, H.; Motta, M.F.; Farias, J.P.; Afonso, C.R.M.; Ramirez, A.J. New insight on the solidification path of an alloy 625 weld overlay. J. Mater. Res. Technol. 2013, 2, 228–237. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Levine, L.E.; Allen, A.J.; Stoudt, M.R.; Lindwall, G.; Lass, E.A.; Williams, M.E.; Idell, Y.; Campbell, C.E. Effect of heat treatment on the microstructural evolution of a nickel-based superalloy additive-manufactured by laser powder bed fusion. Acta Mater. 2018, 152, 200–214. [Google Scholar] [CrossRef]
- EOS NickeAlloy IN625. Available online: https://www.eos.info/03_system-related-assets/material-related-contents/metal-materials-and-examples/metal-material-datasheet/nickelalloy-inconel/niall-in625-m290_material_data_sheet_06-17_en.pdf (accessed on 13 August 2021).
- Ilavsky, J.; Zhang, F.; Andrews, R.N.; Kuzmenko, I.; Jemian, P.R.; Levine, L.E.; Allen, A.J. Development of combined microstructure and structure characterization facility for in situ and operando studies at the Advanced Photon Source. J. Appl. Crystallogr. 2018, 51, 867–882. [Google Scholar] [CrossRef]
- Zhang, F.; Levine, L.E.; Allen, A.J.; Young, S.W.; Williams, M.E.; Stoudt, M.R.; Moon, K.-W.; Heigel, J.C.; Ilavsky, J. Phase Fraction and Evolution of Additively Manufactured (AM) 15-5 Stainless Steel and Inconel 625 AM-Bench Artifacts. Integr. Mater. Manuf. Innov. 2019, 8, 362–377. [Google Scholar] [CrossRef]
- Andersson, J.-O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar] [CrossRef]
- Software, T.-C. Ni-Based Superalloys Database, Version 8. Available online: http://www.thermocalc.com/products-services/databases/thermodynamic/ (accessed on 1 September 2015).
- Tc-Prisma Version 2.0.3; Thermo-Calc Software Ab: Stockholm, Sweden, 2013.
- Shi, P.F.; Engström, A.; Sundman, B.; Ågren, J. Thermodynamic Calculations and Kinetic Simulations of some Advanced Materials. Mater. Sci. Forum 2011, 675-677, 961–974. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, K.; Sterner, G.; Mason, P. Modeling precipitation kinetics during heat treatment with calphad-based tools. J. Mater. Eng. Perform. 2014, 23, 4193–4196. [Google Scholar] [CrossRef]
- Langer, J.S.; Schwartz, A.J. Kinetics of nucleation in near-critical fluids. Phys. Rev. A 1980, 21, 948–958. [Google Scholar] [CrossRef]
- Kampmann, R.; Wagner, R. Decomposition of Alloys: The early stages. In Proceedings of the 2nd Acta-Scripta Metallurgica Conference, Sonnenberg, Germany, 19–23 September 1983; Pergamon Press: Oxford, UK, 1984; pp. 91–103. [Google Scholar]
- Wagner, R.; Kampmann, R.; Voorhees, P.W. Homogeneous second-phase precipitation. Mater. Sci. Technol. 1991, 5, 309. [Google Scholar]
- Lindwall, G.; Campbell, C.E.; Lass, E.; Zhang, F.; Stoudt, M.R.; Allen, A.J.; Levine, L.E. Simulation of TTT Curves for Additively Manufactured Inconel 625. Met. Mater. Trans. A 2018, 50, 457–467. [Google Scholar] [CrossRef] [Green Version]
- Kirkwood, D. Microsegregation. Mater. Sci. Eng. 1984, 65, 101–109. [Google Scholar] [CrossRef]
- Zhang, F.; Levine, L.E.; Allen, A.J.; Campbell, C.E.; Lass, E.; Cheruvathur, S.; Stoudt, M.R.; Williams, M.E.; Idell, Y. Homogenization kinetics of a nickel-based superalloy produced by powder bed fusion laser sintering. Scr. Mater. 2017, 131, 98–102. [Google Scholar] [CrossRef] [Green Version]
- Stoudt, M.R.; Lass, E.; Ng, D.S.; Williams, M.E.; Zhang, F.; Campbell, C.E.; Lindwall, G.; Levine, L.E. The Influence of Annealing Temperature and Time on the Formation of δ-Phase in Additively-Manufactured Inconel 625. Met. Mater. Trans. A 2018, 49, 3028–3037. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shankar, V.; Rao, K.B.S.; Mannan, S. Microstructure and mechanical properties of Inconel 625 superalloy. J. Nucl. Mater. 2001, 288, 222–232. [Google Scholar] [CrossRef]
- Sundararaman, M.; Mukhopadhyay, P.; Banerjee, S. Precipitation of the δ-Ni3Nb phase in two nickel base superalloys. Met. Mater. Trans. A 1988, 19, 453–465. [Google Scholar] [CrossRef]
- Rai, S.K.; Kumar, A.; Shankar, V.; Jayakumar, T.; Rao, K.B.S.; Raj, B. Characterization of microstructures in Inconel 625 using X-ray diffraction peak broadening and lattice parameter measurements. Scr. Mater. 2004, 51, 59–63. [Google Scholar] [CrossRef]
- Cocks, F.H. A lattice parameter method for the investigation of solid state precipitation. J. Mater. Sci. 1972, 7, 771–780. [Google Scholar] [CrossRef]
- Shaikh, M.; Ahmad, M.; Shoaib, K.; Akhter, J.; Iqbal, M. Precipitation hardening in Inconel*625. Mater. Sci. Technol. 2000, 16, 129–132. [Google Scholar] [CrossRef]
- Karunaratne, M.; Reed, R. Interdiffusion of Niobium and Molybdenum in Nickel between 900–1300 °C. Defect and Diffusion Forum. 2005, 237–240, 420–425. [Google Scholar] [CrossRef]
- Andrews, R.N.; Serio, J.; Muralidharan, G.; Ilavsky, J. An in situ usaxs–saxs–waxs study of precipitate size distribution evolution in a model ni-based alloy. J. Appl. Crystallogr. 2017, 50, 734–740. [Google Scholar] [CrossRef] [Green Version]
- Jia, Q.; Zhang, F.; Rometsch, P.; Li, J.; Mata, J.; Weyland, M.; Bourgeois, L.; Sui, M.; Wu, X. Precipitation kinetics, microstructure evolution and mechanical behavior of a developed Al–Mn–Sc alloy fabricated by selective laser melting. Acta Mater. 2020, 193, 239–251. [Google Scholar] [CrossRef]
- Zhang, F.; Levine, L.E.; Allen, A.J.; Campbell, C.E.; Creuziger, A.A.; Kazantseva, N.; Ilavsky, J. In situ structural characterization of ageing kinetics in aluminum alloy 2024 across angstrom-to-micrometer length scales. Acta Mater. 2016, 111, 385–398. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Zheng, W.-J.; Xiang, J.-Z.; Song, Z.-G.; Pu, E.-X.; Feng, H. Grain Growth Behavior of Inconel 625 Superalloy. J. Iron Steel Res. Int. 2016, 23, 1111–1118. [Google Scholar] [CrossRef]
- Qin, S.; Novak, T.C.; Vailhe, M.K.; Liu, Z.-K.; Beese, A.M. Plasticity and fracture behavior of Inconel 625 manufactured by laser powder bed fusion: Comparison between as-built and stress relieved conditions. Mater. Sci. Eng. A 2021, 806, 140808. [Google Scholar] [CrossRef]
- Beaucage, G. Approximations Leading to a Unified Exponential/Power-Law Approach to Small-Angle Scattering. J. Appl. Crystallogr. 1995, 28, 717–728. [Google Scholar] [CrossRef]
- Johnson, W.C.; Alexander, J.I.D. Interfacial conditions for thermomechanical equilibrium in two-phase crystals. J. Appl. Phys. 1986, 59, 2735–2746. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, X.; Qin, X.; Ding, Y. High-temperature mechanical properties of Inconel-625: Role of carbides and delta phase. Mater. Sci. Technol. 2017, 33, 1610–1617. [Google Scholar] [CrossRef]
- Soni, H.; Gor, M.; Rajput, G.S.; Sahlot, P. A comprehensive review on effect of process parameters and heat treatment on tensile strength of additively manufactured Inconel-625. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Verhoeven, J.D. Fundamentals of Physical Metallurgy; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Wang, G.; Ouyang, H.; Fan, C.; Guo, Q.; Li, Z.; Yan, W.; Li, Z. The origin of high-density dislocations in additively manufactured metals. Mater. Res. Lett. 2020, 8, 283–290. [Google Scholar] [CrossRef]



| Cr | Mo | Nb | Fe | Ti | Al | Co | Si | Mn | C | Ni | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Measured Mass Fraction (%) | 20.7 | 8.83 | 3.75 | 0.72 | 0.35 | 0.28 | 0.18 | 0.13 | 0.03 | 0.01 | balance |
| Standard Range of Mass Fraction (%) | 20.0–23.0 | 8.0–10.0 | 3.15–4.15 | 5.0 max | 0.4 max | 0.4 max | 1.0 max | 0.5 max | 0.5 max | 0.1 max | Balance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Ilavsky, J.; Lindwall, G.; Stoudt, M.R.; Levine, L.E.; Allen, A.J. Solid-State Transformation of an Additive Manufactured Inconel 625 Alloy at 700 °C. Appl. Sci. 2021, 11, 8643. https://doi.org/10.3390/app11188643
Zhang F, Ilavsky J, Lindwall G, Stoudt MR, Levine LE, Allen AJ. Solid-State Transformation of an Additive Manufactured Inconel 625 Alloy at 700 °C. Applied Sciences. 2021; 11(18):8643. https://doi.org/10.3390/app11188643
Chicago/Turabian StyleZhang, Fan, Jan Ilavsky, Greta Lindwall, Mark R. Stoudt, Lyle E. Levine, and Andrew J. Allen. 2021. "Solid-State Transformation of an Additive Manufactured Inconel 625 Alloy at 700 °C" Applied Sciences 11, no. 18: 8643. https://doi.org/10.3390/app11188643
APA StyleZhang, F., Ilavsky, J., Lindwall, G., Stoudt, M. R., Levine, L. E., & Allen, A. J. (2021). Solid-State Transformation of an Additive Manufactured Inconel 625 Alloy at 700 °C. Applied Sciences, 11(18), 8643. https://doi.org/10.3390/app11188643







