Exploring Frontiers of 4D X-ray Tomography
Abstract
:1. Introduction
2. High-Speed X-ray CT
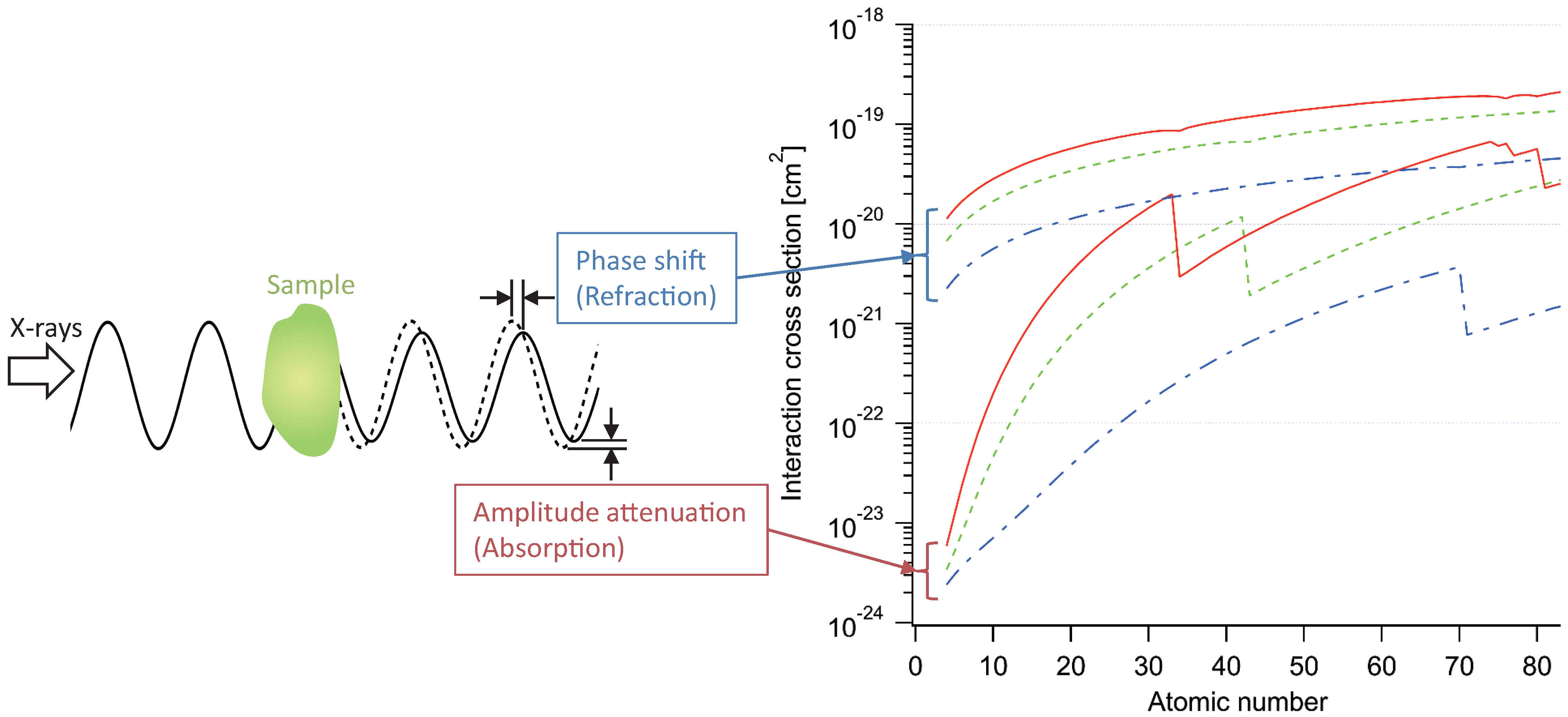
2.1. X-ray Imaging
2.2. X-ray CT
3. High-Speed X-ray CT
3.1. With Sample Rotation
3.2. With Compressed Sensing
3.3. Without Sample Rotation
4. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Fossum, E.R.; Hodongwa, D.B. A review of the pinned photodiode for CCD and CMOS image sensors. IEEE J. Electron Devices Soc. 2014, 2, 33–43. [Google Scholar] [CrossRef]
- Kuroda, R.; Suzuki, M.; Sugawa, S. Over 100 million frames per second high speed global shutter CMOS image sensor. Proc. SPIE 2019, 11051, 1105157. [Google Scholar]
- Als-Nielsen, J.; McMorrow, D. Elements of Modern X-ray Physics, 2nd ed.; Wiley: Chichester, UK, 2011. [Google Scholar]
- Fitzgerald, R. Phase-sensitive x-ray imaging. Phys. Today 2000, 53, 23–26. [Google Scholar] [CrossRef]
- Nugent, K.A. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1–99. [Google Scholar] [CrossRef] [Green Version]
- Bonse, U.; Hart, M. An X-ray interferometer. Appl. Phys. Lett. 1965, 6, 155–156. [Google Scholar] [CrossRef]
- Momose, A.; Takeda, T.; Itai, Y.; Hirano, K. Phase-contrast X-ray computed tomography for observing biological soft tissues. Nat. Med. 1996, 2, 473–475. [Google Scholar] [CrossRef]
- Takeda, T.; Yoneyama, A.; Wu, J.; Thet-Thet-Lwin; Momose, A.; Hyodo, K. In vivo physiological saline-infused hepatic vessel imaging using a two-crystal-interferometer-based phase-contrast X-ray technique. J. Synchrotron Rad. 2012, 19, 252–256. [Google Scholar] [CrossRef]
- Yoneyama, A.; Nambu, A.; Ueda, K.; Yamada, S.; Takeya, S.; Hyodo, K.; Takeda, T. Phase-contrast X-ray imaging system with sub mg/cm3 density resolution. J. Phys. Conf. Ser. 2013, 425, 192007. [Google Scholar] [CrossRef]
- Davis, J.; Gao, D.; Gureyev, T.E.; Stevenson, A.W.; Wilkins, S.W. Phase-contrast imaging of weakly absorbing materials using hard X-rays. Nature 1995, 373, 595–598. [Google Scholar] [CrossRef]
- Chapman, D.; Thomlinson, W.; Johnston, R.E.; Washburn, D.; Pisano, E.; Gmúr, N.; Zhong, Z.; Menk, R.; Arfelli, F.; Sayers, D. Diffraction enhanced x-ray imaging. Phys. Med. Biol 1997, 42, 2015–2025. [Google Scholar] [CrossRef] [Green Version]
- Ando, A.; Sugiyama, H.; Maksimenko, A.; Pattanasiriwisawa, W.; Hyodo, K.; Xiaowei, Z. A new optics for dark-field imaging in X-ray region ‘Owl’. Jpn. J. Appl. Phys. 2001, 40, L844–L846. [Google Scholar] [CrossRef]
- Snigirev, A.; Snigireva, I.; Kohn, V.; Kuznetsov, S.; Schelokov, I. On the possibilities of x-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev. Sci. Instrum. 1995, 66, 5486–5492. [Google Scholar] [CrossRef]
- Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A.; Stevenson, A.W. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Cloetens, P.; Barrett, R.; Baruchel, J.; Guigay, J.-P.; Schlenker, M. Phase objects in synchrotron radiation hard x-ray imaging. J. Phys. D 1996, 29, 133–146. [Google Scholar] [CrossRef]
- Paganin, D.; Mayo, S.C.; Gureyev, T.E.; Miller, P.R.; Wilkins, S.W. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microsc. 2002, 206, 33–40. [Google Scholar] [CrossRef]
- David, C.; Nóhammer, B.; Solak, H.H. Differential x-ray phase contrast imaging using a shearing interferometer. Appl. Phys. Lett. 2002, 81, 3287–3289. [Google Scholar] [CrossRef]
- Momose, A.; Kawamoto, S.; Koyama, I.; Hamaishi, Y.; Takai, K.; Suzuki, Y. Demonstration of x-ray Talbot interferometry. Jpn. J. Appl. Phys. 2003, 42, L866–L868. [Google Scholar] [CrossRef]
- Weitkamp, T.; Diaz, A.; David, C.; Pfeiffer, F.; Stampanoni, M.; Cloetens, P.; Ziegler, E. X-ray phase imaging with a grating interferometer. Opt. Express 2005, 13, 6296–6304. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Takeda, Y.; Suzuki, Y.; Hattori, T. Phase tomography by x-ray Talbot interferometry for biological imaging. Jpn. J. Appl. Phys. 2006, 45, 5254–5262. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Phase retrieval and differential phase-contrast imaging with low-brilliance X-ray sources. Nat. Phys. 2006, 2, 258–261. [Google Scholar] [CrossRef]
- Yashiro, W.; Takeda, Y.; Momose, A. Efficiency of capturing a phase image using cone-beam x-ray Talbot interferometry. J. Opt. Soc. Am. A 2008, 25, 2025–2039. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Weitkamp, T.; Bunk, O.; David, C. Hard-X-ray dark-field imaging using a grating interferometer. Nat. Mater. 2008, 7, 134–137. [Google Scholar] [CrossRef]
- Yashiro, W.; Terui, Y.; Kawabata, K.; Momose, A. On the origin of visibility contrast in x-ray Talbot interferometry. Opt. Express 2010, 18, 16890–16901. [Google Scholar] [CrossRef]
- Feldkamp, L.A.; Davis, L.C.; Kress, J.W. Practical cone-beam algorithm. J. Opt. Soc. Am. A 1984, 1, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Inoue, Y.; Matsuoka, Y.; Kobayashi, S.; Hishida, N.; Yamashita, Y.; Sakai, T.; Yamanaka, S.; Imanishi, T.; Ishiyama, T. “Subrina” x-ray CT scanner, sub-second scanning type. Shimadzu Rev. 2000, 57, 225–231. [Google Scholar]
- Yashiro, W.; Noda, D.; Kajiwara, K. Sub-10-ms X-ray tomography using a grating interferometer. Appl. Phys. Express 2017, 10, 052501. [Google Scholar] [CrossRef] [Green Version]
- Yashiro, W.; Ueda, R.; Kajiwara, K.; Noda, D.; Kudo, H. Millisecond-order X-ray phase tomography with compressed sensing. Jpn. J. Appl. Phys. 2017, 56, 112503. [Google Scholar] [CrossRef]
- Yashiro, W.; Kamezawa, C.; Noda, D.; Kajiwara, K. Millisecond-order X-ray phase tomography with a fringe-scanning method. Appl. Phys. Express 2018, 11, 122501. [Google Scholar] [CrossRef]
- García-Moreno, F.; Kamm, P.H.; Neu, T.R.; Búlk, F.; Mokso, R.; Schlepútz, C.M.; Stampanoni, M.; Banhart, J. Using X-ray tomoscopy to explore the dynamics of foaming metal. Nat. Commun. 2019, 10, 3762. [Google Scholar] [CrossRef]
- Voegeli, W.; Kajiwara, K.; Kudo, H.; Shirasawa, T.; Liang, X.; Yashiro, W. Multibeam X-ray optical system for high-speed tomography. Optica 2020, 7, 514–517. [Google Scholar] [CrossRef]
- Yokozeki, S.; Suzuki, T. Shearing Interferometer Using the Grating as the Beam Splitter. Appl. Opt. 1971, 10, 1575–1580. [Google Scholar] [CrossRef]
- Talbot, H.F. Facts relating to optical science. Philos. Mag. 1836, 9, 401–407. [Google Scholar]
- Patorski, K. The self-imaging phenomenon and its applications. Prog. Opt. 1989, 27, 1–108. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge U. Press: Cambridge, UK, 1999. [Google Scholar]
- Yoneyama, A.; Baba, R.; Kawamoto, R. Quantitative analysis of the physical properties of CsI, GAGG, LuAG, CWO, YAG, BGO, and GOS scintillators using 10-, 20- and 34-keV monochromated synchrotron radiation. Opt. Mater. Express 2021, 11, 398–411. [Google Scholar] [CrossRef]
- Kamada, K.; Endo, T.; Tsutumi, K.; Yanagida, T.; Fujimoto, Y.; Fukabori, A.; Yoshikawa, A.; Pejchal, J.; Nikl, M. Composition engineering in cerium-doped (Lu,Gd)3(Ga,Al)5O12 single-crystal scintillators. Cryst. Growth Des. 2011, 11, 4484–4490. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef]
- Schreiber, H.; Bruning, J.H. Optical Shop Testing, 3rd ed.; Malacara, D., Ed.; Wiley: Hoboken, NJ, USA, 2007; Chapter 14. [Google Scholar]
- Hack, E.; Burke, J. Invited review article: Measurement uncertainty of linear phase-stepping algorithms. Rev. Sci. Instrum. 2011, 82, 061101. [Google Scholar] [CrossRef]
- Mashita, R.; Yashiro, W.; Kaneko, D.; Bito, Y.; Kishimoto, H. High-speed rotating device for X-ray tomography with 10 ms temporal resolution. J. Synchrotron Rad. 2021, 28, 322–326. [Google Scholar] [CrossRef]
- Available online: https://www.youtube.com/watch?v=4D2RLSmY0kg (accessed on 26 August 2021).
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Li, M.H.; Yang, H.Q.; Kudo, H. An accurate iterative reconstruction algorithm for sparse objects: Application to 3D blood vessel reconstruction from a limited number of projections. Phys. Med. Biol. 2002, 47, 2599–2609. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Pan, X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 2008, 53, 4777–4807. [Google Scholar] [CrossRef] [Green Version]
- Defrise, M.; Vanhove, C.; Liu, X. An algorithm for total variation regularization in high-dimensional linear problems. Inverse Probl. 2011, 27, 065002. [Google Scholar] [CrossRef]
- Kudo, H.; Yamazaki, F.; Nemoto, T.; Takaki, K. A very fast iterative algorithm for TV-regularized image reconstruction with applications to low-dose and few-view CT. Proc. SPIE 2016, 9967, 996711. [Google Scholar]
- Wang, T.; Kudo, H.; Yamazaki, F.; Liu, H. A fast regularized iterative algorithm for fan-beam CT reconstruction. Phys. Med. Biol. 2019, 64, 145006. [Google Scholar] [CrossRef]
- Yashiro, W.; Voegeli, W.; Wada, T.; Kato, H.; Kajiwara, K. Fabrication of multi-blade crystals for hard-X-ray multi-beam imaging system. Jpn. J. Appl. Phys. 2020, 59, 092001. [Google Scholar] [CrossRef]
- Momose, A.; Yashiro, W.; Maikusa, H.; Takeda, Y. High-speed X-ray phase imaging and X-ray phase tomography with Talbot interferometer and white synchrotron radiation. Opt. Express 2009, 17, 12540–12545. [Google Scholar] [CrossRef]
- Lambert, J.; Mokso, R.; Cantat, I.; Cloetens, P.; Glazier, J.A.; Graner, F.; Delannay, R. Coarsening Foams Robustly Reach a Self-Similar Growth Regime. Phys. Rev. Lett. 2010, 104, 248304. [Google Scholar] [CrossRef] [PubMed]
- Bieberle, M.; Barthel, F.; Menz, H.J.; Mayer, H.-G.; Hampel, U. Ultrafast three-dimensional X-ray computed tomography. Appl. Phys. Lett. 2011, 98, 034101. [Google Scholar] [CrossRef]
- Finegan, D.P.; Scheel, M.; Robinson, J.B.; Tjaden, B.; Hunt, I.; Mason, T.J.; Millichamp, J.; Michiel, M.D.; Offer, G.J.; Hinds, G.; et al. In-operando high-speed tomography of lithium-ion batteries during thermal runaway. Nat. Commun. 2015, 6, 6924. [Google Scholar] [CrossRef]
- Ruhlandt, A.; Töpperwien, M.; Krenkel, M.; Mokso, R.; Salditt, T. Four dimensional material movies: High speed phase-contrast tomography by backprojection along dynamically curved paths. Sci. Rep. 2017, 7, 6487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laurien, E.T.; Stürzel, T.; Zhou, M. Unsteady void measurements within debris beds using high speed X-ray tomography. Nucl. Eng. Des. 2017, 312, 277–283. [Google Scholar] [CrossRef]
- Banowski, M.; Beyer, M.; Szalinski, L.; Lucas, D.; Hampel, U. Comparative study of ultrafast X-ray tomography and wire-mesh sensors for vertical gas–liquid pipe flows. Flow Meas. Instrum. 2017, 53, 95–106. [Google Scholar] [CrossRef]
- Vegso, K.; Wu, Y.L.; Takano, H.; Hoshino, M.; Momose, A. Development of pink-beam 4D phase CT for in-situ observation of polymers under infrared laser irradiation. Sci. Rep. 2019, 9, 7404. [Google Scholar] [CrossRef] [Green Version]
- Shirasawa, T.; Liang, X.; Voegeli, W.; Arakawa, E.; Kajiwara, K.; Yashiro, W. High-speed multi-beam X-ray imaging using a lens coupling detector system. Appl. Phys. Express 2020, 13, 077002. [Google Scholar] [CrossRef]
- Yashiro, W.; Shirasawa, T.; Kamezawa, C.; Voegeli, W.; Arakawa, E.; Kajiwara, K. A multi-beam X-ray imaging detector using a branched optical fiber bundle. Jpn. J. Appl. Phys. 2020, 59, 038003. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yashiro, W.; Voegeli, W.; Kudo, H. Exploring Frontiers of 4D X-ray Tomography. Appl. Sci. 2021, 11, 8868. https://doi.org/10.3390/app11198868
Yashiro W, Voegeli W, Kudo H. Exploring Frontiers of 4D X-ray Tomography. Applied Sciences. 2021; 11(19):8868. https://doi.org/10.3390/app11198868
Chicago/Turabian StyleYashiro, Wataru, Wolfgang Voegeli, and Hiroyuki Kudo. 2021. "Exploring Frontiers of 4D X-ray Tomography" Applied Sciences 11, no. 19: 8868. https://doi.org/10.3390/app11198868
APA StyleYashiro, W., Voegeli, W., & Kudo, H. (2021). Exploring Frontiers of 4D X-ray Tomography. Applied Sciences, 11(19), 8868. https://doi.org/10.3390/app11198868





