Effect of Stirrup on Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Series
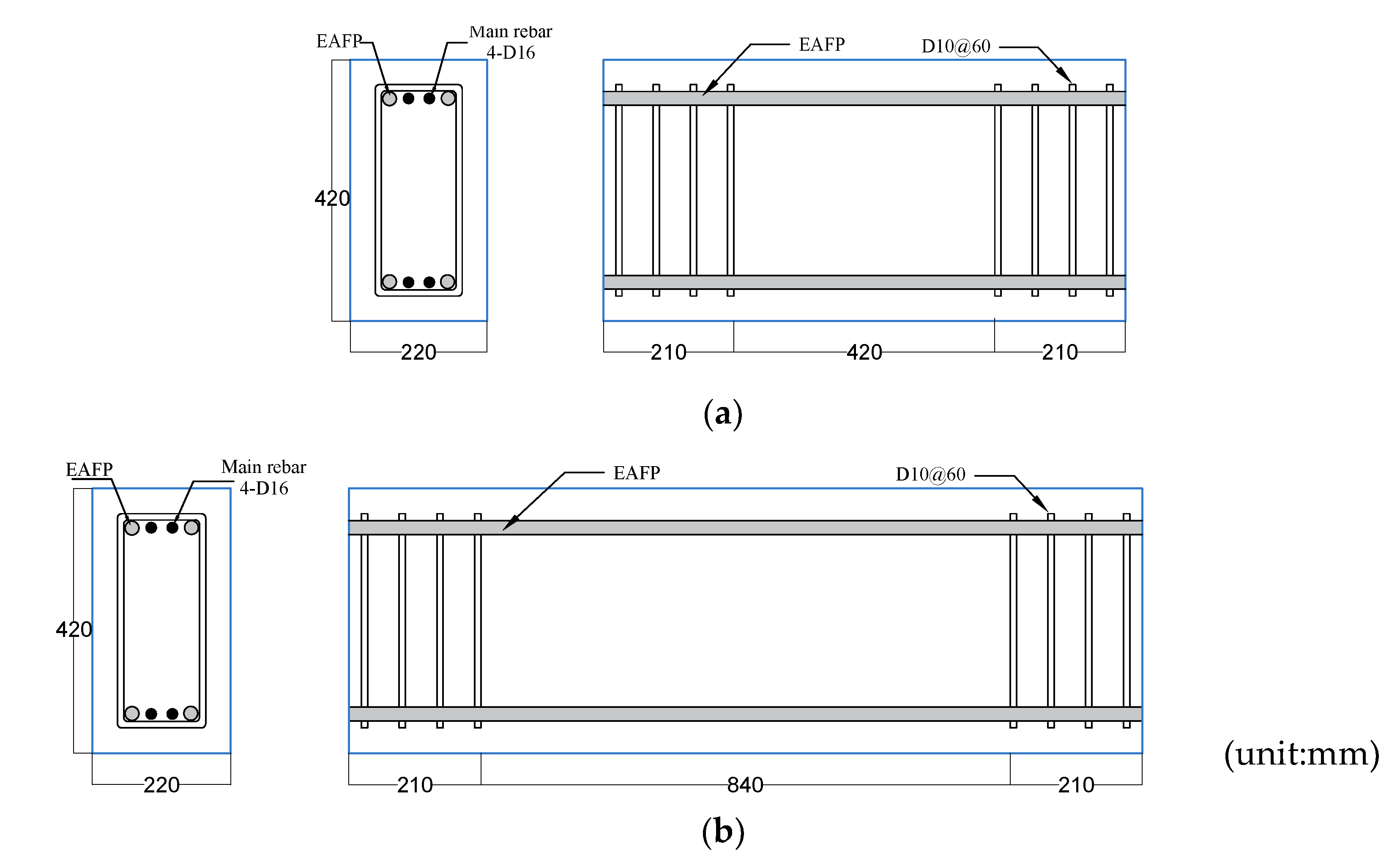
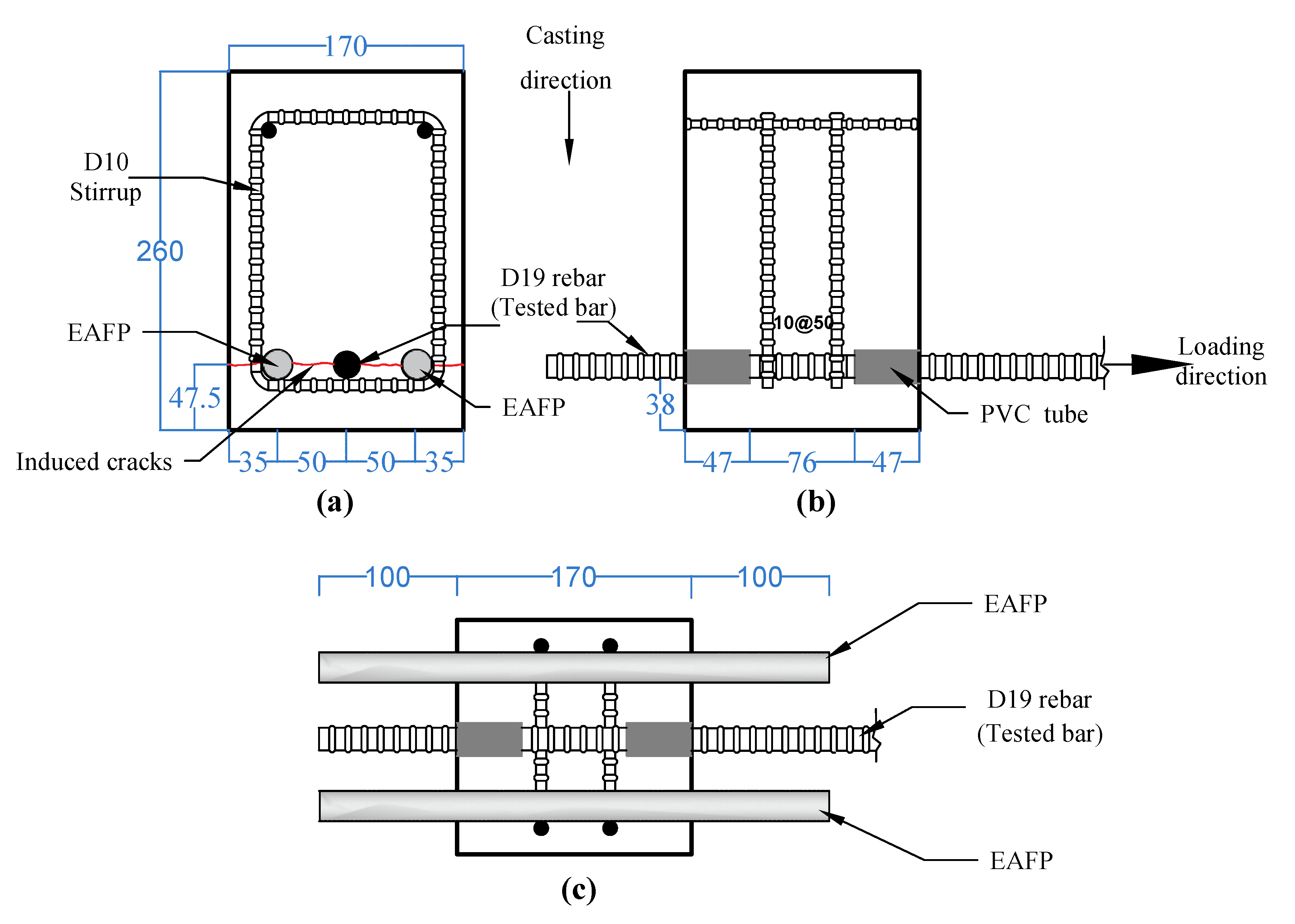
2.2. Specimen Overview
2.3. Used Materials
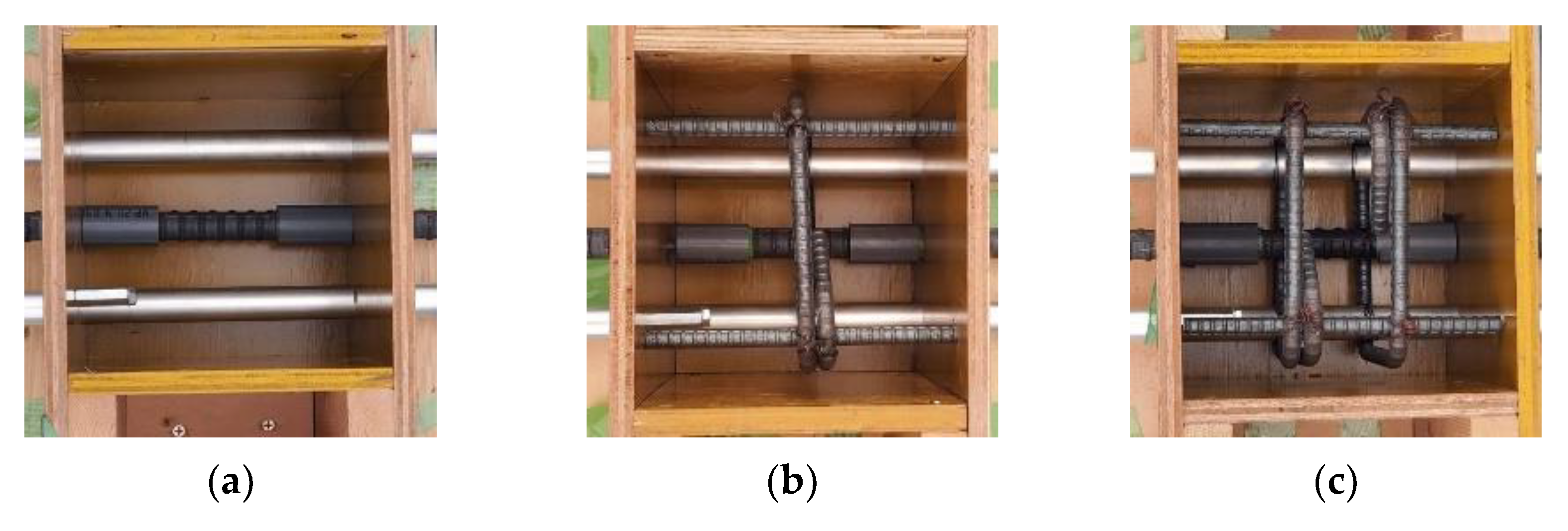
2.4. Crack Simulation by EAFP
2.5. Loading and Measurement Method
3. Experimental Results
3.1. Crack Simulation by EAFP
3.2. Results of the Pull-Out Test
3.2.1. Failure Mode
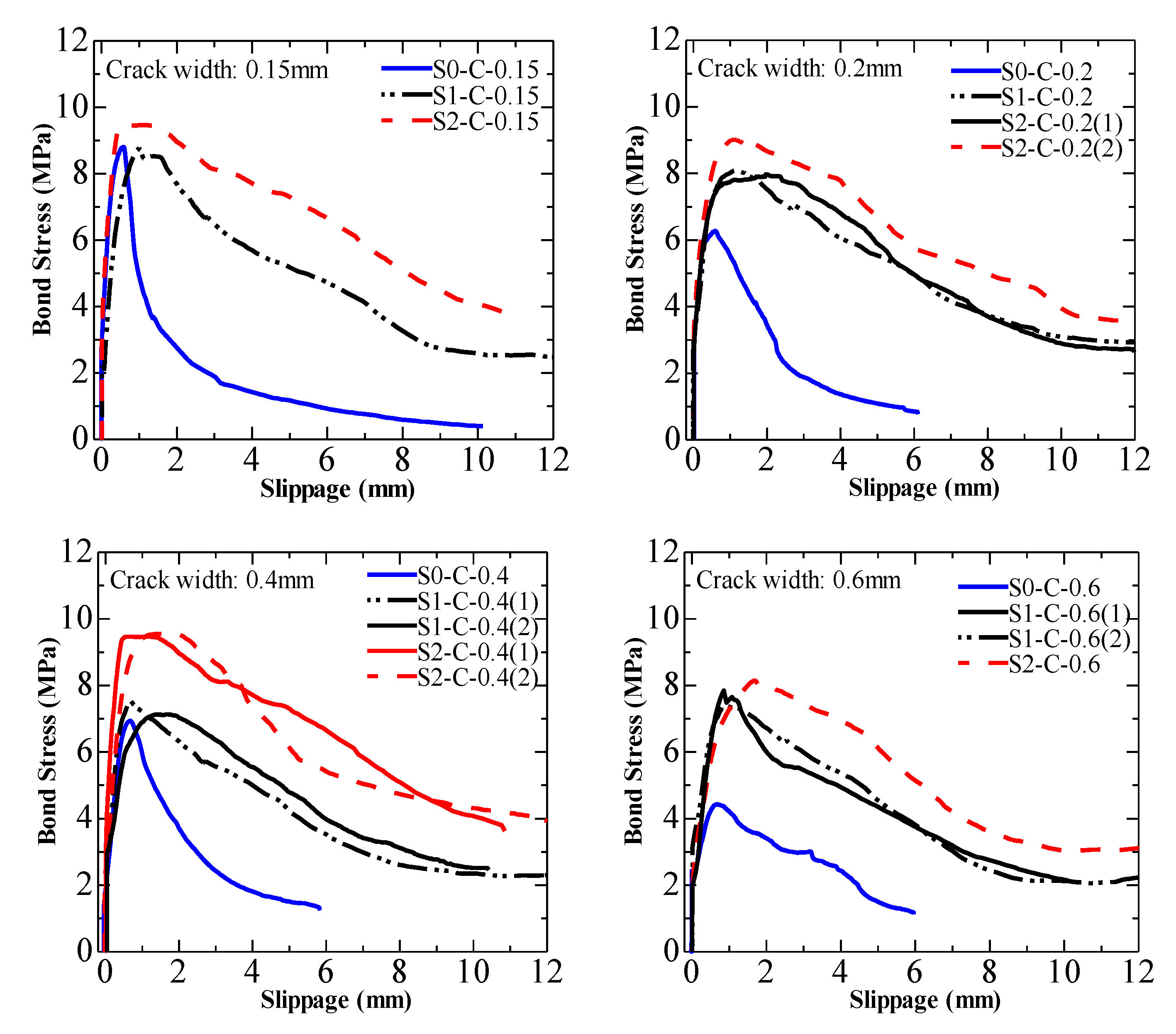
3.2.2. Bond Stress and Slippage
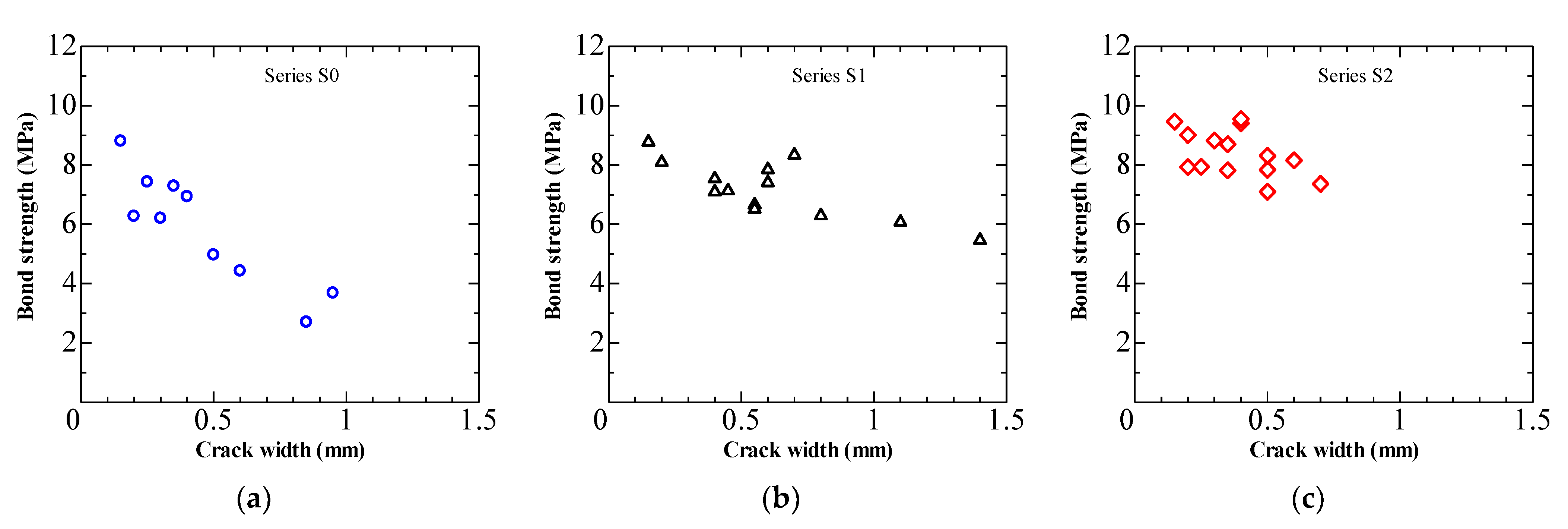
3.2.3. Bond Strength in Cracked Specimens
4. Evaluation of Bond Strength Degradation in Cracked Specimen with Stirrup
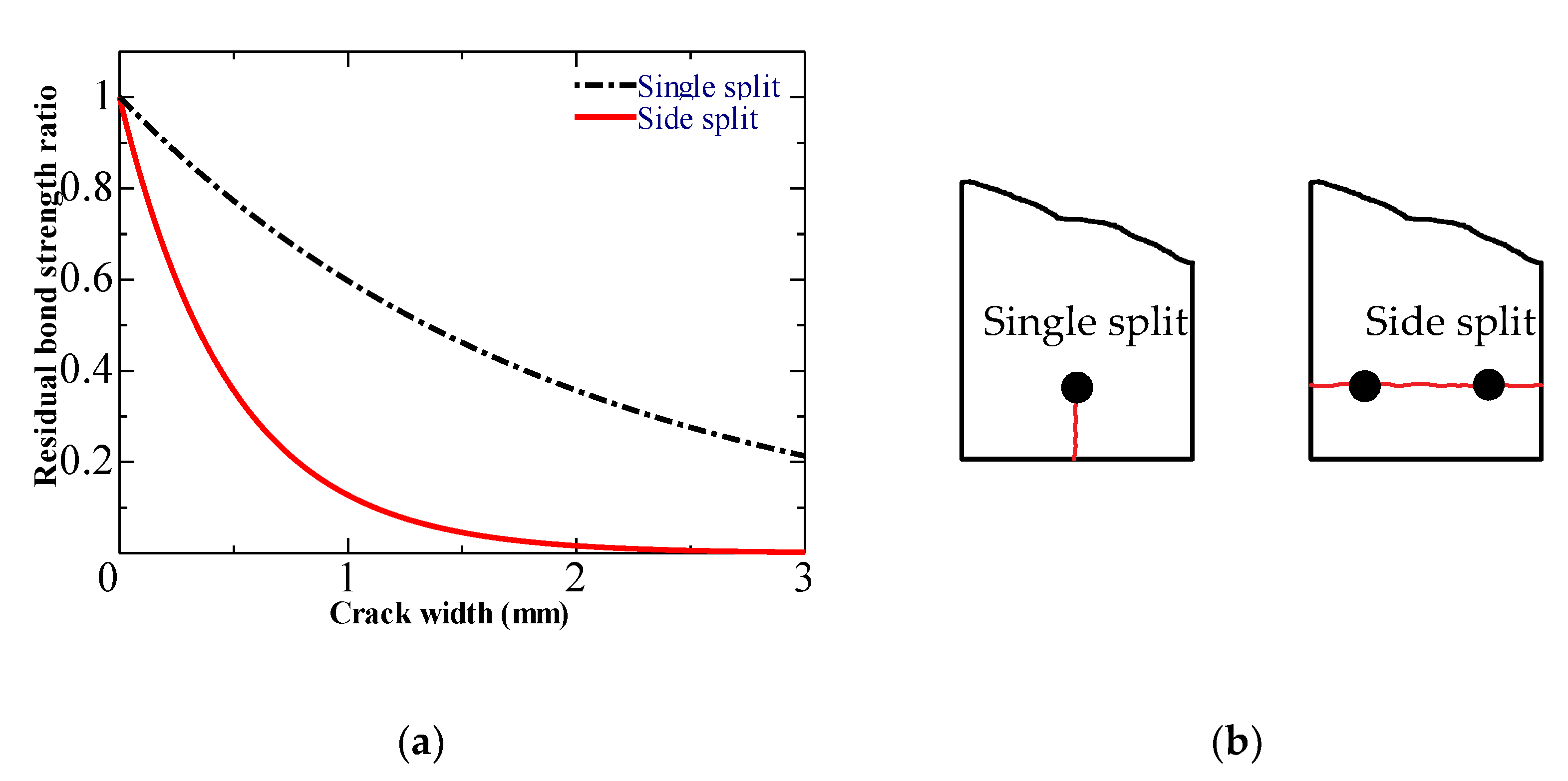
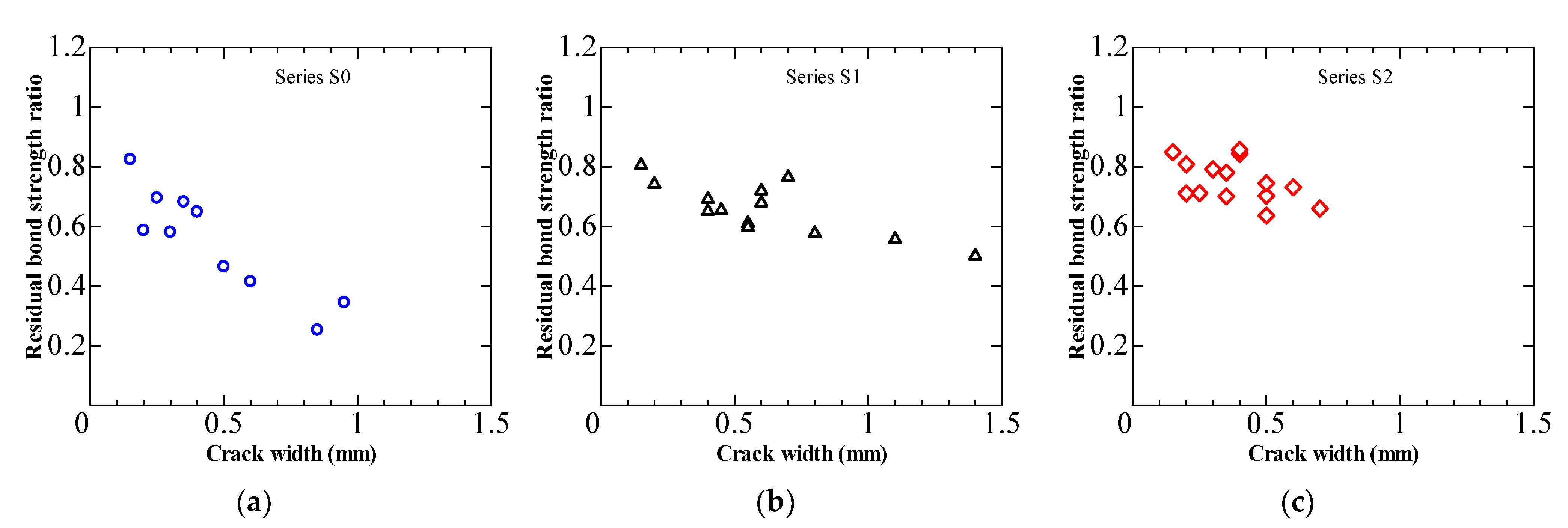
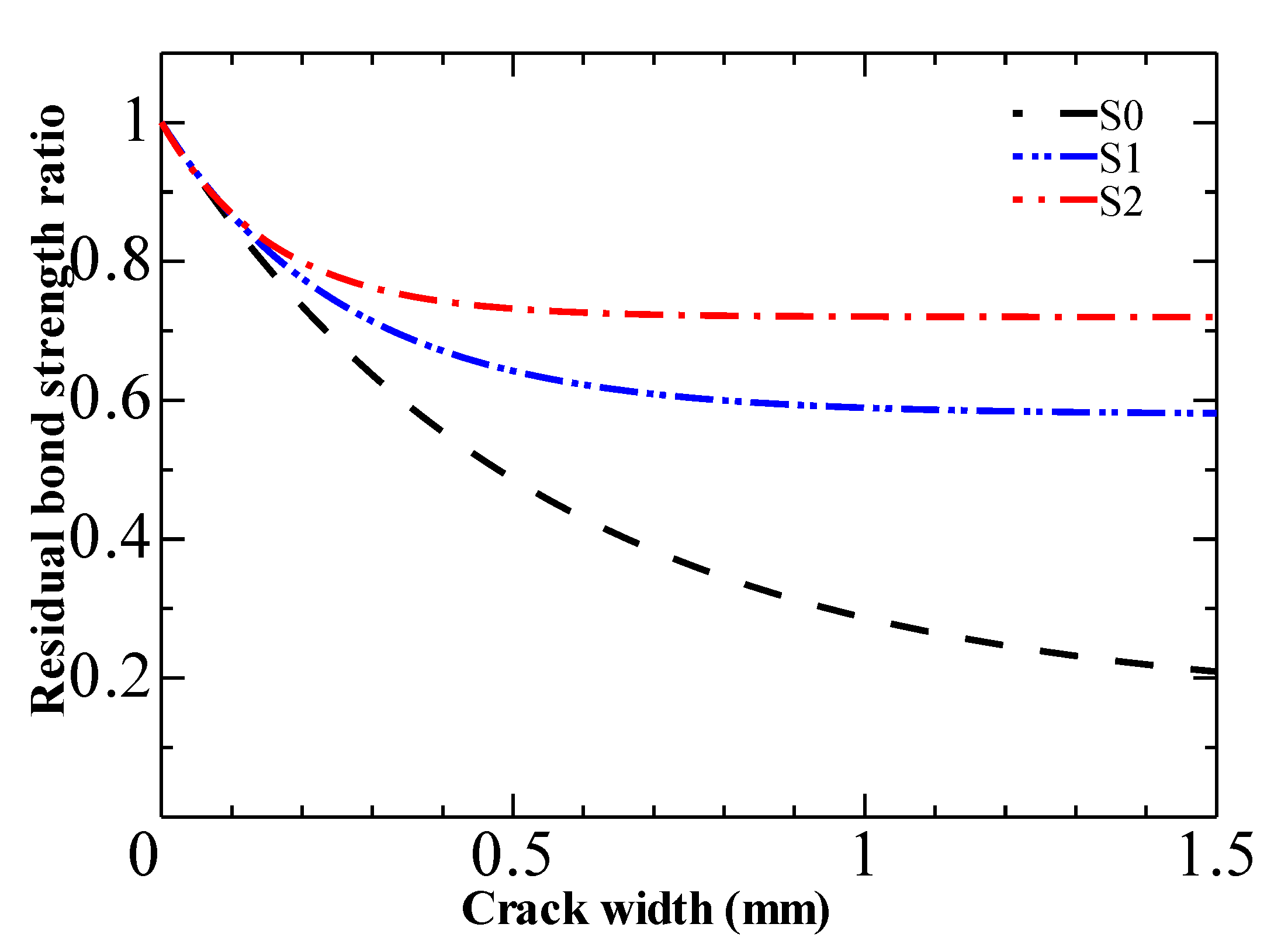
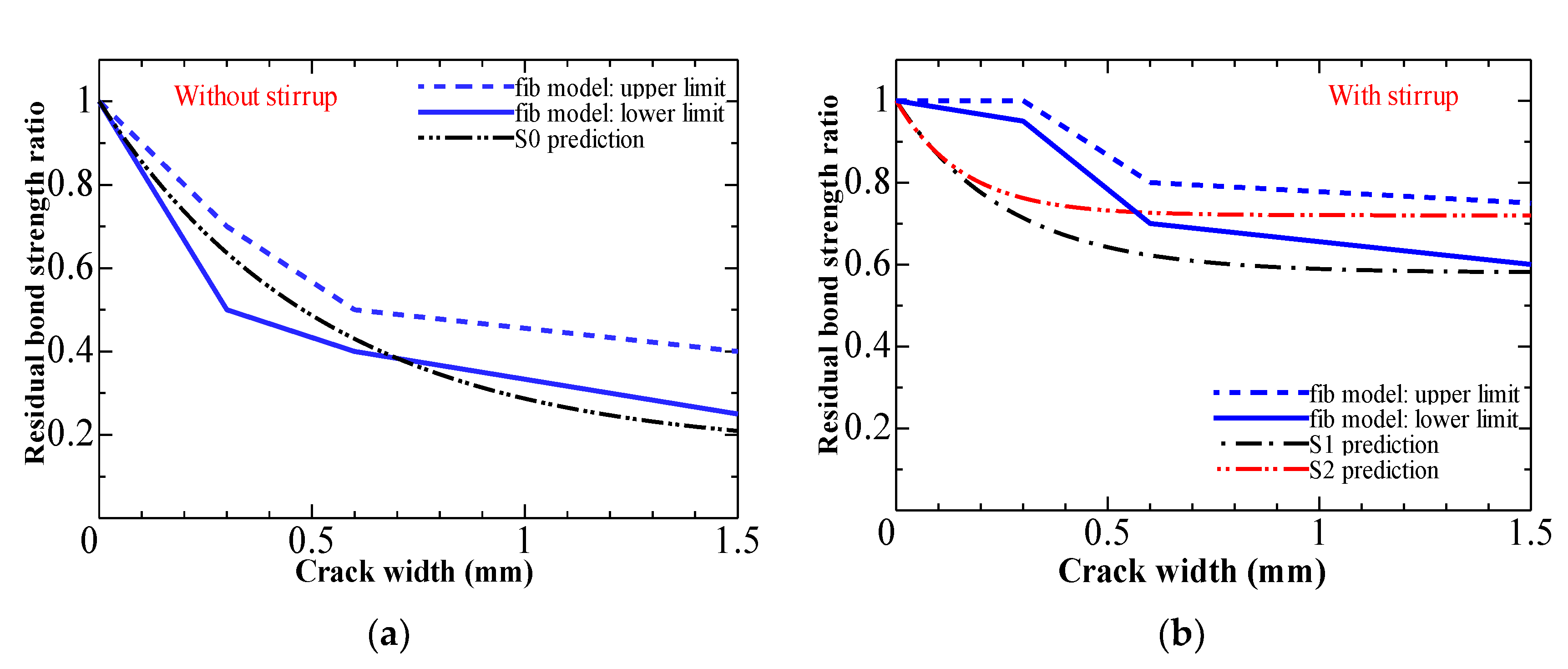
4.1. Bond Degradation and Surface Crack Width Relationship
4.2. Comparison of the Test Results with Fib Model
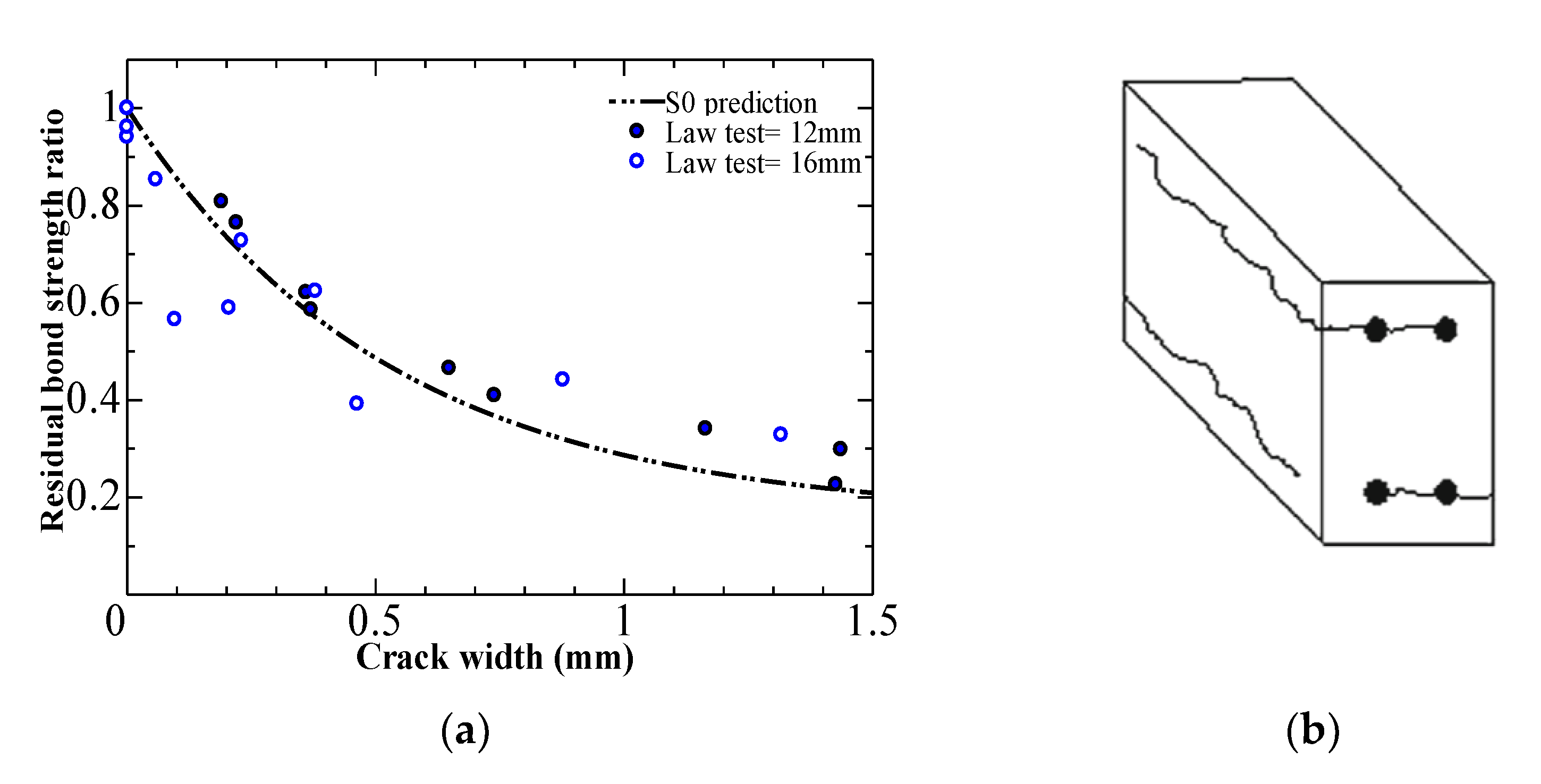
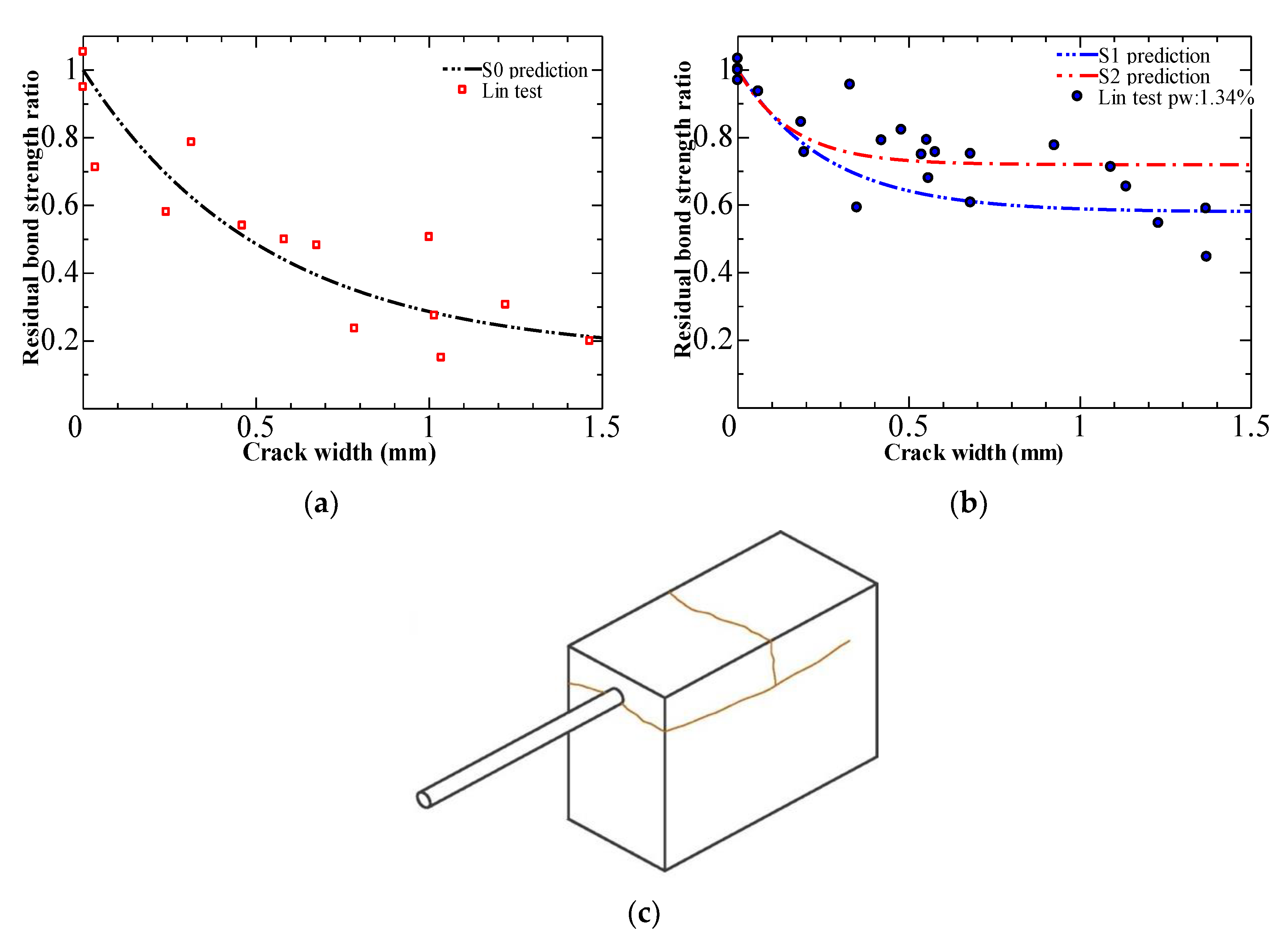
4.3. Comparison of the Proposed Formulas with Experimental Results in the Literature
5. Conclusions
- (1)
- By restraining the induced crack widening, stirrups can significantly limit the bond strength degradation in cracked concrete.
- (2)
- While ignoring the ambiguity related to corrosion product or rate, crack induced by EAFP can quantify the net amount of damage due to corrosion.
- (3)
- The coefficient of variation is 12% for specimens without stirrup from Law et al. And for specimen without and with stirrup from Lin et al., the coefficients of variation are 14% and 17%, respectively. The proposed formulas for bond degradation in cracked concrete can provide a satisfactory prediction
- (4)
- More bond tests based on cracked specimens with smaller stirrup ratios are needed, and the effect on the bond of rebar profile change due to corrosion should be investigated further.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oyado, M.; Kanakubo, T.; Yamamoto, Y.; Kuroiwa, T. Bending Performance of Corroded RC Beams Used for Many Years. In Proceedings of the 2nd Asian Concrete Federation International Conference, Bali, Indonesia, 20–21 November 2006. [Google Scholar]
- Castel, A.; François, R.; Arliguie, G. Mechanical Behaviour of Corroded Reinforced Concrete Beams—Part 1: Experimental Study of Corroded Beams. Mater. Struct. 2000, 33, 539–544. [Google Scholar] [CrossRef]
- Dong, W.; Ye, J.; Murakami, Y.; Oshita, H.; Suzuki, S.; Tsutsumi, T. Residual Load Capacity of Corroded Reinforced Concrete Beam Undergoing Bond Failure. Eng. Struct. 2016, 127, 159–171. [Google Scholar] [CrossRef]
- Cairns, J.; Plizzari, G.A.; Du, Y.; Law, D.W.; Franzoni, C. Mechanical Properties of Corrosion-Damaged Reinforcement. ACI Mater. J. 2005, 102, 256. [Google Scholar]
- Park, R.; Pauley, T. Strength and Deformation of Members with Shear. In Reinforced Concrete Structures; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1975; pp. 270–345. ISBN 978-0-470-17283-4. [Google Scholar]
- Tepfers, R.; Achillides, Z.; Azizinamini, A.; Balázs, G.; Bigaj-van-Vliet, A.; Cabrera, J.; Cairns, J.; Cosenza, E.; den Uijl, J.; Eligehausen, R.; et al. Fib Bulletin 10: Bond of Reinforcement in Concrete; Fib Bulletins; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2000; ISBN 978-2-88394-050-5. [Google Scholar]
- Lin, H.; Zhao, Y.; Feng, P.; Ye, H.; Ozbolt, J.; Jiang, C.; Yang, J.-Q. State-of-the-Art Review on the Bond Properties of Corroded Reinforcing Steel Bar. Constr. Build. Mater. 2019, 213, 216–233. [Google Scholar] [CrossRef]
- Mancini, G.; Tondolo, F. Effect of Bond Degradation Due to Corrosion—a Literature Survey. Struct. Concr. 2014, 15, 408–418. [Google Scholar] [CrossRef]
- Auyeung, Y.; Balaguru, P.; Lan, C. Bond Behavior of Corroded Reinforcement Bars. ACI Mater. J. 2000, 97. [Google Scholar] [CrossRef]
- Tondolo, F. Bond Behaviour with Reinforcement Corrosion. Constr. Build. Mater. 2015, 93, 926–932. [Google Scholar] [CrossRef]
- Hanjari, K.Z.; Coronelli, D.; Lundgren, K. Bond Capacity of Severely Corroded Bars with Corroded Stirrups. Mag. Concr. Res. 2011, 63, 953–968. [Google Scholar] [CrossRef] [Green Version]
- Fang, C.; Lundgren, K.; Chen, L.; Zhu, C. Corrosion Influence on Bond in Reinforced Concrete. Cem. Concr. Res. 2004, 34, 2159–2167. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Yang, J.-Q.; Feng, P.; Ozbolt, J.; Ye, H. Effects of the Corrosion of Main Bar and Stirrups on the Bond Behavior of Reinforcing Steel Bar. Constr. Build. Mater. 2019, 225, 13–28. [Google Scholar] [CrossRef]
- Blomfors, M.; Zandi, K.; Lundgren, K.; Coronelli, D. Engineering Bond Model for Corroded Reinforcement. Eng. Struct. 2018, 156, 394–410. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Ožbolt, J.; Reinhardt, H.-W. Bond Strength Evaluation of Corroded Steel Bars via the Surface Crack Width Induced by Reinforcement Corrosion. Eng. Struct. 2017, 152, 506–522. [Google Scholar] [CrossRef]
- Law, D.W.; Tang, D.; Molyneaux, T.K.C.; Gravina, R. Impact of Crack Width on Bond: Confined and Unconfined Rebar. Mater. Struct. 2011, 44, 1287–1296. [Google Scholar] [CrossRef]
- Fischer, C.; Ožbolt, J. An Appropriate Indicator for Bond Strength Degradation Due to Reinforcement Corrosion. In Proceedings of the 8th International Conference on Fracture Mechanics of Concrete and Concrete Structures, Toledo, Spain, 10–14 March 2013. [Google Scholar]
- Koulouris, K.; Apostolopoulos, C. An Experimental Study on Effects of Corrosion and Stirrups Spacing on Bond Behavior of Reinforced Concrete. Metals 2020, 10, 1327. [Google Scholar] [CrossRef]
- Mak, M.W.T.; Lees, J. Assessment of Corrosion-Induced Bond Deterioration in Reinforced Concrete: Towards a Splitting Crack-Based Approach. In Proceedings of the IABSE Congress—Resilient Technologies for Sustainable Infrastructure, Christchurch, New Zealand, 3–5 February 2021. [Google Scholar]
- Mak, M.W.T.; Desnerck, P.; Lees, J.M. Corrosion-Induced Cracking and Bond Strength in Reinforced Concrete. Constr. Build. Mater. 2019, 208, 228–241. [Google Scholar] [CrossRef]
- Wang, Y.; Geem, Z.W.; Nagai, K. Bond Strength Assessment of Concrete-Corroded Rebar Interface Using Artificial Neutral Network. Appl. Sci. 2020, 10, 4724. [Google Scholar] [CrossRef]
- Yang, Y.; Nakamura, H.; Miura, T.; Yamamoto, Y. Effect of Corrosion-Induced Crack and Corroded Rebar Shape on Bond Behavior. Struct. Concr. 2019, 20, 2171–2182. [Google Scholar] [CrossRef]
- Desnerck, P.; Lees, J.M.; Morley, C.T. Bond Behaviour of Reinforcing Bars in Cracked Concrete. Constr. Build. Mater. 2015, 94, 126–136. [Google Scholar] [CrossRef]
- Brantschen, F.; Faria, D.M.V.; Fernández Ruiz, M.; Muttoni, A. Bond Behaviour of Straight, Hooked, U-Shaped and Headed Bars in Cracked Concrete. Struct. Concr. 2016, 17, 799–810. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Guizani, L.; Ouellet-Plamondon, C.M. On Bond-Slip Response and Development Length of Steel Bars in Pre-Cracked Concrete. Constr. Build. Mater. 2019, 199, 560–573. [Google Scholar] [CrossRef]
- Syll, A.S.; Aburano, T.; Kanakubo, T. Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes. Struct. Concr. 2021, 1–17. [Google Scholar] [CrossRef]
- Aburano, T.; Syll, A.S.; Kanakubo, T. Structural Performance of RC Beams with Induced Corrosion Cracks by Aluminum Pipe Filled with an Expansion Agent. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Bhargava, K.; Ghosh, A.K.; Mori, Y.; Ramanujam, S. Corrosion-Induced Bond Strength Degradation in Reinforced Concrete—Analytical and Empirical Models. Nucl. Eng. Des. 2007, 237, 1140–1157. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y. Effects of Confinements on the Bond Strength between Concrete and Corroded Steel Bars. Constr. Build. Mater. 2016, 118, 127–138. [Google Scholar] [CrossRef]
- Zhou, H.; Lu, J.; Xv, X.; Dong, B.; Xing, F. Effects of Stirrup Corrosion on Bond–Slip Performance of Reinforcing Steel in Concrete: An Experimental Study. Constr. Build. Mater. 2015, 93, 257–266. [Google Scholar] [CrossRef]
- Giuriani, E.; Plizzari, G.; Schumm, C. Role of Stirrups and Residual Tensile Strength of Cracked Concrete on Bond. J. Struct. Eng. 1991, 117, 1–18. [Google Scholar] [CrossRef]
- Yasojima, A.; Kanakubo, T. Bond Splitting Strength of RC Members Based on Local Bond Stress and Slip Behavior. In Proceedings of the 11th International Conference on Fracture, Turin, Italy, 20–25 March 2005. No. 4486. [Google Scholar]
- Yasojima, A.; Kanakubo, T. Local Bond Splitting Behavior of RC Members with Lateral Reinforcement. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. Paper ID 05-03-0033. [Google Scholar]
- Apostolopoulos, C.A.; Koulouris, K.F.; Apostolopoulos, A.C. Correlation of Surface Cracks of Concrete Due to Corrosion and Bond Strength (between Steel Bar and Concrete). Adv. Civ. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Walraven, J. Model Code 2010—First Complete Draft, Volume 2; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2010; ISBN 978-2-88394-095-6. [Google Scholar]






| Series | Specimen Name | Induced Crack Target | Stirrup Spacing (mm) | Stirrup Ratio (%) |
|---|---|---|---|---|
| S0 | S0-C- (crack in mm) | 0.15 mm to 1.0 mm | 0 | 0 |
| S1 | S1-C- (crack in mm) | 0.15 mm to 1.5 mm | 76 * | 1.10 |
| S2 | S2-C- (crack in mm) | 0.15 mm to 1.5 mm | 50 | 1.68 |
| Series (Number of Specimens) | Specimen Name | Induced Crack Width (mm) | At maximum Load | Failure Mode | |
|---|---|---|---|---|---|
| Bond Stress (MPa) | Slip (mm) | ||||
| S0 (10) | S0-C-0.15 | 0.15 | 8.81 | 0.58 | Face split |
| S0-C-0.20 | 0.20 | 6.27 | 0.60 | Face split | |
| S0-C-0.25 | 0.25 | 7.43 | 0.43 | Side split | |
| S0-C-0.30 | 0.30 | 6.21 | 0.46 | Side split | |
| S0-C-0.35 | 0.35 | 7.29 | 0.56 | Side split | |
| S0-C-0.40 | 0.40 | 6.93 | 0.68 | Side split | |
| S0-C-0.50 | 0.50 | 4.97 | 0.65 | Side split | |
| S0-C-0.60 | 0.60 | 4.43 | 0.69 | Side split | |
| S0-C-0.85 | 0.85 | 2.70 | 1.11 | Side split | |
| S0-C-0.95 | 0.95 | 3.69 | 1.04 | Side split | |
| S1 (13) | S1-C-0.15 | 0.15 | 8.77 | 1.00 | Face split |
| S1-C-0.20 | 0.20 | 8.09 | 1.15 | Face split | |
| S1-C-0.40(1) | 0.40 | 7.54 | 0.69 | Face split | |
| S1-C-0.40(2) | 0.40 | 7.10 | 1.36 | Face split | |
| S1-C-0.45 | 0.45 | 7.13 | 1.69 | Face split | |
| S1-C-0.55(1) | 0.55 | 6.66 | 1.49 | Side split | |
| S1-C-0.55(2) | 0.55 | 6.51 | 2.41 | Side split | |
| S1-C-0.60(1) | 0.60 | 7.40 | 0.92 | Side split | |
| S1-C-0.60(2) | 0.60 | 7.84 | 0.85 | Side split | |
| S1-C-0.70 | 0.70 | 8.33 | 1.47 | Side split | |
| S1-C-0.80 | 0.80 | 6.29 | 2.33 | Side split | |
| S1-C-1.10 | 1.10 | 6.07 | 2.27 | Side split | |
| S1-C-1.40 | 1.40 | 5.46 | 2.09 | Side split | |
| S2 (13) | S2-C-0.15 | 0.15 | 9.46 | 1.09 | Face split |
| S2-C-0.20(1) | 0.20 | 7.93 | 2.09 | Face split | |
| S2-C-0.20(2) | 0.20 | 9.01 | 1.03 | Face split | |
| S2-C-0.25 | 0.25 | 7.94 | 1.56 | Face split | |
| S2-C-0.30 | 0.30 | 8.82 | 1.94 | Face split | |
| S2-C-0.35 | 0.35 | 7.82 | 1.34 | Face split | |
| S2-C-0.40(1) | 0.40 | 9.40 | 1.26 | Face split | |
| S2-C-0.40(2) | 0.40 | 9.55 | 1.88 | Face split | |
| S2-C-0.50(1) | 0.50 | 7.84 | 1.37 | Face split | |
| S2-C-0.50(2) | 0.50 | 7.10 | 1.88 | Side split | |
| S2-C-0.50(3) | 0.50 | 8.31 | 1.69 | Side split | |
| S2-C-0.60 | 0.60 | 8.16 | 1.68 | Side split | |
| S2-C-0.70 | 0.70 | 7.36 | 1.29 | Side split | |
| Series | pw (%) | a | b |
|---|---|---|---|
| S0 | 0 | 0.84 | −1.89 |
| S1 | 1.10 | 0.42 | −3.05 |
| S2 | 1.68 | 0.28 | −6.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syll, A.S.; Shimokobe, H.; Kanakubo, T. Effect of Stirrup on Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes. Appl. Sci. 2021, 11, 8874. https://doi.org/10.3390/app11198874
Syll AS, Shimokobe H, Kanakubo T. Effect of Stirrup on Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes. Applied Sciences. 2021; 11(19):8874. https://doi.org/10.3390/app11198874
Chicago/Turabian StyleSyll, Amadou Sakhir, Hiroki Shimokobe, and Toshiyuki Kanakubo. 2021. "Effect of Stirrup on Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes" Applied Sciences 11, no. 19: 8874. https://doi.org/10.3390/app11198874
APA StyleSyll, A. S., Shimokobe, H., & Kanakubo, T. (2021). Effect of Stirrup on Bond Strength Degradation in Concrete Cracked by Expansion Agent Filled Pipes. Applied Sciences, 11(19), 8874. https://doi.org/10.3390/app11198874







