A New Method to Determine the Steel Fibre Content of Existing Structures—Evaluation and Validation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Concrete Mix Design
2.2. Experimental Setup
2.2.1. Basic Setup
2.2.2. Advanced Test Setup for Cylindrical Specimens
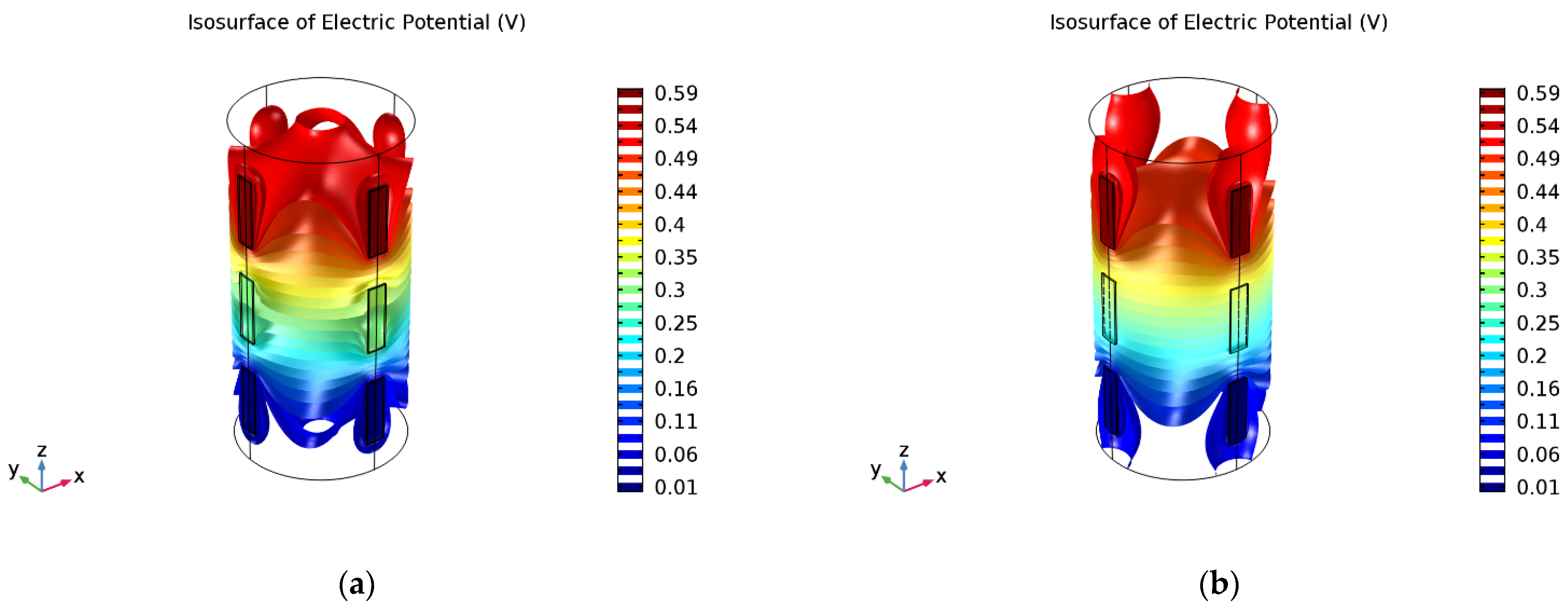
2.3. Modelling of the Current Flow
2.4. Evaluation of the Results
3. Results and Discussion
3.1. Tests on Concrete Cubes as Additional Specimens
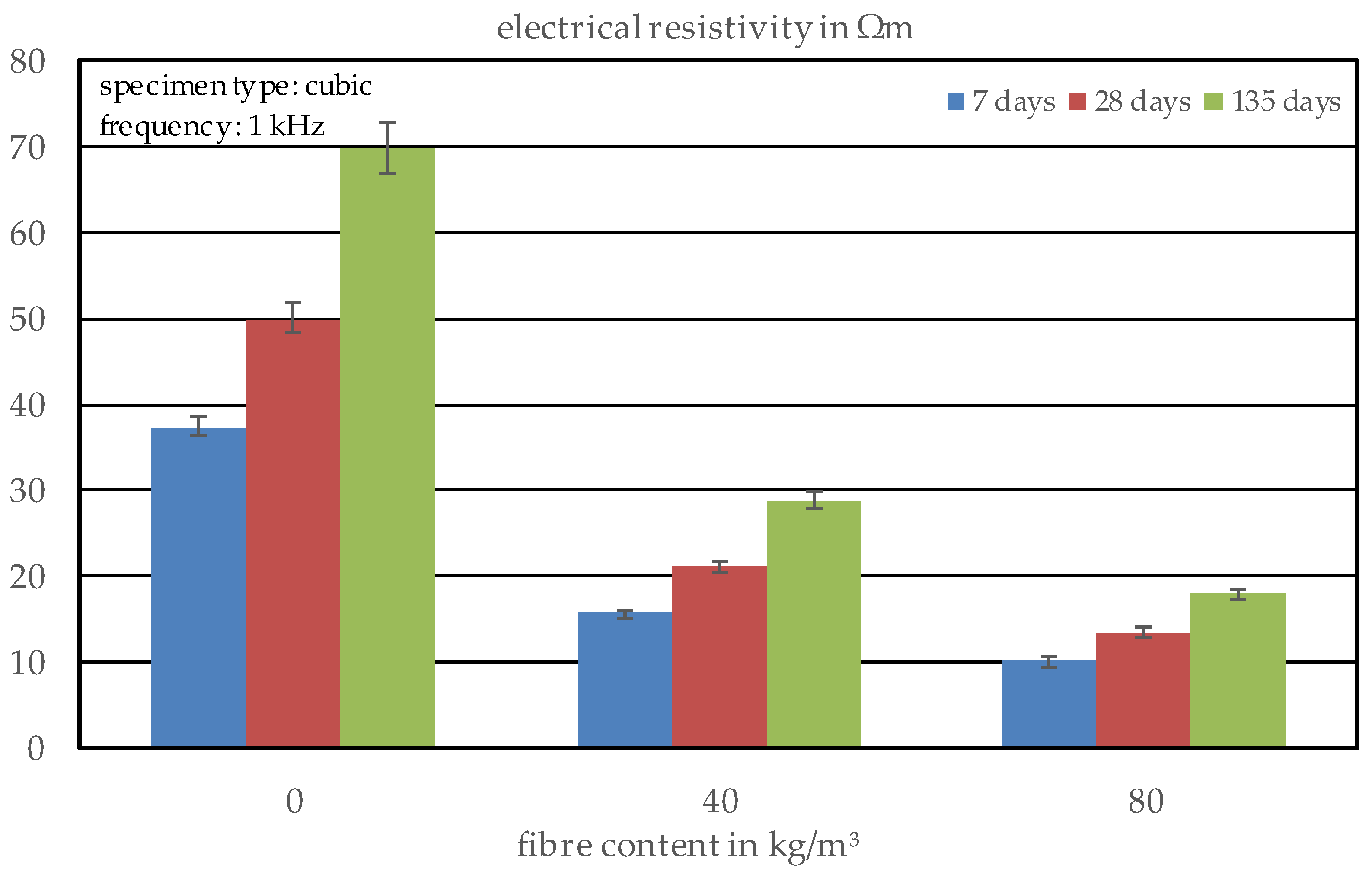
3.1.1. General Evaluation of the Cubic Specimens
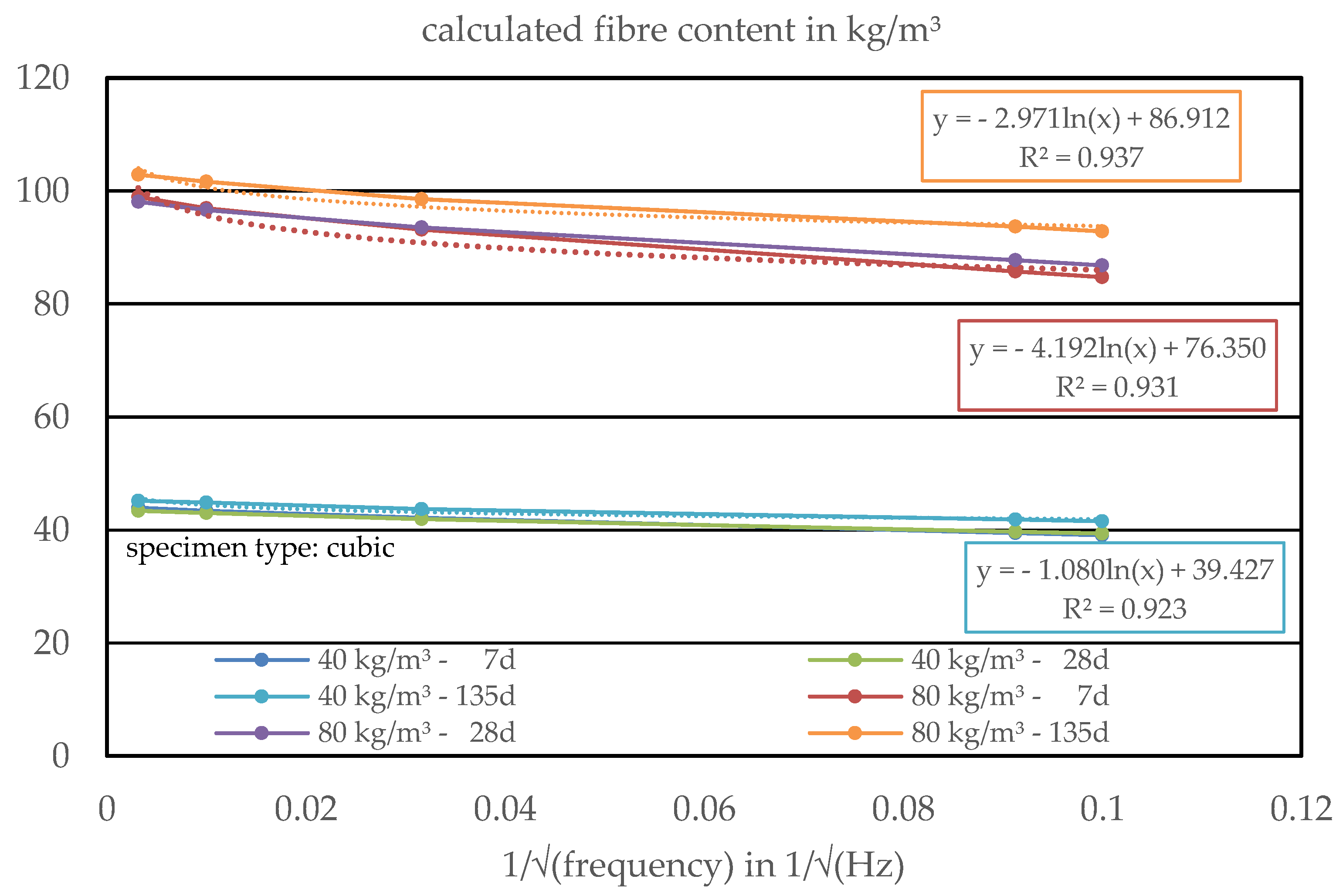
3.1.2. Estimation of the Fibre Content and Orientation
3.2. Testing of Drilling Core Samples
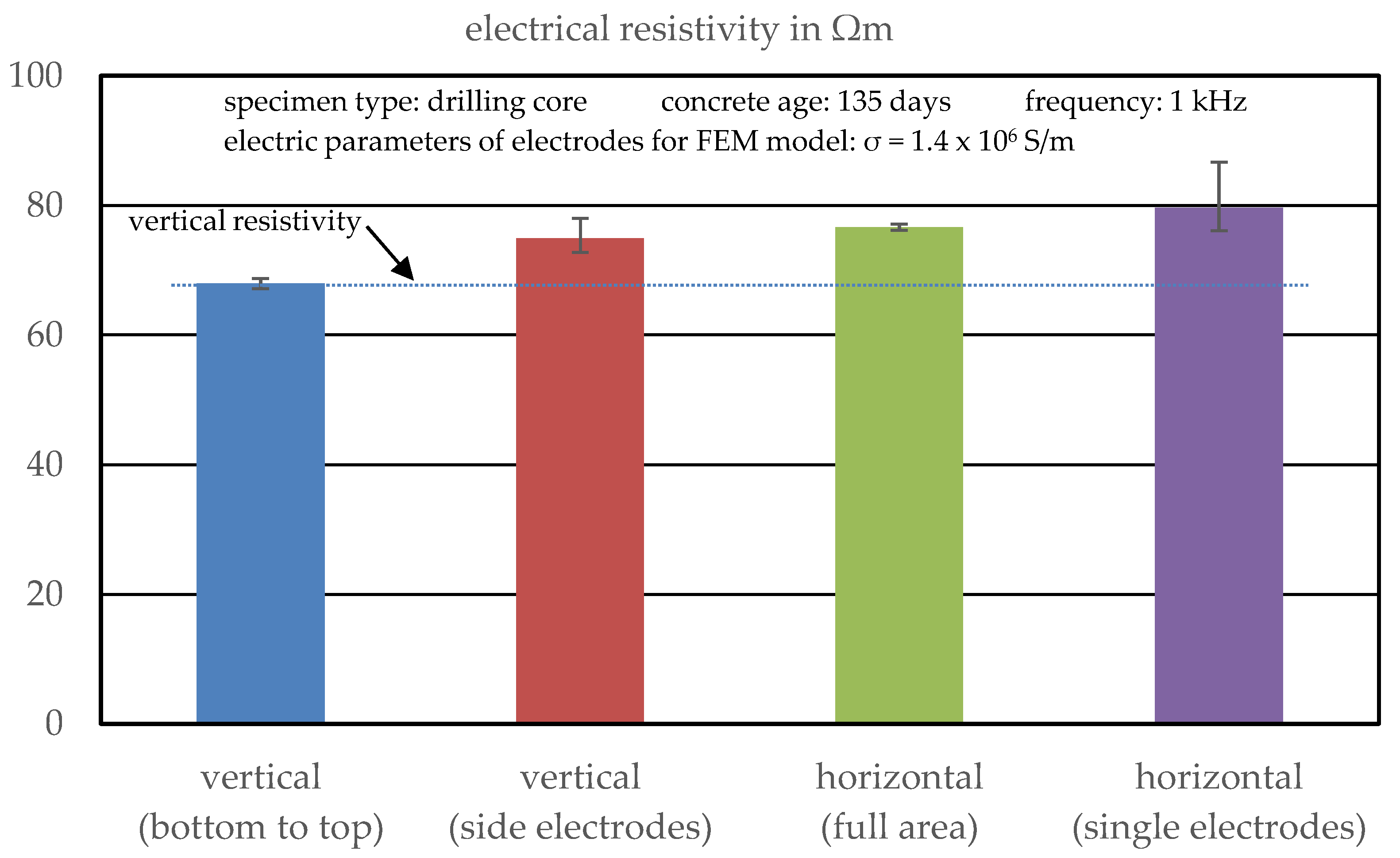
3.2.1. Effect of the k-Value Based on the FEM Model
3.2.2. Statistical Analysis of the Test Results
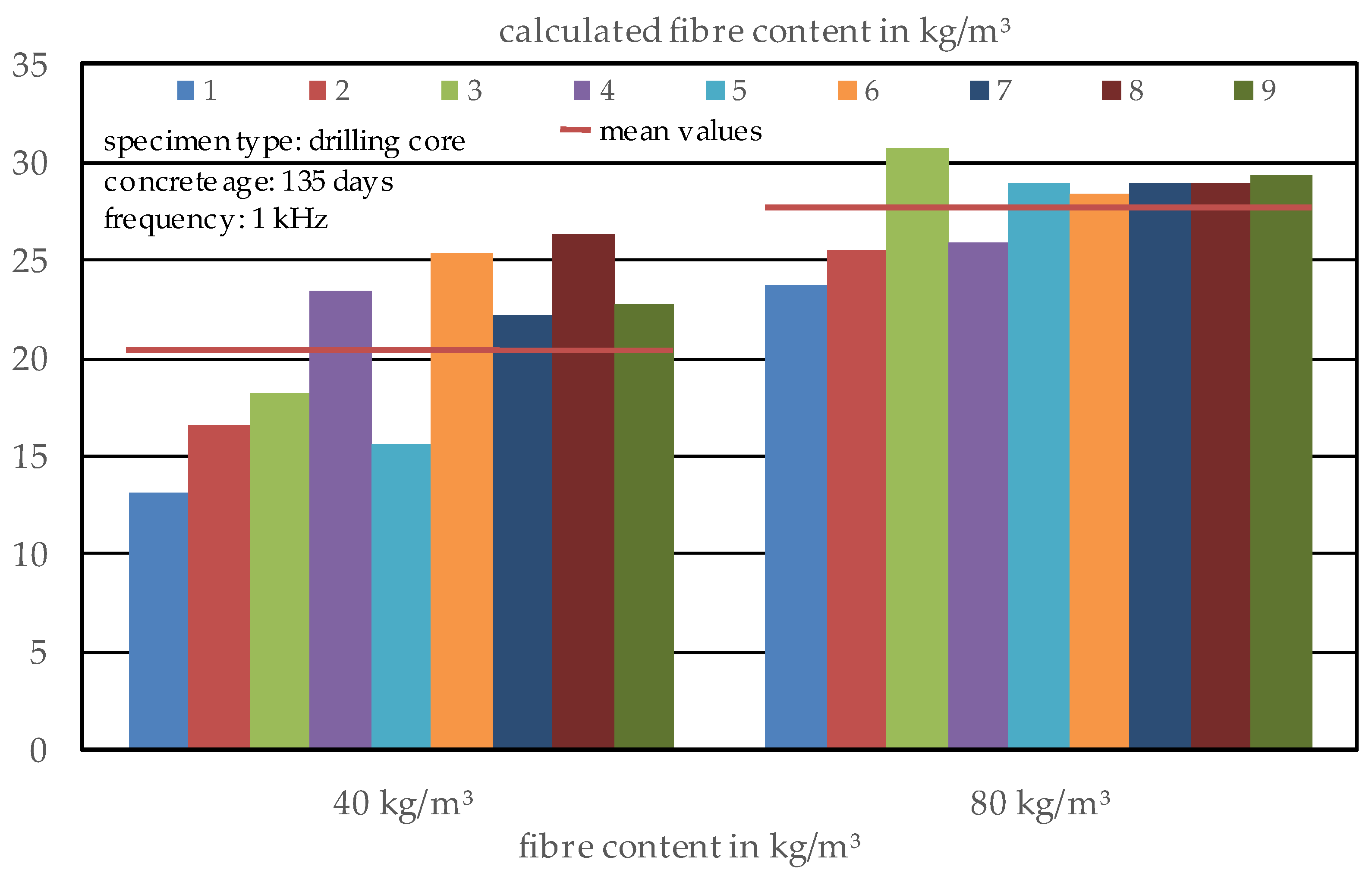
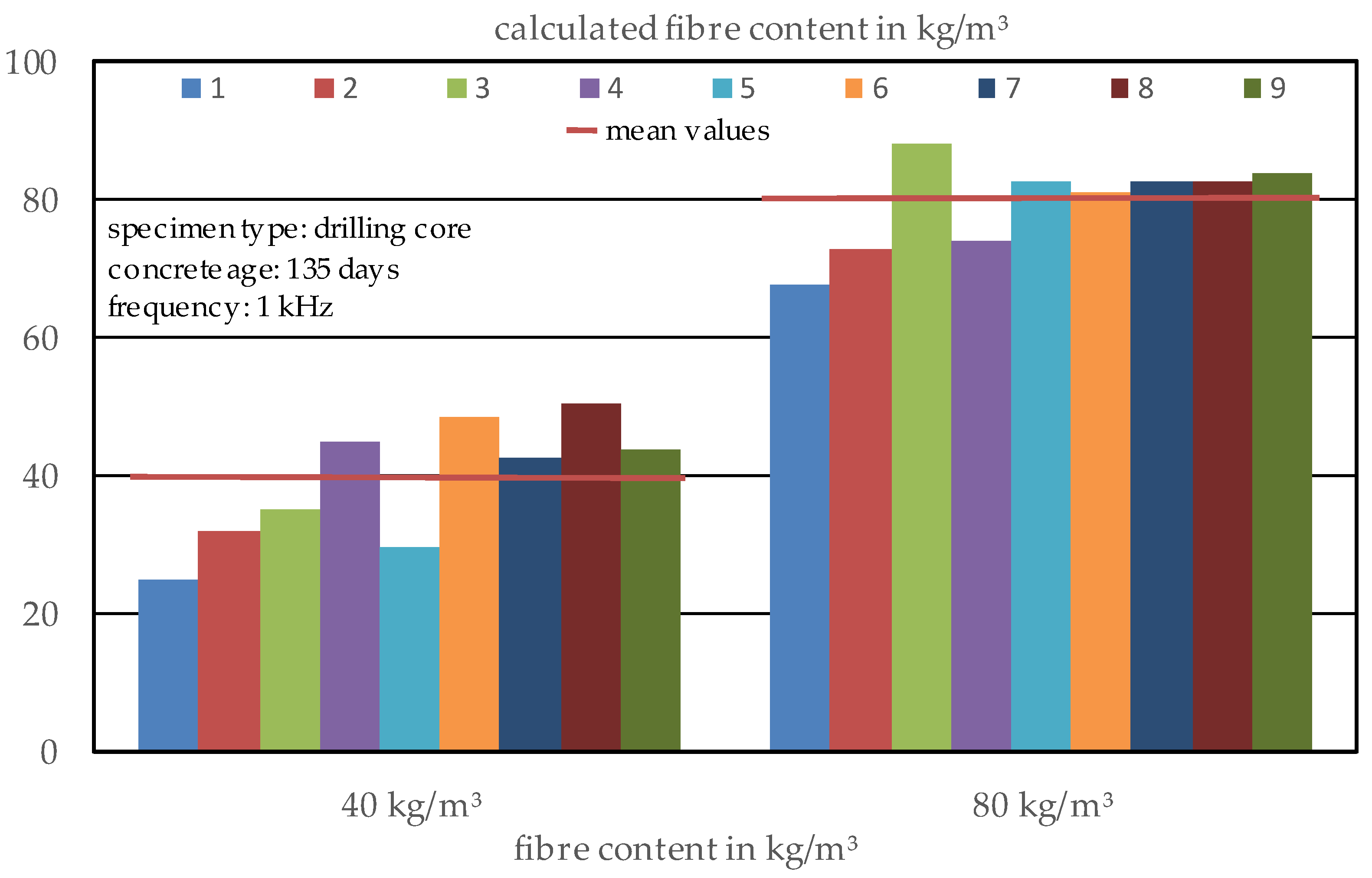
3.2.3. Estimation of the Fibre Content
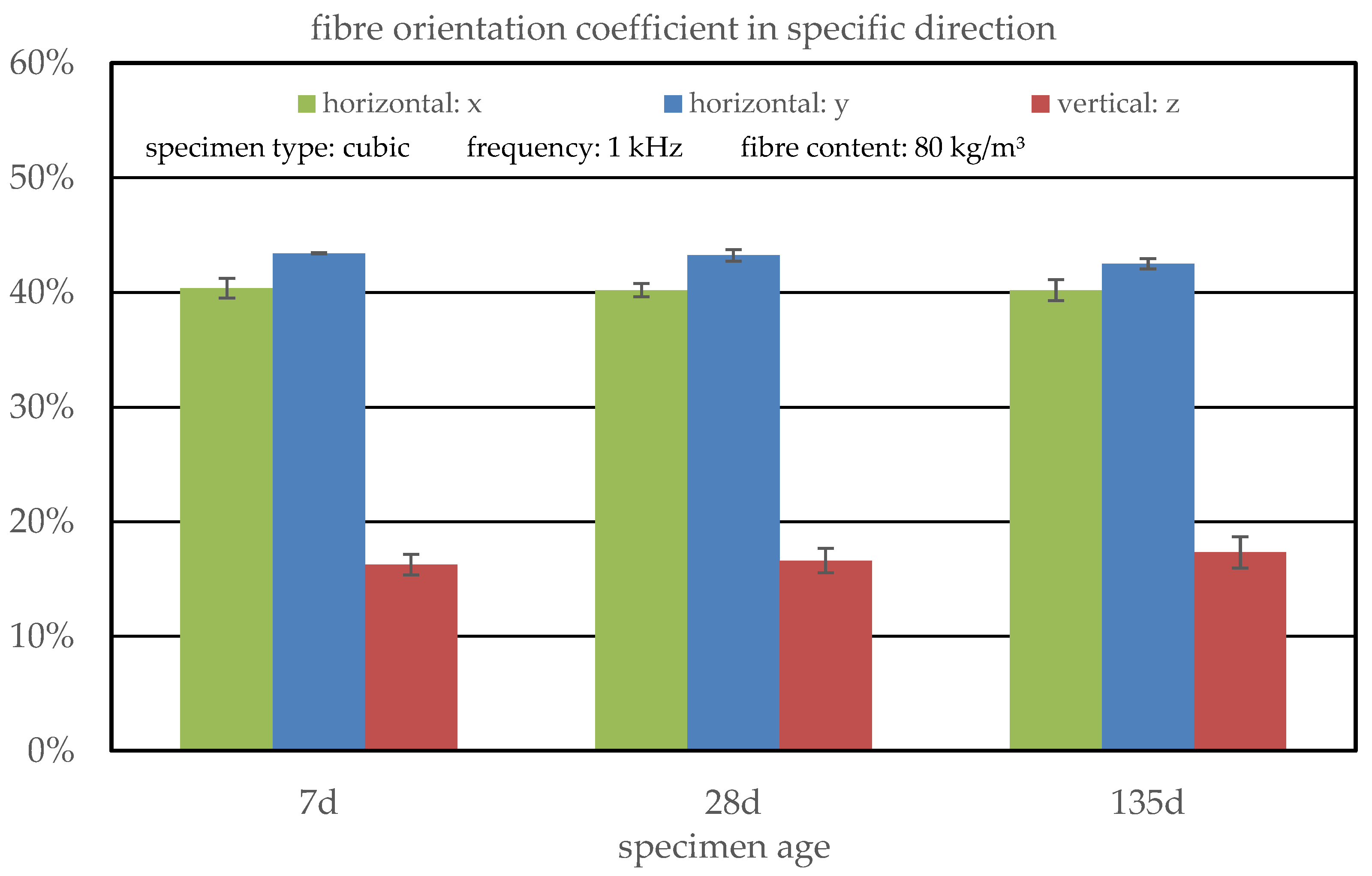
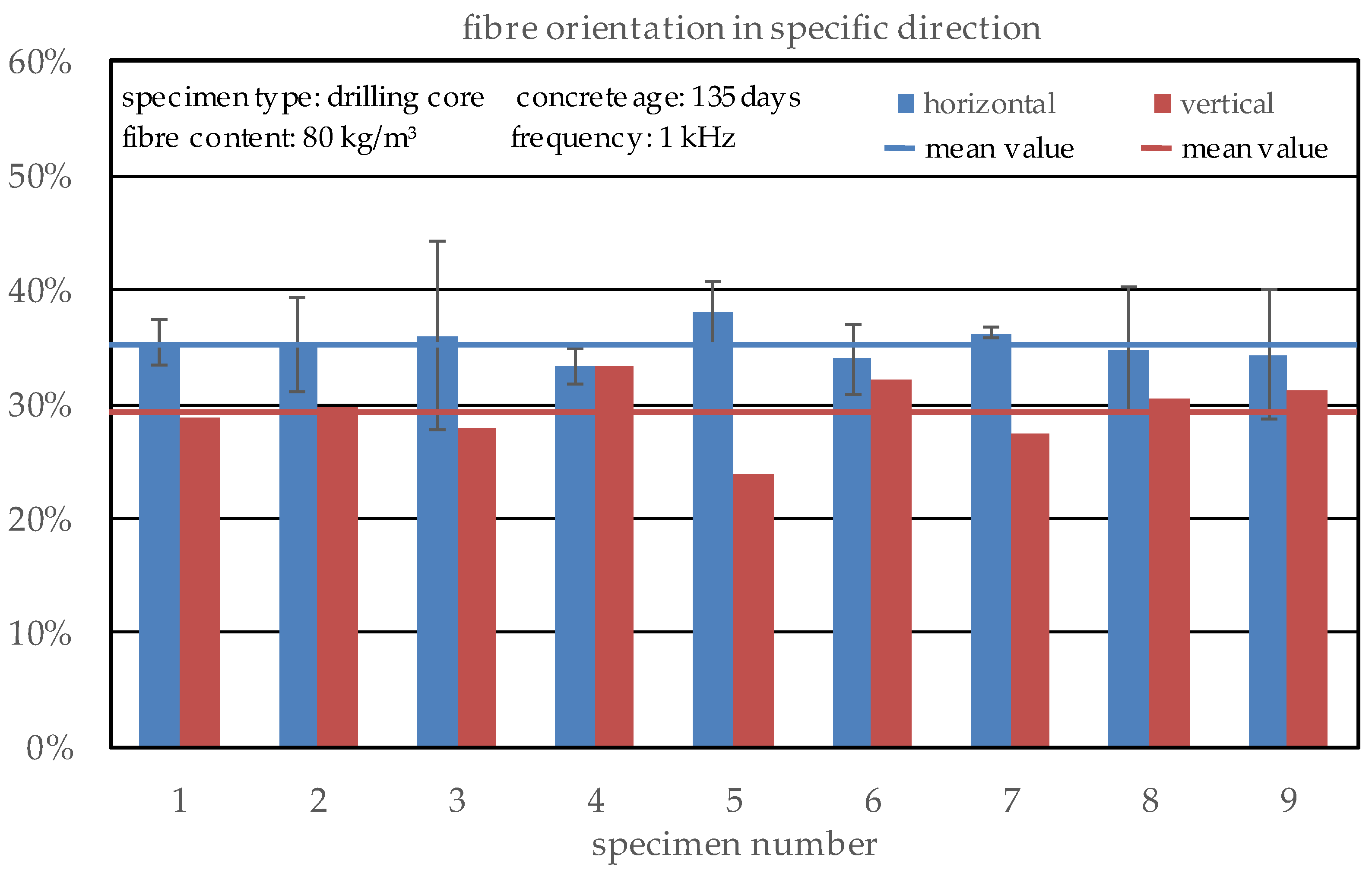
3.2.4. Estimation of the Fibre Orientation
4. Conclusions
- In contrast to AC-IS, the used method, based on electrical resistivity measurements, is much easier to use. However, similar models can be adapted to calculate both fibre content and orientation. One limitation in the application is the small amount of data that is used to calibrate the equations for the calculation of the fibre content for drilling cores which are needed to analyse structural elements or buildings.
- Based on the data gained in this study, a coefficient dependent on the expected value was found to calculate an adjusted fibre aspect ratio as a new coefficient for the literature’s model for specimens with small dimensions where probably a huge number of fibres are truncated through the drilling process and thus the effective fibre length is much smaller than the original one.
- With this coefficient, the fibre content of drilling cores can be estimated in a satisfying way, and thus the basis for the analysis of the fibre content of existing structures in an easy way has been provided. Independent of such a factor, the orientation of the fibres inside a specimen can be calculated comparative from the electrical resistivity in different directions, which can be measured with the cylindrical test setup very easily and fast.
- The results show that the newly developed method is suitable for rapid and non-destructive structural diagnosis based on drilling cores using electrical resistivity measurements.
- In further studies, the authors will focus on the verification of the correlation between the fibre content and the coefficient for adjusting the aspect ratio, especially by a variety of specimen size and fibre lengths. Additionally, different concretes with deviant compositions will be analysed to see if those calculations are applicable in a universal way or if additional adjustments are needed in some cases. Finally, the test setup and the models will be adjusted for several geometries in case of precast elements or existing structural elements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Electrode A | Electrode B | k-Value | ||
|---|---|---|---|---|
| Height Level | Angle | Height Level | Angle | |
| all | 0° | all | 180° | 0.071866 |
| all | 90° | all | 270° | |
| 1 | 0° | 1 | 180° | 0.026653 |
| 1 | 90° | 1 | 270° | |
| 3 | 0° | 3 | 180° | |
| 3 | 90° | 3 | 270° | |
| 2 | 0° | 2 | 180° | 0.027555 |
| 2 | 90° | 2 | 270° | |
| 1 | all | 2 | all | 0.086957 |
| 2 | all | 3 | all | |
| 1 | all | 3 | all | 0.054714 |
| Electrode A | Electrode B | k-Value | ||
|---|---|---|---|---|
| Height Level | Angle | Height Level | Angle | |
| all | 0° | all | 180° | 0.063497 |
| all | 90° | all | 270° | |
| 1 | 0° | 1 | 180° | 0.023066 |
| 1 | 90° | 1 | 270° | |
| 3 | 0° | 3 | 180° | |
| 3 | 90° | 3 | 270° | |
| 2 | 0° | 2 | 180° | 0.023768 |
| 2 | 90° | 2 | 270° | |
| 1 | all | 2 | all | 0.076614 |
| 2 | all | 3 | all | |
| 1 | all | 3 | all | 0.048069 |
References
- Cleven, S.; Raupach, M.; Matschei, T. Electrical Resistivity of Steel Fibre-Reinforced Concrete—Influencing Parameters. Materials 2021, 14, 3408. [Google Scholar] [CrossRef] [PubMed]
- Cleven, S.; Raupach, M.; Matschei, T. A New Method to Determine the Steel Fibre Content of Existing Structures—Test Setup and Numerical Simulation. Appl. Sci. 2022, 12, 561. [Google Scholar] [CrossRef]
- Gettu, R.; Gardner, D.R.; Saldívar, H.; Barragán, B.E. Study of the distribution and orientation of fibers in SFRC specimens. Mater. Struct. Mater. Constr. 2005, 38, 31–37. [Google Scholar] [CrossRef]
- Gouri Mohan, L.; Nazeer, M.; Nizad, A.; Suresh, S. Fibre reinforced concrete—A state-of-the-art review. Int. J. Earth Sci. Eng. 2010, 3, 634–642. [Google Scholar]
- Martinelli, P.; Colombo, M.; Pujadas, P.; De la Fuente, A.; Cavalaro, S.; Di Prisco, M. Characterization tests for predicting the mechanical performance of SFRC floors: Identification of fibre distribution and orientation effects. Mater. Struct. Mater. Constr. 2021, 54, 1–16. [Google Scholar] [CrossRef]
- Molins, C.; Aguado, A.; Saludes, S. Double Punch Test to control the energy dissipation in tension of FRC (Barcelona test). Mater. Struct. 2008, 42, 415–425. [Google Scholar] [CrossRef] [Green Version]
- Barnett, S.J.; Lataste, J.; Parry, T.; Millard, S.G.; Soutsos, M.N. Assessment of fibre orientation in ultra high performance fibre reinforced concrete and its effect on flexural strength. Mater. Struct. Mater. Constr. 2010, 43, 1009–1023. [Google Scholar] [CrossRef]
- Kobaka, J.; Katzer, J.; Ponikiewski, T.A. combined electromagnetic induction and radar-based test for quality control of steel fibre reinforced concrete. Materials 2019, 12, 3507. [Google Scholar] [CrossRef] [Green Version]
- Luo, T.; Zhang, C.; Sun, C.; Zheng, X.; Ji, Y.; Yuan, X. Experimental investigation on the freeze–thaw resistance of steel fibers reinforced rubber concrete. Materials 2020, 13, 1260. [Google Scholar] [CrossRef] [Green Version]
- Rossi, B.; Wolf, S. Steel fibre reinforced concrete for the future of tunnel lining segments—A durable solution. In Proceedings of the Tunnels and Underground Cities: Engineering and Innovation Meet Archaeology, Architecture and Art; CRC Press: Boca Raton, FL, USA, 2019; Volume 1, pp. 2978–2985. [Google Scholar] [CrossRef]
- Woo, L.Y.; Wansom, S.; Ozyurt, N.; Mu, B.; Shah, S.P.; Mason, T.O. Characterizing fiber dispersion in cement composites using AC-Impedance Spectroscopy. Cem. Concr. Compos. 2005, 27, 627–636. [Google Scholar] [CrossRef]
- Zak, G.; Park, C.B.; Benhabib, B. Estimation of Three-Dimensional Fibre-Orientation Distribution in Short-Fibre Composites by a Two-Section Method. J. Compos. Mater. 2000, 35, 316–339. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Q.; Chen, Y.; Shi, Y.; Ling, Y. Durability of steel fiber-reinforced concrete containing SiO2 nano-particles. Materials 2019, 12, 2184. [Google Scholar] [CrossRef] [Green Version]
- Cugat, V.; Cavalaro, S.H.P.; Bairán, J.M.; de la Fuente, A. Safety format for the flexural design of tunnel fibre reinforced concrete precast segmental linings. Tunn. Undergr. Space Technol. 2020, 103, 103500. [Google Scholar] [CrossRef]
- Herrmann, H.; Boris, R.; Goidyk, O.; Braunbrück, A. Variation of bending strength of fiber reinforced concrete beams due to fiber distribution and orientation and analysis of microstructure. In Proceedings of the IOP Conference Series: 4th International Conference on Innovative Materials, Structures and Technologies (IMST 2019), Riga, Latvia, 25–27 September 2019; IOP Publishing: Bristol, UK, 2019; Volume 660, p. 012059. [Google Scholar] [CrossRef]
- Tarawneh, A.; Almasabha, G.; Alawadi, R.; Tarawneh, M. Innovative and reliable model for shear strength of steel fibers reinforced concrete beams. Structures 2021, 32, 1015–1025. [Google Scholar] [CrossRef]
- Plizzari, G.A. Fiber reinforced concrete for repairing and strengthening RC structures: Some recent advancements. In Proceedings of the MATEC Web Conference, International Conference on Concrete Repair, Rehabilitation and Retrofitting (ICCRRR 2018), Cape Town, South Africa, 19–21 November 2018; Volume 199. [Google Scholar] [CrossRef]
- Balázs, G.L.; Czoboly, O.; Lublóy, É.; Kapitány, K.; Barsi, Á. Observation of steel fibres in concrete with computed tomography. Constr. Build. Mater. 2017, 140, 534–541. [Google Scholar] [CrossRef]
- Ferrara, L.; Faifer, M.; Toscani, S. A magnetic method for non destructive monitoring of fiber dispersion and orientation in steel fiber reinforced cementitious composites—part 1: Method calibration. Mater. Struct. 2012, 45, 575–589. [Google Scholar] [CrossRef]
- Komárková, T. Design of Methodology for Non-Destructive Testing of Steel-Reinforced-Fiber-Concrete. Key Eng. Mater. 2016, 714, 179–185. [Google Scholar] [CrossRef]
- Lataste, J.F.; Behloul, M.; Breysse, D. Characterisation of fibres distribution in a steel fibre reinforced concrete with electrical resistivity measurements. NDT E Int. 2008, 41, 638–647. [Google Scholar] [CrossRef]
- Lee, S.; Oh, J.; Cho, J. Fiber orientation factor on rectangular cross-section in concrete members. Int. J. Eng. Technol. 2015, 7, 470–473. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Xia, J.; Chin, C.; Jones, S. Fibre distribution characterization of ultra-high performance fibre-reinforced concrete (uhpfrc) plates using magnetic probes. Materials 2020, 13, 5064. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ruan, X.; Akiyama, M.; Zhang, M.; Xin, J.; Lim, S. Modelling method of fibre distribution in steel fibre reinforced concrete based on X-ray image recognition. Compos. Part B Eng. 2021, 223, 109124. [Google Scholar] [CrossRef]
- Mattarneh, A.-H. Electromagnetic quality control of steel fiber concrete. Constr. Build. Mater. 2014, 73, 350–356. [Google Scholar] [CrossRef]
- Park, T.; Her, S.; Jee, H.; Yoon, S.; Cho, B.; Hwang, S.; Bae, S. Evaluation of orientation and distribution of steel fibers in high-performance concrete column determined via micro-computed tomography. Constr. Build. Mater. 2021, 270. [Google Scholar] [CrossRef]
- Ponikiewski, T.; Katzer, J. X-ray computed tomography of fibre reinforced self-compacting concrete as a tool of assessing its flexural behaviour. Mater. Struct. /Mater. Constr. 2016, 49, 2131–2140. [Google Scholar] [CrossRef] [Green Version]
- Torrents, J.M.; Blanco, A.; Pujadas, P.; Aguado, A.; Juan-García, P.; Sánchez-Moragues, M.Á. Inductive method for assessing the amount and orientation of steel fibers in concrete. Mater. Struct. Mater. Constr. 2012, 45, 1577–1592. [Google Scholar] [CrossRef] [Green Version]
- Woo, L.Y.; Kidner, N.J.; Wansom, S.; Mason, T.O. Combined Time Domain Reflectometry and AC-Impedance Spectroscopy of Fiber-Reinforced Fresh-Cement Composites. Cem. Concr. Res. 2007, 37, 89–95. [Google Scholar] [CrossRef]
- Testing Fresh Concrete—Part 5: Flow Table Test; German Version EN 12350-5:2019; DIN EN 12350-5:2019-09; Beuth Publishing DIN: Berlin, Germany, 2019. [CrossRef]
- Testing Fresh Concrete—Part 6: Density; German Version EN 12350-6:2019; DIN EN 12350-6:2019-09; Beuth Publishing DIN: Berlin, Germany, 2019. [CrossRef]
- Testing Fresh Concrete—Part 7: Air Content—Pressure Methods; German Version EN 12350-7:2019; DIN EN 12350-7:2019-09; Beuth Publishing DIN: Berlin, Germany, 2019. [CrossRef]
- Reichling, K.; Raupach, M. Measurement and visualisation of the actual concrete resistivity in consideration of conductive layers and reinforcement bars. In Rehabilitation and Retrofitting III, Proceedings of the 3rd International Conference on Concrete Repair, Rehabilitation and Retrofitting, Cape Town, South Africa, 3–5 September 2018; Taylor Francis Group: Abingdon, UK, 2012; pp. 707–714. [Google Scholar]






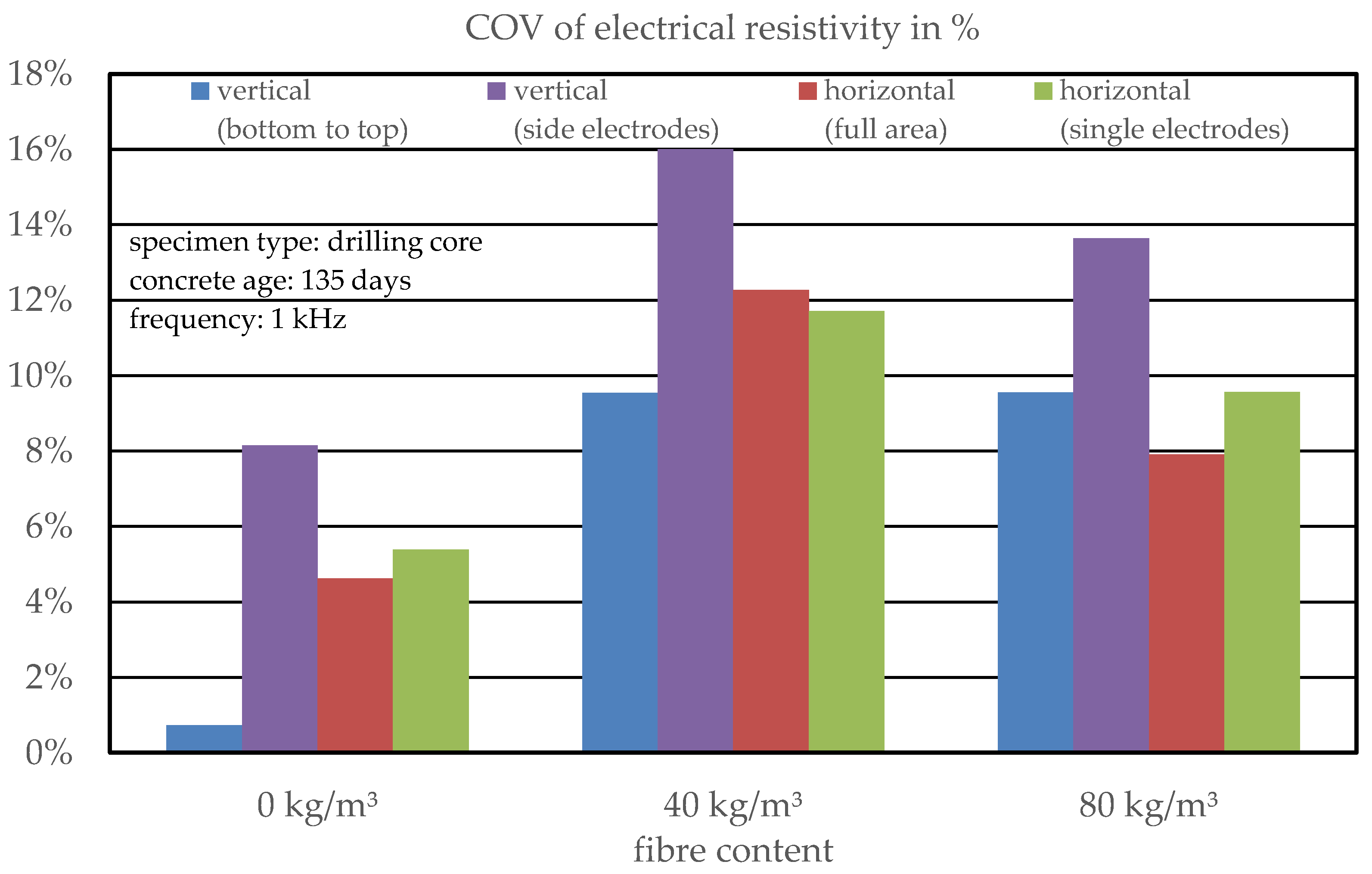

| Parameter | Unit | 32-60-300-00 |
|---|---|---|
| CEM I 32.5 R | kg/m3 | 300.0 |
| Water | kg/m3 | 180.0 |
| Sand 0–4 mm | kg/m3 | 845.5 |
| Gravel 4–16 mm | kg/m3 | 1004.0 |
| Water/cement ratio | - | 0.60 |
| Grain size distribution | - | A/B16 |
| Steel fibre type | - | Macrofibre 60 mm |
| Steel fibre content | kg/m3 | 0, 40, 80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cleven, S.; Raupach, M.; Matschei, T. A New Method to Determine the Steel Fibre Content of Existing Structures—Evaluation and Validation. Appl. Sci. 2022, 12, 454. https://doi.org/10.3390/app12010454
Cleven S, Raupach M, Matschei T. A New Method to Determine the Steel Fibre Content of Existing Structures—Evaluation and Validation. Applied Sciences. 2022; 12(1):454. https://doi.org/10.3390/app12010454
Chicago/Turabian StyleCleven, Simon, Michael Raupach, and Thomas Matschei. 2022. "A New Method to Determine the Steel Fibre Content of Existing Structures—Evaluation and Validation" Applied Sciences 12, no. 1: 454. https://doi.org/10.3390/app12010454
APA StyleCleven, S., Raupach, M., & Matschei, T. (2022). A New Method to Determine the Steel Fibre Content of Existing Structures—Evaluation and Validation. Applied Sciences, 12(1), 454. https://doi.org/10.3390/app12010454







