Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction
Abstract
:1. Introduction
2. The Dynamic Model and Numerical Methodology
2.1. The Equation of Motion
2.2. Discretization of the System Model
3. Results and Discussion
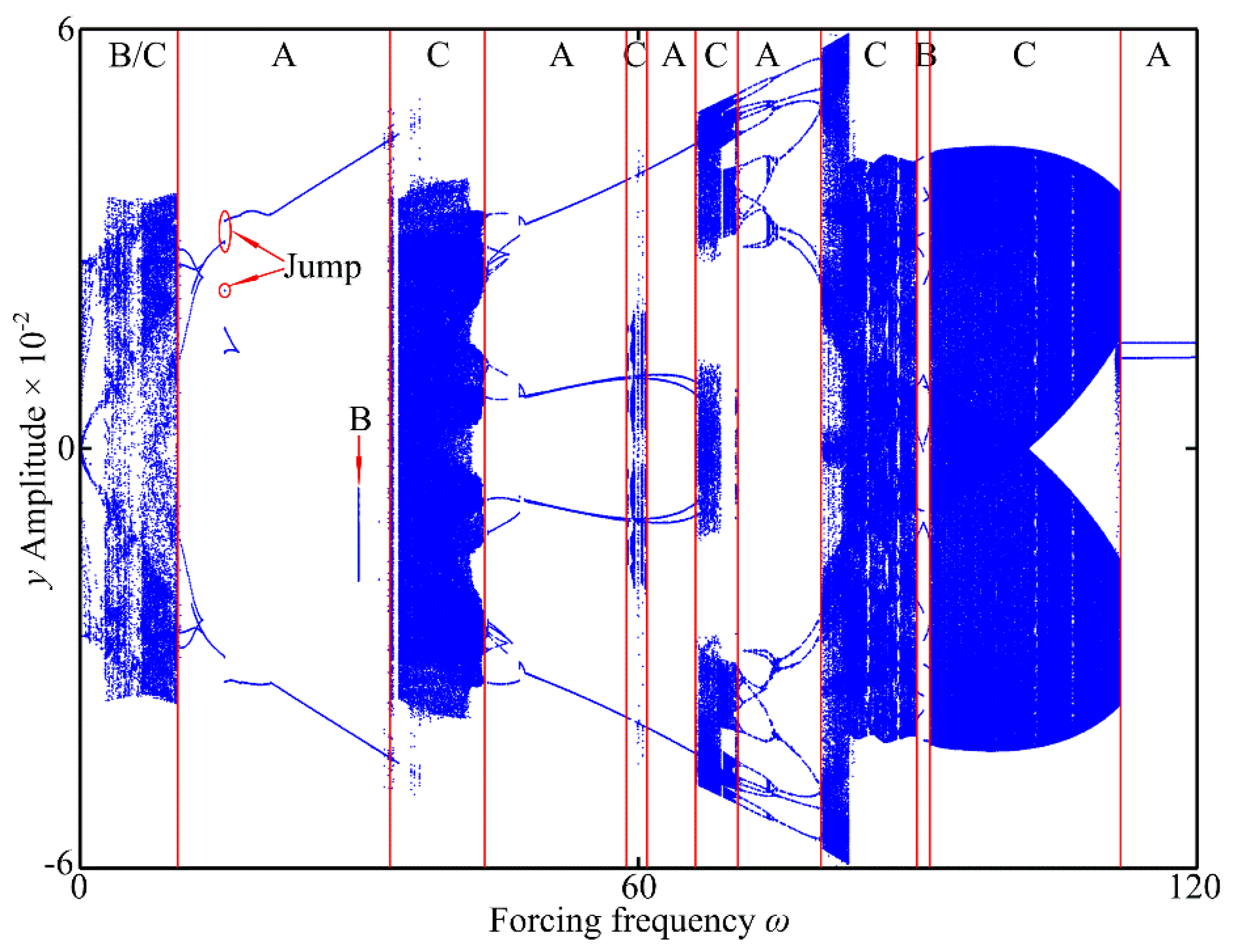
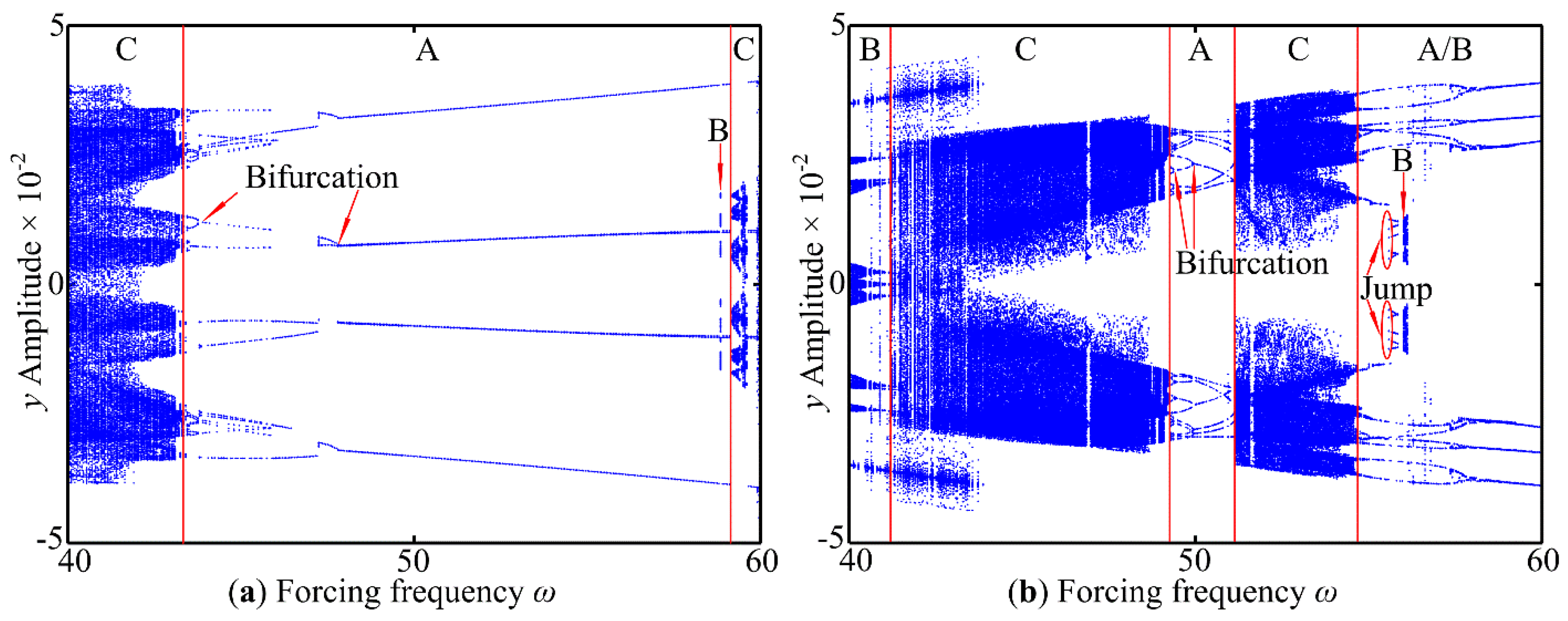
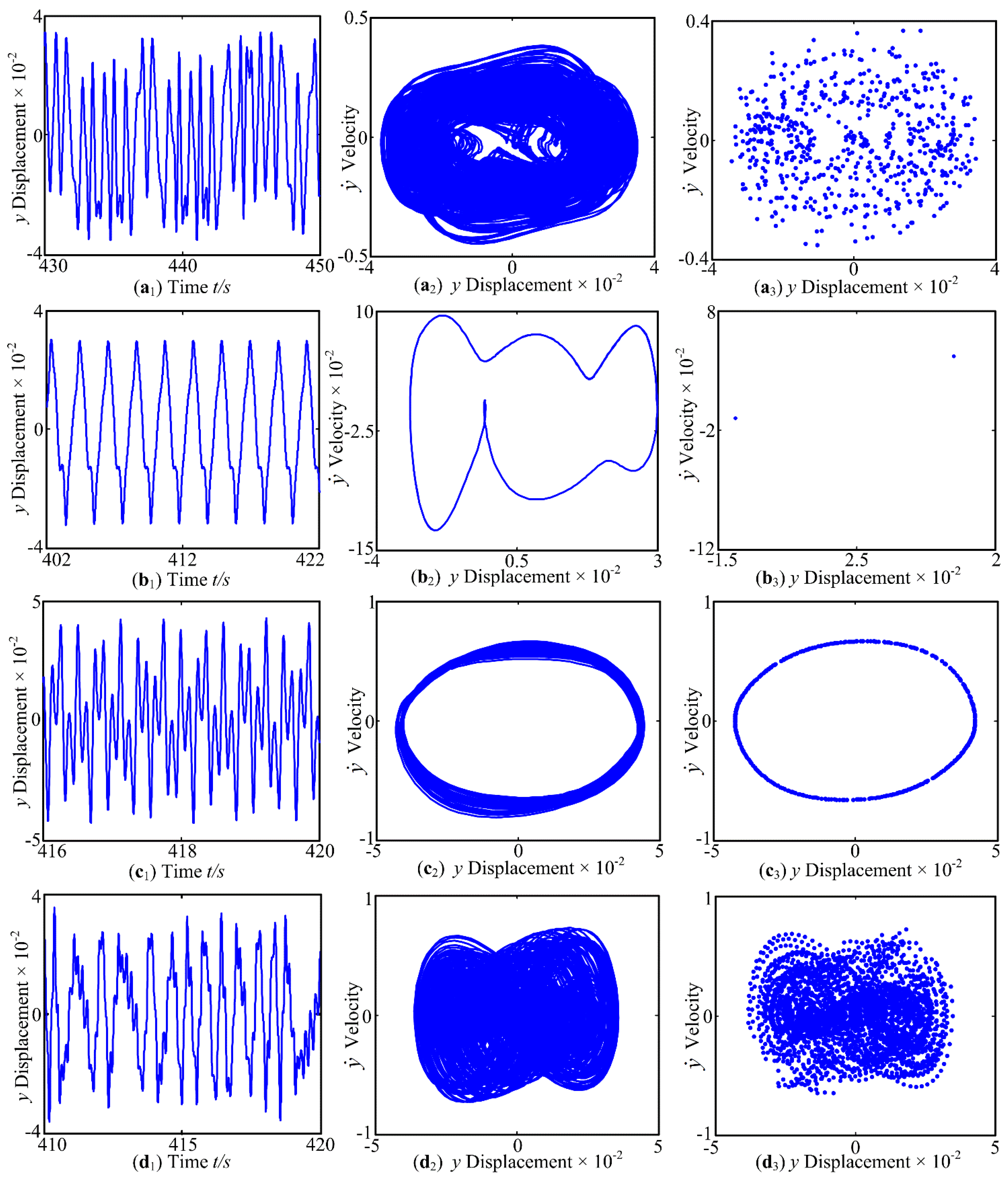
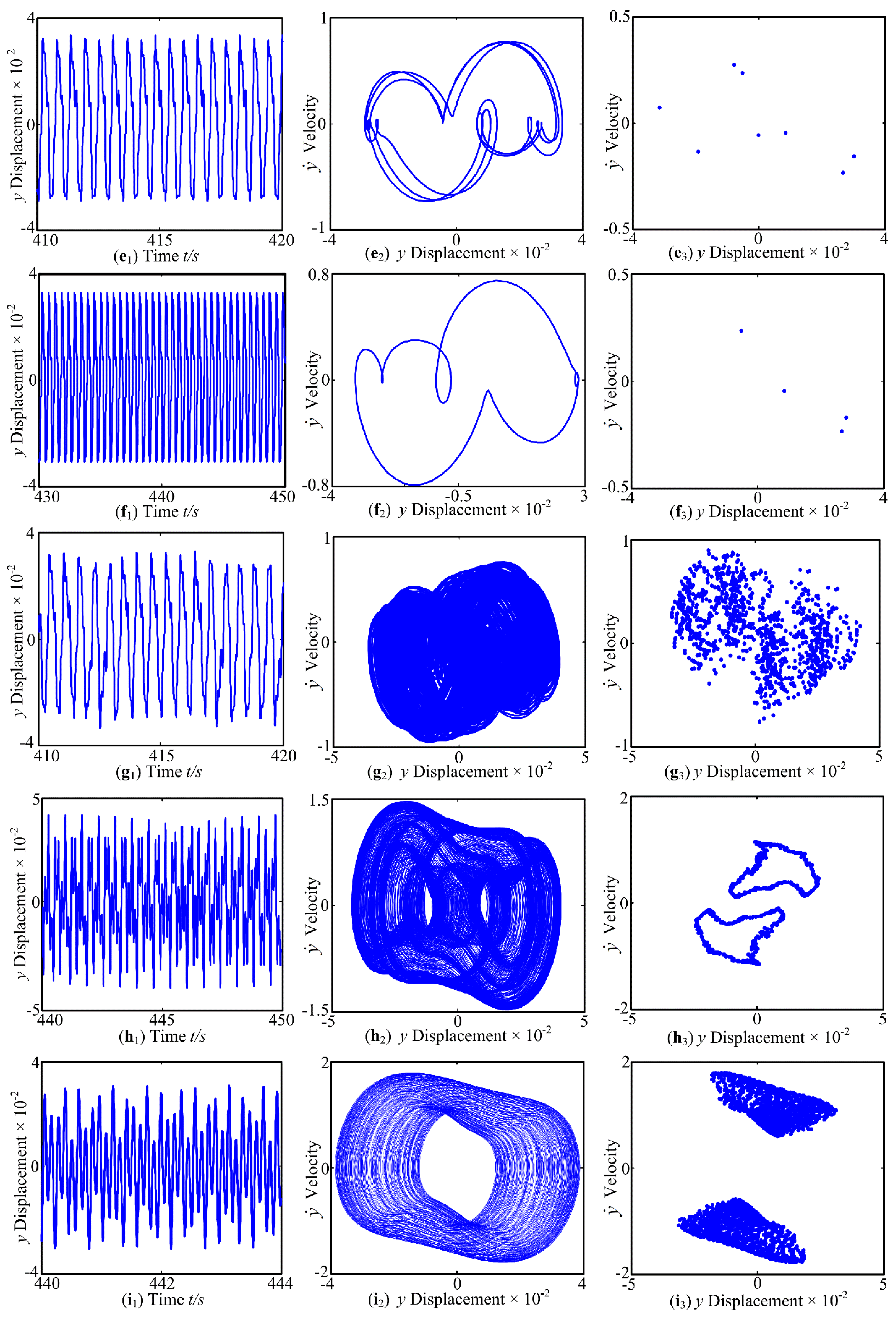
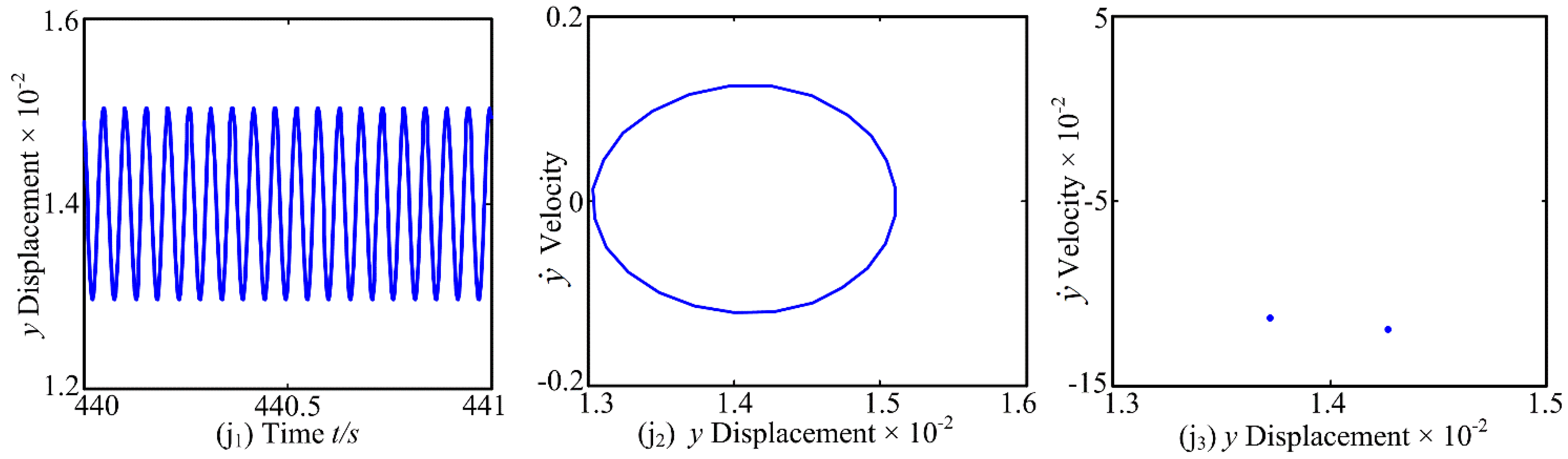
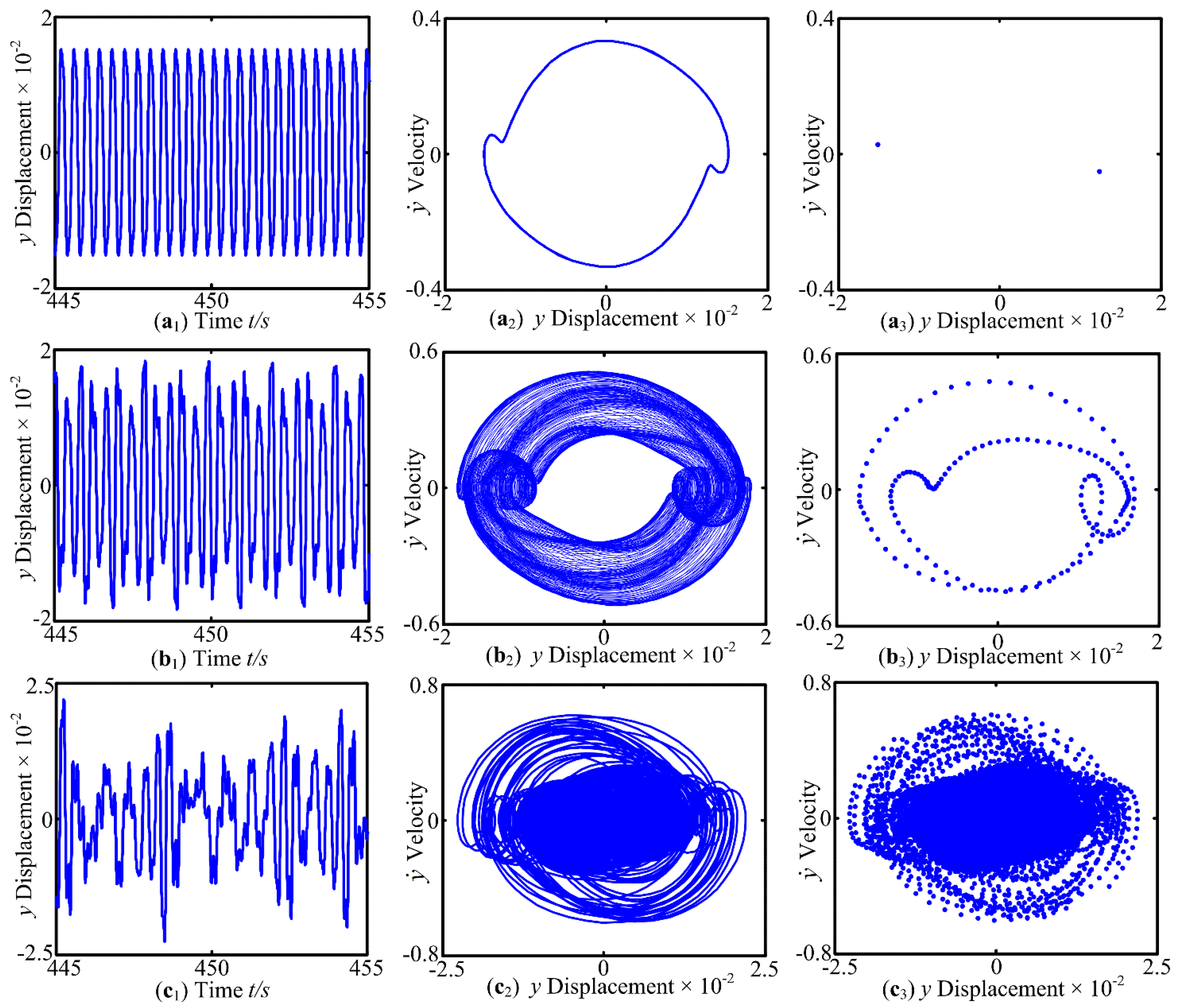
3.1. The Effect of Forcing Frequency ω on Dynamic Characteristics
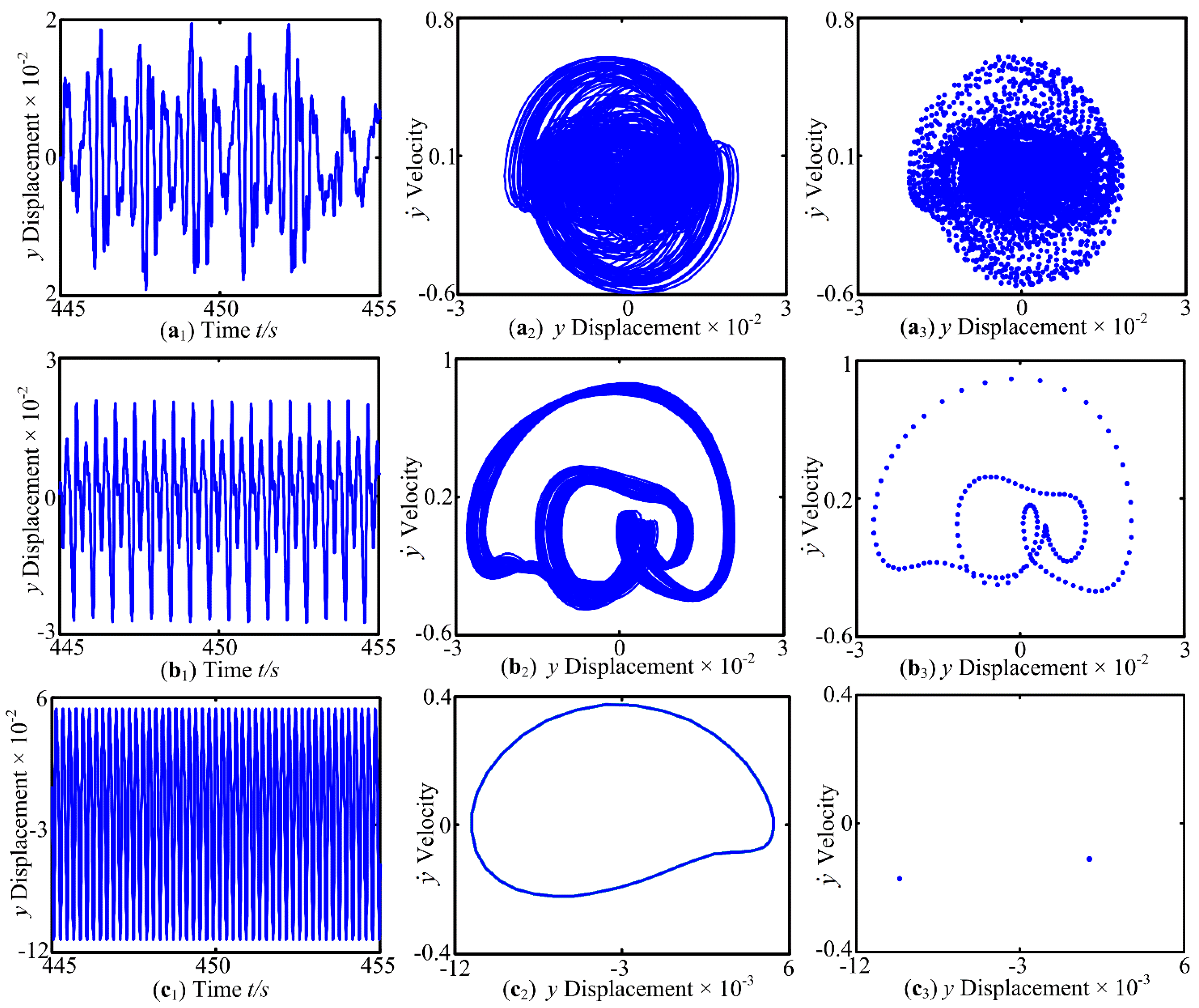
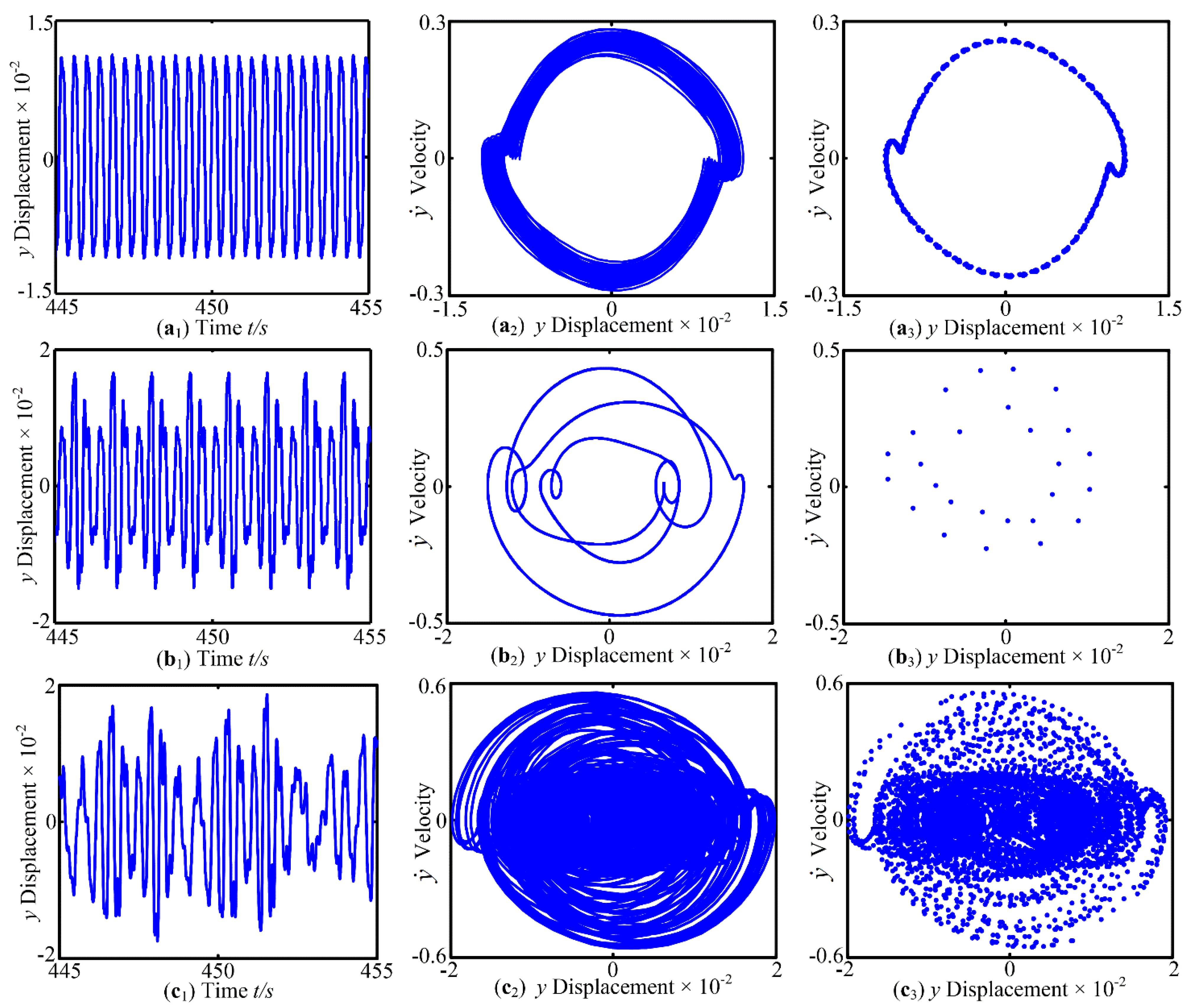
3.2. The Effect of Perturbation Amplitude μ on Dynamic Characteristics
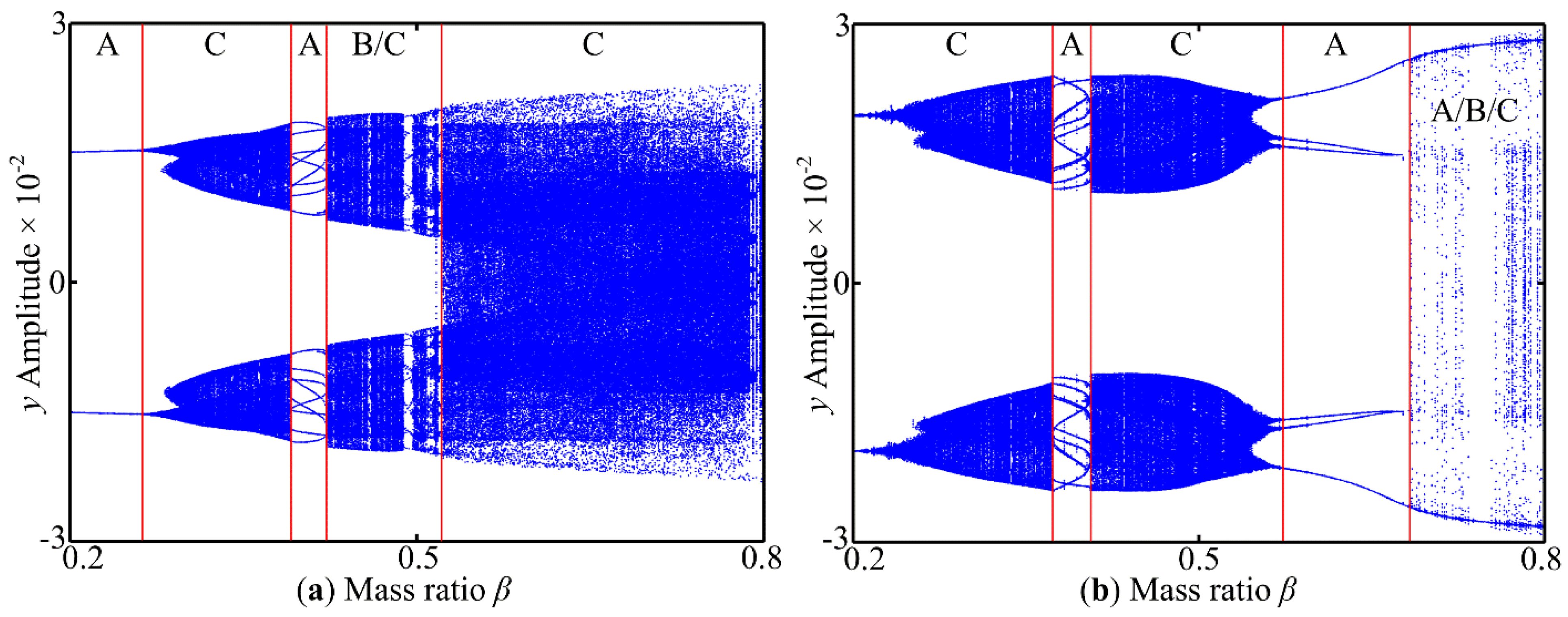
3.3. The Effect of Mass Ratio β on Dynamic Characteristics
3.4. The Effect of Flow Velocity u0 on Dynamic Characteristics
4. Conclusions
- (1)
- Under the control parameter of forcing frequency ω, the vibration system exhibits periodic motion, quasi-periodic motion and chaotic behavior, and the phenomenon of jumping discontinuity appears. In addition, a period-doubling reverse bifurcation from chaotic motion to periodic motion is exhibited. The support stiffness causes a change in the inherent characteristics, which has an impact on the dynamic of the system.
- (2)
- With the increase in the perturbation amplitude μ, the periodic motion, quasi-periodic motion, chaotic behavior, jump discontinuity phenomenon and period-doubling bifurcations phenomenon of the system are transformed. In addition, under certain combinations of supporting stiffness, the region of chaotic motion becomes smaller and the area of periodic motion grows. The support stiffness can, to a certain extent, cause a change of the inherent characteristics of the system.
- (3)
- As mentioned above, with the increase in the mass ratio β and flow velocity u0, the intensity of chaotic motion increases, and the system exhibits periodic and quasi-periodic responses and chaotic motion. Moreover, under certain combinations of supporting stiffness, periodic motion increases and the chaotic region shrinks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghasemloonia, A.; Rideout, D.G.; Butt, S.D. A review of drillstring vibration modeling and suppression methods. J. Pet. Sci. Eng. 2015, 131, 150–164. [Google Scholar] [CrossRef]
- Liu, Y.; Joseph, P.C.; Sa, R.D. Numerical and experimental studies of stick–slip oscillationsin drill-strings. Nonlinear Dyn. 2017, 90, 2959–2978. [Google Scholar] [CrossRef] [Green Version]
- Real, F.F.; Batou, A.; Ritto, T.G.; Desceliers, C.; Aguiar, R.R. Hysteretic bit/rock interaction model to analyze the torsional dynamics of a drill string. Mech. Syst. Signal Process. 2018, 111, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Kamel, J.M.; Yigit, A.S. Modeling and analysis of stick–slip and bit bounce in oil well drillstrings equipped with dragbits. J. Sound Vib. 2014, 333, 6885–6899. [Google Scholar] [CrossRef]
- Liang, F.; Gao, A.; Yang, X.D. Dynamical analysis of spinning functionally graded pipes conveying fluid with multiple spans. Appl. Math. Model. 2020, 83, 454–469. [Google Scholar] [CrossRef]
- Liang, F.; Yang, X.D.; Qian, Y.J.; Zhang, W. Transverse free vibration and stability analysis of spinning pipes conveying fluid. Int. J. Mech. Sci. 2018, 137, 195–204. [Google Scholar] [CrossRef]
- Liang, F.; Yang, X.D.; Zhang, W.; Qian, Y.J. Dynamical modeling and free vibration analysis of spinning pipes conveying fluid with axial deployment. J. Sound Vib. 2018, 417, 65–79. [Google Scholar] [CrossRef]
- Liang, F.; Yang, X.D.; Zhang, W.; Qian, Y.J. Vibrations in 3D space of a spinning supported pipe exposed to internal and external annular flows. J. Fluids Struct. 2019, 87, 247–262. [Google Scholar] [CrossRef]
- Guzek, A.; Shufrin, I.; Pasternak, E.; Dyskin, A. Influence of drilling mud rheology on the reduction of vertical vibrations in deep rotary drilling. J. Pet. Sci. Eng. 2015, 135, 375–383. [Google Scholar] [CrossRef]
- Shen, H.; Padoussis, M.P.; Wen, J.; Yu, D.; Wen, X. The beam-mode stability of periodic functionally-graded-material shells conveying fluid. J. Sound Vib. 2014, 333, 2735–2749. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. Nonlinear response of fluid-conveying functionally graded cylindrical shells subjected to mechanical and thermal loading conditions. Compos. Struct. 2017, 168, 675–684. [Google Scholar] [CrossRef]
- Zhou, X.W.; Dai, H.L.; Wang, L. Dynamics of axially functionally graded cantilevered pipes conveying fluid. Compos. Struct. 2018, 190, 112–118. [Google Scholar] [CrossRef]
- An, C.; Su, J. Dynamic behavior of axially functionally graded pipes conveying fluid. Math. Probl. Eng. 2017, 2017, 6789634. [Google Scholar] [CrossRef] [Green Version]
- Volpi, L.P.; Lobo, D.M.; Ritto, T.G. A stochastic analysis of the coupled lateral-torsional drill string vibration. Nonlinear Dyn. 2021, 103, 49–62. [Google Scholar] [CrossRef]
- Zhu, K.; Chung, J. Nonlinear lateral vibrations of a deploying Euler–Bernoulli beam with a spinning motion. Int. J. Mech. Sci. 2015, 90, 200–212. [Google Scholar] [CrossRef]
- Huo, Y.L.; Wang, Z.M. Dynamic analysis of a vertically deploying/retracting cantilevered pipe conveying fluid. J. Sound Vib. 2016, 360, 224–238. [Google Scholar] [CrossRef]
- Vaziri, V.; Oladunjoye, I.O.; Kapitaniak, M.; Aphale, S.S.; Wierci, G.M. Parametric analysis of a sliding-mode controller to suppress drill-string stick-slip vibration. Meccanica 2020, 55, 2475–2492. [Google Scholar] [CrossRef]
- Eftekhari, M.; Hosseini, M. On the stability of spinning functionally graded cantilevered pipes subjected to fluid-thermomechanical loading. Int. J. Struct. Stab. Dyn. 2016, 16, 1550062. [Google Scholar] [CrossRef]
- Kapitaniak, M.; Hamaneh, V.V.; Chávez, J.P.; Nandakumar, K.; Wiercigroch, M. Unveiling complexity of drill-String vibrations: Experiments and modeling. Int. J. Mech. Sci. 2015, 101–102, 324–337. [Google Scholar] [CrossRef]
- Gupta, S.K.; Wahi, P. Global axial-torsional dynamics during rotary drilling. J. Sound Vib. 2016, 375, 332–352. [Google Scholar] [CrossRef]
- Lian, Z.; Qiang, Z.; Lin, T.; Wang, F. Experimental and numerical study of drill string dynamics in gas drilling of horizontal wells. J. Nat. Gas Sci. Eng. 2015, 27, 1412–1420. [Google Scholar] [CrossRef]
- Boukredera, F.S.; Hadjadj, A.; Youcefi, M.R. Drilling vibrations diagnostic through drilling data analyses and visualization in real time application. Earth Sci. Inform. 2021, 7, 1–18. [Google Scholar]
- Lenwoue, A.R.K.; Deng, J.; Feng, Y.; Li, H.; Oloruntoba, A.; Selabi, N.; Marembo, M.; Sun, Y. Numerical Investigation of the Influence of the Drill String Vibration Cyclic Loads on the Development of the Wellbore Natural Fracture. Energies 2021, 14, 2015. [Google Scholar] [CrossRef]
- Moharrami, M.J.; Martins, C.; Shiri, H. Nonlinear integrated dynamic analysis of drill strings under stick-slip vibration. Appl. Ocean. Res. 2021, 108, 102521. [Google Scholar] [CrossRef]
- Kapluno, V.J.; Khajiyeva, L.A.; Martyniuk, M.; Sergaliyev, A.S. On the dynamics of drilling. Int. J. Eng. Sci. 2020, 146, 103184. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, W.; Chávez, J.P.; Sa, R.D. Torsional stick-slip vibrations and multistability in drill-strings. Appl. Math. Model. 2019, 76, 545–557. [Google Scholar] [CrossRef]
- Mfs, A.; Ed, B.; Nvdwa, B. Nonlinear dynamic modeling and analysis of borehole propagation for directional drilling. Int. J. Non-Linear Mech. 2019, 113, 178–201. [Google Scholar]
- Salehi, M.M.; Moradi, H. Nonlinear multivariable modeling and stability analysis of vibrations in horizontal drill string. Appl. Math. Model. 2019, 71, 525–542. [Google Scholar] [CrossRef]
- Zhang, H.; Di, Q.; Li, N.; Wang, W.; Chen, F. Measurement and simulation of nonlinear drillstring stick-slip and whirling vibrations. Int. J. Non-Linear Mech. 2020, 125, 103528. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Huang, L.; Zhang, R.; Liu, B.; Wang, J.; Li, L. Modeling of torsional oscillation of drillstring dynamics. Nonlinear Dyn. 2019, 96, 267–283. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Wang, R.; Liu, B.; Guo, S. The chaotic dynamics of drilling. Nonlinear Dyn. 2016, 83, 2013–2018. [Google Scholar] [CrossRef]
- Lu, C.; Wu, M.; Chen, L.; Cao, W. An event-triggered approach to torsional vibration control of drill-string system using measurement-while-drilling data. Control. Eng. Pract. 2020, 106, 104668. [Google Scholar] [CrossRef]
- Vromen, T.; Dai, C.H.; Nathan, V.; Oomen, T.; Astrid, P.; Doris, P. Mitigation of Torsional Vibrations in Drilling Systems: A Robust Control Approach. IEEE Trans. Control Syst. Technol. 2017, 27, 249–265. [Google Scholar] [CrossRef]
- Panda, L.N.; Kar, R.C. Non-linear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances. Nonlinear Dyn. 2007, 49, 9–30. [Google Scholar] [CrossRef]
- Panda, L.N.; Kar, R.C. Non-linear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances. J. Sound Vib. 2008, 309, 375–406. [Google Scholar] [CrossRef]
- Jin, J.D.; Song, Z.Y. Parametric resonances of supported pipes conveying pulsating fluid. J. Fluids Struct. 2005, 20, 763–783. [Google Scholar] [CrossRef]
- Kapitaniak, M.; Vaziri, V.; Chávez, J.P.; Wiercigroch, M. Experimental studies of forward and backward whirls of drill-string. Mech. Syst. Signal Process. 2018, 100, 454–465. [Google Scholar] [CrossRef] [Green Version]
- Wang, L. A further study on the non-linear dynamic of simply supported pipes conveying pulsating fluid. Int. J. Non-Linear Mech. 2009, 44, 115–121. [Google Scholar] [CrossRef]
- Jin, J.D. Stability and chaotic motions of a restrained pipe conveying fluid. J. Sound Vib. 1997, 208, 427–439. [Google Scholar] [CrossRef]
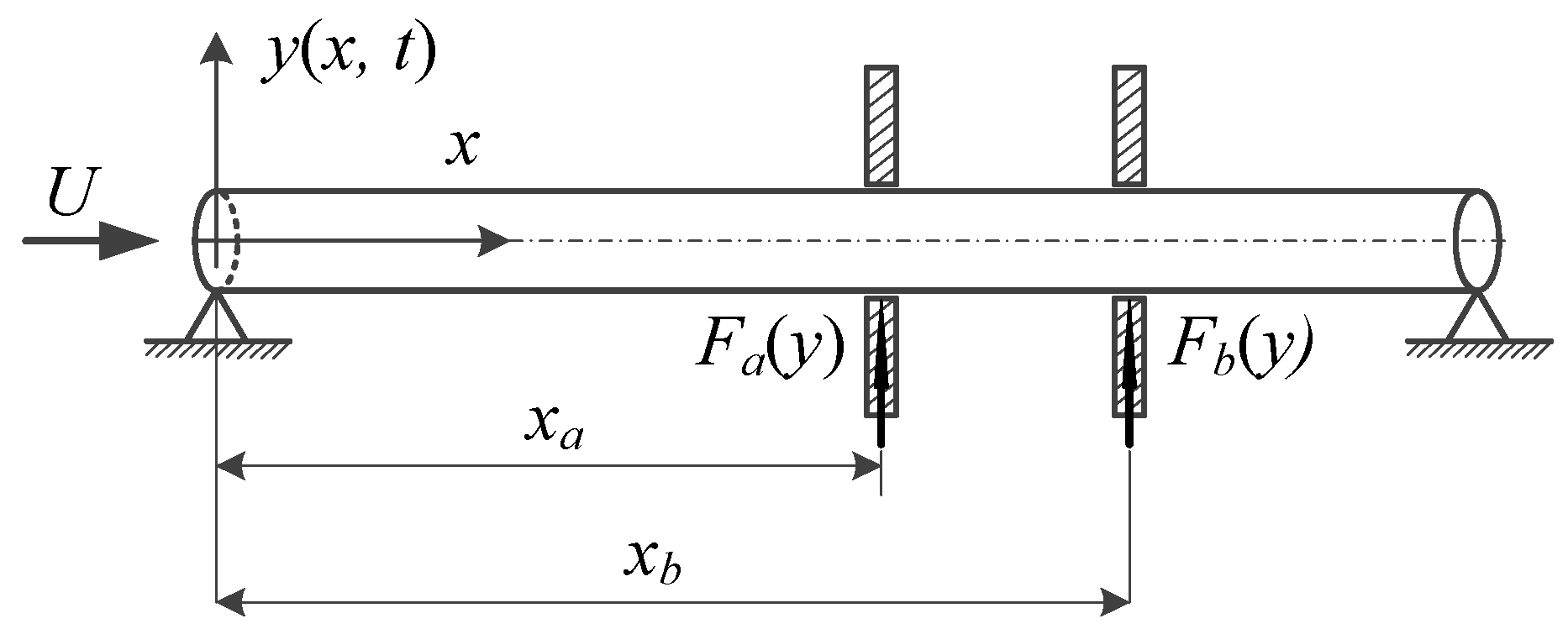



| Item | Notation | Value |
|---|---|---|
| Density of cutting fluid Density of drilling shaft | ρf ρz | 8.65 × 102 kg/m3 7.8 × 103 kg/m3 |
| Young’s modulus | E | 2.14 × 1011 Pa |
| Internal diameter External diameter | d1 d2 | 7.68 × 10−2 m 1.27 × 10−2 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Liu, X.; Song, G.; Zhou, S. Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction. Appl. Sci. 2021, 11, 9047. https://doi.org/10.3390/app11199047
Wang R, Liu X, Song G, Zhou S. Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction. Applied Sciences. 2021; 11(19):9047. https://doi.org/10.3390/app11199047
Chicago/Turabian StyleWang, Rongpeng, Xiaoqin Liu, Guiqiu Song, and Shihua Zhou. 2021. "Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction" Applied Sciences 11, no. 19: 9047. https://doi.org/10.3390/app11199047
APA StyleWang, R., Liu, X., Song, G., & Zhou, S. (2021). Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction. Applied Sciences, 11(19), 9047. https://doi.org/10.3390/app11199047





