Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor
Abstract
1. Introduction
2. Disturbance Torque Model of the Sun-Tracking Solar Array
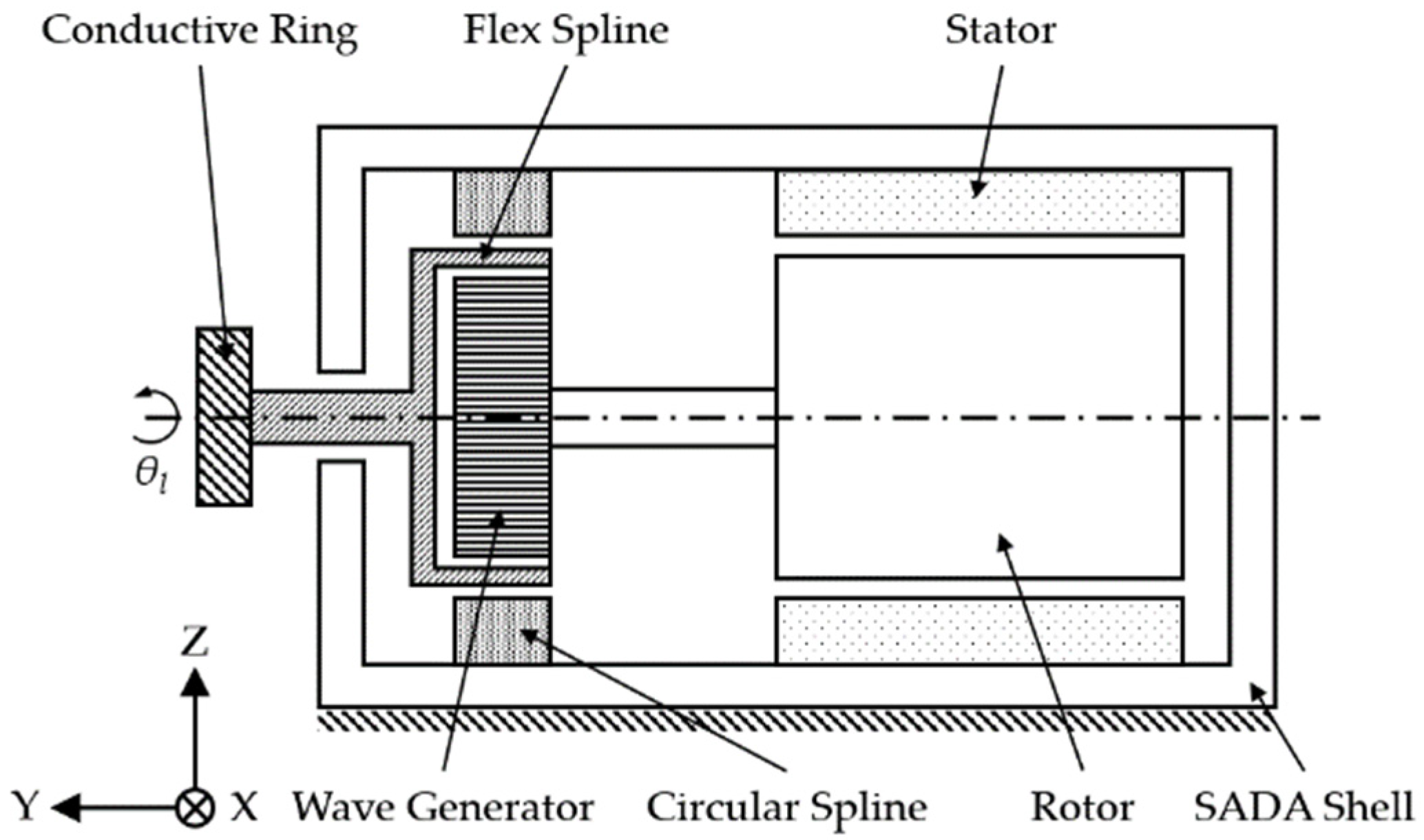
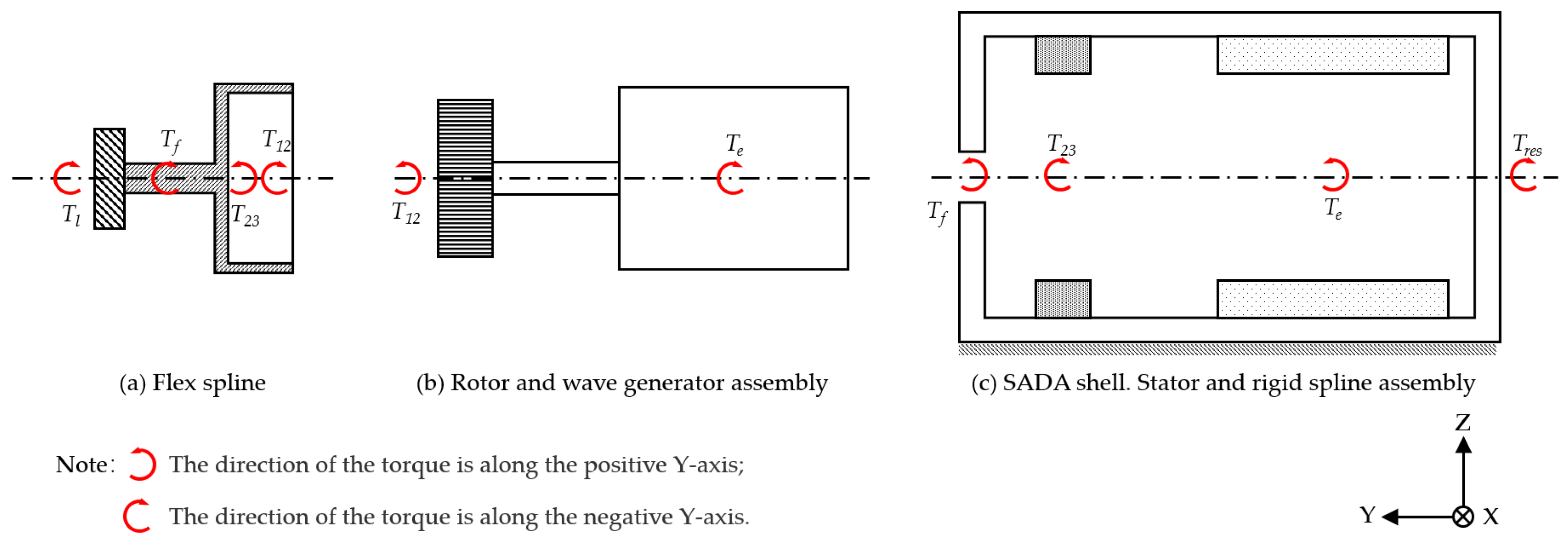
2.1. Electromagnetic Torque Model of Stepping Motors
2.2. Friction Torque Model
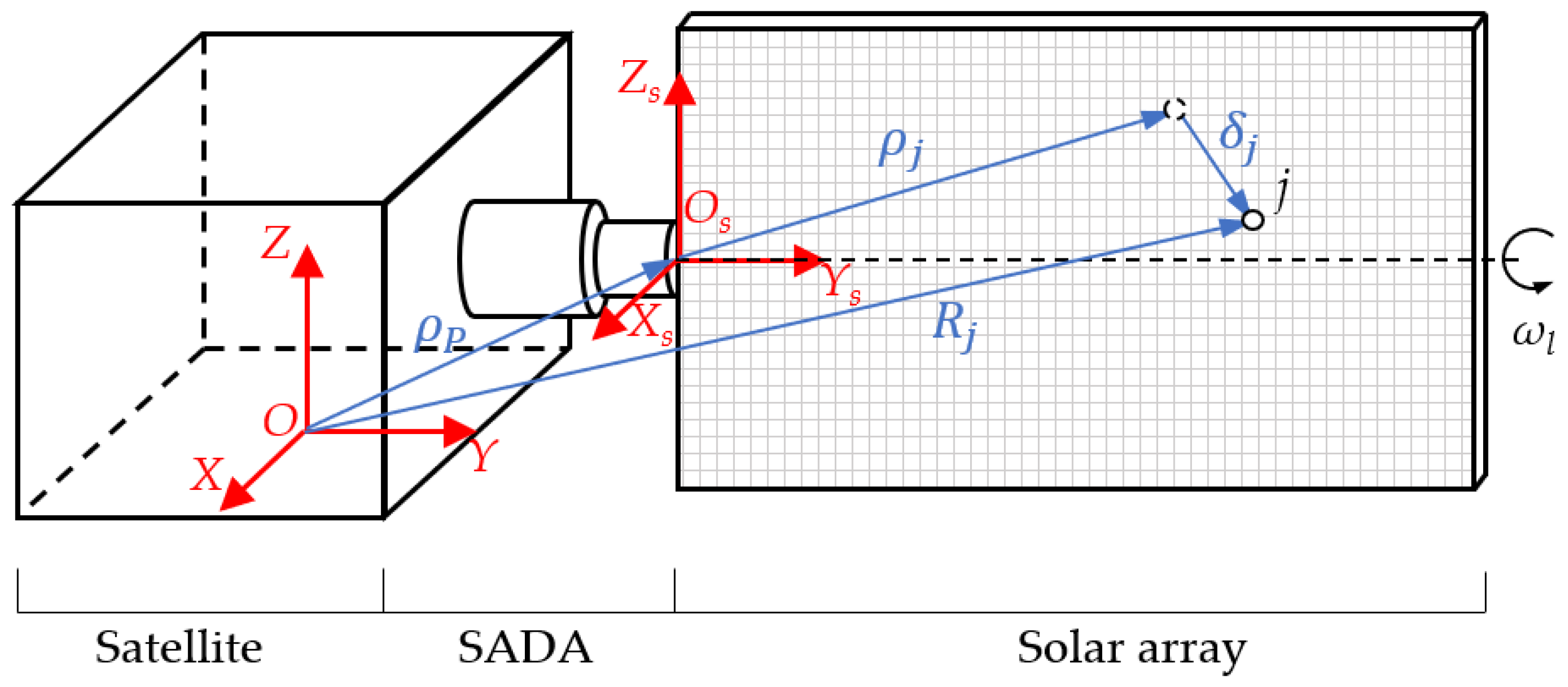
2.3. Dynamics Model of the Solar Array
2.4. Disturbance Torque Model
3. Solar Array Simulator
3.1. The Dynamic Characteristics of the Solar Array
3.2. Structure of the SAS
4. Validation of the Proposed Disturbance Torque Model
4.1. Experimental Results
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aglietti, G.; Langley, R.S.; Rogers, E.; Gabriel, S. Model Building and Verification for Active Control of Microvibrations with Probabilistic Assessment of the Effects of Uncertainties. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 389–399. [Google Scholar] [CrossRef]
- Zhang, Z.; Aglietti, G.S.; Ren, W. Coupled microvibration analysis of a reaction wheel assembly including gyroscopic effects in its accelerance. J. Sound Vib. 2013, 332, 5748–5765. [Google Scholar] [CrossRef]
- Li, L.; Tan, L.; Kong, L.; Wang, D.; Yang, H. The influence of flywheel micro vibration on space camera and vibration suppression. Mech. Syst. Signal Process. 2018, 100, 360–370. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Jiang, J. Coupled dynamic analysis of a single gimbal control moment gyro cluster integrated with an isolation system. J. Sound Vib. 2014, 333, 345–363. [Google Scholar] [CrossRef]
- Zhang, Y.; Zang, Y.; Li, M.; Wang, Y.; Li, W. Active-passive integrated vibration control for control moment gyros and its application to satellites. J. Sound Vib. 2017, 394, 1–14. [Google Scholar] [CrossRef]
- Chen, S.; Xuan, M.; Xin, J.; Liu, Y.; Gu, S.; Li, J.; Zhang, L. Design and experiment of dual micro-vibration isolation system for optical satellite flywheel. Int. J. Mech. Sci. 2020, 179, 105592. [Google Scholar] [CrossRef]
- Chen, S.; Xuan, M.; Zhang, L.; Gu, S.; Gong, X.-X.; Sun, H.-Y. Simulating and Testing Microvibrations on an Optical Satellite Using Acceleration Sensor-Based Jitter Measurements. Sensors 2019, 19, 1797. [Google Scholar] [CrossRef]
- Alkomy, H.; Shan, J. Modeling and validation of reaction wheel micro-vibrations considering imbalances and bearing disturbances. J. Sound Vib. 2020, 492, 115766. [Google Scholar] [CrossRef]
- Sattar, M.; Wei, C. Analysis of Coupled Torsional Disturbance Behavior of Micro-stepped Solar Array Drives. J. Sound Vib. 2018, 442, 572–597. [Google Scholar] [CrossRef]
- Wang, H.-j.; Wang, W.; Wang, X.; Zou, G.-y.; Fan, X.-w. Space Camera Image Degradation Induced by Satellite Micro-vibration. Acta Photon. Sin. 2013, 42, 1212–1217. [Google Scholar] [CrossRef]
- Woodard, S. Upper Atmosphere Research Satellite In-Flight Dynamics Study: Lessons Learned. J. Spacecraft Rockets 2000, 37, 794–800. [Google Scholar] [CrossRef][Green Version]
- Farley, R.; Ngo, S. Development of the solar array deployment and drive system for the XTE spacecraft. In Proceedings of the 29th Aerospace Mechanisms Symposium, Houston, TX, USA, 17–19 May 1995; pp. 268–282. [Google Scholar]
- Elsodany, N.; Rezeka, S.; Maharem, N. Adaptive PID control of a stepper motor driving a flexible rotor. World Pumps 2011, 50, 127–136. [Google Scholar] [CrossRef]
- Xia, L. The Primary Research on Low-frequence Resonate of Step-motor and it’s Damping Methods. J. Shenyang Polytech. Univ. 1994, 3, 73–78. [Google Scholar]
- Bodson, M.; Sato, J.; Silver, S. Spontaneous speed reversals in stepper motors. IEEE Trans. Control Syst. Technol. 2006, 4, 369–373. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, W.; Wu, S.; Wang, G. Experiment and Simulation of Electromagnetic Stiffness for Stepper Motor. Appl. Mech. Mater. 2010, 29–32, 1567–1573. [Google Scholar] [CrossRef]
- Si, Z.; Liu, Y.; Li, K. Research on modeling and driver design of solar array drive assembly. Aerosp. Control Appl. 2010, 36, 13–19. [Google Scholar]
- Gasbarri, P.; Monti, R.; Angelis, C.; Sabatini, M. Effects of uncertainties and flexible dynamic contributions on the control of a spacecraft full-coupled model. Acta Astronaut. 2012, 94, 515–526. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.; Xia, M.; He, S.; Li, H.; Wu, Q. Research on a six-degree-of-freedom disturbance force and moment simulator for space micro-vibration experiments. J. Sound Vib. 2018, 432, 530–548. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.; Zhang, Y.; Tang, L.; Guan, X. Inner structural vibration isolation method for a single control moment gyroscope. J. Sound Vib. 2016, 361, 78–98. [Google Scholar] [CrossRef]
- Sun, X.; Yang, B.; Zhao, L.; Sun, X. Optimal design and experimental analyses of a new micro-vibration control payload-platform. J. Sound Vib. 2016, 374, 43–60. [Google Scholar] [CrossRef]
- Zhu, S.; Lei, Y.; Wu, X.-f.; Zhang, D.-P. Effect of drive mechanisms on dynamic characteristics of spacecraft tracking-drive flexible systems. J. Sound Vib. 2015, 343, 194–215. [Google Scholar] [CrossRef]
- Kapun, A.; Hace, A. Identification of Stepping Motor Parameters. In Proceedings of the EUROCON 2007—The International Conference on Computer as a Tool, Warsaw, Poland, 9–12 September 2007. [Google Scholar] [CrossRef]
- B’Elanger, P.; Taghirad, H. An Experimental Study on Modelling and Identification of Harmonic Drive Systems. In Proceedings of the Proceedings of 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996. [Google Scholar]
- Jamaludin, Z.; Brussel, H.; Swevers, J. Friction Compensation of an XY Feed Table Using Friction-Model-Based Feedforward and an Inverse-Model-Based Disturbance Observer. IEEE Trans. Ind. Electron. 2009, 56, 3848–3853. [Google Scholar] [CrossRef]
- Acarnley, P. Stepping Motors: A Guide to Theory and Practice, 4th ed.; IET: London, UK, 2002; pp. 85–86. [Google Scholar]
- Girard, A. Modal effective mass models in structural dynamics. In Proceedings of the 9th Conference International Modal Analysis Conference (IMAC), Florence, Italy, 15–18 April 1991; pp. 45–50. [Google Scholar]
- Füllekrug, U.; Sinapius, J.M. Identification of Modal Parameters, Generalized and Effective Masses During Base-Driven Tests. Aerosp. Sci. Technol. 1998, 7, 469–480. [Google Scholar] [CrossRef]
- Irvine, T. Effective Modal Mass and Modal Participation Factors. Available online: http://www.vibrationdata.com/tutorials2/ModalMass.pdf (accessed on 25 September 2021).
- Wijker, J. Modal Effective Mass. In Spacecraft Structures; Springer: Berlin, Germany, 2008; pp. 247–264. [Google Scholar]
- Masterson, R.A.; Miller, D.W.; Grogan, R.L. Development and validation of reaction wheel disturbance models: Empirical model. J. Sound Vib. 2002, 249, 575–598. [Google Scholar] [CrossRef]
- Cheng, T.-S.; Chao, Y.C.; Wu, C.Y.; Li, Y.-H.; Nakamura, Y.; Lee, K.Y.; Yuan, T.; Leu, T.-S. Experimental and numerical investigation of microscale hydrogen diffusion flames. Proc. Combust. Inst. 2005, 30, 2489–2497. [Google Scholar] [CrossRef]
- Yu, Y.; Gong, X.; Zhang, L.; Jia, H.; Xuan, M. Full-Closed-Loop Time-Domain Integrated Modeling Method of Optical Satellite Flywheel Micro-Vibration. Appl. Sci. 2021, 11, 1328. [Google Scholar] [CrossRef]

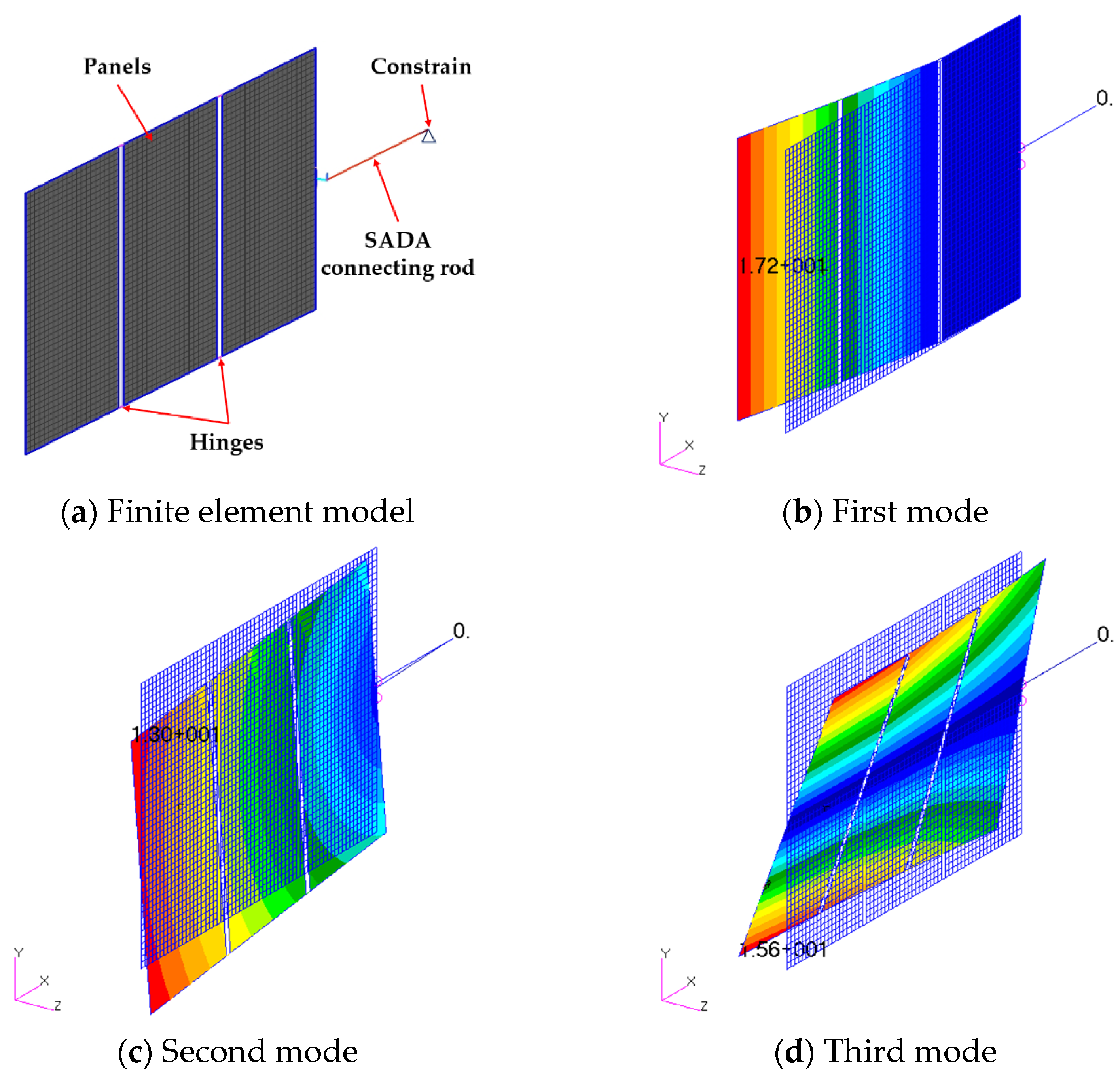
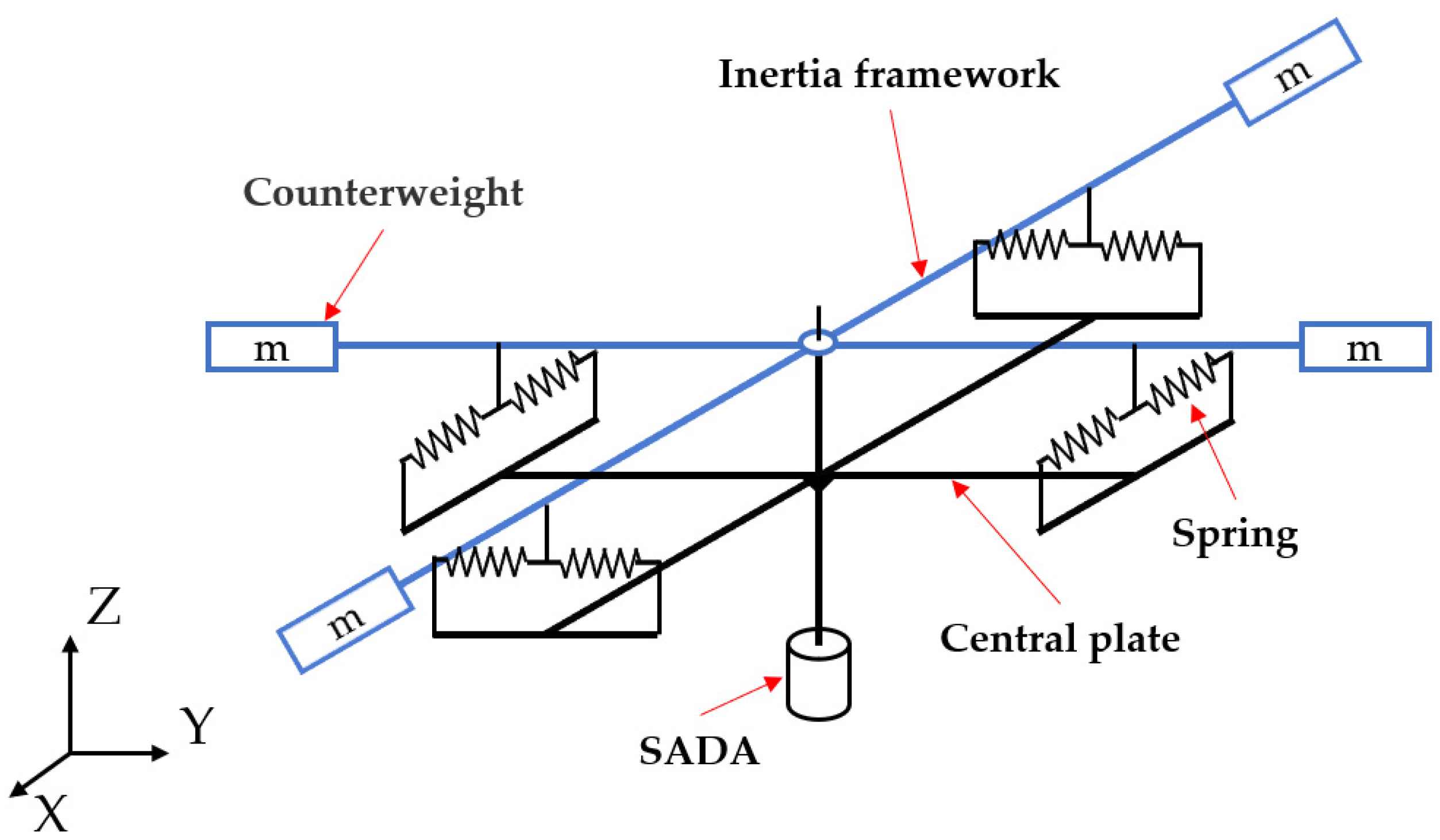
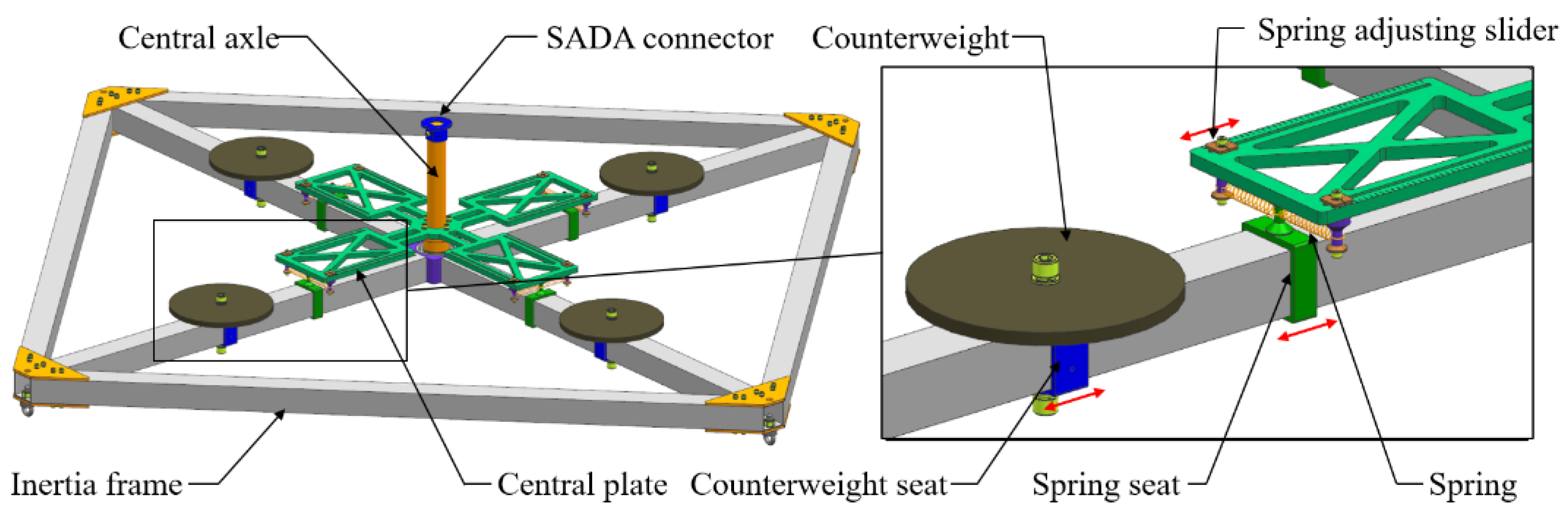
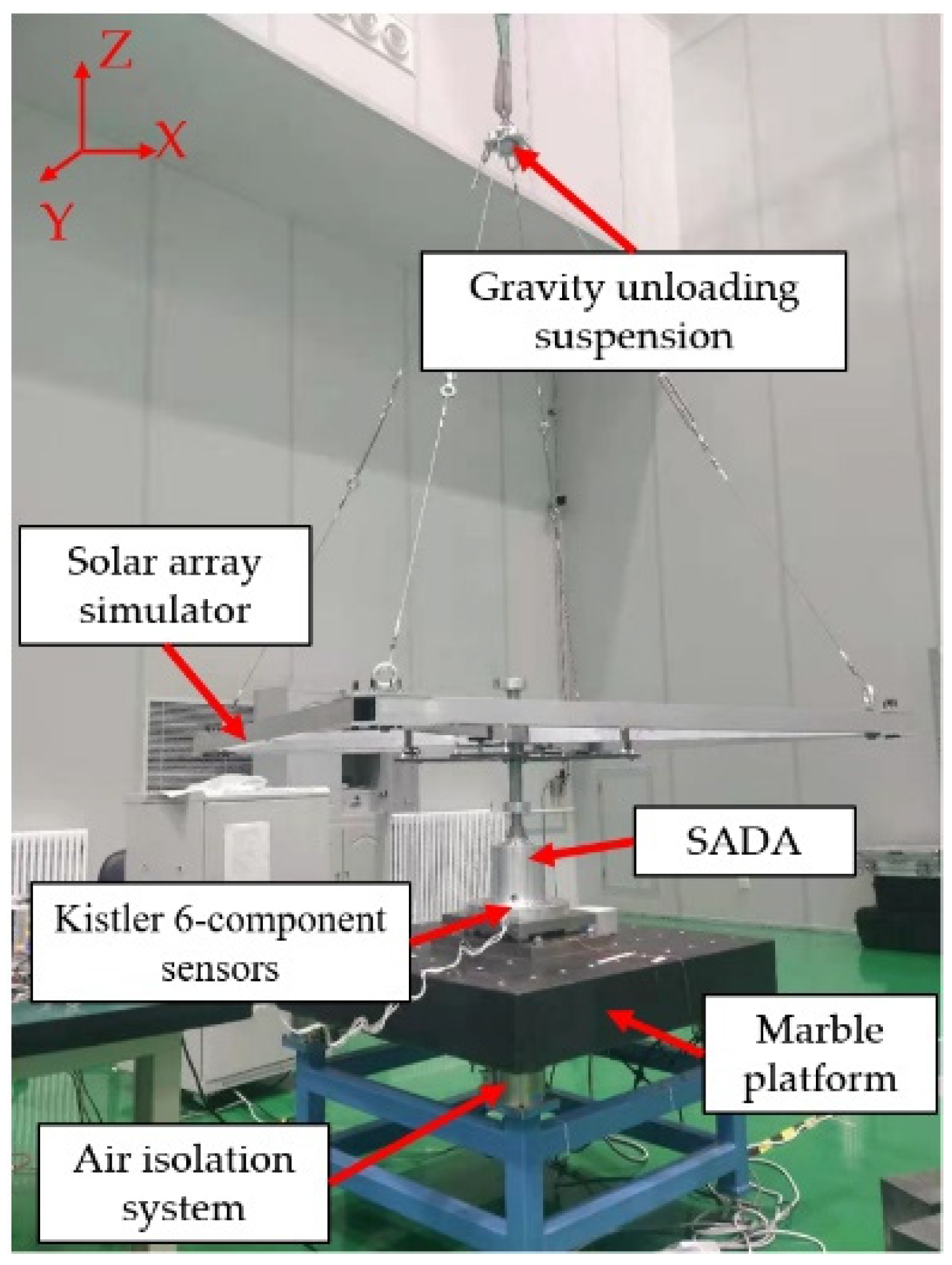
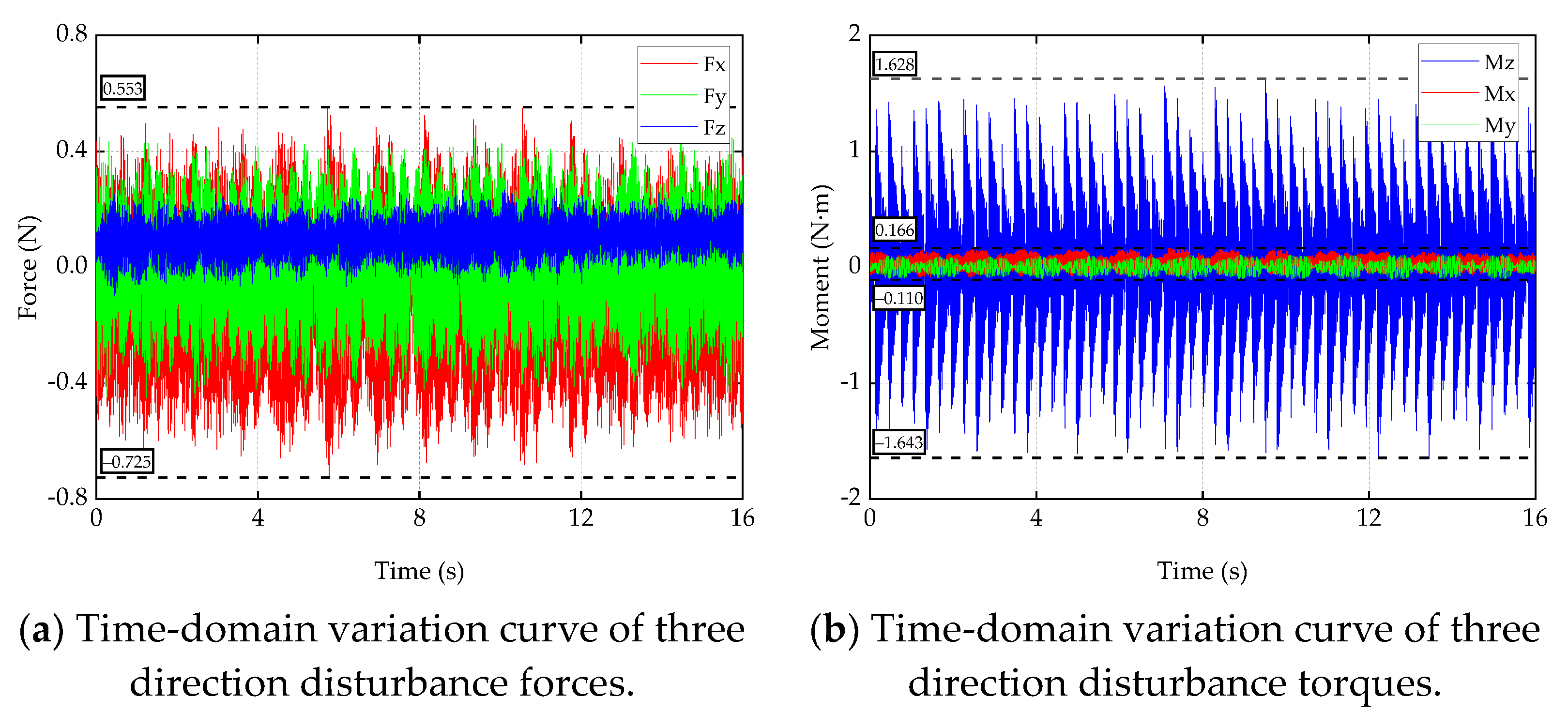





| Mode | Frequency (Hz) | Modal Effective Mass (kg·m2) | Modal Effective Mass Fraction |
|---|---|---|---|
| 1 | 0.22 | 3.82 × 10−16 | 4.97 × 10−16 |
| 2 | 0.55 | 2.80 × 10−4 | 3.64 × 10−5 |
| 3 | 1.18 | 7.44 | 0.967 |
| 4 | 1.28 | 3.46 × 10−4 | 4.50 × 10−5 |
| 5 | 2.46 | 3.40 × 10−5 | 4.42 × 10−6 |
| 6 | 4.17 | 1.31 × 10−3 | 1.70 × 10−4 |
| 7 | 4.45 | 2.07 × 10−1 | 2.69 × 10−2 |
| 8 | 8.98 | 2.19 × 10−2 | 2.85 × 10−3 |
| 9 | 9.09 | 4.86 × 10−3 | 6.32 × 10−4 |
| 10 | 11.6 | 1.48 × 10−2 | 1.92 × 10−3 |
| Total | - | 7.69 | 0.999 |
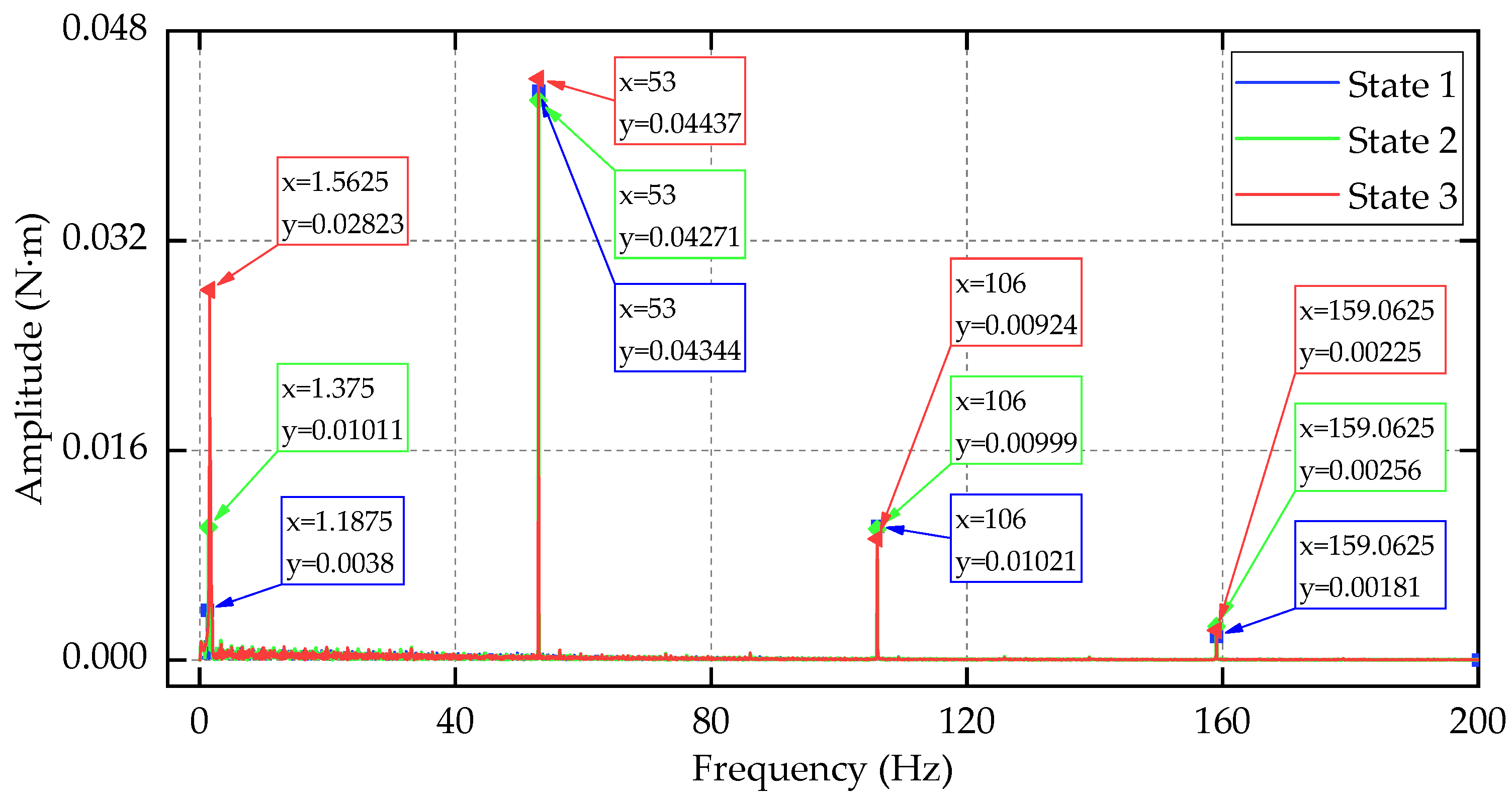
| State No. | Modal Frequency (Hz) | Rotational Inertia (kg·m2) |
|---|---|---|
| 1 | 1.19 | 8.18 |
| 2 | 1.39 | 8.18 |
| 3 | 1.59 | 8.18 |
| 4 | 1.19 | 15.69 |
| 5 | 1.19 | 22.99 |
| Symbol | Parameter | Value (Unit) |
|---|---|---|
| z | Number of rotor teeth | 50 |
| b | Beat number | 4 |
| n | Subdivisions | 16 |
| I | Current Amplitude | 0.6 A |
| Km | Motor torque constant | 0.3 Nm/A |
| Kd | Detent torque constant | 0.01 Nm/A |
| Jr | Moment of inertia of SADA rotor | 0.2 kg·cm2 |
| Jwg | Moment of inertia of wave generator | 0.052 kg·cm2 |
| R | Winding resistance | 6 Ω |
| L | Self-induction coefficient | 13 mH |
| h | Reduction ratio | 100 |
| Cruising speed of solar array | 0.06°/s | |
| KP | Proportional coefficient | 500 |
| KI | Integral coefficient | 6000 |
| KD | Differential coefficient | 0 |
| Tc | Coulomb friction coefficient for motor | 0.0246 |
| Ts | Static friction coefficient for motor | 0.0462 |
| ωs | Stribeck velocity for motor | 0.003°/s |
| σ | Viscous friction coefficient for motor | 0.0255 |
| Number of contact pairs of ring and brush | 320 | |
| p | Pressure of a single point | 0.042 N |
| μ | The friction factor | 1.53 |
| r | The radius of conductive ring | 0.0265 m |
| No. | Test (Hz) | Finite Element Model (Hz) | Relative Error |
|---|---|---|---|
| 1 | 1.189 | 1.187 | 0.419% |
| 2 | 18.72 | 18.16 | 2.99% |
| 3 | 18.76 | 18.27 | 3.15% |
| Components | Natural Frequency | Driving Frequency | 2nd-Order Harmonic | 3rd-Order Harmonic |
|---|---|---|---|---|
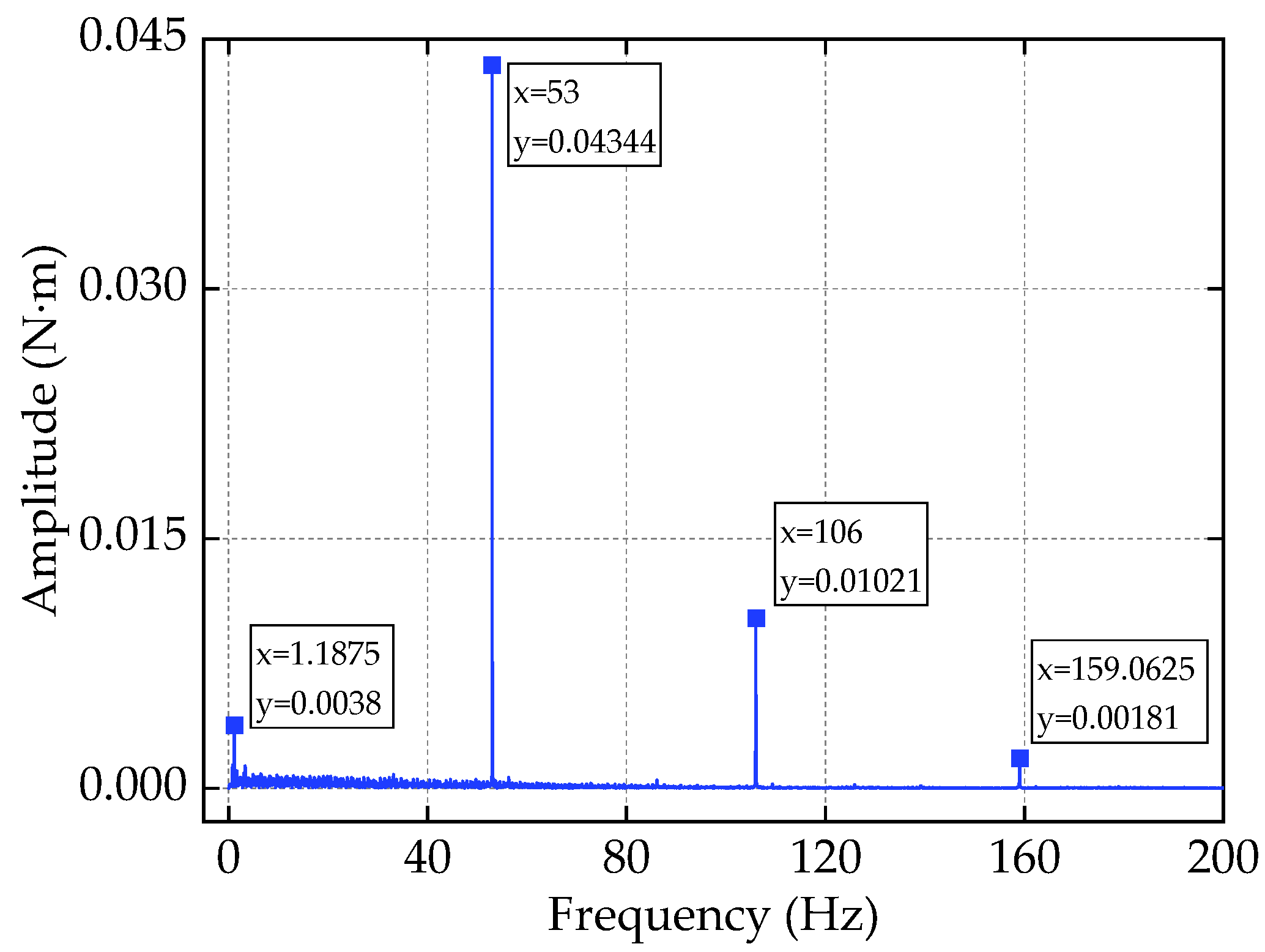
| Test (Hz) | 1.189 | 53 | 106 | 159.0625 |
| Simulation (Hz) | 1.18749 | 53.31217 | 106.68683 | 159.999 |
| Absolute error (Hz) | 0.00151 | 0.31217 | 0.68683 | 0.93650 |
| Relative error (%) | 0.127 | 0.589 | 0.648 | 0.5888 |
| Components | Natural Frequency | Driving Frequency | 2nd-Order Harmonic | 3rd-Order Harmonic |
|---|---|---|---|---|
| Experiments (Nm) | 0.0038 | 0.04344 | 0.01021 | 0.00181 |
| Simulation (Nm) | 0.00399 | 0.03661 | 0.01249 | 0.002198 |
| Absolute error (Nm) | 0.00019 | 0.00683 | 0.00228 | 0.000388 |
| Relative error (%) | 5.00 | 15.72 | 22.33 | 21.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Guan, Y.; Zhang, D.; Chen, S.; Zhao, C.; Zhang, L. Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor. Appl. Sci. 2021, 11, 9076. https://doi.org/10.3390/app11199076
Yu J, Guan Y, Zhang D, Chen S, Zhao C, Zhang L. Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor. Applied Sciences. 2021; 11(19):9076. https://doi.org/10.3390/app11199076
Chicago/Turabian StyleYu, Jisong, Yongliang Guan, Daowei Zhang, Shanbo Chen, Chunjuan Zhao, and Lei Zhang. 2021. "Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor" Applied Sciences 11, no. 19: 9076. https://doi.org/10.3390/app11199076
APA StyleYu, J., Guan, Y., Zhang, D., Chen, S., Zhao, C., & Zhang, L. (2021). Simulation and Experimental Research on the Disturbance Behavior of a Sun-Tracking Solar Array Driven by a Stepping Motor. Applied Sciences, 11(19), 9076. https://doi.org/10.3390/app11199076






