Green Shipping—Multifunctional Marine Scrubbers for Emission Control: Silencing Effect
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
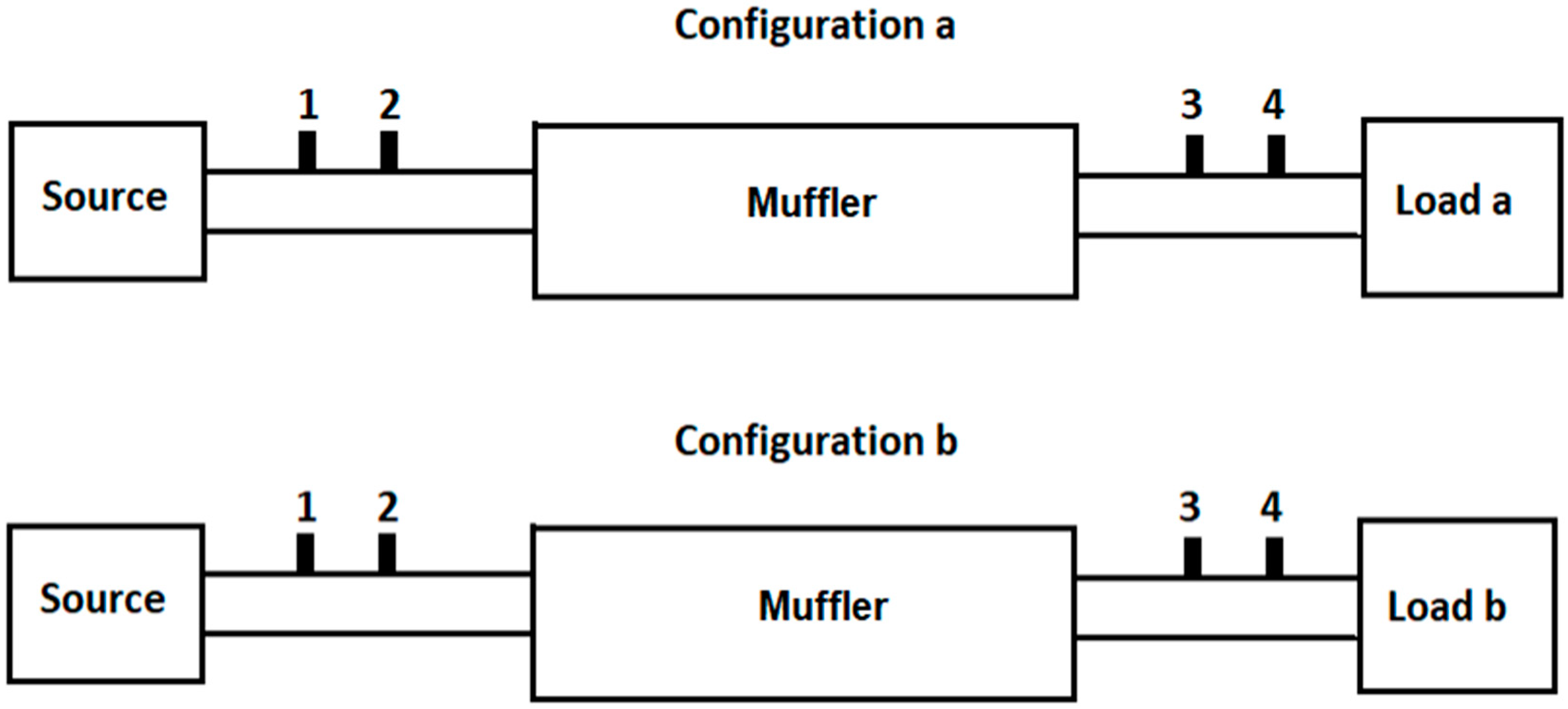
2.1. Transmission Loss Measurements and Calculations
2.1.1. Experimental Techniques for Transmission Loss Measurements
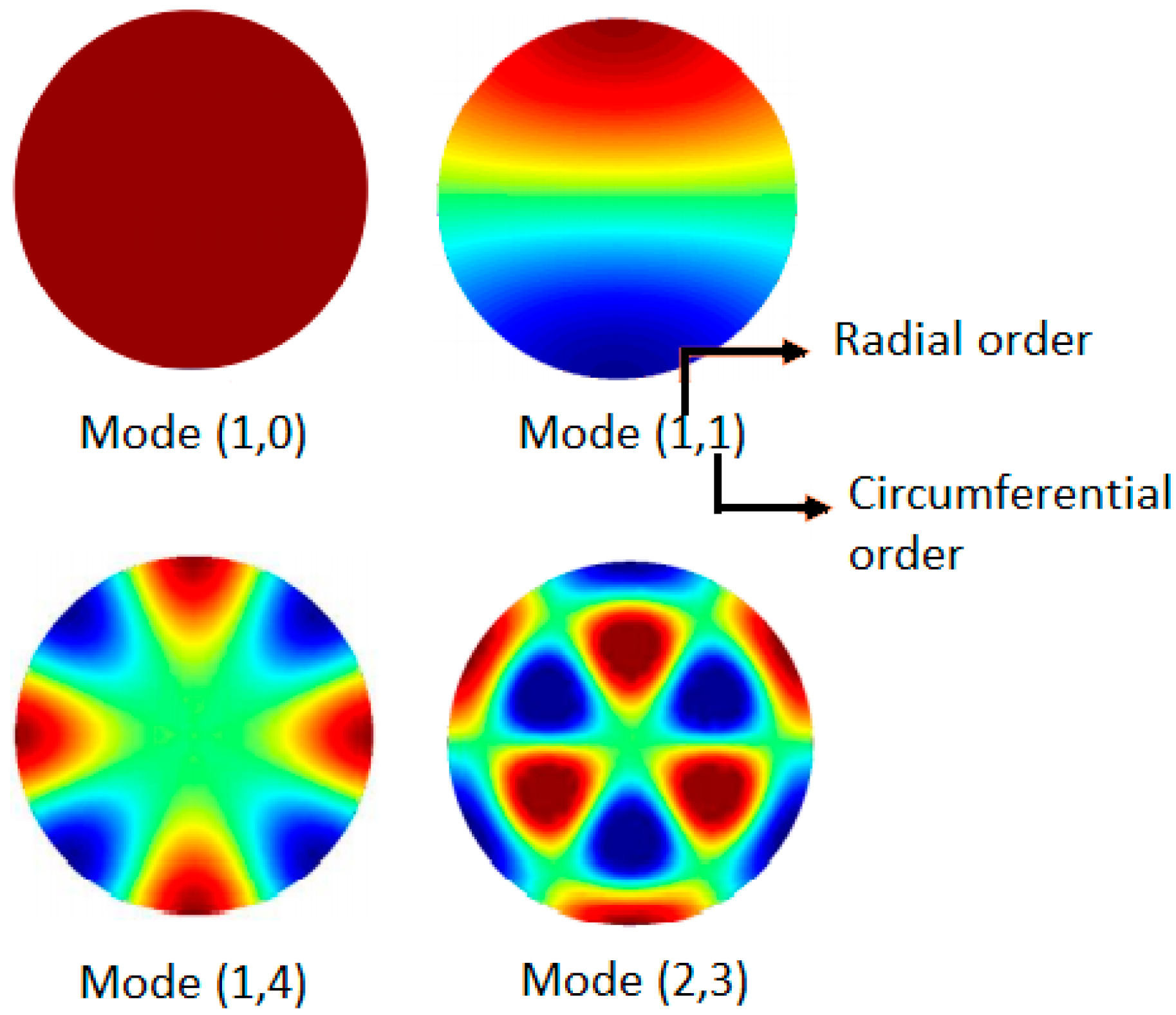
2.1.2. Numerical Methods to Evaluate Transmission Loss
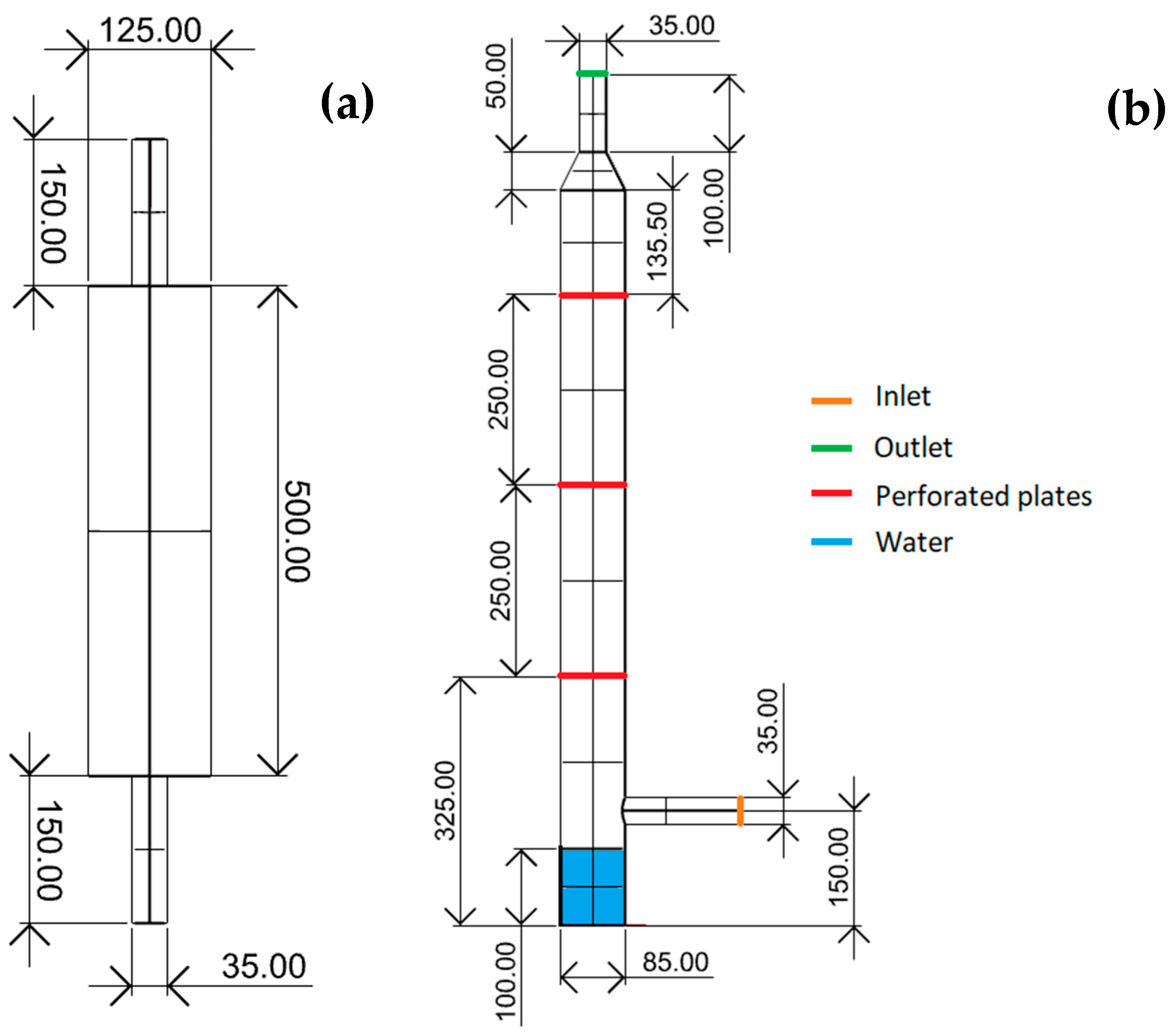
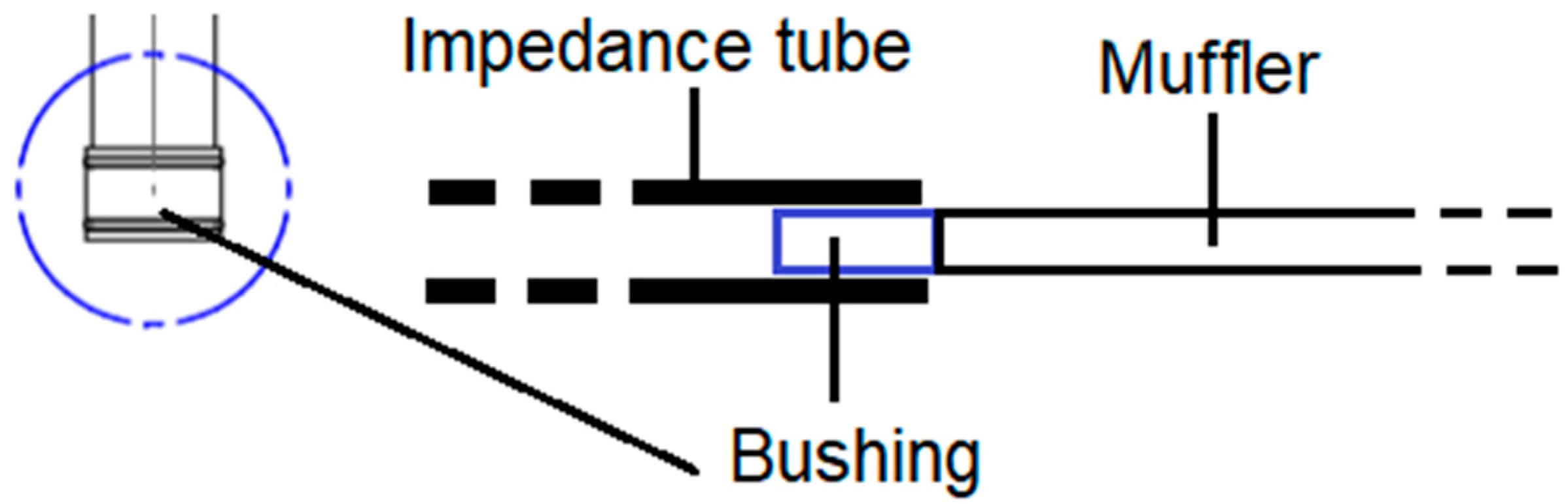
2.2. The Case Studies: Experimental Tests and Numerical Analyses
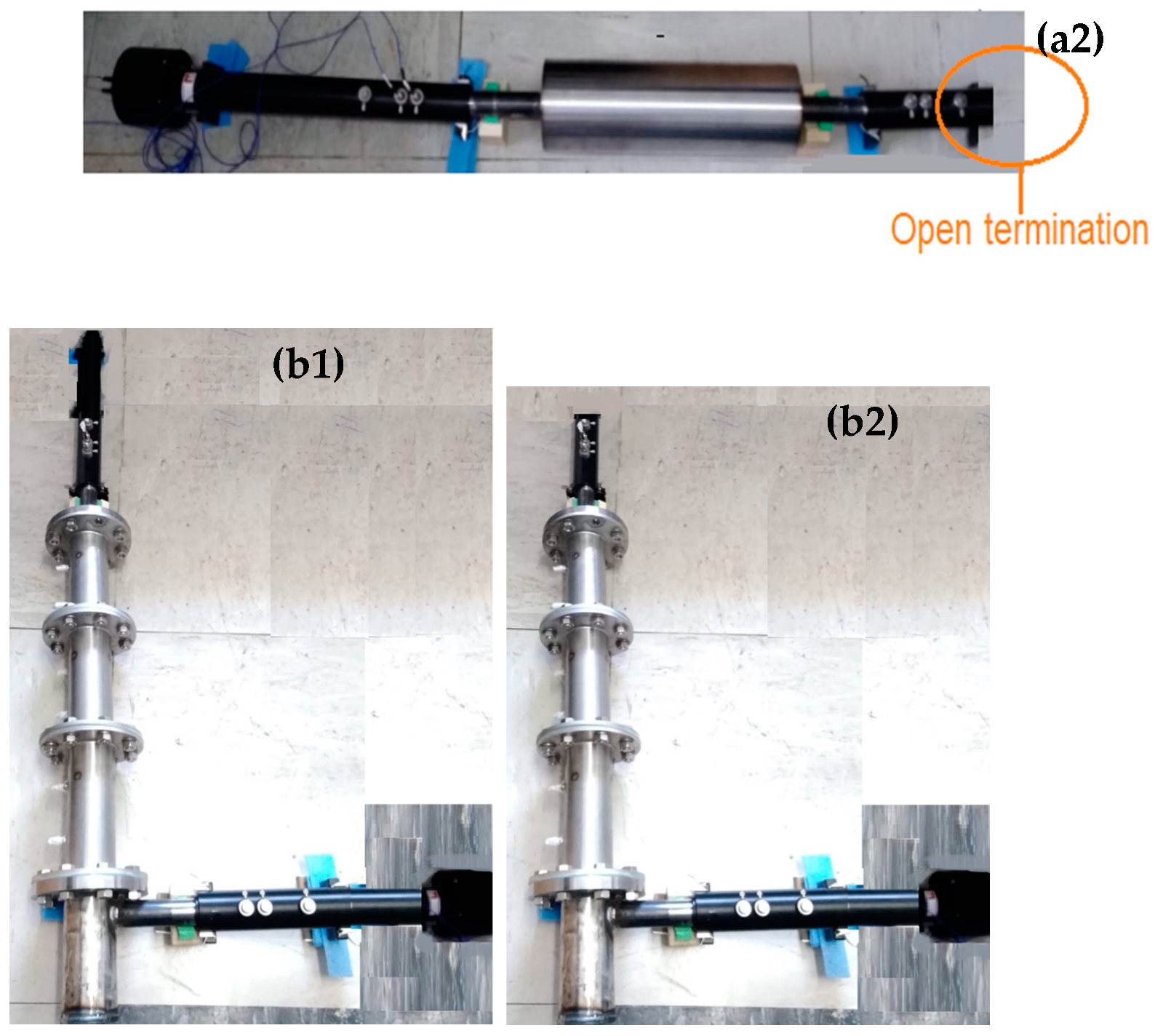
2.2.1. Transmission Loss Experimental Measurements
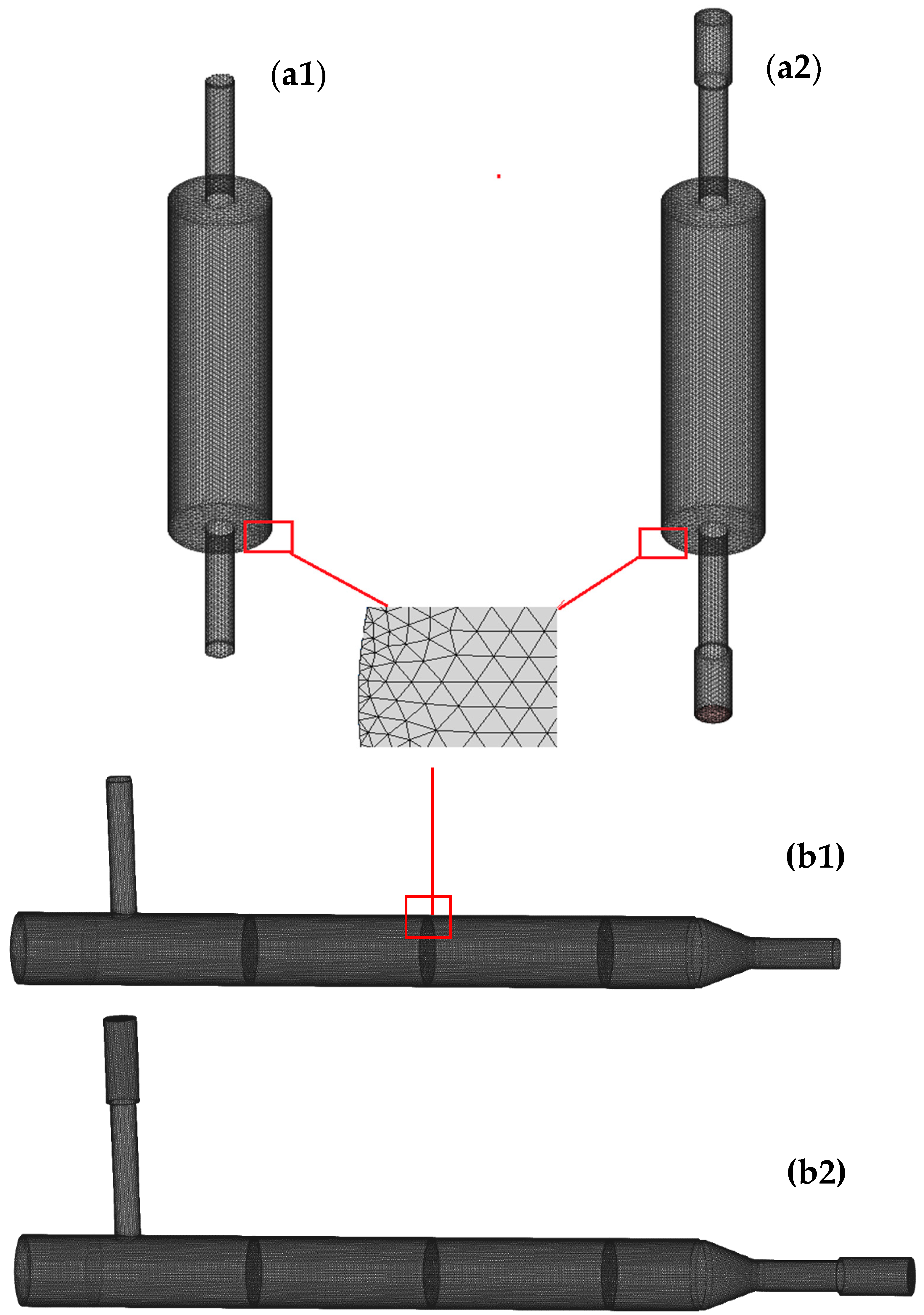
2.2.2. FEM Simulations of Transmission Loss
3. Results and Discussion
3.1. Simple Expansion Chamber
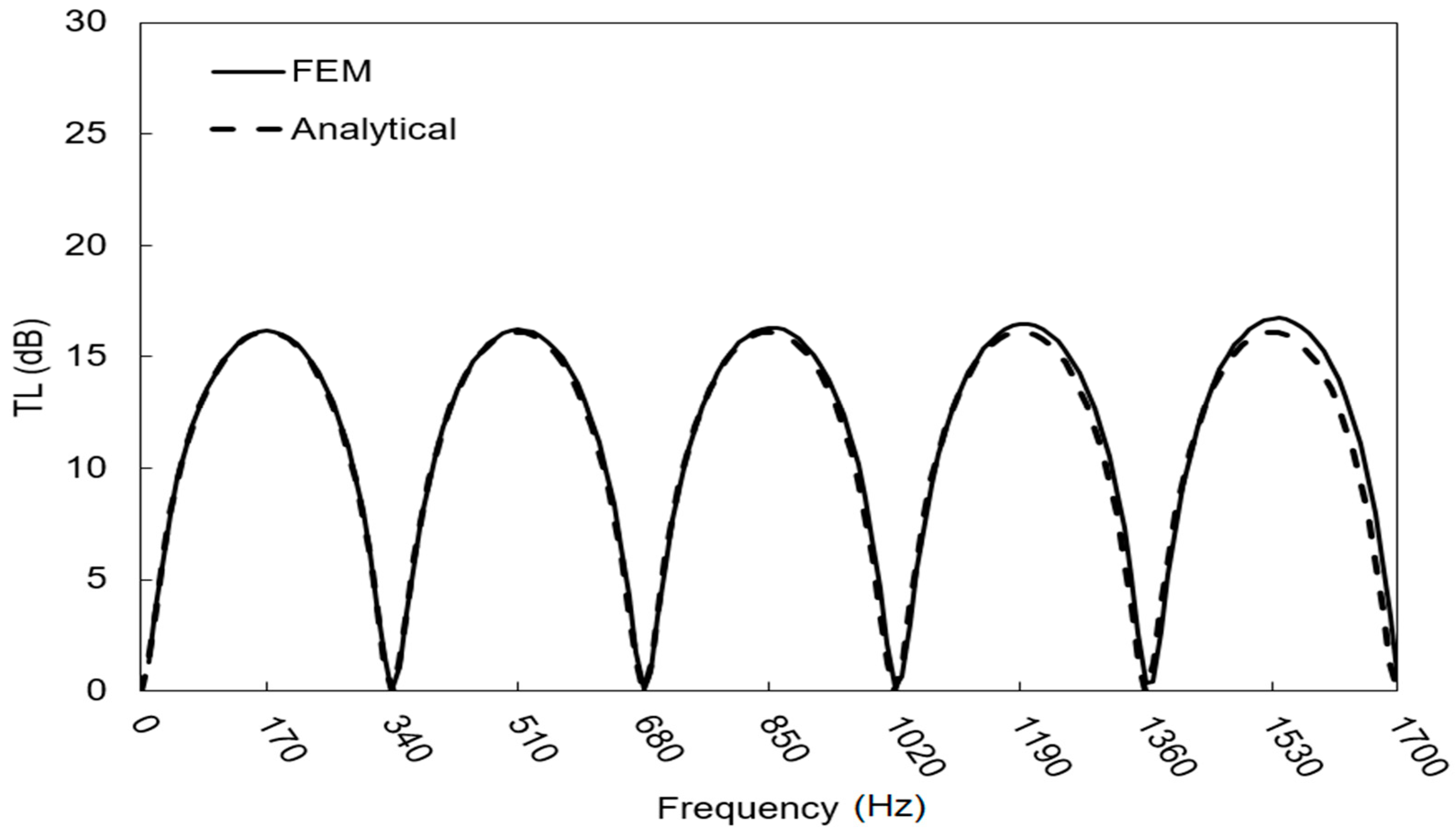
3.1.1. Experimental Transmission Loss Assessment
3.1.2. FEM Transmission Loss Assessment
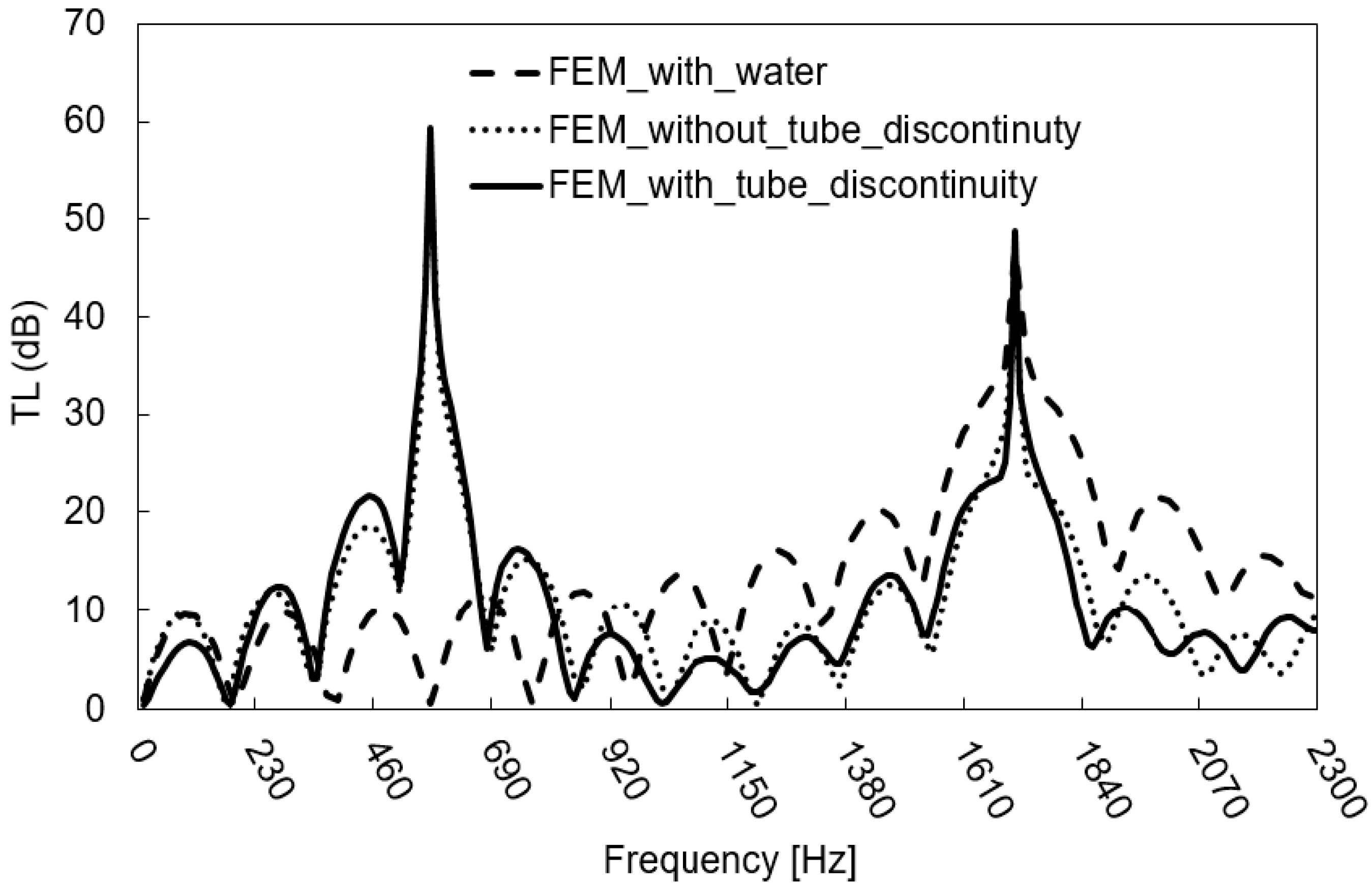
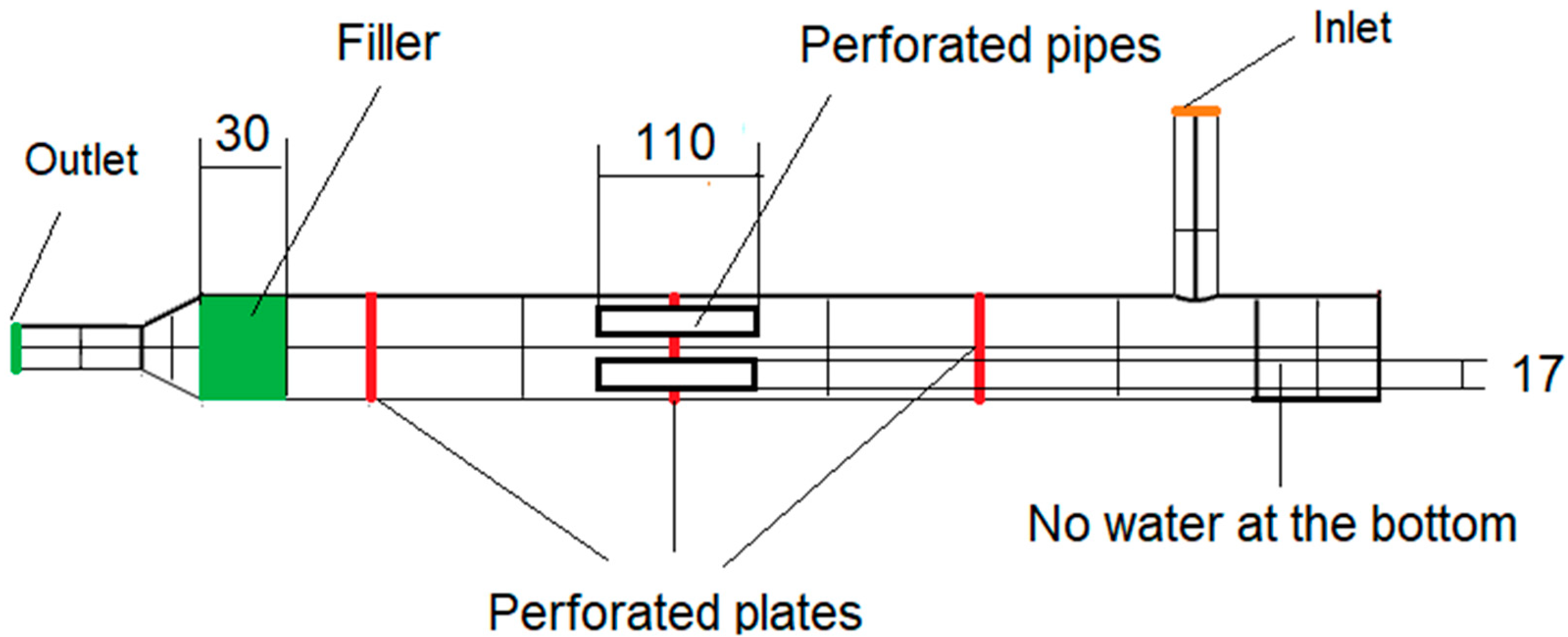
3.2. Model-Scale Scrubber
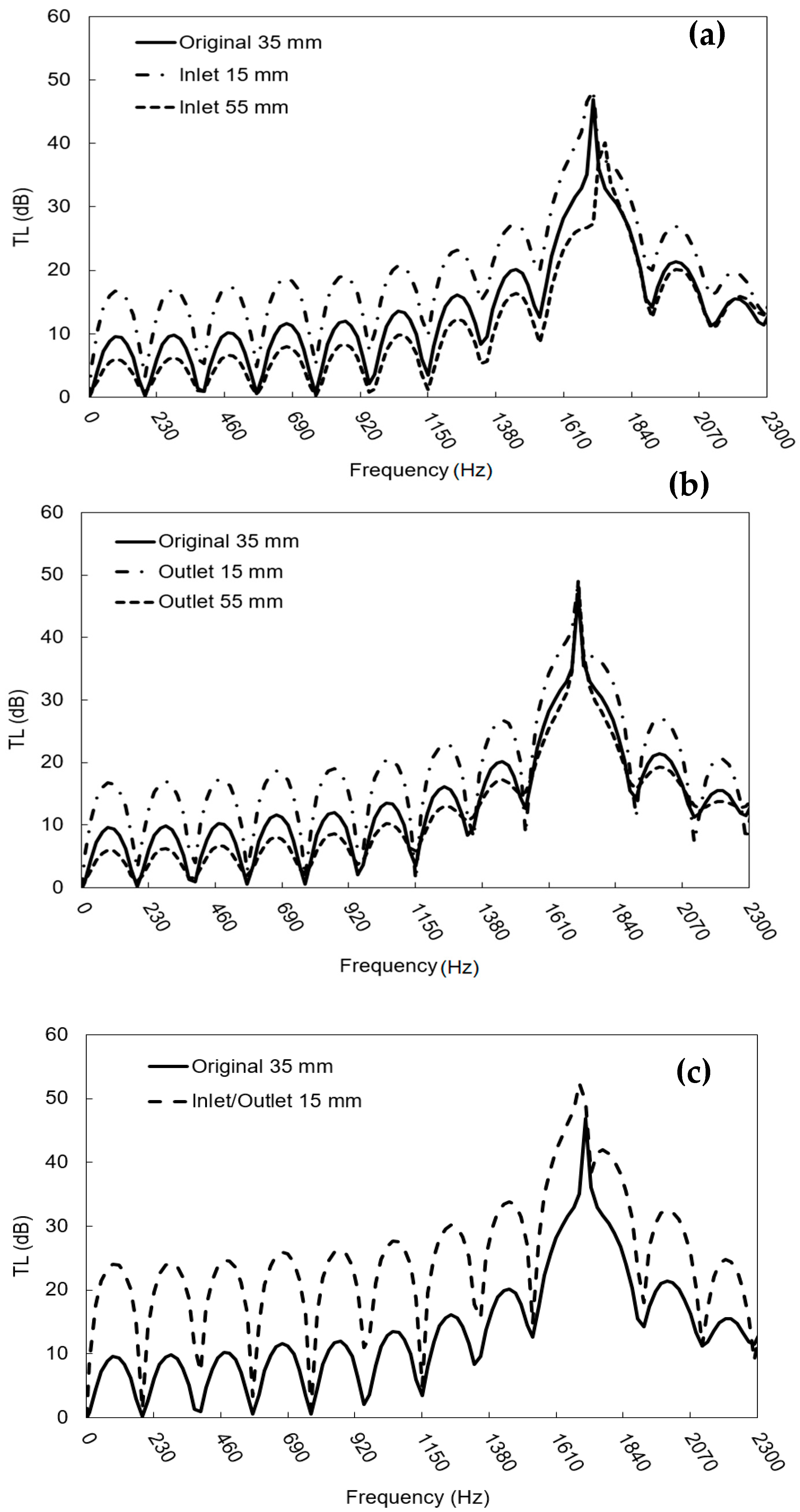
3.3. Effects of Scrubber Design on Transmission Loss
4. Conclusions
- The importance of the geometry of the experimental set-up (i.e., connection between prototype and impedance tube) on the measured TL (Section 3.1 and Section 3.2);
- The removal of the water at the bottom of the scrubber (e.g., letting the water to directly flow out), allowing the TL increase at low frequencies (Section 3.2);
- Decreasing the inlet and outlet pipe diameter of the scrubber, allowing its TL to increase along the entire frequency range (Section 3.3);
- The addition of perforated pipes and/or a filler inside of the scrubber is possible to increase the TL and change the fundamental frequencies of the system (Section 3.3).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Lv, L. Design and Evaluation of an Integrated SCR and Exhaust Muffler from Marine Diesels. J. Mar. Sci. Technol. 2015, 20, 505–519. [Google Scholar] [CrossRef]
- MARPOL 73/78. Annex VI-Regulations for the Prevention of Air Pollution from Ships, Chapter 3-Requirements for Control of Emissions from Ships, Regulation 13—Nitrogen Oxides (NOx); International Maritime Organization (IMO): London, UK, 2008. [Google Scholar]
- MARPOL 73/78. Annex VI-Regulations for the Prevention of Air Pollution from Ships, Chapter 3-Requirements for Control of Emissions from Ships, Regulation 14- Sulphure Oxides (SOx); International Maritime Organization (IMO): London, UK, 2008. [Google Scholar]
- Ushakov, S.; Stenersen, D.; Einang, P.M.; Ask, T.Ø. Meeting Future Emission Regulation at Sea by Combining Low-Pressure EGR and Seawater Scrubbing. J. Mar. Sci. Technol. 2020, 25, 482–497. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, Y.; Fagerholt, K.; Zhou, J. Reducing Sulfur and Nitrogen Emissions in Shipping Economically. Transp. Res. Part D: Transp. Environ. 2021, 90, 102641. [Google Scholar] [CrossRef]
- Johnsen, K.; Kock, F.; Strøm, A.; Chryssakis, C. Global Sulphur Cap 2020 Update. 2019, p. 52. Available online: https://www.dnvgl.com/maritime/publications/global-sulphur-cap-2020.html (accessed on 22 December 2020).
- Oil Price Information. Available online: https://www.petrolbunkering.com/price-information/ (accessed on 22 February 2021).
- Lindstad, H.E.; Rehn, C.F.; Eskeland, G.S. Sulphur Abatement Globally in Maritime Shipping. Transp. Res. Part D Transp. Environ. 2017, 57, 303–313. [Google Scholar] [CrossRef] [Green Version]
- Scrubbers Shown to Have Lower Climate Impact than Low-Sulphur Fuel, Wärtsilä Corporation. Available online: https://Www.Wartsila.Com/Media/News/22-09-2020-Scrubbers-Shown-to-Have-Lower-Climate-Impact-than-Low-Sulphur-Fuel-2786812 (accessed on 29 December 2020).
- Boscarato, I.; Hickey, N.; Kašpar, J.; Prati, M.V.; Mariani, A. Green Shipping: Marine Engine Pollution Abatement Using a Combined Catalyst/Seawater Scrubber System. 1. Effect of Catalyst. J. Catal. 2015, 328, 248–257. [Google Scholar] [CrossRef] [Green Version]
- International Maritime Organization. Resolution MSC.337(91), Code on Noise Levels on Board Schips; IMO: London, UK, 2012. [Google Scholar]
- Lloyd’s Register, ShipRight procedures, Additional Design & Construction Procedure (ADP), Procedure for the Determination of Airborne Noise Emissions from Marine Vessels, January 2019. Available online: https://www.lr.org/en/shipright-procedures/#accordion-additionaldesign&constructionprocedure(adp) (accessed on 28 December 2020).
- NAM KyoungHun. Scrubber with Noise Reduction on Ship. Korean Patent KR102039134 (B1), 5 November 2019.
- Sridhara, B.S.; Crocker, M.J. Review of Theoretical and Experimental Aspects of Acoustical Modeling of Engine Exhaust Systems. J. Acoust. Soc. Am. 1994, 95, 2363–2370. [Google Scholar] [CrossRef]
- Tao, Z.; Seybert, A.F. A Review of Current Techniques for Measuring Muffler Transmission Loss. J. Passeng. Car Mech. Syst. J. 2003, 112, 2096–2100. [Google Scholar]
- Beranek, L.L.; Ver, I.L. Noise and Vibration Control Engineering, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005; ISBN 10-0471449423. [Google Scholar]
- Dokumaci, E. Duct Acoustics: Fundamentals and Applications to Mufflers and Silencers; Cambridge University Press: Cambridge, UK, 2021; ISBN 9781108887656. [Google Scholar] [CrossRef]
- Bodén, H.; Glav, R. Exhaust and intake noise and acoustical design of mufflers and silencers. In Handbook of Noise and Vibration Control; Crocker, M.J., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Chapter 85. [Google Scholar] [CrossRef]
- Chung, J.Y.; Blaser, D.A. Transfer Function Method of Measuring In-duct Acoustic Properties. II. Experiment. J. Acoust. Soc. Am. 1980, 68, 914–921. [Google Scholar] [CrossRef]
- Chung, J.Y.; Blaser, D.A. Transfer Function Method of Measuring In-duct Acoustic Properties. I. Theory. J. Acoust. Soc. Am. 1980, 68, 907–913. [Google Scholar] [CrossRef]
- ISO 10534: Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedances Tubes—Part 2: Transfer Function Method; International Organization for Standardization: Geneva, Switzerland, 2001.
- Munjal, M.L. Acoustics of Ducts and Mufflers, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; ISBN 10 1118443128. [Google Scholar]
- Munjal, M.L.; Doige, A.G. Theory of a Two Source-Location Method for Direct Experimental Evaluation of the Four-Pole Parametersof an Acoustic Element. J. Sound Vib. 1990, 141, 323–333. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, W.; Guo, L.-X. A CFD Results-Based Approach to Investigating Acoustic Attenuation Performance and Pressure Loss of Car Perforated Tube Silencers. Appl. Sci. 2018, 8, 545. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.D.; Ji, Z.L. Transmission Loss Prediction of Reactive Silencers Using 3-D Time-Domain CFD Approach and Plane Wave Decomposition Technique. Appl. Acoust. 2016, 112, 25–31. [Google Scholar] [CrossRef]
- Bing, W.; Yongjuan, W.; Cheng, X. Study of Transmission Loss on Muffler. RJASET 2013, 5, 5556–5560. [Google Scholar] [CrossRef]
- Tan, W.-H.; Ripin, Z.M. Analysis of Exhaust Muffler with Micro-Perforated Panel. J. Vibroeng. 2013, 15, 558–573. [Google Scholar]
- Katz, B.F.G. Method to Resolve Microphone and Sample Location Errors in the Two-Microphone Duct Measurement Method. J. Acoust. Soc. Am. 2000, 108, 2231–2237. [Google Scholar] [CrossRef] [PubMed]
- MSC Software-Hexagon. Actran 2020 User’s Guide, Volume, Installation, Operations, Theory and Utilities; Free Field Technologies: Mont-Saint-Guibert, Belgium, 2020. [Google Scholar]
- Marburg, S.; Nolte, B. Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods; Springer: Berlin, Germany, 2008; ISBN 978-3-540-77447-1. [Google Scholar]
- Marburg, S. Six boundary elements per wavelength: Is that enough? J. Comput. Acoust. 2002, 10, 25–51. [Google Scholar] [CrossRef]
- Kurowski, P.M. Finite Element Analysis for Design Engineers, 2nd ed.; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Maa, D.-Y. Potential of Microperforated Panel Absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Wartsila Italia S.p.A.; Trieste, Italy. Personal communication, 2021.
- Yang, Y.; Jia, H.; Lu, W.; Sun, Z.; Yang, J. Impedance-Matching Acoustic Bend Composed of Perforated Plates and Side Pipes. J. Appl. Phys. 2017, 122, 054502. [Google Scholar] [CrossRef] [Green Version]
- Dubno, J.R.; Eckert, M.A.; Lee, F.-S.; Matthews, L.J.; Schmiedt, R.A. Classifying Human Audiometric Phenotypes of Age-Related Hearing Loss from Animal Models. J. Assoc. Res. Otolaryngol. 2013, 14, 687–701. [Google Scholar] [CrossRef] [PubMed]
- Weston, D.E. The Theory of the Propagation of Plane Sound Waves in Tubes. Proc. Phys. Soc. B 1953, 66, 695–709. [Google Scholar] [CrossRef]
- Gao, Z.; Saine, K.; Hynninen, A.; Tanttari, J. Large engine exhaust noise in real life and measurement techniques in practice. In Proceedings of the 26th International Congress on Sound and Vibration, Montreal, QC, Canada, 7–11 July 2019. [Google Scholar]








| c (m/s) | ρ (kg/m3) | μ (Pa/s) | |
|---|---|---|---|
| Air | 340.0 | 1.225 | 1.78 × 10−5 |
| Water | 1448.9 | 999.1 | 1.14 × 10−3 |
| Max | Mean | Min | |
|---|---|---|---|
| Jacobian | 1 | 1 | 1 |
| Aspect Ratio | 6.42 | 1.76 | 1.03 |
| n | Analytical fmin (Hz) | Experimental fmin (Hz) | Delta fmin (%) | Analytical fmax (Hz) | Experimental fmax (Hz) | Delta fmax (%) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.0 | 170 | 220 | +29.4 |
| 1 | 340 | 348 | +2.4 | 510 | 508 | −0.4 |
| 2 | 680 | 685 | +0.7 | 850 | 919 | +8.1 |
| 3 | 1020 | 1050 | +2.9 | 1190 | 1226 | +3.0 |
| 4 | 1360 | 1382 | +1.6 | 1530 | 1520 | −0.7 |
| n | Analytical Amplitudes (dB) | Experimental Amplitudes (dB) | Delta Amplitudes (dB) |
|---|---|---|---|
| 0 | 16.1 | 16.6 | +0.5 |
| 1 | 16.1 | 19.0 | +2.9 |
| 2 | 16.1 | 12.8 | −3.3 |
| 3 | 16.1 | 20.2 | +4.1 |
| 4 | 16.1 | 15.6 | −0.6 |
| n | FEM fmin (Hz) | Delta fmin (%) | FEM fmax (Hz) | Delta fmax (%) | FEM Amplitudes (dB) | Delta Amplitudes (dB) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0.0 | 170 | 0.0 | 16.1 | 0.0 |
| 1 | 348 | 0.0 | 510 | 0.0 | 16.1 | 0.0 |
| 2 | 680 | 0.0 | 850 | 0.0 | 16.1 | 0.0 |
| 3 | 1040 | 0.0 | 1190 | 0.0 | 16.5 | +0.4 |
| 4 | 1370 | 0.0 | 1530 | 0.0 | 16.7 | +0.6 |
| n | FEM Discontinuty fmin (Hz) | Delta fmin (%) | FEM Discontinuty fmax (Hz) | Delta fmax (%) | FEM Discontinuty Amplitudes (dB) | Delta Amplitudes (dB) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0.0 | 220 | 0.0 | 16.3 | −0.3 |
| 1 | 348 | 0.0 | 510 | +0.4 | 19.3 | +0.3 |
| 2 | 680 | −0.7 | 860 | −5.7 | 12.0 | −0.8 |
| 3 | 1040 | −0.9 | 1220 | −0.5 | 19.5 | −0.7 |
| 4 | 1370 | −0.9 | 1510 | −0.7 | 16.4 | +0.8 |
| n | Experimental fmin (Hz) | FEM fmin (Hz) | Delta fmin (%) | Experimental fmax (Hz) | FEM fmax (Hz) | Delta fmax (%) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.0 | 119 | 120 | +0.8 |
| 1 | 195 | 190 | −2.6 | 288 | 290 | +0.7 |
| 2 | 351 | 350 | −0.3 | 448 | 460 | +2.7 |
| 3 | 511 | 510 | −0.2 | 584 | 570 | −2.4 |
| 4 | 668 | 675 | +1.0 | 731 | 750 | +2.6 |
| 5 | 838 | 840 | +0.2 | 911 | 930 | +2.1 |
| 6 | 1008 | 1020 | +1.2 | 1110 | 1130 | +1.8 |
| 7 | 1206 | 1220 | +1.2 | 1304 | 1310 | +0.5 |
| 8 | 1376 | 1375 | −0.1 | 1467 | 1480 | +0.9 |
| 9 | 1527 | 1545 | +1.2 | 1632 | 1660 | +1.7 |
| 10 | 1674 | 1680 | +0.4 | 1754 | 1710 | −2.5 |
| 11 | 1848 | 1860 | +0.6 | 1918 | 1930 | +0.6 |
| 12 | 2015 | 2020 | +0.2 | 2098 | 2100 | +0.1 |
| 13 | 2182 | 2160 | −1.0 | 2248 | 2250 | +0.1 |
| n | Experimental Amplitudes (dB) | FEM Amplitudes (dB) | Delta Amplitudes (dB) |
|---|---|---|---|
| 0 | 9.4 | 6.3 | −3.1 |
| 1 | 14.8 | 12.2 | −2.6 |
| 2 | 23.0 | 21.2 | −1.8 |
| 3 | 67.3 | 62.5 | −4.8 |
| 4 | 18.0 | 16.2 | −1.8 |
| 5 | 9.0 | 7.4 | +1.6 |
| 6 | 5.2 | 5.3 | +0.1 |
| 7 | 8.6 | 7.2 | −1.4 |
| 8 | 9.4 | 13.4 | +4.0 |
| 9 | 13.7 | 23.1 | +9.4 |
| 10 | 49.9 | 48.8 | −1.1 |
| 11 | 15.0 | 10.2 | −4.8 |
| 12 | 10.2 | 7.3 | −2.9 |
| 13 | 6.1 | 9.2 | +3.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyaw Oo D’Amore, G.; Biot, M.; Mauro, F.; Kašpar, J. Green Shipping—Multifunctional Marine Scrubbers for Emission Control: Silencing Effect. Appl. Sci. 2021, 11, 9079. https://doi.org/10.3390/app11199079
Kyaw Oo D’Amore G, Biot M, Mauro F, Kašpar J. Green Shipping—Multifunctional Marine Scrubbers for Emission Control: Silencing Effect. Applied Sciences. 2021; 11(19):9079. https://doi.org/10.3390/app11199079
Chicago/Turabian StyleKyaw Oo D’Amore, Giada, Marco Biot, Francesco Mauro, and Jan Kašpar. 2021. "Green Shipping—Multifunctional Marine Scrubbers for Emission Control: Silencing Effect" Applied Sciences 11, no. 19: 9079. https://doi.org/10.3390/app11199079
APA StyleKyaw Oo D’Amore, G., Biot, M., Mauro, F., & Kašpar, J. (2021). Green Shipping—Multifunctional Marine Scrubbers for Emission Control: Silencing Effect. Applied Sciences, 11(19), 9079. https://doi.org/10.3390/app11199079







