Integration of Functional Link Neural Networks into a Parameter Estimation Methodology
Abstract
:1. Introduction
2. Conventional LSM-Based RSM
3. Proposed Dual-Response Model Based on Functional Link NNs
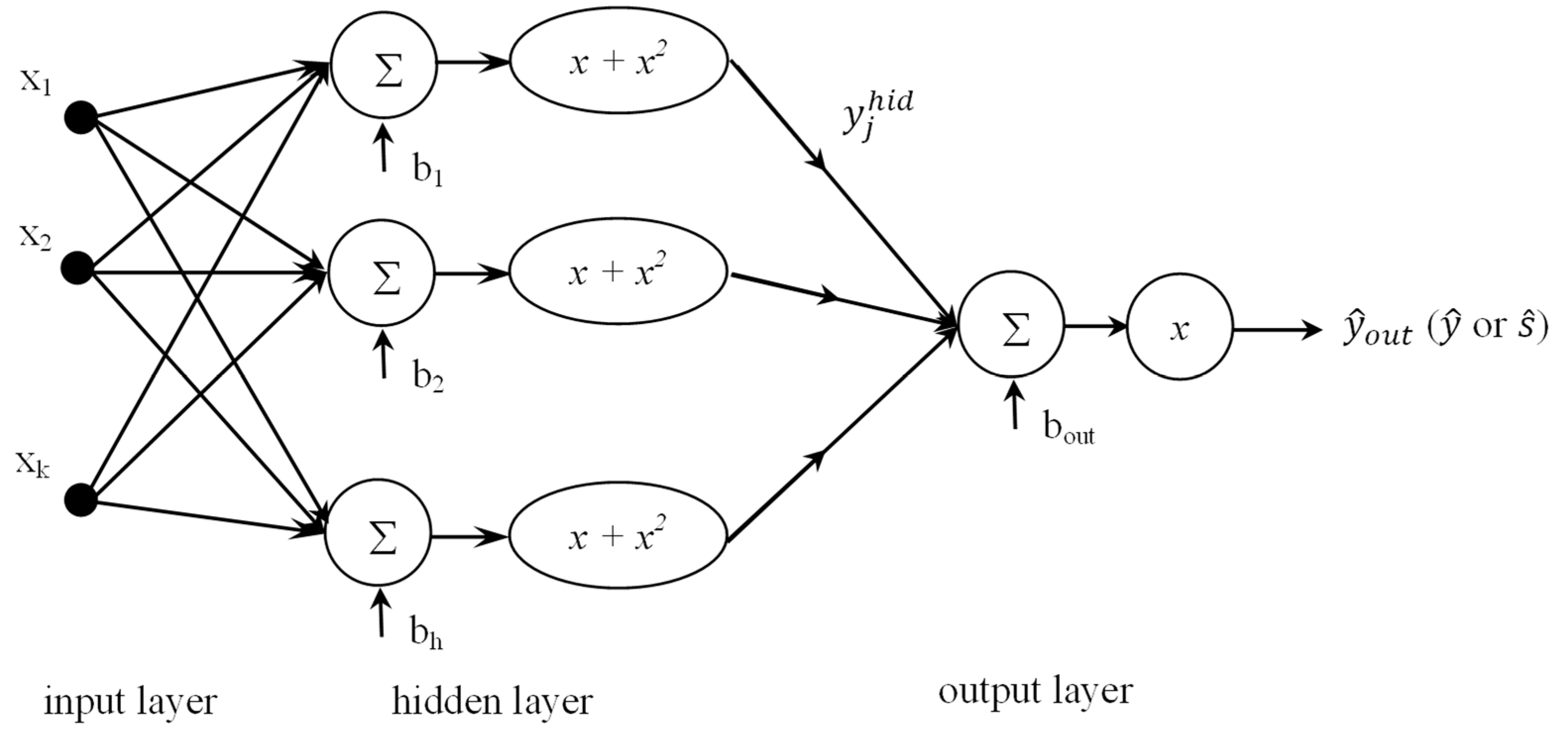
3.1. Proposed Functional Link NN
3.2. Learning Algorithm
3.3. Number of Hidden Neurons
4. Case Study
5. Conclusions and Further Studies
Author Contributions
Funding
Conflicts of Interest
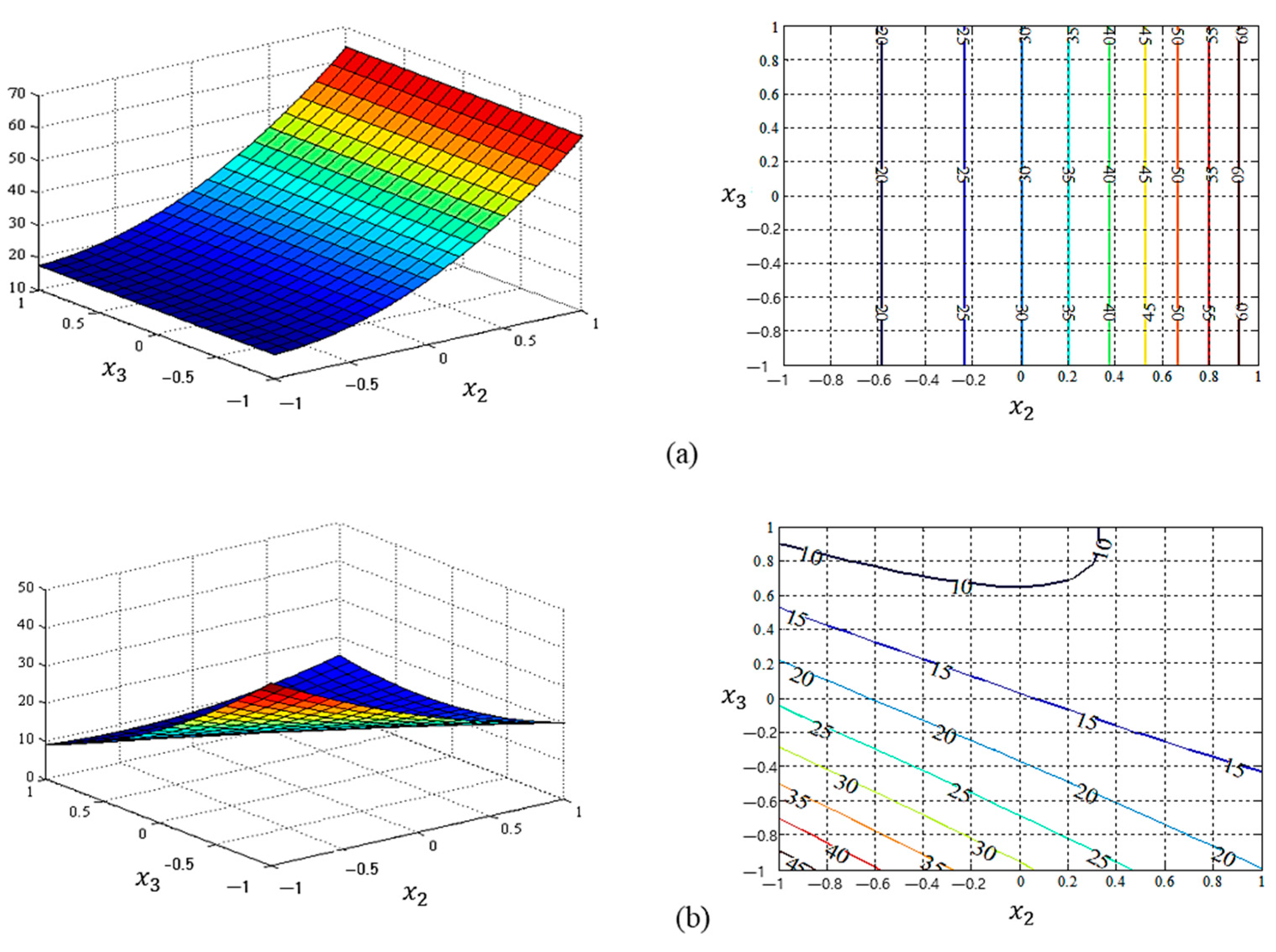
Appendix A. The Estimated Regression Formulas of the Process Mean and Standard Deviation



Appendix B. MATLAB Codes to Perform Estimative Regression Functions of Means and Standard Deviations by Using the Proposed NN Method
| MAIN FUNCTION %% Preparation %% data load dataprint.mat Target_mean = 500; y_mean = [dataprint(:,7)]; y_std = [dataprint(:,8)]; y_var = [dataprint(:,9)]; format long g %% prepare data X_NN = [dataprint(:,1:3)]’; y_mean_NN = y_mean’; y_std_NN = y_std’; y_var_NN = y_var’; samplesize_mean = size(y_mean_NN,2); sample_mean = size(y_mean_NN,1); samplesize_std = size(y_std_NN,2); sample_std = size(y_std_NN,1); [m,n] = size(X_NN); best1 = 1; best2 = 1; minBIC1 = 10e10; minBIC2 = 10e10; for i = 1:25 [net1, err1] = create_Poly2_mean(X_NN, y_mean_NN, i); mse1 = mse(err1); BIC1 = samplesize_mean*log(mse1/samplesize_mean) + m*log(samplesize_mean); if BIC1 <= minBIC1 minBIC1 = BIC1; best1 = i; end end Hidden_neuron_mean = best1; [net_mean_trained, err1] = create_Poly2_mean(X_NN, y_mean_NN, best1); mean_fun = @(x) sim(net_mean_trained, x); W_in_hid_mean = net_mean_trained.IW{1,1}; W_hid_out_mean = net_mean_trained.LW{2,1}; b_in_hid_mean = net_mean_trained.b{1,1}; b_hid_out_mean = net_mean_trained.b{2,1}; for j = 1:25 [net2, err2] = create_Poly2_std(X_NN, y_std_NN, j); mse2 = mse(err2); BIC2 = samplesize_std*log(mse2/samplesize_std) + m*log(samplesize_std); if BIC2 <= minBIC2 minBIC2 = BIC2; best2 = j; end end Hidden_neuron_std = best2; [net_std_trained, err2] = create_Poly2_std(X_NN, y_std_NN, best2); std_fun = @(x) sim(net_std_trained, x); W_in_hid_std = net_std_trained.IW{1,1}; W_hid_out_std = net_std_trained.LW{2,1}; b_in_hid_std = net_std_trained.b{1,1}; b_hid_out_std = net_std_trained.b{2,1}; %% NN_MSE: Optimal solutions options = optimset(‘Algorithm’,’interior-point’); objfun_NN = @(x) (mean_fun(x)-Target_mean)^2 + std_fun(x)^2; [x_opt_NN fval_opt_NN] = fmincon(objfun_NN, x0, [[], [[], [[], [[], lb, ub,[[],options); meanfun_opt_NN = mean_fun(x_opt_NN); stdfun_opt_NN = std_fun(x_opt_NN); results_MSE_NN = [x_opt_NN’ meanfun_opt_NN abs(meanfun_opt_NN-Target_mean) stdfun_opt_NN^2 fval_opt_NN] SUB-FUNCTION (TRAIN MEAN FUNCTION) |
| function [net,err] = create_Poly2_mean(inputs, targets, numHiddenNeurons) Number_Input = size(inputs,1); Number_Output = size(targets,1); net = Poly2_mean(Number_Input,Number_Output,numHiddenNeurons); %% Train and Apply Network net.trainFcn = ‘trainlm’; net.performFcn = ‘mse’; net.trainParam.epochs = 1000; net.trainParam.goal = 1e-5; net.trainParam.lr = 0.05;net.trainParam.show = 50; net.trainParam.showWindow = true; net.trainParam.max_fail = 100; net.divideFcn = ‘dividerand’; net = init(net); net.plotFcns = {‘plotperform’,’plottrainstate’,’plotregression’,’plotfit’}; [net,tr] = train(net,inputs,targets); bestEpoch = tr.best_epoch; trained = sim(net,inputs); err = targets-trained; end SUB-FUNCTION (TRAIN STANDARD DEVIATION FUNCTION) function [net,err] = create_Poly2_std(inputs, targets, numHiddenNeurons) Number_Input = size(inputs,1); Number_Output = size(targets,1); net = Poly2_std(Number_Input,Number_Output,numHiddenNeurons); %% Train and Apply Network net.trainFcn = ‘trainlm’; net.performFcn = ‘mse’; net.trainParam.epochs = 1000; net.trainParam.goal = 1e-5; net.trainParam.lr = 0.05; net.trainParam.show = 50; net.trainParam.showWindow = true; net.trainParam.max_fail = 100; net.divideFcn = ‘dividerand’; net = init(net); net.plotFcns = {‘plotperform’,’plottrainstate’,’plotregression’,’plotfit’}; [net,tr] = train(net,inputs,targets); bestEpoch = tr.best_epoch; trained = sim(net,inputs); err = targets-trained; end SUB-FUNCTION (CREATE MEAN FUNCTION) function net = Poly2_mean(Number_Input, Number_Output, numHiddenNeurons) net = network; %% Architect net.numInputs = 1; net.numLayers = 2; net.biasConnect(1) = 1; net.biasConnect(2) = 1; net.inputConnect(1,1) = 1; net.outputConnect = [0 1]; net.layerConnect = [0 0; 1 0]; %% layer1 net.inputs{1}.size = Number_Input; net.layers{1}.size = numHiddenNeurons; net.layers{1}.transferFcn = ‘Polyfunc2’; net.layers{1}.initFcn = ‘initnw’; %% layer2net.layers{2}.size = Number_Output; net.layers{2}.transferFcn = ‘purelin’; net.layers{2}.initFcn = ‘initnw’; %% net functionnet.initFcn = ‘initlay’; end SUB-FUNCTION (CREATE STANDARD DEVIATION FUNCTION) function net = Poly2_std(Number_Input, Number_Output, numHiddenNeurons) net = network; %% Architect net.numInputs = 1; net.numLayers = 2; net.biasConnect(1) = 1; net.biasConnect(2) = 1; net.inputConnect(1,1) = 1;net.outputConnect = [0 1]; net.layerConnect = [0 0; 1 0]; %% layer1 net.inputs{1}.size = Number_Input; net.layers{1}.size = numHiddenNeurons; net.layers{1}.transferFcn = ‘Polyfunc2_std’; net.layers{1}.initFcn = ‘initnw’; %% layer2 net.layers{2}.size = Number_Output; net.layers{2}.transferFcn = ‘purelin’; net.layers{2}.initFcn = ‘initnw’; %% net function net.initFcn = ‘initlay’; end SUB-FUNCTION (INTEGRATE FUNCTIONAL LINK TRANSFER FUNCTION INTO NN-BASED MEAN FUNCTION) function out1 = Polyfunc2(in1,in2,in3,in4) fn = mfilename; boiler_transfer %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Name function n = name n = ‘Quadratic’; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Output range function r = output_range(fp) r = [-inf +inf]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Active input range function r = active_input_range(fp) r = [-inf +inf]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Defaults function fp = param_defaults(values) fp = struct; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Names function names = param_names names = {}; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Check function err = param_check(fp) err = ‘‘; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Apply Transfer Function function a = apply_transfer(n,fp) a = n.^2 + n; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Derivative of Y w/respect to X function da_dn = derivative(n,a,fp) da_dn = 2*n +1; SUB-FUNCTION (INTEGRATE FUNCTIONAL LINK TRANSFER FUNCTION INTO NN-BASED STANDARD DEVIATION FUNCTION) function out1 = Polyfunc2_std(in1,in2,in3,in4) fn = mfilename; boiler_transfer %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Name function n = name n = ‘Quadratic polynomial Function’; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Output range function r = output_range(fp) r = [-inf +inf]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Active input range function r = active_input_range(fp) r = [-inf +inf]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Defaults function fp = param_defaults(values) fp = struct; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Names function names = param_names names = {}; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Parameter Checkfunction err = param_check(fp)err = ‘‘;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Apply Transfer Function function a = apply_transfer(n,fp) a = n + n.^2–11; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Derivative of Y w/respect to X function da_dn = derivative(n,a,fp) da_dn = 1 + 2*n; |
References
- Bendell, A.; Disney, J.; Pridmore, W.A. Taguchi Methods: Applications in World Industry; International Foundation for Science Publications: Bedford, UK, 1989; pp. 1–26. [Google Scholar]
- Dehnad, K. Quality Control, Robust Design and the Taguchi Method; Wadsworth and Brooks/Cole: Pacific Grove, CA, USA, 1989; pp. 243–254. [Google Scholar]
- Taguchi, G. Introduction to Quality Engineering: Designing Quality Into Products and Processes; Kraus International Publications: White Plains, NY, USA, 1986; pp. 153–176. [Google Scholar]
- León, R.V.; Shoemaker, A.C.; Kacker, R.N. Performance measures independent of adjustment: An explanation and extension of Taguchi’s signal-to-noise ratios. Technometrics 1987, 29, 253–265. [Google Scholar] [CrossRef]
- Box, G.E.P. Signal-to-noise ratios, performance criteria, and transformations. Technometrics 1988, 30, 1–17. [Google Scholar] [CrossRef]
- Box, G.; Bisgaard, S.; Fung, C. An explanation and critique of Taguchi’s contributions to quality engineering. Qual. Reliab. Eng. Int. 1988, 4, 123–131. [Google Scholar] [CrossRef]
- Nair, V.N.; Abraham, B.; MacKay, J.; Box, G.; Kacker, R.N.; Lorenzen, T.J.; Lucas, J.M.; Myers, R.H.; Vining, G.G.; Nelder, J.A.; et al. Taguchi’s parameter design: A panel discussion. Technometrics 1992, 34, 127–161. [Google Scholar] [CrossRef]
- Vining, G.G.; Myers, R.H. Combining Taguchi and response surface philosophies: A dual response approach. J. Qual. Technol. 1990, 22, 38–45. [Google Scholar] [CrossRef]
- Del Castillo, E.; Montgomery, D.C. A nonlinear programming solution to the dual response problem. J. Qual. Technol. 1993, 25, 199–204. [Google Scholar] [CrossRef]
- Copeland, K.A.F.; Nelson, P.R. Dual response optimization via direct function minimization. J. Qual. Technol. 1996, 28, 331–336. [Google Scholar] [CrossRef]
- Lin, D.K.J.; Tu, W. Dual response surface optimization. J. Qual. Technol. 1995, 27, 34–39. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 1st ed.; John Wiley & Sons: New York, NY, USA, 1995; pp. 1–12. [Google Scholar]
- Box-Steffensmeier, J.M.; Brady, H.E.; Collier, D. (Eds.) Oxford handbooks online. In The Oxford Handbook of Political Methodology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Lee, S.B.; Park, C.S. Development of robust design optimization using incomplete data. Comput. Ind. Eng. 2006, 50, 345–356. [Google Scholar] [CrossRef]
- Cho, B.R.; Choi, Y.; Shin, S. RETRACTED ARTICLE: Development of censored data-based robust design for pharmaceutical quality by design. Int. J. Adv. Manuf. Technol. 2010, 49, 839–851. [Google Scholar] [CrossRef]
- Cho, B.R.; Shin, S. Quality improvement and robust design methods to a pharmaceutical research and development. Math. Probl. Eng. 2012, 2012, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Luner, J.J. Achieving continuous improvement with the dual approach: A demonstration of the Roman catapult. Qual. Eng. 1994, 6, 691–705. [Google Scholar] [CrossRef]
- Cho, B.R.; Park, C.S. Robust design modeling and optimization with unbalanced data. Comput. Ind. Eng. 2005, 48, 173–180. [Google Scholar] [CrossRef]
- Irie, B.; Miyake, S. Capabilities of three-layered perceptrons. In Proceedings of the IEEE International Conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; pp. 641–648. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signal. Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Funahashi, K. On the approximate realization of continuous mappings by neural networks. Neural Netw. 1989, 2, 183–192. [Google Scholar] [CrossRef]
- Rowlands, H.; Packianather, M.S.; Oztemel, E. Using artificial neural networks for experimental design in off-line quality. J. Syst. Eng. 1996, 6, 46–59. [Google Scholar]
- Shin, S.; Hoang, T.T.; Le, T.H.; Lee, M.Y. A new robust design method using neural network. J. Nanoelectron. Optoelectron. 2016, 11, 68–78. [Google Scholar] [CrossRef]
- Arungpadang, T.R.; Kim, Y.J. Robust parameter design based on back propagation neural network. Korean Manag. Sci. Rev. 2012, 29, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Le, T.H.; Jang, H.; Shin, S. Determination of the Optimal Neural Network Transfer Function for Response Surface Methodology and Robust Design. Appl. Sci. 2021, 11, 6768. [Google Scholar] [CrossRef]
- Su, C.T.; Hsieh, K.L. Applying neural network approach to achieve robust design for dynamic quality characteristics. Int. J. Qual. Reliab. Manag. 1998, 15, 509–519. [Google Scholar] [CrossRef]
- Cook, D.F.; Ragsdale, C.T.; Major, R.L. Combining a neural network with a genetic algorithm for process parameter optimization. Eng. Appl. Artif. Intell. 2000, 13, 391–396. [Google Scholar] [CrossRef]
- Chow, T.T.; Zhang, G.Q.; Lin, Z.; Song, C.L. Global optimization of absorption chiller system by genetic algorithm and neural network. Energy Build. 2002, 34, 103–109. [Google Scholar] [CrossRef]
- Chang, H.H. Applications of neural networks and genetic algorithms to Taguchi’s robust design. Int. J. Electron. Bus. 2005, 3, 90–96. [Google Scholar]
- Chang, H.H.; Chen, Y.K. Neuro-genetic approach to optimize parameter design of dynamic multiresponse experiments. Appl. Soft Comput. 2011, 11, 436–442. [Google Scholar] [CrossRef]
- Arungpadang, T.A.R.; Tangkuman, S.; Patras, L.S. Dual Response Approach in Process Capability based on Hybrid Neural Network-Genetic Algorithms. JoSEPS 2019, 1, 117–122. [Google Scholar] [CrossRef] [Green Version]
- Villa-Murillo, A.; Carrión, A.; Sozzi, A. Forest-Genetic method to optimize parameter design of multiresponse experiment. Intel. Artif. 2020, 23, 9–25. [Google Scholar]
- Radosław, W.; Krzysztof, G.; Agnieszka, K.; Monika, J.M. Optimisation of ANN topology for predicting the rehydrated apple cubes colour change using RSM and GA. Neural Comput. Appl. 2018, 30, 1795–1809. [Google Scholar]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions [With discussion]. J. R. Stat. Soc. B 1951, 13, 1–38. [Google Scholar]
- Myers, R.H. Response surface methodology—Current status and future directions. J. Qual. Technol. 1999, 31, 30–44. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. WIREs Comp. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Box, G.E.P.; Draper, N.R. Empirical Model—Building and Response Surfaces; John Wiley & Sons: New York, NY, USA, 1987; pp. 1–669. [Google Scholar]
- Khuri, A.I.; Cornell, J.A. Response Surface: Design and Analyses, 1st ed.; CRC Press: New York, NY, USA, 1987; pp. 1–536. [Google Scholar]
- Hartman, E.J.; Keeler, J.D.; Kowalski, J.M. Layered neural networks with Gaussian hidden units as universal approximations. Neural Comput. 1990, 2, 210–215. [Google Scholar] [CrossRef]
- Javadikia, P.; Rafiee, S.; Garavand, A.T.; Keyhani, A. Modeling of moisture content in tomato drying process by ANN-GA technique. In Proceedings of the 1st International Econference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 13–14 October 2011; IEEE Publications: Piscataway, NJ, USA, 2011; Volume 2011, pp. 162–165. [Google Scholar]
- Duch, W.; Jankowski, N. Transfer functions: Hidden possibilities for better neural networks. In Proceedings of the ESANN 2001, 9th European Symposium on Artificial Neural Networks, Bruges, Belgium, 25–27 April 2001; pp. 81–94. [Google Scholar]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef] [Green Version]





| Treatment Combinations | Coefficients | |
|---|---|---|
| Constant | 327.630 | 34.883 |
| 177.000 | 11.527 | |
| 109.430 | 15.323 | |
| 131.460 | 29.190 | |
| 32.000 | 4.204 | |
| −22.389 | −1.316 | |
| −29.056 | 16.778 | |
| 66.028 | 7.720 | |
| 75.472 | 5.109 | |
| 43.583 | 14.082 | |
| Objective | Response Function | Training Algorithm | Structure | No. of Epoch |
|---|---|---|---|---|
| Mean | mse | Trainlm | 3-21-1 | 13 |
| Std | mse | Trainlm | 3-2-1 | 12 |
| Weight | Bias | ||||
|---|---|---|---|---|---|
| 0.96075 | 0.11736 | 1.54028 | 2.10096 | 3.63174 | 1.00092 |
| 0.75123 | 0.38223 | 0.73934 | 1.62200 | 0.77913 | |
| −0.28537 | −0.34012 | −0.80124 | 2.30133 | 3.88614 | |
| 1.17461 | 0.63199 | 1.11264 | 1.73056 | 1.68918 | |
| 0.27560 | 0.60510 | −0.26521 | −0.48992 | −0.70557 | |
| −0.72625 | 0.41018 | 0.21240 | −0.11370 | −0.84332 | |
| −0.45138 | −0.37180 | 0.56006 | −1.03860 | −0.39605 | |
| −0.40578 | −0.11631 | −0.02559 | −0.09612 | −0.44870 | |
| 0.75884 | −0.59636 | −0.37276 | −0.29991 | −0.43415 | |
| 2.86524 | 1.95064 | 1.96605 | 4.72650 | 5.36510 | |
| −1.13144 | −0.73588 | −1.17218 | 0.84079 | −1.47882 | |
| −0.06226 | −0.41228 | −0.58818 | 0.40969 | 0.05234 | |
| 0.32760 | −0.75682 | −0.67588 | −0.11504 | −0.02238 | |
| −0.01851 | −0.81573 | 0.01320 | −0.27318 | −0.58988 | |
| 0.11633 | 0.16928 | 0.17376 | −0.45037 | −0.88337 | |
| −0.68532 | 0.37096 | −0.27889 | −0.27210 | 0.04470 | |
| −0.27500 | −0.52907 | 0.34659 | −0.85252 | −0.31859 | |
| 0.91857 | 0.59698 | 0.76126 | 0.59614 | 0.80572 | |
| 0.29861 | −0.39570 | 0.10545 | 0.28709 | 0.51167 | |
| 0.56297 | −0.03477 | −0.09037 | 0.43088 | 0.67887 | |
| 0.10126 | −0.37625 | −0.01066 | −0.64268 | −0.36799 | |
| Weight | Bias | ||||
|---|---|---|---|---|---|
| −2.04505 | −3.02946 | −4.90330 | 0.86246 | −4.32652 | −0.01267 |
| −0.38368 | −1.22474 | −0.62419 | −2.32404 | −2.08030 | |
| Estimation Model | Optimal Factor Settings | Process Mean | Process Bias | Process Variance | EQL | ||
|---|---|---|---|---|---|---|---|
| LSM | 1.0000 | 0.07153 | −0.25028 | 494.67226 | 5.32773 | 1977.53266 | 2005.91742 |
| Proposed NN | 0.99999 | 0.99999 | −0.79327 | 496.39189 | 3.60810 | 450.64771 | 463.66611 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.-H.; Tang, M.; Jang, J.H.; Jang, H.; Shin, S. Integration of Functional Link Neural Networks into a Parameter Estimation Methodology. Appl. Sci. 2021, 11, 9178. https://doi.org/10.3390/app11199178
Le T-H, Tang M, Jang JH, Jang H, Shin S. Integration of Functional Link Neural Networks into a Parameter Estimation Methodology. Applied Sciences. 2021; 11(19):9178. https://doi.org/10.3390/app11199178
Chicago/Turabian StyleLe, Tuan-Ho, Mengyuan Tang, Jun Hyuk Jang, Hyeonae Jang, and Sangmun Shin. 2021. "Integration of Functional Link Neural Networks into a Parameter Estimation Methodology" Applied Sciences 11, no. 19: 9178. https://doi.org/10.3390/app11199178
APA StyleLe, T.-H., Tang, M., Jang, J. H., Jang, H., & Shin, S. (2021). Integration of Functional Link Neural Networks into a Parameter Estimation Methodology. Applied Sciences, 11(19), 9178. https://doi.org/10.3390/app11199178





