Prediction of Beck Depression Inventory Score in EEG: Application of Deep-Asymmetry Method
Abstract
:1. Introduction
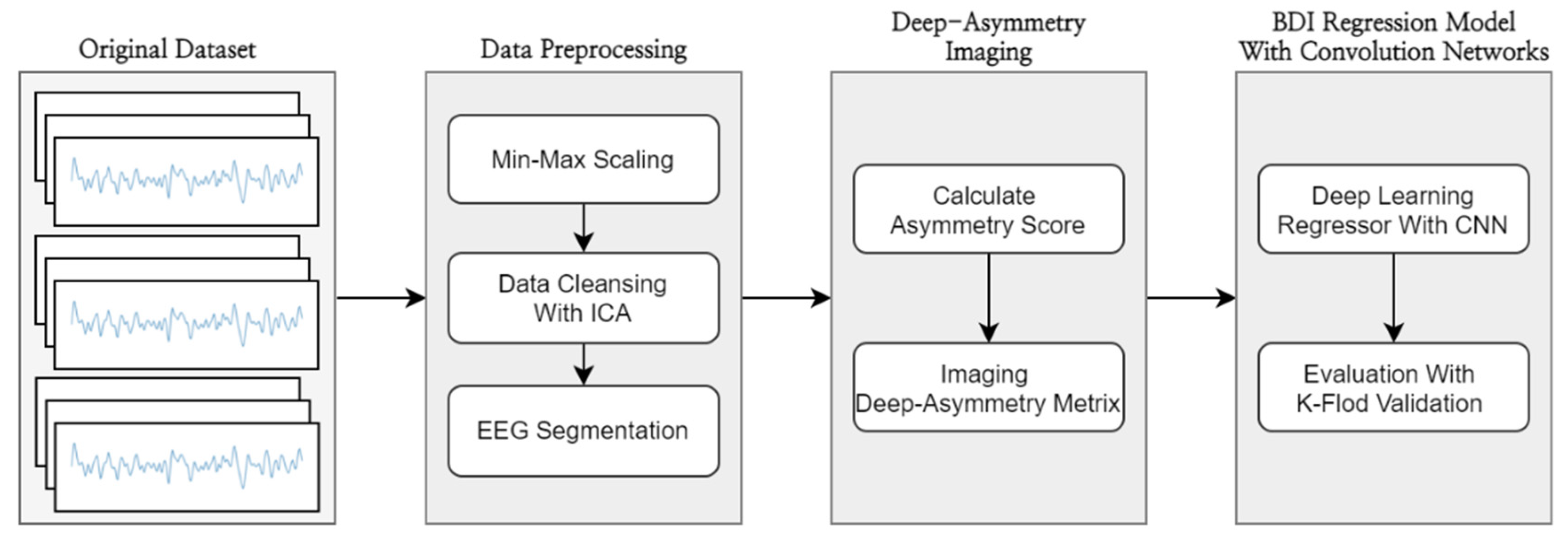
2. Materials and Methods
2.1. Dataset
2.2. Data Preprocessing
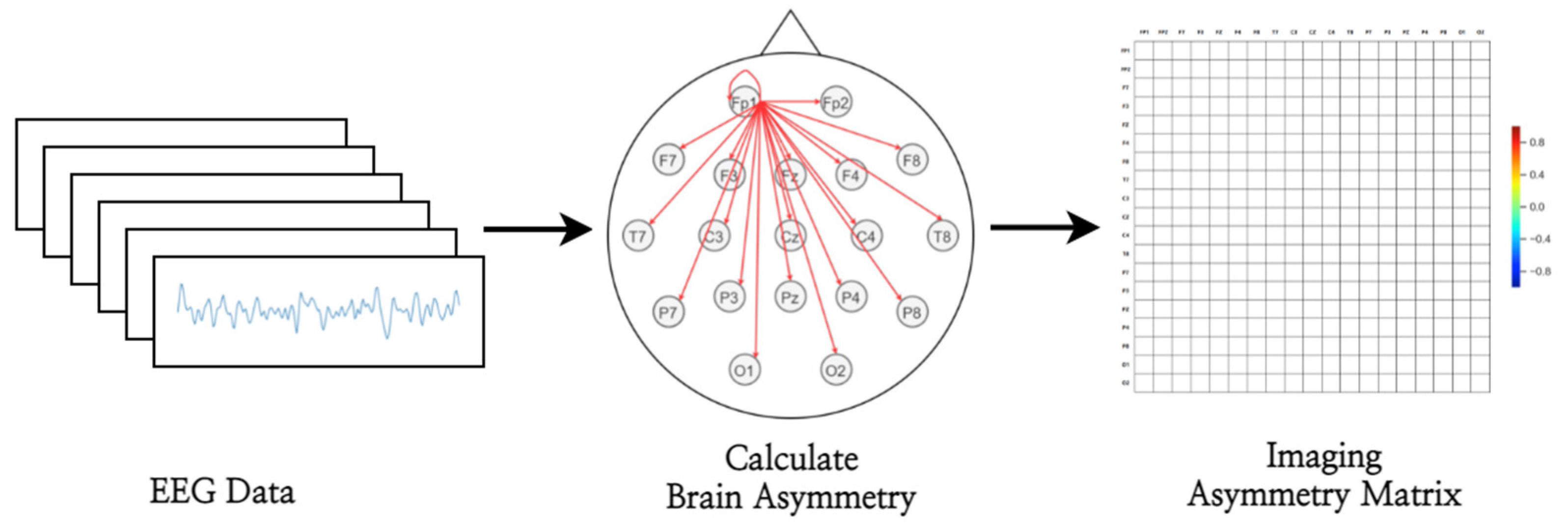
2.3. Deep-Asymmetry Imaging
2.3.1. Brain Asymmetry Score Calculator
2.3.2. Asymmetry Matrix Imager
2.4. BDI Regression Model
2.5. Evaluation Metrics
2.6. Model Training
3. Results
3.1. Deep-Asymmetry Image
3.2. BDI Regression Model Performance
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, Y.-T.; Kim, Y.S.; Yi, B.-K.; Kim, S.M. Clinical decision support functions and digitalization of clinical documents of electronic medical record systems. Healthc. Inform. Res. 2019, 25, 115–123. [Google Scholar] [CrossRef] [Green Version]
- Garg, A.X.; Adhikari, N.K.; McDonald, H.; Rosas-Arellano, M.P.; Devereaux, P.J.; Beyene, J.; Sam, J.; Haynes, R.B. Effects of computerized clinical decision support systems on practitioner performance and patient outcomes: A systematic review. JAMA 2005, 293, 1223–1238. [Google Scholar] [CrossRef]
- Parekh, R. What Is Depression? Available online: https://www.psychiatry.org/patients-families/depression/what-is-depression (accessed on 1 July 2021).
- Smith, K.M.; Renshaw, P.F.; Bilello, J. The diagnosis of depression: Current and emerging methods. Compr. Psychiatry 2013, 54, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Association: Arlington, VA, USA, 2013.
- Brenner, L. Beck Anxiety Inventory. Encyclopedia of Clinical Neuropsychology. 2011. Available online: http://www.springerreference.com/docs/html/chapterdbid/184603 (accessed on 1 July 2021).
- Williams, J.B. A structured interview guide for the Hamilton Depression Rating Scale. Arch. Gen. Psychiatry 1988, 45, 742–747. [Google Scholar] [CrossRef]
- Shetty, P.; Mane, A.; Fulmali, S.; Uchit, G. Understanding masked depression: A Clinical scenario. Indian J. Psychiatry 2018, 60, 97. [Google Scholar] [PubMed]
- Rekik, I.; Allassonnière, S.; Carpenter, T.K.; Wardlaw, J.M. Medical image analysis methods in MR/CT-imaged acute-subacute ischemic stroke lesion: Segmentation, prediction and insights into dynamic evolution simulation models. A critical appraisal. Neuroimage Clin. 2012, 1, 164–178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nouretdinov, I.; Costafreda, S.G.; Gammerman, A.; Chervonenkis, A.; Vovk, V.; Vapnik, V.; Fu, C.H.Y. Machine learning classification with confidence: Application of transductive conformal predictors to MRI-based diagnostic and prognostic markers in depression. NeuroImage 2011, 56, 809–813. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.L.; Shen, H.; Liu, L.; Hu, D. Unsupervised classification of major depression using functional connectivity MRI. Hum. Brain Mapp. 2014, 35, 1630–1641. [Google Scholar] [CrossRef]
- Durongbhan, P.; Zhao, Y.; Chen, L.; Zis, P.; De Marco, M.; Unwin, Z.C.; Venneri, A.; He, X.; Li, S.; Zhao, Y. A dementia classification framework using frequency and time-frequency features based on EEG signals. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 826–835. [Google Scholar] [CrossRef] [Green Version]
- Aslan, Z.; Akin, M. Automatic Detection of Schizophrenia by Applying Deep Learning over Spectrogram Images of EEG Signals. Traitement Signal 2020, 37, 235–244. [Google Scholar] [CrossRef]
- Lee, S.-H.; Lim, J.S.; Kim, J.-K.; Yang, J.; Lee, Y. Classification of normal and epileptic seizure EEG signals using wavelet transform, phase-space reconstruction, and Euclidean distance. Comput. Methods Programs Biomed. 2014, 116, 10–25. [Google Scholar] [CrossRef]
- De Aguiar Neto, F.S.; Rosa, J.L.G. Depression biomarkers using non-invasive EEG: A review. Neurosci. Biobehav. Rev. 2019, 105, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.L.; Coan, J.A.; Towers, D.N.; Allen, J.J. Frontal EEG asymmetry during emotional challenge differentiates individuals with and without lifetime major depressive disorder. J. Affect. Disord. 2011, 129, 167–174. [Google Scholar] [CrossRef] [Green Version]
- Cantisani, A.; Koenig, T.; Horn, H.; Müller, T.; Strik, W.; Walther, S. Psychomotor retardation is linked to frontal alpha asymmetry in major depression. J. Affect. Disord. 2015, 188, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Mumtaz, W.; Xia, L.; Ali, S.S.A.; Yasin, M.A.M.; Hussain, M.; Malik, A.S. Electroencephalogram (EEG)-based computer-aided technique to diagnose major depressive disorder (MDD). Biomed. Signal Process. Control 2017, 31, 108–115. [Google Scholar] [CrossRef]
- Mahato, S.; Paul, S. Classification of depression patients and normal subjects based on electroencephalogram (EEG) signal using alpha power and theta asymmetry. J. Med. Syst. 2020, 44, 28. [Google Scholar] [CrossRef]
- Mahato, S.; Paul, S. Detection of major depressive disorder using linear and non-linear features from EEG signals. Microsyst. Technol. 2019, 25, 1065–1076. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adeli, H.; Subha, D.P. Automated EEG-based screening of depression using deep convolutional neural network. Comput. Methods Programs Biomed. 2018, 161, 103–113. [Google Scholar] [CrossRef]
- Mumtaz, W.; Qayyum, A. A deep learning framework for automatic diagnosis of unipolar depression. Int. J. Med. Inform. 2019, 132, 103983. [Google Scholar] [CrossRef] [PubMed]
- Kwon, H.; Park, J.; Kang, S.; Lee, Y. Imagery Signal-Based Deep Learning Method for Prescreening Major Depressive Disorder. In Proceedings of the Cognitive Computing—ICCC 2019, Cham, Switzerland, 25–30 June 2019; pp. 180–185. [Google Scholar]
- Kwon, H.; Kang, S.; Park, W.; Park, J.; Lee, Y. Deep Learning based Pre-screening method for Depression with Imagery Frontal EEG Channels. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 16–18 October 2019; pp. 378–380. [Google Scholar]
- Li, X.; La, R.; Wang, Y.; Hu, B.; Zhang, X. A Deep Learning Approach for Mild Depression Recognition Based on Functional Connectivity Using Electroencephalography. Front. Neurosci. 2020, 14, 192. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; La, R.; Wang, Y.; Niu, J.; Zeng, S.; Sun, S.; Zhu, J. EEG-based mild depression recognition using convolutional neural network. Med. Biol. Eng. Comput. 2019, 57, 1341–1352. [Google Scholar] [CrossRef]
- Saeedi, A.; Saeedi, M.; Maghsoudi, A.; Shalbaf, A. Major depressive disorder diagnosis based on effective connectivity in EEG signals: A convolutional neural network and long short-term memory approach. Cogn. Neurodyn. 2021, 15, 239–252. [Google Scholar] [CrossRef]
- Loh, H.; Ooi, C.; Aydemir, E.; Tuncer, T.; Dogan, S.; Acharya, U.R. Decision support system for major depression detection using spectrogram and convolution neural network with EEG signals. Expert Syst. 2021, e12773. [Google Scholar] [CrossRef]
- Kang, M.; Kwon, H.; Park, J.-H.; Kang, S.; Lee, Y. Deep-Asymmetry: Asymmetry Matrix Image for Deep Learning Method in Pre-Screening Depression. Sensors 2020, 20, 6526. [Google Scholar] [CrossRef] [PubMed]
- Valstar, M.; Schuller, B.; Smith, K.; Eyben, F.; Jiang, B.; Bilakhia, S.; Schnieder, S.; Cowie, R.; Pantic, M. AVEC 2013: The continuous audio/visual emotion and depression recognition challenge. In Proceedings of the 3rd ACM International Workshop on Audio/Visual Emotion Challenge, Barcelona, Spain, 21 October 2013; pp. 3–10. [Google Scholar]
- Valstar, M.; Schuller, B.; Smith, K.; Almaev, T.; Eyben, F.; Krajewski, J.; Cowie, R.; Pantic, M. Avec 2014: 3d Dimensional affect and depression recognition challenge. In Proceedings of the 4th International Workshop on Audio/Visual Emotion Challenge, Orlando, FL, USA, 7 November 2014; pp. 3–10. [Google Scholar]
- Zhu, Y.; Shang, Y.; Shao, Z.; Guo, G. Automated Depression Diagnosis Based on Deep Networks to Encode Facial Appearance and Dynamics. IEEE Trans. Affect. Comput. 2018, 9, 578–584. [Google Scholar] [CrossRef]
- Melo, W.C.d.; Granger, E.; Hadid, A. Depression Detection Based on Deep Distribution Learning. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 4544–4548. [Google Scholar] [CrossRef] [Green Version]
- Cavanagh, J.F.; Bismark, A.; Frank, M.J.; Allen, J.J. Larger error signals in major depression are associated with better avoidance learning. Front. Psychol. 2011, 2, 331. [Google Scholar] [CrossRef] [Green Version]
- Cavanagh, J.F. EEG: Probabilistic Selection and Depression. OpenNeuro 2021. [Google Scholar] [CrossRef]
- Klem, G.H. The ten-twenty electrode system of the international federation. the internanional federation of clinical nenrophysiology. Electroencephalogr. Clin. Neurophysiol. Suppl. 1999, 52, 3–6. [Google Scholar]
- Patro, S.G.; Sahu, K.K. Normalization: A Preprocessing Stage. IARJSET 2015, 2, 20–22. [Google Scholar] [CrossRef]
- Jung, T.-P.; Makeig, S.; Humphries, C.; Lee, T.-W.; Mckeown, M.J.; Iragui, V.; Sejnowski, T.J. Removing electroencephalographic artifacts by blind source separation. Psychophysiology 2000, 37, 163–178. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef] [Green Version]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Weisstein, E.W. Simpson’s Rule. Available online: https://mathworld.wolfram.com/SimpsonsRule.html (accessed on 1 July 2021).
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the ICML 2010, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Stone, M. An asymptotic equivalence of choice of model by cross-validation and Akaike’s criterion. J. R. Stat. Soc. Ser. B 1977, 39, 44–47. [Google Scholar] [CrossRef]
- Park, J.-I.; Jeon, M. The stigma of mental illness in Korea. J. Korean Neuropsychiatr. Assoc. 2016, 55, 299–309. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-S.; Yang, B.-H.; Oh, D.-Y.; Kim, K. EEG A1, A2, and Percent Asymmetry Indices in Major Depressive Disorder; The Importance of Symptom Severity of Depression and Anxiety. J. Korean Neuropsychiatry 2007, 46, 179–184. [Google Scholar]
- Jung, K.H.; Lee, J.S.; Lee, J.H. Power Spectral Analysis EEG Characteristics of Major Depressive Disorder. Korean J. Clin. Psychol. 2008, 27, 581–593. [Google Scholar]
- Meerwijk, E.L.; Ford, J.M.; Weiss, S.J. Resting-state EEG delta power is associated with psychological pain in adults with a history of depression. Biol. Psychol. 2015, 105, 106–114. [Google Scholar] [CrossRef] [Green Version]
- Canolty, R.T.; Knight, R.T. The functional role of cross-frequency coupling. Trends Cogn. Sci. 2010, 14, 506–515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fitzgerald, P.J.; Watson, B.O. Gamma oscillations as a biomarker for major depression: An emerging topic. Transl. Psychiatry 2018, 8, 177. [Google Scholar] [CrossRef] [PubMed]
- Poppelaars, E.S.; Harrewijn, A.; Westenberg, P.M.; van der Molen, M.J.W. Frontal delta-beta cross-frequency coupling in high and low social anxiety: An index of stress regulation? Cogn. Affect. Behav. Neurosci. 2018, 18, 764–777. [Google Scholar] [CrossRef]
- Miskovic, V.; Moscovitch, D.A.; Santesso, D.L.; McCabe, R.E.; Antony, M.M.; Schmidt, L.A. Changes in EEG Cross-Frequency Coupling During Cognitive Behavioral Therapy for Social Anxiety Disorder. Psychol. Sci. 2011, 22, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Seghier, M.L.; Price, C.J. Interpreting and Utilising Intersubject Variability in Brain Function. Trends Cogn. Sci. 2018, 22, 517–530. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Ahmed, K.I.U.; Mostafa, R.; Hadjileontiadis, L.; Khandoker, A. Evidence of Variabilities in EEG Dynamics During Motor Imagery-Based Multiclass Brain–Computer Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 371–382. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Baumert, M. Intra- and Inter-subject Variability in EEG-Based Sensorimotor Brain Computer Interface: A Review. Front. Comput. Neurosci. 2020, 13, 87. [Google Scholar] [CrossRef] [Green Version]
- Lei, Z.; Samaras, D.; Tomasi, D.; Volkow, N.; Goldstein, R. Machine learning for clinical diagnosis from functional magnetic resonance imaging. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 1211–1217. [Google Scholar] [CrossRef]
- Chikara, R.K.; Ko, L.-W. Prediction of Human Inhibition Brain Function with Inter-Subject and Intra-Subject Variability. Brain Sci. 2020, 10, 726. [Google Scholar] [CrossRef]
- Teo, J.; Hou, C.L.; Mountstephens, J. Deep learning for EEG-Based preference classification. AIP Conf. Proc. 2017, 1891, 020141. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, Y.; Moradi, M.H. Prediction of Depression Severity Scores Based on Functional Connectivity and Complexity of the EEG Signal. Clin. EEG Neurosci. 2020, 52, 52–60. [Google Scholar] [CrossRef]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 30 June 2016; pp. 2921–2929. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Wang, Z.; Yang, J. Diabetic retinopathy detection via deep convolutional networks for discriminative localization and visual explanation. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- LaValle, S.M.; Branicky, M.S.; Lindemann, S.R. On the relationship between classical grid search and probabilistic roadmaps. Int. J. Robot. Res. 2004, 23, 673–692. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Mockus, J. Bayesian Approach to Global Optimization: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 37. [Google Scholar]
- Yoon, Y.; Kim, Y.-H. Optimizing Taxon Addition Order and Branch Lengths in the Construction of Phylogenetic Trees Using Maximum Likelihood. J. Bioinform. Comput. Biol. 2020, 18, 2050003. [Google Scholar] [CrossRef] [PubMed]









| Layer | Kernel Size (Pool Size) | Activation | Output Shape | Param # |
|---|---|---|---|---|
| Convolution 1D | 4 | ReLU | 5117, 64 | 4928 |
| MaxPooling 1D | 2 | 2558, 64 | 0 | |
| Convolution 1D | 2 | ReLU | 2557, 32 | 4128 |
| MaxPooling 1D | 2 | 1278, 32 | 0 | |
| Convolution 1D | 2 | ReLU | 1277, 16 | 1040 |
| MaxPooling 1D | 2 | 638, 16 | 0 | |
| Flatten | 10,208 | 0 | ||
| Dense | ReLU | 64 | 653,376 | |
| Dense | linear | 1 | 65 |
| Layer | Kernel Size (Pool Size) | Activation | Output Shape | Param # |
|---|---|---|---|---|
| Convolution 2D | 2 × 2 | ReLU | 683, 28, 16 | 208 |
| MaxPooling 2D | 2 × 2 | 341, 14, 16 | 0 | |
| Batch Normalization | 341, 14, 16 | 64 | ||
| Convolution 2D | 2 × 2 | ReLU | 340, 13, 16 | 520 |
| MaxPooling 2D | 2 × 2 | 170, 6, 8 | 0 | |
| Convolution 2D | 2 × 2 | ReLU | 168, 4, 4 | 292 |
| MaxPooling 2D | 2 × 2 | 84, 2, 4 | 0 | |
| Flatten | 672 | 0 | ||
| Dense | ReLU | 256 | 172,288 | |
| Dropout (0.25) | 256 | 0 | ||
| Dense | linear | 1 | 257 |
| Layer | Kernel Size (Pool Size) | Activation | Output Shape | Param # |
|---|---|---|---|---|
| Convolution 2D | 3 × 3 | ReLU | 62, 62, 32 | 896 |
| MaxPooling 2D | 2 × 2 | 31, 31, 32 | 0 | |
| Batch Normalization | 31, 31, 32 | 128 | ||
| Convolution 2D | 3 × 3 | ReLU | 29, 29, 64 | 18,496 |
| MaxPooling 2D | 2 × 2 | 14, 14, 64 | 0 | |
| Convolution 2D | 3 × 3 | ReLU | 12, 12, 128 | 73,856 |
| MaxPooling 2D | 2 × 2 | 6, 6, 128 | 0 | |
| Flatten | 4608 | 0 | ||
| Dense | ReLU | 256 | 1,179,904 | |
| Dropout (0.25) | 256 | 0 | ||
| Dense | linear | 1 | 257 |
| Signal-Based Baseline Model | Image-Based Baseline Model | Deep-Asymmetry Model | |
|---|---|---|---|
| Epoch | 20 | 10 | 10 |
| Batch size (step per epoch) | 128 | 48 (100) | 48 (100) |
| Loss Function | MSE | MSE | MSE |
| Optimizer | Adam | Adam | Adam |
| Learning rate | 0.001 | 0.0001 | 0.0001 |
| Band | RMSE | MAE |
|---|---|---|
| Delta | 10.30 | 9.14 |
| Theta | 10.39 | 9.58 |
| Alpha | 10.27 | 9.18 |
| Beta | 10.11 | 9.01 |
| Broadband | 10.11 | 8.91 |
| Band | RMSE | MAE |
|---|---|---|
| Broadband | 9.38 | 7.95 |
| Band | RMSE | MAE |
|---|---|---|
| Delta | 3.46 | 2.23 |
| Theta | 5.09 | 3.40 |
| Alpha | 4.17 | 2.76 |
| Beta | 4.45 | 2.83 |
| Broadband | 8.51 | 6.77 |
| Dataset | Method | RMSE | |
|---|---|---|---|
| [32] | AVEC2013 | Deep learning model based on joint-tuning layers | 9.82 |
| AVEC2014 | 9.55 | ||
| [33] | AVEC2013 | Deep learning model based on expectation loss | 8.25 |
| AVEC2014 | 8.23 | ||
| [61] | EEG dataset | A machine learning model based on functional connectivity feature extraction in EEG signals | 7.69 |
| Proposed | EEG dataset [35] | Deep learning model based on convolutional network using a deep-asymmetry image | 3.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.; Kang, S.; Lee, Y. Prediction of Beck Depression Inventory Score in EEG: Application of Deep-Asymmetry Method. Appl. Sci. 2021, 11, 9218. https://doi.org/10.3390/app11199218
Kang M, Kang S, Lee Y. Prediction of Beck Depression Inventory Score in EEG: Application of Deep-Asymmetry Method. Applied Sciences. 2021; 11(19):9218. https://doi.org/10.3390/app11199218
Chicago/Turabian StyleKang, Min, Seokhwan Kang, and Youngho Lee. 2021. "Prediction of Beck Depression Inventory Score in EEG: Application of Deep-Asymmetry Method" Applied Sciences 11, no. 19: 9218. https://doi.org/10.3390/app11199218
APA StyleKang, M., Kang, S., & Lee, Y. (2021). Prediction of Beck Depression Inventory Score in EEG: Application of Deep-Asymmetry Method. Applied Sciences, 11(19), 9218. https://doi.org/10.3390/app11199218






