Mechanical and Acoustic Emission (AE) Characteristics of Rocks under Biaxial Confinements
Abstract
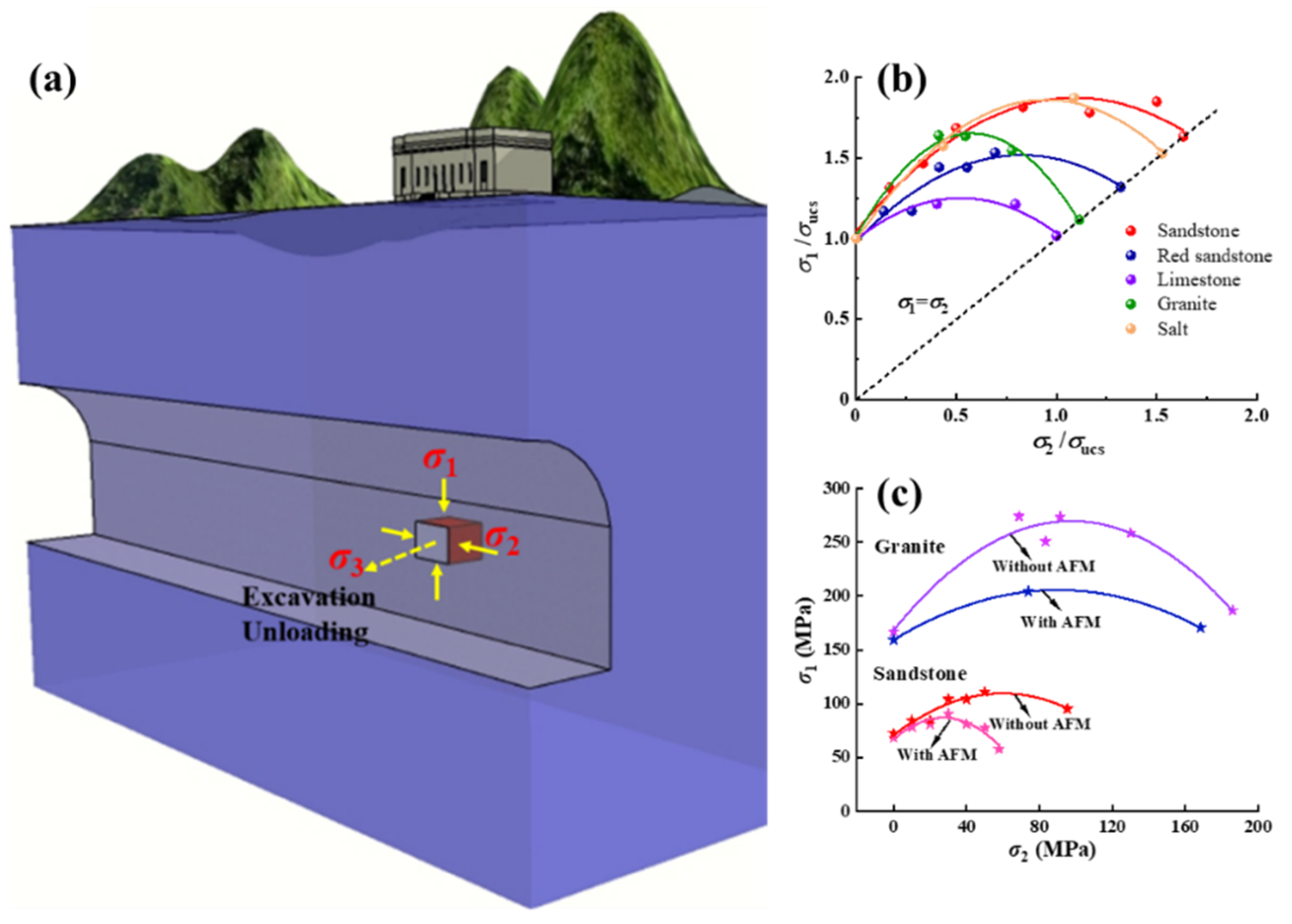
:1. Introduction
2. Experimental Methodology
2.1. Rock Specimens
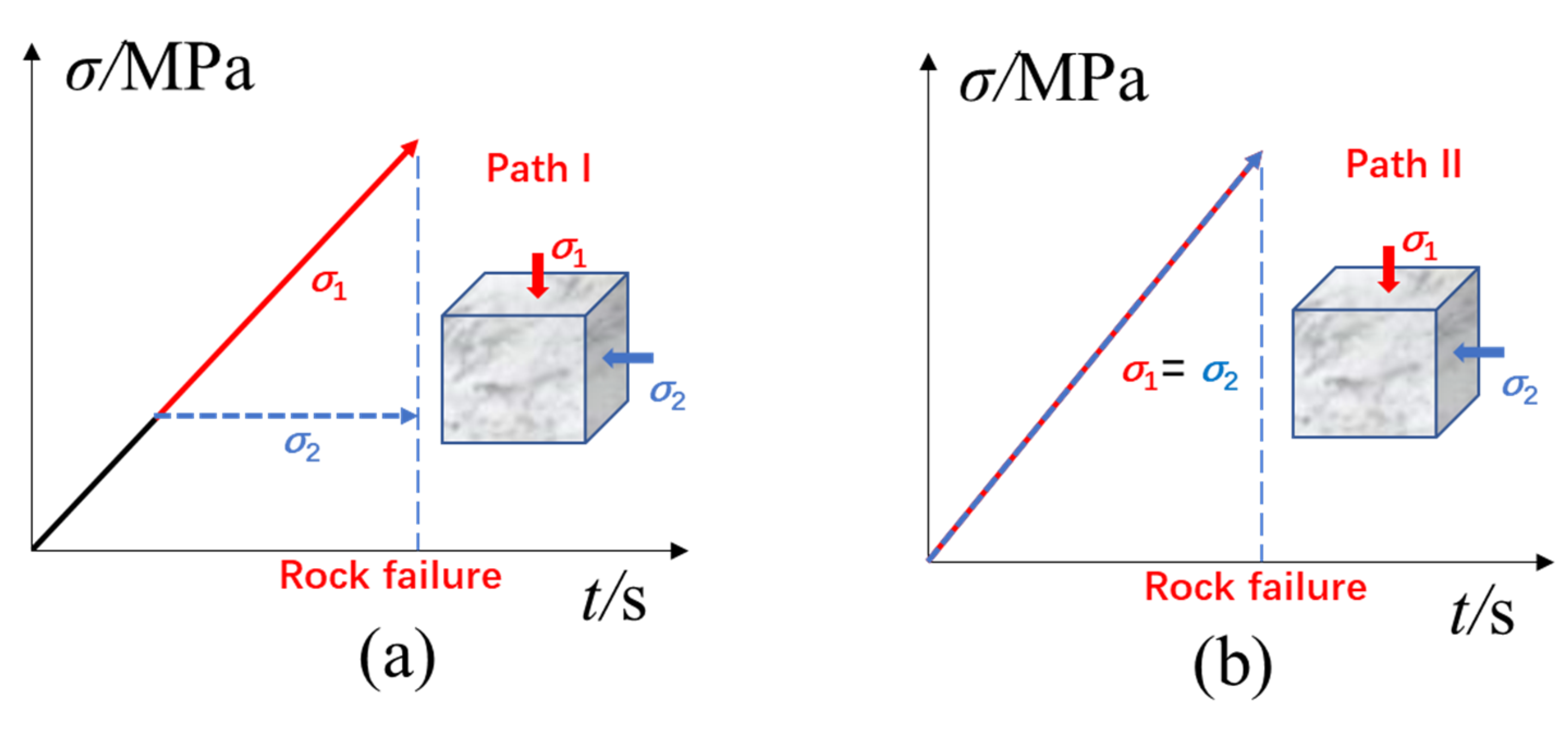
2.2. Stress Paths
2.3. Anti-Friction Measures
2.4. Testing Apparatus
3. Results and Discussion
3.1. Basic Mechanical Parameters of Rocks
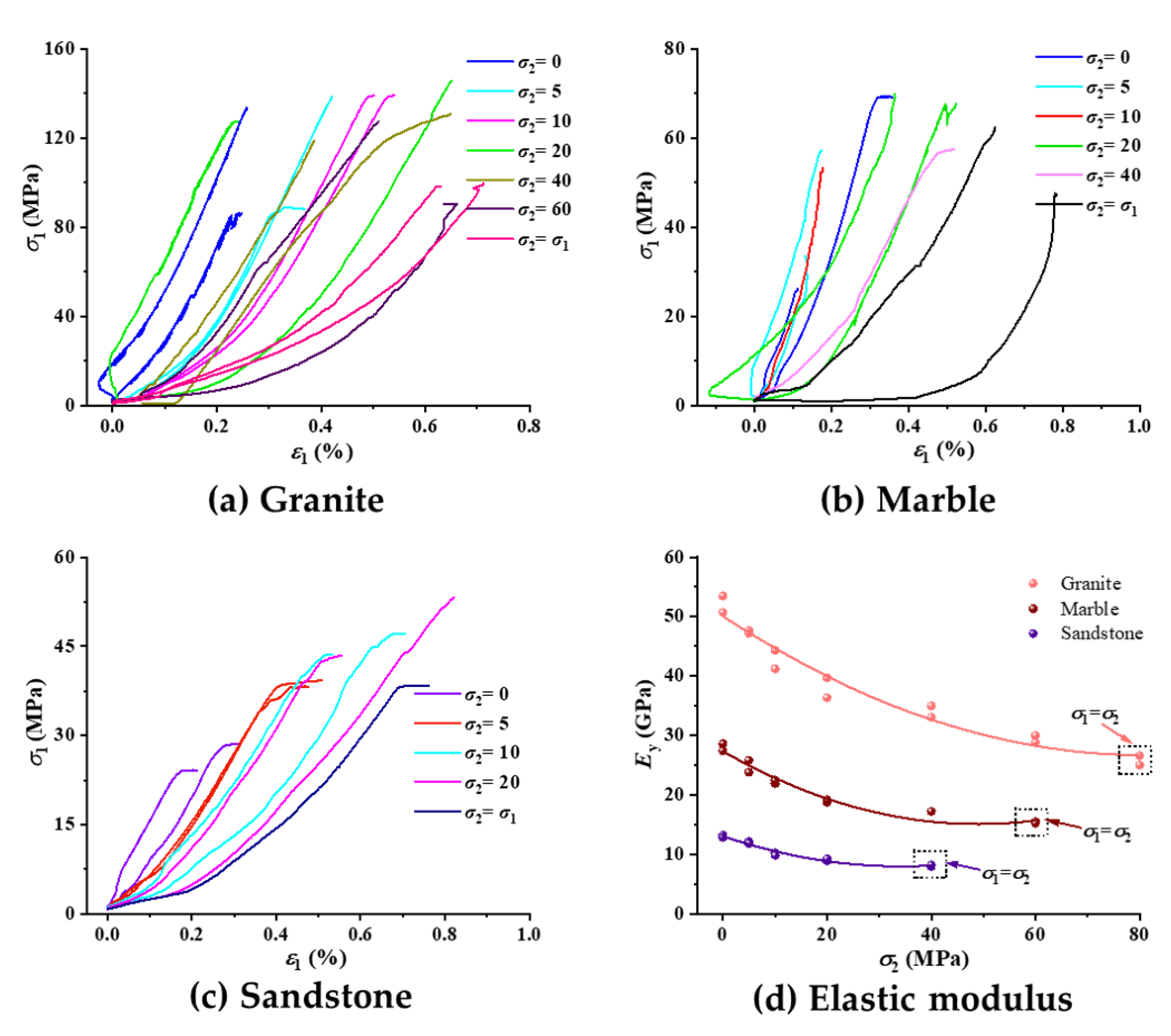
3.2. Stress–Strain Properties
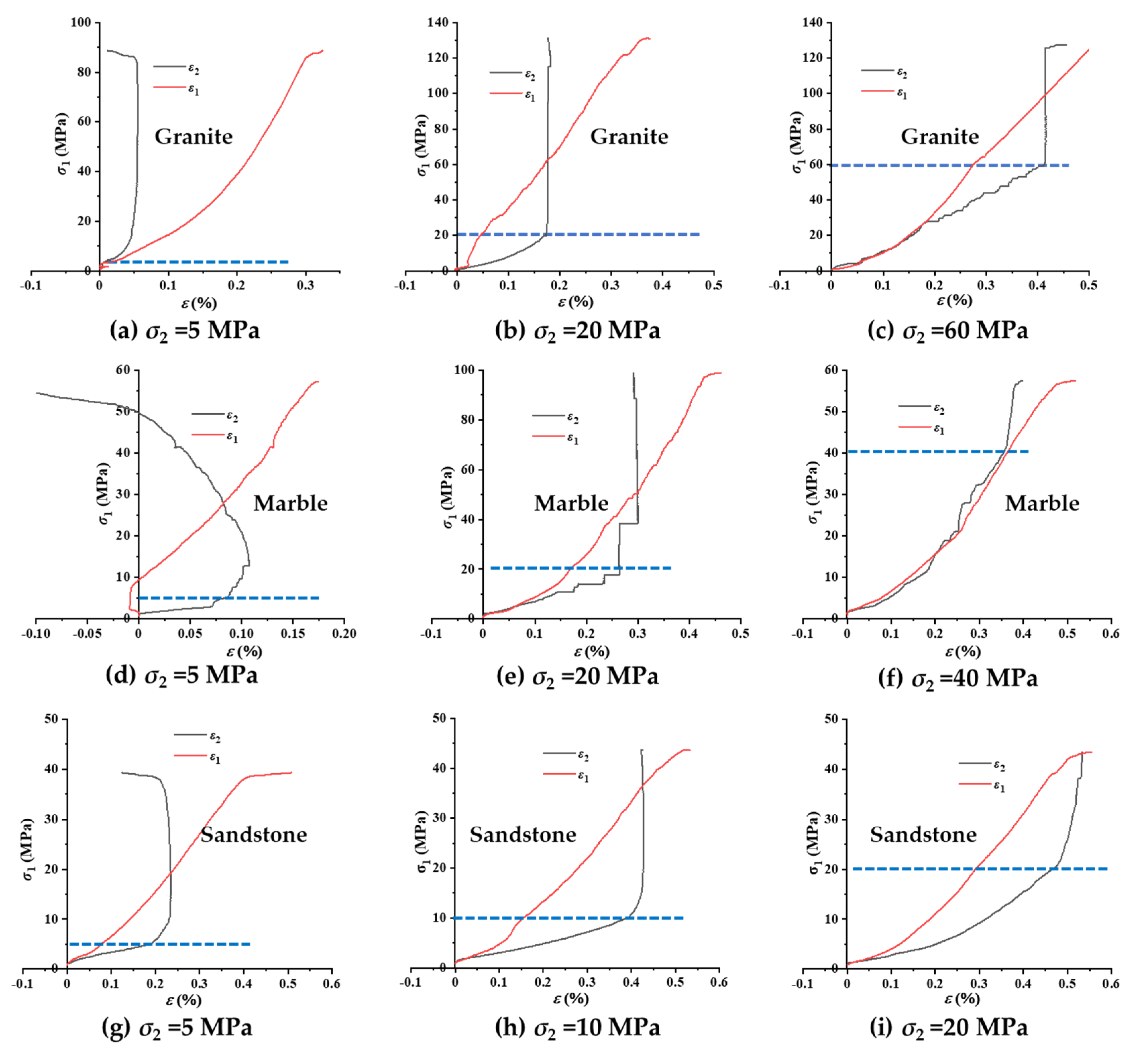
3.2.1. Axial Strain
3.2.2. Lateral Strain
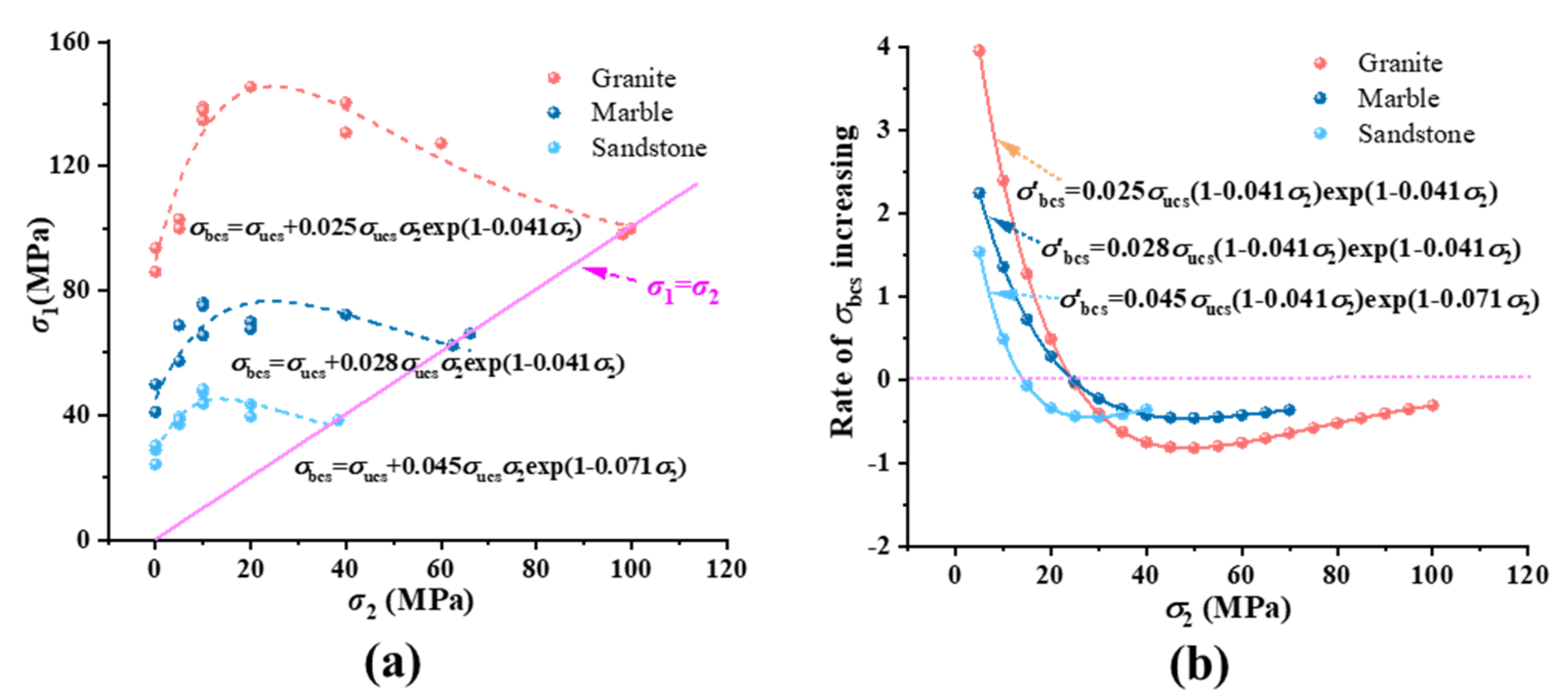
3.3. Biaxial Compressive Strength
3.4. AE Characteristics
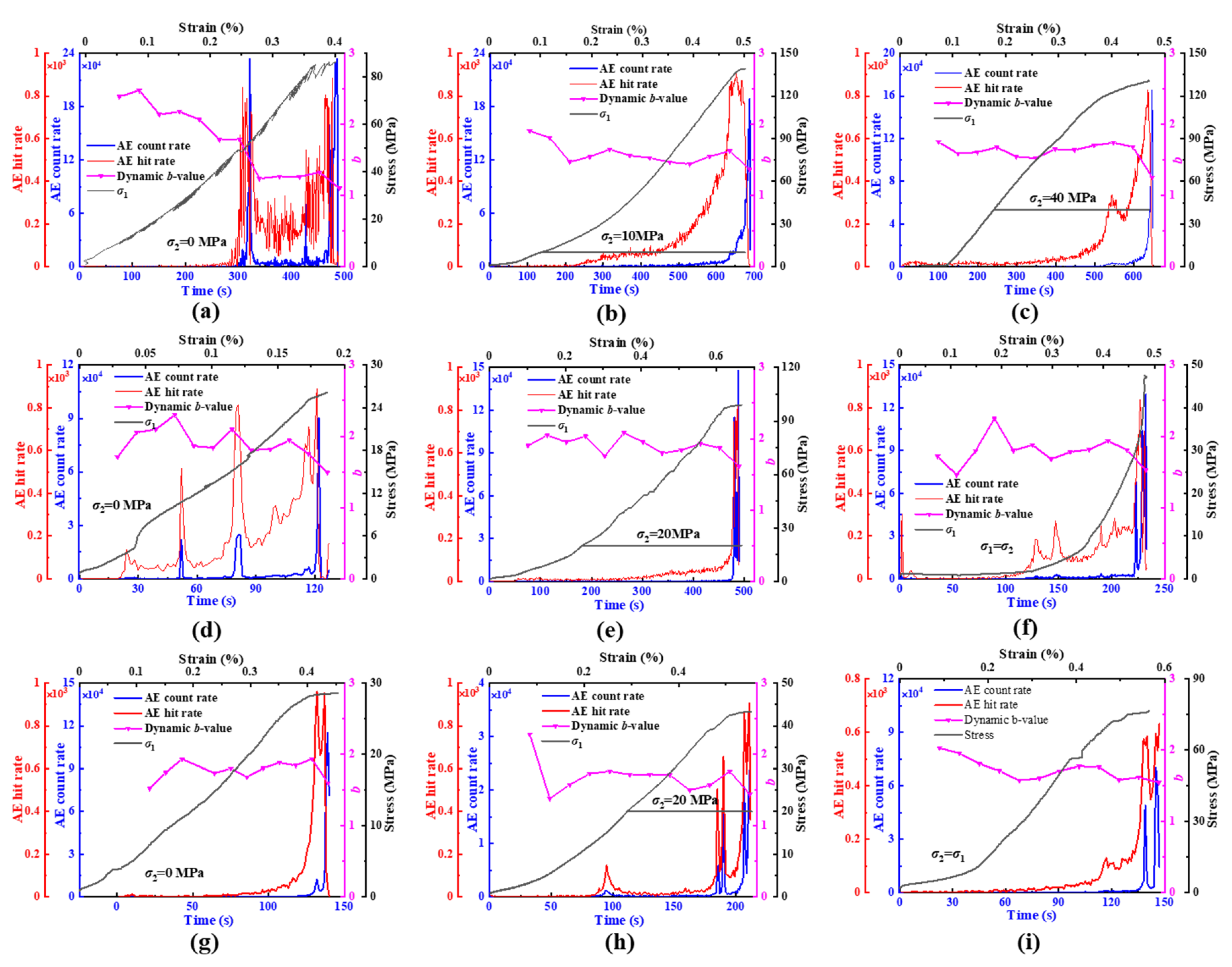
3.4.1. AE Hit Rate, AE Count Rate, and Dynamic b-Value
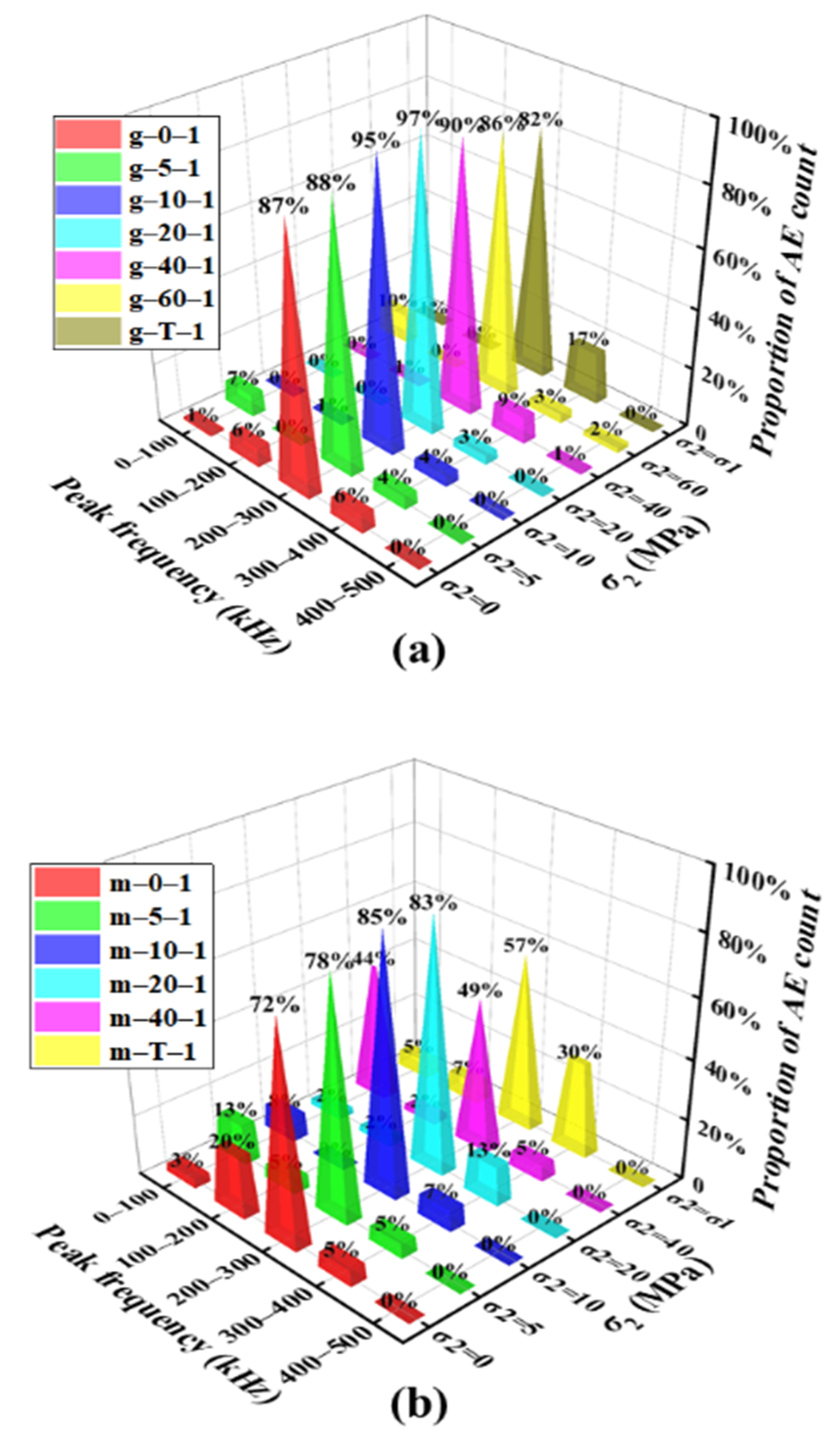
3.4.2. AF-RA Distribution
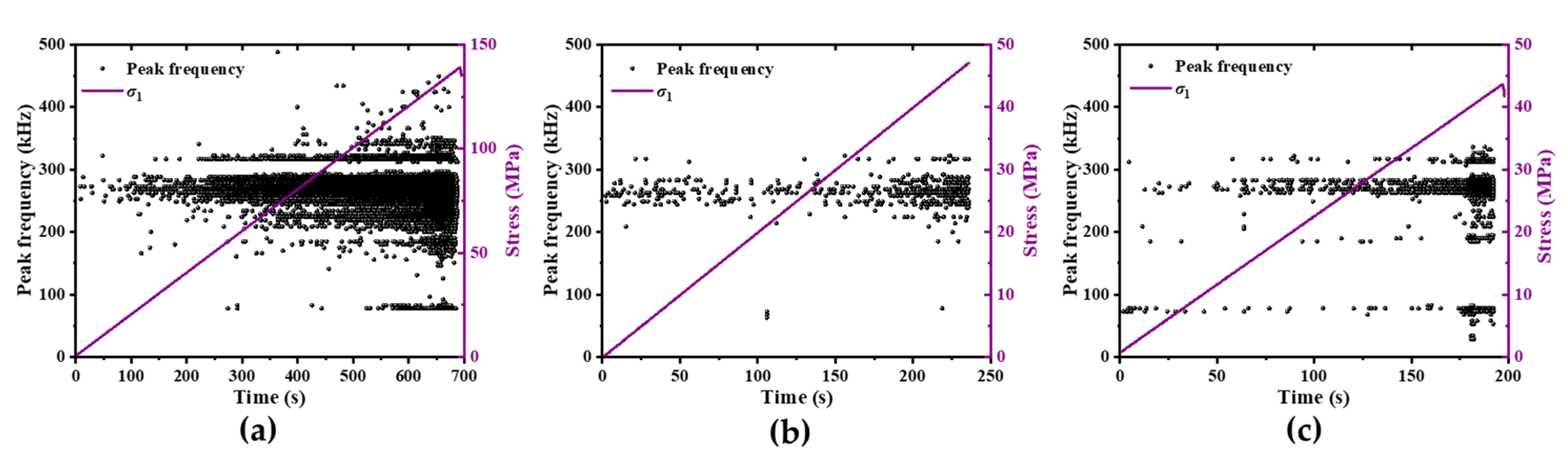
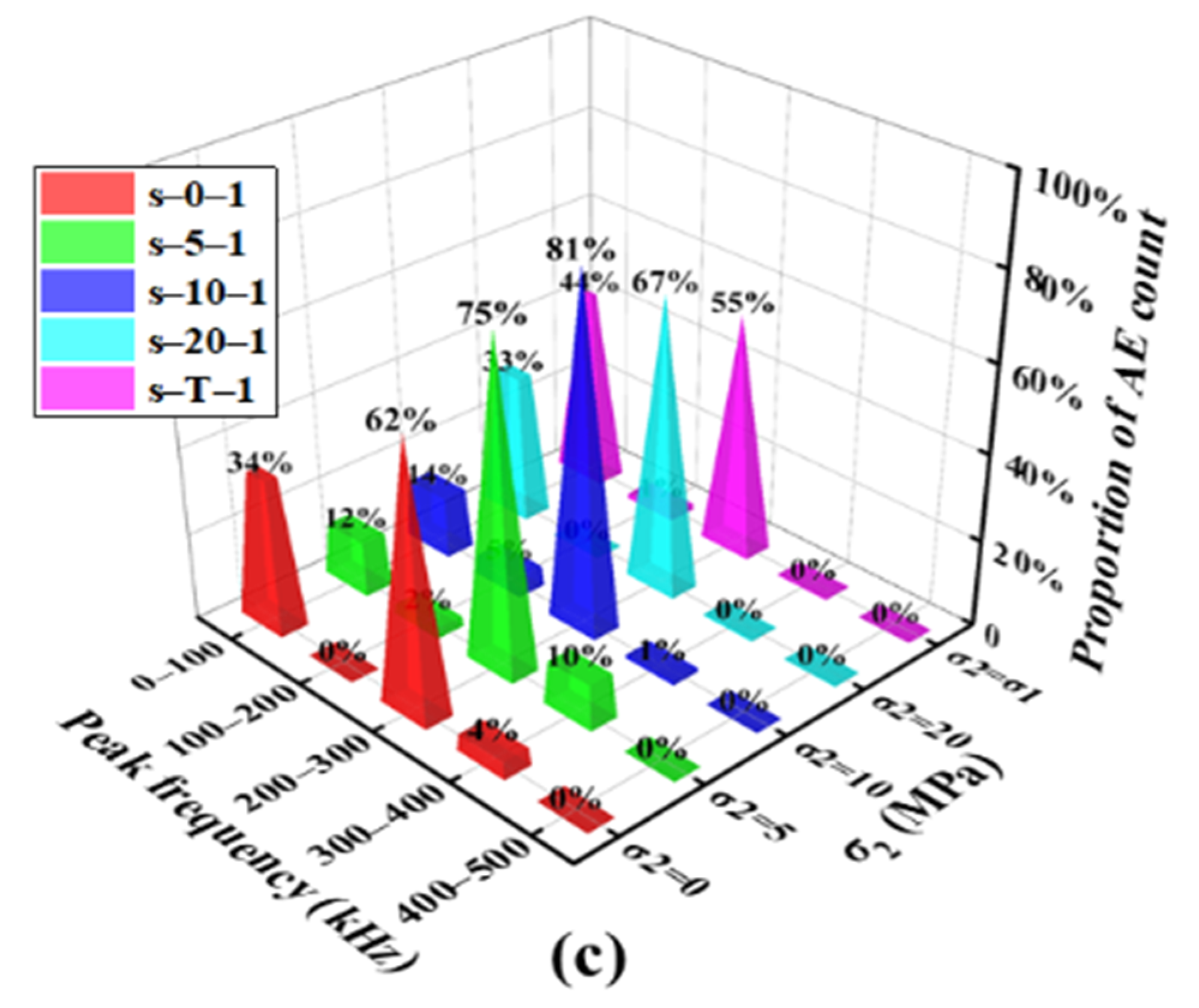
3.4.3. Peak Frequency
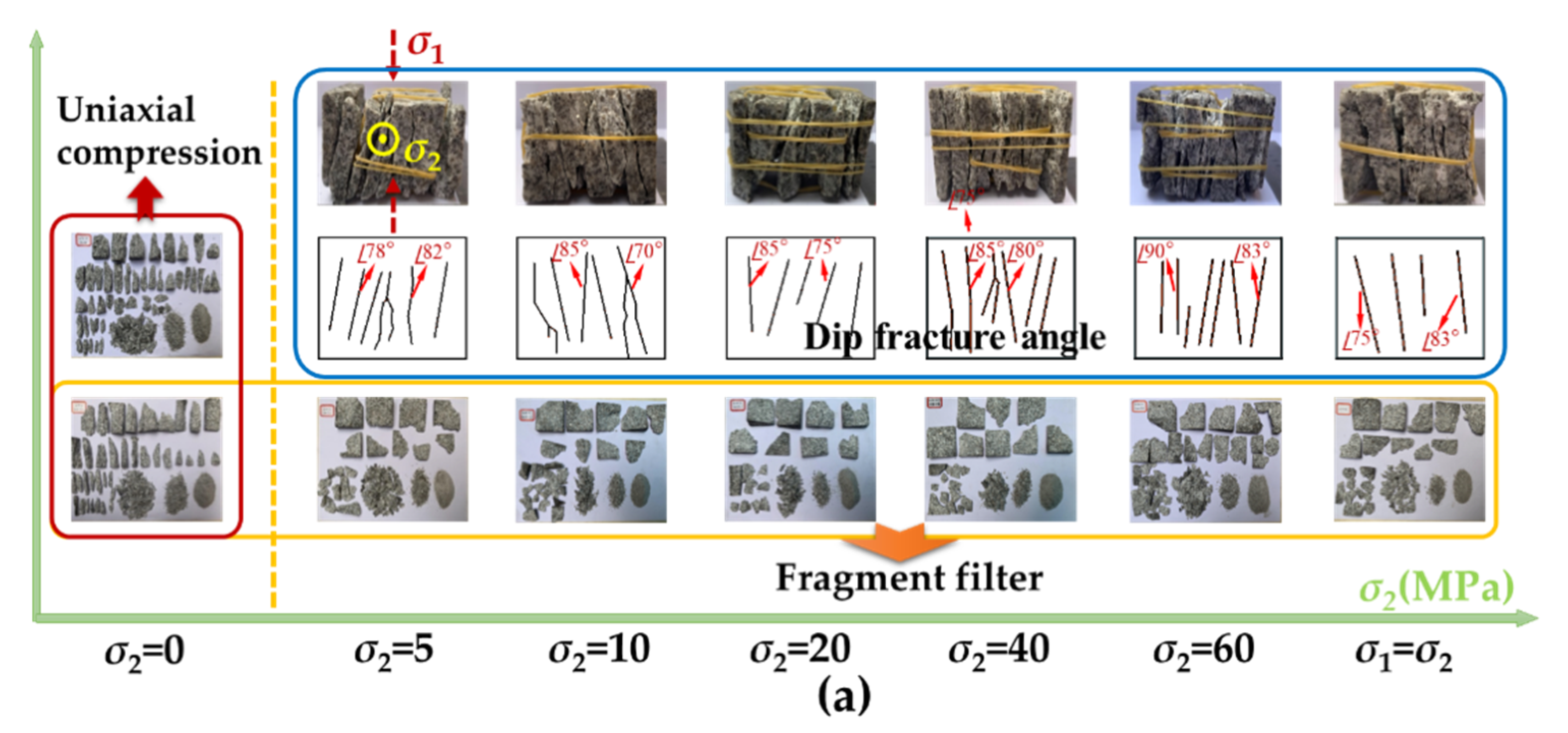
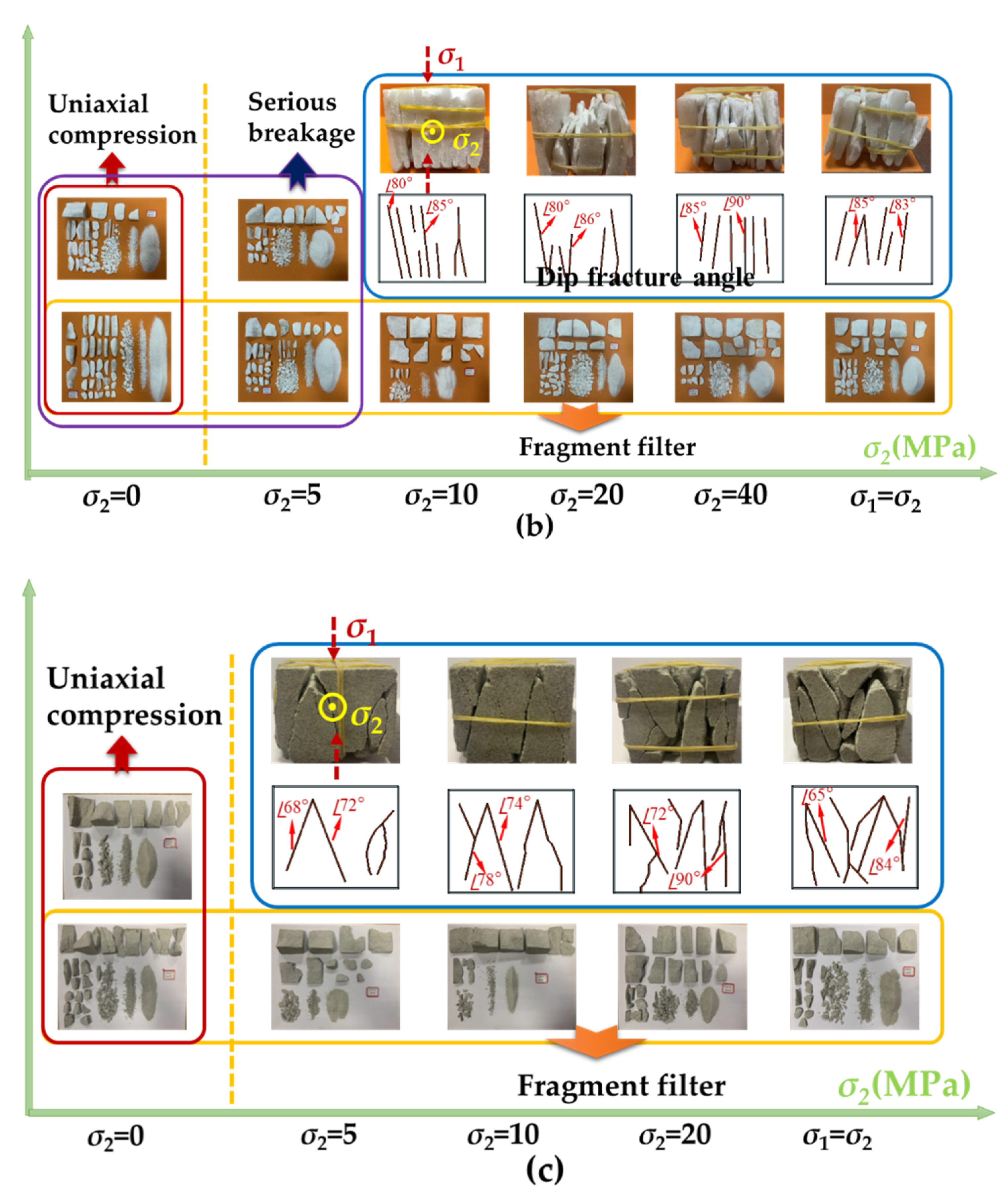
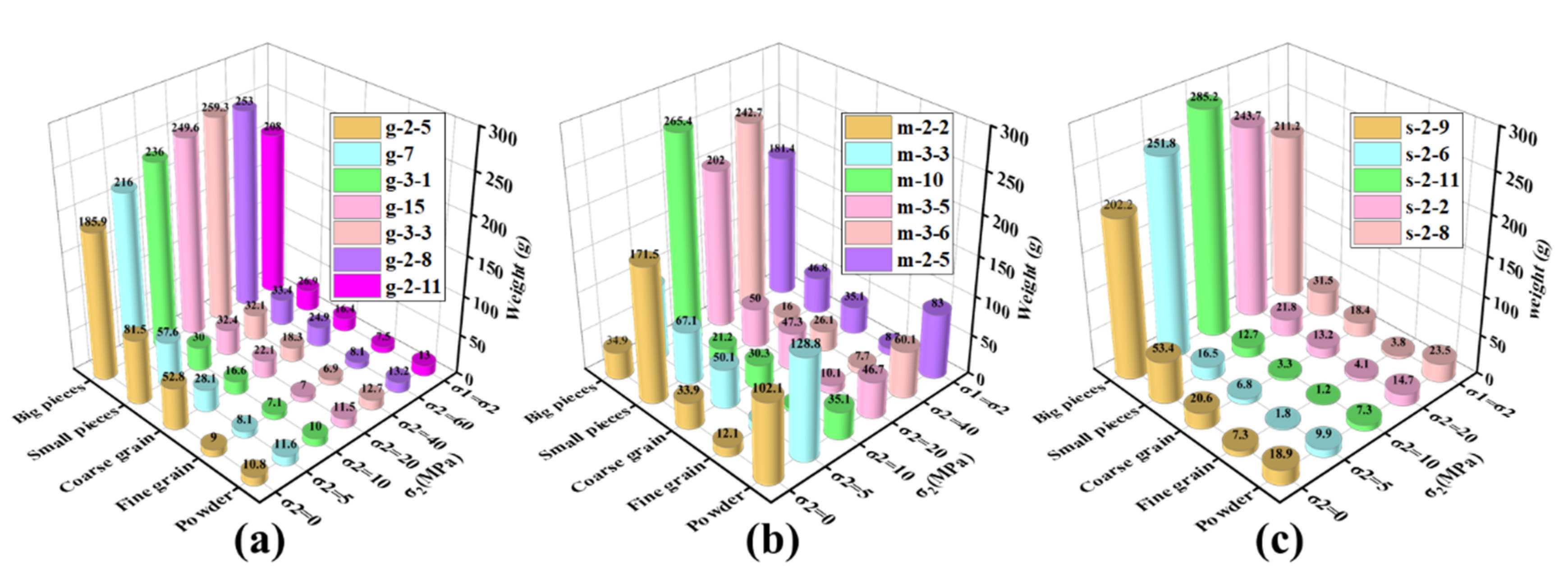
3.5. Failure Mode
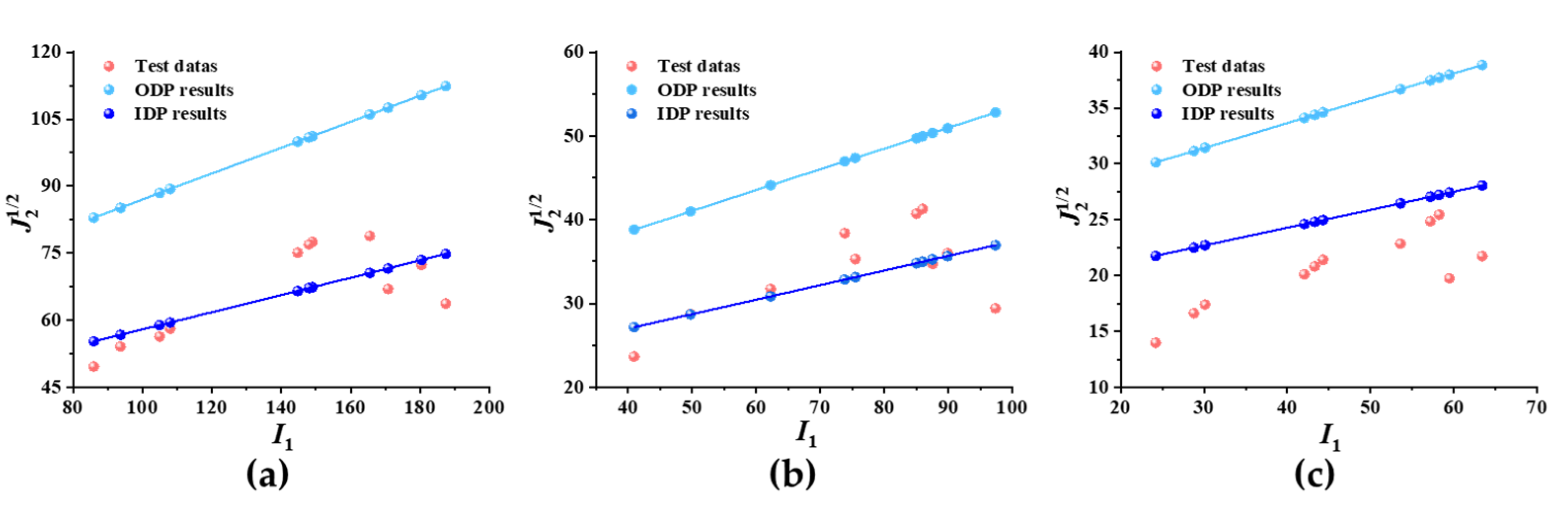
4. Strength Criterion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, K.; Li, X.; Yang, C.; Zhou, J.; Chen, S.; Manoj, K. Experimental investigations on mechanical performance of rocks under fatigue loads and biaxial confinements. J. Cent. South. Univ. 2020, 27, 2985–2998. [Google Scholar]
- Du, K.; Li, X.; Tao, M.; Wang, S. Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests. Int. J. Rock. Mech. Min. 2020, 133, 104411. [Google Scholar]
- Du, K.; Tao, M.; Li, X.; Zhou, J. Experimental Study of Slabbing and Rockburst Induced by True-Triaxial Unloading and Local Dynamic Disturbance. Rock. Mech. Rock. Eng. 2016, 49, 3437–3453. [Google Scholar]
- Wang, S.; Li, X.; Yao, J.; Gong, F.; Li, X.; Du, K.; Tao, M.; Huang, L.; Du, S. Experimental investigation of rock breakage by a conical pick and its application to non-explosive mechanized mining in deep hard rock. Int. J. Rock. Mech. Min. 2019, 122, 104063. [Google Scholar]
- Wang, S.; Sun, L.; Li, X.; Wang, S.; Du, K.; Li, X.; Feng, F. Experimental investigation of cuttability improvement for hard rock fragmentation using conical cutter. Int. J. Geomech. 2021, 21, 06020039. [Google Scholar]
- Cai, X.; Zhou, Z.; Du, X. Water-induced variations in dynamic behavior and failure characteristics of sandstone subjected to simulated geo-stress. Int. J. Rock. Mech. Min. 2020, 130, 104339. [Google Scholar]
- Sagong, M.; Park, D.; Yoo, J.; Lee, J.S. Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression. Int. J. Rock. Mech. Min. 2011, 48, 1055–1067. [Google Scholar]
- Zhu, W.C.; Liu, J.; Tang, C.A.; Zhao, X.D.; Brady, B.H. Simulation of progressive fracturing processes around underground excavations under biaxial compression. Tunn. Undergr. Space Tech. 2004, 20, 231–247. [Google Scholar]
- Cai, X.; Zhou, Z.; Zang, H.; Song, Z. Water saturation effects on dynamic behavior and microstructure damage of sandstone: Phenomena and mechanisms. Eng. Geol. 2020, 276, 105760. [Google Scholar]
- Mitri, H.S.; Rispoli, A.; Bétournay, M.C. Strength and Behavior of Biaxially Loaded Limestone Rock. In Alaska Rocks 2005, The 40th U.S. Symposium on Rock Mechanics (USRMS): Rock Mechanics for Energy, Mineral and Infrastructure Development in the Northern Regions; OnePetro: Anchorage, AL, USA, 2005. [Google Scholar]
- Du, K.; Su, R.; Tao, M.; Yang, C.; Momeni, A.; Wang, S. Specimen shape and cross-section effects on the mechanical properties of rocks under uniaxial compressive stress. Bull. Eng. Geol. Environ. 2019, 78, 6061–6074. [Google Scholar]
- Mitri, H.S. Mechanical Behaviour of Biaxially Loaded Coalmine Sandstone; The International Young Scholars’ Symposium on Rock Mechanics: Beijing, China, 2008. [Google Scholar]
- Cai, M. Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries—Insight from numerical modeling. Int. J. Rock. Mech. Min. 2007, 45, 763–772. [Google Scholar]
- Sainoki, A.; Maina, D.; Schwartzkopff, A.K.; Obara, Y.; Karakus, M. Impact of the intermediate stress component in a plastic potential function on rock mass stability around a sequentially excavated large underground cavity. Int. J. Rock. Mech. Min. 2018, 127, 104233. [Google Scholar]
- Bobet, A.; Einstein, H.H. Fracture coalescence in rock-type materials under uniaxial and biaxial compression. Int. J. Rock. Mech. Min. 1998, 35, 863–888. [Google Scholar]
- Xie, H.; Li, L.; Ju, Y.; Peng, R.; Yang, Y. Energy analysis for damage and catastrophic failure of rocks. Sci. China. Technol. Sci. 2011, 54, 119–209. [Google Scholar]
- Yang, X.; Jing, H.; Chen, K. Numerical simulations of failure behavior around a circular opening in a non-persistently jointed rock mass under biaxial compression. Int. J. Min. Sci. Technol. 2016, 26, 729–738. [Google Scholar]
- Zhong, Z.; Deng, R.; Lv, L.; Fu, X.; Yu, J. Fracture mechanism of naturally cracked rock around an inverted U-shaped opening in a biaxial compression test. Int. J. Rock. Mech. Min. 2018, 103, 242–253. [Google Scholar]
- Feng, X.; Kong, R.; Zhang, X.; Yang, C. Experimental Study of Failure Differences in Hard Rock under True Triaxial Compression. Rock. Mech. Rock. Eng. 2019, 52, 2109–2122. [Google Scholar]
- Chang, C.; Hairnso, B. True triaxial strength and deformability of the German Continental Deep Drilling Program (KTB) deep hole amphibolite. J. Geophys. Res. 2000, 105, 18999–19013. [Google Scholar]
- Haimson, B.; Chang, C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite. Int. J. Rock. Mech. Min. 2000, 37, 285–296. [Google Scholar]
- Labuz, J.F.; Bridell, J.M. Reducing Frictional Constraint in Compression Testing Through Lubrication. Int. J. Rock. Mech. Min. Geomech. Abstr. 1993, 30, 451–455. [Google Scholar]
- Maso, J.; Lerau, J. Mechanical behaviour of Darney sandstone (Vosges, France) in biaxial compression. Int. J. Rock. Mech. Min. Geomech. Abstr. 1980, 17, 109–115. [Google Scholar] [CrossRef]
- Yun, X.; Mitri, H.S.; Yang, X.; Wang, Y. Experimental investigation into biaxial compressive strength of granite. Int. J. Rock. Mech. Min. 2010, 47, 334–341. [Google Scholar] [CrossRef]
- Fan, P.; Li, Y.; Zhao, Y.; Dong, L.; Ma, L. End friction effect of Mogi type of true-triaxial test apparatus. Chin. J. Rock Mech. Eng. 2017, 36, 2720–2730. [Google Scholar]
- Wang, S.; Li, X.; Du, K.; Wang, S.; Tao, M. Experimental study of the triaxial strength properties of hollow cylindrical granite specimens under coupled external and internal confining stresses. Rock. Mech. Rock. Eng. 2018, 51, 2015–2031. [Google Scholar] [CrossRef]
- Akai, K.; Mori, H. Study on the Failure Mechanism of a Sand-Stone under Combined Compressive Stresses. Jpn. Soc. Civ. Eng. 1967, 1967, 11–24. [Google Scholar] [CrossRef]
- Mogi, K. Effect of the intermediate principal stress on rock failure. J. Geophys. Res. 1967, 72, 5117–5131. [Google Scholar] [CrossRef]
- Antonaci, P.; Bocca, P.; Masera, D. Fatigue crack propagation monitoring by Acoustic Emission signal analysis. Eng. Fract. Mech. 2012, 81, 26–32. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Mpalaskas, A.C.; Ntalakas, D.; Matikas, T.E. Effect of wave distortion on acoustic emission characterization of cementitious materials. Constr. Build. Mater. 2012, 35, 183–190. [Google Scholar] [CrossRef]
- Spies, T.; Eisenblätter, J. Acoustic emission investigation of microcrack generation at geological boundaries. Eng. Geol. 2001, 61, 181–188. [Google Scholar] [CrossRef]
- Shiotania, T.; Ohtsub, M.; Ikeda, K. Detection and evaluation of AE waves due to rock deformation. Constr. Build. Mater. 2001, 15, 235–246. [Google Scholar] [CrossRef]
- Chen, G.; Sun, X.; Wang, J.; Wang, D.; Zhu, Z. Detection of cracking behaviors in granite with open precut cracks by acoustic emission frequency spectrum analysis. Arab. J. Geosci. 2020, 13, 26–32. [Google Scholar] [CrossRef]
- He, M.; Miao, J.; Feng, J. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock. Mech. Min. 2010, 47, 286–298. [Google Scholar] [CrossRef]
- Du, K.; Yang, C.; Su, R.; Tao, M.; Wang, S. Failure properties of cubic granite, marble, and sandstone specimens under true triaxial stress. Int. J. Rock. Mech. Min. 2020, 130, 104309. [Google Scholar] [CrossRef]
- Aggelis, D.G.; Mpalaskas, A.C.; Matikas, T.E. Investigation of different fracture modes in cement-based materials by acoustic emission. Cement. Concrete. Res. 2013, 48, 1–8. [Google Scholar] [CrossRef]
- Aggelis, D.G. Classification of cracking mode in concrete by acoustic emission parameters. Mech. Res. Commun. 2011, 38, 153–157. [Google Scholar] [CrossRef]
- Cai, M.; Morioka, H.; Kaiser, P.K.; Tasaka, Y.; Kurose, H.; Minami, M.; Maejim, T. Back-analysis of rock mass strength parameters using AE monitoring data. Int. J. Rock. Mech. Min. 2007, 44, 538–549. [Google Scholar] [CrossRef]
- Lei, X.; Masuda, K.; Nishizawa, O.; Jouniaux, L.; Liu, L.; Ma, W.; Satoh, T.; Kusunose, K. Detailed analysis of acoustic emission activity during catastrophic fracture of faults in rock. J. Struct. Geol. 2004, 26, 247–258. [Google Scholar] [CrossRef]
- Tham, L.G.; Liu, H.; Tang, C.A.; Lee, P.K.; Tsui, Y. On Tension Failure of 2-D Rock Specimens and Associated Acoustic Emission. Rock Mech. Rock Eng. 2005, 38, 1–19. [Google Scholar] [CrossRef]
- Chang, S.H.; Lee, C.I. Estimation of cracking and damage mechanisms in rock under triaxial compression by moment tensor analysis of acoustic emission. Int. J. Rock. Mech. Min. 2004, 41, 1069–1086. [Google Scholar] [CrossRef]
- Moradian, Z.A.; Ballivy, G.; Rivard, P.; Gravel, C.; Rousseau, B. Evaluating damage during shear tests of rock joints using acoustic emissions. Int. J. Rock. Mech. Min. 2010, 47, 590–598. [Google Scholar] [CrossRef]
- Ishida, T.; Kanagaw, T.; Kanaori, Y. Source distribution of acoustic emissions during an in-situ direct shear test: Implications for an analog model of seismogenic faulting in an inhomogeneous rock mass. Eng. Geol. 2010, 110, 66–76. [Google Scholar] [CrossRef] [Green Version]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Notched marble plates under tension: Detecting pre-failure indicators and predicting entrance to the “critical stage”. Fatigue. Fract. Eng. M 2018, 41, 776–786. [Google Scholar] [CrossRef]
- Triantis, D.; Kourkoulis, S.K. An Alternative Approach for Representing the Data Provided by the Acoustic Emission Technique. Rock. Mech. Rock. Eng. 2018, 51, 2433–2438. [Google Scholar] [CrossRef]
- Mogi, K. Study of Elastic Shocks Caused by the Fracture of Heterogeneous Materials and Its Relations to Earthquake Phenomena. Bull. Earthq. Res. Inst. 1962, 40, 125–173. [Google Scholar]
- Scholz, C. The Frequency-Magnitude Relation of Microfracturing in Rock and Its Relation to Earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Lei, X.L. How Do Asperities Fracture? An Experimental Study of Unbroken Asperities. Earth Planet. Sci. Lett. 2003, 213, 347–359. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar]
- Rao, M.V.M.S.; Lakshmi, K.J.P. Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture. Curr. Sci. India 2005, 89, 1577–1582. [Google Scholar]
- Rao, M.V.M.S.; Prasanna Lakshmi, K.J.; Nagaraja Rao, G.M.; Vijayakumar, K.; Udayakumar, S. Precursory icrocracking and brittle failure of Latur basalt and migmatite gneiss under compressive loading. Curr. Sci. India 2011, 101, 1053–1059. [Google Scholar]
- Aggelis, D.G.; Soulioti, D.V.; Sapouridis, N.; Barkoula, N.M.; Paipetis, A.S.; Matikas, T.E. Acoustic emission characterization of the fracture process in fibre reinforced concrete. Constr. Build. Mater. 2011, 25, 4126–4131. [Google Scholar] [CrossRef]
- Loukidis, A.; Triantis, D.; Stavrakas, I.; Pasiou, E.D.; Kourkoulis, S.K. Comparative Ib-value and F-function analysis of Acoustic Emissions from elementary and structural tests with marble specimens. Mater. Des. Process. Commun. 2020, e176. [Google Scholar] [CrossRef] [Green Version]
- Gay, N.C. Fracture growth around openings in large blocks of rock subjected to uniaxial and biaxial compression. Int. J. Rock. Mech. Min. 1976, 13, 231–243. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Colmenares, L.B.; Zoback, M.D. A statistical evaluation of intact rock failure criteria constrained by poly axial test data for five different rocks. Int. J. Rock Mech. Min. Sci. 2002, 39, 695–729. [Google Scholar] [CrossRef]
- Feng, F.; Li, X.; Du, K.; Li, D.; Rostami, J.; Wang, S. Comprehensive Evaluation of Strength Criteria for Granite, Marble, and Sandstone Based on Polyaxial Experimental Tests. Int. J. Geomech. 2020, 20, 04019155. [Google Scholar] [CrossRef]





| Rock Types | (MPa) | (MPa) | Loading Rate (MPa/s) |
|---|---|---|---|
| Granite | 0, 5, 10, 20, 40, 60 | 0 | 0.2 |
| Marble | 0, 5, 10, 20, 40 | 0 | 0.2 |
| Sandstone | 0, 5, 10, 20 | 0 | 0.2 |
| Rock Types | (MPa) | (GPa) | ||
|---|---|---|---|---|
| Granite | 89.86 | 52.25 | 0.25 | 4.26 |
| Marble | 45.39 | 27.67 | 0.27 | 3.58 |
| Sandstone | 27.71 | 12.07 | 0.31 | 2.34 |
| Rock Type | Specimen NO. | (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|---|
| Granite | g-0-1 | 0 | 0 | 86.12 | 86.12 |
| g-0-2 | 0 | 0 | 93.68 | 93.68 | |
| g-5-1 | 0 | 5 | 103.00 | 103.00 | |
| g-5-2 | 0 | 5 | 99.95 | 99.95 | |
| g-10-1 | 0 | 10 | 134.73 | 134.73 | |
| g-10-2 | 0 | 10 | 138.98 | 138.98 | |
| g-10-3 | 0 | 10 | 138.00 | 138.00 | |
| g-20-1 | 0 | 20 | 145.50 | 145.50 | |
| g-40-1 | 0 | 40 | 130.80 | 130.80 | |
| g-40-2 | 0 | 40 | 140.40 | 140.40 | |
| g-60-1 | 0 | 60 | 127.40 | 127.40 | |
| g-T-1 | 0 | 98.10 | 98.10 | ||
| g-T-2 | 0 | 99.80 | 99.80 | ||
| Marble | m-0-1 | 0 | 0 | 49.80 | 49.80 |
| m-0-2 | 0 | 0 | 40.98 | 40.98 | |
| m-5-1 | 0 | 5 | 68.85 | 68.85 | |
| m-5-2 | 0 | 5 | 57.30 | 57.30 | |
| m-10-1 | 0 | 10 | 76.00 | 76.00 | |
| m-10-2 | 0 | 10 | 65.50 | 65.50 | |
| m-10-3 | 0 | 10 | 75.02 | 75.02 | |
| m-20-1 | 0 | 20 | 69.90 | 69.90 | |
| m-20-2 | 0 | 20 | 67.56 | 67.56 | |
| m-40-1 | 0 | 40 | 72.30 | 72.30 | |
| m-T-1 | 0 | 66.11 | 66.11 | ||
| m-T-2 | 0 | 62.40 | 62.40 | ||
| Sandstone | s-0-1 | 0 | 0 | 28.80 | 28.80 |
| s-0-2 | 0 | 0 | 24.20 | 24.20 | |
| s-0-3 | 0 | 0 | 30.14 | 30.14 | |
| s-5-1 | 0 | 5 | 37.06 | 37.06 | |
| s-5-2 | 0 | 5 | 39.30 | 39.30 | |
| s-5-3 | 0 | 5 | 38.30 | 38.30 | |
| s-10-1 | 0 | 10 | 47.20 | 47.20 | |
| s-10-2 | 0 | 10 | 43.60 | 43.60 | |
| s-10-3 | 0 | 10 | 48.24 | 48.24 | |
| s-20-1 | 0 | 20 | 39.49 | 39.49 | |
| s-20-2 | 0 | 20 | 43.40 | 43.40 | |
| s-T-1 | 0 | 38.40 | 38.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Liu, M.; Yang, C.; Tao, M.; Feng, F.; Wang, S. Mechanical and Acoustic Emission (AE) Characteristics of Rocks under Biaxial Confinements. Appl. Sci. 2021, 11, 769. https://doi.org/10.3390/app11020769
Du K, Liu M, Yang C, Tao M, Feng F, Wang S. Mechanical and Acoustic Emission (AE) Characteristics of Rocks under Biaxial Confinements. Applied Sciences. 2021; 11(2):769. https://doi.org/10.3390/app11020769
Chicago/Turabian StyleDu, Kun, Minghui Liu, Chengzhi Yang, Ming Tao, Fukang Feng, and Shaofeng Wang. 2021. "Mechanical and Acoustic Emission (AE) Characteristics of Rocks under Biaxial Confinements" Applied Sciences 11, no. 2: 769. https://doi.org/10.3390/app11020769
APA StyleDu, K., Liu, M., Yang, C., Tao, M., Feng, F., & Wang, S. (2021). Mechanical and Acoustic Emission (AE) Characteristics of Rocks under Biaxial Confinements. Applied Sciences, 11(2), 769. https://doi.org/10.3390/app11020769







