Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach
Abstract
Featured Application
Abstract
1. Introduction
- In this study, a non-probabilistic wavelet packet transform method is proposed that resolves the problem of uncertainties in vibration-based damage detection. The damaged and undamaged structure’s acceleration responses are decomposed to obtain the wavelet pocket relative energies of the signal.
- Different levels of detection of structural damage, including the occurrence of damage, location and severity of it, are evaluated using a computational approach. Furthermore, the effect of different levels of uncertainties on damage identification are presented.
- Furthermore, the applicability of WWLS-SVM to act as a non-probabilistic surrogate model for damage detection of structures, with consideration of uncertainties, will be examined through simulating a damage in the benchmark model.
2. Main Steps of the Proposed Damage Detection Procedure
3. Feature Extraction Using Wavelet Packet Transform (WPT)
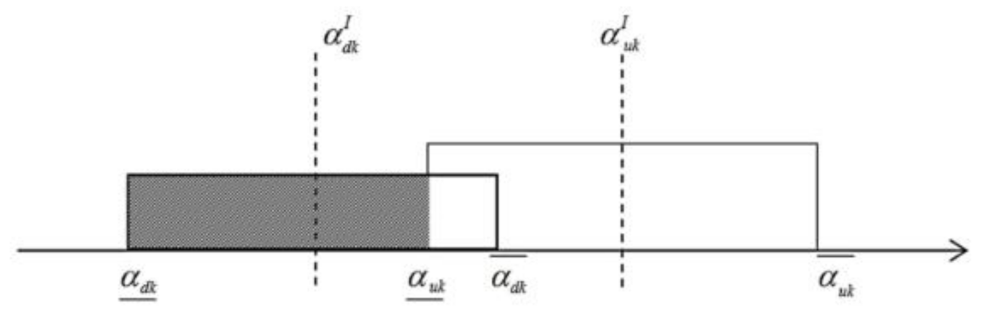
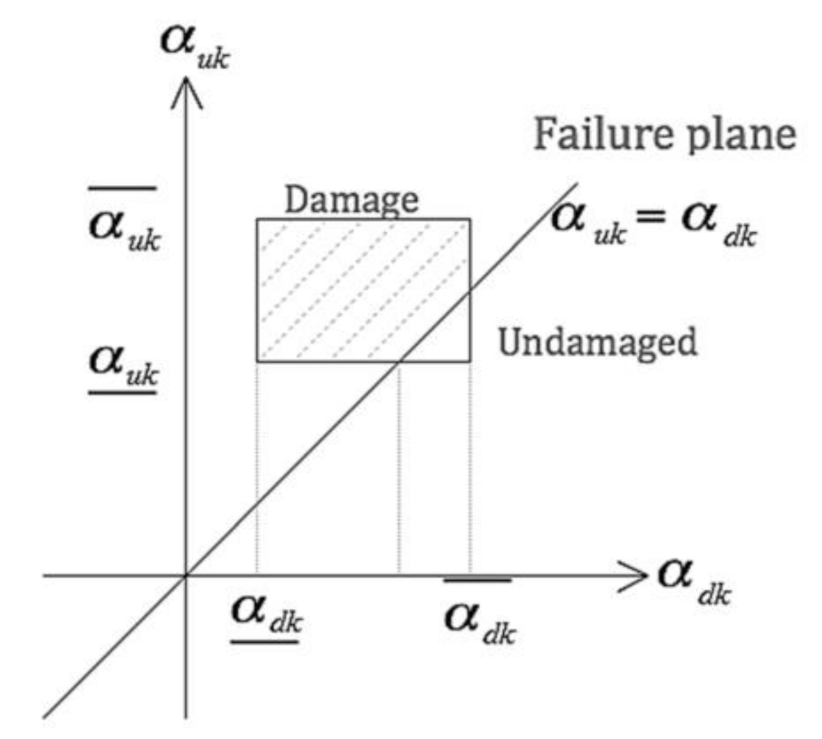
4. Interval Analysis Method for Consideration of Uncertainties
- = value of ESP in the damaged stat
- = value of ESP in undamaged (healthy) state.
- number of damage cases.
- number of segments of structures.
- interval number or vector representation
- number of sensor on structure
- is the acquiring number
Possibility of Damage Existence (PoDE) and Damage Measure Index (DMI)
5. Wavelet Weighted Least Squares Support Vector Machine (WWLS-SVM)
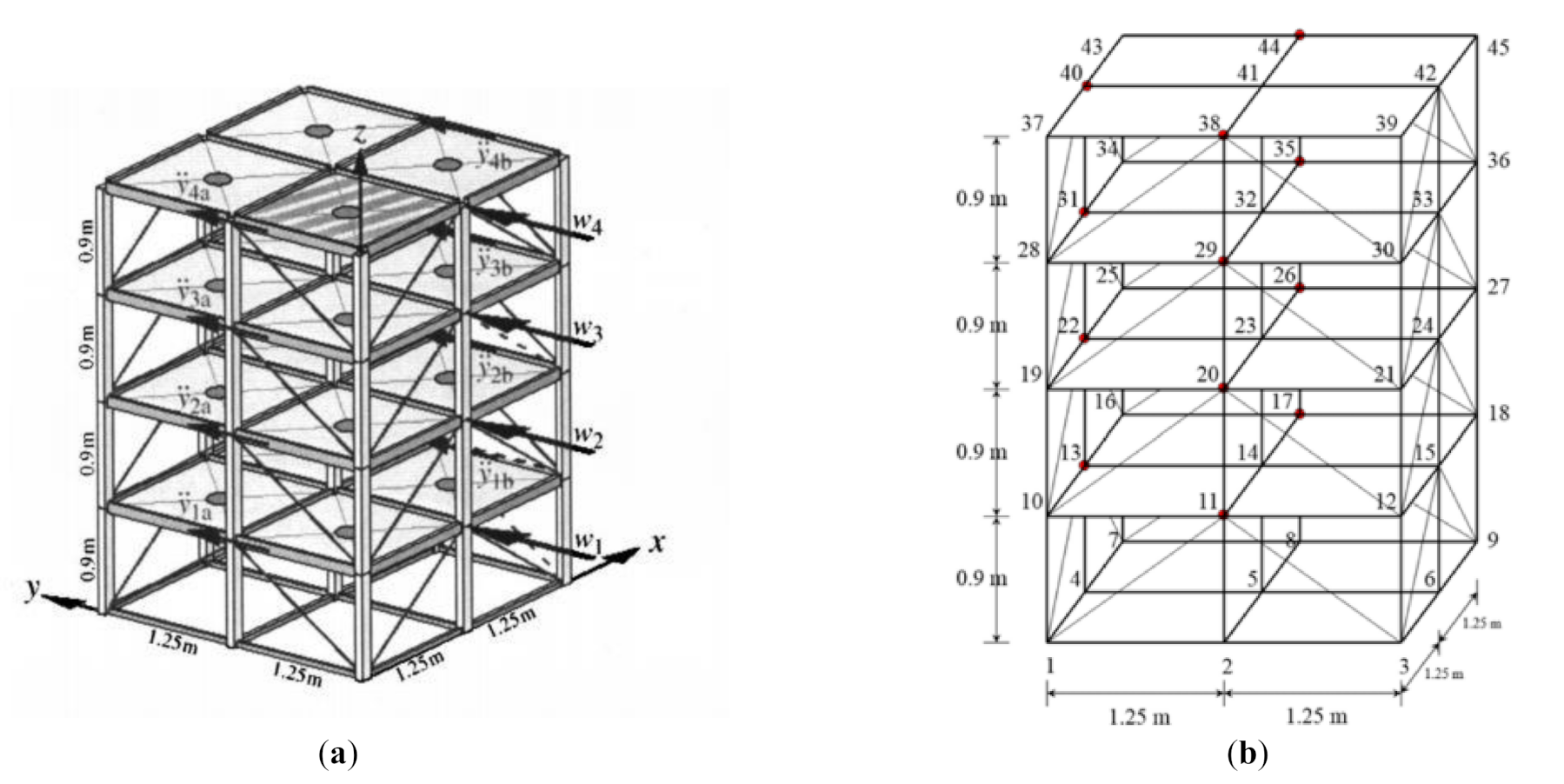
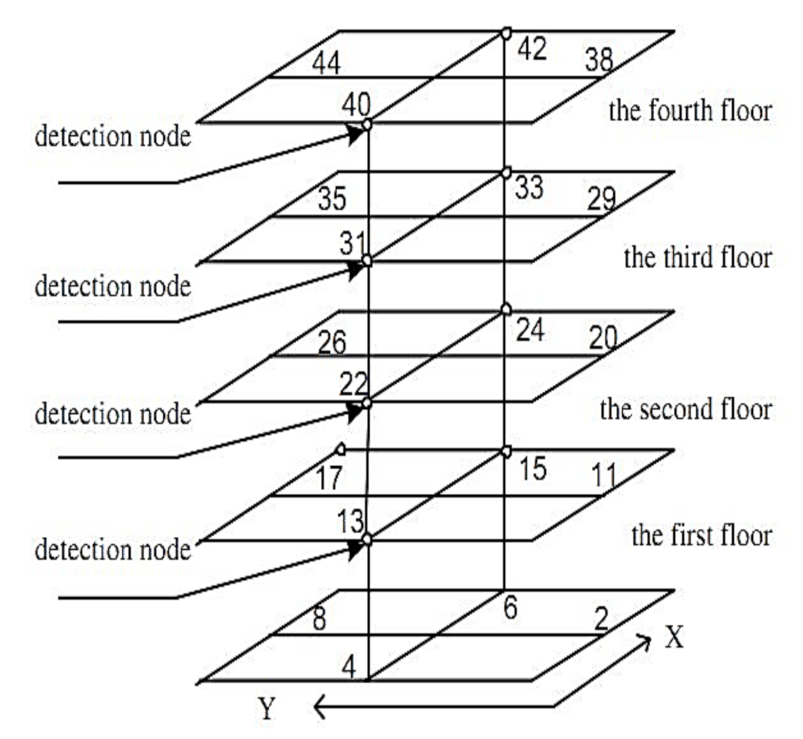
6. Damage Detection of IASC-ASCE Structural Health Monitoring Benchmarks
6.1. Feature Extraction and Training Phase for Damage Cases 4 and 5
6.2. First Phase—Comparing the Performance of PoDE and PDE
6.3. Second Phase—Evaluation of Damage Severities
6.4. Third Phase—Influence of Various Noise Levels on the Identification Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 1118443217. [Google Scholar]
- Toh, G.; Park, J. Review of Vibration-Based Structural Health Monitoring Using Deep Learning. Appl. Sci. 2020, 10, 1680. [Google Scholar]
- Rainieri, C.; Magalhaes, F.; Gargaro, D.; Fabbrocino, G.; Cunha, A. Predicting the variability of natural frequencies and its causes by Second-Order Blind Identification. Struct. Health Monit. 2019, 18, 486–507. [Google Scholar]
- Fathnejat, H.; Ahmadi-nedushan, B. Meta-heuristic algorithms and group method of data handling An efficient two-stage approach for structural damage detection using meta-heuristic algorithms and group method of data handling surrogate model. Front. Struct. Civ. Eng. 2020, 14, 907–929. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueño, R. Emerging artificial intelligence methods in structural engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-Driven Structural Health Monitoring and Damage Detection through Deep Learning: State-of-the-Art Review. Sensors 2020, 20, 2778. [Google Scholar]
- Padil, K.H.; Bakhary, N.; Hao, H. The use of a non-probabilistic artificial neural network to consider uncertainties in vibration-based-damage detection. Mech. Syst. Signal Process. 2017, 83, 194–209. [Google Scholar] [CrossRef]
- Mo, J.; Wang, L.; Qiu, Z.; Shi, Q. A nonprobabilistic structural damage identification approach based on orthogonal polynomial expansion and interval mathematics. Struct. Control Health Monit. 2019, 26, e2378. [Google Scholar]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with uncertainty in model updating for damage assessment: A review. Mech. Syst. Signal Process. 2015, 123–149. [Google Scholar] [CrossRef]
- Ghiasi, R.; Ghasemi, M.R. Optimization-based method for structural damage detection with consideration of uncertainties-a comparative study. Smart Struct. Syst. 2018, 22, 561–574. [Google Scholar]
- Bakhary, N.; Hao, H.; Deeks, A.J. Damage detection using artificial neural network with consideration of uncertainties. Eng. Struct. 2007, 29, 2806–2815. [Google Scholar] [CrossRef]
- Shu, J.; Zhang, Z.; Gonzalez, I.; Karoumi, R. The application of a damage detection method using Artificial Neural Network and train-induced vibrations on a simplified railway bridge model. Eng. Struct. 2013, 52, 408–421. [Google Scholar] [CrossRef]
- Qiu, Z.; Wang, L. The need for introduction of non-probabilistic interval conceptions into structural analysis and design. Sci. China Phys. Mech. Astron. 2016, 59, 114632. [Google Scholar]
- Abdulkareem, M.; Bakhary, N. Non-probabilistic wavelet method to consider uncertainties in structural damage detection. J. Sound Vib. 2018, 433, 77–98. [Google Scholar] [CrossRef]
- Ghiasi, R.; Torkzadeh, P.; Noori, M. A machine-learning approach for structural damage detection using least square support vector machine based on a new combinational kernel function. Struct. Health Monit. 2016, 15, 302–316. [Google Scholar] [CrossRef]
- Khatibinia, M.; Gharehbaghi, S. Seismic Reliability-Based Design Optimization of Reinforced Concrete Structures Including Soil-Structure Interaction Effects. In Earthquake Engineering-From Engineering Seismology to Optimal Seismic Design of Engineering Structures; Intechopen: London, UK, 2015; pp. 267–304. [Google Scholar]
- Suykens, J.A.K.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar]
- Padil, K.H.; Bakhary, N.; Abdulkareem, M.; Li, J.; Hao, H. Non-probabilistic method to consider uncertainties in frequency response function for vibration-based damage detection using Artificial Neural Network. J. Sound Vib. 2020, 467, 115069. [Google Scholar]
- Wang, X.; Xia, Y.; Zhou, X.; Yang, C. Structural damage measure index based on non-probabilistic reliability model. J. Sound Vib. 2014, 333, 1344–1355. [Google Scholar] [CrossRef]
- Kankanamge, Y.; Hu, Y.; Shao, X. Application of wavelet transform in structural health monitoring. Earthq. Eng. Eng. Vib. 2020, 19, 515–532. [Google Scholar]
- Ravanfar, S.A.; Razak, H.A.; Ismail, Z.; Hakim, S.J.S. Damage Detection Based on Wavelet Packet Transform and Information Entropy. In Structural Health Monitoring; Springer: Cham, Switzerland, 2014; Volume 5, pp. 223–229. [Google Scholar]
- Johnson, E.A.; Lam, H.F.; Katafygiotis, L.S.; Beck, J.L. Phase I IASC-ASCE structural health monitoring benchmark problem using simulated data. J. Eng. Mech. 2003, 130, 3–15. [Google Scholar]
- Gurley, K.; Kareem, A. Applications of wavelet transforms in earthquake, wind and ocean engineering. Eng. Struct. 1999, 21, 149–167. [Google Scholar]
- Luckey, D.; Fritz, H.; Legatiuk, D.; Dragos, K.; Smarsly, K. Artificial intelligence techniques for smart city applications. In International Conference on Computing in Civil and Building Engineering; Springer: Cham, Switzerland, 2020; pp. 3–15. [Google Scholar]
- Yen, G.G.; Lin, K.-C. Wavelet packet feature extraction for vibration monitoring. IEEE Trans. Ind. Electron. 2000, 47, 650–667. [Google Scholar]
- Sun, Z.; Chang, C.-C. Vibration based structural health monitoring: Wavelet packet transform based solution. Struct. Infrastruct. Eng. 2007, 3, 313–323. [Google Scholar]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar]
- Han, J.-G.; Ren, W.-X.; Sun, Z.-S. Wavelet packet based damage identification of beam structures. Int. J. Solids Struct. 2005, 42, 6610–6627. [Google Scholar]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar]
- Boller, C. Structural Health Monitoring—An Introduction and Definitions. In Encyclopedia of Structural Health Monitoring; Wiley Online Library: Hoboken, NJ, USA, 2009. [Google Scholar]
- Daubechies, I. Ten Lectures on Wavelets; Siam: Philadelphia, PA, USA, 1992; Volume 61, ISBN 1611970105. [Google Scholar]
- Ravanfar, S.A. Vibration-Based Structural Damage Detection and System Identification Using Wavelet Multiresolution Analysis. Ph.D. Thesis, University of Malaya, Kuala Lumpur, Malaysia, 2017. [Google Scholar]
- Ghiasi, R.; Torkzadeh, P.; Noori, M. Structural damage detection using artificial neural networks and least square support vector machine with particle swarm harmony search algorithm. Int. J. Sustain. Mater. Struct. Syst. 2014, 4, 303–320. [Google Scholar]
- Nazin, S.A.; Polyak, B.T. Interval parameter estimation under model uncertainty. Math. Comput. Model. Dyn. Syst. 2005, 11, 225–237. [Google Scholar]
- Lantz, B. Black Box Methods—Neural Networks and Support Vector Machines. In Machine Learning with R.; Jones, J., Sheikh, A., Eds.; Packt Publishing: Birmingham, UK, 2013; pp. 205–242. [Google Scholar]
- Rosenblueth, E. Point estimates for probability moments. Proc. Natl. Acad. Sci. USA 1975, 72, 3812–3814. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar]
- Suykens, J.A.K.; Horvath, G.; Basu, S.; Micchelli, C.; Vandewalle, J. Advances in Learning Theory: Methods, Models and Applications; IOS Press: Amsterdam, The Netherlands, 2003; ISBN 978-1-58603-341-5. [Google Scholar]
- Khatibinia, M.; Javad Fadaee, M.; Salajegheh, J.; Salajegheh, E. Seismic reliability assessment of RC structures including soil–structure interaction using wavelet weighted least squares support vector machine. Reliab. Eng. Syst. Saf. 2013, 110, 22–33. [Google Scholar]
- Seyedpoor, S.M.; Salajegheh, J.; Salajegheh, E.; Gholizadeh, S. Optimum shape design of arch dams for earthquake loading using a fuzzy inference system and wavelet neural networks. Eng. Optim. 2009, 41, 473–493. [Google Scholar]
- He, H.; Yan, W. Structural damage detection with wavelet support vector machine: Introduction and applications. Struct. Control Heal. Monit. 2007, 14, 162–176. [Google Scholar]
- Oh, C.K.; Beck, J.L. A Bayesian learning method for structural damage assessment of phase I IASC-ASCE Benchmark problem. KSCE J. Civ. Eng. 2018, 22, 987–992. [Google Scholar]
- Azimi, M.; Pekcan, G. Structural health monitoring using extremely compressed data through deep learning. Comput. Civ. Infrastruct. Eng. 2019. [Google Scholar] [CrossRef]
- Dyke, S. Report on the Building Structural Health Monitoring Problem Phase 1 Analytical. Available online: https://datacenterhub.org/resources/2806/supportingdocs (accessed on 1 December 2020).
- Das, S.; Saha, P. Structural health monitoring techniques implemented on IASC–ASCE benchmark problem: A review. J. Civ. Struct. Health Monit. 2018, 8, 689–718. [Google Scholar]
- Ghasemi, M.R.; Ghiasi, R.; Varaee, H. Probability-Based Damage Detection of Structures Using Surrogate Model and Enhanced Ideal Gas Molecular Movement Algorithm. In Advances in Structural and Multidisciplinary Optimization: Proceedings of the 12th World Congress of Structural and Multidisciplinary Optimization (WCSMO12); Schumacher, A., Vietor, T., Fiebig, S., Bletzinger, K.-U., Maute, K., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 1657–1674. ISBN 978-3-319-67988-4. [Google Scholar]
- Kook, O.C. Bayesian Learning for Earthquake Engineering Applications and Structural Health Monitoring; Earthquake Engineering Research Laboratory: Pasadena, CA, USA, 2007. [Google Scholar]
- Yuen, K.-V.; Au, S.K.; Beck, J.L. Two-stage structural health monitoring approach for phase I benchmark studies. J. Eng. Mech. 2004, 130, 16–33. [Google Scholar]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Department of Building Technology and Structural Engineering, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Yuan, F.-G.; Zargar, S.A.; Chen, Q.; Wang, S. Machine learning for structural health monitoring: Challenges and opportunities. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; SPIE Digital Library; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11379, p. 1137903. [Google Scholar]

| Surrogate Model | Training Input | Testing Input | Output | |
|---|---|---|---|---|
| Lower bound | WWLS-SVM 1 | of Acc. response with negative | of Acc. response with negative ω | |
| Upper bound | WWLS-SVM 2 | of Acc. response with positive | of Acc. response with pitive ω |
| Description | Case | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 12 DOF model 120 DOF model | O | O | O | O | O |
| Symmetric Mass Asymmetric Mass | O | O | O | O | O |
| Ambient Excitation Shaker on Roof | O | O | O | O | O |
| Damage Patterns: Remove Followings (1) All Braces in the 1st Story (2) All Braces in the 1st and 3rd Story (3) One Brace in the 1st Story (4) One Brace in the 1st and 3rd Story (5) 4 and Loosen Floor Beam at 1st Level (6) 2/3 Stiffness in One Brace at 1st Story | O O | O O | O O | O O O O | O O O O O O |
| Damage Case | Damage Patten | Story 1 | Story 2 | Story 3 | Story 4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Target Damage Cases 4&5 | 1 | 100 | 100 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 100 | 100 | 0.00 | 0.00 | 100 | 100 | 0.00 | 0.00 | |
| 3 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.00 | 100 | 0.00 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | |
| 5 | 0.00 | 100 | 0.00 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | |
| 6 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Prediction Damage Case 4 PoDE | 1 | 100 | 100 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 100 | 100 | 0.00 | 0.00 | 100 | 100 | 0.00 | 0.00 | |
| 3 | 2.00 | 100 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.00 | 100 | 0.00 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | |
| Prediction Damage Case 5 PoDE | 1 | 100 | 98 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 98 | 100 | 2.00 | 4.00 | 100 | 95 | 0.00 | 0.00 | |
| 3 | 2.00 | 97 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 4.00 | 100 | 0.00 | 0.00 | 100 | 1.00 | 0.00 | 0.00 | |
| 5 | 0.00 | 100 | 0.00 | 0.00 | 100 | 0.00 | 0.00 | 0.00 | |
| 6 | 0.00 | 99 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Prediction Damage Case 4 PDE | 1 | 100 | 99 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 100 | 100 | 3.00 | 1.00 | 100 | 99 | 0.00 | 0.00 | |
| 3 | 7.00 | 95 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 8.00 | 98 | 0.00 | 0.00 | 99 | 8.00 | 0.00 | 0.00 | |
| Prediction Damage Case 5 PDE | 1 | 90 | 91 | 0.00 | 0.00 | 1.00 | 5.00 | 0.00 | 0.00 |
| 2 | 79 | 91 | 7.00 | 14.00 | 80 | 90 | 6.00 | 2.00 | |
| 3 | 18.00 | 90 | 0.00 | 0.00 | 2.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 10.00 | 90 | 0.00 | 0.00 | 95 | 12.00 | 0.00 | 0.00 | |
| 5 | 13.00 | 87 | 1.00 | 1.00 | 98 | 15.00 | 1.00 | 0.00 | |
| 6 | 14.00 | 92 | 0.00 | 0.00 | 1.00 | 4.00 | 0.00 | 0.00 | |
| Method | RMSE | Total Time (s) |
|---|---|---|
| FE model (PDE) | ||
| FE model (PoDE) | ||
| Probabilistic WWLS-SVM surrogate model (PDE) | ||
| Non-Probabilistic WWLS-SVM surrogate model (PoDE) |
| Damage Case | Damage Patten | Story 1 | Story 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Target Damage Cases 4&5 | 1 | 0.45 | 0.71 | 0.45 | 0.71 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.45 | 0.71 | 0.45 | 0.71 | 0.45 | 0.71 | 0.45 | 0.71 | |
| 3 | 0.00 | 0.36 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.00 | 0.36 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | |
| 5 | 0.00 | 0.36 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | |
| 6 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Prediction Damage Case 4 | 1 | 0.44 | 0.70 | 0.44 | 0.70 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.43 | 0.70 | 0.44 | 0.69 | 0.44 | 0.74 | 0.42 | 0.68 | |
| 3 | 0.05 | 0.35 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.00 | 0.32 | 0.00 | 0.01 | 0.19 | 0.00 | 0.02 | 0.00 | |
| Prediction Damage Case 5 | 1 | 0.42 | 0.69 | 0.40 | 0.67 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.40 | 0.68 | 0.44 | 0.70 | 0.44 | 0.67 | 0.40 | 0.68 | |
| 3 | 0.00 | 0.30 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.06 | 0.38 | 0.00 | 0.07 | 0.19 | 0.01 | 0.03 | 0.00 | |
| 5 | 0.00 | 0.29 | 0.00 | 0.00 | 0.20 | 0.00 | 0.04 | 0.00 | |
| 6 | 0.00 | 0.18 | 0.00 | 0.04 | 0.00 | 0.00 | 0.00 | 0.00 | |
| Train Uncertainties | Element | Test Uncertainties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 2% | 5% | 15% | 20% | ||||||||
| PoDE | DMI | PoDE | DMI | PoDE | DMI | PoDE | DMI | PoDE | DMI | |||
| 0% | S1 | 100 | 0.43 | 100 | 0.41 | 100 | 0.38 | 100 | 0.39 | 100 | 0.32 | |
| 100 | 0.70 | 100 | 0.73 | 99 | 0.65 | 85 | 0.58 | 85 | 0.51 | |||
| S2 | 0 | 0.00 | 0 | 0.00 | 5.12 | 0.01 | 0 | 0.00 | 47.1 | 0.30 | ||
| 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 21.10 | 0.20 | 38 | 0.27 | |||
| S3 | 100 | 0.44 | 99 | 0.40 | 100 | 0.49 | 80 | 0.30 | 95 | 0.39 | ||
| 100 | 0.71 | 100 | 0.69 | 100 | 0.65 | 100 | 0.79 | 65 | 0.40 | |||
| S4 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 12 | 0.09 | 0 | 0.00 | ||
| 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 13.15 | 0.09 | |||
| 2% | S1 | 100 | 0.38 | 100 | 0.39 | 100 | 0.46 | 100 | 0.46 | 100 | 0.46 | |
| 100 | 0.68 | 100 | 0.67 | 100 | 0.69 | 99 | 0.69 | 90 | 0.69 | |||
| S2 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 19 | 0.12 | 39 | 0.12 | ||
| 0 | 0.00 | 0 | 0.00 | 7.12 | 0.04 | 17.12 | 0.10 | 7.12 | 0.10 | |||
| S3 | 100 | 0.39 | 100 | 0.39 | 98 | 0.35 | 98 | 0.35 | 95 | 0.35 | ||
| 100 | 0.69 | 100 | 0.75 | 100 | 0.65 | 94 | 0.65 | 90 | 0.65 | |||
| S4 | 0 | 0.00 | 4.11 | 0.02 | 0 | 0.00 | 0.0 | 0.00 | 2.2 | 0.01 | ||
| 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 4.0 | 0.04 | 0 | 0.00 | |||
| 5% | S1 | 100 | 0.38 | 100 | 0.40 | 100 | 0.48 | 100 | 0.39 | 79 | 0.30 | |
| 100 | 0.67 | 100 | 0.65 | 100 | 0.66 | 98 | 0.66 | 100 | 0.59 | |||
| S2 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 20.1 | 0.09 | 2.1 | 0.01 | ||
| 8.16 | 0.05 | 6.15 | 0.04 | 0 | 0.04 | 12.01 | 0.04 | 35 | 0.15 | |||
| S3 | 100 | 0.46 | 100 | 0.39 | 100 | 0.41 | 97 | 0.49 | 100 | 0.41 | ||
| 98.11 | 0.65 | 100 | 0.69 | 100 | 0.65 | 100 | 0.61 | 76 | 0.55 | |||
| S4 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 1.65 | 0.00 | ||
| 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 10.2 | 0.12 | 14.2 | 0.12 | |||
| 15% | S1 | 100 | 0.40 | 100 | 0.40 | 100 | 0.40 | 100 | 0.46 | 78 | 0.46 | |
| 86 | 0.61 | 97 | 0.67 | 97 | 0.67 | 100 | 0.72 | 100 | 0.72 | |||
| S2 | 0 | 0.00 | 0 | 0.00 | 14.01 | 0.14 | 0 | 0.00 | 55 | 0.34 | ||
| 0 | 0.00 | 13.11 | 0.10 | 0 | 0.00 | 4.41 | 0.01 | 0 | 0.00 | |||
| S3 | 100 | 0.39 | 100 | 0.39 | 100 | 0.49 | 100 | 0.49 | 87.12 | 0.37 | ||
| 82 | 0.61 | 91 | 0.63 | 100 | 0.69 | 100 | 0.74 | 98 | 0.74 | |||
| S4 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 15.34 | 0.09 | ||
| 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | |||
| 20% | S1 | 70 | 0.29 | 81 | 0.29 | 94 | 0.32 | 100 | 0.32 | 100 | 0.40 | |
| 90 | 0.60 | 90 | 0.60 | 88.12 | 0.67 | 98 | 0.67 | 100 | 0.69 | |||
| S2 | 0 | 0.00 | 0 | 0.00 | 11 | 0.03 | 31 | 0.13 | 0 | 0.00 | ||
| 54 | 0.30 | 33 | 0.13 | 0 | 0.00 | 14 | 0.03 | 0 | 0.00 | |||
| S3 | 49 | 0.24 | 79 | 0.33 | 100 | 0.44 | 100 | 0.40 | 100 | 0.41 | ||
| 61 | 0.50 | 80 | 0.81 | 100 | 0.81 | 100 | 0.78 | 100 | 0.75 | |||
| S4 | 16.12 | 0.08 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | 0 | 0.00 | ||
| 38.11 | 0.17 | 10.12 | 0.06 | 0 | 0.00 | 20.1 | 0.20 | 0 | 0.00 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghiasi, R.; Noori, M.; Altabey, W.A.; Silik, A.; Wang, T.; Wu, Z. Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach. Appl. Sci. 2021, 11, 770. https://doi.org/10.3390/app11020770
Ghiasi R, Noori M, Altabey WA, Silik A, Wang T, Wu Z. Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach. Applied Sciences. 2021; 11(2):770. https://doi.org/10.3390/app11020770
Chicago/Turabian StyleGhiasi, Ramin, Mohammad Noori, Wael A. Altabey, Ahmed Silik, Tianyu Wang, and Zhishen Wu. 2021. "Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach" Applied Sciences 11, no. 2: 770. https://doi.org/10.3390/app11020770
APA StyleGhiasi, R., Noori, M., Altabey, W. A., Silik, A., Wang, T., & Wu, Z. (2021). Uncertainty Handling in Structural Damage Detection via Non-Probabilistic Meta-Models and Interval Mathematics, a Data-Analytics Approach. Applied Sciences, 11(2), 770. https://doi.org/10.3390/app11020770








