Numerical Investigation on the Influence of the Streamlined Structures of the High-Speed Train’s Nose on Aerodynamic Performances

Abstract

The structural design of the streamlined shape is the basis for high-speed train aerodynamic design. With use of the delayed detached-eddy simulation (DDES) method, the influence of four different structural types of the streamlined shape on aerodynamic performance and flow mechanism was investigated. These four designs were chosen elaborately, including a double-arch ellipsoid shape, a single-arch ellipsoid shape, a spindle shape with a front cowcatcher and a double-arch wide-flat shape. Two different running scenes, trains running in the open air or in crosswind conditions, were considered. Results reveal that when dealing with drag reduction of the whole train running in the open air, it needs to take into account how air resistance is distributed on both noses and then deal with them both rather than adjust only the head or the tail. An asymmetrical design is feasible with the head being a single-arch ellipsoid and the tail being a spindle with a front cowcatcher to achieve the minimum drag reduction. The single-arch ellipsoid design on both noses could aid in moderating the transverse amplitude of the side force on the tail resulting from the asymmetrical vortex structures in the flow field behind the tail. When crosswind is considered, the pressure distribution on the train surface becomes more disturbed, resulting in the increase of the side force and lift. The current study reveals that the double-arch wide-flat streamlined design helps to alleviate the side force and lift on both noses. The magnitude of side force on the head is 10 times as large as that on the tail while the lift on the head is slightly above that on the tail. Change of positions where flow separation takes place on the streamlined part is the main cause that leads to the opposite behaviors of pressure distribution on the head and on the tail. Under the influence of the ambient wind, flow separation occurs about distinct positions on the train surface and intricate vortices are generated at the leeward side, which add to the aerodynamic loads on the train in crosswind conditions. These results could help gain insight on choosing a most suitable streamlined shape under specific running conditions and acquiring a universal optimum nose shape as well.

1. Introduction

As the running speed of high-speed trains increases, aerodynamics play a much greater role in the safety and amenity issues of high-speed trains [1,2]. Consequently, it is crucial to improve the aerodynamic performance of high-speed trains [3]. As near-ground vehicles with a large slenderness ratio and intricate structures [3,4], high-speed trains cover a variety of running environments and experience prominent unsteady characteristics in the ambient flow field [5,6]. The geometric design, along with running environments, act as major roles to affect aerodynamic performance of a high-speed train. However, running environments, restricted by road conditions and construction cost, cannot be changed greatly to improve the high-speed train’s performance, whereas the geometric design becomes a favorable approach to improvement. The structural design for a high-speed train includes shape designs of both noses [7,8,9], design of key components [10,11], and smooth design of the whole train [3]. Generally speaking, the head and the tail are identical for the convenience of dispatch and operation, and their performance to a large degree determines the whole train’s aerodynamic performance. Kwon Hyeokbin et al. [12], Lee Jongsoo et al. [13], and Kim I et al. [14] studied the influence of the streamlined nose on the micropressure wave through two-dimensional design. Vytla V V et al. [15] carried out multiobjective optimization on geometric shapes of a high-speed train based on self-adaptive surrogate models. Krajnovic S [16] performed an optimization of the train’s front for the crosswind stability and optimization of vortex generators (VGs) for the purpose of drag reduction. Ku YC et al. [17] proposed a vehicle modeling function (VMF) parametric method to parameterize the high-speed train’s head and tail, and analyzed the influence of key design variables of the streamlined shape on the train aerodynamic performance. Yao et al. [18] starting from the previous work proposed a three-dimensional parametric method suitable for engineering design of the streamlined shape of high-speed trains, and further performed a multiobjective aerodynamic optimization with use of particle swarm optimization method.

High-speed trains’ streamlined noses are designed with complicated surfaces and characterized by geographical and cultural environments of the countries where they are employed. Present parametric methods are mainly based on a given existing shape, but have trouble in designing unique and original streamlined shapes [6,19], even the authors’ new three-dimensional method [18,20,21] failed this goal. Therefore, the research based on current parametric methods could most likely achieve, other than a universally optimum nose shape, an optimized design for some particular and existing shapes. The streamlined structure is the determinant for types of the head and tail. As a result, the study of its impacts upon the aerodynamic performance of high-speed trains is fundamental for obtaining the nose shapes of the train with the best aerodynamic performance. Raghuathan S et al. [22] carried out experiments for high-speed trains’ noses with four different lengths and four different variation rates of cross-sectional area in a wind tunnel to study their influence on the drag and lift of the train model. Chen et al. [23] studied the influence of some key design variables, namely the length of the head, characteristic sectional profiles, cowcatcher, cab window, and cross section of the train body, on the drag and lift force of the train model. Hemida H. et al. [24] made use of LES to study the length of the train head’s influence on ambient flow field. Yang et al. [3] compared and analyzed the aerodynamic performance of CRH380A and CRH380B which have been in service in China for over nine years. These studies have mainly described the relationships between the geometric shapes and aerodynamic performance but not yet specifically pointed out how the streamlined structures of the noses affect the flow field around a train.

Aiming at four typical streamlined structures of high-speed trains’ noses, the current study numerically studies ambient flow field and analyzes these four structures’ influence upon aerodynamic loads and slipstream, in order to gain theoretical insight on acquiring a universal optimum nose shape. This paper is organized into five sections. Section 2 mainly introduces the popular streamlined structures all over the world, and the reason why the four typical structures are chosen is also explained there. Section 3 introduces the numerical methodologies adopted in the paper, and the computational models, computational conditions, mesh configurations, and method validation are also included. Section 4 provides the results obtained from numerical simulations. Analysis and discussion on these results is presented to understand the influence due to the difference of streamlined structures on flow field and aerodynamic loads. Section 5 concludes the research by listing the main research outcomes along with providing suggestions for future work.

2. Streamlined Structures of High-Speed Train’s Head

The geometric design of the streamlined nose is key to the shape design of high-speed trains, severely affected by the running speed, operating environments, load capacity, and local culture [3]. Figure 1 shows the four latest nose shapes, namely CR400AF, CR400BF for China Fuxing EMU, the TGV in France, and ALFA-X for Japan Shinkansen. The streamlined structures of these four nose shapes are distinct from each other. Among them CR400AF and CR400BF have medium lengths, while a double-arch design [25] gives CR400AF a better streamline and CR400BF looks weighty with the single-arch design. Both shapes are to meet the demand of riding comfort, energy saving, and environmental protection under the circumstances that complicated tunnels and viaducts are popular along Chinese railways and trains are bound to carry numerous passengers. By contrast, railway tunnels in Europe are fewer and passengers are mainly concentrated in metropolitans, which gives rise to the short clean and single-arch design of the TGV heads, considering that load capacity can be expanded without the hindrance of tunnels. However, since Japanese high-speed rail owns a long history tracing back to an earlier date than any other country in the world, an unavoidable issue is left behind that the size of the tunnels are too narrow due to previous construction. What is more, the mountainous landscape in Japan requires trains to run through tunnels one after another. Therefore, the goal of high-speed train design is mainly coping with the pressure wave and micropressure wave in the tunnels. ALFA-X is the latest Japanese high-speed rail innovation which has not yet been put into the market. Its head is structured as double-arch ellipsoid with a length up to 22 m to alleviate the aerodynamic effects.

The optimization of high-speed train nose shape can be carried out under a unique running scenario as long as the railway is built on a rather singular type of landscape. However, for countries in possession of developed railway systems covering diverse environments and immense span, it is difficult to reduce the cost for design, construction and maintenance if optimum streamlined noses are designed for each scenario. As a consequence, obtaining an optimum nose shape for specific running scenario becomes a major task for high-speed train studies. The streamlined structure of the nose shape determines the aerodynamic performance of the train. To design the optimum nose shape, the streamlined type of the nose shape needs to be determined in advance, which is reflected by the aerodynamic performance of the train [22,23]. Consequently, the fundamental work of nose shape optimization is to study the flow mechanism of the streamlined structures.

There are a variety of nose shapes, of which the basic streamlined types include spindle, ellipsoid, wide-flat shape, and so on [25]. Figure 2 shows four traditional high-speed trains’ head streamlined structures—double-arch ellipsoid, single-arch ellipsoid, a spindle shape with a front cowcatcher, and a double-arch wide-flat shape.

As shown in Figure 2, the cross sections and areas of the four trains are different from each other. To eliminate the influence of different cross sections on the ambient flow field, a uniform cross section is achieved by modifying every nose shape. In addition, the train model is also locally simplified to facilitate the numerical analysis. The modified four streamlined shapes on the base of the noses in Figure 2 are labeled as TP1, TP2, TP3, and TP4, respectively, which are shown in Figure 3. It can be observed that the length of each head is distinct, with TP1 and TP3 being 12 m, TP2 being 7.5 m, and TP4 being 14 m. The distance from the first bogie to the nose tip varies from each other, and the structure of the cowcatchers and the way it guides the air are different as well. Particularly, the cowcatcher of TP3 and its nose shape are integrated together, just as shown in Figure 3.

3. Numerical Algorithms

3.1. DDES

Detached-eddy simulation (DES) method [26], as a mixed scheme of Reynolds Averaged Navier–Stokes (RANS) method and large eddy simulation (LES) method, owns its particular advantage in solving flow with large Reynolds number and apparent separations. In the simulation of the ground transports where there may exist large flow separation, DES presents high precision on the prediction of aerodynamic drag and flow separations [27]. The flow field around the high-speed train is significantly unsteady. More precise flow structures could be obtained with use of the DES method as long as the computational mesh is fine enough [6,28]. The most frequently used DES methods include two kinds: DES based on SA turbulence model [29] and DES based on k-w [30] and SST k-w turbulence model [31]. These two methods both can result in problems such as MSD and cell-induced separation. To overcome these problems, Menter et al. modified dissipation rate for SST k-w as:

$$\tilde{\omega }=\omega \varphi$$

(1)

$$\varphi =\max \left(\frac{l_t}{C_{\mathrm{DES}}\Delta }F,1\right)$$

(2)

where $l_t=\frac{\sqrt{k}}{{\beta }^{*}\omega }$, $\Delta$ is the maximal value between the centers of computational cell and adjacent cells. $F=1-F_2$, while the expression of $F_2$ takes the form as:

$$F_2=\tanh \left({\left(\max \left(\frac{2\sqrt{k}}{{\beta }^{*}\omega d},\frac{500v}{d^2\omega }\right)\right)}^2\right)$$

(3)

When $\varphi =1$ the RANS model is adopted, while LES model is utilized when $\varphi >1$.

$$C_{\mathrm{DES}}=C_{\mathrm{DES},k-\omega }{F}_1+C_{\mathrm{DES},k-\epsilon }\left(1-F_1\right)$$

(4)

In which, $C_{\mathrm{DES},k-\omega }$ and $C_{\mathrm{DES},k-\epsilon }$ are set as 0.78 and 0.61, respectively.

$$F_1=\tanh \left({\left[\min \left(\max \left(\frac{\sqrt{k}}{0.09\omega d},\frac{500v}{d^2\omega }\right),\frac{2k}{d^{2}C{D}_{k\omega }}\right)\right]}^4\right)$$

(5)

In which, $d$ denotes the distance between the first cell and the wall, while $v$ is the coefficient of kinematic viscosity.

$$C{D}_{k\omega }=\max \left(\frac{1}{\omega }\nabla k\cdot \nabla \omega ,{10}^{-20}\right)$$

(6)

3.2. Algorithm and Mesh Validation

To validate the prediction accuracy of the numerical algorithms, a wind tunnel experiment was carried out on a simplified train model. The wind tunnel is a low-speed open wind tunnel with an 8 × 6 m cross section in Mianyang, Sichuan Province. The turbulence intensity of the incoming flow is 0.2%. The train model and the test section of the wind tunnel are shown in Figure 4. The train model is fixed with the subgrade by the force-measuring balances, which are mounted on the geometry center of each carriage. They are placed on a turntable, which could be used to adjust the angle of the train model and the incoming flow. As shown in Figure 4, the test model is a 1:8 scaled model with windshields and bogies included, and takes the subgrade and tracks into consideration. The scaled model takes a length of 4 m, a height of 0.4375 m, and a width of 0.4225 m. The velocity of the incoming flow is 60 m/s. The Reynolds number is 1.28 × 106 taking the height of the model as the characteristic length.

Meanwhile, in order to determine a proper mesh configuration for the current analysis, two mesh configurations are proposed on the wind tunnel model, just as

Table 1. Mesh parameters.

	Boundary Layers	Minimum Size of a Cell	Number of Cells
Coarse mesh	15	10 mm	29.82 million
Fine mesh	20	1.5 mm	69.22 million

shows.

Without special notification the aerodynamic loads on the train are all evaluated in the form of dimensionless coefficients as follows:

$$\text{Pressure coefficient }(\mathrm{Cp}):C_p=P/0.5\rho V^2$$

(7)

$$\text{Drag coefficient }(\mathrm{Cd}):C_{di}=F_{di}/0.5\rho V^{2}S$$

(8)

$$\text{Side force coefficient }(\mathrm{Cs}):C_{si}=F_{si}/0.5\rho V^{2}S$$

(9)

$$\text{Lift coefficient }(\mathrm{Cl}):C_{li}=F_{li}/0.5\rho V^{2}S$$

(10)

where P denotes the relative pressure, ρ is the air density, and V is the train velocity as well as the speed of incoming flow in the tunnel experiment. S represents the maximum cross section area, which is 10 m² in this study. The order i, ranging from 1 to 8, represents the number of each carriage. When w is used it represents the whole train. When i equals 0, it denotes the streamlined shape of the head, while 9 the streamlined shape of the tail.

The pressure and forces on the train in the wind tunnel experiment are measured by means of steady tests, so the time-averaged computational results are taken for comparisons. In Figure 5, plots of pressure coefficients (Cp) of the head and the tail profile are presented, with computation and experiments included. It could be found that results from both coarse mesh and fine mesh are in accordance with the experiment, while the two are consistent in the head and fine mesh performs better compared to the experiment than coarse mesh around the tail, indicating that the adopted numerical algorithms could obtain the flow data around the train precisely.

Table 2. Comparison of Cd among numerical simulations and wind tunnel experiment.

	H-Cd	M-Cd	T-Cd	W-Cd
Wind tunnel	0.1346	0.0808	0.1323	0.3477
Coarse mesh	0.1276	0.0770	0.1565	0.3611
Fine mesh	0.1325	0.0809	0.1447	0.3581

lists the coefficients obtained by two mesh configurations as well as the experiment. It can be reported that total drag coefficients (W-Cd) obtained by both kinds of mesh are nearly the same, but the drag coefficient for each carriage of the fine mesh configuration agrees better with that of the experiment. The errors of H-Cd, M-Cd, and T-Cd with fine mesh are 1.6%, 0.1%, and 9.4%, respectively. Therefore, although the pressure coefficients along the longitudinal section of the streamlined shape for both mesh configurations agree well with the experiment, the fine mesh configuration was adopted for current study due to its excellent performance in predicting the drag coefficients for each carriage of the train model. For the following analysis on streamlined structures of high-speed trains, the adopted mesh configuration is in accordance with the fine mesh in this section.

3.3. Boundary Conditions

The geometry of TP1 is shown in Figure 6. TP1 is an eight-grouped model, with the simplified bogies and windshields included. Meanwhile, components such as pantographs, doors, and windows are all neglected. For TP2, TP3, and TP4, the difference from TP1 only exists in the streamlined shapes. The cross section area S is 11.2 m², while the train body height H is 3.5 m. For the convenience of analyzing the aerodynamic performance of each component, the orders of each carriage and each bogie are prescribed as shown in Figure 6. From small to large the numbers represent the parts from the head to the tail, while the streamlined part of the train is also named independently for further analysis.

The x axis is set along the train axis, with the origin set on the middle of the train. The z axis is set to the vertical direction, as Figure 5 shows. The y axis could be decided in accordance with the right-hand rule. The computational domain is shown in Figure 5. Taking the height of the train as the characteristic length H, the inlet boundary is 55H away from the head nose and the outlet boundary is 85H away from the tail nose. The height and width of the computational domain are 28 H and 56H, respectively.

The velocity of the train is 350 km/h, so that the Mach number is 0.2858. As a result, the incoming flow could be assumed as incompressible. The turbulence model used with DDES is the SST k-w two-equation model. The temporal terms for all of the DDES simulations were discretized by using a second-order implicit scheme. The diffusive and subgrid fluxes were discretized with a second-order central difference scheme. The convective term was discretized using a second-order upwind scheme. Studies from Baker [2] reveal that the Strouhal number of the shedding vortex in the wake ranges from 0.11 to 0.14. As a result, the time step used in the current study is 5 × 10⁻⁴ s [6]. The number of inner iterations in each time step is 10. The total computational time is 2 s.

The velocity inlet boundary with a velocity of 350 km/h and the pressure outlet boundary with the relative pressure of 0 Pa were adopted for the INLET and OUTLET boundary in Figure 7. The lateral sides and top of the computational domain were set as slip walls, while the ground was set as the moving wall with a speed of 350 km/h in the same direction as the inlet stream. For the simulation in a crosswind condition the velocity of the incoming flow is the resultant velocity of the train and the wind. The INLET boundary and the windward side boundary were taken as the inlet boundaries. Meanwhile, the OUTLET boundary and the leeward side boundary were set as the pressure outlet boundaries. The rest of the boundary conditions remain the same.

3.4. Computational Grids

The commercial software STAR-CCM+ 13.04 was adopted for mesh generation. The Cartesian grids were generated for the volume mesh and prism grids were generated near the train surface. The standard wall function was used to control the number of cells in the prism layers. A total of 20 layers of prism grids were generated with an increasing ratio of 1.1 and a total length of 30 mm, which keeps the value of y+ of the first layer near the train surface around 30. As seen in Figure 6, the region around the train is locally densified. The minimum size of a cell in this region is 12 mm and the total amount of the computational grids is about 170 million. The grids on the longitudinal section of the domain and the local components are shown in Figure 8.

4. Results and Discussion

4.1. Flow Mechanism for Trains Running in the Open Air without Crosswind

The most frequent circumstance where a high-speed train operates is the static open environment. In this situation, drag of the whole train, the side force, and train-induced air flow represent the key variables to the aerodynamic performance of the train.

The aerodynamic drag is firstly focused on. As a major part in the total drag of the train [3], the inviscid drag is determined by the pressure distribution on the train body. Figure 9 shows the contours of the time-averaged pressure on the head and the tail of the four models. The nose tip of the leading streamline is the stagnation point, which owns the highest pressure. However, for different streamlined structures, the distribution and area of high pressure in the stagnation zone differ from each other. The high pressure region of TP2 is the largest, while that of TP3 is the least due to the integrated design between the cowcatcher and the nose. Yet, for TP4 whose cowcatcher is moved backwards to behind the nose tip, a rather large high pressure zone is induced around the cowcatcher. To alleviate this problem an airflow-guiding design is adopted around the cowcatcher for E6′s nose. As seen from Figure 10, it is obvious that there is a secondary high pressure zone at the transition from the nose to the cab window for the trains with double-arch structures. In contrast, TP2 with the single-arch shape has only one high pressure zone at the nose tip. Due to great bending of the cab window, the airflow accelerates rapidly, resulting in significant negative pressure over this zone, which is the reason why negative drag appears around this region for TP2. The third high pressure zone appears at the rear of the first bogie for each nose shape. That is because the air flows quickly underneath and then impinges hard on the back of the bogie cabin, generating a high pressure zone consequently. The pressure distribution of this area is mainly determined by how the air flows by the cowcatcher. For TP2 and TP4 whose air flows bilaterally by the train with the guidance of cowcatchers, there is less air impingement around the bogie thus less impact upon the rear of the bogie cabin. In light of this, to reduce the pressure force around the bogie region, some pumping devices could be mounted at the rear of the bogie cabin according to the pressure distribution. The pressure distributions on the head and tail remain the same, except that the pressure on the head varies more drastically. This kind of distribution also explains why the drag along the head and that along the tail act oppositely as mentioned above.

Viscous force is the other major part of the total drag of the high-speed train. The smoother and straighter the train body is, the more viscous force contributes to the total resistance. Owing to great slenderness, the development of a turbulent boundary layer on the train surface affects the distribution of shear force to a large degree. When the nose streamlined structure changes, the location where the flow separation occurs also alters, thus, the turbulent boundary layer will be influenced. Figure 10a shows the distributions of accumulated pressure force, shear force, and total drag along the train body of TP1. It can be seen that on regions with irregular components pressure force contributes more, while on regions where the cross section of the train remains constant, shear force takes the lead. The variation of the nose streamlined structure does not relate to obvious changes of the proportion that pressure force and shear force make up the total drag. As a result, to reduce the total drag over the whole high-speed train, the reduction of pressure drag should be mainly focused on. The distributions of shear force coefficients of four models along the train body are given in Figure 10b. It could be found that shear force fluctuates massively about the irregular region of the train. Shear force around the streamlined region on the head is relatively large and that around the streamlined region on the tail is rather small. Shear force around the bogies is apparently smaller than that around the regions with constant cross section. From the streamlined head to the tail, fluctuation amplitude of shear force gradually becomes smaller and reaches the lowest at the trailing nose tip. Similar shear force magnitude is measured around the constant cross-sectional regions for the four models. Among these four models, the minimum shear force around the streamlined regions could be observed on TP4.

Shear force originates from the viscosity effect of the turbulent boundary layer on the train. Figure 11 shows the velocity profile within the boundary layer at different cross sections for the four models. It can be seen that the boundary layer grows thicker as the airflow runs from head to tail, exceeding as much as 1.5 m or 40% of the train height around the constant cross-sectional region on the tail. The amplitude of velocity variation is rather huge around the streamlined region on the head, because the boundary layer is not fully developed and the pressure gradient is enormous, causing shear force to oscillate significantly. Around the constant cross-sectional region on the leading car, the boundary layer gradually develops and the inner flow within the boundary layer stabilizes. As the boundary layer develops along the train body, its thickness increases gradually, meanwhile the pressure gradient near the train surface becomes smaller and smaller, leading to reduction of shear force. The pressure gradient of TP4 is the largest over the constant cross-sectional region on the leading car, resulting in the largest shear force on the corresponding regions among the four models. For the middle carriages, the pressure gradients of the four models are similar. Consequently, the shear forces of the four models tend to be similar too. Around the constant cross-sectional region on the trailing carriage, the pressure gradient of TP4 is still the most significant and naturally its shear force becomes the biggest among the models. As for the streamlined region on the trailing car, owing to the longest streamline, the flow separation location of TP4 is the furthest away from the trailing nose tip. As a result, the distance from where the boundary flow is broken to the nose tip of TP4 is also the longest.

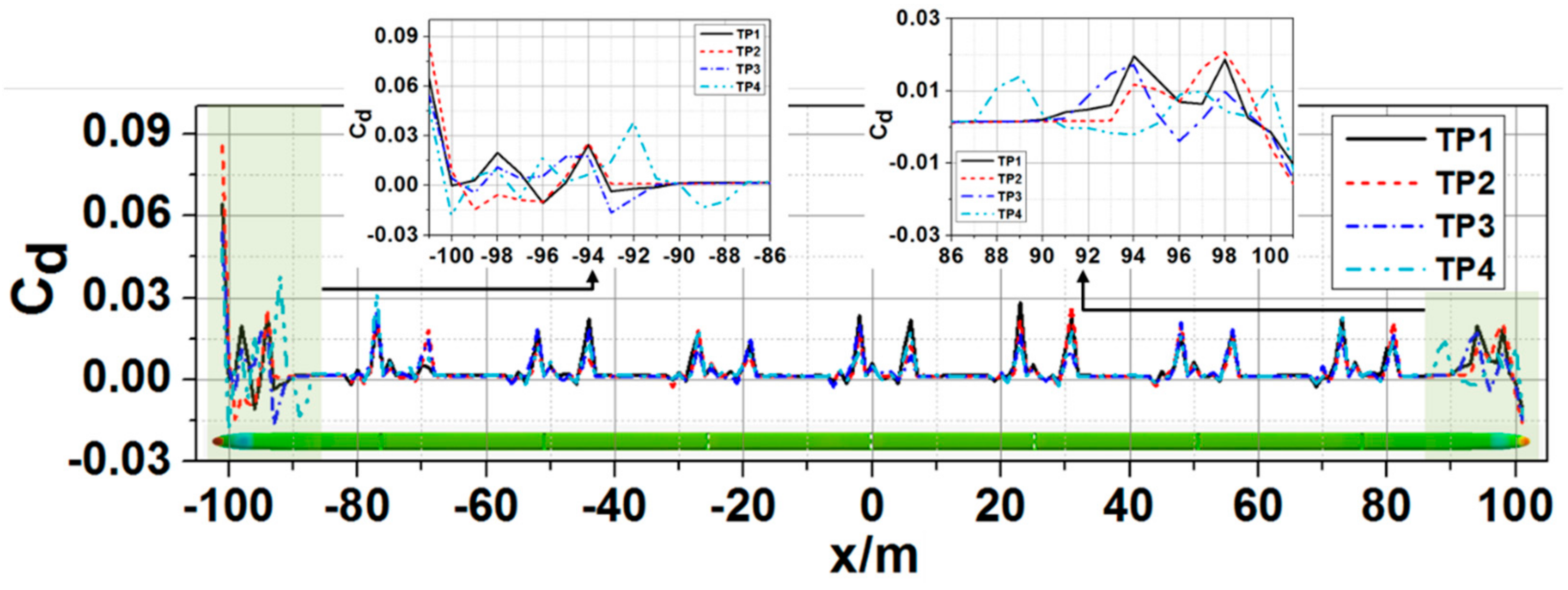
Figure 12 shows plots of accumulated Cd on four computational models along the x axis at t = 2 s. It could be observed that Cd fluctuates severely on the head, the tail, and bogies. In the region where the cross section remains constant, Cd keeps a relatively low value but increases apparently around the bogie regions. The distribution of Cd varies from each other along the streamlined shape for the four models. For TP1 whose nose is constructed in double-arch ellipsoid, the first peak appears at the transition from the head nose to the cab window and a minimum in the middle of the cab window. After that, the second peak of Cd appears about the rear of the first bogie cabin. Built in single-arch ellipsoid, Cd of TP2 turns to be the largest compared to the other three at the leading nose tip. However, it drops rapidly afterwards until the middle of the cab window. It keeps negative in the following 4 m along the streamline until the rear of the first bogie cabin, where the first Cd peak appears. TP3 is constructed in a spindle with a cowcatcher in the front. The drag of TP3 along the streamline remains positive and also meets its peak at the rear of the first bogie cabin. As for TP4 whose shape is a wide-flat double-arch, Cd at the nose tip is the minimum. After the stagnation around the nose tip Cd drops sharply to under zero and then unsteadily increases until it reaches the top at the rear of the first bogie cabin. However, Cd along the streamlined shape on the tail performs adversely to that on the head but its amplitude reduces apparently. Therefore, it can be seen that when the streamlined head and tail are designed symmetrically, the drag distributions along both streamlined shapes, other than only head or tail, should be considered to achieve the minimum drag of the train. However, if the streamlined head and tail could be designed differently, a recommendation could be proposed that the head can be designed in single-arch ellipsoid while the tail can take the form of a spindle with a cowcatcher in the front.

Time-averaged Cd of the four models is given in

Table 3. Time-averaged Cd of the four models.

Models	Cdw	Cd1	Cd2	Cd3	Cd4	Cd5	Cd6	Cd7	Cd8
TP1	0.764	0.172	0.081	0.079	0.085	0.084	0.085	0.083	0.096
TP2	0.752	0.157	0.084	0.075	0.078	0.086	0.087	0.076	0.109
TP3	0.752	0.173	0.082	0.079	0.085	0.080	0.080	0.080	0.093
TP4	0.733	0.162	0.081	0.078	0.076	0.081	0.083	0.080	0.092

. From the given data it can be seen that the whole Cd of TP1 is the highest while that of TP4 is the lowest, dropping by 4.2% compared to TP1. On the other hand, the whole Cd of TP2 and TP3 remains close to each other. Specifically, Cd of the leading car of TP2 is the smallest while that of the trailing car is the largest among the four models. For TP3, the Cd of the leading car is the largest while that of the trailing car is close to TP4. The Cd of the middle carriages for TP2 and TP3 remain close to each other, which is in accordance with the drag distribution shown in Figure 10b. The Cd of the leading car for TP4 increases by 3.2% to TP2. However, the Cd of middle carriages and the trailing car is the smallest among all the models. Although the aerodynamic drag coefficients of streamlined head and tail are almost similar for TP1 and TP3, the Cd of middle carriages for TP1 is relatively larger than TP3. It could be concluded that when performing drag reduction of a high-speed train, not only the drag of the leading and trailing streamlines should be considered, but also the streamlined variation influence on the middle carriages. In brief, the drag reduction design should aim at the drag of the whole train.

Since the high-speed train is running very close to the ground, ground effect makes a significant contribution to the aerodynamic performance of the bogie system [28,32]. Drag of the bogies makes up 27% of the whole resistance [3]. For the convenience of analyzing the influence of streamlined structures on the aerodynamic performance of the bogies, each bogie as well as the corresponding cabin are divided separately from the carriage, so there are 16 bogie systems in total. Figure 13 shows the time-averaged Cd of each bogie system (with BOGIE representing the bogie and BOTTOM representing the bogie cabin) for the four models. It could be observed that Cd of BOGIE-1 is evidently larger than any other BOGIE. Cd of all BOGIEs is not so distinct except BOGIE-1, while in detail for one bogie system Cd of the cabin is far more considerable than Cd of the bogie. The drag coefficient of BOGIE-1 is close to each other for TP1 and TP3, while Cd of BOGIE-1 for TP2 is the lowest, dropping by about 26% compared to TP3. Judging from total drag of the bogie system, TP2 and TP4 own similar drag while TP1 has the most significant resistance, growing by 8.2% compared to TP2. The first bogie is the most sensitive in drag performance to the streamlined structures under the nose tip. However, because of the fully developed turbulent flow around the wake region, the last bogie of the train is not sensitive to the streamlined structures at all. The influence of the streamlined structures on the last bogie could be neglected.

As mentioned above, streamlined structures influence the flow details around the first bogie region to a large degree. As the clearance H between the streamlined head and the ground varies, the flux and velocity of air flowing through this clearance to the first bogie cabin also change. Figure 14 shows the velocity contour of the longitudinal section around the first bogie region and pressure contour of the first bogie. It could be seen that after flowing by the stagnant zone ahead of the nose tip and the cowcatcher, the flow accelerates within the clearance. Due to the sudden expansion of free space in the cabin, more flow separation could be observed. Stagnation could also be observed on the front of the bogie while most of the flow gets inside the cabin and becomes more turbulent. A high pressure region is generated at the rear of the cabin due to the impingement of the flow. Specifically, the guidance effect of the cowcatcher design plays an important role in the aerodynamic performance of the system. The flow is guided along the train surface until it reaches the bogie region. If the sides of the cabin shrink too much, just as TP1 shows, it would be much easier for the guided flow going inside the cabin and further generating larger drag on the cabin. For TP2, the sides of the bogie cabin shrink less compared to TP1. Consequently, less flow could impinge on the cabin, and less high pressure region around the cabin could be observed. Due to the integration design of the cowcatcher and the streamline for TP3, the stagnation point lowers down to the region near the bottom of the streamline. Thus, more flow gathers around the clearance and lateral sides of the train, resulting in much higher pressure and a larger high pressure zone in the rear of the cabin. For TP4, it could be seen clearly that the flow is guided away from the bogie cabin, so that no high pressure region could be observed in the cabin. Three key design variables that influence the flow details around the bogie region could be found out, which are the streamlined structure of the streamline, the height of the clearance, and the distance between the front of the cowcatcher and the front of the bogie cabin. When designing the bottom structures of the nose, the main idea should be decreasing the amount of air entering the bogie cabin. For many engineering practices a design of a fully-wrapped apron board around the bogie is applied, yet this scheme hinders the detection and maintenance of the bogie. A more practical scheme should be trying to find the balance point among the three key variables.

The train-induced wind is also a key index to evaluate the aerodynamic design of a high-speed train [33,34] and the nose shape streamlined structure affects the train-induced wind substantially. This study refers to the train-induced wind regulated in TSI [33] at standard positions (z = 0.2 m, y = 3 m; z = 1.44 m, y = 3 m) to contrastively analyze how train-induced wind reacts to the nose streamlined structures. Figure 15 shows the curves of time-averaged velocity of the train-induced wind at standard positions for the four models. It is obvious that the maximum wind appears in the wake flow field. At the same position, the velocity of the train-induced wind grows when near the ground. The streamlined structure of the streamline does not evidently affect the train-induced wind around the head but significantly disturbs that around the tail. At z = 0.2 m, the wind velocity firstly oscillates at the streamlined region on the head. After that the train-induced wind grows steadily until reaching a peak as near as the maximum at the middle of the train. Then, the wind velocity unsteadily drops to the secondary minimum around the trailing nose tip. The wind again ultimately speeds up to the maximum in the wake flow field about 25 m away from the trailing nose tip. The maximum velocities of the train-induced wind of TP1, TP2, TP3, and TP4 are 12.6, 15.1, 15.1, and 17.3 m/s, respectively. At z = 1.44 m, the behavior of the train-induced wind velocity is in accordance with the situation at z = 0.2 m around the streamlined region on the head. After passing by the head, the wind accelerates gradually but drops suddenly at the trailing nose tip. Then the velocity of the train wind climbs up again and eventually arrives at the maximum in the wake flow field about 50 m away from the trailing nose tip. The maximum train-induced wind velocity of TP1 and TP2 are 4.7 m/s while those of TP3 and TP4 are 6.8 m/s.

Since the high-speed train is symmetrical along the y axis, the side force on the leading car and middle carriages can be ignored. Due to the vortex shedding in the wake flow, strong asymmetric characteristics could be observed in the wake flow, and strong fluctuation of side force could be found on the trailing car [2,6], which affects severely the amenity of the train. Figure 16 shows the time histories of coefficients of the side force (Cs) of the four models. It is clear that the side force on tails of four models vibrates about zero and the time-averaged value approaches zero in spite of large amplitude. The smallest amplitude of Cs on TP2 is about 0.072 while the largest amplitude of Cs on the TP4 is about 0.1. The amplitude of TP1 and of TP4 are 0.085 and 0.075, respectively.

For a high-speed train with eight carriages, the length of the train is 60 times larger than its height, indicating that the flow has already been fully turbulent when the boundary layer develops as far as to the trailing car. Prominent flow separation could be found on the streamlined trailing, resulting in complicated vortex shedding in the wake. Figure 17 exhibits the contour of vorticity at a particular cross section (X = 95 m) around the last bogie in the trailing car at different timesteps for the four models. As shown in Figure 17, the train body is surrounded by vortices with distinct sizes and intensity. Moreover, the vortices at both sides of the train are asymmetrical. As time changes, the sizes and intensity of vortices alter continuously, exhibiting apparent unsteady features. Specifically, TP2 owns the shortest nose and this section does change too much from the constant cross section of the main body. As a result, flow separation for TP2 is not that drastic so the sizes of vortices are rather small. On the contrary, TP4 which has the longest nose generates the strongest and largest vortices, since its streamlined shape changes so dramatically at this section that the flow separation magnifies. TP1 and TP3 both have the same length of nose. The section of the former is nearly elliptical, making large vortices mainly scatter at both sides of the train. However, the section of the latter is almost wide-flat, leading to the emergence of large vortices on top of the train. These phenomena also explain why the side force vibration movement of TP1 is greater than that of TP3.

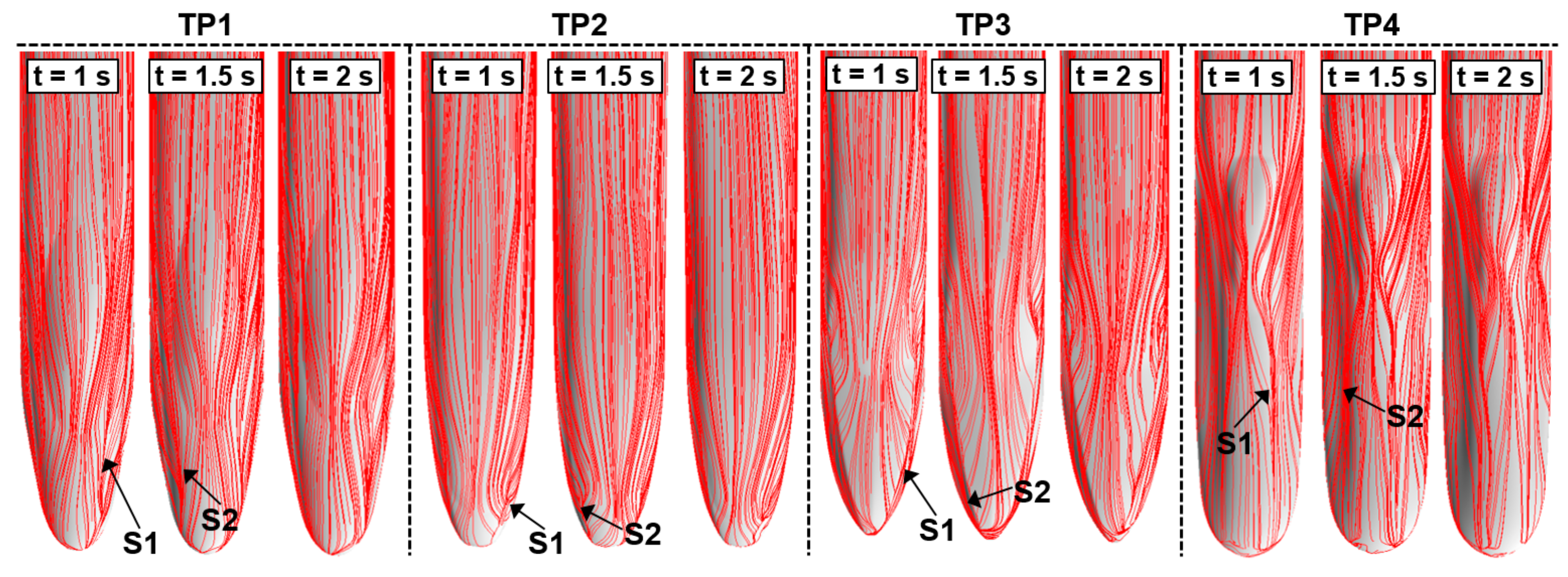
Figure 18 shows surface streamlines on the trailing car at different timesteps. Two distinct separation lines can be found on the streamlined nose region and their positions develop as time flows by, showing remarkable unsteady characteristics for the generation and detachment of vortices. Since the vortices at both sides of the trailing nose repeatedly generate and detach from the surface, the separation lines sway about the central axis. Taking TP3 as an example, as Figure 17 and Figure 18 show, at t = 1 s S2 is far from the central line while S1 is closer to the center, generating a peak for the side force of the trailing car. Afterwards when it comes to t = 1.5 s, the situation is quite the other way around as compared to t = 1 s, leaving the side force of the trailing car down in the trough. At t = 2 s S1 and S2 are basically symmetrical along the central axis, hence the side force of the trailing car tends to be zero. This example further sheds light on the fact that the side force of the trailing car is induced by the asymmetrical development of trailing vortices by a wide margin. In contrast with other models, TP3 have longer distance between the separation lines and the central axis, indicating that smaller vortices will be generated, so that the amplitude of the side force of the trailing car will be lower, too. The flow separation around the trailing streamline of TP4 is the most complicated. The separation lines are firstly generated around the cab window and possess the longest tracks covering the major upper surface of the train, indicating that the trailing vortices generate and then detach from the upper surface, which could lead to the enlargement of side force amplitude. TP2, on the other hand, has the shortest nose and the shortest separation lines, generating vortices of smaller sizes and creating better conditions to minimize side force magnitude. Compared with TP3, TP1 has separation lines much closer to the center, giving rise to larger vortices and larger magnitude of side force as well. Therefore, the wide-flat streamlined structure is prone to amplification of the side force of the trailing car while the single-arch ellipsoid streamlined structure is better at reducing the magnitude of the side force of the trailing car.

4.2. Flow Mechanism in Crosswind Conditions

The environmental wind is an essential factor that should be taken into consideration when designing a high-speed train. Under windy circumstances, the ambient flow field of the train will behave quite distinctly [20,21], increasing the aerodynamic loads on the train to a large degree and posing a threat to the safe operation. To study the nose shape streamlined structures and their influence on the aerodynamic performance of the high-speed train subjected to strong crosswind, the velocity of the crosswind is set as 20 m/s perpendicular to the train motion. The high-speed train runs at a speed of 350 km/h. In crosswind conditions the side force of the leading and trailing cars significantly increases and tends to be the main aerodynamic load on the train. Figure 19 shows the distributions of coefficients of accumulated side force for the four models at t = 2 s. It could be found that side force around the streamlined region takes the major part as compared with other regions and the distribution forms of the side force of the leading car and that of the trailing car are adverse. In terms of magnitude, side force on the head is much stronger yet that on the middle carriages is weaker. Meanwhile, the side force increases at regions with the bogies and windshields. Around the streamlined region on the head, TP2′s side force shifts most drastically, which rises to the maximum soon after the nose then goes down slowly to zero. Due to its shortest nose among all models, the side force of TP2 owns the shortest route from the peak to zero. TP1, TP3, and TP4 all share a same pattern of side force distribution that the force firstly drops after the nose then goes up to the top, and eventually goes down to about zero. For trailing streamlined regions four noses share the same side force behavior that the absolute side force ascends then descends after the same-cross section region on the train. In particular, TP4 has a much steadier form of side force performance and its maximum of absolute side force around the head and around the tail are smaller than the other models due to its longest nose shape.

From Figure 20 which shows the time-averaged pressure contours of four nose shapes, it can be discovered that the high pressure zone around the head stagnant point moves windward and a significant low pressure zone appears at the leeward side of the streamlined region, which promotes the side force on the head. At the tail there is also an intensive low pressure zone leeward and a high pressure zone occupies the cab glass surface as well as the tail nose tip. This kind of pressure distribution is opposite to the pattern on the head, so is the side force of the tail. For the main body region with a uniform section area, an obvious low pressure zone emerges at the transition from the windward side to the top but has a rather small size, which exerts a negligible impact on the side force. The nose shape streamlined structures determine the pattern of the pressure covers. For TP1 shaped in a double-arch ellipsoid structure, the elliptical cab glass is the main feature for this structure. It blocks the windward flow around the head streamlined region to some degree and causes the area of the windward high pressure zone and that of the leeward low pressure zone to expand at the same time. The flow separation line above the tail streamlined region travels across the cab glass and the elliptical nose tip, which also marks the boundary of the high pressure zone and the low pressure zone. The high pressure zone ahead of the tail nose tip is larger than the low pressure zone around the cab glass, which suppresses the lift on the tail. TP2 gets a short nose with a single-arch ellipsoid structure. Even though the high pressure zone in the windward side is small, the low pressure zone on top of the train and at the leeward side is dominant in size and intensity. The apparent high pressure zone only exists around the tail nose. Its low pressure zone around the windward side of the tail streamlined region and on the top is clearly larger than its high pressure zone. These facts are disadvantageous for reducing the side force and the lift. For TP3 who has a double-arch spindle structure with a front-mounted cowcatcher, the front of the cab glass is almost wide-flat, causing the flow to separate at the leeward side after passing by this region. As a result, the size of the high pressure zone around the cab glass grows and the low pressure zone leeward shrinks, decreasing the side force and the lift on the head. Lastly, for TP4 which is built in a wide-flat double-arch structure, its nose as long as 16 m can direct the air from the nose tip to the leeward side well. The low pressure zone at the leeward side of the head almost disappears and the high pressure zone moves back to the windward side of the cab glass. The flow separation line on top of the tail travels across the cab glass and then goes straight backwards. The area of the low pressure zone in the windward side drops and the high pressure zone on top of the streamlined region increases, which significantly restrains the lift and the side force both on the head and tail. Overall, the wide-flat double-arch structure is more feasible under crosswind circumstances, with its pressure distribution more beneficial to the reduction of the side force and lift on the head and tail.

To explain why the pressure around the head streamlined region and around the tail streamlined region are asymmetrical, Figure 21 presents the instantaneous velocity contours of different sections and pressure contours of the head and tail for four models. Around the head streamlined region, the air is impeded by the windward side around the nose and gets stagnant. This phenomenon clearly slows down the air and creates a high pressure zone around the windward side of the stagnant point. After that the air carries on its way to the top at a growing speed, leading to a decrease of surface pressure to the negative zone. When the air arrives at the bottom of the leeward side, it interacts with the flow from the bottom and generates vortices. The nose streamlined structure determines how the air flows around the streamlined regions. Like the wide-flat structure, it is not an ideal barrier to the air flow in front of the nose and permits the air to go freely to the leeward side. It also hinders the air to accelerate on the top, narrowing down the low pressure zone leeward. On the other hand, for the single-arch ellipsoid which has a larger exposure to the wind, it expands the size of the low pressure zone on top of the train and the leeward side as the air flow speeds up quickly on top of the train. For the trailing streamlined region, the separation position deviates from the transition of the leeward side and the top to the windward side. As far as to the tail nose tip, the separation is located on the top of the windward side. This flow pattern with great separation forces the air to speed up windward and the velocity windward is far greater than that leeward, causing a powerful negative pressure zone windward and a positive pressure zone on top of the streamlined region and at its leeward side. In general, how the nose structure influences the flow mechanism around the tail copies the way it influences the head.

In wind-free conditions, the side force of the head fluctuates around zero and the time-averaged side force on the tail is close to zero. However, in crosswind conditions, the wind destroys the flow field symmetry along the central axis of the train, resulting in the increase of the aerodynamic loads. Figure 22 depicts the side force in time domain on the head and tail for four models. It is clear that coefficients of side force (Cs) for all models’ heads are considerable and pointing leeward. Their actual side force is nearly 60 kN. To be specific, TP2′s Cs is slightly greater than that of TP1 and of TP3 in terms of average and maximum. TP4′s Cs is apparently lower than the other three. Additionally, from Figure 22b we notice that the side force on the tail points windward, and the tail Cs drops by an order of magnitude compared to the head Cs, implying that the tail side force is less influenced by the streamlined structure of the streamline.

Figure 23 shows the time histories of lift coefficients on the head and tail for four models. In crosswind conditions, lift on the head and on the tail are positive with the former slightly larger than the latter. Compared to the lift in wind-free conditions, the head lift in crosswind conditions is three times larger and the tail lift grows by an order of magnitude except TP4. In terms of the head lift, TP1 has the greatest magnitude while TP4 has the least. As for the lift of the trailing car, TP4 owns the least lift, with its time-averaged value being half of the others. TP3 has the greatest time-averaged value and TP1 has the most significant magnitude. Specifically, the peak of the lift of TP4 is near to the trough of the lift of TP1.

The side force and lift on the head and tail in crosswind conditions are mainly determined by the ambient flow field features. Figure 24 shows the vorticity contours at different sections of four noses. It could be discovered that the energy of the flow field mainly gathers around the leeward side and vortex structures leeward are extraordinarily complicated and unsteady. A tiny vortex V1 is formed around the bottom of the head in the leeward side and as it moves towards the tail it gradually vanishes. Meanwhile the flow separation occurs around the transition from the leeward side to the top and another vortex V2 is generated. V2 also develops towards the tail and deviates from the leeward train. The vortex core of V2 core grows larger and larger, and then breaks down into smaller vortices with different intensity around the tail. The flow separation near the transition from the top of the main body to the leeward side breeds a vortex V3 around the leeward side of the train. V3 attaches closely to the train as it travels towards the tail. This behavior is the most influential to the train’s aerodynamic performance. However, vortices at the leeward side of the head are not fully developed and are less significant in size and intensity. They are less important to the performance of the train. Yet vortices at the leeward side of the middle and the tail are maturely developed and are vital to the pressure distribution on the leeward train, thus, further affect the performance of the middle carriages and the trailing car. Due to TP2′s shortest nose, V2 is formed at the closest place to the head nose tip. On the contrary, TP4 has the longest nose, so the V2′s generation in this case is the other way around. Besides, V2′s core grows up at the slowest speed as it moves to TP4′s tail. In the middle of the train, vortices at the leeward side of the train are developed for all cases, regardless of different nose shapes.

To further illustrate vortices at the leeward side of the train, Figure 25 shows the iso-surface of Q (Q = 100) for the four models, in which vortex labels are the same as in Figure 24. It could be found that V1 is generated in the leeward side around the first bogie of the leading car and grows larger as it travels downstream. It nearly disappears around the conjunction of CAR2 and CAR3. Therefore, V1 only affects the aerodynamic performance of CAR1 and CAR2 and its influence on other compartments can be ignored. V2 comes into being tightly around the main body with a uniform section, then moves away from the train. The vortex core of V2 magnifies gradually. Until the middle of the train it ceases to change its distance to the train and then travels parallel to the train and eventually enters the wake flow field. V3 emerges at the middle of CAR2 and stays close to the train as it propagates. It interacts with other vortices generated around the trailing streamlined region, creating an intricate trailing vortex system. V4 is generated out of the flow separation around the trailing nose and then moves leeward. V4 influences the aerodynamic performance of the trailing car the most while its impact on other parts of the train are so small that it can be neglected. The streamlined structure of the nose shape is the least important to V1. The longer the nose is, the nearer V2 is born to the tail. Its vortex core near the head gets smaller as the nose grows longer. As V3 comes out of the flow separation around the transition from the top of the main body to the leeward side, the streamlined structure of the nose does not affect V3 to a large degree. Yet, the nose streamlined structure is most crucial to V4. For example, after generation at the trailing nose tip on TP1 and TP4, V4 gets mixed up with vortices at the leeward side straightforward, resulting in the breakdown of large vortices into small ones at the rear of the wake flow field. As for TP2, V4 moves windward after being formed at the trailing nose tip, then mixes with vortices at the leeward side. Apart from that, large vortices of TP2 remain complete in the wake flow field. For TP3, after V4′s generation around the trailing nose tip, V4 goes parallel to the wake flow field and does not interact that much with vortices leeward.

In crosswind conditions the aerodynamic forces on the train are massively increased while the loads on the leading car keep the major part. As a consequence, the safety of the head is of great vitality to the overall design of the train.

Table 4. Comparison of the time-averaged Cd on the whole train, Cs and Cl of the leading car for the four models.

Models	Cdw	Cs	Cl
TP1	1.175	1.024	0.486
TP2	1.193	1.045	0.499
TP3	1.185	1.026	0.442
TP4	1.168	0.951	0.451

lists the time-averaged coefficients of drag on the whole train (Cdw), the side force coefficient (Cs), and the lift coefficient (Cl) of the leading car. It can be discovered that Cdw under crosswind circumstances increases by 50% in contrast with that in a static environment for all four models. Cdw on each model does not differ from each other obviously. Cs of the leading car for TP2 is the greatest while that of TP4 is the least, with the latter decreasing by 9% compared to the former. Cs of the leading car for TP1 is almost the same as that of TP3. Meanwhile, Cl of the leading car is nearly half of Cs for the four models, among which TP2 is the biggest while TP3 is the smallest, dropping by 11.4% compared to the former. TP4 and TP3 have similar head Cl while TP1 and TP2 have close head Cl as well. Generally speaking, the wide-flat double-arch structure can better improve the aerodynamic performance of the high-speed train in crosswind conditions.

5. Conclusions

The study of the nose shape streamlined structure is fundamental to the design of a high-speed train’s nose. This study validated the precision of the DDES method and the viability of the mesh configuration referring to the wind tunnel experimental data. Then targeted at the eight-grouped high-speed train model, streamlined structures such as double-arch ellipsoid, single-arch ellipsoid, a spindle with a front-mounted cowcatcher, double-arch wide-flat shape, and their impacts on the train aerodynamic performance under static and crosswind environmental circumstances were analyzed by means of DDES. Main conclusions are drawn as follows.

When there is no wind and the length of the nose remains the same, to alleviate the drag on the whole train the pressure distribution on the head and tail should both be considered if the head and tail are designed symmetrically. In other words, we should not only focus on the aerodynamic loads on head or tail. However, if the head and tail could be designed asymmetrically, the low drag design of high-speed trains could be achieved with the head nose shaping in single-arch ellipsoid and the tail taking the form of a spindle with a front-mounted cowcatcher. The asymmetrically developing vortices around the trailing nose lead to considerable fluctuations of the side force of the trailing car. These vortices also render the time-averaged side force of the trailing car nearly zero, but the side force fluctuates with rather obvious amplitude. The single-arch ellipsoid streamlined structure can moderate the amplitude of the side force well.

In crosswind conditions, the stagnant point on the head nose tends to lean at the windward side, enlarging the intensity and size of the windward high pressure zone and that of the leeward low pressure zone. It also remarkably aggravates the aerodynamic side force and lift. The wide-flat double-arch structure is more advantageous to the reduction of the side force and the lift on the leading and trailing car. Primary emphasis should firstly be laid on the head when conducting the design in crosswind conditions.

Considering the specific operation scenario of high-speed trains, the current study could aid in the preference of the streamlined shape for engineering application. However, since the running scenarios of high-speed trains, such as trains passing by a tunnel or trains passing by each other, are also frequently met, the influence of typical streamlined shapes on pressure waves or aerodynamic loads is also needed. Meanwhile, aerodynamic shape optimization on the streamlined shape with best performance among these four types is required. Future study can be carried out by focusing on these specific aspects.