Simulation of Crack Propagation in Reinforced Concrete Elements
Abstract
:1. Introduction
2. General Crack Propagation
- For random cracking, concrete tensile strength scattering along the longitudinal axis of the specimen is required. Therefore, the CPM can map different statistical distributions;
- It must be possible to calculate steel and concrete strains separately over the entire length of the specimen. Thus, both materials shall be represented separately;
- A bond stress–slip relationship is required for the interaction of both materials. This should be definable in a general mathematical form to be able to take into account different loading levels and material configurations.
3. Crack Propagation Model (CPM)
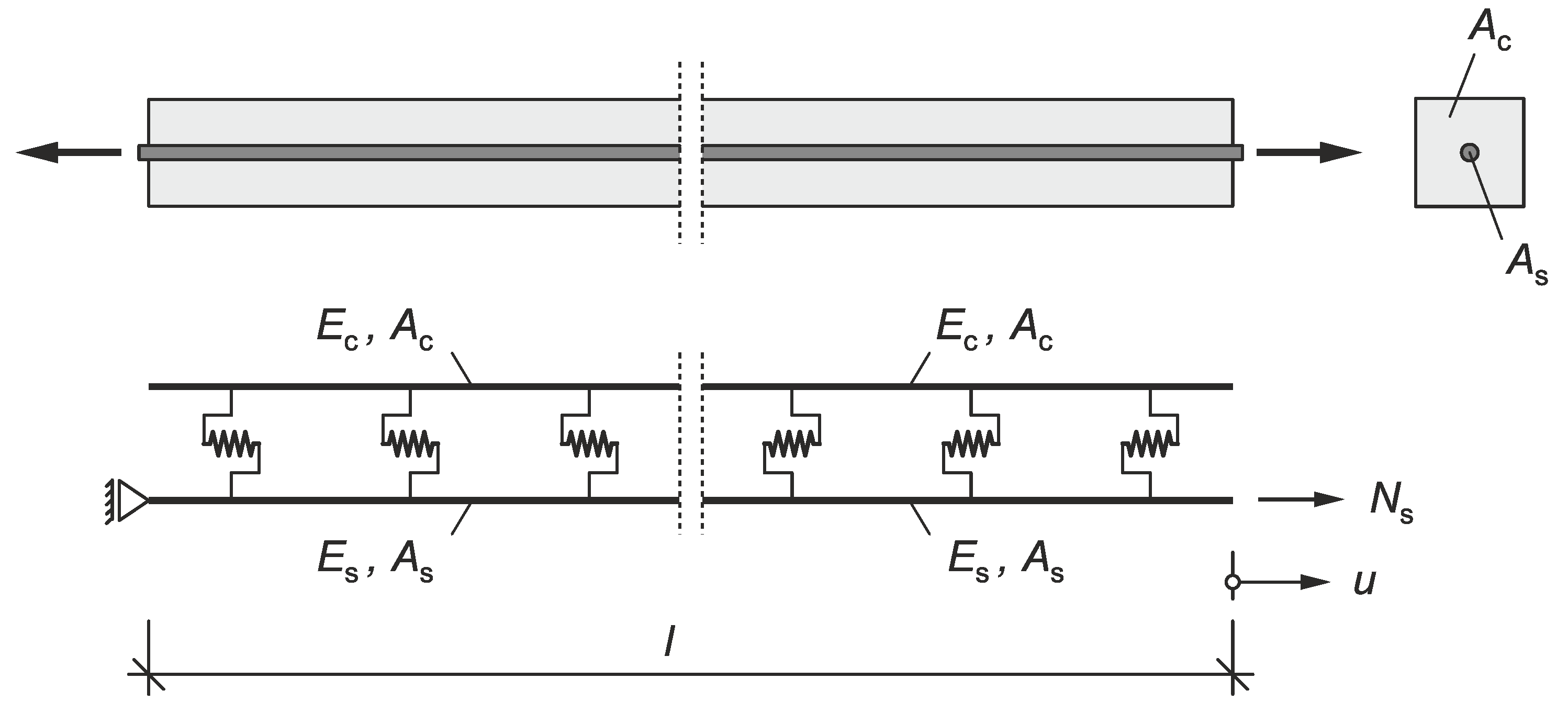
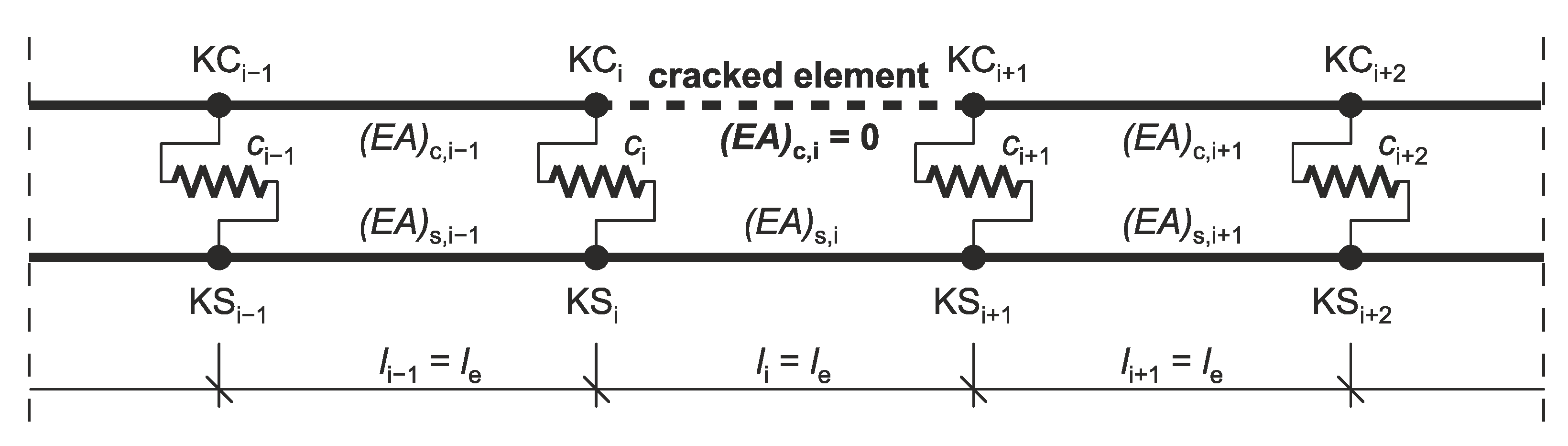
3.1. Model Setup
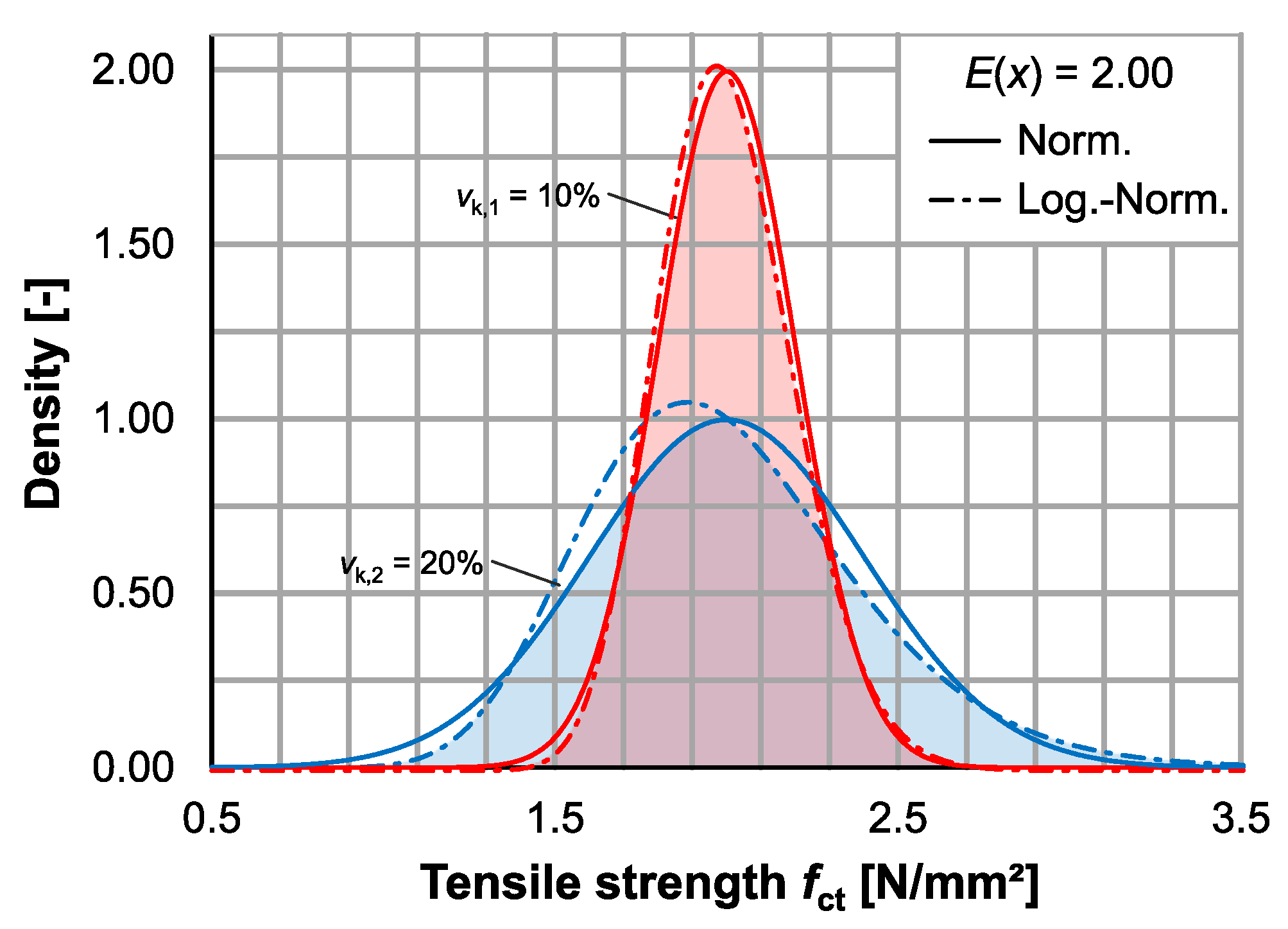
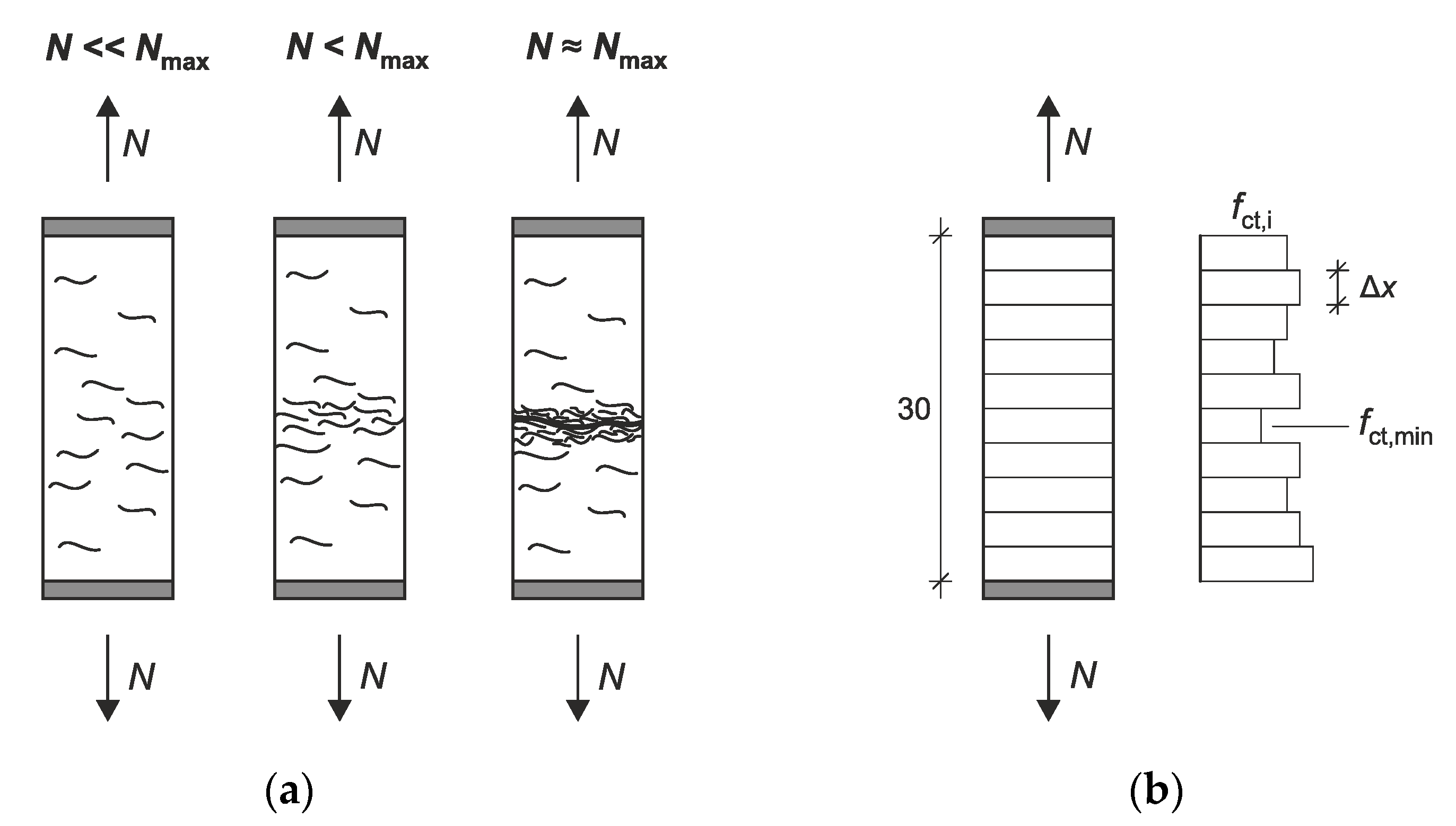
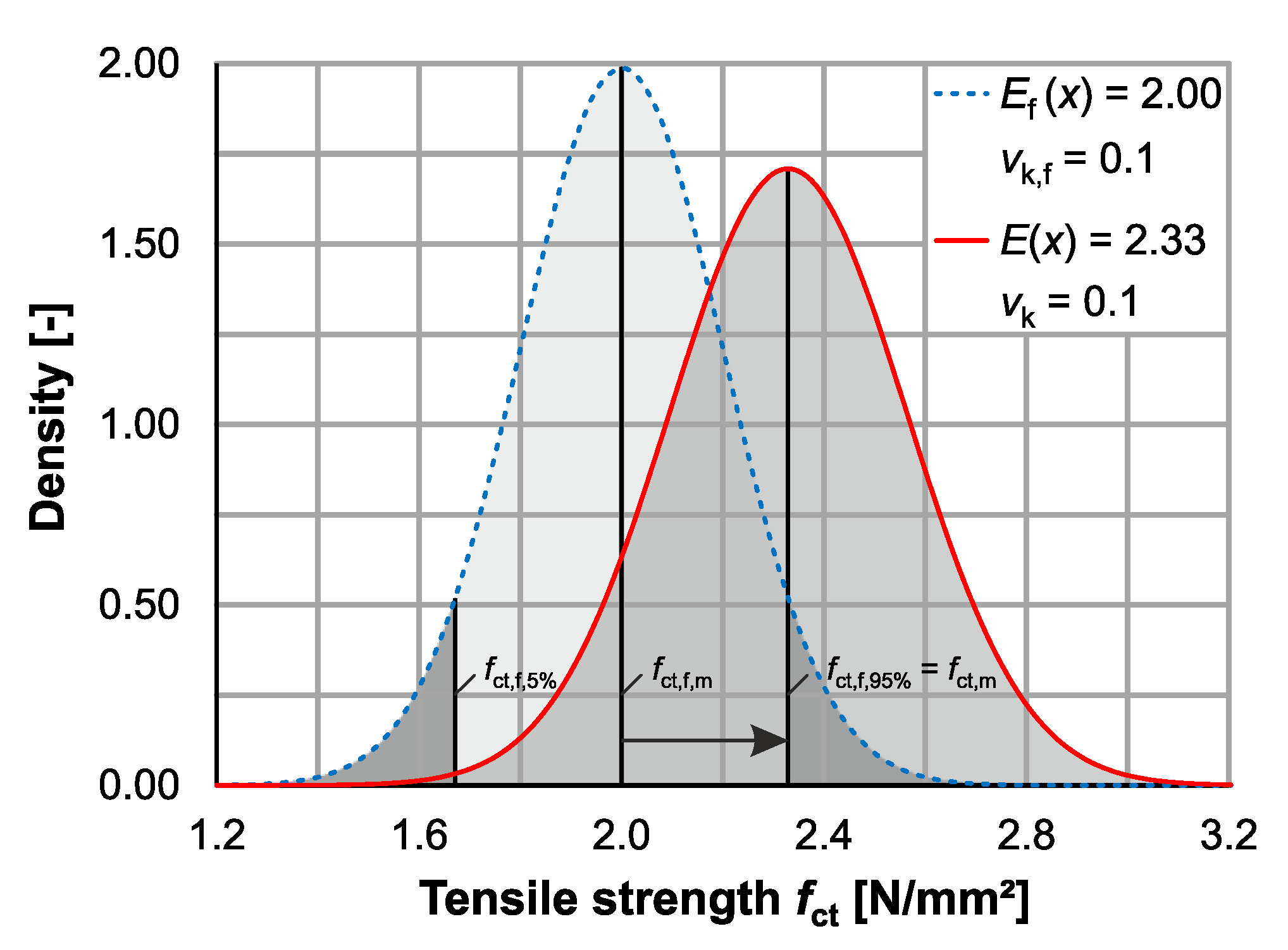
3.2. Distribution of Tensile Strength
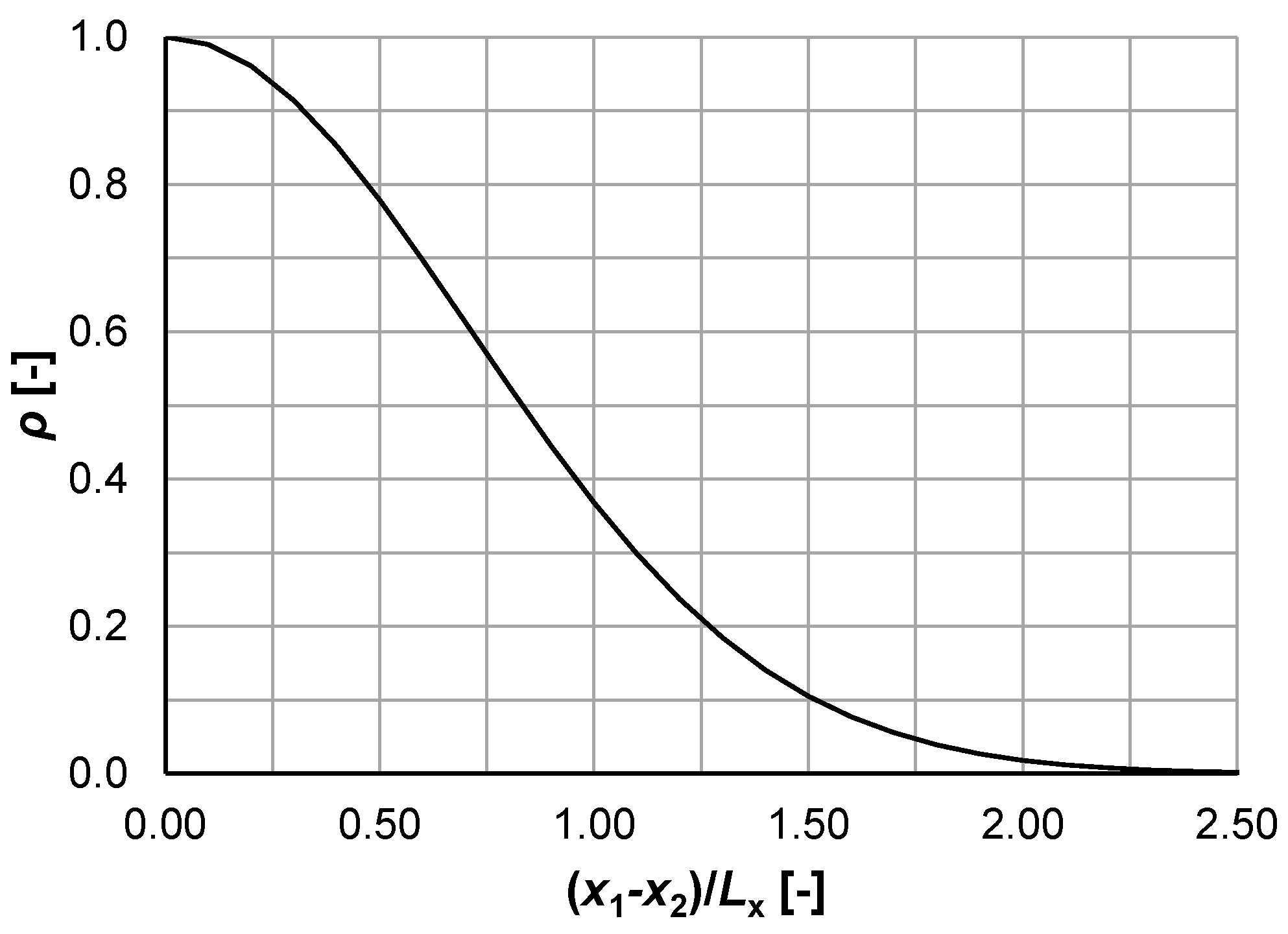
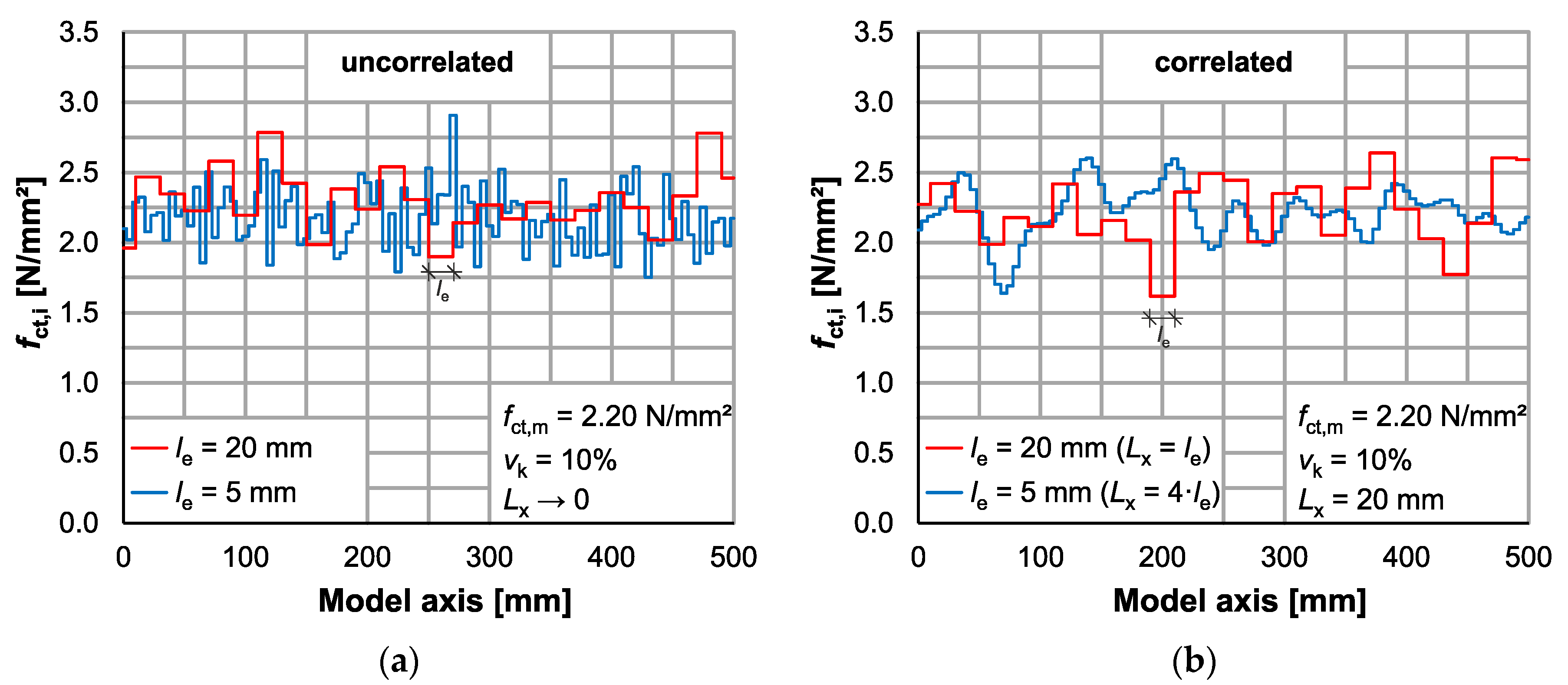
3.3. Element Size and Autocorrelation
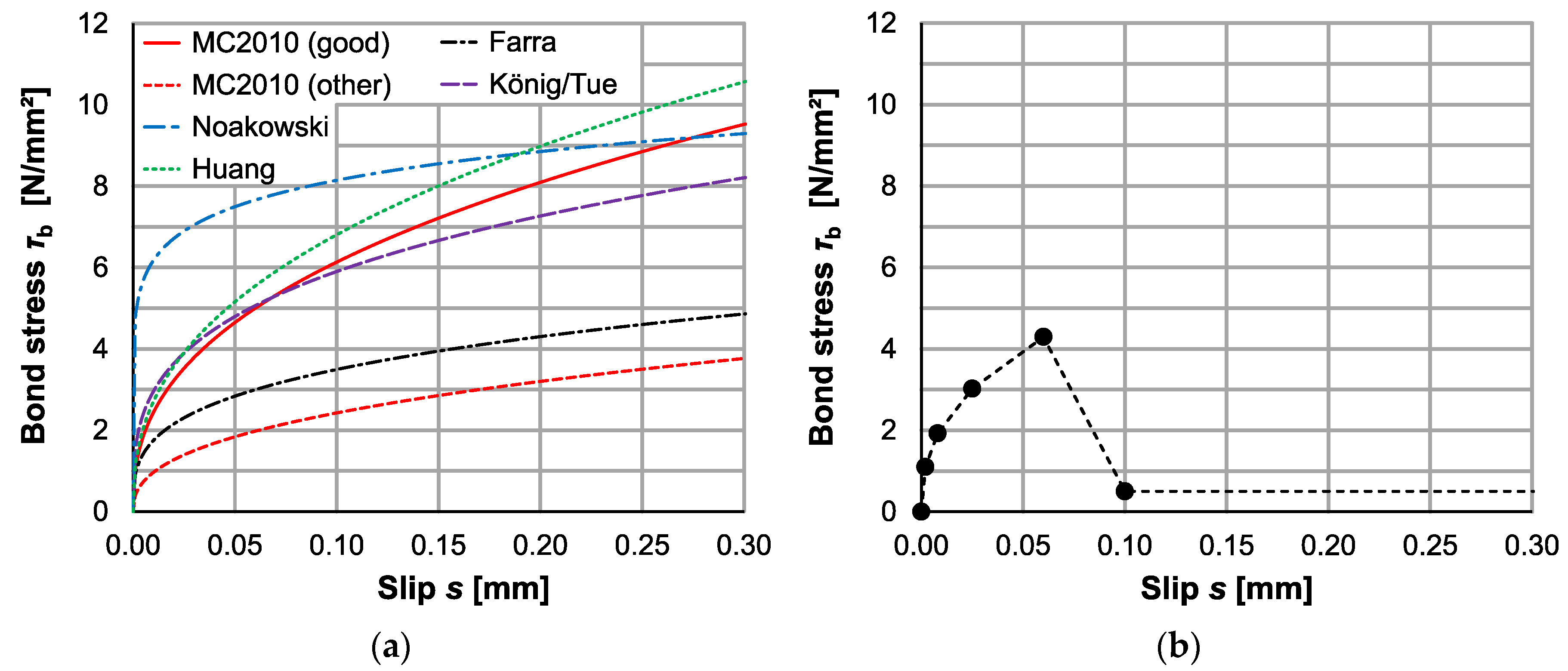
3.4. Bond–Slip Relationship
3.5. Model Features and Advantages
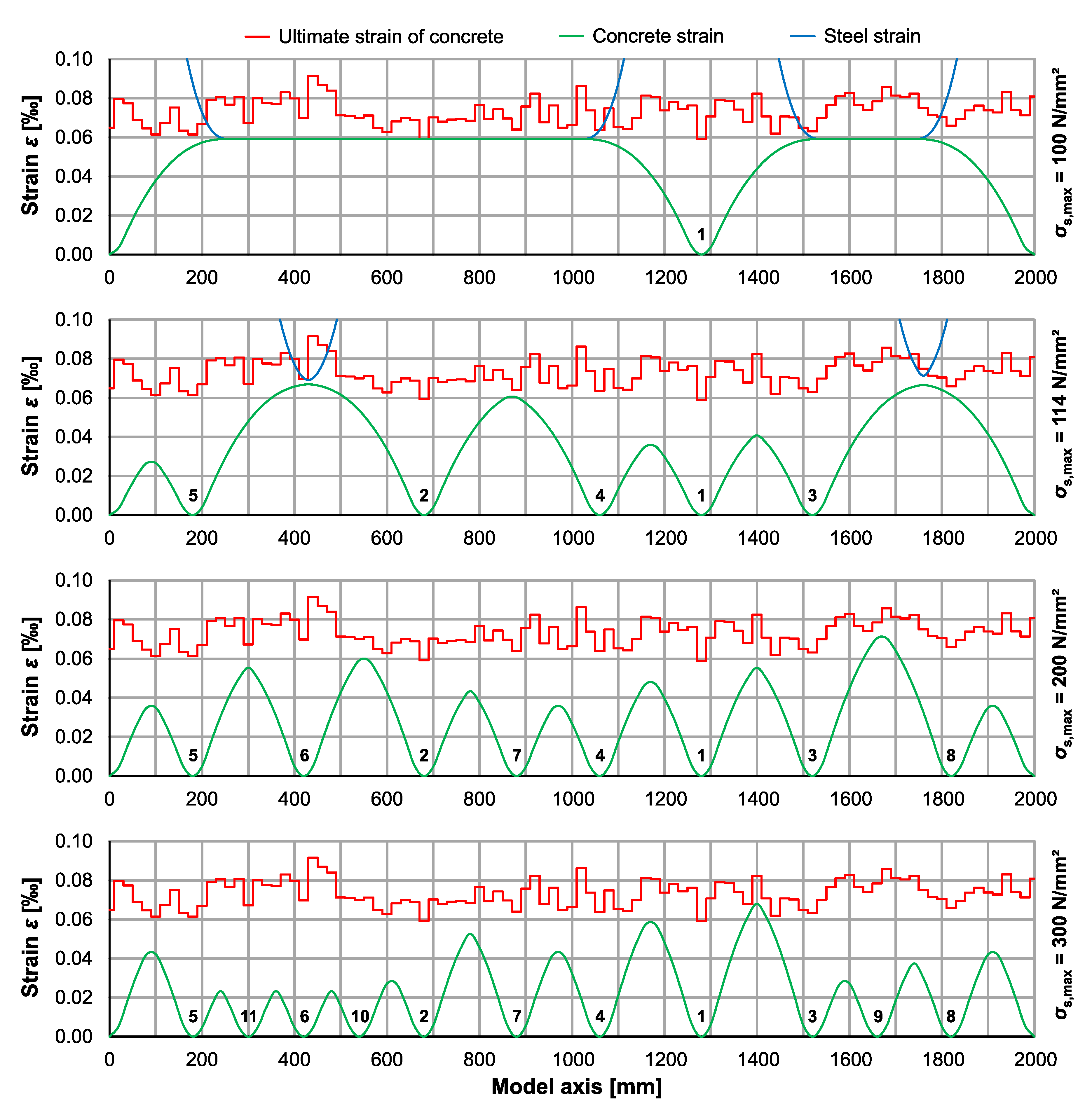
4. Simulation and Calculation Procedure
5. Comparison with Experiments
- Varying the coefficient of variation and correlation length to determine the distribution of the tensile strength along the model axis has only a limited effect on the results;
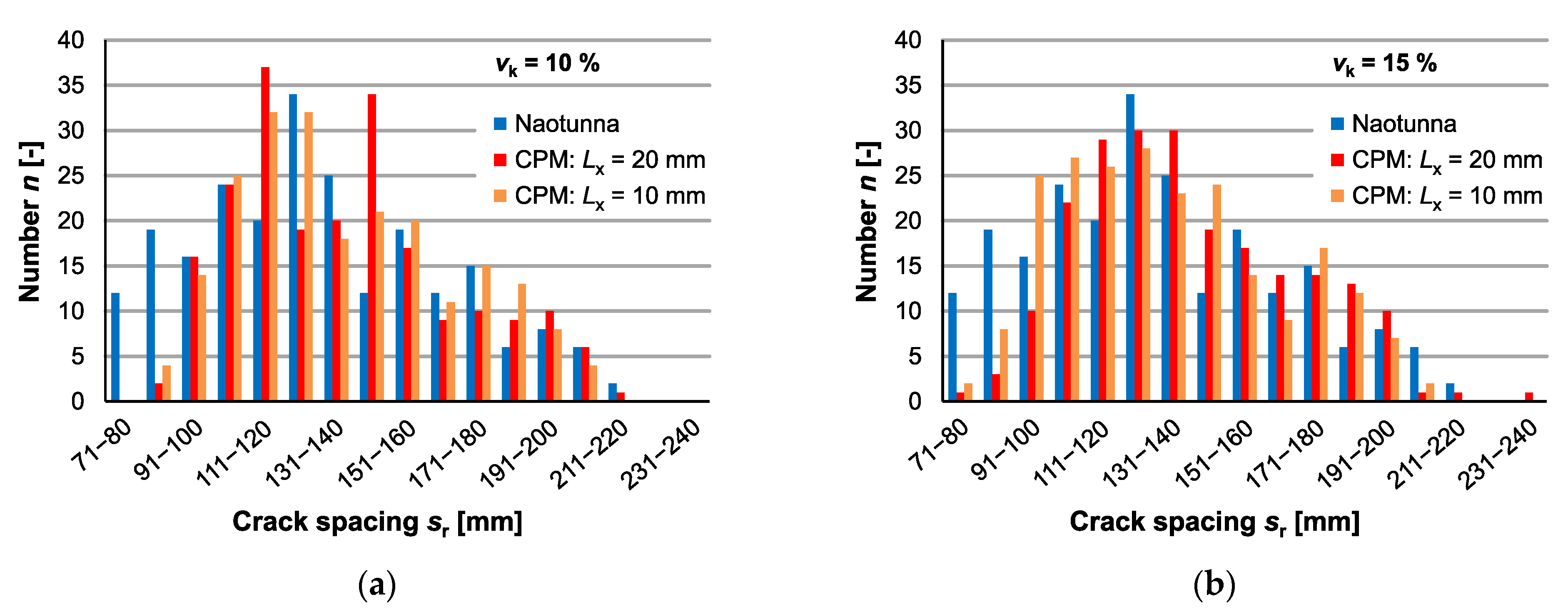
- The range of very small crack spacings () is underestimated for vk = 10% and vk = 15%, as well as for Lx = 20 mm and Lx = 10 mm (see Figure 15);
- The experimental value sr,0.95/sr,m = 1.5 is estimated with adequate accuracy by the CPM (sr,0.95/sr,m = 1.4) (see Table 4);
- The comparison of the median and mean values of the experimental results show a positive skew (skewed to the right) (see Table 4) indicating a log-normal distribution of the crack spacing sr.
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Base, G.D.; Read, J.B.; Beeby, A.W.; Taylor, H.P.J. An Investigation of the Crack Control Characteristics of Various Types of Bar in Reinforced Concrete Beams, Report 18, Part 1; Cement and Concrete Association Research: London, UK, 1966. [Google Scholar]
- Rüsch, H.; Rehm, G. Versuche mit Betonformstählen, Teil I-III. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1963; Volume 140, pp. 160–165. [Google Scholar]
- Empelmann, M. Zum nichtlinearen Trag- und Verformungsverhalten von Stabtragwerken aus Konstruktionsbeton unter besonderer Berücksichtigung von Betriebsbeanspruchungen. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 1995. [Google Scholar]
- Häußler-Combe, U.; Hartig, J. Rissbildung von Stahlbeton bei streuender Betonzugfestigkeit. Bauingenieur 2010, 85, 460–470. [Google Scholar]
- Empelmann, M.; Cramer, J. Rissbreiten an biegebeanspruchten Bauteilen. Beton Stahlbetonbau 2018, 113, 291–297. [Google Scholar] [CrossRef]
- Empelmann, M.; Cramer, J. Modell zur Beschreibung der zeitabhängigen Rissbreitenentwicklung in Stahlbetonbauteilen. Beton Stahlbetonbau 2019, 114, 327–336. [Google Scholar] [CrossRef]
- Empelmann, M.; Cramer, J. Time-dependent development of crack widths in reinforced concrete structures. In Concrete Innovations in Materials, Design and Structures, Proceedings of the fib Symposium, Kraków, Poland, 27–29 May 2019; International Federation for Structural Concrete: Lausanne, Switzerland, 2019. [Google Scholar]
- Liao, W.-C.; Chen, P.-S.; Hung, C.-W.; Wagh, S.K. An Innovative Test Method for Tensile Strength of Concrete by Applying the Strut-and-Tie Methodology. Materials 2020, 13, 2776. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J.; Taha, M.R. Experimental and Numerical Evaluation of Direct Tension Test for Cylindrical Concrete Specimens. Adv. Civ. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Joint Committee for Structural Safety (JCSS). Probabilistic Model Code—Part III. 2002. Available online: https://www.jcss-lc.org/jcss-probabilistic-model-code (accessed on 9 November 2020).
- Mirza, S.A.; Hatzinikolas, M.; MacGregor, J.G. Statistical description of strength of concrete. ASCE J. Struct. Div. 1979, 105, 1021–1037. [Google Scholar]
- Fédération Internationale du Béton (Fib). Fib Model Code for Concrete Structures 2010; Fédération Internationale du Béton: Lausanne, Switzerland, 2013. [Google Scholar] [CrossRef]
- DIN EN 1992-1-1:2004 + AC:2010. In Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; Beuth: Berlin, Germany, 2011.
- Voigt, J. Beitrag zur Bestimmung der Tragfähigkeit Bestehender Stahlbetonkonstruktionen auf Grundlage der Systemzuverlässigkeit. Ph.D. Thesis, University of Siegen, Siegen, Germany, 28 February 2014. [Google Scholar]
- Rüsch, H.; Sell, R.; Rackwitz, R. Statistische Analyse der Betonfestigkeit. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1969; Volume 206. [Google Scholar]
- Tue, N.V.; Schenck, G.; Schwarz, J. Eine kritische Betrachtung des zusätzlichen Sicherheitsbeiwertes für hochfesten Beton. Bauingenieur 2007, 82, 39–46. [Google Scholar]
- Schwennicke, A. Zur Berechnung von Stahlbetonbalken und -Scheiben im gerissenen Zustand unter Berücksichtigung der Mitwirkung des Betons zwischen den Rissen. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 1983. [Google Scholar]
- Koch, R. Verformungsverhalten von Stahlbetonstäben unter Biegung und Längszug im Zustand II, auch bei Mitwirkung des Betons zwischen den Rissen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 1976. [Google Scholar]
- Heilmann, H.G. Beziehungen zwischen Zug- und Druckfestigkeit des Betons. Beton 1969, 19, 68–70. [Google Scholar]
- Blaschke, F.; Losekamp, C.; Mehlhorn, G. Zugtragverhalten von Beton nach langandauernder statischer sowie schwellender Zugvorbelastung. Beton Stahlbetonbau 1994, 89, 204–205. [Google Scholar] [CrossRef]
- Duda, H. Bruchmechanisches Verhalten von Beton unter monotoner und zyklischer Zugbeanspruchung. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1991; Volume 419. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Struct. 1983, 16, 155–177. [Google Scholar] [CrossRef] [Green Version]
- Jahn, M. Zum Ansatz der Betonzugfestigkeit bei den Nachweisen zur Trag- und Gebrauchsfähigkeit von unbewehrten und bewehrten Betonbauteilen. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1983; Volume 341. [Google Scholar]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Ahrens, A. Ein stochastisches Simulationskonzept zur Lebensdauerermittlung von Stahlbeton- und Spannbetontragwerken und seine Umsetzung an einer Referenzbrücke. Ph.D. Thesis, Ruhr-Universität Bochum, Bochum, Germany, 3 December 2010. [Google Scholar]
- Vanmarcke, E. Random Fields: Analysis and Synthesis; Rev. and expanded new ed.; World Scientific Publication: Singapore, 2010. [Google Scholar] [CrossRef]
- Real, M.D.V.; Filho, A.C.; Maestrini, S.R. Response variability in reinforced concrete structures with uncertain geometrical and material properties. Nucl. Eng. Des. 2003, 226, 205–220. [Google Scholar] [CrossRef]
- Tepfers, R.; Achillides, Z.; Azizinamini, A.; Balázs, G.; Bigaj-Van-Vliet, A.; Cabrera, J.; Cairns, J.; Cosenza, E.; Uijl, J.D.; Eligehausen, R.; et al. Fib Bulletin 10, Bond of reinforcement in concrete. In Fib Bulletins; Fédération Internationale du Béton: Lausanne, Switzerland, 2000; Volume 10. [Google Scholar]
- Farra, B. Influence de la résistance du béton et de son adhérence avec l’armature sur la fissuration. Ph.D. Thesis, Ecole Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 1995. [Google Scholar]
- König, G.; Tue, N.V. Grundlagen und Bemessungshilfen für die Rissbreitenbeschränkung im Stahlbeton und Spannbeton. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1996; Volume 466. [Google Scholar]
- Noakowski, P. Nachweisverfahren für Verankerung, Verformung, Zwangbeanspruchung und Rissbreite, Kontinuierliche Theorie der Mitwirkung des Betons auf Zug. Rechenhilfen für die Praxis. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1988; Volume 394. [Google Scholar]
- Huang, Z.; Engstrom, B.; Magnusson, J. Experimental and Analytical Studies of the Bond Behaviour of Deformed Bars in High Strength Concrete, Preceedings of the 4th International Symposium on the Utilization of High Strength/High Performance Concrete, Paris, France, 29–31 May 1996; Pr. Ponts et Chaussées: Paris, France, 1996; Volume 3, pp. 1115–1124. [Google Scholar]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V.; Earthquake Engineering Research Center. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; Report No. UCB/EERC-83/23; University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Kreller, H. Zum nichtlinearen Trag- und Verformungsverhalten von Stahlbetonstabtragwerken unter Last- und Zwangeinwirkung. In Heftreihe des Deutschen Ausschuss für Stahlbeton, 1st ed.; Beuth: Berlin, Germany, 1990; Volume 409. [Google Scholar]
- Comite Euro-International Du Beton. CEB-FIP Model Code 1990. In CEB Bulletin; Thomas Telford Ltd.: London, UK, 1993; Volume 213–214. [Google Scholar] [CrossRef]
- Naotunna, C.N.; Samarakoon, S.S.M.M.K.; Fosså, K.T. Experimental and theoretical behavior of crack spacing of specimens subjected to axial tension and bending. Struct. Concr. 2020, 1–18. [Google Scholar] [CrossRef]
- Meinhardt, M.; Keuser, M.; Braml, T. Numerical Simulation of Crack Propagation Using Spatially Varying Material Parameters, Proceedings of the 2018 Fib Congress, Melbourne, Australia, 7–11 October 2018; International Federation for Structural Concrete: Lausanne, Switzerland, 2019. [Google Scholar]
- Kaklauskas, G.; Gribniak, V. Effects of shrinkage on tension stiffening in RC members. In Structural Concrete and Time, Proceedings for the 2005 Fib Symposium, La Plata, Argentina, 28–30 September 2005; International Federation for Structural Concrete: La Plata, Argentina, 2005. [Google Scholar]
- Rimkus, A.; Gribniak, V. Experimental investigation of cracking and deformations of concrete ties reinforced with multiple bars. Constr. Build. Mater. 2017, 148, 49–61. [Google Scholar] [CrossRef]
- Mobasher, B.; Stang, H.; Shah, S. Microcracking in fiber reinforced concrete. Cem. Concr. Res. 1990, 20, 665–676. [Google Scholar] [CrossRef]






| Model | Bond Conditions | τb,max | s1 | α |
|---|---|---|---|---|
| MC2010 [12] | Good | 1.0 | 0.40 | |
| MC2010 [12] | All other cases | 1.8 | 0.40 | |
| Farra [29] | Mean | 1.0 | 0.30 | |
| König and Tue [30] | 1.0 | 0.30 | ||
| Noakowski [31] | Good | 1.0 | 0.12 | |
| Huang [32] | Good | 1.0 | 0.40 |
| Geometry | ||
| Reinforcement ratio | ρ | 2% |
| Diameter of reinforcing bar | ∅ | 16 mm |
| Length of model | l | 2000 mm |
| Element length | le | 20 mm |
| Material | ||
| Concrete: C20/25 | ||
| Mean value of compressive strength of concrete | fcm | 28 N/mm2 |
| Mean value of tensile strength of concrete | fct,m | 2.2 N/mm2 |
| Mean value of modulus of elasticity of concrete | Ecm | 30,000 N/mm2 |
| Reinforcement: B500 | ||
| Modulus of elasticity of reinforcing steel | Es | 200,000 N/mm2 |
| Bond–slip relationship | ||
| Model Code 2010 (good bond conditions) | ||
| Bond stress | ||
| Reduction factor | ||
| Scattering | ||
| Tensile strength of concrete | ||
| Coefficient of variation | vk | 10% |
| Correlation length | Lx | 20 mm |
| Geometry | ||
| Reinforcement ratio | ρ | 8% |
| Diameter of reinforcing bar | ∅ | 32 mm |
| Length of model | l | 2000 mm |
| Element length | le | 10 mm |
| Material | ||
| Concrete | ||
| Mean value of compressive strength of concrete | fcm | 35 N/mm2 |
| Mean value of tensile strength of concrete | fct,m | 3.2 N/mm2 |
| Mean value of modulus of elasticity of concrete | Ecm | 32,000 N/mm2 |
| Reinforcement: B500 | ||
| Modulus of elasticity of reinforcing steel | Es | 200,000 N/mm2 |
| Bond slip relationship | ||
| Model Code 2010 (good bond conditions) | ||
| Bond stress | ||
| Reduction factor | ||
| Scattering | ||
| Tensile strength of concrete | 18 distributions (in each case) | |
| Coefficient of variation | vk | 10% (15%) |
| Correlation length | Lx | 20 mm (10 mm) |
| Naotunna [36] | CPM: vk = 10% | CPM: vk = 15% | |||
|---|---|---|---|---|---|
| Lx = 20 mm | Lx = 10 mm | Lx = 20 mm | Lx = 10 mm | ||
| Total number n 1 | 230 | 214 | 217 | 215 | 224 |
| Mean (section) sr,m | 131–140 mm | 141–150 mm | 141–150 mm | 141–150 mm | 131–140 mm |
| Median (section) | 121–130 mm | 131–140 mm | 131–140 mm | 131–140 mm | 121–130 mm |
| 95th percentile (section) sr,0.95 | 191–200 mm | 191–200 mm | 191–200 mm | 191–200 mm | 181–190 mm |
| sr,0.95/sr,m | ~1.5 | ~1.4 | ~1.4 | ~1.4 | ~1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cramer, J.; Javidmehr, S.; Empelmann, M. Simulation of Crack Propagation in Reinforced Concrete Elements. Appl. Sci. 2021, 11, 785. https://doi.org/10.3390/app11020785
Cramer J, Javidmehr S, Empelmann M. Simulation of Crack Propagation in Reinforced Concrete Elements. Applied Sciences. 2021; 11(2):785. https://doi.org/10.3390/app11020785
Chicago/Turabian StyleCramer, Jonas, Sara Javidmehr, and Martin Empelmann. 2021. "Simulation of Crack Propagation in Reinforced Concrete Elements" Applied Sciences 11, no. 2: 785. https://doi.org/10.3390/app11020785





