Surrogate Model for Multi-Component Diffusion of Uranium through Opalinus Clay on the Host Rock Scale
Abstract
:Featured Application
Abstract
1. Introduction
2. Methods
2.1. Geochemical System of the Opalinus Clay
2.2. Integrating Sorption Processes
2.3. Modelling Multi-Component Diffusion
2.4. Modelling Single-Component Diffusion
3. Model Calibration
4. Results
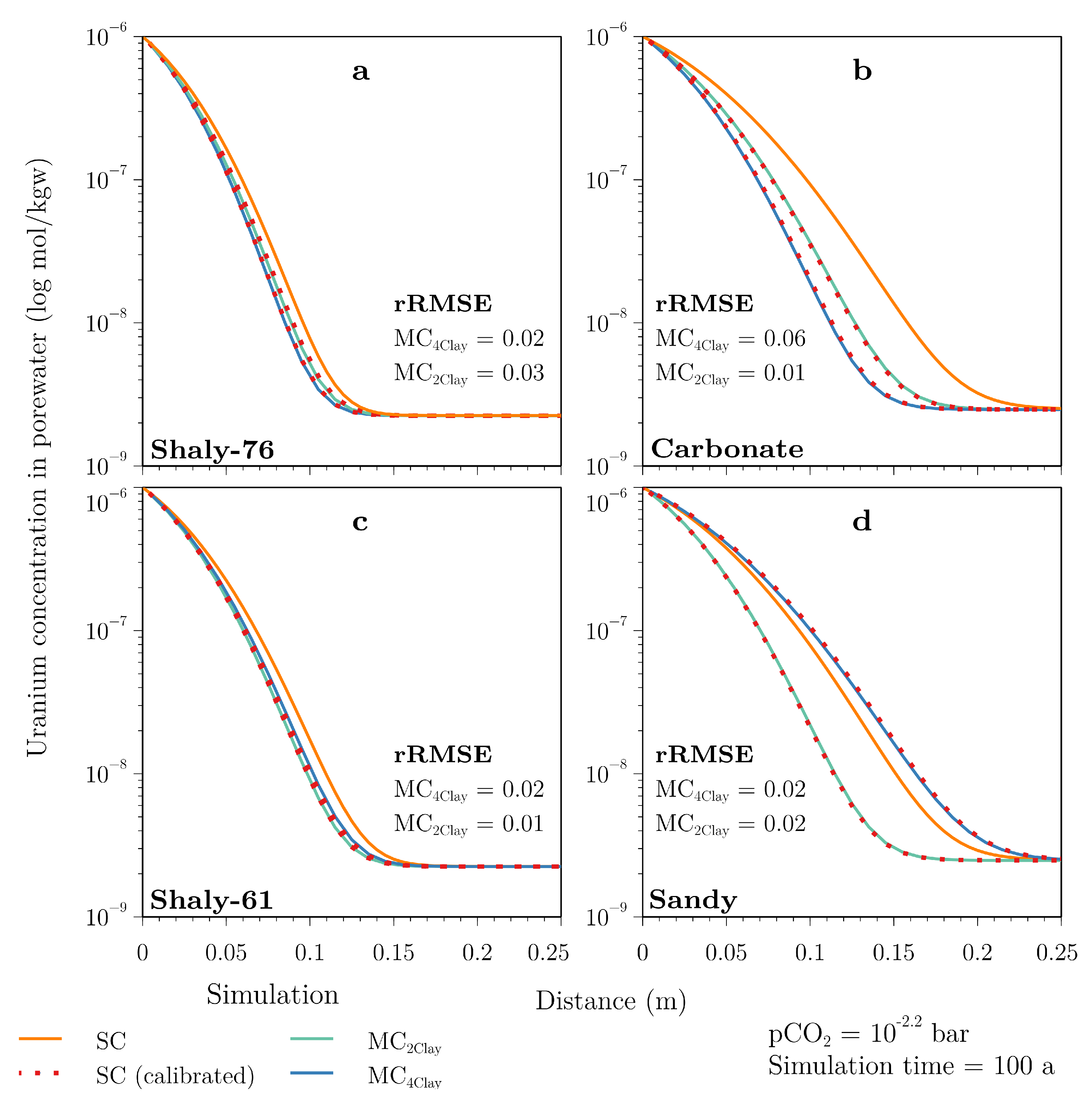
4.1. Multi- and Single-Component Simulations on the Metre-Scale
4.2. Multi-Component Diffusion for Varying Total Amounts of Minerals on the Metre-Scale
4.3. Transfer of Multi-Component Diffusion Simulations to the Host Rock Scale
5. Discussion
5.1. Differences between Single- and Multi-Component Diffusion Approach
5.2. Effect of Varying Mineralogy on Multi-Component Diffusion
5.3. Implications for the Host Rock Scale
6. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DDL | Diffuse double layer |
| Effective diffusion coefficient (m/s) | |
| Pore diffusion coefficient (m/s) | |
| Self-diffusion coefficient in water (m/s) | |
| Porosity (-) | |
| Distribution coefficient (kg/m) | |
| MC | Multi-component |
| n | medium-specific, empirical exponent in Archie’s law (-) |
| pCO | Partial pressure of carbon dioxide (bar) |
| pzc | point of zero charge |
| rRMSE | Relative root mean square error (-) |
| SC | Single-component |
| SCM | Surface complexation model |
References
- IAEA. Scientific and Technical Basis for the Geological Disposal of Radioactive Wastes; Technical Report; International Atomic Energy Agency: Vienna, Austria, 2003. [Google Scholar]
- Nagra. Project Opalinus Clay—Safety Report; Nagra Technical Report; NTB 02-05; Negra: Wettingen, Switzerland, 2002. [Google Scholar]
- Delay, J.; Rebours, H.; Vinsot, A.; Robin, P. Scientific investigation in deep wells for nuclear waste disposal studies at the Meuse/Haute Marne underground research laboratory, Northeastern France. Phys. Chem. Earth 2007, 32, 42–57. [Google Scholar] [CrossRef]
- Mazurek, M.; Gautschi, A.; Marschall, P.; Vigneron, G.; Lebon, P.; Delay, J. Transferability of geoscientific information from various sources (study sites, underground rock laboratories, natural analogues) to support safety cases for radioactive waste repositories in argillaceous formations. Phys. Chem. Earth 2008, 33, S95–S105. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Wersin, P. Multicomponent diffusion modeling in clay systems with application to the diffusion of tritium, iodide, and sodium in opalinus clay. Environ. Sci. Technol. 2007, 41, 5002–5007. [Google Scholar] [CrossRef] [PubMed]
- Appelo, C.A.J.; Van Loon, L.R.; Wersin, P. Multicomponent diffusion of a suite of tracers (HTO, Cl, Br, I, Na, Sr, Cs) in a single sample of Opalinus Clay. Geochim. Cosmochim. Acta 2010, 74, 1201–1219. [Google Scholar] [CrossRef]
- Tournassat, C.; Bourg, I.C.; Steefel, C.I.; Bergaya, F. Surface Properties of Clay Minerals. Dev. Clay Sci. 2015, 6, 5–31. [Google Scholar] [CrossRef]
- Altmann, S. ‘Geo’chemical research: A key building block for nuclear waste disposal safety cases. J. Contam. Hydrol. 2008, 102, 174–179. [Google Scholar] [CrossRef]
- Bossart, P.; Bernier, F.; Birkholzer, J.; Bruggeman, C.; Connolly, P.; Dewonck, S.; Fukaya, M.; Herfort, M.; Jensen, M.; Matray, J.M.; et al. Mont Terri rock laboratory, 20 years of research: Introduction, site characteristics and overview of experiments. Swiss J. Geosci. 2017, 110, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Pearson, F.J.; Arcos, D.; Bath, A.; Boisson, J.Y.; Fernández, A.M.; Gäbler, H.E.; Gaucher, E.C.; Gautschi, A.; Griffault, L.; Hernán, P.; et al. Mont Terri Project—Geochemistry of Water in the Opalinus Clay Formation at the Mont Terri Rock Laboratory; Technical Report 5; Federal Office for Water and Geology (FOWG): Bern, Switzerland, 2003. [Google Scholar]
- Hennig, T.; Stockmann, M.; Kühn, M. Simulation of diffusive uranium transport and sorption processes in the Opalinus Clay. Appl. Geochem. 2020, 123. [Google Scholar] [CrossRef]
- Metz, V.; Geckeis, H.; González-Robles, E.; Loida, A.; Bube, C.; Kienzler, B. Radionuclide behaviour in the near-field of a geological repository for spent nuclear fuel. Radiochim. Acta 2012, 100, 699–713. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of input and examples for PHREEQC Version 3—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. In U.S. Geological Survey Techniques and Methods; U.S. Geological Survey: Denver, CO, USA, 2013; Volume Book 6, Chapter A43; p. 497. [Google Scholar]
- Kerisit, S.; Liu, C. Molecular simulation of the diffusion of uranyl carbonate species in aqueous solution. Geochim. Cosmochim. Acta 2010, 74, 4937–4952. [Google Scholar] [CrossRef]
- Liu, C.; Shang, J.; Zachara, J.M. Multispecies diffusion models: A study of uranyl species diffusion. Water Resour. Res. 2011, 47, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Wersin, P.; Mazurek, M.; Mäder, U.K.; Gimmi, T.; Rufer, D.; Lerouge, C.; Traber, D. Constraining porewater chemistry in a 250 m thick argillaceous rock sequence. Chem. Geol. 2016, 434, 43–61. [Google Scholar] [CrossRef] [Green Version]
- Joseph, C.; Van Loon, L.R.; Jakob, A.; Steudtner, R.; Schmeide, K.; Sachs, S.; Bernhard, G. Diffusion of U(VI) in Opalinus Clay: Influence of temperature and humic acid. Geochim. Cosmochim. Acta 2013, 109, 74–89. [Google Scholar] [CrossRef]
- Keesmann, S.; Noseck, U.; Buhmann, D.; Fein, E.; Schneider, A. Modellrechnungen zur Langzeitsicherheit von Endlagern in Salz- und Granitformationen; Technical Report GRS-206; Gesellschaft für Anlagen- und Reaktorsicherheit (GRS) mbH: Koln, Germany, 2005. [Google Scholar]
- Wersin, P.; Gaucher, E.C.; Gimmi, T.; Leupin, O.X.; Mäder, U.K.; Pearson, F.J.; Thoenen, T.; Tournassat, C. Geochemistry of Porewaters in Opalinus Clay at Mont Terri: Experimental Data and Modelling; Mont Terri Project, Technical Report; TR 2008-06; Mont Terri Project: St. Ursanne, Switzerland, 2009. [Google Scholar]
- Bradbury, M.H.; Baeyens, B. Derivation of In-Situ Opalinus Clay Porewater Compositions from Experimental and Geochemical Modelling Studies; Nagra Technical Report, NTB 97-07; Nagra: Wettingen, Switzerland, 1997. [Google Scholar]
- Pearson, F.J.; Tournassat, C.; Gaucher, E.C. Biogeochemical processes in a clay formation in situ experiment: Part E—Equilibrium controls on chemistry of pore water from the Opalinus Clay, Mont Terri underground research laboratory, Switzerland. Appl. Geochem. 2011, 26, 990–1008. [Google Scholar] [CrossRef] [Green Version]
- Vinsot, A.; Appelo, C.A.J.; Cailteau, C.; Wechner, S.; Pironon, J.; De Donato, P.; De Cannière, P.; Mettler, S.; Wersin, P.; Gäbler, H.E. CO2 data on gas and pore water sampled in situ in the Opalinus Clay at the Mont Terri rock laboratory. Phys. Chem. Earth 2008, 33, 54–60. [Google Scholar] [CrossRef]
- Wersin, P.; Leupin, O.X.; Mettler, S.; Gaucher, E.C.; Mäder, U.; De Cannière, P.; Vinsot, A.; Gäbler, H.E.; Kunimaro, T.; Kiho, K.; et al. Biogeochemical processes in a clay formation in situ experiment: Part A—Overview, experimental design and water data of an experiment in the Opalinus Clay at the Mont Terri underground research laboratory, Switzerland. Appl. Geochem. 2011, 26, 931–953. [Google Scholar] [CrossRef]
- Lerouge, C.; Blessing, M.; Flehoc, C.; Gaucher, E.C.; Henry, B.; Lassin, A.; Marty, N.; Matray, J.; Proust, E.; Rufer, D.; et al. Dissolved CO2 and alkane gas in clay formations. Procedia Earth Planet. Sci. 2015, 13, 88–91. [Google Scholar] [CrossRef] [Green Version]
- Gaucher, E.C.; Lassin, A.; Lerouge, C.; Fléhoc, C.; Marty, N.C.M.; Benoit, H.; Tournassat, C.; Altmann, S.; Vinsot, A.; Buschaert, S. CO2 Partial Pressure in Clayrocks: A General Model; Water-Rock Interaction WRI-13; HAL (archive hal-00664967): Guanajuato, Mexico, 2010; pp. 855–858. [Google Scholar]
- Bossart, P.; Thury, M. Characteristics of the Opalinus Clay at Mont Terri; Reports of the Swiss Geological Survey, No. 3; Swiss Geological Survey: Wabern, Switzerland, 2008. [Google Scholar]
- Marques Fernandes, M.; Vér, N.; Baeyens, B. Predicting the uptake of Cs, Co, Ni, Eu, Th and U on argillaceous rocks using sorption models for illite. Appl. Geochem. 2015, 59, 189–199. [Google Scholar] [CrossRef] [Green Version]
- Stockmann, M.; Schikora, J.; Becker, D.A.; Flügge, J.; Noseck, U.; Brendler, V. Smart Kd-values, their uncertainties and sensitivities—Applying a new approach for realistic distribution coefficients in geochemical modeling of complex systems. Chemosphere 2017, 187, 277–285. [Google Scholar] [CrossRef]
- Dzombak, D.A.; Morel, F.M.M. Surface Complexation Modeling: Hydrous Feric Oxide; Jon Wiley and Sons: New York, NY, USA, 1990; p. 393. [Google Scholar]
- Hyun, S.P.; Cho, Y.H.; Hahn, P.S.; Kim, S.J. Sorption mechanism of U(VI) on a reference montmorillonite: Binding to the internal and external surfaces. J. Radioanal. Nucl. Chem. 2001, 250, 55–62. [Google Scholar] [CrossRef]
- Joseph, C.; Stockmann, M.; Schmeide, K.; Sachs, S.; Brendler, V.; Bernhard, G. Sorption of U(VI) onto Opalinus Clay: Effects of pH and humic acid. Appl. Geochem. 2013, 36, 104–117. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Modelling the sorption of Mn(II), Co(II), Ni(II), Zn(II), Cd(II), Eu(III), Am(III), Sn(IV), Th(IV), Np(V) and U(VI) on montmorillonite: Linear free energy relationships and estimates of surface binding constants for some selected heavy metals and actinide. Geochim. Cosmochim. Acta 2005, 69, 875–892. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B.; Geckeis, H.; Rabung, T. Sorption of Eu(III)/Cm(III) on Ca-montmorillonite and Na-illite. Part 2: Surface complexation modelling. Geochim. Cosmochim. Acta 2005, 69, 5403–5412. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Experimental and Modelling Investigations on Na-Illite: Acid-Base Behaviour and the Sorption of Strontium, Nickel, Europium and Uranyl; Nagra Technical Report, NTB 04-02; Nagra: Wettingen, Switzerland, 2005. [Google Scholar]
- Hartmann, E.; Geckeis, H.; Rabung, T.; Lützenkirchen, J.; Fanghänel, T. Sorption of radionuclides onto natural clay rocks. Radiochim. Acta 2008, 96, 699–707. [Google Scholar] [CrossRef]
- Wigger, C.; Van Loon, L.R. Effect of the pore water composition on the diffusive anion transport in argillaceous, low permeability sedimentary rocks. J. Contam. Hydrol. 2018, 213, 40–48. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Vinsot, A.; Mettler, S.; Wechner, S. Obtaining the porewater composition of a clay rock by modeling the in- and out-diffusion of anions and cations from an in-situ experiment. J. Contam. Hydrol. 2008, 101, 67–76. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Multicomponent diffusion in clays. In Water Pollution in Natural Porous Media; Instituto Geologica de Espana: Madrid, Spain, 2007; Volume 1, pp. 3–13. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Solute transport solved with the Nernst-Planck equation for concrete pores with ‘free’ water and a double layer. Cem. Concr. Res. 2017, 101, 102–113. [Google Scholar] [CrossRef]
- Gratwohl, P. Diffusion in Natural Porous Media: Contaminant Transport, Sorption/Desorption and Dissolution Kinetics; Kluwer Academic Publishers: London, UK, 1958. [Google Scholar]
- Van Loon, L.R.; Glaus, M.A.; Müller, W. Anion exclusion effects in compacted bentonites: Towards a better understanding of anion diffusion. Appl. Geochem. 2007, 22, 2536–2552. [Google Scholar] [CrossRef]
- Van Loon, L.R.; Leupin, O.X.; Cloet, V. The diffusion of SO42- in Opalinus Clay: Measurements of effective diffusion coefficients and evaluation of their importance in view of microbial mediated reactions in the near field of radioactive waste repositories. Appl. Geochem. 2018, 95, 19–24. [Google Scholar] [CrossRef]
- Van Loon, L.R.; Soler, J.M.; Jakob, A.; Bradbury, M.H. Effect of confining pressure on the diffusion of HTO, 36Cl- and 125I- in a layered argillaceous rock (Opalinus Clay): Diffusion perpendicular to the fabric. Appl. Geochem. 2003, 18, 1653–1662. [Google Scholar] [CrossRef]
- Mazurek, M.; Alt-Epping, P.; Bath, A.; Gimmi, T.; Waber, H. Natural Tracer Profiles Across Argillaceous Formations: The CLAYTRAC Project; Technical Report; Nuclear Energy Agency and Organisation for Economic Co-Operation and Development: Paris, France, 2009. [Google Scholar]
- Van Loon, L.R.; Mibus, J. A modified version of Archie’s law to estimate effective diffusion coefficients of radionuclides in argillaceous rocks and its application in safety analysis studies. Appl. Geochem. 2015, 59, 85–94. [Google Scholar] [CrossRef]
- Van Loon, L.R.; Soler, J.M.; Bradbury, M.H. Diffusion of HTO, 36Cl- and 125I- in Opalinus Clay samples from Mont Terri: Effect of confining pressure. J. Contam. Hydrol. 2003, 61, 73–83. [Google Scholar] [CrossRef]
- Zorn, T. Untersuchungen der Sorption von Uran(VI) an das Gestein Phyllit zur Bestimmung von Oberflächenkomplexierungskonstanten. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2000. [Google Scholar]
- Arnold, T.; Zorn, T.; Zänker, H.; Bernhard, G.; Nitsche, H. Sorption behavior of U(VI) on phyllite: Experiments and modeling. J. Contam. Hydrol. 2001, 47, 219–231. [Google Scholar] [CrossRef]
- Tournassat, C.; Tinnacher, R.M.; Grangeon, S.; Davis, J.A. Modeling uranium(VI) adsorption onto montmorillonite under varying carbonate concentrations: A surface complexation model accounting for the spillover effect on surface potential. Geochim. Cosmochim. Acta 2018, 220, 291–308. [Google Scholar] [CrossRef]
- Philipp, T.; Shams Aldin Azzam, S.; Rossberg, A.; Huittinen, N.; Schmeide, K.; Stumpf, T. U (VI) sorption on Ca-bentonite at (hyper)alkaline conditions – Spectroscopic investigations of retention mechanisms. Sci. Total. Environ. 2019, 676, 469–481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lauper, B.; Jaeggi, D.; Deplazes, G.; Foubert, A. Multi-proxy facies analysis of the Opalinus Clay and depositional implications (Mont Terri rock laboratory, Switzerland). Swiss J. Geosci. 2018, 111, 383–398. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Unit | Shaly-76 | Shaly-61 | Sandy | Carb-Rich |
|---|---|---|---|---|---|
| pH | - | 7.13 | 7.50 | 7.40 | 7.28 |
| mmol/L | 281 | 230 | 121 | 195 | |
| mmol/L | 1.93 | 1.47 | 0.87 | 0.73 | |
| mmol/L | 21.97 | 16.79 | 5.91 | 15.89 | |
| mmol/L | 18.90 | 16.03 | 6.73 | 16.37 | |
| mmol/L | 0.46 | 0.47 | 0.35 | 0.44 | |
| mol/L | 29.62 | 8.37 | 9.81 | 9.81 | |
| nmol/L | 2.28 | 2.28 | 2.52 | 2.52 | |
| mmol/L | 327 | 273 | 121 | 242 | |
| mmol/L | 16.79 | 12.30 | 6.94 | 16.03 | |
| mol/L | 21.65 | 21.65 | 10.65 | 10.65 | |
| Alkalinity | mmol/L | 3.85 | 1.24 | 2.61 | 2.05 |
| I | mol/L | 0.38 | 0.32 | 0.16 | 0.28 |
| DDL | nm | 0.49 | 0.54 | 0.76 | 0.57 |
| Illite | wt.% | 20 | 17 | 17 | 8 |
| IS mixed | wt.% | 16 | 12 | 8 | 6 |
| Kaolinite | wt.% | 30 | 26 | 13 | 8 |
| Chlorite | wt.% | 10 | 6 | 7 | 4 |
| ∑Clay | wt.% | 76 | 61 | 45 | 26 |
| Calcite | wt.% | 14 | 11 | 17 | 42 |
| Dolomite | wt.% | n.a. | 2 | 2 | 3 |
| Siderite | wt.% | 1 | 4 | 2 | 2 |
| Porosity | - | 0.166 | 0.162 | 0.137 | 0.155 |
| wet water content | - | 0.068 | 0.070 | 0.055 | 0.063 |
| dry bulk density | kg/m | 2290 | 2280 | 2365 | 2320 |
| wet bulk density | kg/m | 2458 | 2456 | 2498 | 2480 |
| Parameter | Shaly-76 | Shaly-61 | Sandy | Carb-Rich | ||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | |
| Porosity (-) | 0.191 | 0.141 | 0.191 | 0.141 | 0.177 | 0.130 | 0.171 | 0.155 |
| wet water content (-) | 0.051 | 0.086 | 0.051 | 0.086 | 0.053 | 0.078 | 0.053 | 0.075 |
| dry bulk density (kg/m) | 2230 | 2410 | 2230 | 2410 | 2260 | 2400 | 2280 | 2400 |
| wet bulk density (kg/m) | 2420 | 2530 | 2420 | 2530 | 2440 | 2530 | 2450 | 2530 |
| Rock per kg porewater (kg/kg) | 11.55 | 16.95 | 11.55 | 16.95 | 12.36 | 18.17 | 13.20 | 15.24 |
| Scenario | Parameter | Shaly-76 | Shaly-61 | Sandy | Carb-Rich |
|---|---|---|---|---|---|
| MC | (10 m/kg) | 4.04 | 3.09 | 1.55 | 1.43 |
| (10 m/s) | 1.50 | 1.60 | 2.25 | 1.00 | |
| MC | (10 m/kg) | 4.04 | 3.09 | 1.55 | 1.43 |
| (10 m/s) | 1.00 | 1.10 | 2.00 | 1.00 | |
| MC | (10 m/kg) | 4.04 | 3.09 | 1.55 | 1.43 |
| (10 m/s) | 2.20 | 2.65 | 4.50 | 1.25 | |
| MC | (10 m/kg) | 3.64 | 2.71 | 1.10 | 1.29 |
| (10 m/s) | 1.50 | 1.40 | 0.80 | 1.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hennig, T.; Kühn, M. Surrogate Model for Multi-Component Diffusion of Uranium through Opalinus Clay on the Host Rock Scale. Appl. Sci. 2021, 11, 786. https://doi.org/10.3390/app11020786
Hennig T, Kühn M. Surrogate Model for Multi-Component Diffusion of Uranium through Opalinus Clay on the Host Rock Scale. Applied Sciences. 2021; 11(2):786. https://doi.org/10.3390/app11020786
Chicago/Turabian StyleHennig, Theresa, and Michael Kühn. 2021. "Surrogate Model for Multi-Component Diffusion of Uranium through Opalinus Clay on the Host Rock Scale" Applied Sciences 11, no. 2: 786. https://doi.org/10.3390/app11020786
APA StyleHennig, T., & Kühn, M. (2021). Surrogate Model for Multi-Component Diffusion of Uranium through Opalinus Clay on the Host Rock Scale. Applied Sciences, 11(2), 786. https://doi.org/10.3390/app11020786






