1. Introduction
In the field of medical imaging, segmentations are extremely useful for a plethora of tasks, including image-based diagnosis, lesion detection, image fusion, surgical planning or computer-aided surgery. For the prostate, in particular, fusion-guided biopsy and focal therapies are quickly gaining popularity due to the improved sensitivity and specificity for lesion detection [
1], and the low complication profile [
2], respectively, although they are still not fully accepted in clinical guidelines.
Nevertheless, accurate prostate segmentations are still hard and laborious to obtain, since they have to be manually annotated by expert radiologists and, even then, the inter- and intra-observer variability may be significant due to factors such as the lack of clear boundaries between neighboring tissues or the huge size and texture variation of this gland among patients. In our experiments, 14 images were segmented by a second expert, and the inter-expert agreement was found to be of 0.8794 in terms of Sørensen-Dice Similarity Coefficient (
DSC) and 1.5619 mm in terms of the Average Boundary Distance (ABD). Very similar results were obtained in [
3], with experts achieving a
DSC and an ABD of 0.83 and 1.5 mm, respectively. Because of this, automatic segmentation algorithms for the prostate are increasingly sought-after.
Before the rise of Deep Learning (DL) around 2012 [
4], many different techniques for automatic prostate segmentation coexisted. For instance, in [
5], MR images of the prostate were segmented by using voxel threshold-based classification followed by 3D statistical shape modeling. An alternative approach suggested by [
6] attempted to match the probability distributions of the photometric variables inside the object of interest with an appearance model, and then evolved the shape of the object until both distributions matched best. Another technique that has been widely used in the literature for medical image segmentation is atlas matching, which consists in non-rigidly registering a set of labeled atlas images to the image of interest, and then somehow combining all resulting segmentations into a single one [
7].
Despite the strengths of these methods, the true revolution in this field came with the advent of CNNs, which are a kind of DL algorithm formed by a stack of convolutional filters and non-linear activation functions, wherein the filter parameters are learned by stochastic gradient descent. New CNN architectures have been steadily raising state-of-the-art performance in computer vision tasks, such as image classification [
8], image segmentation [
9] or object detection [
10]. Similarly, this trend has carried over to medical imaging, and prostate segmentation in particular.
One of the first approaches to CNN-based segmentation consisted in sliding a classification CNN over a whole image to provide pixel-wise classifications, which then were combined into a single segmentation mask [
11]. Shortly after, fully convolutional neural networks for semantic segmentation were proposed [
12]; they allowed for much faster training and inference, as the whole image was processed at once, and also made a better use of spatial information by utilizing activation maps from different layers. Later, the U-net architecture [
9] introduced the encoder-decoder design with skip connections that is still predominantly used. In a U-net, the image is first processed through an encoder CNN, which is similar to a classification CNN. The output of the encoder is then connected to the input of the decoder CNN, which is an inverted version of the encoder where the pooling operators have been exchanged by up-scaling convolutions. Additionally, skip connections transfer information from the encoder to the decoder at several stages other than the output. This idea, in combination with residual connections [
13] and a cost function based on
DSC, was quickly extended from two-dimensional (2D) convolutions to 3D convolutions by the V-net [
14], in order to better deal with 3D medical images. Similar to the transition from pixel-wise classification to fully convolutional CNNs, 3D-CNNs are better able to use the context of the whole image and provide faster speeds in comparison with a per-slice 2D segmentation.
In the field of prostate segmentation in MR imaging, many different CNN architectures building on top of the V-net or the U-net have been proposed. For instance, ref. [
15] proposed the addition of deep supervision, ref. [
16] used a more recent densenet-resenet architecture [
13,
17,
18] introduced a boundary-aware cost function. Prostate segmentation in 3D Ultrasound (US) imaging, although much less prevalent, has experienced a similar development, with a recent paper employing the attention mechanism to exploit the information from several layers [
19]. Some of these architectural choices, and several others, will be further elaborated in
Section 2.
Despite the high performances reported by many of the aforementioned papers, it could be argued that they all incur in a common pitfall: they are designed to perform well on one single prostate dataset. Therefore, it is unknown how robust the model would be when applied to any other dataset. This kind of robustness is paramount if the model is to be applied in a real-life scenario, where the images may come from many different scanners, and may be analyzed by many different experts. Furthermore, robustness is also desirable in the sense that the produced segmentations should be accepted by different experts, despite their possibly varying criteria for segmentation; in other words, the produced segmentations should ideally behave like an average prediction from several experts.
In this paper, a robust algorithm based on CNNs for MR and US prostate image segmentation is proposed. It leverages both common and not-so-common design choices, such as a hybrid densenet-resnet architecture (
Section 2.3), deep supervision (
Section 2.4), 3D data augmentation (
Section 2.5), a cyclic learning rate (
Section 2.7), checkpoint ensembling (
Section 2.8) and a simple yet effective post-processing technique to increase the resolution of the segmentations known as Neural Resolution Enhancement (
Section 2.9). This technique, besides improving the segmentation performance, allows the CNN to produce segmentations with resolutions beyond that of the original image. Furthermore, the model is trained on five different datasets simultaneously (
Section 2.1), achieving an excellent performance on all of them. Finally, the weights obtained from this model are used to train (through transfer learning) an US segmentation model on two different datasets, achieving also an excellent performance on them both. Results are presented both quantitatively (
Section 3.1), by presenting the metrics (
Section 2.10) achieved on every dataset, and qualitatively (
Section 3.2), by showing images of the predicted and Ground Truth (GT) segmentations on several patients. The paper is closed by a discussion, (
Section 4), about the clinical impact of the proposed model, and a brief conclusion (
Section 5).
2. Materials and Methods
2.1. Description of the Datasets
One of the main strengths of this study is the use of five different prostate T2-weighted MR datasets. As shown in
Table 1, there is a significant variability in scanner manufacturers, resolutions and magnetic field strengths, among other factors. Datasets “Girona” [
20], “Promise12” [
21] and “Prostate-3T” [
22] are all freely available for download on the Internet, while “IVO” comes from the Valencian Institute of Oncology, and “Private” comes from a private institution which has decided to remain anonymous. Furthermore, Promise12 is an ongoing prostate segmentation challenge, wherein 50 MR prostate images are provided along with their segmentation masks (dataset “Promise12”), and 30 additional images are provided without segmentations as a test set (dataset “Promise12_test”). The participants must submit their predictions to the challenge server, where they are evaluated. Hence, “Promise12_test” will only be used for testing.
In addition to that, the prostate segmentations follow varying criteria depending on the expert who segmented them. In “IVO” dataset, three different radiologists with two, five and seven years of experience in prostate cancer imaging took turns to perform the segmentations. In “Private” dataset, a single medical physicist with two years of experience in MR prostate imaging segmented all the images. In “Promise12”, each of the four rows in
Table 1 corresponds to a different medical center and, by extension, were also segmented by at least one different expert each, although an expert from the Promise12 challenge [
21] corrected some of them. For the other datasets, no further information about the segmentations is known.
Regarding exclusion criteria, before separating the images into any subsets, all segmentations were examined and those with obvious errors were directly excluded. Therefore, no corrections were made, so as to better preserve the particular criteria from each expert (except for the “Private” dataset, in which all segmentations were revised). The number of samples (N) in
Table 1 is computed after this filtering. As a special mention, 18 images from “Prostate-3T”, which were also present in “Promise12” or “Promise12_test” (although with different GT segmentations), were also discarded; and other 30 images from “Prostate-3T” (half of the original dataset), which systematically left many slices in the base and apex unsegmented, had to be discarded as well.
Figure 1 shows the center slice of a sample from each of the datasets.
For the 3D-US segmentation model, two different datasets were employed: “IVO” and “Private”, both coming from the same institutions as their homonymous MR datasets. For “IVO” (
images), five different urologists with six to thirty years of experience segmented the images, while for “Private” (
images), it was two urologists with more than ten years of experience; no exclusion criteria were applied. Images from both datasets were captured using Hitachi scanners at spacings of 0.20 mm to 0.41 mm in any axis.
Figure 1 shows the center slice of a sample from each axis. Unfortunately, no further segmented datasets were found on the Internet for this image modality.
2.2. Image Pre-Processing
Before using the images to train the CNN, they all had to be pre-processed to alleviate their heterogeneity. First, their intensity was normalized by applying Equation (
1) to every image
I, such that 98% of the voxels in
fall within the range
.
Then, the center crop of each image (and its respective segmentation mask) was taken, using a size of and a spacing of (1, 1, 3) mm for the MR images, and a size of and a spacing of (0.75, 0.75, 0.75) mm for the US images. B-Spline interpolation of third order was employed for all image interpolation tasks, while Gaussian label interpolation was used for the masks.
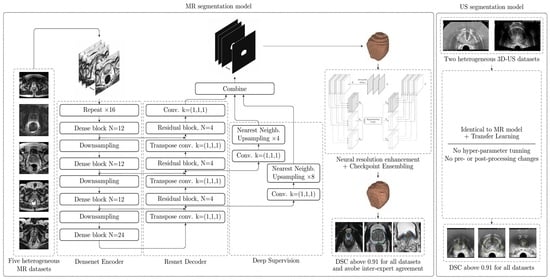
2.3. Hybrid Densenet-Resnet Architecture
The proposed CNN architecture (
Figure 2) is based on the V-Net and, more precisely, on the architecture proposed by [
16], which combines a densenet [
17] encoder with a resnet [
13] decoder. All design decisions were guided by validation results.
The full architecture is sufficiently described in
Figure 2. Therefore, only a few interesting design choices will be discussed here. Firstly, the proposed Dense block includes a residual connection, which empirically helped the CNN converge faster. Secondly, every Dense block contains between 12 and 24 “standard” convolutions (kernel of size (3, 3, 3)), as well as several “bottleneck” convolutions (kernel of size (1, 1, 1)), for a total of 72 “standard” convolutions, which is a huge number compared to similar architectures such as V-net (with only 12 convolutions in its resnet-based encoder) or BOWDA-net [
23] (with 28 convolutions in its densenet-based encoder). This makes the encoder better capable of learning more complex representations of the input data. Comparatively, the decoder can have a simpler resnet architecture, since the heavy lifting (which is feature extraction) has already been done by the encoder. Thirdly, channel-wise PReLU was employed as activation function [
24], as it provides a slightly better performance at a negligible additional computational cost. A channel-wise PReLU function is similar to a ReLU (Rectified Linear Unit) [
25] function, but with a learnable slope
for the negative inputs (instead of being just zero);
is shared among all activations in a channel, but is different for every channel. Fourthly, transpose convolutions were used in the decoder, since they were found to provide a better performance when compared to upsampling followed by a convolution.
Due to the huge memory requirements intrinsic to the densenet architecture, very small batch sizes had to be employed (4 for the MR dataset, and 2 for the US dataset), as well as a technique known as Gradient Checkpointing [
26], which allows to reduce the Graphics Processing Unit (GPU) memory requirements at the cost of increased computation times. It works by keeping a fraction of the CNN activations in memory at any given time (instead of all of them), and recomputing the rest when they are needed.
2.4. Deep Supervision
To further improve the performance of the CNN, a simple implementation of Deep Supervision [
27] is used. Unlike regular CNNs, which predict the segmentation mask from the last layer only, deeply supervised CNNs attempt to predict it from several intermediate layers as well. In
Figure 2 this is implemented by the branches to the right of the decoder, which take the activation maps at two points along the decoder, reduce the number of channels to one by means of a “bottleneck” convolution, and then upsample them to the CNN output resolution using Nearest Neighbors interpolation. During training, the final output of the CNN is averaged with these intermediate predictions while, during inference, only the final output is considered. A similar implementation for this technique is also successfully used by [
15].
Figure 3 shows the GT mask of a prostate MR image, as well as the final and intermediate predictions, which are used for Deep Supervision. As it can be seen, intermediate predictions resemble a downscaled version of the final mask.
As demonstrated in [
27], Deep Supervision serves a twofold purpose: on one hand, it forces all the layers throughout the network to learn features which are directly useful for the task of image segmentation; on the other hand, the gradients are better able to flow towards the deeper layers, which accelerates training, and helps prevent problems related to gradient vanishing.
2.5. Online Data Augmentation
Online data augmentation was used to artificially increase the amount and variability of the training images, thus improving the generalization capabilities of the model and, ultimately, its performance. Before feeding an image to the CNN during training, the following transformations were sequentially applied to it:
- 1.
3D rotation along a random axis with random magnitude in the range radians.
- 2.
3D shift of random magnitude in the range mm along every axis.
- 3.
3D homogeneous scaling of random magnitude in the range times.
- 4.
Flipping along x-axis with probability 1/2.
- 5.
Adding Normally distributed noise with a random magnitude in the range relative to the normalized image.
When required, a random number would be sampled from the uniform distribution and then scaled and shifted to the appropriate range.
2.6. Model Training
For both the MR and US segmentation models, images were split into three subsets: training (70% of the images), validation (15%) and test (15%). These proportions were computed dataset-wise, such that the relative representation of each datset on every subset was the same. The MR training set was used to update the weights of the CNN through stochastic gradient descent (Adam optimizer with default parameters), while the MR validation set was used to choose the best set of hyper-parameters (such as learning rate schedule, CNN depth, CNN width, input resolution or even internal CNN architecture). Once the MR segmentation model was considered final, the CNN was retrained one last time using both MR training and validation subsets, and the results were evaluated in the MR test subset.
For the US segmentation model no hyper-parameters were changed, except the input size and spacing (to better fit the prostate in the image, as discussed in
Section 2.2) and the batch size (due to GPU memory limitations, as discussed in
Section 2.3). Furthermore, transfer learning was employed [
28]: the weights from the MR segmentation model were used as an initialization to the US segmentation model, thus leveraging the feature extraction capabilities of the pre-trained model. The US model was directly trained using both US training and validation subsets (as no validation subset was actually required), and the results were evaluated in the US test subset.
2.7. Cyclic Learning Rate
A cyclic learning rate [
29] was chosen for training, as it presents several advantages with respect to a fixed schedule. Firstly, an optimal fixed schedule must be learned from the data, which is cumbersome and requires extensive trial and error; secondly, this cyclic schedule will allow us to use a technique known as Checkpoint Ensembling, which will be explained in
Section 2.8. Thirdly, a cyclic learning rate supposedly helps the optimizer escape saddle point plateaus, which is desirable. The chosen cyclic schedule is a decaying triangular wave (schedule known as “triangular2” in [
29]) of period 48 epochs (at 180 batches per epoch), with a minimum learning rate of
, a maximum of
, and a decay such that the maximum value of the wave is halved every period. The CNN was trained for six periods (a total of 288 epochs).
2.8. Checkpoint Ensembling
Checkpoint Ensembling [
30] is a strategy that allows to capture the effects of traditional ensembling methods within a single training process. It works by collecting checkpoints of the best
k weights (those that lead to the best validation scores of the CNN during its training process). Then, during inference, for each input to the CNN,
k predictions are obtained and combined into a single one (by averaging, for instance). In theory, this method makes a compound prediction from weights which may have settled into different local minima, thus simulating the compound segmentation proposal from several experts.
As for our model, using a cyclic learning rate opens up the possibility of using weight checkpoints that coincide with the minima of the learning rate schedule, as it is at these points where the gradient stabilizes most, and local minima are supposedly reached. Therefore, in our particular case, six checkpoints will be used for Checkpoint Ensembling. As a bonus, this technique incurs in no additional costs, other than inference costs, which are obviously increased by a factor of six. Traditional ensembling was also tested, although finally discarded, as it did not provide any performance improvements and incurred in much higher training costs.
2.9. Neural Resolution Enhancement
The last technique that will be discussed is Neural Resolution Enhancement [
31], which leverages the properties of any already trained image segmentation CNN to intelligently increase the resolution of the output mask at no cost, even beyond the resolution of the original image.
To understand how this method operates, let us describe how a threefold increase in the resolution along the z-axis would be performed (refer to
Figure 4). First, the resolution of the input image
X is triplicated along the z-axis (by using bicubic interpolation, for instance), therefore becoming
. Then, three new images (
) are built by taking z-slices from
in such a way that they have the same size (dimensions) and spacing (voxel size) as
X, but are offset by different sub-voxel amounts along z-axis (in fact, note that
). Then,
and
are fed through the CNN, and three segmentation masks are obtained (
). Finally, all three predictions are combined by stacking them in the correct order, hence obtaining
, which is a predicted mask with three times the resolution of
X along the z-axis. This same procedure could be applied to any number of dimensions simultaneously, although the inference cost would scale abruptly, as all the possible sub-voxel displacement combinations would have to be computed.
This method, albeit simple, is extremely powerful, as it allows to predict (rather than to interpolate) segmentation masks beyond the resolution of the original image. The problem of interpolation is therefore shifted from the mask domain to the image domain, where the conveyed information is still complete and not yet binarized. Furthermore, it can be applied to any already trained segmentation CNN, as a simple post-processing step.
Figure 5 shows an example application.
In the context of our problem, z-axis resolution is triplicated to reduce the impact of the final mask interpolation. This is: once the CNN outputs a segmentation mask, it must be transformed back to the space of the original input image (same resolution, spacing, physical orientation, position, etc.). Although this is necessarily a lossy process, by leveraging this technique, the predicted mask can have a higher resolution, which significantly mitigates the issue.
2.10. Evaluation Metrics and Loss
As it is customary in semantic segmentation problems,
DSC was employed as the main evaluation metric, which guided most design decisions.
DSC is defined in Equation (
2), where N denotes the total number of voxels in an image,
represents the prediction of the CNN at voxel
i,
is the GT label at voxel
i, and
is a small arbitrary value that prevents division by zero.
As a loss function,
DSC is much better able to deal with unbalanced segmentation masks in comparison with binary cross-entropy. However, several studies acknowledge its deficiencies along the boundaries of the mask [
23], or when the target is very small [
32] (as in lesion segmentation). Ref. [
23], for instance, utilizes a composite loss which penalizes wrong segmentations proportionally to the distance to the boundary of the GT. Despite multiple attempts at incorporating a similar loss to our model, we finally decided against it, since it did not provide any performance advantages during validation. Therefore, the finally used loss function
is directly derived from
DSC, as illustrated in Equation (
3).
In addition to
DSC, two distance-based metrics were also employed: Average Boundary Distance (ABD) and 95th percentile Hausdorff Distance (HD95). These metrics were computed as described in the Promise12 challenge [
21] and represent the average and the 95th percentile largest distance (in mm) between the surface of the predicted mask and the GT mask, respectively.
When comparing these metrics among groups, the Wilcoxon signed-rank test was employed, which is the non-parametric equivalent of the paired t-test. The Wilcoxon test was needed due to the distribution of the metrics in the test set not being normal (p-value ≤ 0.001 using D’Agostino and Pearson’s normality test for DSC, ABD and HD95 results).
3. Results
3.1. Quantitative Results
The quantitative test results (in terms of
DSC, HD95 and ABD metrics) for both MR and US segmentation models (globally, and by dataset) are shown in
Table 2. Both models achieve a mean and median
DSC above the 0.91 threshold for all datasets, meaning that they are very strong performers and, more interestingly, that they are robust to the heterogeneity of the various datasets. As an exception, the mean
DSC on the “Girona” dataset falls to around 0.90 due to a single relatively weak prediction (
DSC of 0.8467) dragging down the mean of this extremely small set, as evidenced by the otherwise inexplicably high median value. Also, the mean
DSC for the MR segmentation model on the “Private” dataset is exceptionally high, probably due to it being the only dataset where GT segmentations were revised.
These observations are further supported by the HD95 metric. For all MR and US datasets, it sits mostly just below 4 mm in average. Since the slices in a typical prostate MR image are about 3 mm apart, achieving an HD95 below 3 mm is extremely unlikely due to the different criteria regarding how far the base and the apex should extend. Thus, an average HD95 below 4 mm is a very good result. Finally, the ABD metric lies mainly below 1 mm in average for all MR datasets, and below 1.2 mm for the US datasets.
For comparison purposes, a second segmentation (GT2) was created for the first three datasets by one of the IVO experts.
Table 3 shows the mean
DSC of the predictions of the model against each of the GTs (GT and GT2), as well as the mean
DSC of the GTs against themselves (the inter-expert agreement). As it can be seen, the
DSC of the model against both GT and GT2 surpasses by a large margin the inter-expert agreement (except for one case), suggesting that the model is more robust and reliable than any given expert by itself. Two Wilcoxon tests confirm that these differences in
DSC are statistically significant (at a significance threshold of 0.05).
Since most authors focus on performing well in one single dataset, it is difficult to compare these results against other published models. As an exception [
16] used a private dataset (with diffusion-weighted MR images and ADC-maps in addition to the T2-weighted MR images) in conjunction with “Promise12”, achieving an impressive mean
DSC of 0.9511 on their own dataset, but only a mean
DSC of 0.8901 on “Promise12_test”.
Regarding 3D-US image segmentation, few publications were found (most use 2D-US), and none employed more than one dataset. As for recent 3D-US papers, ref. [
19] achieved a mean
DSC of 0.90 by leveraging an attention mechanism. Ref. [
33] obtained a
DSC 0.919 by using a contour-refinement post-processing step, however, the results are not reported on a proper test set, but rather, using leave-one-out cross-validation. More recently, ref. [
34] achieved an excellent 0.941 mean
DSC by applying a 2D U-Net on radially sampled slices of the 3D-US and then reconstructing the full 3D volume. As an example on the problem of 2D-US segmentation, ref. [
35] achieved a mean
DSC of 93.9 by using an ensemble of five CNNs. This last result, however, is not directly comparable, as in 2D-US segmentation the
DSC is evaluated on a per-slice basis, instead of the prostate as a whole.
Promise12 is an ongoing prostate segmentation challenge, wherein 50 MR prostate images are provided along with their segmentation masks (dataset “Promise12”), and 30 additional images are provided without segmentations as a test set (dataset “Promise12_test”).
Table 4 shows the performance of the model on “Promise12_test” along with the five best entries to the Promise12 challenge. For this specific dataset, the predicted segmentation masks are uploaded and evaluated in the servers of the challenge, and the results are publicly posted online thereafter [
36].
As it should be expected, the mean and median for our model are similar to the results obtained for the other test sets (
Table 2). Also, comparing it to the other entries (
Table 4), our model achieves very similar results for all metrics; yet, its Challenge Score falls behind. That said, this is also to be expected since, unlike the other contestants, no fine-tuning was performed to improve the results for this dataset in particular. BOWDA-net [
23], for example, uses an adversarial domain adaptation strategy to transform the images from a second training dataset to the domain of the “Promise12” dataset, therefore improving the performance only on “Promise12_test”. Lastly, our model used just 41 out of the 50 images provided in the “Promise12” dataset for training, as two were discarded and seven were used for testing. When comparing our model against each of the others with a Wilcoxon test, only the first contender (MSD-Net) was found to be significantly (
p-value ≤ 0.01) better in all metrics, while the fourth contender (nnU-Net) was better in terms of
DSC (
p-value = 0.037) and ABD (
p-value = 0.030), but not HD95 (
p-value = 0.439). The nnU-Net [
37] is a very recent and interesting method that tries to automate the process of adapting a CNN architecture to a new dataset by making use of a sensible set of heuristics. Regarding the MSD-Net, unfortunately, its specifics are yet to be published as of the writing of this paper.
Ultimately, beating this challenge was never the focus of this paper. No other single model (to the author’s knowledge) is able to perform as consistently as ours in so many different datasets simultaneously. This is of utmost importance if such a model is to be used in a real-life scenario, where the MR images may come from many different scanners, and may be analyzed by many different experts.
3.2. Qualitative Results
To asses these results qualitatively, in
Figure 6a–n, the center 100 mm × 100 mm crop (85 mm × 85 mm in the case of US images) of three slices from the worst and best performing images (in terms of
DSC) from each dataset have been represented, along with the GT (in red), the GT2 (in blue, when available) and the predicted segmentations (in green). Figures were generated using Python library plot_lib [
38].
Regarding the worst cases, despite being the poorest performers, the differences are relatively small and often the model proposal is arguably superior to the GT. Furthermore, the central slices are almost identical in all instances, and it is only towards base and apex where the differences emerge. One of such discrepancies is the point at which the apex and the base begin, which oftentimes depends on the segmentation criteria, as it can be seen, for instace, in
Figure 6a, where the CNN indicates the presence of prostate in the rightmost slice (at the base), while the GT label does not (although GT2 does). Finally, at several ambiguous instances (such as in the middle slice of
Figure 6a and the rightmost slice of
Figure 6b,j), the predicted mask (in green) behaves as an average between both experts. As discussed, this is a very desirable property for the model to have, and this is what allows it to outperform single experts on their own (as demonstrated in
Table 3).
As for the best cases, it can be seen that they are mostly represented by larger prostates, as they are comparatively easier to segment, and also the
DSC metric is biased towards them. As a curiosity, the rightmost slice in
Figure 6n shows how the model has learned to avoid segmenting the catheter balloon that is used in prostate biopsies, the procedure during which the US images were acquired.
In terms of HD95, the worst MR case, which corresponds to an HD95 of 7.2 mm, is shown in
Figure 7. As it can be seen, two slices from the apex are missed by the algorithm, hence amounting to a minimum of
mm of error, plus some extra mm. The worst performing MR case in terms of ABD coincides with the worst performing prostate in terms of
DSC, which can be found in
Figure 6d.
3.3. Ablation Studies
Table 5 contains the results of the ablation studies, which were performed by changing one single aspect of the baseline MR model at a time. Wilcoxon tests were performed against the baseline to check for significance (
p-value
). Also, a single experiment was performed on the US model by retraining it without the use of transfer learning.
Firstly, the two post-processing techniques discussed in this paper (Checkpoint Ensembling and Neural Resolution Enhancement) are analyzed. Both show high statistical significance (p-values ) in terms of DSC and ABD. In fact, out of all the experiments conducted in this Section, only these two were found to make a statistically significant difference, probably since the worsening of the metrics, even if minor, is sustained for all images. These post-processing methods affect in no way the training process or the model, as they are applied at a later stage; therefore they are a simple and free bonus in performance, only at the cost of increased inference time.
Secondly, a battery of tests involving architectural changes (which require retraining) is presented. Even if none of these experiments showed statistical significance, several conclusions can still be extracted cautiously.
The first two experiments are an attempt to lower the complexity of the baseline model by either reducing the number of resolution levels of the network, or the amount of layers (this is: “standard” convolutions) per level. In both cases, even if the differences with respect to the baseline were small, a decrease in performance can be observed for the majority of the metrics, which justifies the use of the more complex baseline architecture if possible.
In the next two experiments, models based exclusively on the resnet architecture (with residual connections applied every four consecutive convolutions) were employed. Despite having as much as four times the amount of parameters as compared to the baseline, these models were the worst performing out of all analyzed in this Section, hence showing the power of the densenet architecture.
The next test consisted in replacing the PReLU activations with ReLU activations. Despite this having a very small influence in performance, the metrics are overall better in the baseline, and PReLU is therefore preferred given its negligible impact on model complexity.
For the following test, Deep Supervision was deactivated. In general, most of the metrics show a small improvement with this architectural modification. In our internal validation tests, this technique seemed to provide a small boost in performance and, as such, it was added to the final model. Furthermore, it stabilized the initial steps of the training procedure. However, in light of these results, its usefulness remains now in question.
For the last test, the US segmentation model was retrained using random weight initialization, instead of using the weights from the MR model for transfer learning. Although the fine-tuned model converged faster, the results suggest that training from scratch might be preferable in situations like this one, where the amount of training data is sufficient. In any event, the generality of the architecture and pre-/post-processing methodology still holds, even if the weights of the MR prostate segmentation model are not particularly useful for the problem of US prostate segmentation.
4. Discussion
In this paper, a robust and generalizable model for accurate prostate segmentation has been proposed.
To achieve robustness, the model was trained with five very challenging and heterogeneous MR prostate datasets (and two US prostate datasets) with GTs originating from many different experts with varying segmentation criteria. Additionally, several key design choices, such as the use of Checkpoint Ensembling and a relatively heavy data augmentation regime, were explicitly made.
In clinical practice, the MR and US images may originate from many different scanners, with widely different characteristics (field intensities, scanner manufacturers, use of endorectal coil, etc.), to which any segmentation algorithm should be robust by design. As we have seen in
Table 2, the proposed model has a similarly good performance for all images, no matter the dataset nor its specific characteristics.
Furthermore, such an algorithm may be used by different experts with varying criteria for segmenting the prostate. Even if it is impossible to please every criterion simultaneously, the proposed model is shown to behave as an average prediction among the different experts, as seen for instance in the rightmost slice of
Figure 6j. This is corroborated by
Table 3, where it shows a significantly higher overlap with any given expert (it tries to please all criteria), than the experts between themselves.
Concerning generalizability, the proposed architecture can be very easily applied to different tasks by means of transfer learning. In this paper, the MR segmentation model is simply retrained, with no hyperparameter tuning or image pre- or post-processing changes (other than the change of input resolution), on the problem of US prostate segmentation, achieving equally good performances despite the smaller dataset sizes, as seen in
Table 2.
The main clinical applications of the proposed model lie in the context of fusion-guided biopsy and focal therapies on the prostate, which require an accurate segmentation of both MR and US prostate images. These segmentations are employed to perform registration between both modalities, which is needed to transfer the prostate lesions detected by the radiologists in the preoperative MR to the intraoperative US image in order to guide the procedure.
The proposed model can undercut, and even eliminate, the need of manual segmentations, which require expertise, are very time-consuming, and are prone to high inter- and intra-expert variability. Hence, more accurate segmentations may lead to better inter-modal prostate image registration and better prognosis in the aforementioned procedures; while almost instant results can be of particular interest for the segmentation of intraoperative US images, where the urologist currently has to spend around ten minutes manually performing this task next to the sedated patient.
Finally, a technique known as Neural Resolution Enhancement was employed as a post-processing step to reduce the impact of the lossy CNN output interpolation. This method, which leverages any already trained segmentation CNN, can also be used to improve the resolution of the output mask even beyond that of the original input image, as discussed in
Figure 5.
This technique could be especially appealing for simulating the biomechanical behavior of the prostate, which is required by many registration algorithms and surgical simulators. To function properly, such simulations demand very high resolution meshes of the prostate geometry, which are inherently impossible to obtain due to the reduced resolution of the original MR and US images. However by using Neural Resolution Enhancement, a much higher resolution mask is obtained, which is not the result of mere interpolation, but rather a prediction of the missing geometry by combining the contextual information contained in the original image with the knowledge that the CNN has acquired about the general shape of this gland.