Hybrid Early Warning System for Rock-Fall Risks Reduction
Abstract
1. Introduction
- We developed a prediction model-based machine learning technology to predict the possibility of rock-fall.
- We developed a detection model-based computer vision algorithms to detect and track rock-fall events.
- We combined the detection and the prediction models in a hybrid reliable risk reduction model to increase the model reliability.
- We developed a hybrid early warning system to reduce the rock-fall risks.
2. Study Area and Problems
3. Data Used
4. Methodology
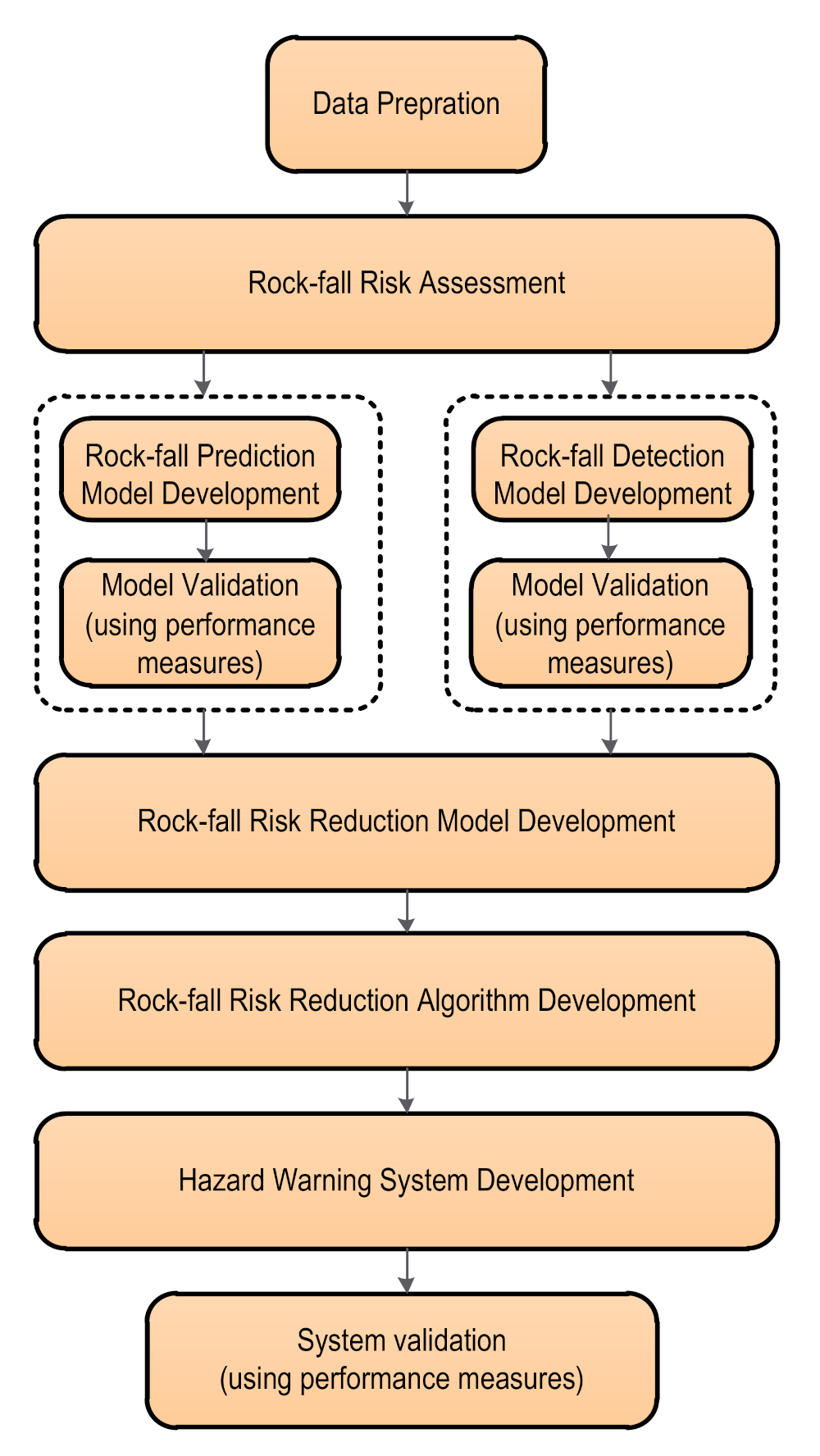
4.1. Overall Methodology
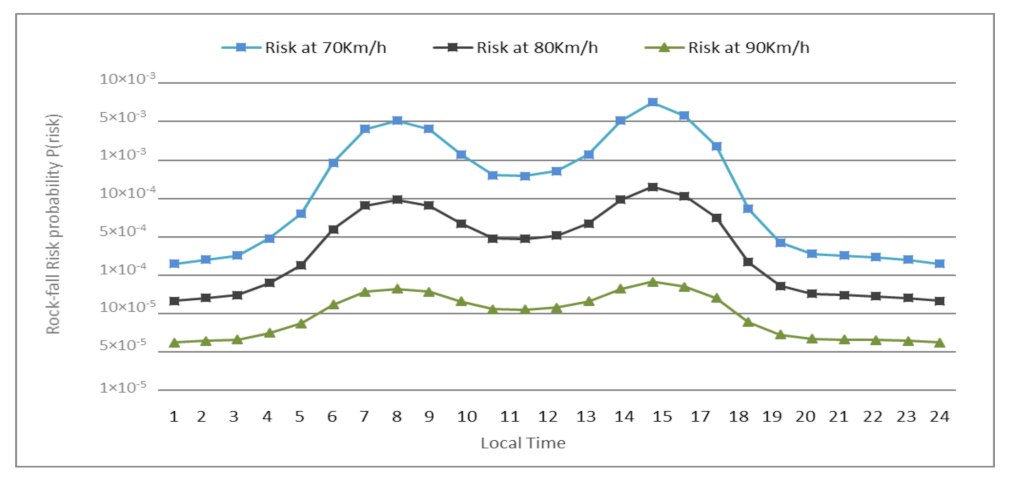
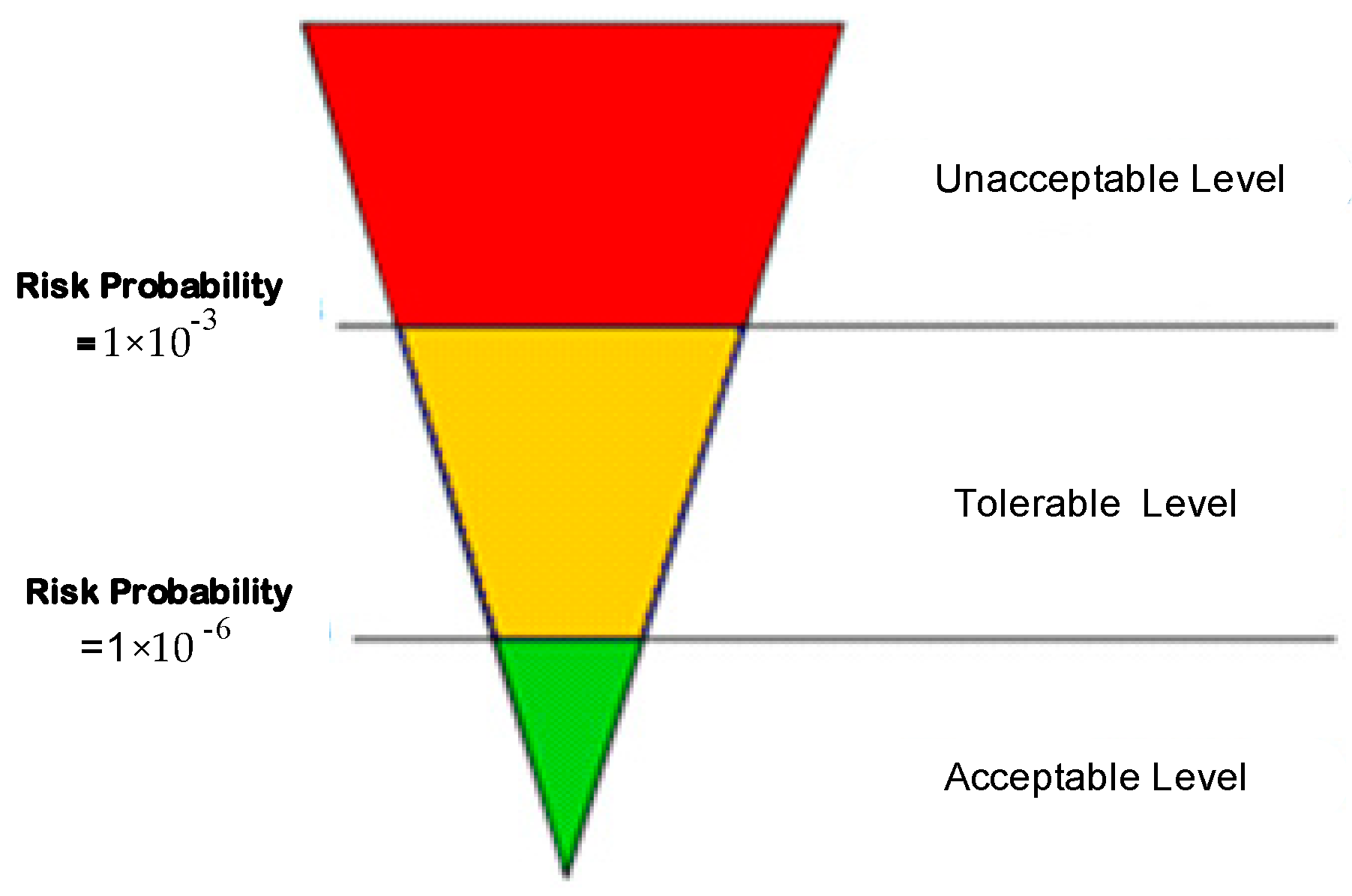
4.2. Rock-Fall Risk Assessment
4.3. Rock-Fall Prediction Model Development
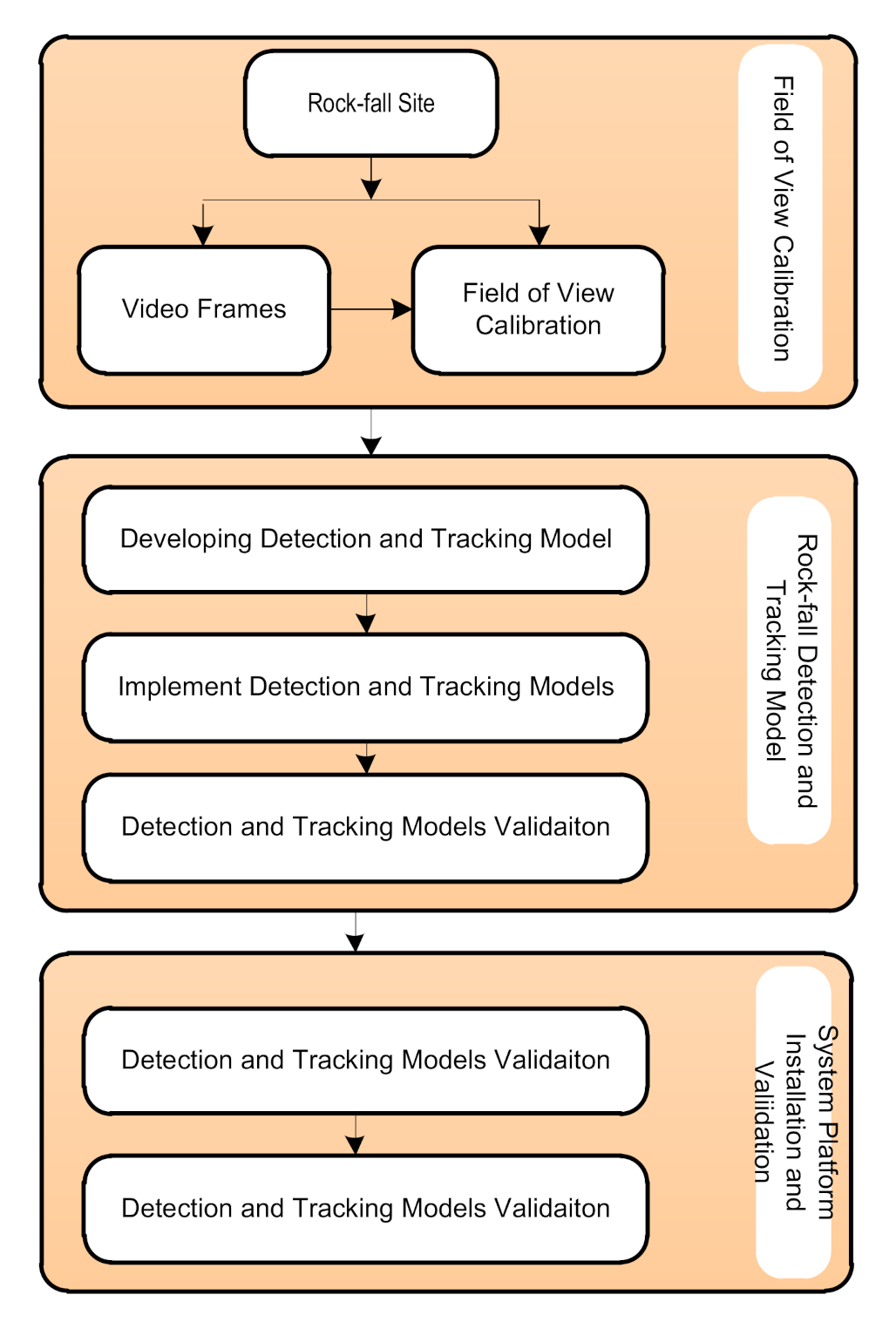
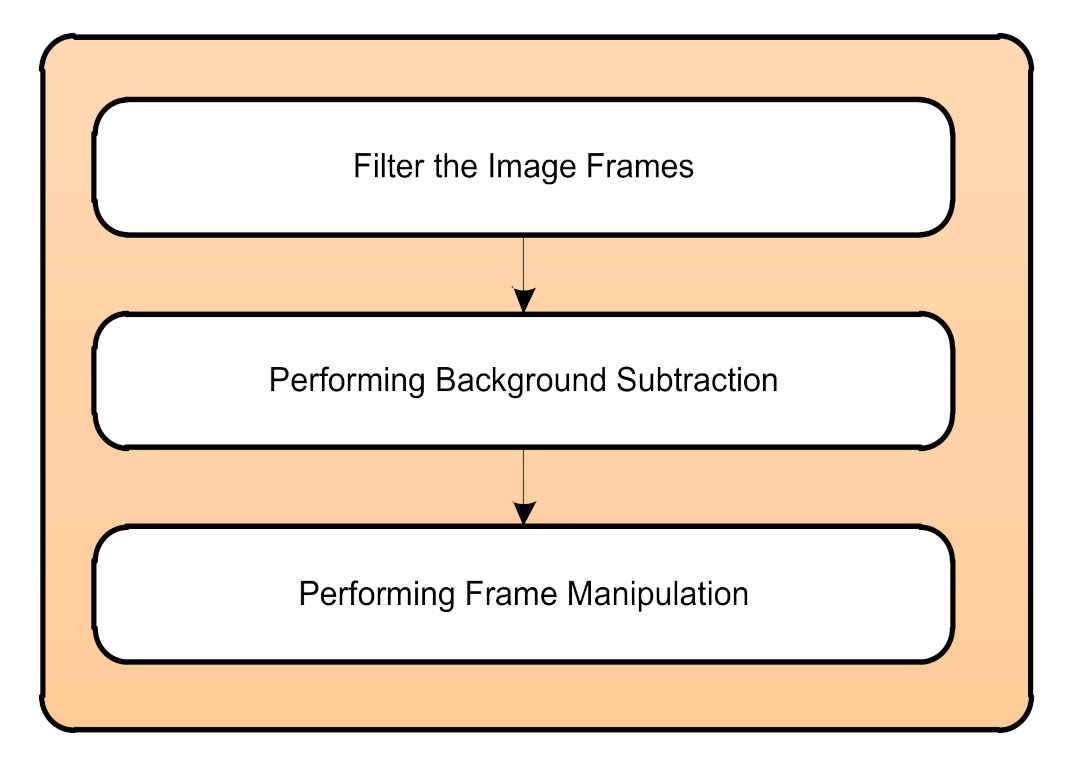
4.4. Rock-Fall Detection Model Development
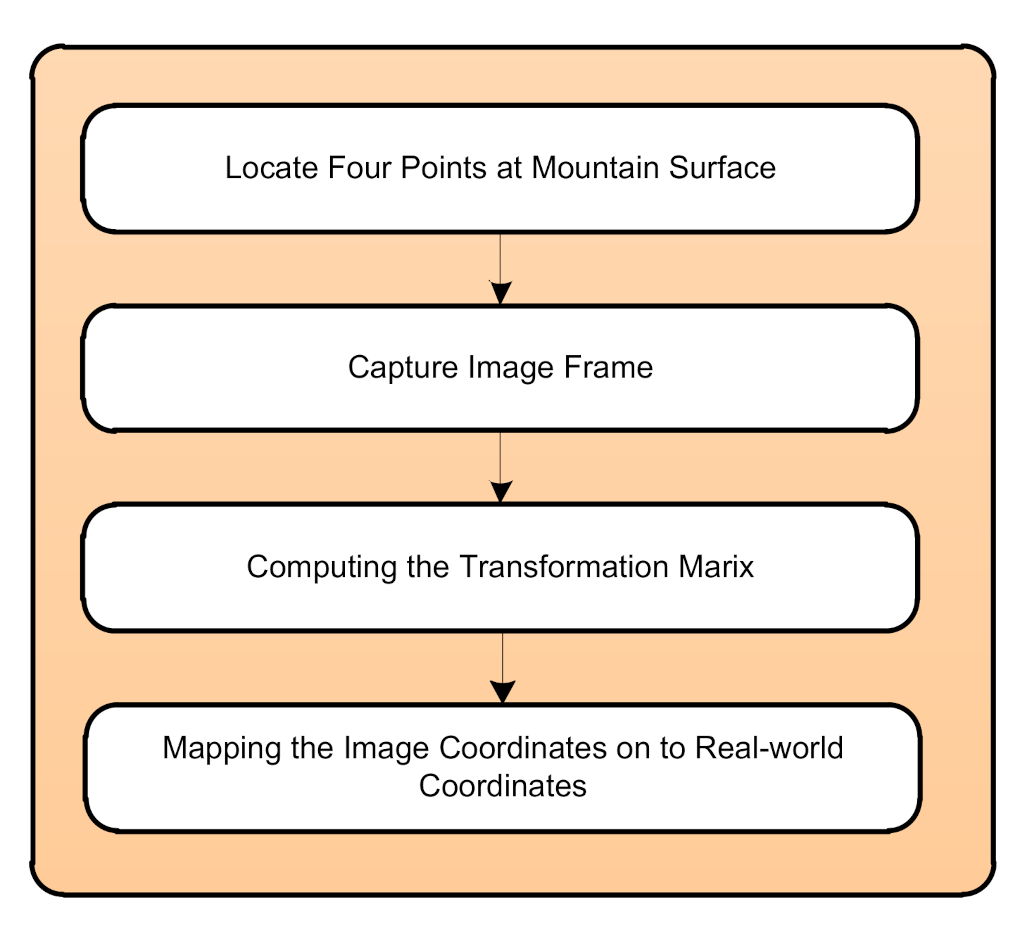
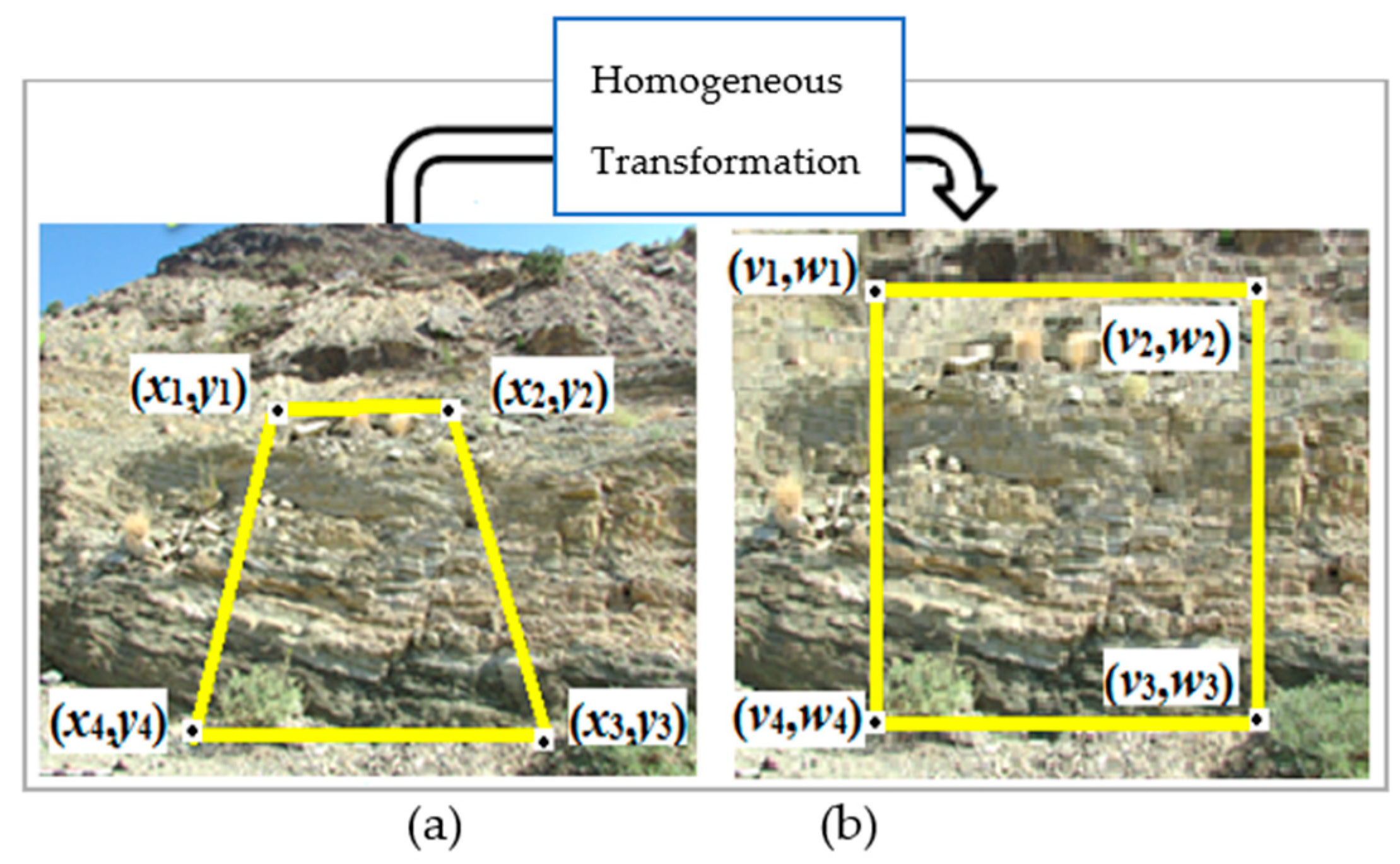
Field of View Calibration
4.5. Rock-Fall Detection Process
4.6. Hybrid Risk Reduction Model
4.7. Risk Reduction Algorithm
| Algorithm 1. To compute a rock-fall risk, classifying the risk level, and performing the rock-fall risk reduction action |
| Step 1: Inputs |
| Read (video frames from camera) |
| Read (weather data from sensors) |
| Step 2: Detect the moving rocks: |
| according to Equation (6) |
| Step 3: Predict the rock fall event p(x): |
| according to Equation (2) |
| Step 4: Compute the rock fall risk |
| according to Equation (3) |
| Step 5: Classify the hazard level: |
| Classifying the hazard level in to three levels |
| if () |
| then Unacceptable level |
| if () |
| then Tolerable level |
| if () |
| then Acceptable level |
| Step 6: Perform the rock-fall risk reduction action |
| Generate light and sound alarms |
| in case of Unacceptable level (Red light+ sound) |
| in case of Tolerable level (Yellow light) |
| in case of Acceptable level (Green light) |
| Save (x1, x2, x3, p(x)) every 30 min |
| Step 7: Return to Step 1 |
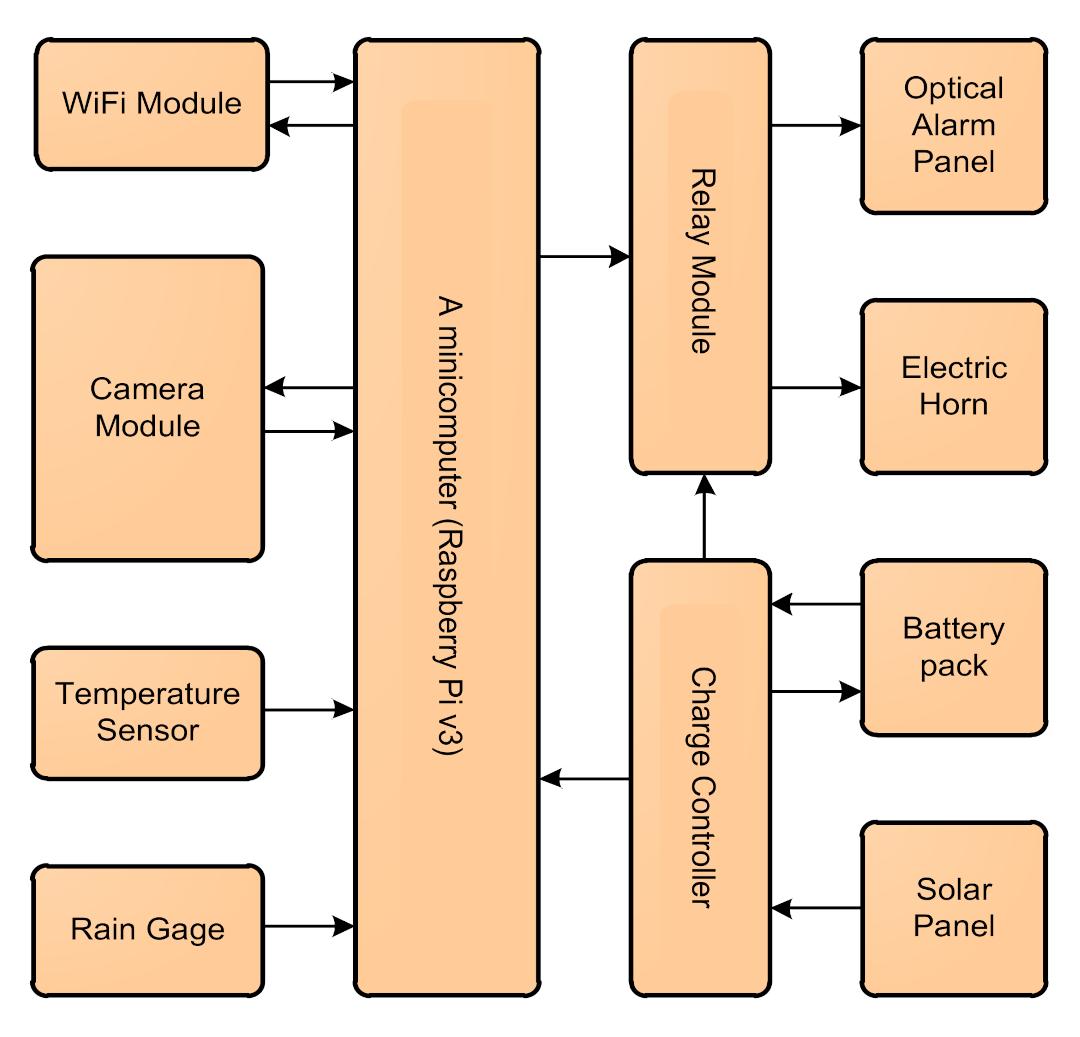
4.8. Hybrid Early Warning System
4.8.1. Hardware Components
4.8.2. Software
4.8.3. Platform Installation
4.9. System Validation
5. Results and Discussion
5.1. Risk Assessment
5.2. Prediction Model Results
5.3. Detection Model Results
5.4. Hybrid Risk Reduction Model Results
5.5. Model Validation
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Z.; Lei, W.; Wu, P.; Li, B.; Fang, Y. A New Efficient Algorithm for Hazardous Material Transportation Problem via Lane Reservation. IEEE Access 2019, 7, 175290–175301. [Google Scholar] [CrossRef]
- Youssef, A.M.; Maerz, N.H. Overview of some geological hazards in the Saudi Arabia. Environ. Earth Sci. 2013, 70, 3115–3130. [Google Scholar] [CrossRef]
- Maerz, N.H.; Youssef, A.M.; Pradhan, B.; Bulkhi, A. Remediation and mitigation strategies for rock fall hazards along the highways of Fayfa Mountain, Jazan Region, Kingdom of Saudi Arabia. Arab. J. Geosci. 2015, 8, 2633–2651. [Google Scholar] [CrossRef]
- Bourrier, F.; Dorren, L.; Nicot, F.; Berger, F.; Darve, F. Toward objective rockfall trajectory simulation using a stochastic impact model. Geomorphology 2009, 110, 68–79. [Google Scholar] [CrossRef]
- Azzoni, A.; La Barbera, G.; Zaninetti, A. Analysis and prediction of rockfalls using a mathematical model. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 709–724. [Google Scholar] [CrossRef]
- Bunce, C.; Cruden, D.; Morgenstern, N. Assessment of the hazard from rock fall on a highway: Reply. Can. Geotech. J. 1998, 35, 410. [Google Scholar] [CrossRef]
- Katz, O.; Reichenbach, P.; Guzzetti, F. Rock fall hazard along the railway corridor to Jerusalem, Israel, in the Soreq and Refaim valleys. Nat. Hazards 2011, 56, 649–665. [Google Scholar] [CrossRef]
- Asteriou, P.; Tsiambaos, G. Effect of impact velocity, block mass and hardness on the coefficients of restitution for rockfall analysis. Int. J. Rock Mech. Min. Sci. 2018, 106, 41–50. [Google Scholar] [CrossRef]
- Dadashzadeh, N.; Duzgun, H.; Yesiloglu-Gultekin, N. Reliability-based stability analysis of rock slopes using numerical analysis and response surface method. Rock Mech. Rock Eng. 2017, 50, 2119–2133. [Google Scholar] [CrossRef]
- Ersöz, T.; Topal, T. Assessment of rock slope stability with the effects of weathering and excavation by comparing deterministic methods and slope stability probability classification (SSPC). Environ. Earth Sci. 2018, 77, 547. [Google Scholar] [CrossRef]
- Sharma, P.; Verma, A.K.; Negi, A.; Jha, M.K.; Gautam, P. Stability assessment of jointed rock slope with different crack infillings under various thermomechanical loadings. Arab. J. Geosci. 2018, 11, 431. [Google Scholar] [CrossRef]
- Shen, W.; Zhao, T.; Dai, F.; Zhou, J.; Xu, N. Investigation of Rockfall Impact Against Gravel Cushion via a Discrete Element Approach. In Proceedings of the China-Europe Conference on Geotechnical Engineering, Cham, Switzerland, 13–16 August 2018; pp. 1521–1525. [Google Scholar]
- Budetta, P. Assessment of rockfall risk along roads. Nat. Hazards Earth Syst. Sci. 2004, 4, 71–81. [Google Scholar] [CrossRef]
- Luciano, P. Quantitative risk assessment of rockfall hazard in the amalfi coastal road. Available online: https://upcommons.upc.edu/handle/2099.1/4937 (accessed on 1 February 2021).
- Sun, S.-Q.; Li, L.-P.; Li, S.-C.; Zhang, Q.-Q.; Hu, C. Rockfall Hazard Assessment on Wangxia Rock Mass in Wushan (Chongqing, China). Geotech. Geol. Eng. 2017, 35, 1895–1905. [Google Scholar] [CrossRef]
- Paronuzzi, P. Rockfall-induced block propagation on a soil slope, northern Italy. Environ. Geol. 2009, 58, 1451–1466. [Google Scholar] [CrossRef]
- Chen, G.; Zheng, L.; Zhang, Y.; Wu, J. Numerical Simulation in Rockfall Analysis: A Close Comparison of 2-D and 3-D DDA. Rock Mech. Rock Eng. 2013, 46, 527–541. [Google Scholar] [CrossRef]
- Li, L.; Lan, H. Probabilistic modeling of rockfall trajectories: A review. Bull. Int. Assoc. Eng. Geol. 2015, 74, 1163–1176. [Google Scholar] [CrossRef]
- Steiakakis, C.; Partsinevelos, P.; Tripolitsiotis, A.; Agioutantis, Z; Mertikas, S.; Vlahou, G. Design and System Architecture of the GEOIM Rockfall Monitoring System. In 5th Interdisciplinary Workshop on Rockfall Protection-RocExs; RocExs: Lecco, Italy, 2014. [Google Scholar]
- Collins, D.S.; Toya, Y.; Hosseini, Z.; Trifu, C.I. Real Time Detection of Rock Fall Events Using a Microseismic Railway Monitoring System; Geohazards: Kingstone, ON, Canada, 2014. [Google Scholar]
- Gracchi, T.; Lotti, A.; Saccorotti, G.; Lombardi, L.; Nocentini, M.; Mugnai, F.; Gigli, G.; Barla, M.; Giorgetti, A.; Antolini, F. A method for locating rockfall impacts using signals recorded by a microseismic network. Geoenviron. Disasters 2017, 4, 26. [Google Scholar] [CrossRef]
- Pieš, M.; Hájovský, R. Use of accelerometer sensors to measure the states of retaining steel networks and dynamic barriers. In Proceedings of the 2018 19th International Carpathian Control Conference (ICCC), Szilvasvarad, Hungary, 28–31 May 2018; pp. 416–421. [Google Scholar]
- Caviezel, A.; Schaffner, M.; Cavigelli, L.; Niklaus, P.; Buhler, Y.; Bartelt, P.; Magno, M.; Benini, L. Design and Evaluation of a Low-Power Sensor Device for Induced Rockfall Experiments. IEEE Trans. Instrum. Meas. 2017, 67, 767–779. [Google Scholar] [CrossRef]
- Lato, M.; Hutchinson, J.; Diederichs, M.; Ball, D.; Harrap, R. Engineering monitoring of rockfall hazards along transportation corridors: Using mobile terrestrial LiDAR. Nat. Hazards Earth Syst. Sci. 2009, 9, 935–946. [Google Scholar] [CrossRef]
- Hartmeyer, I.; Keuschnig, M.; Schrott, L. Implementing a long-term monitoring site focusing on permafrost and rockfall interaction at the Kitzsteinhorn (3.203 m), Hohe Tauern Range, Austria–A status report from the MOREXPERT project. In Conference Volume of the 5th Symposium for Research in Protected Areas; Sekretariat des Nationalparkrates Hohe Tauern: Osttirol, Austria, 2013; Volume 2. [Google Scholar]
- Tonini, M.; Abellán, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014, 8, 95–110. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D. J.; Kromer, R.; Lato, M.; Edwards, T. Effects of sampling interval on the frequency-magnitude relationship of rockfalls detected from terrestrial laser scanning using semi-automated methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Gigli, G.; Morelli, S.; Fornera, S.; Casagli, N. TXT-tool 4.039-3.1: Terrestrial Laser Scanner and Geomechanical Surveys for the Rapid Evaluation of Rock Fall Susceptibility Scenarios. In Landslide Dynamics: ISDR-ICL Landslide Interactive Teaching Tools; Springer: Cham, Switzerland, 2018; pp. 477–491. [Google Scholar]
- Fantini, A.; Fiorucci, M.; Martino, S. Rock falls impacting railway tracks: Detection analysis through an artificial intelligence camera prototype. Wirel. Commun. Mob. Comput. 2017, 2017, 9386928. [Google Scholar] [CrossRef]
- Shirzadi, A.; Saro, L.; Joo, O.H.; Chapi, K. A GIS-based logistic regression model in rock-fall susceptibility mapping along a mountainous road: Salavat Abad case study, Kurdistan, Iran. Nat. Hazards 2012, 64, 1639–1656. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A.; Agliardi, F. Assessment of rockfall susceptibility by integrating statistical and physically-based approaches. Geomorphology 2008, 94, 419–437. [Google Scholar] [CrossRef]
- Abaker, M.; Abdelmaboud, A.; Osman, M.; Alghobiri, M.; Abdelmotlab, A. A Rock-fall Early Warning System Based on Logistic Regression Model. Intell. Autom. Soft Comput. 2021, 28, 843–856. [Google Scholar] [CrossRef]
- Aoun, A.G. Aqabats Shaar and Dele Two Obstacles in the Life Test. 2010. Available online: https://www.okaz.com.sa/article/365122 (accessed on 11 January 2021).
- Al-Andijani, T. The Geological Survey Completes the Study of Rockfalls in Aqabat Shaar in the Asir Region. 2005. Available online: https://www.alriyadh.com/82375 (accessed on 17 January 2021).
- Was. Rockslides Cause the Hurdles of Shaar and Dhula to Be Closed, and “Asir Transport” Begins Their Maintenance. 2020. Available online: https://www.spa.gov.sa/2117551 (accessed on 19 February 2021).
- Delonca, A.; Gunzburger, Y.; Verdel, T. Statistical correlation between meteorological and rockfall databases. Nat. Hazards Earth Syst. Sci. 2014, 14, 1953–1964. [Google Scholar] [CrossRef]
- D’Amato, J.; Hantz, D.; Guerin, A.; Jaboyedoff, M.; Baillet, L.; Mariscal, A. Influence of meteorological factors on rockfall occurrence in a middle mountain limestone cliff. Nat. Hazards Earth Syst. Sci. 2016, 16, 719–735. [Google Scholar] [CrossRef]
- Berti, M.; Martina, M.L.V.; Franceschini, S.; Pignone, S.; Simoni, A.; Pizziolo, M. Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J. Geophys. Res. Space Phys. 2012, 117, F4. [Google Scholar] [CrossRef]
- Collins, B.D.; Stock, G.M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 2016, 9, 395–400. [Google Scholar] [CrossRef]
- Shirzadi, A.; Chapi, K.; Shahabi, H.; Solaimani, K.; Kavian, A.; Bin Ahmad, B. Rock fall susceptibility assessment along a mountainous road: An evaluation of bivariate statistic, analytical hierarchy process and frequency ratio. Environ. Earth Sci. 2017, 76, 152. [Google Scholar] [CrossRef]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating Rockfall Risk: Some Critical Aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef]
- Kaewfak, K.; Huynh, V.-N.; Ammarapala, V.; Ratisoontorn, N. A Risk Analysis Based on a Two-Stage Model of Fuzzy AHP-DEA for Multimodal Freight Transportation Systems. IEEE Access 2020, 8, 153756–153773. [Google Scholar] [CrossRef]
- Wang, X.; Frattini, P.; Crosta, G.B.; Zhang, L.; Agliardi, F.; Lari, S.; Yang, Z. Uncertainty assessment in quantitative rockfall risk assessment. Landslides 2013, 11, 711–722. [Google Scholar] [CrossRef]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Tian, G.; Liu, Y.; Tang, M. Logistic regression analysis of non-randomized response data collected by the parallel model in sensitive surveys. Aust. N. Z. J. Stat. 2019, 61, 134–151. [Google Scholar] [CrossRef]
- Huang, S.; Lyu, Y.; Peng, Y.; Huang, M. Analysis of Factors Influencing Rockfall Runout Distance and Prediction Model Based on an Improved KNN Algorithm. IEEE Access 2019, 7, 66739–66752. [Google Scholar] [CrossRef]
- Wang, X.-T.; Li, S.-C.; Ma, X.-Y.; Xue, Y.-G.; Hu, J.; Li, Z.-Q. Risk Assessment of Rockfall Hazards in a Tunnel Portal Section Based on Normal Cloud Model. Pol. J. Environ. Stud. 2017, 26, 2295–2306. [Google Scholar] [CrossRef]
- Kromer, R.; Lato, M.; Hutchinson, D.J.; Gauthier, D.; Edwards, T. Managing rockfall risk through baseline monitoring of precursors using a terrestrial laser scanner. Can. Geotech. J. 2017, 54, 953–967. [Google Scholar] [CrossRef]
- Park, J.G.; Lee, C. Bayesian rule-based complex background modeling and foreground detection. Opt. Eng. 2010, 49, 027006. [Google Scholar] [CrossRef]
- Budetta, P.; Nappi, M. Comparison between qualitative rockfall risk rating systems for a road affected by high traffic intensity. Nat. Hazards Earth Syst. Sci. 2013, 13, 1643. [Google Scholar] [CrossRef][Green Version]
- Gholizadeh, R.; Londono, S.L.M.; Barahona, M.J.P. Expectation Bayesian Estimation of System Reliability Based on Failures. Methodol. Comput. Appl. Probab. 2018, 21, 367–385. [Google Scholar] [CrossRef]
- Szydłowski, T.; Surmiński, K.; Batory, D. Drivers’ Psychomotor Reaction Times Tested with a Test Station Method. Appl. Sci. 2021, 11, 2431. [Google Scholar] [CrossRef]
- Zeng, G. On the confusion matrix in credit scoring and its analytical properties. Commun. Stat. Theory Methods 2019, 49, 2080–2093. [Google Scholar] [CrossRef]
- Nesticò, A.; He, S.; De Mare, G.; Benintendi, R.; Maselli, G. The ALARP Principle in the Cost-Benefit Analysis for the Acceptability of Investment Risk. Sustainability 2018, 10, 4668. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Average vehicle lengths | 5.4 m |
| Average number of vehicles driving on the road every day (NV) | 6245 vehicles |
| Average vehicle speed range (Vv) | 70 to 90 Km/h |
| Vulnerability of the vehicle regarding rock-fall incidents V(D:T) | 1 |
| Rock-fall frequency (fh) | 0.07 Per day |
| Independent Variable | Coefficient (β) | Std. Error | Wald | Significant Probability |
|---|---|---|---|---|
| Slope-angle | 0.306 | 0.132 | 5.419 | 0.020 |
| Rainfall-rate | 0.425 | 0.165 | 6.669 | 0.010 |
| Temperature variation | 0.915 | 0.421 | 4.712 | 0.030 |
| Rock Code | Rock Size cm3 | Detect Object | Disappearance Frequency N | Traceability |
|---|---|---|---|---|
| A1 | 24.53 | 0 | 0 | 0.0000 |
| A2 | 37.06 | 1 | 21 | 0.9475 |
| A3 | 49.00 | 1 | 15 | 0.9625 |
| B1 | 160.93 | 1 | 14 | 0.9650 |
| B2 | 196.25 | 1 | 12 | 0.9700 |
| B3 | 184.00 | 1 | 12 | 0.9700 |
| C1 | 382.68 | 1 | 10 | 0.9750 |
| C2 | 508.32 | 1 | 7 | 0.9825 |
| C3 | 657.04 | 1 | 6 | 0.9850 |
| D1 | 1052.97 | 1 | 5 | 0.9875 |
| D2 | 1012.00 | 1 | 5 | 0.9875 |
| D3 | 1235.05 | 1 | 4 | 0.9900 |
| E1 | 1880.49 | 1 | 3 | 0.9925 |
| E2 | 2297.01 | 1 | 3 | 0.9925 |
| E3 | 3041.87 | 1 | 2 | 0.9950 |
| Rock Code | Rock Size cm3 | Detect Object | Disappearance Frequency N | Traceability |
|---|---|---|---|---|
| A1 | 24.53 | 0 | -- | 0.0000 |
| A2 | 37.06 | 0 | -- | 0.0000 |
| A3 | 49.00 | 0 | -- | 0.0000 |
| B1 | 160.93 | 1 | 22 | 0.9450 |
| B2 | 196.25 | 1 | 20 | 0.9500 |
| B3 | 184.00 | 1 | 20 | 0.9500 |
| C1 | 382.68 | 1 | 16 | 0.9600 |
| C2 | 508.32 | 1 | 14 | 0.9650 |
| C3 | 657.04 | 1 | 13 | 0.9675 |
| D1 | 1052.97 | 1 | 11 | 0.9725 |
| D2 | 1012.00 | 1 | 11 | 0.9725 |
| D3 | 1235.05 | 1 | 11 | 0.9725 |
| E1 | 1880.49 | 1 | 9 | 0.9775 |
| E2 | 2297.01 | 1 | 7 | 0.9825 |
| E3 | 3041.87 | 1 | 6 | 0.9850 |
| Parameter | Value |
|---|---|
| Driver reaction time | 0.4 to 2 s |
| Brake Engagement time | 2 s |
| Average acceleration | 10 m/s2 |
| Average vehicle lengths | 5.4 m |
| Average number of vehicles driving on the road every day (NV) | 6245 vehicles |
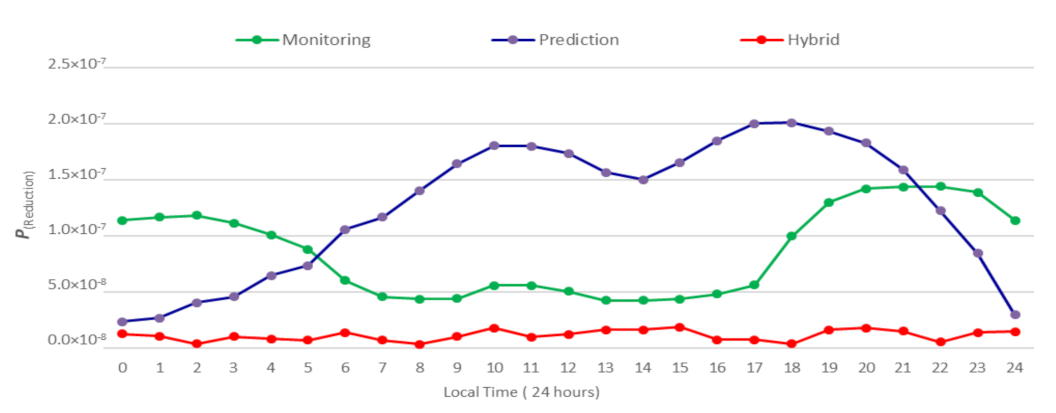
| Monitoring | Prediction | Hybrid | |
|---|---|---|---|
| Lowest | 4.26 × 10−8 | 2.35 × 10−8 | 3.38 × 10−9 |
| Highest | 1.44 × 10−7 | 2.01 × 10−7 | 1.88 × 10−8 |
| Average | 8.62 × 10−8 | 1.27 × 10−7 | 1.13 × 10−8 |
| Data Type | Observed Rock-Fall Even | Predicted Rock-Fall Even | Percentage C | |
|---|---|---|---|---|
| Not occur 0 | Occurs 1 | |||
| Training Data | Not occur 0 | TN = 69 | FP = 11 | 86.3% |
| Occurs 1 | FN = 16 | TP = 38 | 70.4% | |
| Overall Percentage | 79.9% | |||
| Validation data | Not occur 0 | TN = 32 | FP = 5 | 86.5% |
| Occurs 1 | FN = 6 | TP = 15 | 71.4% | |
| Overall Percentage | 81.0% | |||
| Test Period | TP FN | FP N | Sensitivity % | Specificity % | Accuracy % | |
|---|---|---|---|---|---|---|
| 1 | 19 1 | 3 | 17 | 95 | 85 | 90 |
| 2 | 18 2 | 1 | 19 | 90 | 95 | 92.5 |
| 3 | 17 3 | 3 | 17 | 85 | 85 | 85 |
| 4 | 19 1 | 1 | 19 | 95 | 95 | 95 |
| 5 | 18 2 | 0 | 20 | 90 | 100 | 95 |
| 6 | 16 4 | 1 | 19 | 90 | 95 | 87.5 |
| 7 | 17 3 | 0 | 20 | 80 | 100 | 92.5 |
| 8 | 18 2 | 3 | 17 | 90 | 85 | 87.5 |
| 9 | 18 2 | 2 | 18 | 90 | 90 | 90 |
| Monitoring | Prediction | Hybrid | |
|---|---|---|---|
| Sensitivity | 71.4% | 88.8% | 96.7% |
| Specificity | 86.3% | 92.2% | 99.1% |
| Accuracy | 81.0% | 90.6 | 97.9% |
| Reliability | 0.79 | 0.9 | 0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmaboud, A.; Abaker, M.; Osman, M.; Alghobiri, M.; Abdelmotlab, A.; Dafaalla, H. Hybrid Early Warning System for Rock-Fall Risks Reduction. Appl. Sci. 2021, 11, 9506. https://doi.org/10.3390/app11209506
Abdelmaboud A, Abaker M, Osman M, Alghobiri M, Abdelmotlab A, Dafaalla H. Hybrid Early Warning System for Rock-Fall Risks Reduction. Applied Sciences. 2021; 11(20):9506. https://doi.org/10.3390/app11209506
Chicago/Turabian StyleAbdelmaboud, Abdelzahir, Mohammed Abaker, Magdi Osman, Mohammed Alghobiri, Ahmed Abdelmotlab, and Hatim Dafaalla. 2021. "Hybrid Early Warning System for Rock-Fall Risks Reduction" Applied Sciences 11, no. 20: 9506. https://doi.org/10.3390/app11209506
APA StyleAbdelmaboud, A., Abaker, M., Osman, M., Alghobiri, M., Abdelmotlab, A., & Dafaalla, H. (2021). Hybrid Early Warning System for Rock-Fall Risks Reduction. Applied Sciences, 11(20), 9506. https://doi.org/10.3390/app11209506






