A Hybrid Spatial Indexing Structure of Massive Point Cloud Based on Octree and 3D R*-Tree

Abstract

The spatial index structure is one of the most important research topics for organizing and managing massive 3D Point Cloud. As a point in Point Cloud consists of Cartesian coordinates $(x,y,z)$, the common method to explore geometric information and features is nearest neighbor searching. An efficient spatial indexing structure directly affects the speed of the nearest neighbor search. Octree and kd-tree are the most used for Point Cloud data. However, octree or KD-tree do not perform best in nearest neighbor searching. A highly balanced tree, 3D R*-tree is considered the most effective method so far. So, a hybrid spatial indexing structure is proposed based on octree and 3D R*-tree. In this paper, we discussed how thresholds influence the performance of nearest neighbor searching and constructing the tree. Finally, an adaptive way method adopted to set thresholds. Furthermore, we obtained a better performance in tree construction and nearest neighbor searching than octree and 3D R*-tree.

1. Introduction

Currently, the study of autonomous vehicles and robots is a research hotspot. With the development of computer technology and the increasing demand for digitalization, the 3-dimension (3D) model has captured increasing research attention for decades [1]. For example, the 2D map which is widely used in robots cannot support robots to complete complex tasks, such as scene understanding. The 3D map becomes more and more significant for a robot. The 3D data is collected by 3D LiDAR, RGB-D camera, etc., which run at very high frequency. It is inevitable that huge amounts of data will be generated. So, it is urgent to choose an effective organizing and management method for 3D data.

The 3D coordinates $(x,y,z)$ of each point correspond to the geometry component of the Point Cloud, which may contain one or more additional components (attributes), such as color, reflectance, and normal vectors, etc. Point Cloud data is a typical structure of 3D data, which is the set of points with 3D coordinates. The 3D sensors are widely used in various applications, and the technology is relatively mature, while the data processing technology lags behind to some extent. Due to the massive data, disorder, irregularity, sparsity, high resolution, and lack of topological relations or texture information [2], the Point Cloud data processing is complex and challenging. Most feature analyses are based on the relationship between point and neighbors; therefore, Nearest Neighbor ($NN$) search is frequently conducted. The efficiency of query operation directly affects processing Point Cloud data [3]. Furthermore, the 3D coordinate is the primary form of 3D vector data, the basis of 3D geometric modeling, and the object of operation and analysis on vector space. So, it is of great significance to efficiently organize the Point Cloud data.

Currently, the hierarchical partition is usually used to subdivide Point Cloud data space, and the most commonly used data structures are Grid, octree [4], KD-tree [5] and R-tree [6]. Grid divides the data space equally into grids with a fixed resolution, disregarding whether points exist inside or not. So, it is easy to implement. Paper [7] adopts a hash-like structure for storing a multi-dimensional spatial data, and it has the potential to process Point Cloud data. Octree is a 3-dimension extension of Quad-tree [8] or an adaptive Grid structure, and is widely recognized as a promising representation of Point Cloud [9]. It can divide the data space rigidly (i.e., with a fixed target depth or leaf size) or adaptively [10]. If the Point Cloud data distributes uniformly, octree can achieve a better retrieval performance. Otherwise, the octree is unbalanced, such that it will be difficult to perform query or other operations effectively. Since the most frequent operation of Point Cloud data is $NN$ searching during subsequent processing, it is important to design an efficient index structure to increase efficiency of spatial query [11]. For this reason, a hybrid spatial index method combining octree and R*-tree [12] to organize Point Cloud data is proposed.

2. Related Work

2.1. Single Indexing Structure

With the widely utilized of 3D sensors, the volume of Point Cloud data is increasing dramatically. Point Cloud data organization and management have been attracting more and more attention, whose core technology are the spatial index methods. Among these methods, R-tree is a highly balanced tree structure in theory. However, the query efficiency is expected to improve because the overlaps between nodes are ignored, which affect the query efficiency greatly. R+-tree [13] intends to decrease the overlaps and has improved the R-tree to some extent. R*-tree [12] is the best-improved version of R-tree so far, which decreases the number of nodes and the area of overlaps between nodes. Hilbert R-tree [14] utilizes Hilbert-curve to sort R-tree nodes, and improves the storage utilization. Among these spatial index methods, octree and KD-tree are the most frequently used in 3D Point Cloud data organization [15]. In fact, octree performs badly if the data distributes non-uniformly, and KD-Tree would be very deep when data is huge. The single indexing method is no longer satisfies the real-time requirement, and the hybrid indexing method comes into being.

2.2. Hybrid Indexing Structure

Although the single index methods mentioned above are used widely and some improved versions are put forward, there are certain defects and limitations insoluble, such as the tree is too deep or unbalanced and so on. To overcome the shortcoming of single index methods, more and more scholars try to design hybrid index technology. Some proposed strategies are combining with different index structures organically and achieve a better performance in query operation [9,11,16,17,18,19].

KDB-tree [16], combining KD-tree and B-tree, builds a balanced tree by dynamically adjusting. Thereby, it improves the query speed. KD-octree [17], combining KD-tree and octree, constructs a relatively balanced tree using KD-tree, and then constructs octree at each leaf node of KD-tree. In this way, it overcomes the disadvantage that the tree is too deep and cannot query quickly. Octree forest [20] intends to organize Point Cloud data to obtain a better performance of query. Meanwhile, it is just a truncated octree which cuts the octree off at a certain level and then obtains the octree forest. Paper [21] proposed a spatial index method for 3D Point Cloud data. The method consists of two levels; the top-level is a octree and the bottom-level is a set of R-tree corresponding to the leaf nodes of octree. Meanwhile, the leaf nodes are encoded and sorted with Morton-code. There are also other similar methods; while these methods’ performances are almost on a par, each of them has strengths and weaknesses. Therefore, the hybrid index methods need to be further researched.

3. Materials and Methods

This section is arranged as follows: Octree and 3D R*-tree are described firstly, a new encoding method is proposed to associate 3D R*-tree with octree. Furthermore, then the hybrid structure is proposed to improve the performance of the spatial index. Finally, a $kNN$ searching algorithm is designed refer to the hybrid structure. The $kNN$ searching is a basic algorithm to process Point Cloud data, such as normal estimation, feature extraction, etc. So, $kNN$ is mainly used as a performance evaluation index of different structures. Two types of Point Cloud data are used in the next section, randomly generated and acquired by an RGB-D camera scanning a lab. Random data is used to test the performance under different data sizes (1K, 4K, 16K, 64K, 256K), where 1K = 1000 points.

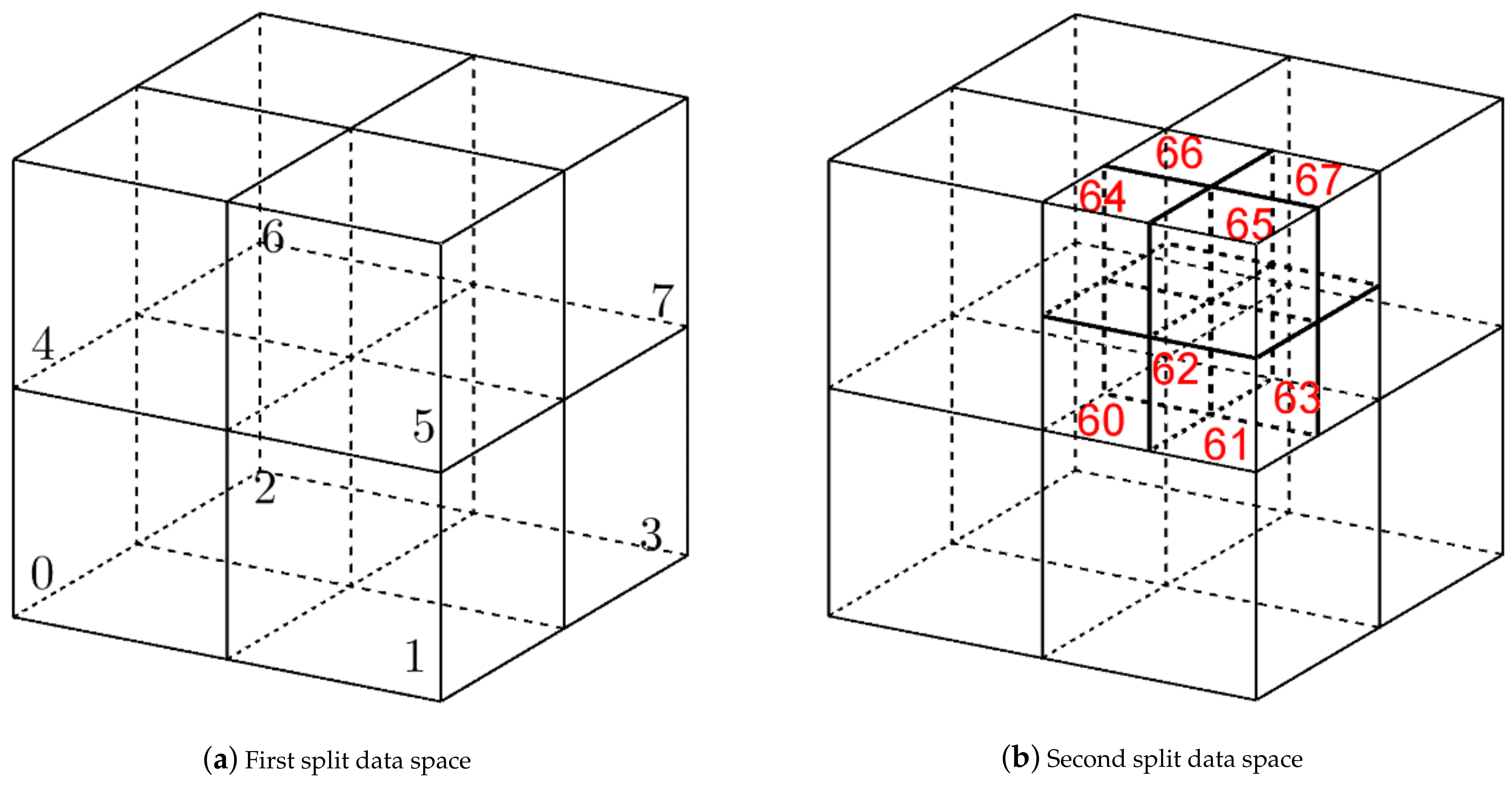
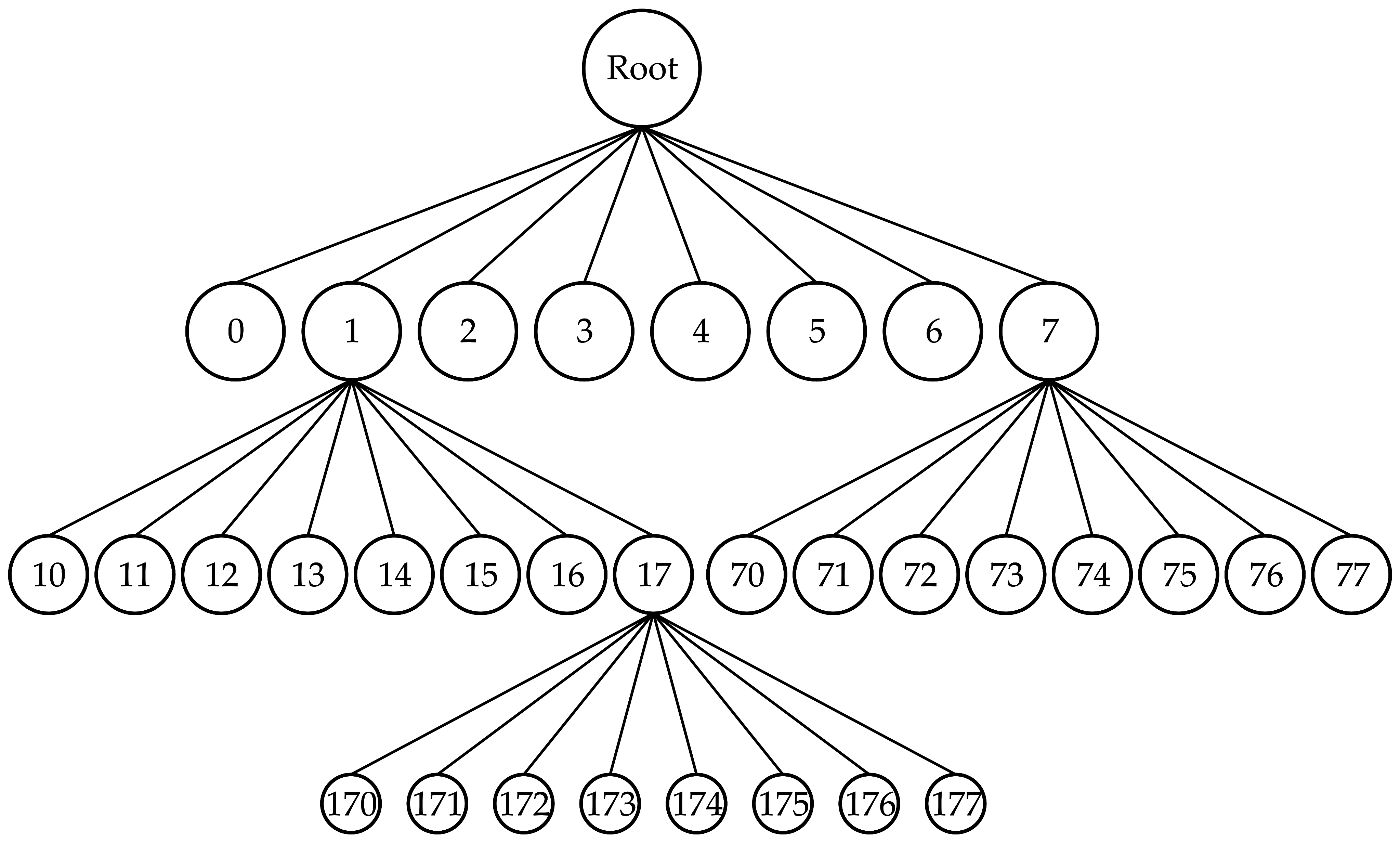
3.1. Octree Encoding/Decoding

Generally, octree includes regular octree and linear octree [22]. The former stores data in leaf nodes and non-leaf nodes, while the latter only stores data in leaf nodes. Reasonable thresholds can limit the depth of the tree. At the same time, when the octree is constructed, Morton-code [23] is used to encode and sort leaf nodes of octree, aiming at improving the efficiency of Point Cloud data retrieval. Currently, the octree’s threshold (depth or leaf size) setting is usually fixed or adaptive experientially. In the data structure research, through the judgment of threshold conditions and related recursive loops, the final goal of 3D Point Cloud data integration is to achieve a fast query.

Octree is a 3D extension of Quad-tree [24] and inherits the fast partition of Quad-tree. It can be used to model 3D geometry and space, which is essential in space planning [25], computer animation, and machine vision [26]. Octree subdivides 3D space into $2^n\times 2^n\times 2^n$ subspaces, where n is the octree depth. Data space is divided into eight subspaces if the space contains geometric object entities, and each subspace is subdivided into eight sub-subspaces if there are entities in subspace, so on and so forth until the terminating condition is reached. Octree is considered as an important revolution of data structure in real 3D space partition. When the tree is constructed, leaf nodes are encoded with a certain regularity to achieve efficient retrieval of Point Cloud data, such as Morton- code [27], Gray-code [28], Hilbert-code [14], etc.

Regular octree occupies a vast amount of memory. The recursively generating and querying operation makes it very time-consuming, especially when the volume of data is so large that the tree is deep. Linear octree [22] improves regular octree and speeds up query operation. It only stores data in leaf nodes. One of the most important things is that the nodes are stored in linear arrays or linear chains according to locate code. Linear octree’s nodes are generated fast and don’t need to change tree greatly when a particular node is divided into smaller sub cubes. Since a linear table is created corresponding to the node, it is more suitable for massive Point Cloud data processing and modeling. For computing locate code, Morton-code is used widely benefiting from the implementation easily by bit operation.

Octree’s leaf nodes are encoded by Morton-code. Assuming the depth of octree is n, an n bits $octal$ number can represent a node uniquely. For convenience, an n bits $decimal$ number is used. In fact, $M=m_{n-1}\cdots m_k\cdots m_2{m}_1{m}_0$ is the same regardless of octal or decimal. The code of a node consists of the code of its parent node’s and its own. If a node with code $m_p$ is split into eight sub-nodes, the code of sub-nodes can be calculated by $M=10·m_p+m_i$, where $m_i$ is the code of i-th sub-node and decided by the z-order as shown in Figure 1. Figure 2 shows the Morton-code of octree nodes.

As mentioned earlier, octree will become unbalanced when processing non-uniformly distributed data. We limit the depth of octree and build 3D R*-tree at each leaf node. Figure 1 shows the process of how octree splits the data space and Morton-code encodes nodes. The location code (Morton-code) represents the identifier (id) of the 3D R*-tree.

Compared with kd-tree, octree reduces the height of the tree. Given a point, we can quickly locate the node in which it lays by computing its Morton-code other than traverse the whole tree like kd-tree does. For robots or unmanned aerial vehicles (UAV), the distribution of Point Cloud is non-uniformly, which is obtained by LiDAR or RGB-D camera and represents the environment model of the real world. The threshold $leaf\_size$ setting is crucial to the performance of octree. If $leaf\_size$ is set too large, query operation will be slowed down, if it is too small, the octree will be deeper dramatically and influence the efficiency. Octree is more suitable for regular data, which is a well-known fact. However, the Point Cloud obtained from sensors (LiDAR, RGB-D camera) which are mounted on robot or UAV is always irregular.

3.2. 3D R*-Tree

R- tree, a hierarchical data structure, extends B-tree [29] from 1 to dimension to k-dimension space. Consequently, it is a highly balanced tree and a dynamic structure inherited from B-tree. It is a famous indexing method for multi-dimensional data for spatial query operation. Basic operations can be conducted conveniently, such as inserting, deleting, and querying. Each node in the tree stores the Minimum Bounding k-dimensional Rectangle (MBR) covering its child nodes rather than the actual data, thereby saving the memory space by 50% at least. However, R-tree ignores the overlaps between MBRs and results in increasing the time of querying. In classical R-tree, if two objects lay in two different nodes, it is impossible to merge them into one node, albeit they are near in spatial. Because it follows the principle of minimizing area, ignoring other factors such as overlap.

By researching what factors affect the R-tree’s performance, R*-tree [12] is proposed to minimize the rectangle area, overlaps, and margins of the rectangle. R*-tree makes the MBR of node approaching a square and greatly improves the performance. Generally, R*-tree is recognized as the most efficient spatial querying method [13], which is why we adopt 3D R*-tree.

We hope 3D R-tree is a dynamic structure like R-tree, which is considered as a most promising spatial indexing method and has faster query efficiency than octree [30,31]. As 2D R*-tree does, 3D R*-tree also aims at improving query efficiency based on 3D R-tree by minimizing the overlaps, volume of the Minimum Bounding Box (MBB). We hope that points closed in 3D space are in the same MBB. However, the overlap between MBBs becomes highly complex because the shape of 3D objects or distribution of 3D points will become more diverse. 3D R*-tree consists of intermediate nodes and leaf nodes. Unlike octree or kd-tree, nodes of the 3D R*-tree include node ID and MBB $(x_{min},y_{min},z_{min},x_{max},y_{max},z_{max})$.

An example of 3D R*-tree [32] subdividing the Point Cloud data spatial is shown in Figure 3, the dataset is $table\_scene\_lms400.pcd$ [33], a commonly used dataset. We can see that the overlap becomes more and more severe when the tree is deeper, despite the R*-tree adopting a series of rules to minimize the overlaps. In brief, although 3D R*-tree is faster in querying than octree or kd-tree, it is also tough to query when Point Cloud data becomes huge. This is why we design a hybrid structure based on octree and 3D R*-tree.

In conclusion, among the index methods for Point Cloud management, octree is unbalanced in most cases. Kd-tree is too deep when managing large-scale Point Cloud data, although we did not describe the detail above. The 3D R*-tree will overlap each other when the tree becomes deep. The single indexing methods can hardly meet the requirement of managing large-scale Point Cloud data. So, many hybrid index methods are proposed in recent years. Such as combining 3D R*-tree and kd-tree [18], octree and 3D R*-tree [19], quad-tree and 3D R-tree [31], kd-tree and octree [11], octree and kd-tree [3,34], quad-tree and octree [35], etc. The main idea is to improve the imbalance of tree and speed up the query operation. In this paper, a hybrid indexing method based on octree and 3D R*-tree is proposed for the same purpose.

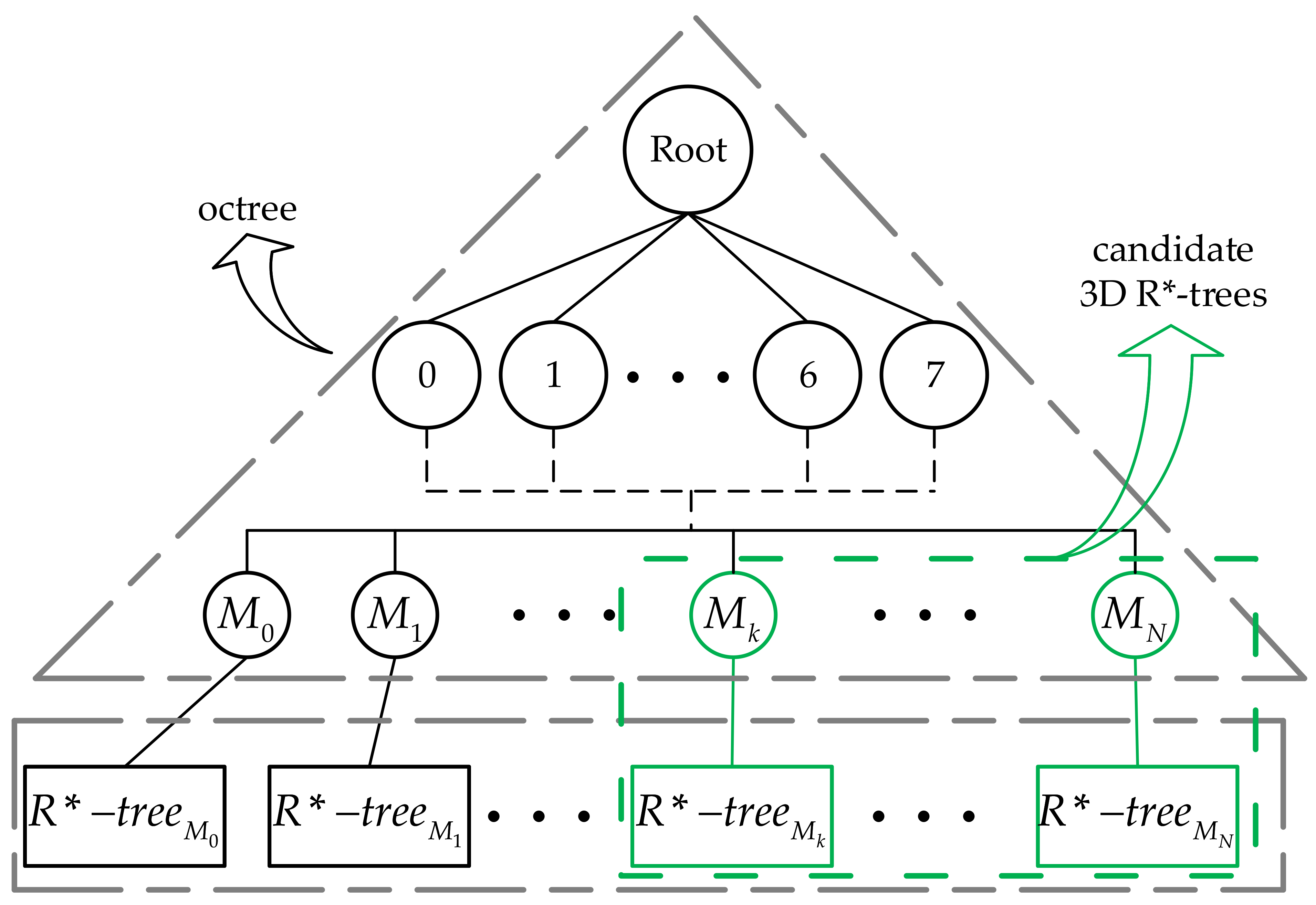
3.3. Hybrid Octree and 3D R*-Tree

This part will describe the details of hybrid spatial index technology. Two steps are needed to build the hybrid structure, (1) building an octree on the whole Point Cloud data, (2) constructing 3D R*-tree on each leaf node of octree. Thresholds: $leaf\_size$ and $dept{h}_{max}$ are required for building octree, $Childre{n}_{max}$ is required for 3D R*-tree, where $leaf\_size$ denotes the maximum number of points in a node, $dept{h}_{max}$ denotes the maximum depth of octree and $Childre{n}_{max}$ denotes the maximum capacity of a 3D R*-tree node. $node\_size$ denotes the actual number of points in the current node and $depth$ denotes the actual depth of the octree. These thresholds are not as easy to set as previously thought. If set too small, computation will increase greatly. If set too large, it seems to be meaningless to establish the tree structure. Generally, thresholds are set according to the distribution of Point Cloud data and the number of searching neighbors. If $k>Childre{n}_{max}$, it is impossible to find k neighbors in the same node and extra time will be taken to search adjacent nodes to find neighbors meeting the requirement.

Concrete steps for constructing hybrid indexing method are described as follows:

(1)

Find the maximum and minimum of x, y, and z over the whole Point Cloud data which are denoted as $(x_{min},x_{max},y_{min},y_{max},z_{min},z_{max})$. The root node is denoted as $(\frac{x_{min}+x_{max}}{2},\frac{y_{min}+y_{max}}{2},\frac{z_{min}+z_{max}}{2})$. Initializing octree: $current\_node=root$;

(2)

For each $current\_node$, judging $node\_size>leaf\_size$ and $depth<dept{h}_{max}$, if so, subdivide $current\_node$ into eight sub-nodes uniformly. Otherwise, stop subdividing. Computing Morton-code for all leaf nodes and sorting them by code. Go to (3);

(3)

A set of 3D R*-tree are constructed on each leaf node with $id$. Initialize 3D R*-tree: $roo{t}_{id}=leaf\_nod{e}_{id}$. Furthermore, insert the points inside $leaf\_nod{e}_{id}$ into corresponding 3D R*-tree. At the same time, judge if $node\_size>Childre{n}_{max}$. If so, implying that nodes in 3D R*-tree are too few to insert all points, then increase the number of cluster centers and dividing nodes of 3D R*-tree dynamically, until the number of points inserted is no more than maximum volume. Go to (4);

(4)

Judge if $point{s}_{insert}<leaf\_siz{e}_{id}$, where $point{s}_{insert}$ is the number of points inserted into corresponding 3D $R^{*}$-$tre{e}_{id}$. If so, go to (3), otherwise, 3D $R^{*}$-$tre{e}_{id}$ is constructed.

The overall hybrid structure is shown in Figure 4. The top-level is octree, and the bottom-level is a set of 3D R*-trees.

3.4. kNN Search

As it is a two-level structure that spatial indexing has proposed in this paper, the $kNN$ searching algorithm is divided into two steps, octree searching and 3D R*-tree searching. Candidate 3D R*-trees are chosen by searching along octree, and then $kNN$ are found by searching along 3D R*-tree.

3.4.1. Octree Searching

To search $kNN$ efficiently, we defined a searching ball $B_r$ which takes query point $(x_{query},y_{query},z_{query})$ as the center and r as the radius, an $octant$ with center $(x_{center},y_{center},z_{center})$ and edge length $(2l_x,2l_y,2l_z)$. There are three cases of relationship between $B_r$ and $octant$ as follows:

(1)

$B_r$ lays inside $octant$;

(2)

$B_r$ contains $octant$;

(3)

$B_r$ intersects with $octant$.

Criteria of them as follows:

(1)

Meeting $|x_{query}-x_{center}|<l_x$, $|y_{query}-y_{center}|<l_y$ and $|z_{query}-z_{center}|<l_z$ at the same time, then $B_r$ lays inside $octant$.

(2)

Meeting $\left(\right|x_{query}-x_{center}|+l_x{)}^2+\left(\right|y_{query}-y_{center}|+l_y{)}^2+\left(\right|z_{query}-z_{center}{|+l_z)}^2<r^2$, then $B_r$ contains $octant$.

(3)

It is a little complicated for this case. Three criteria are included:

(1)

There are three inequalities: $|x_{query}-x_{center}|>r+l_x$, $|y_{query}-y_{center}|>r+l_y$, $|z_{query}-z_{center}|>r+l_z$. If one of them holds, then $B_r$ do not intersect with $octant$;

(2)

There are three inequalities: $|x_{query}-x_{center}|<l_x$, $|y_{query}-y_{center}|<l_y$, $|z_{query}-z_{center}|<l_z$. If none or one of them holds, then $B_r$ do not intersect with $octant$;

(3)

If $\sqrt{x_d^2+y_d^2+z_d^2}\ge r$, then $B_r$ do not intersect with $octant$. Where $x_d=max\left(\right|x_{query}-x_{center}|-l_x)$, $y_d$ and $z_d$ are likewise.

If and only if none of the three criteria above holds, $B_r$ intersects with $octant$.

In conclusion, given a searching ball $B_r$ and a query point $(x_{query},y_{query},z_{query})$, octree searching finds all candidate 3D R*-trees corresponding to encoded leaf nodes which intersect with $B_r$, contained by $B_r$ or contains $B_r$, as shown in Figure 4. The 3D R*-trees corresponding to the leaf nodes will be searched to find $kNN$.

3.4.2. 3D R*-Tree Searching

MBR-based $NN$ search algorithm is proposed in [36], in which two metrics $MINDIST$ and $MINMAXDIST$ are introduced to avoid traversing the entire tree in finding the k nearest neighbors. The algorithm described briefly in Algorithm  1, in which the symbols are defined as: $p_i$ is the i-th dimensional coordinate value of point p, $R(s,t)$ is a $MBR$ where s can be represented as $(x_{min},y_{min},z_{min})$, t can be represented as $(x_{max},y_{max},z_{max})$.

Two metrics are defined as follows:

$MINDIST(p,R)={\displaystyle \sum _{i=1}^3}{|p_i-r_i|}^2$, where

$$r_i=\left\{\begin{array}{cc}{s}_i\hfill & \mathrm{if}{p}_i<s_i,\hfill \\ t_i\hfill & \mathrm{if}{p}_i>t_i,\hfill \\ p_i\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

$MINMAXDIST(p,R)=\underset{k=1,2,3}{min}(|p_k-r{m}_k{|}^2+{\displaystyle \sum _{i=1,i\ne k}^3}|p_i-r{M}_i{|}^2)$ where

$$r{m}_k=\left\{\begin{array}{cc}{s}_k\hfill & \mathrm{if}{p}_k\le s_k+{t_k}^2,\hfill \\ t_k\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

and

$$r{M}_i=\left\{\begin{array}{cc}{s}_i\hfill & \mathrm{if}{p}_k\ge s_i+{t_i}^2,\hfill \\ t_i\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

To date, the hybrid spatial index tree is constructed, and the search algorithm is designed. In the next step, we will show the superiority of the proposed hybrid spatial index method from the perspective of experimental data.

Algorithm 1$kNN$ search

Require:$current\_node$, query point p, number of neighbors k

if $current\_node$ is $leaf\_node$ then

compare distance from p to all points in $current\_node$

update the $current\_best$ $kNN$ and $current\_bestdistance$(top k)

else

generate Active Branch List(ABL): sort the $MBR$s contained in $current\_node$ according $MINDIST$ in ascending order

compute $kMM$: sort $MINMAXDIST$ in ascending order and set $kMM$ to be the k-th $MINMAXDIST$, in other word, $kMM=sorted\left(MINMAXDIST\right)\left[k\right]$

for i = 1:len(ABL) do

if $MINDIST$ of $MBR\left[i\right]$ is greater than $kMM$ then

discard $MBR\left[i\right]$ and other nodes whose $MINDIST$ is greater than $MINDIST\left[i\right]$

break

end if

end for

for i=1:len(ABL) do

search $kNN$ in $MBR\left[i\right]$

end for

for i=1:len(ABL) do

if $MINDIST$ of $MBR\left[i\right]$ is greater than $current\_bestdistance\left[k\right]$ then

discard $MBR\left[i\right]$ and other nodes whose $MINDIST$ is greater than $MINDIST\left[i\right]$

end if

end for

end if

4. Results

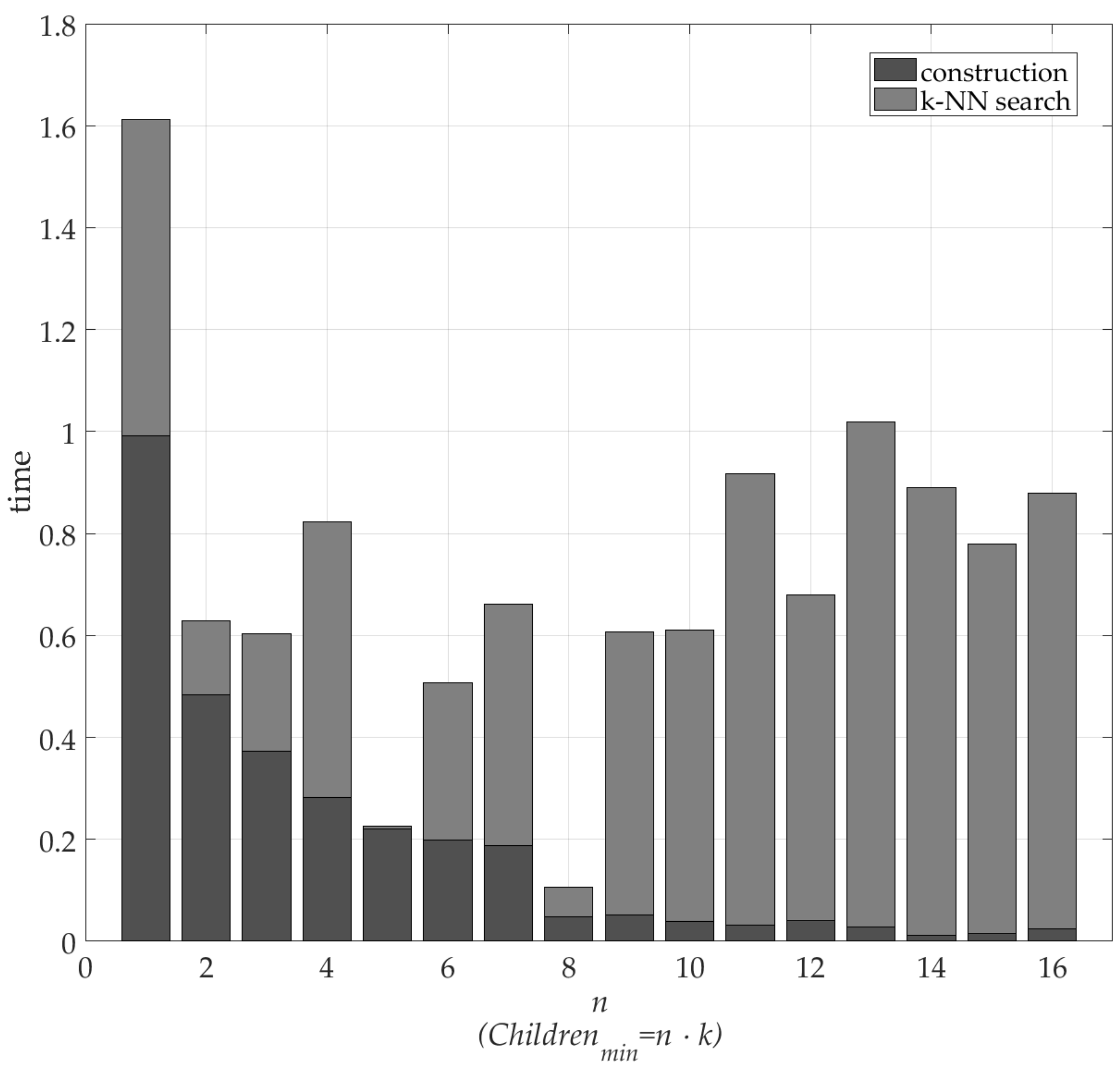
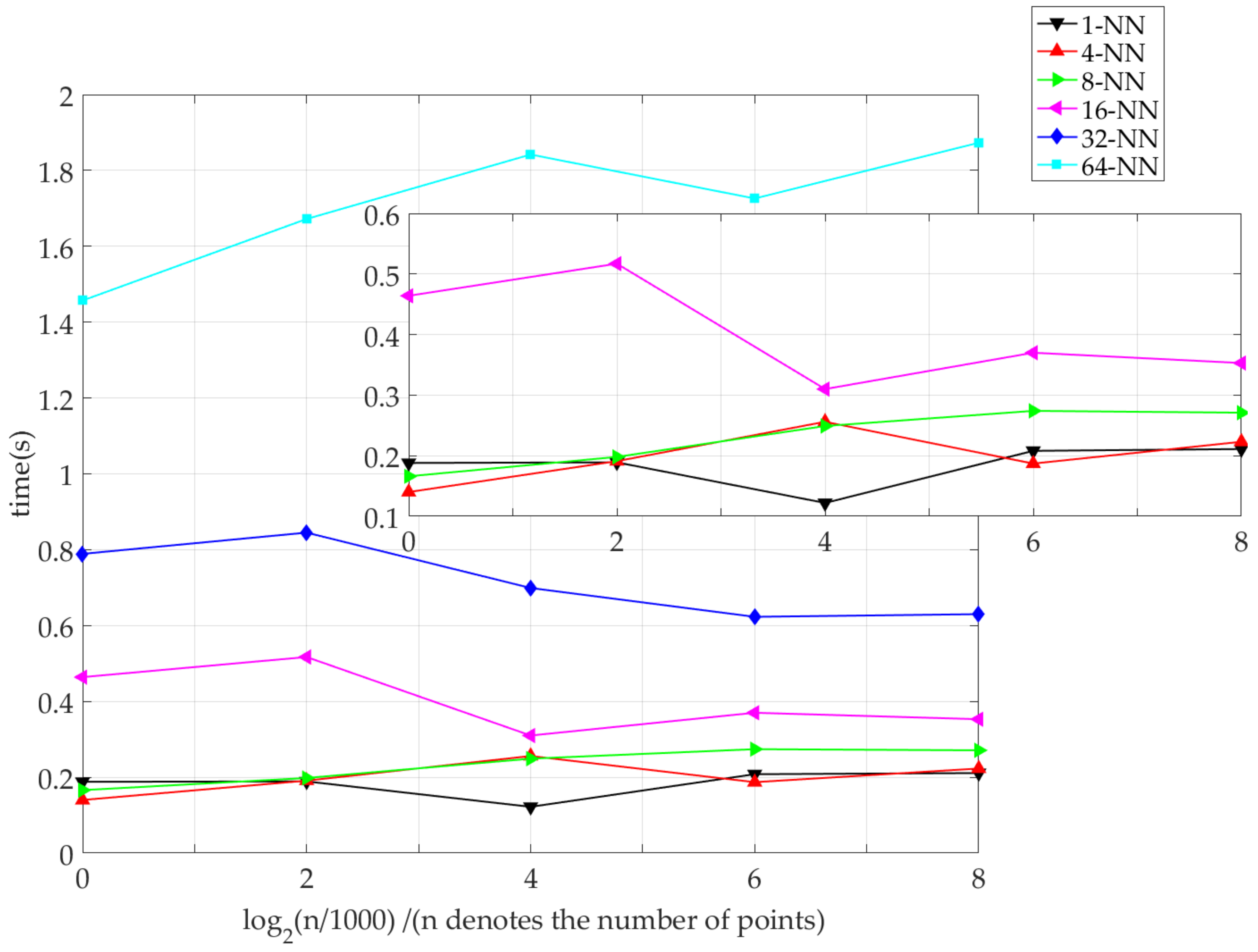
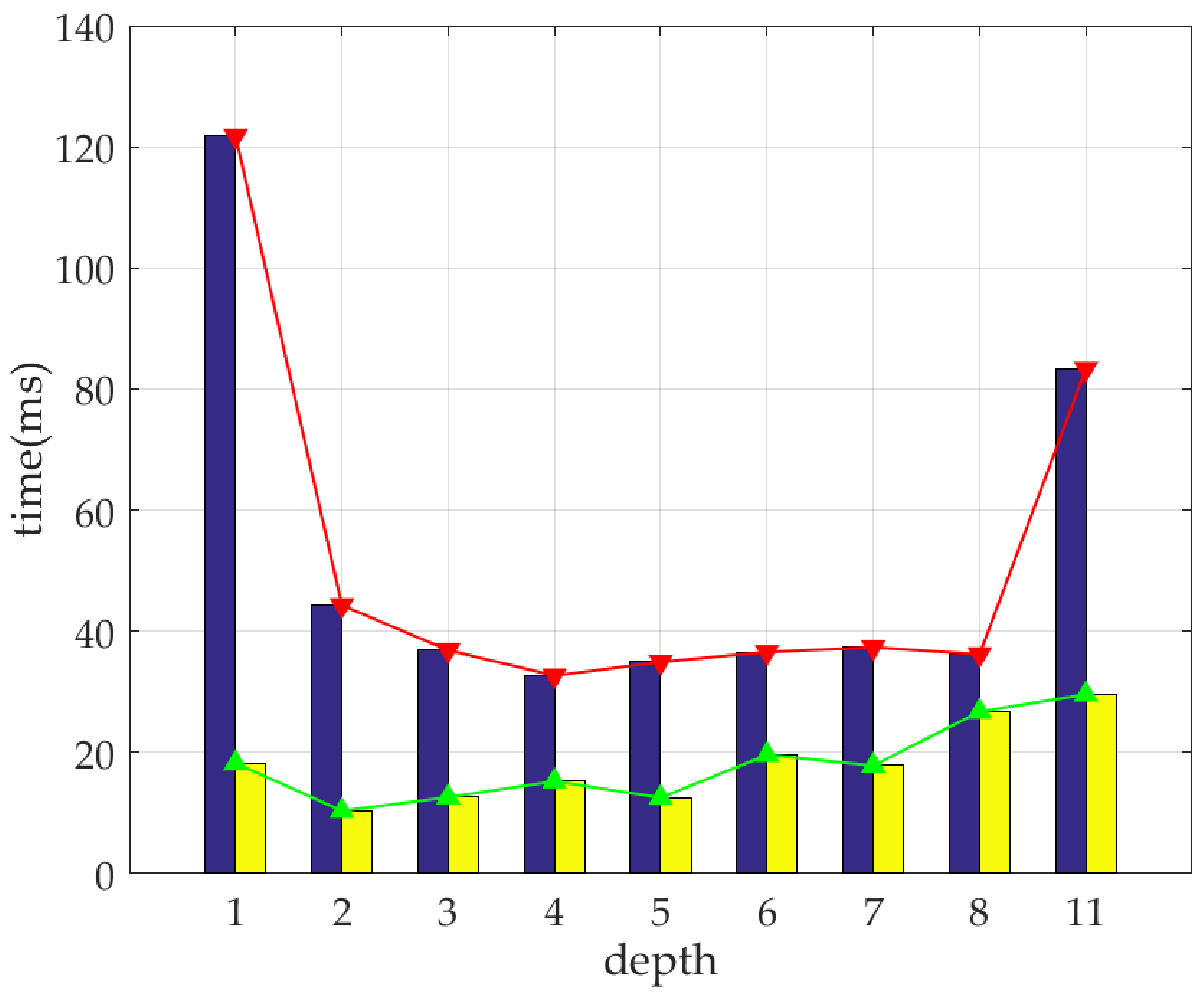
4.1. Thresholds Setting

In this part, the thresholds setting will be discussed firstly. We know that the $Children$ or $depth$ influences the performance of tree construction and query operation. We adopted a fixed $depth$ for octree constructing and a linearly variable $Childre{n}_{min}$ with the number of nearest neighbors needed to be searched for R*-tree constructing: $depth=2$ and $Childre{n}_{min}=n·k$. As shown in Figure 5, time consumed by constructing tree and $kNN$ searching varies with $Childre{n}_{min}$. Note that there is no scale on the y-axis, because the time consumed by constructing tree is far more than $kNN$ searching. For the sake of visualizing, both of them were normalized to the same range of [0,1]. The time consumed by constructing tree decreases with the increasing of $Childre{n}_{min}$, which is reasonable. kNN searching takes the least time when $Childre{n}_{min}=8·k$. Synthetically consider both construction and search time, we came to a conclusion that $Childre{n}_{min}=8·k$ is an optimal choice. However, it is just empirical. In addition, $Childre{n}_{max}=2·Childre{n}_{min}$. Both times are the average of 100 loops.

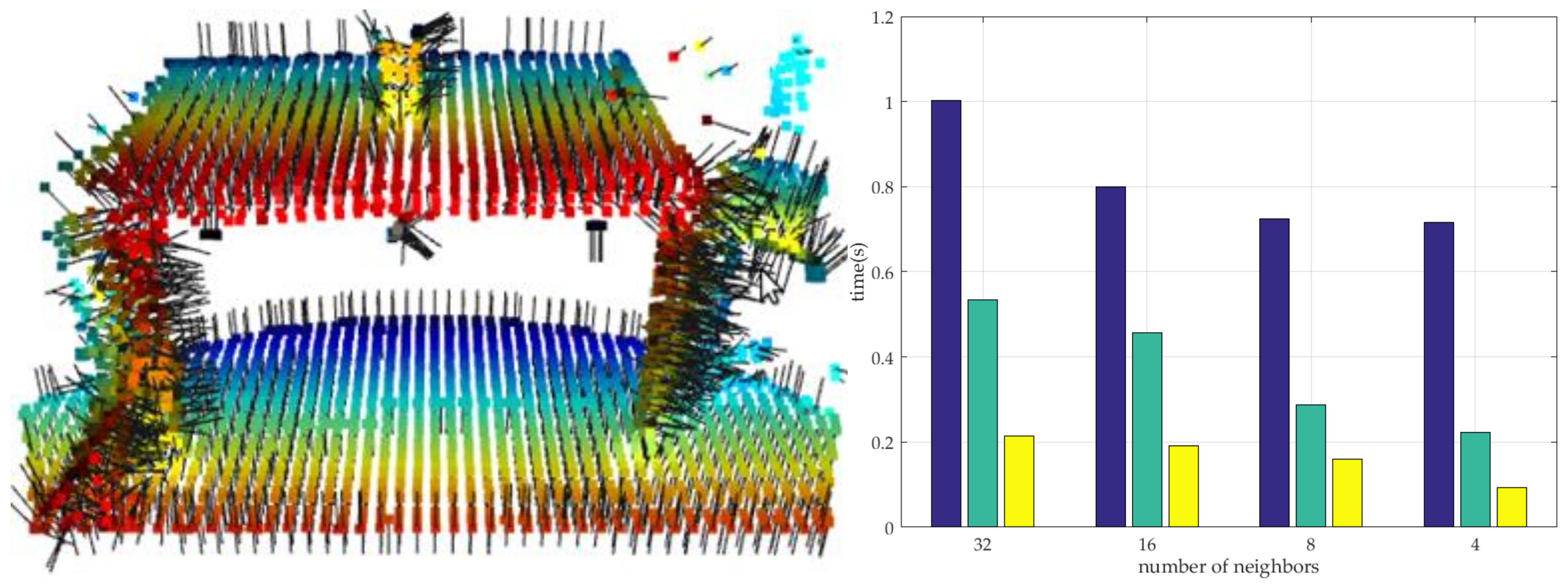
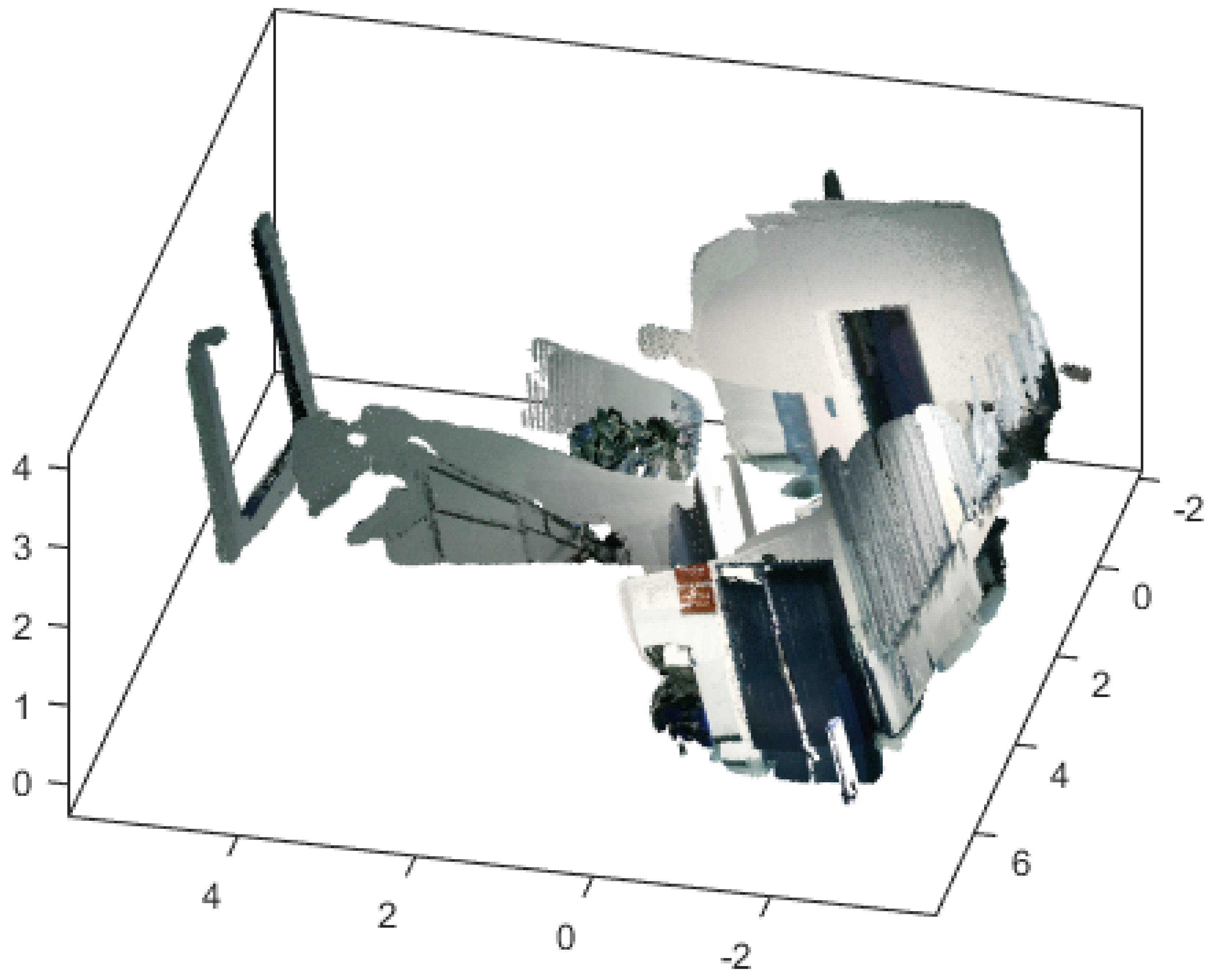
4.2. Verification

To verify the performance of hybrid structure proposed in this paper, randomly generate different sizes of 3D points: 1K, 4K, 16K, 64K, 256K, (1K = 1000), octree $depth=2$, number of neighbors k = $1,4,8,16,32,64$ and $Childre{n}_{min}=8·k$. In this section, construction time was not taken into account. The $kNN$ searching time is shown in Figure 6. We can find that when k is small, searching time is relatively stable, because $Childre{n}_{min}$ is increasing with the increasing of k. When k becomes bigger, $Childre{n}_{min}$ becomes bigger, too. Implying that the capacity of an octant is larger and more points are contained. So, if the query point lies around the center of the octant, the searching time is still stable. When more points near the face, even the corner of an octant, the time will be increasing dramatically. However, in this paper, octree’s $depth$ is limited, so the $octant$ of the octree is bigger, the probability of points near the face or corner of octant is much smaller.

A normal estimation experiment has been made to show the superiority of the hybrid structure proposed in this paper utilizing Point Cloud data table_scene_lms400.pcd mentioned earlier. Firstly, we downsampled the Point Cloud data from 460,400 points to 3309 points. Secondly, estimating normal for each resampled point in Point Cloud. The normal of a point p is the eigenvector corresponding to the minimum eigenvalue computed by point p and its neighbors ($kNN$). Computing normal of each point in Point Cloud will conduct n times of $kNN$ searching, but construct the tree once, where n is the number of points in Point Cloud. The results are shown in Figure 7. The left visualizes the normal of each point, whose direction mostly is downwards. We estimated the normals with 32-$NN$. It is easy to understand that the smaller k is, the less time to search $kNN$, but the less accurate the normal is.

The $depth$ of octree is an important threshold that influences the performance of the hybrid structure. As shown in Figure 8, it is a 3D R*-tree when $depth=1$ and an octree when $depth=11$. The used data is the same as the normal estimation, downsampled table_scene_lms400.pcd with 3309 points. The 3D R*-tree spends more time than octree to construct the structure but less time to search neighbors. When $depth=2,3,\cdots ,8$, the hybrid structure is constructed. We can see that construction time changes with a small magnitude and $kNN$ searching time keeps increasing with the $depth$ increases. A greater $depth$ means more time to construct octree and more candidate 3D R*-trees to search neighbors, because when $depth$ is greater, $leaf\_size$ is less, which implies the $octant$ is smaller and more $octants$ intersect with the search ball $B_r$.

A comparative experiment was conducted applying octree and 3D R*-tree. As shown in Figure 9. the real-world Point Cloud data was collected by an RGB-D camera scanning a laboratory with 888393 points. We test the depth of the tree and the time consumption of tree constructing and $kNN$ searching. The results are shown in

Table 1. Comparison of experimental data. $t_{cons}$ represents the time used by constructing structure, $t_{srch}$ represents the time used by $kNN$ searching.

		Octree	3D R*-Tree	Hybrid Method
	$depth$	7	10	8
$2NN$	$t_{cons}\left(ms\right)$	281	1185	263
	$t_{srch}\left(ms\right)$	68	31	13
	$depth$	5	6	6
$4NN$	$t_{cons}\left(ms\right)$	150	910	176
	$t_{srch}\left(ms\right)$	30	20	6
	$depth$	5	5	5
$8NN$	$t_{cons}\left(ms\right)$	109	778	121
	$t_{srch}\left(ms\right)$	39	12	5
	$depth$	4	4	4
$16NN$	$t_{cons}\left(ms\right)$	115	709	112
	$t_{srch}\left(ms\right)$	20	8	6

, which reveals that the hybrid method proposed in this paper performs better in $kNN$ searching and similar to octree in tree constructing. The 3D R*-tree spends a considerable amount of time in tree constructing but less time in $kNN$ searching than octree. Because R*-tree adopts series of optimizations, unlike octree splits points into eight sub-nodes regardless of the spatial relationship between points. What we take advantage of with 3D R*-tree is the better performance in $kNN$ searching.

5. Discussion

Point Cloud is a set of disordered 3D points. Searching for k nearest neighbors is a general method to extract the geometric information hidden behind the points. Some features can be computed by integrating query point with its neighbors, such as normal estimation. Searching for k nearest neighbors for each point is a task with a huge amount of computation that is dependent on the data management structure. Various tree structures are used to manage Point Cloud. Kd-tree is insensitive to the data distribution. However, when faced with large-scale data, it will be too deep to search efficiently. Octree reduced the depth of the tree by dividing into eight sub-nodes. However, it is sensitive to data distribution. R*-tree is considered the most efficient in searching. However, it cannot be very deep because of overlaps between nodes. Single index structures cannot meet the real-time requirement, and hybrid index structures are widely studied.

It is a fact that most time taken by constructing tree structure, especially R*-tree. It is acceptable because the tree is constructed once, but $kNN$ search repeated are as many times as the number of points to be calculated. The hybrid method proposed in this paper takes about the same time as octree while faster than octree. So, comprehensively considering the time used by tree constructing and $kNN$ searching, the hybrid method performed better than single octree and 3D R*-tree. Some thresholds need to be set and affect the performance of the index structure. This paper sets $Childre{n}_{min}=8·k$, $Childre{n}_{max}=2·Childre{n}_{min}$ empirically. The $depth$ of octree varies with different data.

6. Conclusions

The main contributions of this paper are as follows:

(1)

Proposed a bybrid spatial indexing method;

(2)

Proposed a new octree leaf nodes encoding method is proposed;

(3)

Designed a $kNN$ searching algorithm that refers to the hybrid structure.

The hybrid spatial indexing method intends to efficiently organize and manage large-scale Point Cloud. By setting thresholds adaptively and comparing octree and 3D R*-tree performance, the hybrid method performed better than the single octree and 3D R*-tree. Experiment data confirm that 3D R*-tree conduct better in query operation but worse in tree constructing than octree. Therefore, the hybrid method could complement the two methods and improve the performance both in tree construction and query operation to a certain extent. For structure constructing, hybrid spends about the same time as octree but takes about one-fifth of 3D R*-tree. For $kNN$ searching, hybrid spends less than a half of the 3D R*-tree and about one-fifth of the octree. The $depth$ of octree is fixed in this paper, although we have discussed the influence of $depth$.

The method proposed is just a novel exploration. There are advantages and disadvantages to our approach. Firstly, the octree is constructed with a fixed depth, which implies that the depth will be set differently with different Point Cloud data depth manually. Secondly, 3D R*-tree is sensitive to noisy data because once the noisy data are inserted into the R*-tree, a series of optimization will be conducted to update the R*-tree. While it is meaningful to comprehensively consider the $leaf\_size$ and the number of nearest neighbors.