Sharp and Rounded Cutouts in a Chevron Orifice and Them Impact on the Acoustic and Flow Parameters of Synthetic Jet
Abstract
:1. Introduction
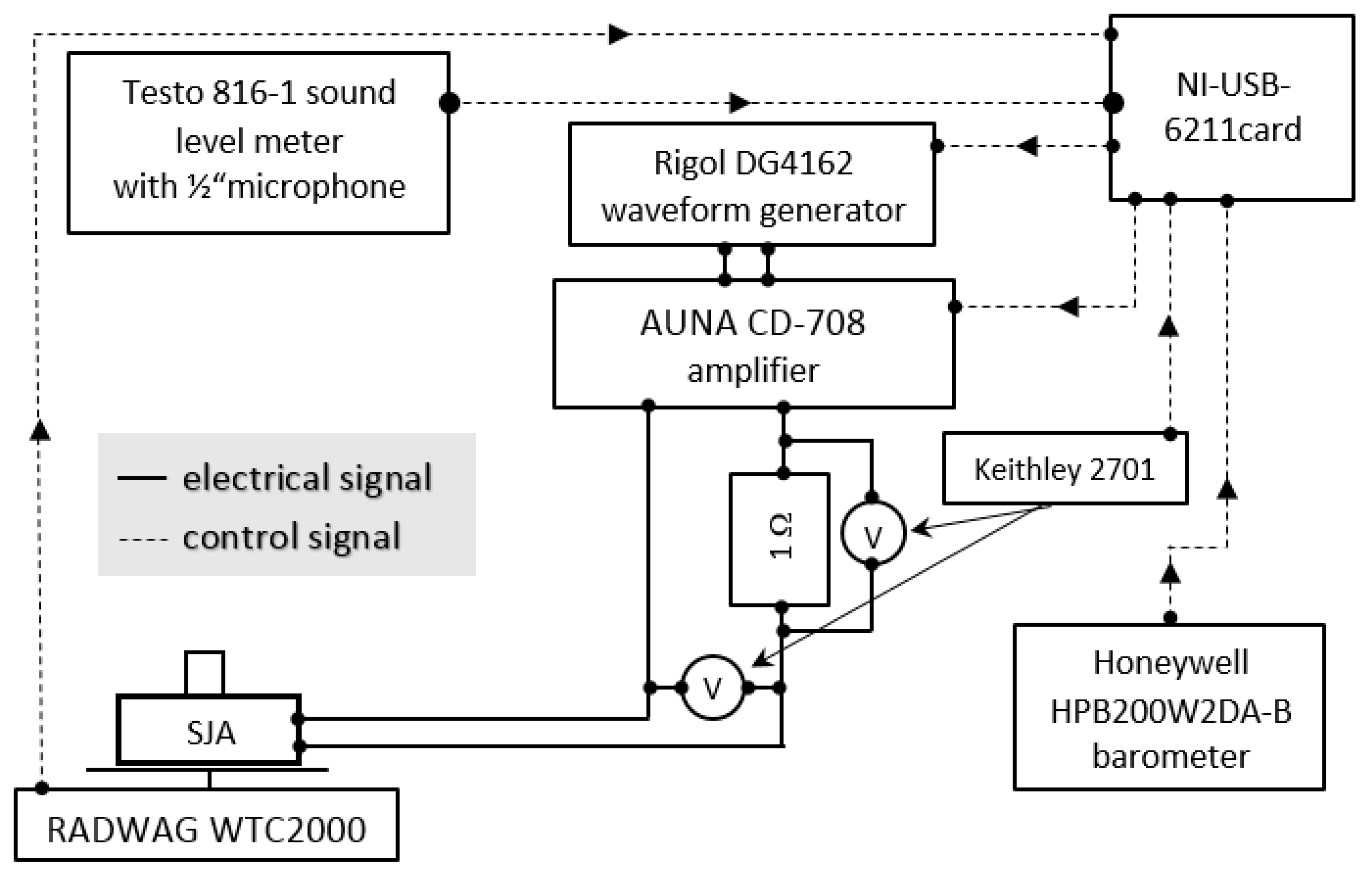
2. Materials and Methods
Data Reduction
3. Results and Discussion
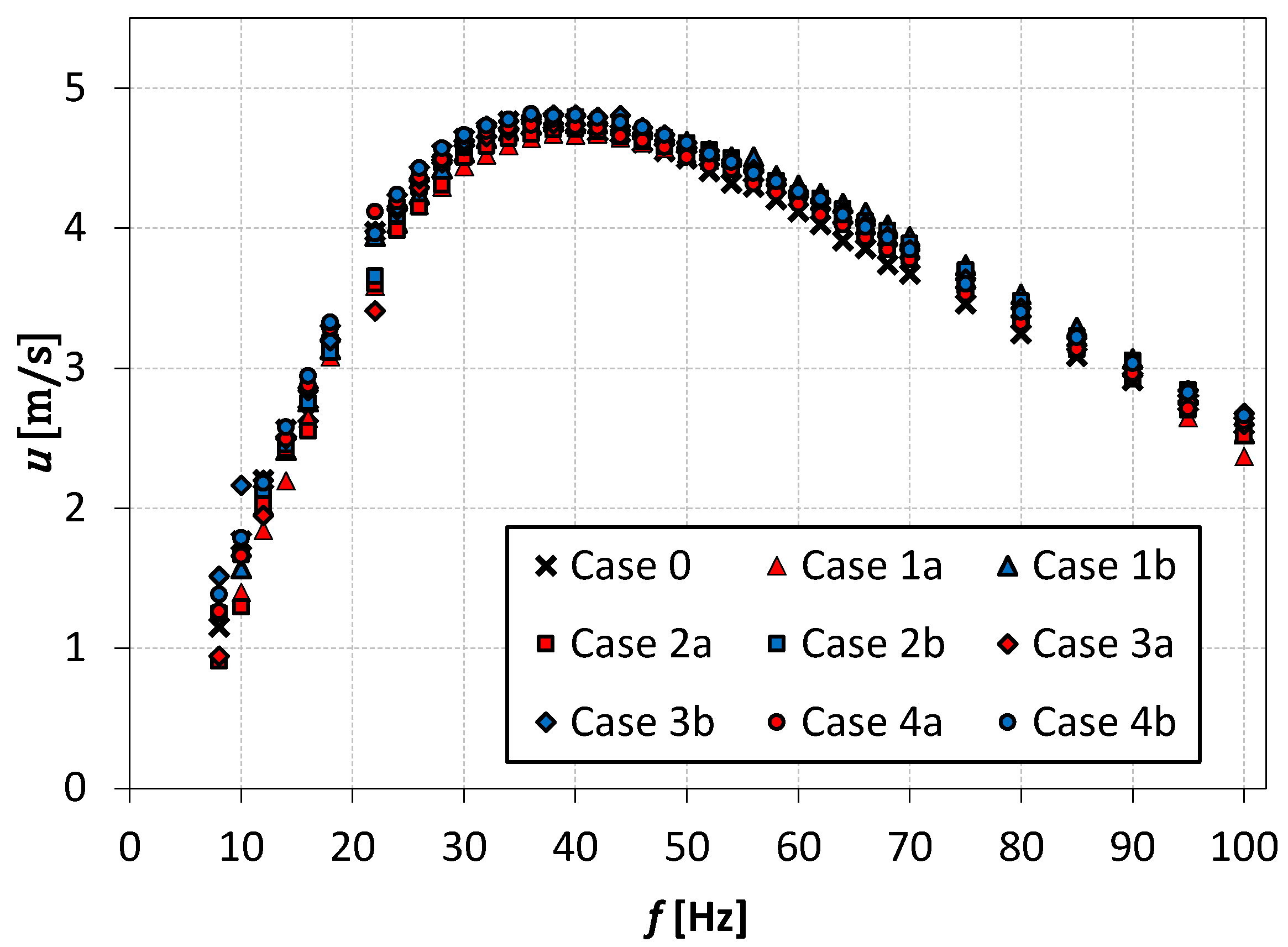
3.1. Resonant Frequency
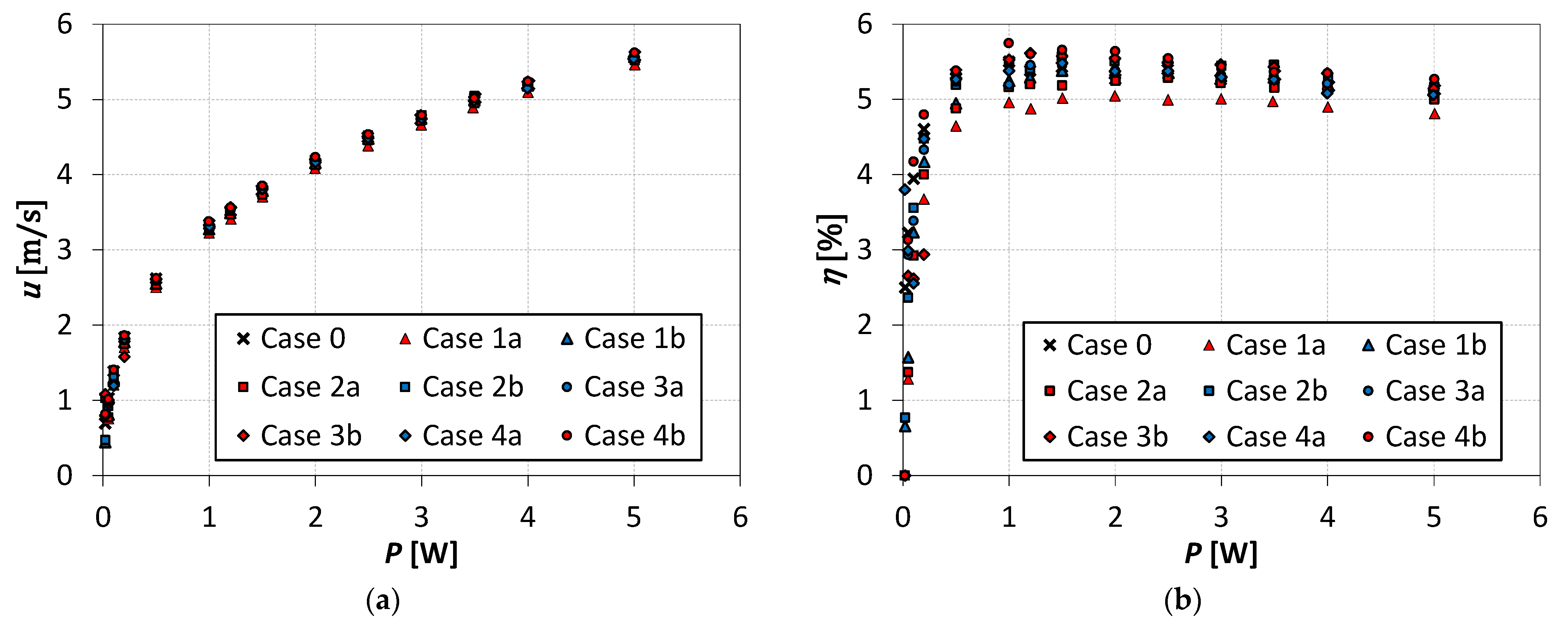
3.2. Flow Parameters
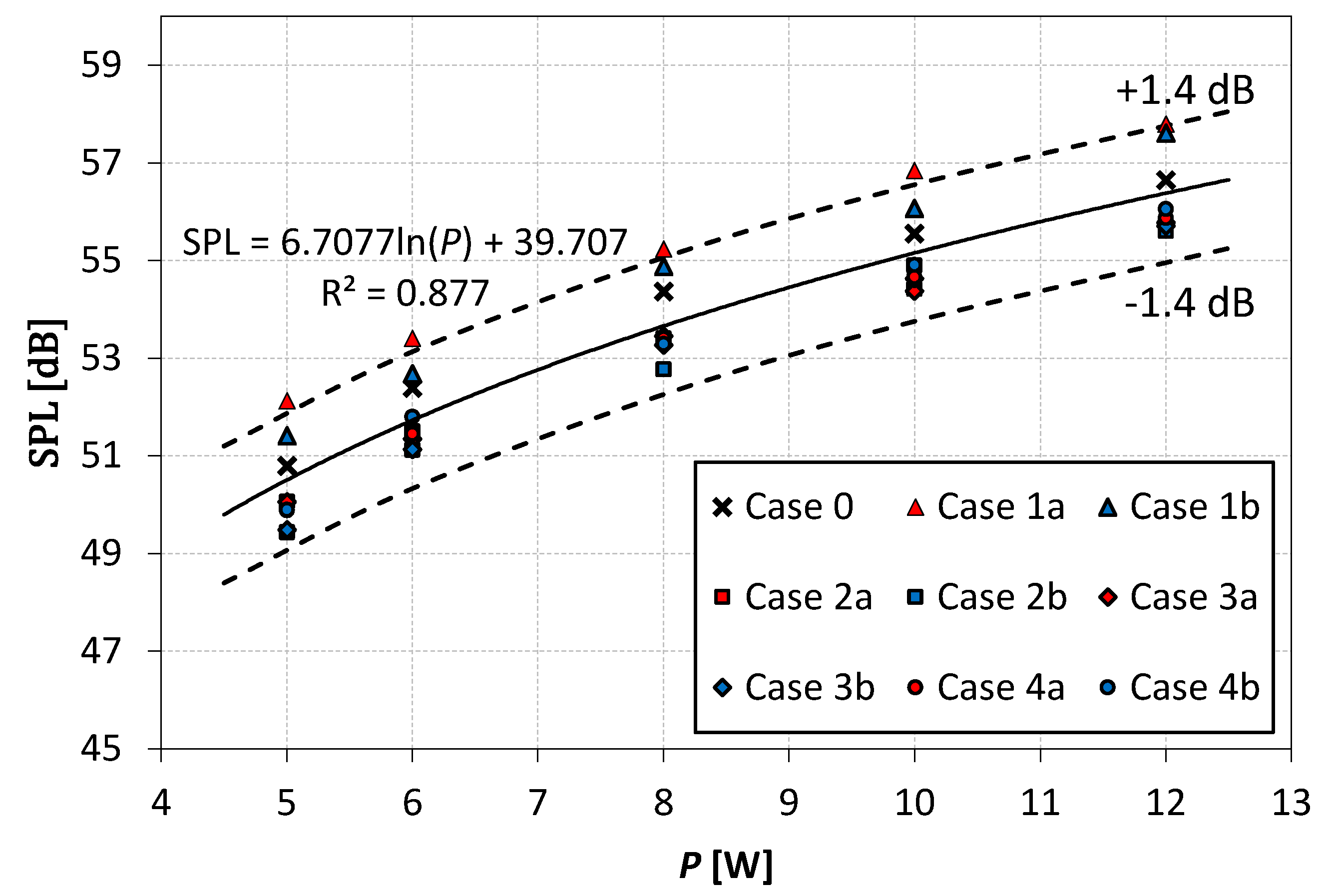
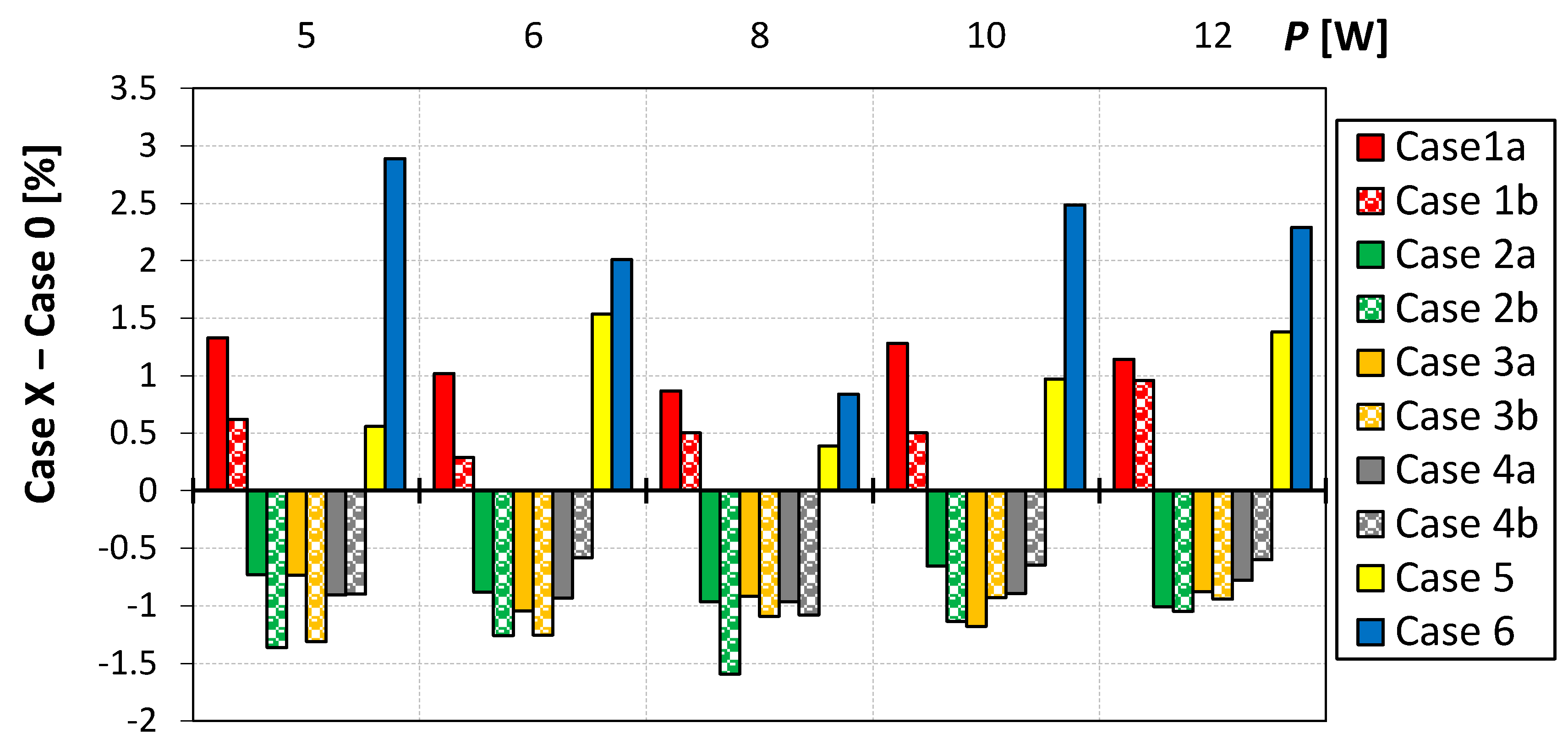
3.3. Noise Level
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gil, P.; Wilk, J.; Smusz, R.; Gałek, R. Centerline heat transfer coefficient distributions of synthetic jets impingement cooling. Int. J. Heat Mass Transf. 2020, 160, 120147. [Google Scholar] [CrossRef]
- Chiatto, M.; Palumbo, A.; de Luca, L. Design approach to predict synthetic jet formation and resonance amplifications. Exp. Therm. Fluid Sci. 2019, 107, 79–87. [Google Scholar] [CrossRef]
- Lyu, Y.W.; Zhang, J.Z.; Tan, J.W.; Shan, Y. Impingement heat transfer on flat and concave surfaces by piston-driven synthetic jet from planar lobed orifice. Int. J. Heat Mass Transf. 2021, 167, 120832. [Google Scholar] [CrossRef]
- Wang, P.; Shen, C. Characteristics of mixing enhancement achieved using a pulsed plasma synthetic jet in a supersonic flow. J. Zhejiang Univ. Sci. A 2019, 20, 701–713. [Google Scholar] [CrossRef]
- Bagherzadeh, A.; Jalali, E.; Sarafraz, M.M.; Akbari, O.; Karimipour, A.; Goodarzi, M.; Bach, Q.-V. Effects of magnetic field on micro cross jet injection of dispersed nanoparticles in a microchannel. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2683–2704. [Google Scholar] [CrossRef]
- Hao, Z.; Liu, G.; Ren, W.; Wang, Y.; Bie, H. Research on the Characteristics of Bluff Body Wake Field Induced by Synthetic Jet with PANS Model. J. Appl. Fluid Mech. 2021, 14, 1053–1063. [Google Scholar] [CrossRef]
- Di Tommaso, R.M.; Fasanella, R.; Nino, E. Lean flame stabilization by means of a coaxial synthetic jet. J. Phys. Conf. Ser. 2020, 1589, 012019. [Google Scholar] [CrossRef]
- Gil, P. Bluff body drag control using synthetic jet. J. Appl. Fluid Mech. 2019, 12, 293–302. [Google Scholar] [CrossRef]
- Geng, L.; Hu, Z.; Lin, Y. Thrust and flow characteristic of double synthetic jet actuator underwater. Ocean Eng. 2019, 176, 84–96. [Google Scholar] [CrossRef]
- Krieg, M.; Mohseni, K. Dynamic modeling and control of biologically inspired vortex ring thrusters for underwater robot locomotion. IEEE Trans. Robot. 2010, 26, 542–554. [Google Scholar] [CrossRef]
- Gil, P. Performance of special type heat sink with an integrated synthetic jet actuator. E3S Web Conf. 2019, 100, 00017. [Google Scholar] [CrossRef] [Green Version]
- Gil, P. Experimental investigation on heat transfer enhancement of air-cooled heat sink using multiple synthetic jets. Int. J. Therm. Sci. 2021, 166, 106949. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). EN ISO 9241-6:2002. Ergonomic Requirements for Office Work with Visual Display Terminals (VDTs)-Part 6: Guidance on the Work Environment (ISO 9241-6:1999); ISO: Geneva, Switzerland, 1999; p. 32. [Google Scholar]
- Colenberg, S.; Jylhä, T.; Arkesteijn, M. The relationship between interior office space and employee health and well-being—A literature review. Build. Res. Inf. 2021, 49, 352–366. [Google Scholar] [CrossRef] [Green Version]
- Bourikas, L.; Gauthier, S.; Khor, N.; En, S.; Xiong, P. Effect of Thermal, Acoustic and Air Quality Perception Interactions on the Comfort and Satisfaction of People in Office Buildings. Energies 2021, 14, 333. [Google Scholar] [CrossRef]
- Zhang, Y.; Ou, D.; Kang, S. The effects of masking sound and signal-to-noise ratio on work performance in Chinese open-plan offices. Appl. Acoust. 2021, 172, 107657. [Google Scholar] [CrossRef]
- Ikhlaq, M.; Yasir, M.; Ghaffari, O.; Arik, M. Acoustics and Heat Transfer Characteristics of Piezoelectric Driven Central Orifice Synthetic Jet Actuators. Exp. Heat Transf. 2021, 1–22. [Google Scholar] [CrossRef]
- Bhapkar, U.S.; Srivastava, A.; Agrawal, A. Acoustic and heat transfer characteristics of an impinging elliptical synthetic jet generated by acoustic actuator. Int. J. Heat Mass Transf. 2014, 79, 12–23. [Google Scholar] [CrossRef]
- Kanase, M.M.; Mangate, L.D.; Chaudhari, M.B. Acoustic aspects of synthetic jet generated by acoustic actuator. J. Low Freq. Noise Vib. Act. Control 2018, 37, 31–47. [Google Scholar] [CrossRef] [Green Version]
- Sadeghian, M.; Bandpy, M.G. Technologies for Aircraft Noise Reduction: A Review. J. Aeronaut. Aerosp. Eng. 2020, 9, 218. [Google Scholar] [CrossRef]
- Xia, H.; Tucker, P.G.; Eastwood, S. Large-eddy simulations of chevron jet flows with noise predictions. Int. J. Heat Fluid Flow 2009, 30, 1067–1079. [Google Scholar] [CrossRef]
- Khan, M.O.A.; Dhabi, A.; Khan, M.O.A.; Dhabi, A.; Dol, S.S.; Dhabi, A. Effects of Chevrons on the Acoustic Noise and Velocity Patterns of Aircraft Nozzles. In Proceedings of the 2020 International Conference on Decision Aid Sciences and Application (DASA) Effects, Sakheer, Bahrain, 8–9 November 2021; pp. 845–849. [Google Scholar]
- Violato, D.; Scarano, F. Three-dimensional evolution of flow structures in transitional circular and chevron jets. Phys. Fluids 2011, 23, 124104. [Google Scholar] [CrossRef] [Green Version]
- Guan, T.; Zhang, J.Z.; Shan, Y.; Hang, J. Conjugate heat transfer on leading edge of a conical wall subjected to external cold flow and internal hot jet impingement from chevron nozzle—Part 1: Experimental analysis. Int. J. Heat Mass Transf. 2017, 106, 329–338. [Google Scholar] [CrossRef]
- Lyu, Y.W.; Zhang, J.Z.; Liu, X.C.; Tan, X.M. Experimental investigation on convective heat transfer induced by piston-driven synthetic jet with a transmission pipe. Exp. Therm. Fluid Sci. 2019, 104, 26–42. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Avallone, F.; Cardone, G. On the flow organization of a chevron synthetic jet. Exp. Therm. Fluid Sci. 2017, 82, 136–146. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Cardone, G. Flow field features of chevron impinging synthetic jets at short nozzle-to-plate distance. Exp. Therm. Fluid Sci. 2019, 106, 202–214. [Google Scholar] [CrossRef]
- Crispo, C.M.; Greco, C.S.; Cardone, G. Convective heat transfer in circular and chevron impinging synthetic jets. Int. J. Heat Mass Transf. 2018, 126, 969–979. [Google Scholar] [CrossRef]
- Smyk, E.; Markowicz, M. Acoustic and flow aspects of synthetic jet actuators with chevron orifices. Appl. Sci. 2021, 11, 652. [Google Scholar] [CrossRef]
- Mangate, L.D.; Chaudhari, M.B. Heat transfer and acoustic study of impinging synthetic jet using diamond and oval shape orifice. Int. J. Therm. Sci. 2015, 89, 100–109. [Google Scholar] [CrossRef]
- Smyk, E.; Wilk, J.; Markowicz, M. Synthetic Jet Actuators with the Same Cross-Sectional Area Orifices-Flow and Acoustic Aspects. Appl. Sci. 2021, 11, 4600. [Google Scholar] [CrossRef]
- Arik, M. An investigation into feasibility of impingement heat transfer and acoustic abatement of meso scale synthetic jets. Appl. Therm. Eng. 2007, 27, 1483–1494. [Google Scholar] [CrossRef]
- Smyk, E. Acoustic aspects of synthetic jet - review. Dev. Mech. Eng. 2020, 16, 4. [Google Scholar] [CrossRef]
- Gil, P. Synthetic jet Reynolds number based on reaction force measurement. J. Fluids Struct. 2018, 81, 466–478, Corrigendum in 2021, 101, 103211. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Acoustics—Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure—Survey Method Using an Enveloping Measurement Surface over a Reflecting Plane (ISO 3746:2010); ISO: Geneva, Switzerland, 2010; p. 48. [Google Scholar]
- Gil, P.; Smyk, E.; Gałek, R.; Przeszłowski, Ł. Thermal, flow and acoustic characteristics of the heat sink integrated inside the synthetic jet actuator cavity. Int. J. Therm. Sci. 2021, 170, 107171. [Google Scholar] [CrossRef]
- Smyk, E.; Przeszłowski, Ł.; Strzelczyk, P.M. Impact of the confinement plate on the synthetic jet. AIP Adv. 2020, 10, 105204, Erratum in 2021, 11, 039901. [Google Scholar] [CrossRef]
- Kordík, J.; Trávníček, Z. Integral Quantities of Axisymmetric Synthetic Jets Evaluated from a Direct Jet Thrust Measurement. Flow Turbul. Combust. 2019, 103, 827–844. [Google Scholar] [CrossRef]
- Gil, P.; Smyk, E. Synthetic jet actuator efficiency based on the reaction force measurement. Sens. Actuators A Phys. 2019, 295, 405–413. [Google Scholar] [CrossRef]
- Broučková, Z.; Trávníček, Z. Visualization study of hybrid synthetic jets. J. Vis. 2015, 18, 581–593. [Google Scholar] [CrossRef]
- Milanovic, I.M.; Zaman, K.B.M.Q. Synthetic jets in cross-flow. Part II: Jets from orifices of different geometry. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003; pp. 1–12. [Google Scholar]
- Girfoglio, M.; Greco, C.S.; Chiatto, M.; de Luca, L. Modelling of efficiency of synthetic jet actuators. Sens. Actuators A Phys. 2015, 233, 512–521. [Google Scholar] [CrossRef]
- Kordík, J.; Trávníček, Z. Optimal diameter of nozzles of synthetic jet actuators based on electrodynamic transducers. Exp. Therm. Fluid Sci. 2017, 86, 281–294. [Google Scholar] [CrossRef]
- Smyk, E.; Wawrzyniak, S.; Peszyński, K. Synthetic jet actuator with two opposite diaphragms. Mech. Mech. Eng. 2020, 24, 17–25. [Google Scholar] [CrossRef]
- Gil, P.; Wilk, J.; Korzeniowski, M. Helmholtz Resonance Frequency of the Synthetic Jet Actuator. Appl. Sci. 2021, 11, 5666. [Google Scholar] [CrossRef]
- De Luca, L.; Girfoglio, M.; Coppola, G. Modeling and Experimental Validation of the Frequency Response of Synthetic Jet Actuators. AIAA J. 2014, 52, 1733–1748. [Google Scholar] [CrossRef]
- Smyk, E. Interference in axisymmetric synthetic jet actuator. EPJ Web Conf. 2017, 143, 02111. [Google Scholar] [CrossRef] [Green Version]
- Hernández-Sánchez, J.F.; Orduña-Bustamante, F.; Velasco-Segura, R. Momentum transfer in the outflow cycle of a Synthetic jet: Comparison between a developed flow and an LE model. arXiv 2021, arXiv:2106.14814. [Google Scholar]
- Persoons, T.; O’Donovan, T.S.; Donovan, T.S.O.; Persoons, T.; Donovan, T.S.O. A pressure-based estimate of synthetic jet velocity. Phys. Fluids 2007, 19, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Jawahar, H.K.; Markesteijn, A.P.; Karabasov, S.A.; Azarpeyvand, M. Effects of Chevrons on Jet-installation Noise. In Proceedings of the AIAA AVIATION 2021 FORUM, Online, 2–6 August 2021; p. 2184. [Google Scholar]
- Tide, P.S.; Srinivasan, K. Effect of chevron count and penetration on the acoustic characteristics of chevron nozzles. Appl. Acoust. 2010, 71, 201–220. [Google Scholar] [CrossRef]
- Akbarali, I.M.; Periyasamy, S. Design and analysis of nozzle for reducing noise pollution. IOSR J. Mech. Civ. Eng. 2020, 17, 6–12. [Google Scholar] [CrossRef]
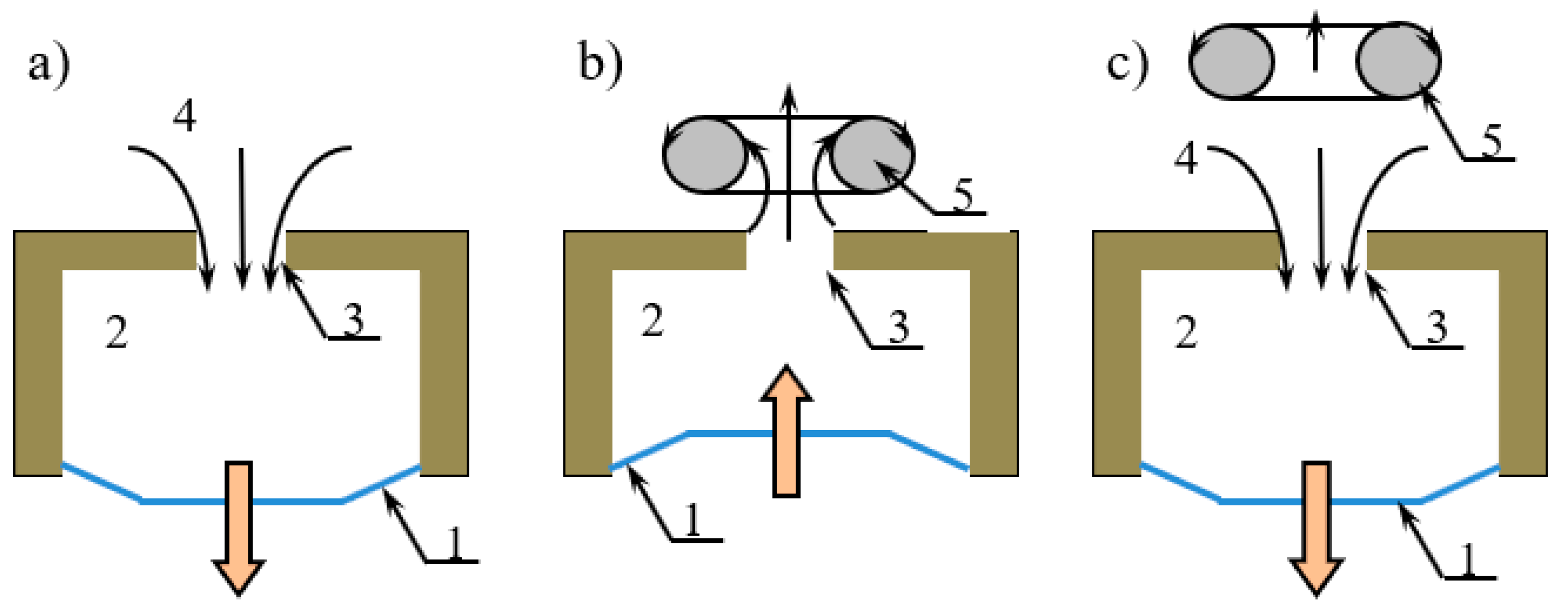
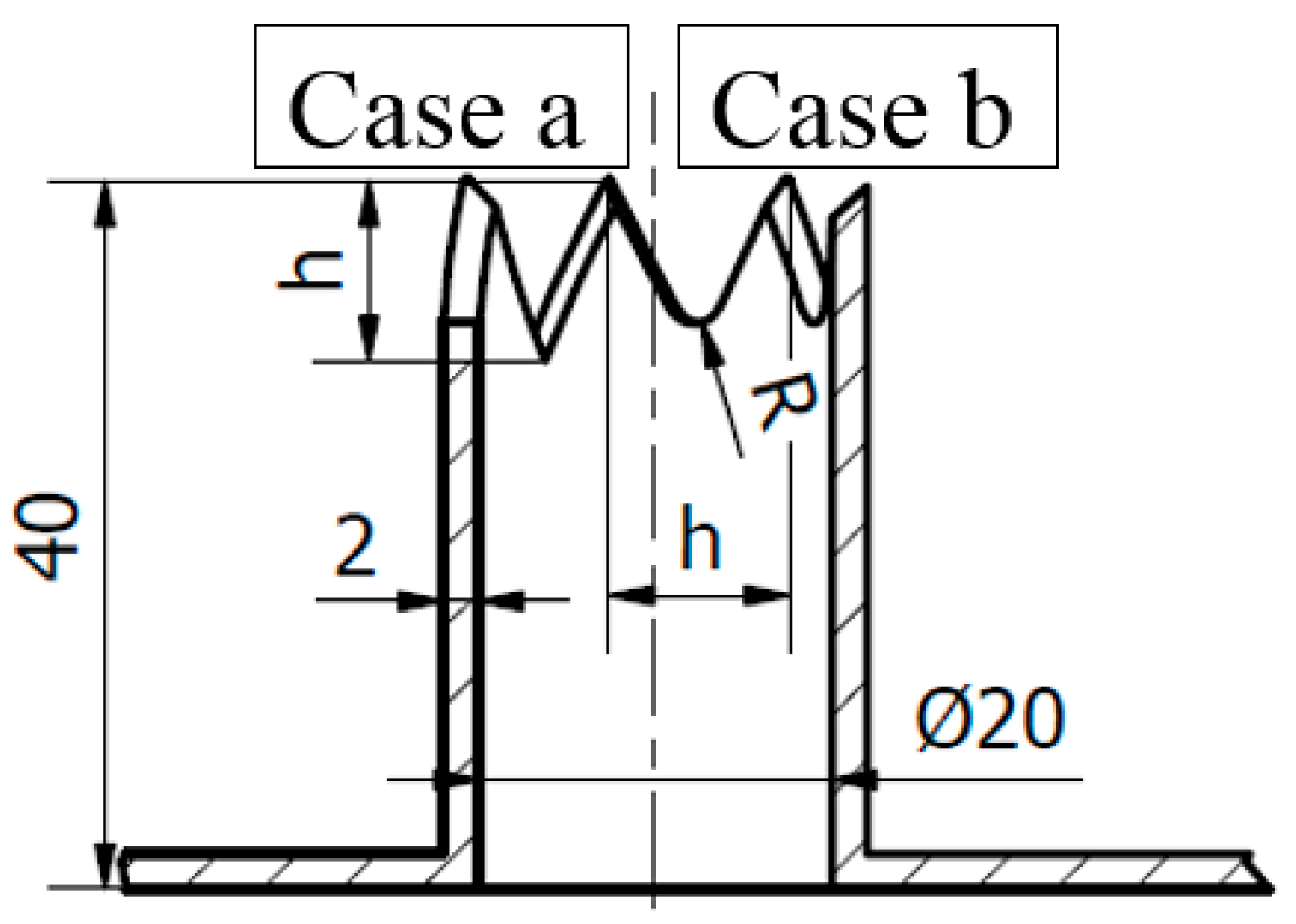

| d [mm] | l [mm] | Number of Chevrons | h [mm] | R [mm] | |
|---|---|---|---|---|---|
| Case 0 | 20 | 40 | - | - | - |
| Case 1a | 20 | 40 | 4 | 18.85 | - |
| Case 1b | 20 | 40 | 4 | 18.85 | 3.14 |
| Case 2a | 20 | 40 | 7 | 10.77 | - |
| Case 2b | 20 | 40 | 7 | 10.77 | 1.80 |
| Case 3a | 20 | 40 | 10 | 7.54 | - |
| Case 3b | 20 | 40 | 10 | 7.54 | 1.26 |
| Case 4a | 20 | 40 | 14 | 5.39 | - |
| Case 4b | 20 | 40 | 14 | 5.39 | 0.90 |
| Case 5 [29] | 20 | 40 | 7 | 15.6 | - |
| Case 6 [29] | 20 | 40 | 7 | 20.8 | - |
| Name | Relative Uncertainty | Absolute Uncertainty |
|---|---|---|
| Power, P | ±0.25% | |
| Force, F | ±1 mN | |
| Efficiency, η | ±0.2% | |
| SPL | ±1.4 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smyk, E. Sharp and Rounded Cutouts in a Chevron Orifice and Them Impact on the Acoustic and Flow Parameters of Synthetic Jet. Appl. Sci. 2021, 11, 9624. https://doi.org/10.3390/app11209624
Smyk E. Sharp and Rounded Cutouts in a Chevron Orifice and Them Impact on the Acoustic and Flow Parameters of Synthetic Jet. Applied Sciences. 2021; 11(20):9624. https://doi.org/10.3390/app11209624
Chicago/Turabian StyleSmyk, Emil. 2021. "Sharp and Rounded Cutouts in a Chevron Orifice and Them Impact on the Acoustic and Flow Parameters of Synthetic Jet" Applied Sciences 11, no. 20: 9624. https://doi.org/10.3390/app11209624
APA StyleSmyk, E. (2021). Sharp and Rounded Cutouts in a Chevron Orifice and Them Impact on the Acoustic and Flow Parameters of Synthetic Jet. Applied Sciences, 11(20), 9624. https://doi.org/10.3390/app11209624






