Fluidization Behavior of Soft Soil Induced by Shield Construction

Abstract

Shield construction will cause the fluidization of soft soil which is characterized by flow plasticity. This paper presents two theoretical models of soil flow behavior based on a fluid mechanics framework to understand the behavior of soft soil during shield tunneling, especially under the shearing action of the shield skin and the cutting wheel. The characteristics of the flow field are discussed, and their relationships with shield construction parameters such as advancing speed, cutting wheel rotation, applied thrust and torque, and water content are analyzed, while the proposed theory is verified by the results of a numerical simulation. Considering the shear-thinning effect of the soil, a closed four-stage shear path to describe the complete process of the soil behavior during shield tunneling is further interpreted. The results indicate that the sheared region produced by the rotating cutting wheel was larger than that produced by the shield shell shearing and that it was significantly affected by soil properties and tunneling parameters. In addition, it is concluded that the sheared region was significantly expanded due to the shear-thinning effect.

1. Introduction

Soft soil, such as mucky, silty clay, is widely distributed in Shanghai, Ningbo and Suzhou. This mucky, silty soil is characterized by a high water content, high compressibility, low permeability, and a high thixotropy with both fluid and solid properties [1,2]. When external force increases to destroy the internal structure of the soil, the soil transforms from solid to liquid, which can be described as the fluidization of the soil [3]. There have been some related studies in the field of submarine slides and foundation pits [4,5,6]. During the process of shield tunneling, the shield skin and cutting wheel will inevitably cause a shearing effect on the surrounding soil and induce the proposed fluidization behavior of the soil. As a result, there is an obvious decrease in the strength and bearing capacity of the sheared soils around the shield, which further increases the range of disturbance to the soil and causes additional downward movement of the shield, increasing the difficulty of the deviation control. Therefore, it is critical to study soil fluidization behavior and its relationship with shield tunneling parameters.

There has been extensive research work undertaken on the influence of shield construction on soil response, among which the most typical has been the Peck formula and its correction formula [7,8,9,10]. Some scholars have used the methods of the model test [11,12,13,14], theoretical analysis [15,16,17,18,19,20,21], and numerical simulation [22,23,24] to study the soil response induced by shield tunneling, but previous studies were generally based on the solid mechanics of elastic and elastoplastic mechanics, which cannot describe the fluid characteristics of a fluid-plastic soil. Moreover, from the perspective of hydrodynamics, shear rate has a great influence on soil responses [25], but existing research hardly considers the influences of shield tunneling speed or cutter head rotation on soil disturbance.

To consider the hydrodynamic characteristics of soft soil, this paper puts forward a theoretical analysis method of soil fluidization behavior induced by shield construction based on a hydrodynamics framework. The influences of water content, shield tunneling speed and cutting wheel rotation on soil behavior are analyzed, and the proposed method is verified by a numerical simulation.

2. Methodology

2.1. Model Assumptions

Soil with a high water content can be described as a mixture of solid and liquid phases, which has both solid and fluid characteristics. When a shield tunnels, the soil around the shield changes gradually from its original intact conditions into weak debris and ultimately into a fluidized turbidity current, especially the soil surrounding the shell and cutting wheel. To interpret this soil behavior, the assumptions were as follows:

(1) Boukpet et al. studied the rheological behavior of soft soil with different water content and proposed that the rheological constitutive can use the Bingham fluid constitutive model, as shown in Equation (1). Additionally, the parameters of the initial yield stress and viscosity coefficient of the soil can be described by a power–law relationship with water content as a variable [26]:

$$\mathit{\tau }={\mathit{\tau }}_c+K\dot{\gamma }={\mathit{\tau }}_c+K\left(-\frac{\mathrm{d}u}{\mathrm{d}r}\right)$$

(1)

where $\dot{\gamma }$ is the shear strain rate(s⁻¹); ${\mathit{\tau }}_c$ is the initial yield stress of the soil (Pa); K is the flow consistency coefficient (Pa·s); r is the distance to the shield center; and u is the flow velocity of the soil surrounding the shield.

(2) The soil is homogeneous and undergoes a steady-state laminar movement under the shearing action of the shield.

2.2. Shield Shell-Soil Shear Flow Model

The flow behavior of the soil around the shield shell occurs when the shear stress of the soil ($\tau$) caused by the applied thrust reaches the initial yield stress ${\tau }_c$, and the sheared region increases with an increasing thrust, as shown by the development of the soil phase in Figure 1. Considering that the soil is homogeneous and the shear velocity is evenly distributed around the shield shell, the sheared region caused by the shield advancing expands evenly along the radial, with a series of concentric iso-velocity shells being formed. To describe the above characteristics, the flow layer can be assumed to be a sleeve mode equiaxed and parallel to the shield shell.

A shield shell-soil shear flow model was established, as shown in Figure 2. Assuming that the shield advances at a uniform speed, the applied force should balance with the shear resistance on the flow layer. Therefore, the force balance equation in the longitudinal direction of the cylindrical soil per unit length within the radius r in the sheared region was obtained:

$$F=2\pi r\tau$$

(2)

where F is the thrust applied on the soil around the shield per unit length.

The radius of the sheared region boundary $r_c$ corresponds to the position where the flow velocity is zero. When r tends to $r_c$, the shear stress approaches ${\tau }_c$. Substituting Equation (2), the radius of the sheared region boundary $r_c$ is as follows:

$$r_c=\frac{F}{2\pi {\tau }_c}$$

(3)

Substituting Equations (2) and (3) into Equation (1):

$$\mathrm{d}u=-\frac{F}{2\pi K}\left(\frac{1}{r}-\frac{1}{r_c}\right)\mathrm{d}r$$

(4)

At the position of the shield skin R, the velocity of the soil is Vs, and at the radius r of the sheared region, the velocity is u. Substituting Equation (4):

$${\displaystyle {\int }_{V_s}^u\mathrm{d}u}=-{\displaystyle {\int }_R^r\frac{F}{2\pi K}\left(\frac{1}{r_{}}-\frac{1}{r_c}\right)}\mathrm{d}r$$

(5)

where R is the radius of the shield shell.

The velocity distribution function solved by the integral is as follows:

$$u=-\frac{F}{2\pi K}\left(\ln \frac{r}{R}-\frac{r-R}{r_c}\right)+\begin{array}{cc}{V}_s& r\in \left[R,r_c\right]\end{array}$$

(6)

Substituting $r=r_c$ and $u=0$ into Equation (6), the speed of the shield advancing is obtained:

$$V_s=\frac{F}{2\pi K}\left(-1+\frac{2\pi {\tau }_{c}R}{F_{}}+\ln \frac{F}{2\pi {\tau }_{c}R}\right)$$

(7)

2.3. Cutting Wheel–Soil Shear Flow Model

Similar to the soil behavior around the shield skin, the soil around the cutting wheel flows when the shear stress of the soil ($\tau$) caused by the applied torque T reaches the initial yield stress ${\tau }_c$. Differently, there is a gradient of linear velocity along the radius of the cutting wheel and the sheared region will start from the edge of the cutting wheel then gradually expand radially and longitudinally. As presented in Figure 3a, the iso-velocity line formed around the cutting wheel should be a curve, and the iso-velocity line with a velocity of zero should converge on the center of the cutting wheel and the shield skin behind the cutting wheel, where the velocity is zero. To describe the above characteristics, a local polar coordinate system was established at the top of the cutting wheel, and the iso-velocity line of the flow field was assumed to be the following Archimedes spiral:

$${\rho }^{\prime }=\frac{2r^{\prime }}{\pi }{\theta }^{\prime }$$

(8)

where ${\rho }^{\prime }$ is the polar diameter in $O^{\prime }$- coordinate system; $r^{\prime }=r-R$; ${\theta }^{\prime }$ is the polar angle in $O^{\prime }$- coordinate system and ${\theta }^{\prime }\in \left[0,3\pi /2\right]$.

Where $\omega$ in Figure 3 is the angular velocity of the cutting wheel.

As shown in Figure 3b, the flow layer of a curved ring in front of the cutter head is determined by the velocity line of ${\rho }^{\prime }$, and the torque increment on the ring element corresponding to the polar angle increment is:

$$\mathrm{d}T=2\pi {\rho }^{\prime }{\left({\rho }^{\prime }\sin {\theta }^{\prime }+R\right)}^2\tau \mathrm{d}{\theta }^{\prime }$$

(9)

Assuming that the applied torque T is balanced with the shear moment on the spiral flow layer, then the applied torque is obtained by integrating the polar angle of the entire spiral flow layer surface:

$$T=\tau {\displaystyle {\int }_0^{3\pi /2}2\pi {\rho }^{\prime }{\left({\rho }^{\prime }\sin {\theta }^{\prime }+R\right)}^2}\mathrm{d}{\theta }^{\prime }$$

(10)

Then the shear stress on the flow layer is as follows:

$$\tau =\frac{T}{{\displaystyle {\int }_0^{3\pi /2}2\pi {\rho }^{\prime }{\left({\rho }^{\prime }\sin {\theta }^{\prime }+R\right)}^2}\mathrm{d}{\theta }^{\prime }}$$

(11)

Substituting the initial yield stress ${\tau }_c$ into Equation (10), the equation corresponding to the ultimate velocity line ${\rho }_c{}^{\prime }$ can be obtained:

$$\frac{T}{{\tau }_c}={\displaystyle {\int }_0^{3\pi /2}2\pi {\rho }_c{}^{\prime }{\left({\rho }_c{}^{\prime }\sin {\theta }^{\prime }+R\right)}^2}\mathrm{d}{\theta }^{\prime }$$

(12)

According to Equation (1), the rheological constitutive equation can be expressed as:

$$\tau ={\tau }_c+K\left(-\frac{du}{d{\rho }^{\prime }}\right)={\tau }_c-K\frac{d{r}^{\prime }}{d{\rho }^{\prime }}\cdot \frac{du}{d{r}^{\prime }}$$

(13)

Substituting Equation (13) into Equation (10):

$$du=-\frac{d{\rho }^{\prime }}{Kd{r}^{\prime }}\left(\frac{T}{S\left(r^{\prime }\right)}-{\tau }_c\right)d{r}^{\prime }$$

(14)

where $S\left(r^{\prime }\right)={\displaystyle {\int }_0^{3\pi /2}2\pi {\rho }^{\prime }{\left({\rho }^{\prime }\sin {\theta }^{\prime }+R\right)}^2}\mathrm{d}{\theta }^{\prime }$.

Substituting the integral boundary condition of $r^{\prime }=0$ and $u=\omega R$ at the edge of the cutting wheel, the velocity integral equation is obtained:

$${\displaystyle {\int }_{\omega R}^{u}du}=-{\displaystyle {\int }_0^{r^{\prime }}\frac{d{\rho }^{\prime }}{Kd{r}^{\prime }}\left(\frac{T}{S\left(r^{\prime }\right)}-{\tau }_c\right)}d{r}^{\prime }$$

(15)

The velocity distribution function is obtained by integration:

$$u=\frac{2\pi n}{60}R-{\displaystyle {\int }_0^{r^{\prime }}\frac{d{\rho }^{\prime }}{Kd{r}^{\prime }}\left(\frac{T}{S\left(r^{\prime }\right)}-{\tau }_c\right)}d{r}^{\prime }$$

(16)

where $n$ is the revolutions per minute of the cutting wheel; $\omega =\frac{2\pi n}{60}$.

Substituting the boundary condition $r^{\prime }=r_c{}^{\prime }$ and $u=0$ at the boundary of the sheared region, the relationship between applied torque T and speed n is established:

$$n=\frac{30}{\pi KR}{\left.{\displaystyle {\int }_0^{{r^{\prime }}_{}}\frac{d{\rho }^{\prime }}{d{r}^{\prime }}\left(\frac{T}{S\left(r^{\prime }\right)}-{\tau }_c\right)}d{r}^{\prime }\right|}_{{r^{\prime }}_c}$$

(17)

The above integral formulas can be calculated with MATLAB.

3. Results

The soil index properties of the kaolin quoted for analysis are shown in

Table 1. Soil index properties [26].

Property	Kaolin
Liquid limit/%	58.4
Plastic limit/%	28
Plastic index/%	30.4
Specific gravity/(kN/m3)	2.6

[26] and the rheological parameters of three groups of moisture content samples are shown in

Table 2. Rheological parameters of soil [26].

w/%	IL	τc/Pa	K/Pa·s
51	0.736	3050	3440
69	1.35	760	672
78	1.7	470	302

. Based on the above soil parameters, a shield applied in the Suzhou Metro Tunnel of Line S1 with a cutter head diameter of 6.86 mm and a shield shell diameter of 6.83 m was selected to analyze the flow behavior of the soil.

3.1. Applied Thrust and Speed

Figure 4 shows the applied thrust-speed curves of the shield shell acting on the soil per unit length. It can be seen from Figure 4 that the speed increased with the increasing thrust, and there was a nonlinear relationship between them, with a large initial increase rate. The thrust required for soil flow decreased with the increase of water content, with the reason being that the soil with high water content had a smaller yield stress and viscosity coefficient, so the ability to resist deformation was smaller.

3.2. Velocity Distribution around the Shield Shell

The advancing speed of the shield was generally 2~100 mm/min (0.033~1.67 mm/s). The velocity distribution of the soil around the shield shell with each moisture content sample was analyzed at the speeds of 0.5 and 1.5 mm/s, as shown in Figure 5. The flow velocity gradually decreased in the radial direction from the shield skin, and the velocity gradient gradually decreased in the radial direction, which means that the farther away from the shield, the slower the velocity decays. The speed of the shield advancing had a significant influence on the flow velocity field of the soil. The radius of the sheared region boundary increased with the increasing shield speed. For a water content of 51%, when the speed was 0.5 mm/s, the radius and the thickness of the sheared region were 3.4774 m and 0.0624 m, respectively; when the speed was 1.5 mm/s, the radius and the thickness of the sheared region were 3.5233 m and 0.1083 m, respectively.

It is worth noting that the soil with a small moisture content had a larger sheared region at the same shield speed, which is contrary to the conclusion that soil with small moisture content has a greater yield stress and stronger deformation resistance. For example, when v = 1.5 mm/s, the radius of the sheared region boundary corresponding to w = 51% was 3.5233 m, and the radius of the sheared region boundary corresponding to w = 78% was 3.4967 m. The reason for this is that the thrust required for a shield to reach the same speed in soil with a low moisture content is much greater than that in soil with a high moisture content, as shown in Figure 4. Therefore, under the combined action of shield thrust and soil yield stress, the soil with the low water content would produce a larger sheared region.

3.3. Torque and Sheared Region Boundary

Figure 6 shows the relationship curves between the applied torque T and the parameter ${r^{\prime }}_c$ of the spiral at the sheared region boundary. The sheared region increased with the increasing torque of the cutting wheel, and the slope of the curves gradually decreased with the increase of the torque. The sheared region boundary of the soils with different moisture contents under the same torque showed obvious differences, and the soil with a high moisture content had a larger sheared region. The reason for this is that the soil with the higher moisture content had poor internal structure, low initial yield strength, and a resulting small deformation resistance.

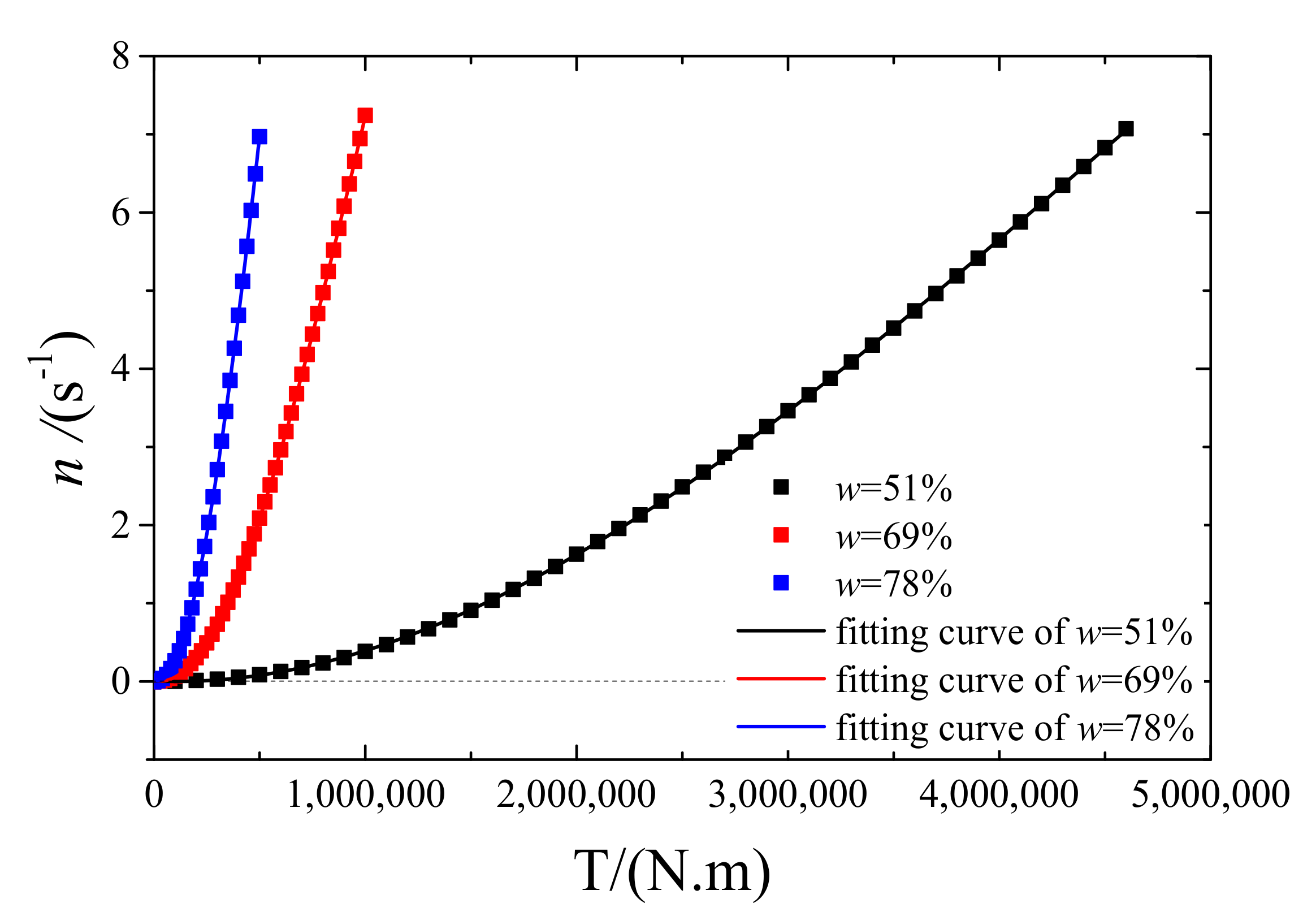
Figure 7 shows the relationship between the applied torque and the revolutions per minute of the cutting wheel. It can be seen from Figure 7 that revolutions of the cutting wheel increased with the increasing torque, and the greater the torque, the greater the revolutions increased. For the soils with different moisture content, the torques required for the shield to reach the same number of revolutions were different, and a small torque was needed in the soil with the highest moisture content.

3.4. Velocity Distribution around the Cutter Head

The revolution of the shield cutting wheel was usually controlled at 0~3 rpm. 1 rpm and 3 rpm were selected to calculate the velocity distribution of soil around the cutting wheel, respectively, as shown in Figure 8. The flow velocity of the soil gradually decreased to zero in the direction away from the cutter head; consistent with the flow velocity field around the shield, the velocity gradient gradually decreased in the direction away from the cutter head. The sheared region was affected by the revolution of the cutting wheel and the moisture content of the soil, therefore, a larger sheared region would be produced when the revolution of the cutter head is high and the soil moisture content is small. It can be seen from Figure 8 that when the moisture content was 51% and the cutter head revolution was 3 rpm, there was a maximum sheared region boundary of 1.7 m (${\theta }^{\prime }=\pi /2$). When the moisture content was 78% and the cutter head speed was 1 rpm, it had a minimum shear boundary of 0.9 m (${\theta }^{\prime }=\pi /2$). Similar to the flow velocity distribution around the shield shell, the larger sheared region corresponding to the soil with the smaller water content was the result of the combined effect of the applied torque and the yield stress of the soil. In addition, the sheared region induced by the cutting wheel was much larger than that caused by the shield shell shearing.

4. Validation

Based on the above analysis, the cutting wheel disturbance was more significant and complicated than the shield shell shearing effect, so the behavior of the soil with a moisture content of 51% induced by the cutting wheel was simulated and verified by using the fluid mechanics numerical analysis software, FLUENT.

The FLUENT software provides four models to simulate non-Newtonian fluids. Among them, the Herschel–Bulkley model is designed for Bingham plastic fluid. In this case, to define the Bingham constitutive model, the parameter of the rheological index in the Herschel–Bulkley model was set to 1, and the corresponding parameters of the soil yield stress ${\tau }_c$ and the flow consistency coefficient $K$ were 3050 Pa and 3440 Pa·s as shown in Table 2. In addition, the limit shear rate was set to 0.001. In the numerical model, a shield with a total length of 9 m and a diameter of 6.83 m was established, and its cutting wheel with a diameter of 6.86 m and a thickness of 90 cm was built. To eliminate border effects, the thickness of the underlying overburden and the width of the soil on both sides of the shield in the model was 3D (where D is the diameter of the cutting wheel), and the length of the soil in front of the cutting wheel was 5D. The cylinder surface attaching to the shield cutting wheel was set as the dynamic surface, and its revolutions were set to 1 rpm and 3 rpm. Moreover, the cylindrical surface of the shield shell and the soil boundaries were set as static surfaces. The numerical model had a total of 757,703 nodes and 148,724 grids by meshing, among which the minimum grid size was 280 mm and the maximum grid size was 560 mm.

Figure 9 shows the flow velocity field when the revolutions of the cutting wheel were 1 rpm and 3 rpm. It can be seen that the iso-velocity line was consistent with the proposed hypothesis of the Archimedes spiral. The boundaries of the sheared region simulated were extracted and compared with the theoretical solution. As shown in Figure 10, the maximum simulated lateral and front thicknesses of the sheared region were 1.5 m and 3 m at n = 1 rpm, and were 3 m and 4 m at n = 3 rpm, which were larger than the maximum theoretical lateral and front sheared region thicknesses of 1.25 m and 2 m at n = 1 rpm, and 2 m and 3.5 m at n = 3 rpm, respectively. The possible reason for this is that the influence of the cutting wheel thickness was not considered in the theoretical calculation, which underestimated the range of the sheared region near the edge of the cutting wheel. In addition, it was found that the theoretical sheared region exceeded the center of the cutting wheel when n = 3 rpm, which was different from the numerical solution. The shear spiral should converge at the center of the cutting wheel because the center speed of the shield cutting wheel was zero, as the numerical solution shown in Figure 9. In this case, the cutting range in front of the cutting wheel would also be expanded to balance the applied torque.

In conclusion, the proposed method is suitable for the case where the number of rotations per minute of the cutter head is small, but for the case of a larger number of cutter head revolutions, the proposed method has limitations. This can be explained by the change of the iso-velocity line mode due to the limitation of the cutter head radius at high revolutions. Therefore, further studies need to be conducted to propose a more precise mode of the iso-velocity line, which can eliminate the above limitations.

5. Discussion

Soft soil such as mucky, silty clay has the characteristics of shear-thinning. For example, in Shanghai and Suzhou, there will be a shear strength reduction of 2~4 times for intact soft soils after being disturbed [27]. In addition, the yield stress and viscosity of the soil also decrease significantly under the disturbance of the shield. The proposed method is suitable for ideal plastic fluid conditions, and the Bingham constitutive model used cannot describe this characteristic of the soil. Therefore, it is necessary to consider the shear-thinning effect of soft soil to further understand the fluidization behavior of soil during shield construction.

Based on the proposed theoretical method, a closed four-stage shear path to describe the shear behavior of soft soil during shield tunneling was presented in Figure 11, which fully considers the shear-thinning effect of the soil. Based on previous studies, a large sheared region will occur first in the intact soil when the cutting wheel arrives with a designed revolution n₀, as the curve of “Path I” shows in Figure 11. As a result, the strength and viscosity of the sheared soil will be greatly reduced due to the shear-thinning effect of the soil. To balance the applied torque, the sheared region will be expanded to compensate for the decrease in the yield stress of the sheared soil. Additionally, the revolutions will also be increased during the stage of “Path II”, as shown in Figure 11. In practice, it is advisable to maintain a stable cutting wheel revolution during tunneling. To keep the revolution from increasing too much, it is necessary to reduce the torque of the cutting wheel appropriately. As the curve of the “Path III” shows in Figure 11, T₁ is the required torque to maintain the designed revolution n₀ in the remolded soil, where the corresponding sheared region will also be reduced. With the shield tunneling, the cutter head contacts the intact soil again and returns to the shear path I, as the curve of the “Path IV” shows in Figure 11. Therefore, the complete process of the soil behavior during the shield tunneling is constituted by the above four shear paths.

It can be seen that the sheared region is significantly expanded due to the shear-thinning characteristics of the soil. Moreover, under the combined action of the shield machine excavation and advancing, the parameters of the soil that the shield encounters are constantly changing, which leads to large fluctuations in the tunneling parameters, and makes it more difficult to maintain parameter stability. Therefore, to minimize the disturbance of the cutter head to the soil and maintain the stability of the excavation parameters, it is recommended to use a lower cutter head revolution and advancing speed when the shield tunnels in soft soil.

6. Conclusions

The motivation for this study was to understand the behavior of soil with high water content during shield tunneling, especially the shearing action of the shield skin and the cutting wheel. In the present paper, two theoretical models of soil fluidization behavior induced by shield tunneling parameters based on the fluid mechanics framework are proposed. The iso-velocity line of the velocity field around the cutting wheel can be described as an Archimedes spiral, and that around the shield shell can be described as a sleeve coaxial with the shield.

The characteristics of the soil plastic flow are presented and their relationships with the shield advancing speed, force applied to the soil around the shield, cutting wheel rotation, torque, and water content are analyzed. Based on the usual design values of shield tunneling parameters, the sheared region produced by the cutting wheel rotating (maximum shear thickness about 4 m) is larger than that produced by the shield shell shearing (maximum shear thickness about 0.1 m). Moreover, it is found that the sheared region is significantly affected by soil moisture content and shear speed. When the shield is tunneling at the same advancing speed or rotation, the sheared region produced in soil with low moisture content (high yield stress and consistency coefficient) is the largest. The results indicate that a large sheared region will be produced in the intact soil, but when the shield is tunneling in soil with high moisture content or in the remolded soil, which has a low yield stress and consistency coefficient, the shield will cause a large sheared region under a small thrust or torque.

The proposed theory was compared with the results of a numerical simulation, and the velocity field induced by the cutting wheel is consistent with the proposed hypothesis of the Archimedes spiral, especially for the case where the number of rotations per minute of the cutter head is small.

The shear-thinning characteristics of soil will reduce its yield stress and viscosity and affect its flow behavior. Considering the shear-thinning effect of the soil, the complete process of soil behavior during shield tunneling has been described by a closed four-stage shear path, which indicates that the sheared region is significantly expanded due to the shear-thinning characteristics of the soil, and that the tunneling parameters fluctuate greatly with stability difficult to maintain.