An Experimental Study on the Mechanical Properties of a High Damping Rubber Bearing with Low Shape Factor

Abstract

A high damping rubber bearing (HDRB) is widely utilized in base-isolation structures due to its good energy dissipation capacity and environmentally friendly properties; however, it is incapable of isolating the vertical vibration caused by earthquakes and subways effectively. Thick rubber bearings with a low shape factor have become one of the important vertical isolation forms. This paper provides an experimental comparative study on high damping rubber bearings with low shape factor (HDRB-LSF), thick lead–rubber bearings (TLRB), and lead–rubber bearings (LRB). The abilities of the bearing and energy dissipation of the above bearings are analyzed contrastively considering the influence of vertical pressure, loading frequency, shear strain, and pre-pressure. Firstly, the HDRB-LSF, TLRB, and LRB are designed according to the Chinese Code for seismic design of buildings. Secondly, cyclic vertical compression tests and horizontal shear tests, as well as their correlation tests, are conducted, respectively. The vibrational characteristics and hysteresis feature of these three bearings are critically compared. Thirdly, a corrected calculation of vertical stiffness for the thick rubber bearings is proposed based on the experimental data to provide a more accurate and realistic tool measuring the vertical mechanical properties of rubber bearings. The test results proved that the HDRB-LSF has the most advanced performance of the three bearings. For the fatigue property, the hysteresis curves of the HDRB-LSF along with TLRB are plump both horizontally and vertically, thus providing a good energy dissipation effect. Regarding vertical stiffness, results from different loading cases show that the designed HDRB-LSF possesses a better vertical isolation effect and preferable environmental protection than LRB, a larger bearing capacity, and, similarly, a more environmentally friendly property than TLRB. Hence, it can avoid the unfavorable resonance effect caused by vertical periodic coupling within the structure. All the experimental data find that the proposed corrected equation can calculate the vertical stiffness of bearings with a higher accuracy. This paper presents the results of an analytical, parametric study that aimed to further explore the low shape factor concepts of rubber bearings applied in three-dimensional isolation for building structures.

1. Introduction

In recent years, basic isolation technology has been extensively applied in building construction and bridge engineering in China and overseas [1,2,3]. By the end of 2020, China had constructed more than 8000 seismic-isolated buildings. The rubber isolation system is currently the most widely used and mature isolation technology, among which the common isolation devices include the ordinary rubber bearing, natural rubber bearing (NRB) [4], LRB [5], HDRB [6], etc. The HDRB has plentiful advantages—such as a simple structure, stable mechanical performance, strong energy dissipation capacity, large stiffness before yielding, environmental protection, etc.—that make it an excellent choice for base-isolation structures. It is made of laminated rubber pads with multi-layer steel plates that are vulcanized and bonded at a high temperature, where the steel plate layers restrain the vertical deformation of the rubber layers from guaranteeing a certain vertical stiffness of the bearing. The rubber layers adapt the high damping material with graphite and other additives to be capable of simultaneously withstanding a vertical load and resist a large horizontal shear displacement. Compared with the ordinary rubber bearing, HDRB can achieve a higher equivalent damping ratio of more than 20% without matching dampers, which saves installation space. HDRB possesses greater stiffness before yielding, a better braking effect on the structure subjected to wind load, more minor damage caused by lead when processing, and is more applicable for those places with special requirements for environmental protection, especially in contrast with the lead–rubber bearing. When the structures are subjected to an earthquake, the HDRB will produce a large deformation and reduce the stiffness, thus achieving a better isolation effect. In recent years, many researchers have conducted studies on HDRB. Burtscher et al. [7] conducted experimental studies on different forms of HDRB and analyzed the influence of the shape factor and steel plate forms on the performance of the bearings. Yamamoto et al. [8] took bidirectional coupling factors into consideration when testing the horizontal shear performance of HDRB. Chen et al. [9] and Xue et al. [10] carried out vertical compression tests along with horizontal shear tests for loading on the designed HDRB. Their results proclaimed a good energy dissipation effect. Bhuiyan et al. [11] proposed a rheological model considering the nonlinear characteristics of HDRB based on the cyclic shear test, monotone relaxation test, and multi-step relaxation test. Dong et al. [12] studied the influence of shear strain and vertical compressive stress on the shear performance of HDRB through the compression–shear performance test, and made an improvement to the restoring force model of the bearing with certain accuracy. Fabio Mazza et al. [13] applied the HDRBs to two typical r.c. framed structures and conducted the structural nonlinear incremental dynamic analyses based on the refined three-spring–two-dashpot model of the bearing.

Rubber bearings, including HDRBs, are generally horizontal isolation bearings, which can reduce the horizontal seismic acceleration response of a structure by about 60%. They are incapable of decreasing or even amplifying vertical seismic effect effectively. This can be explained by the fact that ordinary rubber bearings have a vertical stiffness equivalent to thousands of times their horizontal stiffness, which means that it is likely to obtain a smaller vertical basic period of around 0.1 s and is liable to fall within the striking part of the vertical acceleration spectrum, thus resulting in poor vertical isolation. However, recent large (extra-large) earthquakes in China and abroad indicate that strong vertical ground motions that occur in high-intensity areas, especially near faults areas, may even exceed the horizontal seismic action component. After horizontal seismic action is reduced, vertical ground motion with a high peak value will become the main cause of structural destruction, particularly for medical buildings and industrial facilities. Once damaged, the function of these buildings will be disrupted and the resilience of society will be seriously affected. Hence, scholars have developed several vertical isolation devices and three-dimensional isolation devices. Jia et al. [14] designed a new three-dimensional isolation device containing lead-core rubber pads combined with dish-shaped springs and steel plate dampers. Of those devices, some have undergone complex modeling, which is not conducive to processing, while some need additional dampers to enhance their vertical damping and causing greater vertical stiffness of the bearing. Thick rubber bearings have become one of the most important vertical isolation forms. Compared with an ordinary rubber bearing, there is a conspicuous increase in the thickness of HDRB, generally 4 to 6 times higher than that of the former. The shape factor of ordinary rubber bearing typically ranges from 15 to 30 or more, while that of HDRB is designed to vary from 2 to 5. In 1989, Aiken et al. [15] set the shape factor of the individual 1/4 scale bearings as 2.4 and characterization tests were then conducted. Warn and Vu [16] found that three-dimensional isolation for low and mid-rise structures would be achieved if the shape factors of the elastomeric bearings was set to be less than 4 and significant vertical damping was supplemented. Kanazawa et al. [17] designed a thick rubber bearing with the second shape factor of 4.1, aiming to study the damping effect on the equipment in a nuclear reactor. Zhu et al. [18] selected three thick lead-core rubber bearings with shape factors of 8.0, 12.0, and 16.7, respectively, to conduct basic mechanical properties tests on them. Wang [19] carried out studies on the basic mechanical properties of five thick rubber bearings with shape factors between 4.13 and 5.37 and with different diameters, summarized the law of vertical stiffness parameters of new thick rubber bearings, and then proposed a design method of anti-buckling low-frequency seismic isolation bearings. Liu and Huang [20] compared the vertically seismic response spectrum between prestressed and non-prestressed thick rubber bearings with the shape factor of 3.29. Li et al. [21] conducted a series of experimental studies on shear stiffness, vertical stiffness, deformation performance, fatigue performance, creep performance, and aging performance of thick rubber bearings with the second shape factor of 1.85. The research results of many scholars around the world illustrate that compared with ordinary rubber bearings, thick rubber bearings have smaller vertical stiffness and superior vertical isolation performance, which can avoid the adverse resonance effect caused by the vertical period of vibration coupling with the structure.

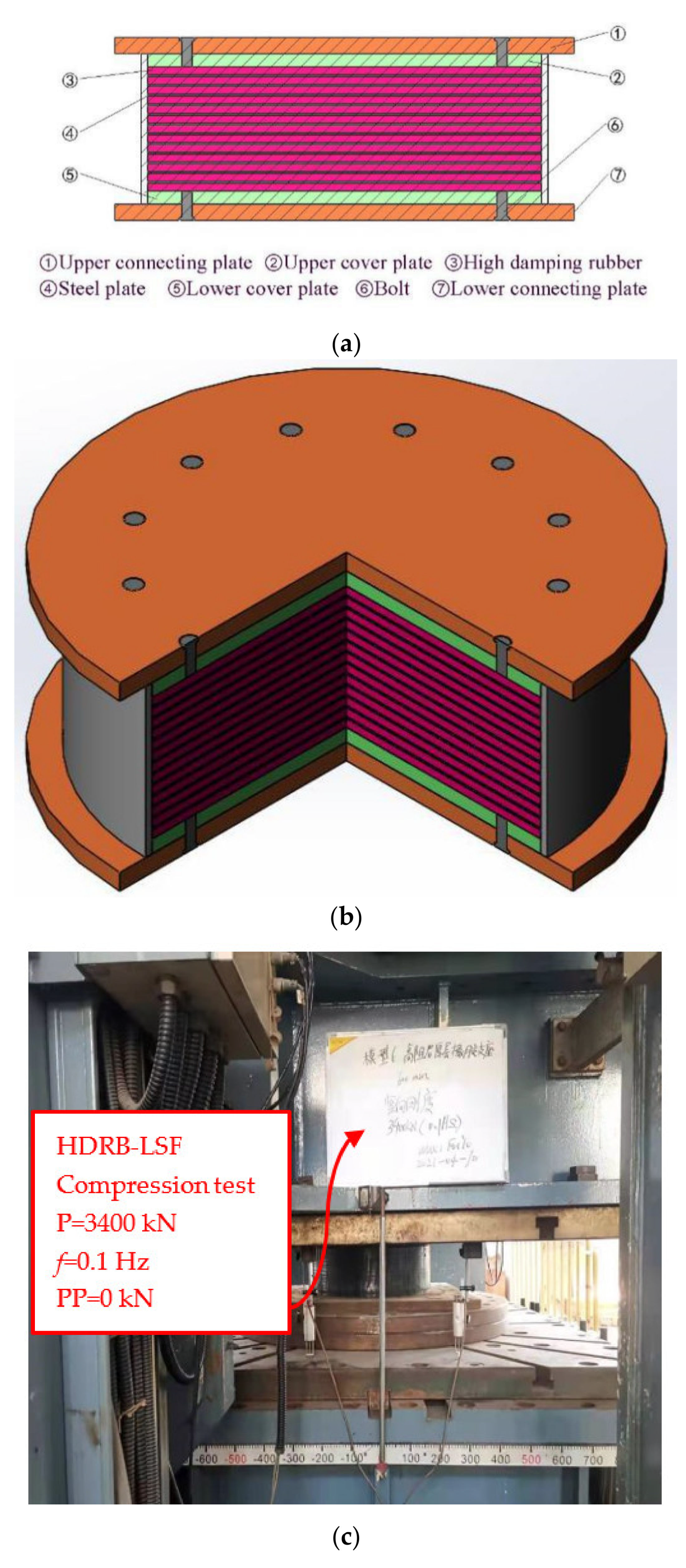
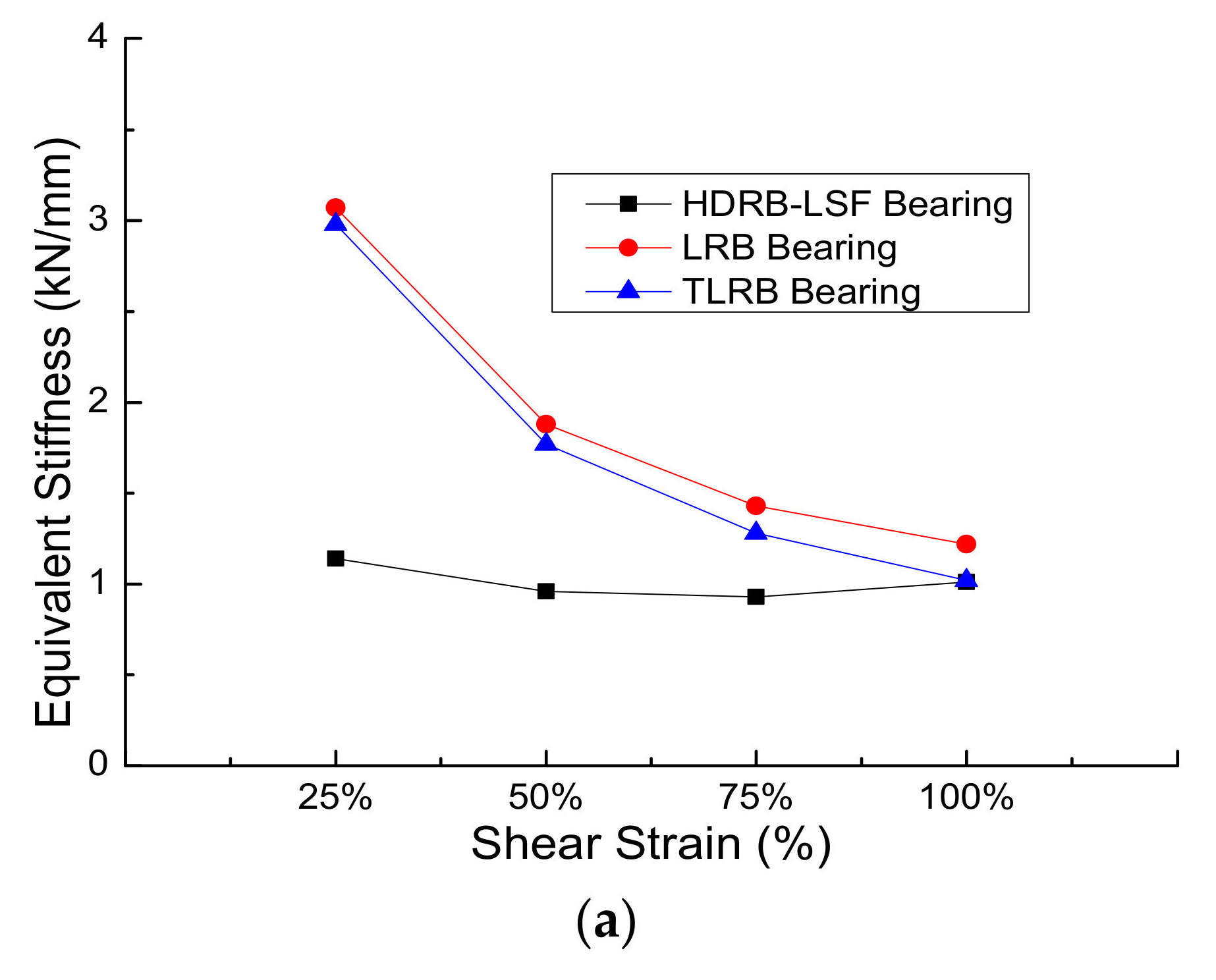
In this paper, three bearings, including HDRB-LSF, TLRB, and LRB, were designed. Then, vertical compression performance tests, horizontal shear performance tests, vertical compression correlation tests, and horizontal shear correlation tests were carried out. The effects of vertical compressive stress, pre-pressure, shear strain, and loading frequency on the performance of the above three bearings were studied. The performance differences of the bearings were compared. Considering that the experimental results of HDRB-LSF displayed a big discrepancy with the theoretical values, a correction method for vertical stiffness of HDRB-LSF was proposed, and the modified values were found to be in good agreement with the experimental results.

2. Experimental Process

2.1. Specimen Design

Three bearings, including HDRB-LSF, TLRB, and LRB were adapted in the test. Figure 1 only displays the configuration of HDRB-LSF. All the bearings were fabricated with a diameter of 600 mm. The thickness and the diameter of the upper and lower sealing plate were 20 mm and 600 mm, respectively. The thickness and the diameter of the upper and lower connecting plates were 25 mm and 700 mm, respectively. The three bearings were designed according to a principle that the total thickness of 156 mm for the rubber pads in the bearings equals.

The first shape factor of the rubber bearing (S₁) is defined as (D − d)/(4t_r), and the second shape factor (S₂) is defined as D/(n_rt_r). D and d denote the diameter of the effective bearing surface and the diameter of the central opening for a bearing, respectively. If the central hole in the bearing is filled with rubber or lead, the opening can be ignored on the basis of the Specification GB/T20688.1-2007 [22]. n_r and t_r are the number and the thickness of rubber layers, respectively. S₁ value of LRB is 37.50, while the S₁ value of TLRB and HDRB-LSF is 12.50. Based on the research experience, t_r and S₁ are important parameters determining the bearing stiffness. The S₁ of LRB is three times that of TLRB and HDRB-LSF, indicating that LRB possesses greater vertical stiffness and more stable bearing capacity vertically. The S₂ value of all the above bearings keeps unchanged at 3.85, explaining that their horizontal stiffness is consistent.

The other dimension parameters of each bearing are listed in

Table 1. Basic parameters of the bearings.

Bearings	D (mm)	dl (mm)	tr (mm)	nr	ts (mm)	ns	S1	S2
HDRB-LSF	600	-	12	13	2.8	12	12.5	3.85
TLRB	600	120	12	13	2.8	12	12.5	3.85
LRB	600	120	4	39	2.8	38	37.5	3.85

, where d_l is the diameter of lead core; n_s and t_s are the numbers and the thickness of steel plates. In the specimens steel plates were made from Q345 material; the rubber pads of HDRB-LSF were made from high damping rubber with a shear modulus of 0.392 MPa and a rubber hardness of 56 HA (Shore hardness); the rubber pads of TLRB and LRB were made from ordinary rubber material with a shear modulus of 0.6 MPa and a rubber hardness of 42 HA. Here, it should be noted that each of the two thick rubber bearings had a small hole in the center when fabricated to facilitate vulcanization. According to the specification: after vulcanization, specimens with a total height of less than 250 mm should be rested for at least 24 h, while other specimens should be rested for more than 48 h. Hence, all the test specimens were rested for more than 48 h after vulcanization and then kept in the testing environment for another 24 h before the test.

The vertical stiffness (K_v) and the horizontal stiffness (K_h) of the ordinary rubber bearing were calculated by Equations (1) and (2) according to the specification GB/T20688.3-2006 [23], where A is the whole effective cross-section area of the bearing; E_c is the modified compressive elastic modulus of laminated rubber under vertical pressure load, which can be obtained from Equation (3); E_v is the volumetric elastic modulus of rubber; E_cb is the apparent elastic modulus of rubber obtained from Equation (4); E₀ represents the elastic modulus of rubber; k is a correction coefficient for the elastic model of rubber material related to rubber hardness; and G is the shear modulus of laminated rubber.

$${}_{{\mathrm{K}}_{\mathrm{v}}=\frac{{\mathrm{E}}_{\mathrm{c}}\mathrm{A}}{{\mathrm{n}}_{\mathrm{r}}{\mathrm{t}}_{\mathrm{r}}}=\frac{\pi \mathrm{D}}{4}{\mathrm{E}}_{\mathrm{c}}{\mathrm{S}}_2}$$

(1)

$${}_{{\mathrm{K}}_{\mathrm{h}}=\frac{\mathrm{GA}}{{\mathrm{n}}_{\mathrm{r}}{\mathrm{t}}_{\mathrm{r}}}}$$

(2)

$${\mathrm{E}}_{\mathrm{c}}=\frac{{\mathrm{E}}_{\mathrm{cb}}\times {\mathrm{E}}_{\mathrm{v}}}{{\mathrm{E}}_{\mathrm{cb}}+{\mathrm{E}}_{\mathrm{v}}}$$

(3)

$${}_{{\mathrm{E}}_{\mathrm{cb}}={\mathrm{E}}_0\left(1+2k{S}_1^2\right)}$$

(4)

For LRB, the computational formula of vertical stiffness (K_v) is the same as an ordinary rubber bearing. However, the shear stiffness obtained from Equation (2) is merely the post-yield stiffness, and its equivalent shear stiffness can be written as

$${\mathrm{K}}_{\mathrm{h}}^{\prime }=\frac{{\mathrm{K}}_{\mathrm{h}}\mathrm{X}+\mathrm{Q}}{\mathrm{X}}$$

(5)

where X is the horizontal shear displacement of the bearing; Q is the yield force of the LRB that linearly correlated with the cross-section area of the lead core and can be acquired by the following formula [24].

$$\mathrm{Q}=\frac{8.367\pi {\mathrm{d}}_l^2}{4}+4.682$$

(6)

where d_l is the diameter of the lead core. It should be pointed out that the role of the lead core should be considered when calculating the vertical stiffness of LRB in Equation (1). The cross-section area A is not the simple addition of lead core cross-section and rubber cross-section but is the relational expression that A = A_r +A_l (E_l/E_c − 1), where A_r and A_l are the cross-section area of rubber and the cross-section area of lead core, respectively; E_l is the elastic modulus of lead core.

We calculated that the designed shear stiffness of HDRB-LSF, TLRB, and LRB are 1.09 kN/mm, 1.35 kN/mm, and 1.35 kN/mm, respectively. The vertical stiffness values of the above three bearings are 706.13 kN/mm, 581.94 kN/mm, and 2116.18 kN/mm, respectively.

2.2. Test Method

The loading device used in the test is shown in Figure 2. Vertical parameters of the compression and shear test device were: the maximum pressure was 20,000 kN, the maximum tension was 6000 kN, the maximum displacement stroke was 700 mm, and the maximum loading speed was 3 mm/s. Horizontal parameters of this device were: the maximum shear test force was ± 6000 kN, the maximum displacement stroke was ±600 mm, and the maximum loading speed was 10 mm/s. Vertical and horizontal loading adopted force control and displacement control, respectively. The acquisition of data relied on an automatic data acquisition system. The vertical pressure was assumed to be P. For the vertical compression performance test, cyclic loading was carried out within the range of P ± 0.3 P. According to the Chinese Specification [19], three loading cycles are recommended for the performance test of rubber bearings. In this test, four cycles were actually loaded to guarantee the data integrity of the third cycle, and the results of the third cycle were extracted to calculate the performance of the bearings.

2.3. Test Cases

Based on the design surface pressure of 12 MPa, according to the Code, and bearing diameter of 600 mm, the specified vertical pressure P was determined as 3400 kN. In order to analyze the influencing factors of vertical stiffness of the three specimens, loading cases with different pre-pressures, vertical pressures, and loading frequencies were successively carried out, as shown in

Table 2. The cases of the vertical compression test.

Cases	Pre-Pressure (kN)	Vertical Pressure (kN)	Loading Frequency (Hz)
Case 1	0	2900	0.01
Case 2	0	2900	0.02
Case 3	0	2900	0.05
Case 4	0	2900	0.1
Case 5	0	3400	0.01
Case 6	0	3400	0.02
Case 7	0	3400	0.05
Case 8	0	3400	0.1
Case 9	0	3700	0.01
Case 10	0	3700	0.02
Case 11	0	3700	0.05
Case 12	0	3700	0.1
Case 13	1700	3400	0.1
Case 14	2040	3400	0.1
Case 15	2720	3400	0.1

. For the horizontal compression and shear performance test, when the specified vertical pressure P (3400 kN) was used, the corresponding shear displacements under 25%, 50%, 75%, and 100% of shear strain γ were, respectively, applied at different loading frequencies of 0.01 Hz, and 0.0082 Hz. When the loading frequency was 0.01 Hz and the shear strain γ was 100%, loading cases with different vertical pressure P of 3400 kN, 4250 kN, and 5100 kN were launched to analyze the shear strain correlation of the horizontal performance for the three specimens, which can be seen in

Table 3. The cases of the horizontal shear test.

Cases	Vertical Pressure (kN)	Shearing Strain γ	Shear Displacement (mm)	Loading Frequency (Hz)
Case 16	3400	±25%	39	0.01
Case 17	3400	±50%	78	0.01
Case 18	3400	±75%	117	0.01
Case 19	3400	±100%	156	0.01
Case 20	3400	±25%	39	0.0082
Case 21	3400	±50%	78	0.0082
Case 22	3400	±75%	117	0.0082
Case 23	3400	±100%	156	0.0082
Case 24	4250	±100%	156	0.01
Case 25	5100	±100%	156	0.01

.

3. Test Results and Analysis

3.1. Vertical Compression Performance of Bearings

The vertical compression performance tests with 100% shear strain were carried out on the three bearings, respectively, under the designed vertical pressure P of 3400 kN and loading frequency of 0.1 Hz (Case 8). Four loading and unloading cycles were conducted for each test case of the three bearings within the range of P ± 0.3 P, and the schematic diagram of vertical loading mode is shown in Figure 3. Figure 4 gives the vertical load–displacement curves of the bearings. It indicates that the vertical energy dissipation effect of HDRB-LSF and TLRB is superior to LRB. With the increase of compressive stress, extrusion deformation occurred in the rubber layer causing the vertical displacement of the bearings. The slopes of hysteresis curves—i.e., the vertical stiffness of the bearings—showed an augmented tendency. Under the action of equal compressive stress, the vertical stiffness of different bearings varied, explaining that the vertical stiffness of a bearing has a close relation with the thickness and the properties of the rubber material.

The third cyclic results of the vertical load–displacement curves of the three bearings under different loading frequencies, pre-pressures, and vertical pressures were obtained, and the effects of these parameters on the vertical stiffness of bearings were analyzed.

3.1.1. Loading Frequency

Test data from cases 1–12 were extracted, and correlation tests of loading frequencies were carried out on three bearings, which aimed to study the influence on hysteresis behavior of high-damping isolation bearings. Due to space limitations, Figure 5 only gives the hysteresis curves of the three bearings at different loading frequencies when the vertical pressure is 3400 kN. It can be seen that the shape of the vertical hysteresis curves for all the bearings obtained by cyclic loading with different loading frequencies are basically the same. Loading frequency has a diverse effect degree on the vertical mechanical properties of different bearings; TLRB is most sensitive to it. With the augment of loading frequency, the vertical stiffness of each bearing presents an increasing trend. When the loading frequency was rather low, it had a slight influence on the vertical performance of the bearings, while the vertical compression displacements observably changed as the loading frequency was relatively high (0.05 Hz and 0.1 Hz).

3.1.2. Vertical Pressure

Figure 6 listed the load–displacement curves of the three bearings under different vertical pressures (2900 kN, 3400 kN, and 3700 kN) at a loading frequency of 0.1 Hz. It explains that the hysteretic curve slopes of the bearings, namely the vertical compression stiffness, increases significantly with the growth of vertical pressure. Among them, the curve shape for LRB is less sensitive to vertical pressure compared to TLRB and HDRB-LSF, which have thick rubber layers. This is due to the fact that as the vertical pressure increases, the thickness of the rubber layer for TLRB and HDRB-LSF diminishes, and the constraint effect of the steel plate is strengthened, ultimately leading to the rapid enlargement of compression modulus of the rubber in the triaxial compression state.

3.1.3. Pre-Pressure

From the extracted test data from cases 1–12, the effect results of different pre-pressures (1700 kN, 2040 kN, and 2720 kN) on the three bearings were obtained, under the vertical pressure of 3400 kN and the loading frequency of 0.1 Hz. The obtained vertical compression load–displacement curves are drawn in Figure 7. As can be seen from the figure, the slopes of the hysteretic curves augment significantly with the growth of pre-pressures, indicating that the pre-pressure has a great influence on the vertical stiffness of the bearings, especially for HDRB-LSF and TLRB.

3.1.4. Results of Vertical Stiffness

We assumed P₁ and P₂ as the small pressure and the larger pressure in the third cycle, and gave them the values of 0.7 P and 1.3 P, respectively. We assumed Y₁ and Y₂ were the smaller displacement and the larger displacement in the third cycle, respectively. The vertical compression stiffness of all the bearings under various test cases was calculated according to Equation (7), as shown in Figure 8, Figure 9 and Figure 10.

$${\mathrm{K}}_{\mathrm{V}}=\frac{{\mathrm{P}}_2-{\mathrm{P}}_1}{{\mathrm{Y}}_2-{\mathrm{Y}}_1}$$

(7)

The error of the vertical stiffness for the bearings is equal to the difference between the theoretical value and the test value divided by the theoretical value. Due to the limited length of the article,

Table 4. Vertical stiffness error between theoretical value and test value (%).

Loading Frequency (Hz)	HDRB-LSF	TLRB	LRB
0.01	68.30	−9.53	1.16
0.02	70.42	−8.49	3.91
0.05	81.96	6.19	7.44
0.1	98.88	22.59	11.32

only shows the comparison results of theoretical and experimental values of vertical stiffness when the vertical pressure is 3400 kN and the pre-pressure is 0 kN.

As can be seen from Figure 8, Figure 9 and Figure 10, under different loading cases the vertical stiffness of LRB is largest in the range between 2050 kN/m and 2450 kN/m. The vertical stiffness of HDRB-LSF takes second place within the range of 1050 kN/m and 1450 kN/m, while the vertical stiffness of TLRB is the lowest, varying from 450 kN/m and 850 kN/m. With the increase in loading frequency, the vertical stiffness of almost all bearings has an increase in different amplitude. When the loading frequency varies from 0.01 Hz to 0.02 Hz, the vertical stiffness values of the HDRB-LSF, LRB, and TLRB improve by 1.3–3.3%, about 2.7%, and 1.1–6.6%, respectively. Whereas when the loading frequency is enlarged from 0.05 Hz to 0.1 Hz, the vertical stiffness values of the HDRB-LSF, LRB, and TLRB improve by 9.1–12.1%, 3.2–4.6%, 13–19.6%. Hence, it can be concluded that the vertical stiffness of LRB is relatively stable, while that of HDRB-LSF and TLRB is sensitive to the change of loading frequency. It can be seen from the table that it is not certain whether the test value or theoretical value is more remarkable for the vertical stiffness of TLRB, while the test values of vertical stiffness for LRB and HDRB-LSF always surpass the theoretical value. Additionally, the margin of error between the test values and the theoretical values of vertical stiffness for the LRB and TLRB are small, which is basically in line with the specific design requirements. The test values of the vertical stiffness for HDRB-LSF are larger than the theoretical value, which means that it is biased towards safety in the bearing design. However, this error has exaggerated what needs to be corrected. The vertical stiffness of LRB is larger than that of HDRB-LSF and TLRB, illustrating that: (1) in the case of equal total thickness of the rubber layer, the larger the number of rubber layers, the greater the vertical stiffness, due to the steel plate that has a strong constraint ability on the transverse deformation of rubber; (2) for the two bearings with thick rubber, the vertical stiffness of the one with the lead core is smaller than the one with high damping rubber, showing that the latter has a marginally worse isolation capability but greater bearing capacity vertically.

3.2. Horizontal Shear Performance

Horizontal shear performance tests were carried out on the three bearings, in which the pressure was slowly and continuously loaded to 3400 kN and remained constant. The shear displacement corresponding to γ = 100% was applied horizontally at a low frequency of 0.01 Hz, and the whole loading process consisted of four cycles. The horizontal stiffness K_h and equivalent damping ratio h_eq of a bearing can be calculated according to Equations (8) and (9):

$${\mathrm{K}}_{\mathrm{h}}=\frac{{\mathrm{Q}}_2-{\mathrm{Q}}_1}{{\mathrm{X}}_2-{\mathrm{X}}_1}$$

(8)

$${\mathrm{h}}_{\mathrm{eq}}(\mathsf{\gamma })=\frac{1}{\pi }.\frac{{\mathrm{W}}_{\mathrm{d}}}{2{\mathrm{K}}_{\mathrm{H}}(\mathsf{\gamma }{\mathrm{T}}_{\mathrm{r}})2}$$

(9)

where Q₁ and Q₂ are the maximum and the minimum shear forces of the third cycle, respectively; X₁ and X₂ denote the positive and the negative maximum displacement of the third cycle, respectively, and X₁ = T_rγ, X₂ = T_r(−γ); and T_r is equal to the product of n_r and t_r. ΔW represents the envelope area of the hysteresis curve.

The horizontal hysteresis curves of the tested bearings are shown in Figure 11. It can be seen from the figure that the curves of the three bearings are respectively in crescent shape (HDRB-LSF) and spindle shape (TLRB and LRB). Among them, the hysteresis curves of HDRB-LSF are relatively less plump, that is, the energy dissipation capacity of which is surprisingly inferior to TLRB and LRB under the same shear deformation condition. The shape of hysteretic curves of each bearing is basically consistent with the specification requirements.

Horizontal shear performances of the bearings are shown in

Table 5. Horizontal performance error between theoretical value and test value.

Bearings		HDRB-LSF	TLRB	LRB
Equivalent stiffness (kN/mm)	Theoretical value	1.09	1.35	1.35
	Test value	1.01	1.02	1.22
	Error (%)	−7.34	−24.44	−9.63
Equivalent damping ratio (%)	Theoretical value	8.06	23.56	28.69
	Test value	9.26	38.89	31.75
	Error (%)	14.89	32.36	10.67

. It shows that under the same vertical pressure and shear strain the horizontal equivalent stiffness of HDRB-LSF is smaller than those of TLRB and LRB, which indicates that under the premise of the equal total thickness of rubbers, the steel plates in HDRB-LSF have less binding force on rubbers than the bearings with lead core.

The energy dissipation capacity of bearings is currently expressed by the equivalent damping ratio. The horizontal equivalent damping ratio of HDRB-LSF was approximately 9% in the third cyclic test (it was about 13% in the first cyclic test), expressing a better energy dissipation capacity than the NRB with a usual equivalent damping ratio of 3%. However, compared to TLRB and LRB with the lead core in the test, the energy dissipation capacity of HDRB-LSF designed in this paper is insufficient and needs improvement. When the vertical pressure is 3400 kN and the shear strain is 100%, the errors between the experimental values and the theoretical values of the horizontal performance of HDRB-LSF and LRB are both less than 15%. In contrast, the errors for TLRB are significant.

In order to quantitatively evaluate the horizontal shear stiffness of the three bearings and studying its relationship with shear deformation, axial pressure, and loading frequency, the third cyclic results of horizontal hysteresis curves of the bearings subjected to various test cases were acquired. Then, the influences of different parameters on the horizontal stiffness and equivalent damping ratio of the three bearings were analyzed.

3.2.1. Shear Strain

The designed vertical pressure of 3400 kN was smoothly exerted in the three bearings and remained unchanged during the whole test process. Under the frequency of 0.01 Hz, horizontal sinusoidal excitation waves were loaded with the shear strains of 25%, 50%, 75%, and 100% in succession, until unloading was completed in all cycles under all shear strains. The data acquisition instrument recorded the data during the whole loading process.

The designed vertical pressure of 3400 kN was smoothly exerted to the three bearings and remained unchanged during the whole test process. Under the frequency of 0.01 Hz, horizontal sinusoidal excitation waves were loaded with the shear strains of 25%, 50%, 75% and 100% in succession, until unloading was completed in all cycles under all shear strains. The data acquisition instrument recorded the data during the whole loading process.

The horizontal shear performance of each bearing can be seen in Figure 12. As the shear displacement aggrandizes, the slopes of the curves gradually reduce, due to the reason that the compression area of the bearing core decreases, which can lessen the constraint of steel plates on the internal rubbers. The hysteresis curves of the bearings become larger as the shear strain grows, indicating that their energy dissipation capacity is strengthened. It should be noted that after multiple loads, points of contraflexure appear on the load–displacement curves, as seen in Figure 12b,c, and the degree of contraflexure on the curves gradually increases as the loading displacement grows.

The test values of horizontal equivalent stiffness and the equivalent damping ratio of the bearings are displayed in Figure 13. It can be seen that under the same shear strain, the horizontal equivalent stiffness of LRB and TLRB are adjacent throughout the test, and the stiffness of the former is slightly larger than that of the latter, while that of HDRB-LSF is the smallest. TLRB has most significant horizontal equivalent damping ratio, followed by LRB and HDRB-LSF, according to priority. The shear strain has an unnoticeable effect on HDRB-LSF and TLRB, but has an obvious impact on LRB whose growth of shear displacement is faster than the increase of the hysteretic curve area [14].

3.2.2. Loading Frequency

Similarly, the remaining vertical pressure of 3400 kN was exerted to the three bearings. Under a shear strain of 100%, horizontal reciprocating loads were applied to all the bearings at successive frequencies of 0.01 Hz and 0.0082 Hz, respectively. The horizontal hysteresis curves, horizontal equivalent stiffness, and equivalent damping ratio of the bearings obtained by the test are shown in Figure 14 and

Table 6. Horizontal performance of the bearings under different loading frequencies.

Loading Frequency (Hz)	Equivalent Stiffness (kN/mm)			Equivalent Damping Ratio (%)
	HDRB-LSF	TLRB	LRB	HDRB-LSF	TLRB	LRB
0.01	1.09	1.35	1.22	9.26	38.89	31.75
0.0082	0.97	1.01	1.21	8.90	38.29	31.15

, respectively. It can be seen that the horizontal equivalent stiffness and equivalent damping ratio of the three bearings all decline with the diminution of loading frequency within a narrow varying range.

3.2.3. Vertical Pressure

Due to the effect of the horizontal overturning moment and vertical seismic action, the vertical pressure on the rubber bearing will change considerably, which will have a certain influence on the shear performance of the bearing. Therefore, it is important to study the pressure correlation of the shear performance for the bearings. The three bearings were slowly and continuously loaded vertically with the vertical pressure loaded to 3400 kN, 4250 kN (1.25 P), and 5100 kN (1.5 P), respectively, and the pressure remained unchanged during the subsequent test. The shear strain was 100% and the horizontal reciprocating load was successively applied to each bearing at the loading frequency of 0.01 Hz. The hysteretic curves of the bearings obtained by the test are shown in Figure 15. The horizontal equivalent stiffness and equivalent damping of the bearings were calculated and are listed in

Table 7. Horizontal performance under different vertical pressures.

	Bearings	Vertical Pressure (kN)
		3400	4250	5100
Equivalent stiffness (kN/mm)	HDRB-LSF	1.01	1.06	0.94
	TLRB	1.02	0.91	0.82
	LRB	1.22	1.21	1.16
Equivalent damping ratio (%)	HDRB-LSF	9.26	10.14	11.39
	TLRB	38.89	43.76	49.30
	LRB	31.80	33.03	34.57

.

As can be seen from the figure and table, HDRB-LSF and LRB are more sensitive to the change of vertical pressure. The horizontal equivalent stiffness of HDRB-LSF increases and then reduces with the growth of vertical pressure, while that of TLRB and LRB gradually decreases with it, which is due to the axial compression and 100% shear deformation caused the out-of-plane distortion of the steel plates, thus reducing the horizontal constraint of the steel plates on the rubber pads. Therefore, the designed surface pressure of the bearing must be strictly limited when it is employed. The equivalent damping ratios of all the three bearings enlarged as the vertical pressure grew, owing to the fact that the higher vertical pressure boosted the triaxial stress of the rubber layer, making the rubber material inside the bearing denser, and magnifying the intermolecular friction of the rubber material, leading to the increase of the hysteretic curve area and equivalent damping ratio. Although the HDRB-LSF has a certain horizontal energy dissipation capacity, the values of the equivalent damping ratio for HDRB-LSF are rather low, owing to the fact that the equivalent damping ratio of high damping rubber material was set to be around 10% when fabricated and considering the constant cost as compared to TLRB and LRB. This paper emphasizes studying the isolation performance law of all the rubber bearings vertically and horizontally used in the base-isolation structures. Hence, the low equivalent damping ratio for HDRB-LSF is acceptable. Of course, a follow-up study of HDRB-LSF will enhance its equivalent damping ratio and reach the corresponding level of the bearings with a lead core.

4. Formula Modification

Therefore, the vertical stiffness of HDRB-LSF and TLRB with thick rubber layer deviates significantly from the theoretical results calculated according to the Lindley Formula and has exceeded the allowable range of engineering design. Hence, the vertical stiffness formulas for the bearing with a thick rubber layer will be revised in this section.

4.1. Theoretical Derivation

As can be seen from Table 4, the test values of vertical stiffness for HDRB-LSF are larger than the theoretical values. When the total thickness of the rubber is constant, the rubber pads of the ordinary thin rubber bearing under pressure are constrained by the steel plates, causing a sizeable vertical stiffness value. Whereas for the thick rubber bearing, the rubber thickness of a single layer is great, leading to the limited constraint effect of the steel plates on the rubber pads and large transverse deformation of the rubber layers, so that its vertical stiffness is more minor. The error of the vertical stiffness between the test value and the theoretical value calculated according to the code is too large to ignore, which cannot adapt to the requirements of engineering design. Hence, the theoretical formula of vertical stiffness must be modified.

It is known from the study that the error of the vertical stiffness for the bearing between the test value and the theoretical value is related to the compressive stress σ and the loading frequency f of the bearing. The theoretical formula can be modified with the following formulas:

$${\mathrm{K}}_{\mathrm{V}}={\mathsf{\varsigma }}_{\mathrm{V}}\frac{{\mathrm{E}}_{\mathrm{c}}\mathrm{A}}{{\mathrm{n}}_{\mathrm{r}}{\mathrm{t}}_{\mathrm{r}}}$$

(10)

$${\mathsf{\varsigma }}_{\mathrm{V}}={\mathsf{\varsigma }}_1\frac{\mathsf{\sigma }}{{\mathsf{\sigma }}_0}{+\mathsf{\varsigma }}_2{\mathrm{f}+\mathsf{\varsigma }}_3$$

(11)

where ${\mathsf{\varsigma }}_{\mathrm{V}}$ is the correction coefficient; ${\mathsf{\varsigma }}_1$, ${\mathsf{\varsigma }}_2$, and ${\mathsf{\varsigma }}_3$ are the correction coefficients, which all can be obtained by the fitting of a polynomial based on the experimental data, and their values are 0.762, 3.599, and 0.8631, respectively; σ₀ is the design compressive stress, i.e., 12 Mpa.

4.2. Modification Results

Figure 16 exhibits the theoretical values, the test values, and the modified theoretical values of the vertical stiffness for HDRB-LSF.

It explains that the modified theoretical values of the vertical stiffness are closer to the test values than the original theoretical values. All the errors between them are less than 1.5%, indicating that the modified method is basically feasible. Moreover, the smaller the vertical pressure, the smaller the error. However, the accuracy of the fitting formula depends on the test samples of the fitting analysis. The test data of the bearings used are few, thus the coverage range of the sample parameters is limited. The applicability of the fitting Equation (9) needs to be further verified in future research.

5. Conclusions

In this paper, three rubber bearings (HDRB-LSF, TLRB, and LRB) were analyzed contrastively via comprehensive experimental studies. The properties of vertical stiffness, horizontal equivalent stiffness, horizontal equivalent damping ratio, and hysteretic curves were tested under different vertical pressures, loading frequencies, shear strain values, and pre-pressures. A corrected calculation for the vertical stiffness of the bearing is proposed based on the results of the study. The results show that the HDRB-LSF possesses stable and reliable performance in the rubber isolation system among all the bearing types. Its vertical stiffness could be accurately calculated by our proposed modified equation. The main conclusions are as follows:

(1)

The vertical stiffness of the bearings increases with the growth of vertical pressure, loading frequency, and pre-pressure. Based on the premise of the equal total thickness of rubber, the vertical stiffness of LRB with thin rubber layer is much larger than that of TLRB and HDRB-LSF with thick rubber layers, and the ratio of LRB to TLRB for the vertical stiffness value reaches approximately 4. The vertical stiffness of TLRB is smaller than HDRB-LSF with equal conditions, which reflects that the material property and the thickness of the rubber material are equally crucial to the mechanical properties of the bearing.

(2)

The horizontal equivalent stiffness of LRB and TLRB with the lead core is greater than that of HDRB-LSF with high damping rubber. When the shear strain and the vertical pressure increase, the horizontal equivalent stiffness of the LRB and TLRB declines, and the gap of the stiffness between them and HDRB-LSF keeps narrowing. The hysteretic curves of HDRB-LSF and TLRB are sensitive to the change of pressure, while those of LRB show little difference. The horizontal mechanical properties of the bearings are affected by loading frequency in different degrees. The equivalent damping ratios of the bearings with lead cores remain above 30%, which is larger than those of HDRB-LSF, according to the designed damping ratios of the three bearings. However, the test results have already exhibited the good energy dissipation capacity of the three bearings. The follow-up study of HDRB-LSF will enhance its equivalent damping ratio, reaching the corresponding level of the bearings with a lead core.

(3)

The errors of the vertical stiffness of the thick rubber bearings between the test value and the theoretical value are exaggerated. Hence, the fitting modification of the theoretical vertical stiffness formula for the HDRB-LSF is carried out. The proposed modification method can better predict the vertical stiffness of the bearing under a certain vertical pressure.

(4)

In summary, unlike the LRB, which is usually used for horizontal isolation, the application of thick rubber bearings including HDRB-LSF and TLRB can simultaneously help important buildings avoid suffering the adverse effects of horizontal and vertical earthquakes on the structure itself and indoor equipment, as well as to improve the post-earthquake recovery of building structures. Compared with TLRB, HDRB-LSF is better suited for the structures when considering their larger bearing capacity and more environmentally friendly characteristics. It should be noted that the surface pressure on the thick rubber bearings should be strictly limited in engineering applications. This paper presents the results of an analytical, parametric study that aimed to further explore the low shape factor concept applied in three-dimensional isolation for building structures.