Recombination of Poly(Acrylic Acid) Radicals in Acidic Aqueous Solutions: A Pulse Radiolysis Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. PAA Solutions Preparation
2.3. PAA Solution Characterization
2.3.1. Dynamic Light-Scattering Measurements (DLS)
2.3.2. Gel Permeation Chromatography (GPC/SEC)
2.3.3. Viscosity Measurements
2.4. Irradiation of PAA Solutions and Model Compounds, Recording the Kinetic Data
2.4.1. Pulse Radiolysis in a Flow System
2.4.2. Pulse Radiolysis in a Stand-Alone Cell
3. Results and Discussion
3.1. Physicochemical Properties of the Studied Systems
3.1.1. Molecular Weights and Dimensions of PAA and OAA
3.1.2. pH and Degree of Dissociation of Carboxylic Groups
3.1.3. Critical Hydrodynamic Concentrations
3.2. Generation and Detection of Free Radicals

3.3. Radical Lifetime as a Function of pH
3.4. Radical Decay Kinetics at pH 2
3.4.1. Kinetic Traces
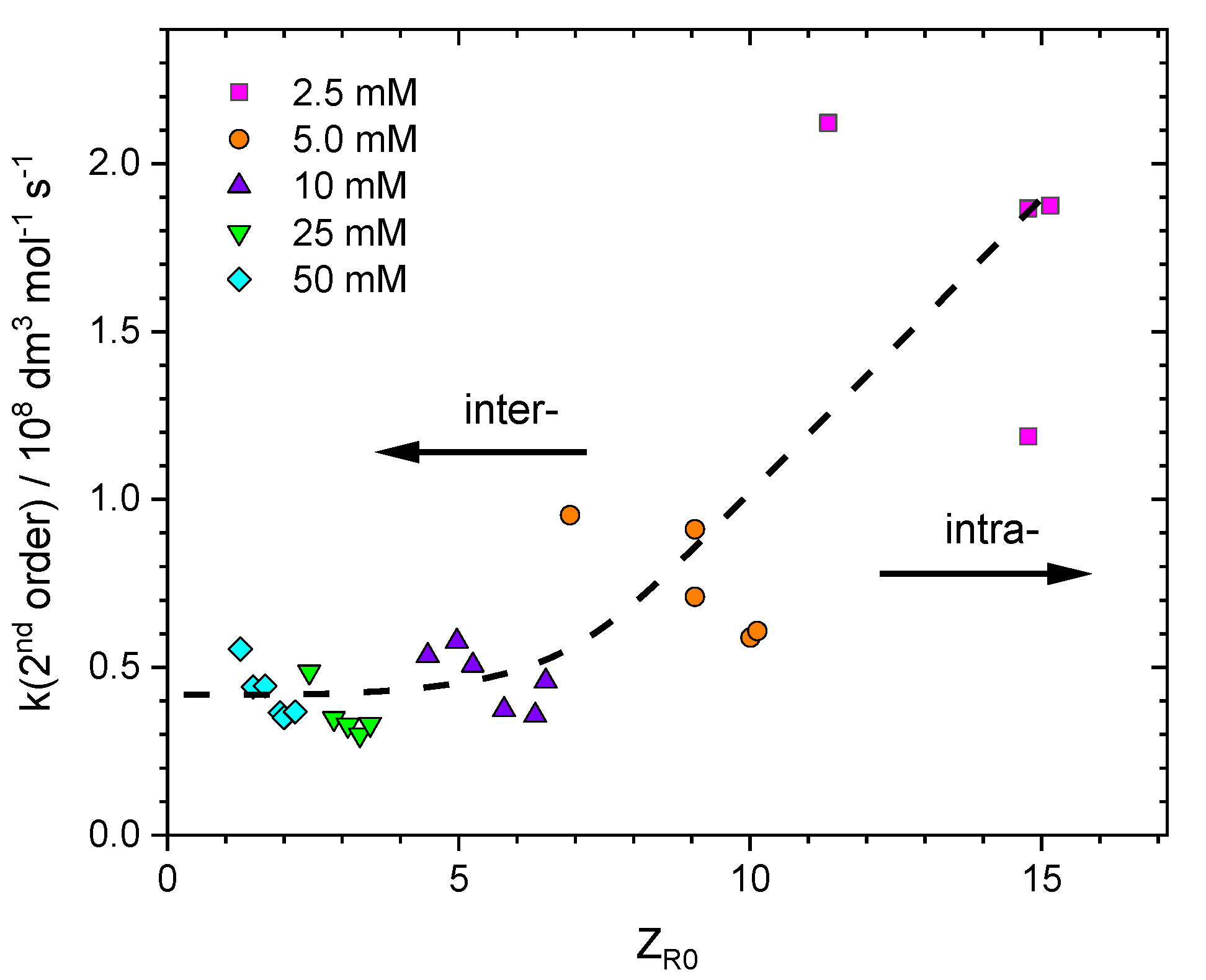
3.4.2. Radical Recombination Rate Constants and Their Dependence on Experimental Parameters
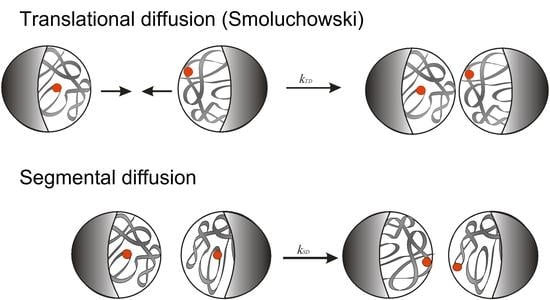
3.4.3. Rate-Determining Step in Intermolecular Recombination of PAA Radicals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reaction | Rate Constant (dm3 mol−1 s−1) | Source |
|---|---|---|
| •OH + PAA → (PAA) • + H2O | 9 × 107 | [53] |
| H• + PAA → (PAA) • + H2 | 5 × 106 | estimate based on [53] |
| eaq− + H3O+ → H• + H2O | 2.3 × 1010 | [81] |
| eaq− + N2O + H2O → •OH + OH− + N2 | 9.1 × 109 | [82] |
| 2 •OH → H2O2 | 5.5 × 109 | [64] |
| H• + •OH → H2O | 7 × 109 | [64] |
| 2 H• → H2 | 8 × 109 | [64] |

References
- Matyjaszewski, K. Atom Transfer Radical Polymerization (ATRP): Current Status and Future Perspectives. Macromolecules 2012, 45, 4015–4039. [Google Scholar] [CrossRef]
- Siegwart, D.J.; Oh, J.K.; Matyjaszewski, K. ATRP in the design of functional materials for biomedical applications. Prog. Polym. Sci. 2012, 37, 18–37. [Google Scholar] [CrossRef] [Green Version]
- Matyjaszewski, K.; Dong, H.; Jakubowski, W.; Pietrasik, J.; Kusumo, A. Grafting from Surfaces for “Everyone”: ARGET ATRP in the Presence of Air. Langmuir 2007, 23, 4528–4531. [Google Scholar] [CrossRef]
- Chen, M.; Zhong, M.; Johnson, J.A. Light-Controlled Radical Polymerization: Mechanisms, Methods, and Applications. Chem. Rev. 2016, 116, 10167–10211. [Google Scholar] [CrossRef] [Green Version]
- Parkatzidis, K.; Wang, H.S.; Truong, N.P.; Anastasaki, A. Recent Developments and Future Challenges in Controlled Radical Polymerization: A 2020 Update. Chem 2020, 6, 1575–1588. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M. Rate Coefficients of Free-Radical Polymerization Deduced from Pulsed Laser Experiments. Prog. Polym. Sci. 2002, 27, 191–254. [Google Scholar] [CrossRef]
- Buback, M. Propagation Kinetics in Radical Polymerization Studied via Pulsed Laser Techniques. Macromol. Symp. 2009, 275–276, 90–101. [Google Scholar] [CrossRef]
- Kockler, K.B.; Haehnel, A.P.; Junkers, T.; Barner-Kowollik, C. Determining Free-Radical Propagation Rate Coefficients with High-Frequency Lasers: Current Status and Future Perspectives. Macromol. Rapid Commun. 2016, 37, 123–134. [Google Scholar] [CrossRef]
- Marien, Y.W.; Edeleva, M.; van Steenberge, P.H.M.; D’hooge, D.R. Exploiting the Pulsed Laser Polymerization-Size Exclusion Chromatography Technique to Retrieve Kinetic Parameters in Radical Polymerization: State-of-the-Art and Future Challenges. Adv. Chem. Eng. 2020, 56, 59–95. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Vana, P.; Davis, T.P. The kinetics of free-radical polymerization. In Handbook of Radical Polymerization; Matyjaszewski, K., Davis, T.P., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; pp. 187–262. ISBN 978-0-471-22045-9. [Google Scholar]
- Vana, P.; Barner-Kowollik, C.; Davis, T.P.; Matyjaszewski, K. Radical polymerization. In Encyclopedia of Polymer Science and Technology; Kroschwitz, J.I., Ed.; John Wiley & Sons: New York, NY, USA, 2004; Volume 11, pp. 359–473. [Google Scholar]
- Wojnarovits, L.; Takacs, E.; Biro, A. Propagation and Size-Dependent Chain Termination Rate Parameters in the Polymerisation of Acrylates in Aqueous Solution as Studied by Pulse Radiolysis. J. Macromol. Sci. A Pure Appl. Chem. 1995, 32, 443–454. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Buback, M.; Egorov, M.; Fukuda, T.; Goto, A.; Olaj, O.F.; Russell, G.T.; Vana, P.; Yamada, B.; Zetterlund, P.B. Critically Evaluated Termination Rate Coefficients for Free-Radical Polymerization: Experimental Methods. Prog. Polym. Sci. 2005, 30, 605–643. [Google Scholar] [CrossRef]
- Russell, G.T.; Gilbert, R.G.; Napper, D.H. Chain-Length-Dependent Termination Rate Processes in Free-Radical Polymerizations. 1. Theory. Macromolecules 1992, 25, 2459–2469. [Google Scholar] [CrossRef]
- Kadlubowski, S.; Grobelny, J.; Olejniczak, W.; Cichomski, M.; Ulanski, P. Pulses of Fast Electrons as a Tool to Synthesize Poly(Acrylic Acid) Nanogels. Intramolecular Cross-Linking of Linear Polymer Chains in Additive-Free Aqueous Solution. Macromolecules 2003, 36, 2484–2492. [Google Scholar] [CrossRef]
- Ashfaq, A.; Clochard, M.-C.; Coqueret, X.; Dispenza, C.; Driscoll, M.S.; Ulański, P.; Al-Sheikhly, M. Polymerization Reactions and Modifications of Polymers by Ionizing Radiation. Polymers 2020, 12, 2877. [Google Scholar] [CrossRef]
- Witcherle, O.; Lim, D. Hydrophylic Gels for Biological Use. Nature 1960, 185, 117–118. [Google Scholar]
- Hoffman, A.S. Hydrogels for Biomedical Applications. Adv. Drug Deliv. Rev. 2002, 54, 3–12. [Google Scholar] [CrossRef]
- Lee, K.Y.; Mooney, D.J. Hydrogels for Tissue Engineering. Chem. Rev. 2001, 101, 1869–1880. [Google Scholar] [CrossRef]
- Rosiak, J.M.; Yoshii, F. Hydrogels and Their Medical Applications. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1999, 151, 56–64. [Google Scholar] [CrossRef]
- Peppas, N.A. Hydrogels in Medicine and Pharmacy; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Rosiak, J.M.; Olejniczak, J. Medical Applications of Radiation Formed Hydrogels. Radiat. Phys. Chem. 1993, 42, 903–906. [Google Scholar] [CrossRef]
- Rosiak, J.M. Radiation Formation of Hydrogels for Drug Delivery. J. Control. Release 1994, 31, 9–19. [Google Scholar] [CrossRef]
- Bromberg, L. Intelligent Hydrogels for the Oral Delivery of Chemotherapeutics. Expert Opin. Drug Deliv. 2005, 2, 1003–1013. [Google Scholar] [CrossRef]
- Rosiak, J.M. Hydrogel dressings HDR. In Radiation Effects on Polymers; ACS Symposium Series 475; Clough, R.C., Shalaby, S.W., Eds.; American Chemical Society: Washington, DC, USA, 1991; pp. 271–299. [Google Scholar] [CrossRef]
- Rosiak, J.; Rucinska-Rybus, A.; Pekala, W. Method of Manufacturing Hydrogel Dressings. U.S. Patent 4,871,490, 3 October 1989. [Google Scholar]
- Ulanski, P.; Rosiak, J.M. Polymeric nano/microgels. In Encyclopedia of Nanoscience and Nanotechnology; Nalwa, H.S., Ed.; American Scientific Publishers: Stevenson Ranch, CA, USA, 2004; pp. 845–871. [Google Scholar]
- Dispenza, C.; Spadaro, G.; Jonsson, M. Radiation Engineering of Multifunctional Nanogels. Top. Curr. Chem. 2016, 374, 69. [Google Scholar] [CrossRef]
- Adamo, G.; Grimaldi, N.; Sabatino, M.A.; Walo, M.; Dispenza, C.; Ghersi, G. E-Beam Crosslinked Nanogels Conjugated with Monoclonal Antibodies in Targeting Strategies. Biol. Chem. 2017, 398, 277–287. [Google Scholar] [CrossRef]
- Rigogliuso, S.; Sabatino, M.A.; Adamo, G.; Grimaldi, N.; Dispenza, C.; Ghersi, G. Polymeric Nanogels: Nanocarriers for Drug Delivery Application. Chem. Eng. Trans. 2012, 27, 247–252. [Google Scholar] [CrossRef]
- Dispenza, C.; Adamo, G.; Sabatino, M.A.; Grimaldi, N.; Bulone, D.; Bondì, M.L.; Rigogliuso, S.; Ghersi, G. Oligonucleotides-Decorated-Poly(N-Vinyl Pyrrolidone) Nanogels for Gene Delivery. J. Appl. Polym. Sci. 2014, 131, 39774. [Google Scholar] [CrossRef]
- Dispenza, C.; Sabatino, M.A.; Ajovalasit, A.; Ditta, L.A.; Ragusa, M.; Purrello, M.; Costa, V.; Conigliaro, A.; Alessandro, R. Nanogel-AntimiR-31 Conjugates Affect Colon Cancer Cells Behaviour. RSC Adv. 2017, 7, 52039–52047. [Google Scholar] [CrossRef] [Green Version]
- Picone, P.; Sabatino, M.A.; Ditta, L.A.; Amato, A.; San Biagio, P.L.; Mulè, F.; Giacomazza, D.; Dispenza, C.; di Carlo, M. Nose-to-Brain Delivery of Insulin Enhanced by a Nanogel Carrier. J. Control. Release 2018, 270, 23–36. [Google Scholar] [CrossRef]
- Picone, P.; Ditta, L.A.; Sabatino, M.A.; Militello, V.; San Biagio, P.L.; di Giacinto, M.L.; Cristaldi, L.; Nuzzo, D.; Dispenza, C.; Giacomazza, D.; et al. Ionizing Radiation-Engineered Nanogels as Insulin Nanocarriers for the Development of a New Strategy for the Treatment of Alzheimer’s Disease. Biomaterials 2016, 80, 179–194. [Google Scholar] [CrossRef]
- Kabanov, A.V.; Vinogradov, S.V. Nanogels as Pharmaceutical Carriers: Finite Networks of Infinite Capabilities. Angew. Chem. Int. Ed. 2009, 48, 5418–5429. [Google Scholar] [CrossRef] [Green Version]
- Soni, K.S.; Desale, S.S.; Bronich, T.K. Nanogels: An Overview of Properties, Biomedical Applications and Obstacles to Clinical Translation. J. Control. Release 2016, 240, 109–126. [Google Scholar] [CrossRef] [Green Version]
- Karg, M.; Pich, A.; Hellweg, T.; Hoare, T.; Lyon, L.A.; Crassous, J.J.; Suzuki, D.; Gumerov, R.A.; Schneider, S.; Potemkin, I.I.; et al. Nanogels and Microgels: From Model Colloids to Applications, Recent Developments, and Future Trends. Langmuir 2019, 35, 6231–6255. [Google Scholar] [CrossRef]
- Matusiak, M.; Rurarz, B.P.; Kadłubowski, S.; Wolszczak, M.; Karczmarczyk, U.; Maurin, M.; Kolesińska, B.; Ulański, P. Synthesis and Properties of Targeted Radioisotope Carriers Based on Poly(Acrylic Acid) Nanogels. Pharmaceutics 2021, 13, 1240. [Google Scholar] [CrossRef]
- Ulański, P.; Janik, I.; Rosiak, J.M. Radiation Formation of Polymeric Nanogels. Radiat. Phys. Chem. 1998, 52, 289–294. [Google Scholar] [CrossRef]
- Kadlubowski, S.; Ulanski, P.; Rosiak, J.M. Synthesis of Tailored Nanogels by Means of Two-Stage Irradiation. Polymer 2012, 53, 1985–1991. [Google Scholar] [CrossRef]
- Matusiak, M.; Kadlubowski, S.; Rosiak, J.M. Nanogels Synthesized by Radiation-Induced Intramolecular Crosslinking of Water-Soluble Polymers. Radiat. Phys. Chem. 2018, 169, 108099. [Google Scholar] [CrossRef]
- Dispenza, C.; Grimaldi, N.; Sabatino, M.A.; Soroka, I.L.; Jonsson, M. Radiation-Engineered Functional Nanoparticles in Aqueous Systems. J. Nanosci. Nanotechnol. 2015, 15, 3445–3467. [Google Scholar] [CrossRef]
- Sabatino, M.A.; Bulone, D.; Veres, M.; Spinella, A.; Spadaro, G.; Dispenza, C. Structure of E-Beam Sculptured Poly(N-Vinylpyrrolidone) Networks across Different Length-Scales, from Macro to Nano. Polymer 2013, 54, 54–64. [Google Scholar] [CrossRef]
- An, J.-C.; Weaver, A.; Kim, B.; Barkatt, A.; Poster, D.; Vreeland, W.N.; Silverman, J.; Al-Sheikhly, M. Radiation-Induced Synthesis of Poly(Vinylpyrrolidone) Nanogel. Polymer 2011, 52, 5746–5755. [Google Scholar] [CrossRef]
- Molyneux, P. Water-Soluble Synthetic Polymers: Properties and Applications; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Bekturov, E.A.; Bakauova, Z.K. Synthetic Water-Soluble Polymers in Solution; Huethig & Wepf: Basel, Switzerland, 1986. [Google Scholar]
- Buchanan, K.J.; Hird, B.; Letcher, T.M. Crosslinked Poly(Sodium Acrylate) Hydrogels. Polym. Bull. 1986, 15, 325–332. [Google Scholar] [CrossRef]
- Kaetsu, I.; Uchida, K.; Morita, Y.; Okubo, M. Synthesis of Electro-Responsive Hydrogels by Radiation Polymerization of Sodium Acrylate. Radiat. Phys. Chem. 1992, 40, 157–160. [Google Scholar] [CrossRef]
- Jabbari, E.; Nozari, S. Swelling Behavior of Acrylic Acid Hydrogels Prepared by γ-Radiation Crosslinking of Polyacrylic Acid in Aqueous Solution. Eur. Polym. J. 2000, 36, 2685–2692. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Hildenbrand, K.; Rosiak, J.M.; von Sonntag, C. Hydroxyl-Radical-Induced Reactions of Poly(Acrylic Acid); a Pulse Radiolysis, EPR and Product Study. Part, I. Deoxygenated Aqueous Solutions. J. Chem. Society Perkin Trans. 2 1996, 1, 13–22. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Hildenbrand, K.; Rosiak, J.M.; von Sonntag, C. Hydroxyl-Radical-Induced Reactions of Poly(Acrylic Acid); a Pulse Radiolysis, EPR and Product Study. Part II. Oxygenated Aqueous Solutions. J. Chem. Society Perkin Trans. 2 1996, 1, 23–28. [Google Scholar] [CrossRef]
- Ulański, P.; Bothe, E.; Hildenbrand, K.; von Sonntag, C.; Rosiak, J.M. The Influence of Repulsive Electrostatic Forces on the Lifetimes of Poly(Acrylic Acid) Radicals in Aqueous Solution. Nukleonika 1997, 42, 425–436. [Google Scholar]
- Ulanski, P.; Rosiak, J.M. Pulse Radiolysis of Poly(Acrylic Acid) in Deoxygenated Aqueous Solution. J. Radioanal. Nucl. Chem. Lett. 1994, 186, 315–324. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Hildenbrand, K.; Rosiak, J.M.; von Sonntag, C. Radiolysis of Poly(Acrylic Acid) in Aqueous Solution. Radiat. Phys. Chem. 1995, 46, 909–912. [Google Scholar] [CrossRef]
- Ulański, P.; Kadłubowski, S.; Rosiak, J.M. Synthesis of Poly(Acrylic Acid) Nanogels by Preparative Pulse Radiolysis. Radiat. Phys. Chem. 2002, 63, 533–537. [Google Scholar] [CrossRef]
- Matusiak, M.; Kadlubowski, S.; Ulanski, P. Radiation-Induced Synthesis of Poly(Acrylic Acid) Nanogels. Radiat. Phys. Chem. 2018, 142, 125–129. [Google Scholar] [CrossRef]
- Dispenza, C.; Sabatino, M.A.; Grimaldi, N.; Mangione, M.R.; Walo, M.; Murugan, E.; Jonsson, M. On the Origin of Functionalization in One-Pot Radiation Synthesis of Nanogels from Aqueous Polymer Solutions. RSC Adv. 2016, 6, 2582–2591. [Google Scholar] [CrossRef]
- Adamo, G.; Grimaldi, N.; Campora, S.; Bulone, D.; Bondì, M.L.; Al-Sheikhly, M.; Sabatino, M.A.; Dispenza, C.; Ghersi, G. Multi-Functional Nanogels for Tumor Targeting and Redox-Sensitive Drug and SiRNA Delivery. Molecules 2016, 21, 1594. [Google Scholar] [CrossRef] [PubMed]
- Grimaldi, N.; Sabatino, M.A.; Przybytniak, G.; Kaluska, I.; Bondì, M.L.; Bulone, D.; Alessi, S.; Spadaro, G.; Dispenza, C. High-Energy Radiation Processing, a Smart Approach to Obtain PVP-Graft-AA Nanogels. Radiat. Phys. Chem. 2014, 94, 76–79. [Google Scholar] [CrossRef]
- Abd El-Rehim, H.A.; Hegazy, E.S.A.; Hamed, A.A.; Swilem, A.E. Controlling the Size and Swellability of Stimuli-Responsive Polyvinylpyrrolidone-Poly(Acrylic Acid) Nanogels Synthesized by Gamma Radiation-Induced Template Polymerization. Eur. Polym. J. 2013, 49, 601–612. [Google Scholar] [CrossRef]
- Henke, A.; Ulanski, P.; Rosiak, J.M. Radiation cross-linked hydrogen-bonding interpolymer complexes. In Hydrogen-Bonded Interpolymer Complexes. Formation, Structure and Applications; Khutoryanskiy, V.V., Staikos, G., Eds.; World Scientific: Singapore, 2009; pp. 259–300. ISBN 978-981-270-785-7. [Google Scholar]
- Ghaffarlou, M.; Sütekin, S.D.; Güven, O. Preparation of Nanogels by Radiation-Induced Cross-Linking of Interpolymer Complexes of Poly (Acrylic Acid) with Poly (Vinyl Pyrrolidone) in Aqueous Medium. Radiat. Phys. Chem. 2018, 142, 130–136. [Google Scholar] [CrossRef]
- Rattanawongwiboon, T.; Ghaffarlou, M.; Sütekin, S.D.; Pasanphan, W.; Güven, O. Preparation of Multifunctional Poly(Acrylic Acid)-Poly(Ethylene Oxide) Nanogels from Their Interpolymer Complexes by Radiation-Induced Intramolecular Crosslinking. Colloid Polym. Sci. 2018, 296, 1599–1608. [Google Scholar] [CrossRef]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical Review of Rate Constants for Reactions of Hydrated Electrons, Hydrogen Atoms and Hydroxyl Radicals (OH/O−) in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef] [Green Version]
- Von Sonntag, C.; Bothe, E.; Ulanski, P.; Deeble, D.J. Pulse Radiolysis in Model Studies toward Radiation Processing. Radiat. Phys. Chem. 1995, 46, 527–532. [Google Scholar] [CrossRef]
- Lacík, I.; Stach, M.; Kasák, P.; Semak, V.; Uhelská, L.; Chovancová, A.; Reinhold, G.; Kilz, P.; Delaittre, G.; Charleux, B.; et al. SEC Analysis of Poly(Acrylic Acid) and Poly(Methacrylic Acid). Macromol. Chem. Phys. 2015, 216, 23–37. [Google Scholar] [CrossRef]
- Karolczak, S.; Hodyr, K.; Łubis, R.; Kroh, J. Pulse Radiolysis System Based on ELU-6E LINAC. J. Radioanal. Nucl. Chem. 1986, 101, 177–188. [Google Scholar] [CrossRef]
- Karolczak, S.; Hodyr, K.; Polowinski, M. Pulse Radiolysis System Based on ELU-6E LINAC. II. Development and Upgrading the System. Radiat. Phys. Chem. 1992, 39, 1–5. [Google Scholar] [CrossRef]
- Schuler, R.H.; Patterson, L.K.; Janata, E. Yields for the Scavenging of OH Radicals in the Radiolysis of N2O-Saturated Aqueous Solutions. J. Phys. Chem. 1980, 84, 2088–2089. [Google Scholar] [CrossRef]
- Burchard, W. Static and Dynamic Light Scattering from Branched Polymers and Biopolymers. Adv. Polym. Sci. 1983, 48, 1–124. [Google Scholar] [CrossRef]
- Serjeant, E.P.; Dempsey, B. Ionisation Constants of Organic Acids in Aqueous Solution; IUPAC Chemical Data Series No. 23; Pergamon Press: Oxford, UK, 1979. [Google Scholar]
- Katchalsky, A.; Gillis, J. Theory of the Potentiometric Titration of Polymeric Acids. Recl. Des Trav. Chim. Des Pays Bas 1949, 68, 879–897. [Google Scholar] [CrossRef]
- Oosawa, F. Polyelectrolytes; Marcel Dekker: New York, NY, USA, 1971. [Google Scholar]
- Morawetz, H. Macromolecules in Solution; Interscience Publishers: New York, NY, USA, 1965. [Google Scholar]
- Charlesby, A. Atomic Radiation and Polymers; Pergamon Press: Oxford, UK, 1960. [Google Scholar]
- Coqueret, X. Obtaining High-Performance Polymeric materials by Radiation. In Radiation Chemistry: From Basics to Applications in Material and Life Sciences; Spotheim-Maurizot, M., Mostafavi, M., Douki, T., Belloni, J., Eds.; EDP Sciences: Les Ulis, France, 2008; pp. 131–150. [Google Scholar]
- Coqueret, X.; Sabharwal, S.; Khairul Zaman, H.M.D.; Czechowska-Biskup, R.; Wach, R.A.; Rosiak, J.M.; Ulanski, P. Introduction to the radiation chemistry of polymers. In The Radiation Chemistry of Polysaccharides; Al-Assaf, S., Coqueret, X., Khairul Zaman, M.H.D., Sen, M., Ulanski, P., Eds.; IAEA: Vienna, Austria, 2016; pp. 25–75. [Google Scholar]
- Buxton, G.V. Radiation chemistry of the liquid state. Water and homogeneous aqueous solutions. In Radiation Chemistry: Principles and Applications; Farhataziz, Rodgers, M.A.J., Eds.; Verlag Chemie: Weinheim, Germany, 1987; pp. 321–349. [Google Scholar]
- Von Sonntag, C. The Chemical Basis of Radiation Biology; Taylor and Francis: London, UK, 1987. [Google Scholar]
- Buxton, G.V. An overview of the radiation chemistry of liquids. In Radiation Chemistry: From Basics to Applications in Material and Life Sciences; Spotheim-Maurizot, M., Mostafavi, M., Douki, T., Belloni, J., Eds.; EDP Sciences: Les Ulis, France, 2008; pp. 3–16. [Google Scholar]
- Jonah, C.D.; Miller, J.R.; Matheson, M.S. The Reaction of Hydrated Electron + Oxonium. Concentration Effects of Acid or Salts. J. Phys. Chem. 1977, 81, 931–934. [Google Scholar] [CrossRef]
- Janata, E.; Schuler, R.H. Rate Constant for Scavenging eaq- in N2O-Saturated Solutions. J. Phys. Chem. 1982, 86, 2078–2084. [Google Scholar] [CrossRef]
- Bartoszek, N.; Ulański, P.; Rosiak, J.M. Reaction of a Low-Molecular-Weight Free Radical with a Flexible Polymer Chain: Kinetic Studies on the OH + Poly(N-Vinylpyrrolidone) Model. Int. J. Chem. Kinet. 2011, 43, 474–481. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Rosiak, J.M.; von Sonntag, C. Radiolysis of the Poly(Acrylic Acid) Model 2,4-Dimethylglutaric Acid: A Pulse Radiolysis and Product Study. J. Chem. Society. Perkin Trans. 2 1996, 1, 5–12. [Google Scholar] [CrossRef]
- Görlich, W.; Schnabel, W. Untersuchungen über der Einfluss der Ladungsdichte auf die Gegenseitige Desaktivierung von Polyion-Makroradikalen. Die Makromol. Chem. 1973, 164, 225–235. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Hildenbrand, K.; von Sonntag, C. Free-Radical-Induced Chain Breakage and Depolymerization of Poly(Methacrylic Acid): Equilibrium Polymerization in Aqueous Solution at Room Temperature. Chem. A Eur. J. 2000, 6, 3922–3934. [Google Scholar] [CrossRef]
- Behar, D.; Rabani, J. Pulse Radiolysis of Poly(Styrenesulfonate) in Aqueous Solutions. J. Phys. Chem. 1988, 92, 5288–5292. [Google Scholar] [CrossRef]
- Ulanski, P.; Bothe, E.; Rosiak, J.M.; von Sonntag, C. OH-Radical-Induced Crosslinking and Strand Breakage of Poly(Vinyl Alcohol) in Aqueous Solution in the Absence and Presence of Oxygen. A Pulse Radiolysis and Product Study. Makromol. Chem. 1994, 195, 1443–1461. [Google Scholar] [CrossRef]
- Ulanski, P.; Rosiak, J.M.; Zainuddin, A. Pulse Radiolysis of Poly(Ethylene Oxide) in Aqueous Solution. II. Decay of Macroradicals. Radiat. Phys. Chem. 1995, 46, 917–920. [Google Scholar] [CrossRef]
- Janik, I.; Ulanski, P.; Hildenbrand, K.; Rosiak, J.M.; von Sonntag, C. Hydroxyl-Radical-Induced Reactions of Poly(Vinyl Methyl Ether): A Pulse Radiolysis, EPR and Product Study in Deoxygenated and Oxygenated Aqueous Solutions. J. Chem. Society. Perkin Trans. 2 2000, 2041–2048. [Google Scholar] [CrossRef]
- Sabharwal, S.; Mohan, H.; Bhardwaj, Y.K.; Majali, A.B. Structure-Reactivity Studies on the Crosslinking of Poly(Vinyl Methyl Ether) in Aqueous Solutions: A Pulse Radiolysis Study. J. Chem. Soc. Faraday Trans. 1996, 92, 4401–4406. [Google Scholar] [CrossRef]
- Jeszka, J.K.; Kadlubowski, S.; Ulanski, P. Monte Carlo Simulations of Nanogels Formation by Intramolecular Recombination of Radicals on Polymer Chain. Dispersive Kinetics Controlled by Chain Dynamics. Macromolecules 2006, 39, 857–870. [Google Scholar] [CrossRef]
- Ulański, P.; Kadłubowski, S.; Jeszka, J.K. Nanogel Formation by Intrachain Radiation-Induced Cross-Linking. Simulation and Experiment. Mater. Sci. Pol. 2006, 24, 467–476. [Google Scholar]
- Dahlgren, B.; Dispenza, C.; Jonsson, M. Numerical Simulation of the Kinetics of Radical Decay in Single-Pulse High-Energy Electron-Irradiated Polymer Aqueous Solutions. J. Phys. Chem. A 2019, 123, 5043–5050. [Google Scholar] [CrossRef] [PubMed]
- Dahlgren, B.; Sabatino, M.A.; Dispenza, C.; Jonsson, M. Numerical Simulations of Nanogel Synthesis Using Pulsed Electron Beam. Macromol. Theory Simul. 2020, 29, 1900046. [Google Scholar] [CrossRef]
- Plonka, A. Developments in Dispersive Kinetics. Prog. React. Kinet. 1991, 16, 157–333. [Google Scholar]
- Plonka, A. Dispersive Kinetics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; ISBN 0-7923-7128-3. [Google Scholar]
- Neta, P.; Simic, M.; Hayon, E. Pulse Radiolysis of Aliphatic Acids in Aqueous Solutions. I. Simple Monocarboxylic Acids. J. Phys. Chem. 1969, 73, 4207–4213. [Google Scholar] [CrossRef]
- Smoluchowski, M. Versuch Einer Mathematischen Theorie der Koagulationskinetik Kolloider Lösungen. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar] [CrossRef] [Green Version]
- Russell, G.T.; Napper, D.H.; Gilbert, R.G. Termination in Free-Radical Polymerizing Systems at High Conversion. Macromolecules 1988, 21, 2133–2140. [Google Scholar] [CrossRef]
- Gillespie, D.T. A General Method for Numerically Simulating the Stochastic Time Evolution of Coupled Chemical Reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Hinsberg, W.; Houle, F. Kinetiscope: A Stochastic Kinetics Simulator. Available online: http://hinsberg.net/kinetiscope/ (accessed on 26 October 2021).







| Parameters | PAA, Nominal Mw 450 kDa | OAA, Nominal Mw 1.8 kDa |
|---|---|---|
| Mw [kDa] | 555 | 3.073 |
| Mn [kDa] | 182 | 0.844 |
| Mw/Mn | 3.05 | 3.64 |
| Z-average Rg [nm] | 99 | <10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matusiak, M.; Kadłubowski, S.; Ulański, P. Recombination of Poly(Acrylic Acid) Radicals in Acidic Aqueous Solutions: A Pulse Radiolysis Study. Appl. Sci. 2021, 11, 10142. https://doi.org/10.3390/app112110142
Matusiak M, Kadłubowski S, Ulański P. Recombination of Poly(Acrylic Acid) Radicals in Acidic Aqueous Solutions: A Pulse Radiolysis Study. Applied Sciences. 2021; 11(21):10142. https://doi.org/10.3390/app112110142
Chicago/Turabian StyleMatusiak, Małgorzata, Sławomir Kadłubowski, and Piotr Ulański. 2021. "Recombination of Poly(Acrylic Acid) Radicals in Acidic Aqueous Solutions: A Pulse Radiolysis Study" Applied Sciences 11, no. 21: 10142. https://doi.org/10.3390/app112110142
APA StyleMatusiak, M., Kadłubowski, S., & Ulański, P. (2021). Recombination of Poly(Acrylic Acid) Radicals in Acidic Aqueous Solutions: A Pulse Radiolysis Study. Applied Sciences, 11(21), 10142. https://doi.org/10.3390/app112110142