1. Introduction
The use of light in space propulsion has been firstly proposed by Eugen Sanger in 1955 [
1]. In his well known article, he considered a pure photon rocket propelled by an antimatter pumped “laser”. Later, with the development of the first laser systems, rockets driven by reflection, transmission or absorption of photons, emitted by a ground-based laser system, have also been proposed [
2,
3]. In 1971, Kantrowitz [
4] and later, in 1972, Mockel [
5] suggested a more practical scheme for space propulsion based on the generation of thrust through the continuous heating of a propellant induced by a laser pulse. Nowadays, several schemes for spacecraft propulsion based on directed energy radiation (DE) or laser ablation propulsion (LAP) are under investigation for deep or interplanetary space exploration over a wide range of spacecraft masses [
6,
7].
In 2000, after the observation [
8,
9,
10] of intense multi–MeV proton emission from solid targets irradiated at ultra–high laser intensities, a substantially new scheme for laser–based space propulsion emerged. This hybrid scheme, which is classifiable as a relativistic laser–driven plasma-acceleration system, can be considered as the connection between LAP engines [
6] and plasma-based electric propulsion [
11]. Horisawa [
12] and Kammash [
13] firstly discussed, in 2000 and 2001 respectively, the laser–accelerated plasma-propulsion system (LAPPS). In their articles, mainly oriented on the possibility of interstellar missions, they considered 100–1000 MeV energy proton bunches, in the wake of the tremendous progress in experimental laser–plasma acceleration that occurred in the early 2000s. An impressive specific impulse in the 10
–10
s range is often reported as a realistic achievable result for these schemes [
6,
13,
14,
15]. According to Ref. [
14], once considering the relativistic effects, the LAPPS specific impulse for a 1 GeV protons exhaust is expected to be
s, which apparently (the meaning of “apparently” will be clarified later) overcomes the performance of the ideal matter–antimatter photon thruster [
16] for which
s. However, despite the remarkable claimed performances, no further development of the LAPPS has been considered until today [
17,
18]. Because of the inadequate expected thrust, LAPPS is generally unmentioned in the list of the advanced space propulsion systems, which are potentially developable in the near future [
19]. In contrast, in the last 10 years, laser–plasma ion acceleration has been widely explored from both theoretical and experimental points of view [
20,
21].
The aim of this work is therefore to revisit the LAPPS scheme, to explore its potentialities and to obtain more accurate figures of merit of its performance. Relying on laser–plasma acceleration parameters, as given by the Target Normal Sheath Acceleration (TNSA) scheme, as the main mechanism of light ions acceleration scheme [
22,
23,
24,
25,
26,
27], we present a general theory able to estimate the LAPPS performance over a large variety of configurations. Remarkably, the results differ by orders of magnitude from previous estimates, potentially making this propulsion system competitive with other mechanisms. Finally, we discuss the possibility of a realistic implementation in a spacecraft by using the current technology.
The article is organized as follows: in
Section 2, we introduce the basic kinematic relations of a rocket–propellant system; a fully covariant formalism of momentum conservation is introduced here for a correct treatment of the relativistic propellant. In
Section 3, the covariant formalism is extended to the dynamics of the rocket, deriving the expression of the engine thrust. In
Section 4, we discuss the complete energy balance of a closed–cycle rocket engine, including the efficiency of the different processes and the channels of energy dissipation. In
Section 5, we discuss the figures of merit and the performance limits of a generic LAPPS engine, relying on the parametrization introduced in
Section 4. In
Section 6, we present a detailed analytical model of a LAPPS engine, where the propellant includes both TNSA–accelerated high–energy particles and low–velocity massive particles accelerated by other mechanisms. The conditions for obtaining the optimization of thrust and impulse of the engine are discussed, for different laser intensities and experimental setups. In
Section 7, we discuss the relevance of radiation contribution in a LAPPS system. Finally, in
Section 8, we summarize the main results obtained in previous sections and discuss possible directions of future research for refining the above described LAPPS model. A nomenclature section is also reported at the end of the paper.
2. Relativistic Propellant
Although only the exhaust flow may move at relativistic velocity, it is convenient to introduce the problem using a fully covariant formalism. A relativistic reaction engine (basically a thruster based on a particle accelerator) expels, in an infinitesimal time interval, an infinitesimal exhaust mass at relativistic velocity with respect to the rocket rest frame. As presented in
Figure 1, the problem can be schematized as a 1D system in which the four-velocity of the rocket is given by:
where
c is the speed of light in vacuum while
is the relativistic factor associated with the scalar rocket velocity
u. We will use the standard Einstein notation in which the 1D covariant four–velocity is given by
, where
is the Minkowski tensor with trace (+,−). The product is given by
(summation over indices). From the differential of the four–velocity
, we can easily construct the scalar relation:
where the rapidity
has been introduced to simplify the notation. Sometimes, the quantities
, which is referred as the proper speed of the rocket, is used instead of the rapidity. If an infinitesimal mass
is expelled from the rocket, the instantaneous conservation of the four-momentum implies:
where
M is the instantaneous rocket mass while
is the propellant four–velocity. Differently from
,
does not correspond to the propellant mass but, more correctly, represents the mass “lost” by the rocket. In fact, a fraction of
is also converted into kinetic energy according to relativistic principles. The limit is represented by the so–called photonic rocket [
1] (a photon–based engine), in which the propellant mass is zero. In this case, the total photons four–momentum is given by
, where
is the wave four-vector. An other independent equation can be retrieved directly from Equation (
3) once contracted with
. Considering that
,
and
we obtain:
where
has been used. As expected, the relevant speed is represented by the propellant relative velocity
, which is measured from the rocket rest frame. In more detail, the term
, which is invariant under Lorentz transformations, has been rearranged to
, expressed in the rocket frame. Thus, Equation (
4) can be used to eliminate
from Equation (
3):
From Equation (
5), once the terms are separated and squared, we finally obtain the differential invariant rocket equation:
where the relation (
2) and
have been used. It is interesting to observe that Equation (
6), which is valid also for photonic rockets, does not contain any explicit propellant relativistic factor. Considering that the rapidity
is an additive function, Equation (
6) can be directly integrated once chosen
as a physical solution, and gives:
where
and
M are the initial rocket mass and the instantaneous rocket mass respectively, calculated in the rocket rest frame. Using the proper speed
instead of rapidity, we find that Equation (
7) is formally identical to the classical non–relativistic Tsiolkovsky’s rocket equation [
28]. However, according to the covariant derivation of Equation (
7), an engine based on photons emission can be simply obtained in the limit of
. As expected, these results are in accordance with a non–covariant derivation [
29].
We are interested in the case of non-relativistic rocket motion (i.e.,
) with a thruster based on a LAPPS. If we define
as the amount of the consumed fuel during the flight, Equation (
7) can be expressed as
where the Taylor’s expansion of the logarithm has been used. Equation (
8), in contrast to Equation (
7), is valid only in the case of non-relativistic rocket motion, for which
. For particle accelerators, differently from chemical fuel engines, the consumed propellant is expected to consist of a small fraction of the entire system mass, so that we may assume
. In this case, considering only the first term in Equation (
8), we obtain
Equation (
9) admits a simple physical interpretation as the classical total momentum of both rocket and propellant are conserved. Here, the propellant mass is defined as the rocket “lost” mass
measured in the rest frame. Again, despite the classical aspect, Equation (
9) remains valid in the case of relativistic (and eventually massless) propellant. Therefore, the laser pulse or the emitted radiation can be considered as a part of propellant. Realistically, in order to produce propulsive capabilities adequate for orbital maneuvering or interplanetary space missions, we need spacecraft velocities
m/s. Considering a conservative fuel–mass ratio of
, the above velocities can be obtained by expelling the propellant at relative velocities
m/s. This suggests that a relativistic speed of the propellant is not mandatory as the condition
seems to fulfill the requirements. This example also fixes the expected order of magnitude for one of the most relevant engine parameters, the specific impulse (see formal definition in Equation (
13))
, where
is the gravitational acceleration measured on Earth at sea level. It is worth mentioning that Equations (
3) and (
4) do not include explicitly the mass wasted for the acceleration of the propellant; a more complete treatment, accounting for the dissipation channels and therefore including the efficiency of the process, will be tackled in a following section. It is however important to anticipate that, in a comprehensive approach, the specific impulse is obtained by substituting the propellant velocity
with an “effective”
, accounting for the efficiency of the system (see Equation (
19)).
3. Engine Thrust
In general, in order to meet the needs of interplanetary robotic (or manned) missions, the travel time
should be limited to years or tens of years according to the classical optimized Hohmann or bi–elliptic transfer orbit maneuverings. A desirable rocket configuration, however, should meet the relation
, where
is the total engine firing time. In this case, all the interplanetary space maneuverings can be considered local. Equation (
7), however, does not contain any information about the time needed to accelerate the rocket up to the desired speed
m/s. For this reason, it is important to derive the relativistic expression of the engine thrust.
In the case of relativistic systems characterized by a variable rest mass, some of the standard covariant relations must be reformulated. In order to avoid any confusion, the simplest way is to consider only kinematic quantities as, for example, the rocket four-acceleration
, where
is the proper time in the rocket frame. In a 1D system, the quantity
, where
is the ordinary acceleration, is invariant under Lorentz transformations. In general, the rapidity and the four–acceleration are related through the expression:
where the definition
has been used. Equation (
10) can also be expressed in terms of the proper velocity
, which clearly shows the physical meaning of this cinematic relation. Finally, from Equations (
7) and (
10), we can find the invariant relation for the relativistic rocket acceleration:
The engine is the only mechanism able to accelerate and decelerate the rocket; thus, the thrust can be defined as the total force
F acting on the system. From the definition
, and considering that force and acceleration are here parallel to the rocket velocity, we need only the expression of the longitudinal acceleration:
. Combining
with Equation (
11), we obtain the engine trust measured in the laboratory space frame:
The specific impulse can be defined, starting from Equation (
12), according to the classical definition:
where
represents the rocket lost mass as it appears from the rocket space frame. As expected,
is an invariant that does not contain any relativistic factor. This property can be directly obtained considering that
is linear in
(see Equation (
7)). In terms of the specific impulse, the engine thrust calculated in the laboratory rest frame is given by:
which is analogous to the classical non–relativistic equation in the limit of
. In Ref. [
14], the alternative relativistic definition of the specific impulse
diverges for
, making this choice ambiguous in the case of comparison with other advanced propulsion schemes, for which the def. (
13) is generally used.
Basically, considering the linear increasing of
with
, we do not obtain a dramatic gain when the propellant approaches the light speed. However,
ranges through several orders of magnitude and the limit
allows for obtaining spacecraft velocities which are compatible with interplanetary (or even interstellar) space missions for
. In this case, the fuel is fully used to accelerate the entire payload overcoming the so–called “rocket tyranny”. In case of non–relativistic rocket motion (
), the firing time
can be defined as the time needed for the engine to consume all the available fuel. In the approximation of
(see Equation (
9)), we find
defining the elementary relations between the thrust
F, the initial rocket mass
, the rocket speed
u, and the firing time
. In the case of a uniform thrust, for an arbitrary weight–thrust ratio of
(i.e.,
), we obtain:
For interplanetary missions ( m/s), the firing time is given by days. By considering a firing time days (realistically, the traveling time is in the range of years for interplanetary missions) and an initial mass Kg, a force N is required. Finally, for a propellant velocity m/s, a total fuel consumption of Kg and an instantaneous fuel consumption of g/s are obtained.
4. Specific Impulse
Besides the general considerations on the rocket dynamics, it becomes important to introduce a more complete approach, including a practical parametrization to calculate the specific impulse of a generic particle accelerator. In this way, it will be possible to analyze the fundamental properties of the LAPPS engine with the appropriate formalism. The calculation of requires determining the relative propellant speed that can be interpreted as the first moment of the velocity distribution of an heterogeneous variety of particles with different masses. For this reason, the optimization of may not coincide with the classical performance optimization of a particle accelerator, independently on the specific acceleration mechanism.
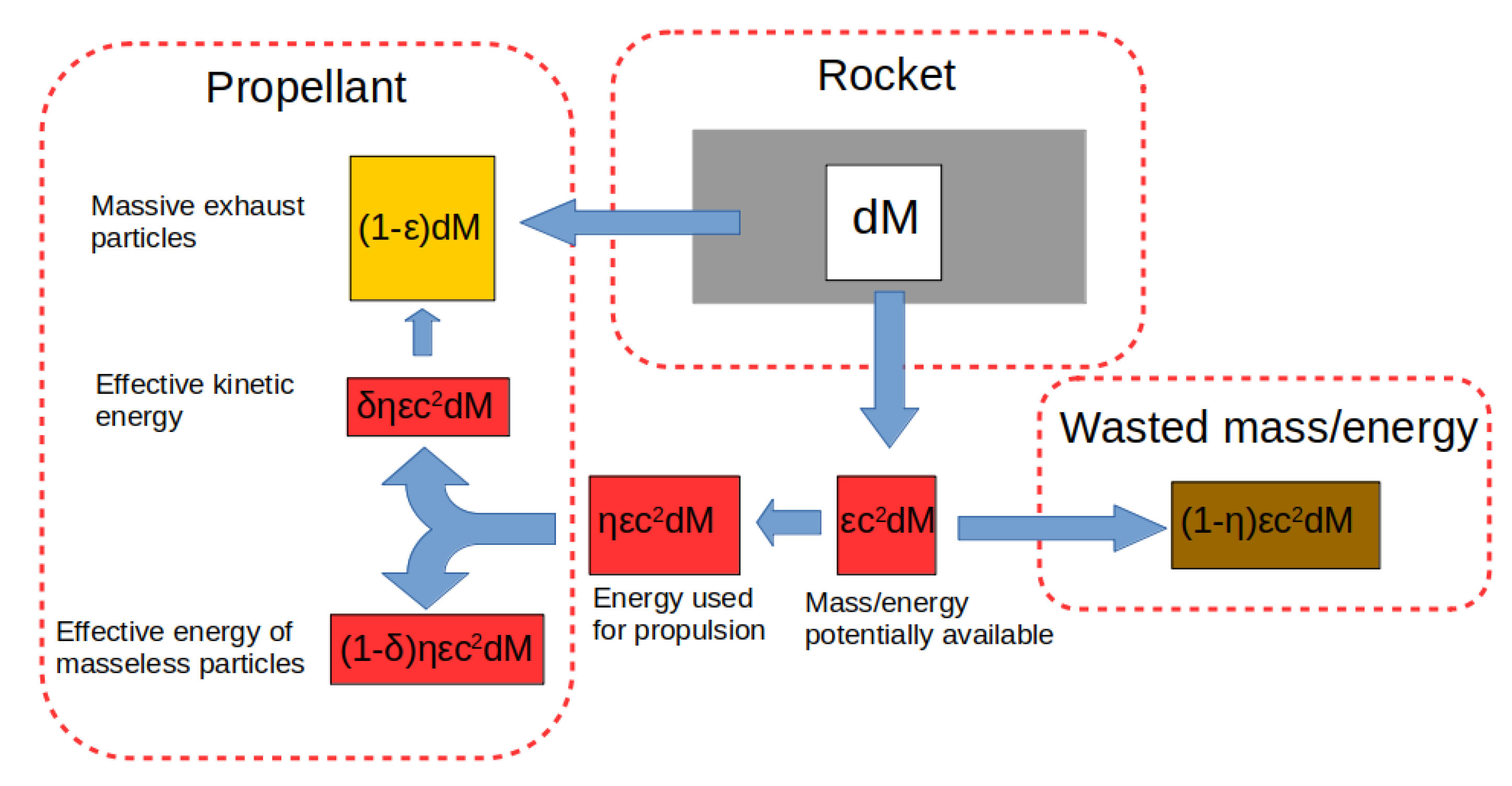
We start considering more in detail the infinitesimal mass
lost by the rocket. We will use the convention introduced by Walter [
30]. According to the scheme presented in
Figure 2, if we define the fraction
as the mass of the massive particles actually expelled,
defines the energy available for utilization. Of the total energy available, in general, only a fraction
is utilized to increase the energy of the propellant of which only a fraction
is used to accelerate massive particles. Thus, in the rocket rest frame, we find:
which simply defines, in terms of the Walter’s parameters
, the fraction of available energy converted into kinetic energy of massive particles. From Equation (
18), we can easily retrieve the propellant speed of massive particles [
30]:
The general invariant solution
of the rocket motion is linear in
, thus it can be used to find the effective exhaust speed in terms of a classical weighted average over velocities. The mass lost by the rocket due to massive particles is
; this fraction includes the rest mass of the expelled particles
and the mass–equivalent energy used to accelerate them
. Note that in the original paper [
30] this term was omitted leading to an error. In the same way, the mass lost by the rocket which is used to “create” massless particles is
. We can therefore calculate a weighted velocity, including both massive and massless particles, as:
Equation (
20) represents the effective propellant speed measured from the rocket rest frame. Basically, in the general Equation (
7),
must be replaced with
to take into account the rocket global efficiency. In terms of Walter’s parameters, i.e., using (
19) and (
20) can be written as:
which corresponds to the corrected solution given by Westmorelend [
31]. The expression (
21) is valid for all the rocket configurations in which both propellant and energy are stored inside (closed cycle). This list does not include, for example, spacecraft propelled by directed energy, jet engines and atmospheric LAP engine as the Myrabo’s lightcraft [
32].
5. LAPPS Performance Limits
We are interested in a rocket in which the engine is based on a LAPPS. As presented in
Figure 3, this implies that a laser system must be installed and powered directly on the rocket. From Equation (
21), we can now define the specific impulse
, which is a generalized form of the impulse already defined in Equation (
13), accounting for all possible channels of energy dissipation; as already said, the effective velocity
is here lower than the propellant speed
. In case of a photon rocket (
and
), in which the laser pulse is directly used as propellant, the specific impulse assumes the form
where
is the energy conversion efficiency of the laser system calculated considering all the energy released by the nuclear reactor. The parameter
indicates the fraction of the available energy wasted by the system. The wasted energy takes into account, among other factors, of heating dissipation and of the orthogonal component of particle velocity, which does not contribute to rocket acceleration. For this reason, in the case of a well collimated laser beam, we obtain
. On the other side, if the laser pulse is focalized (and almost stopped) on a target, as it occurs in a LAPPS, we expect that the photons contribution to the rocket motion can be considered negligible at first order (the EM radiation will be considered later in detail). In this case
, and differentiating Equation (
21), we find that the maximum specific impulse is reached for
where usually
. Equation (
23) indicates that the best performance is obtained when the infinitesimal mass
is almost equally distributed between the rest mass of the accelerated particles
and the available energy
. Consequently, the kinetic energy acquired by the massive propellant becomes
. This quantity is related to the averaged power generated by the nuclear reactor
calculated in the rest frame through
where Equation (
14) has been used, while
characterizes the laser–plasma interaction efficiency. The parameter
indicates, for
, the fraction of the laser pulse energy converted into “parallel” kinetic energy. Considering Equation (
23), the maximum specific impulse which can be obtained in a LAPPS is given by
and gives, once combined with Equation (
24), the expression for the engine thrust
For an ideal system (maximum specific impulse), the relative speed of the massive propellant becomes
Equation (
27) is intrinsically limited by
, which is the fractional amount of available energy that is actually utilized for propulsion. Both laser efficiency
and interaction efficiency
contribute to this limit according to the general relation
where
is the total energy generated by the system (
). From Equation (
28), we also obtain the relation between
and
:
For typical laser systems and targets,
and
are of the same order of magnitude while
. According to Equation (
29), the relation
is therefore usually fulfilled. However, in the limit of
, the conditions
and
become potentially achievable (although without any specific advantages for space propulsion due to the low specific impulse which characterizes this condition).
Realistically, the conditions (
27) and (
28) exclude the possibility of obtaining a relativistic propellant speed from any optimized laser–based closed cycle scheme. This is a general property which depends on the low efficiency of the energy transfer from the power supply to the laser pulse. In conclusion, despite laser–plasma interaction has not yet been discussed in detail, basic properties and limitations of the LAPPS scheme have been already obtained. These results suggest that a space thruster based on laser–plasma interaction should primarily generate a well collimated particle beam with a low fraction of wasted target material. This also implies that schemes, as for example laser–driven plasma-based electron accelerators [
33], where the largest fraction of the target (usually a gas–jet) is not accelerated, are not indicated as thrusters.
7. Radiation Contribution and High Intensity Limit
As well known, high power laser experiments in the TNSA regime produce radiation. From the rocket dynamics point of view, the relevant contributions may come from both bremsstrahlung and recombination X– and
–ray photons emitted from the plasma and produced by the interaction of high-energy electrons with the target. In addition, laser photons which are scattered or reflected during the interaction, can also be taken into account. The specific impulse for a LAPPS engine produced by the photons can be calculated by means of general Equations (
13) and (
20), obtaining a photon contribution to Equation (
46) given by:
The infinitesimal mass lost by the rocket in every laser cycle is then given by
where
is given by Equation (
39), while
takes into account the total energy generated by the system (nuclear energy). The approximation of
is still valid in this model. In the case of a thin target, we immediately find:
where the definitions (
22) and (
28) have been used. As shown in Equation (
60), as long as the term
is negligible with respect to the rest mass of the propellant, also
and therefore can be considered negligible. The upper limit of
corresponds to the photon rocket specific impulse and can be obtained by removing the solid target, i.e., for
and
. In the same way, the total correction to Equation (
48), which is given by
can be considered negligible using current laser technology and solid targets. As already discussed, we are not able to extend the LAPPS model over arbitrary high laser intensities. However, the ultimate limit of high intensity interaction at fixed pulse energy must coincide with the photon rocket, which is independent from the laser intensity and well defined. For this reason, it is interesting to define the condition above which a photon rocket becomes convenient over a LAPPS rocket. Considering that, for a single laser shot, the spacecraft speed gain is proportional to
, we find:
where
has been used with
given by Equation (
53). The threshold (
62), if calculated for typical laser–plasma accelerator parameters, exceeds the intensity range in which the TNSA model is well defined. In other words, an optimized LAPPS scheme is always convenient compared to a pure photon rocket at least for
. This conclusion becomes evident in
Figure 8, where the limit of the photon rocket is reported for a relatively high efficiency of
.
8. Conclusions
The original LAPPS scheme has been revised and expanded starting from the basic principles of closed–cycle engines. A relativistic treatment of the propellant has been used to determine the LAPPS performance limit and the role of the radiation in space propulsion. From a theoretical point of view, we find that optimal results in terms of specific impulse can be obtained well before the achievement of the relativistic limit of the propellant. In fact, it is not convenient to accelerate the particles by consuming a mass () comparable to the mass of the expelled propellant as the specific impulse is linear in even in the relativistic limit; this is a general property of all thrusters based on particle acceleration. For the same reason, we find that the radiation contribution to the propulsion is negligible when the equivalent mass-energy used to accelerate the propellant is negligible with respect to the mass of the vaporized target. In these conditions, the massive fraction of the propellant defines the specific impulse.
The LAPPS has been analyzed in detail by considering a realistic model including the acceleration of ions close to relativistic speed by means of a pure TNSA mechanism, besides an additional amount of particles accelerated to non–relativistic speed during the laser ablation process. The relative weight of these components determines the figures of merit of the LAPSS engine. An analytical description of LAPPS specific impulse and thrust has been obtained as a function of typical laser–plasma interaction parameters. We find that better performances in terms of are reached for high laser intensities using a thin low atomic number target. For intensities close to , a specific impulse can be achieved, with a negligible dependence on secondary acceleration mechanisms. These results suggest that LAPPS is potentially capable of an impressive specific impulse compared to other advanced electric-propulsion schemes. On the other side, the realization of an ideal thrust-mass ratio of 1 N for each tonne is much more challenging as it roughly requires a laser pulse with an energy of and a repetition rate of kHz for a spacecraft of a total mass of few tonnes, which must include a reactor with a thermal power of 20 MW. Moreover, the increase of the thrust implies a drastic reduction of the specific impulse down to values comparable to other advanced schemes. In short, optimized thrusts are obtained when a large amount of mass is accelerated at low velocities rather than when a few particles are brought close to relativistic speed, i.e., when the ion acceleration due to laser ablation becomes dominant with respect to the TNSA scheme. Nevertheless, unlike other closed–cycle electric propulsion, the thrust can be continuously adjusted by varying the laser intensity (e.g., by tuning the relative position of the target with respect to the focal spot) to produce a local increasing of the thrust only when required and thus preserving the possibility of deep space traveling using an ultra–high specific impulse.
Realistically, although the TNSA mechanism is widely explored and well–known, the comprehension of secondary accelerating mechanisms is crucial in LAPPS to correctly characterize its performance, especially in the low intensity limit. For these reasons, dedicated experimental measurements are required in order to fix the free parameters of the theory.