Experimental Study on the Behavior of Polyurethane Springs for Compression Members
Abstract
:1. Introduction
2. Design of Polyurethane Springs
3. Experimental Program
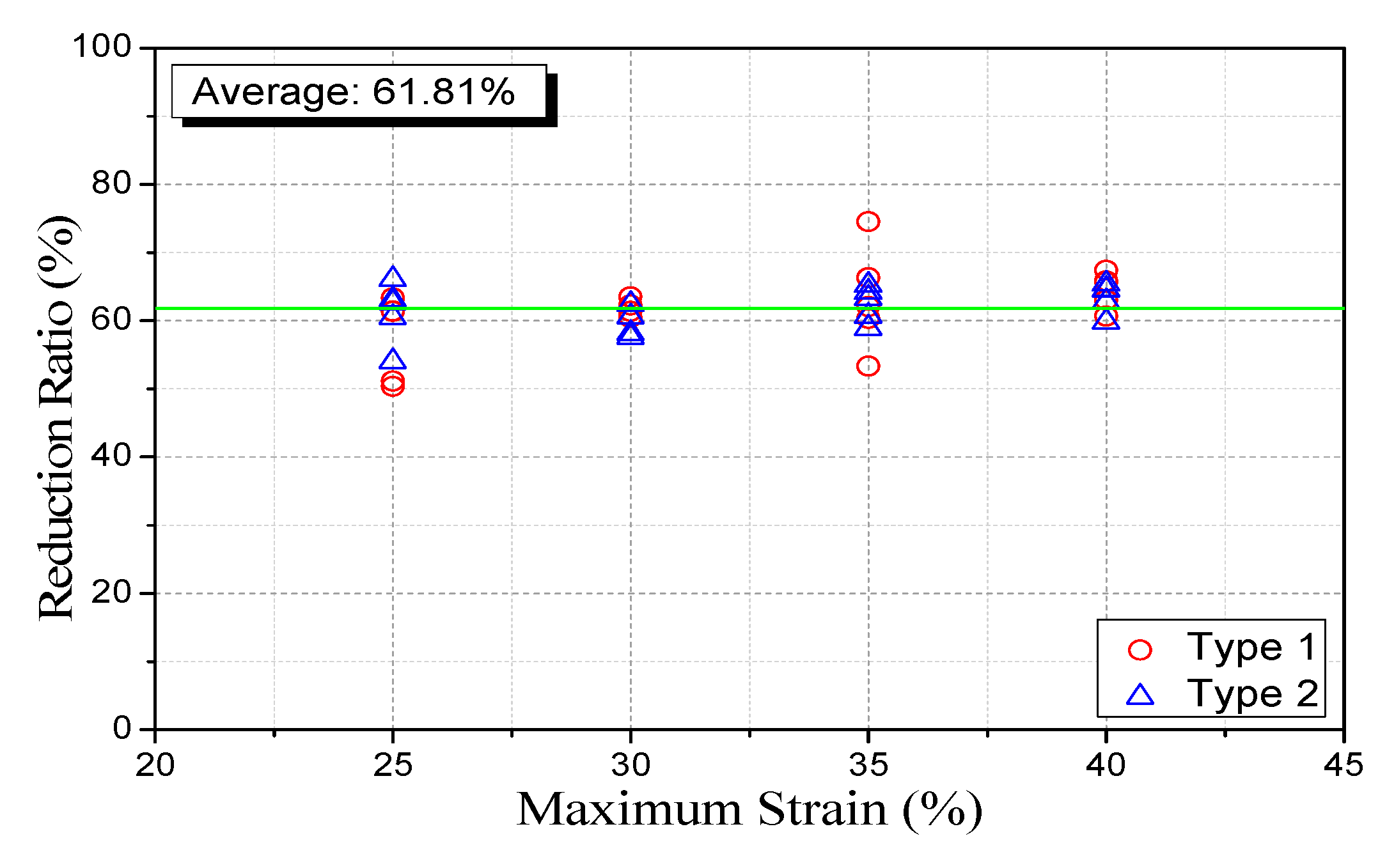
4. Experimental Results and Discussion
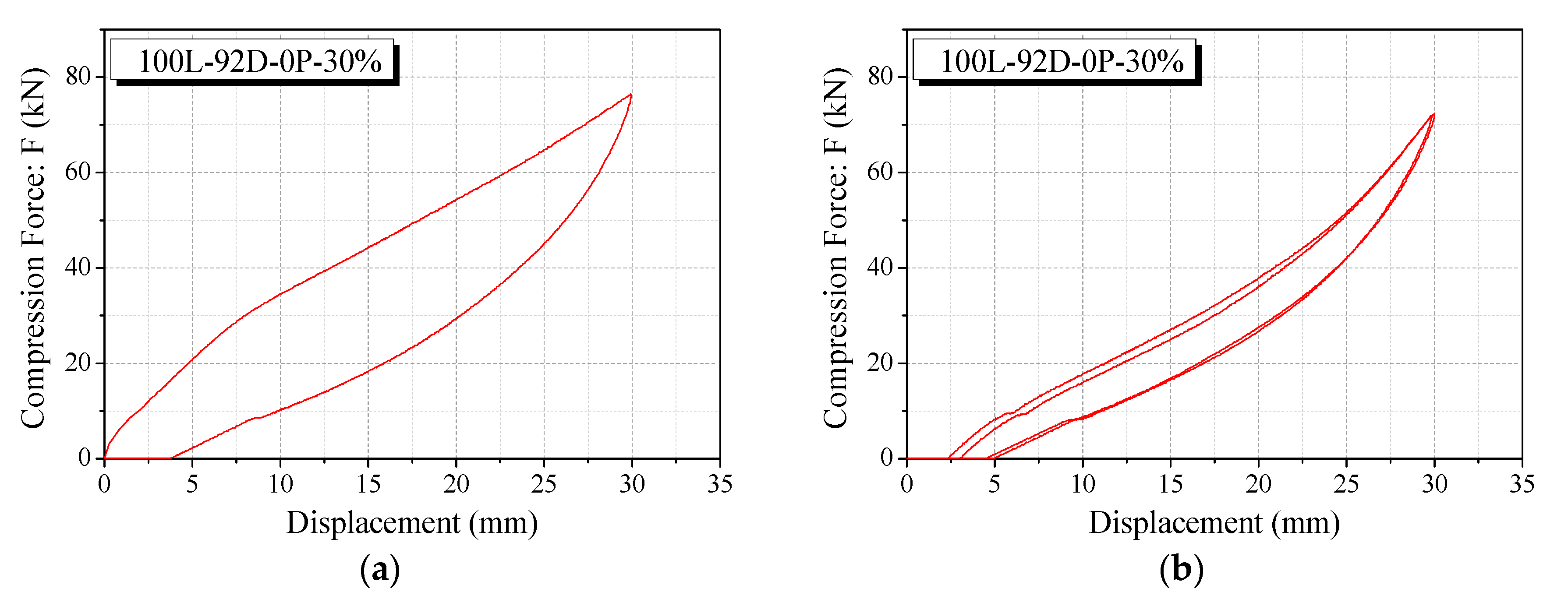
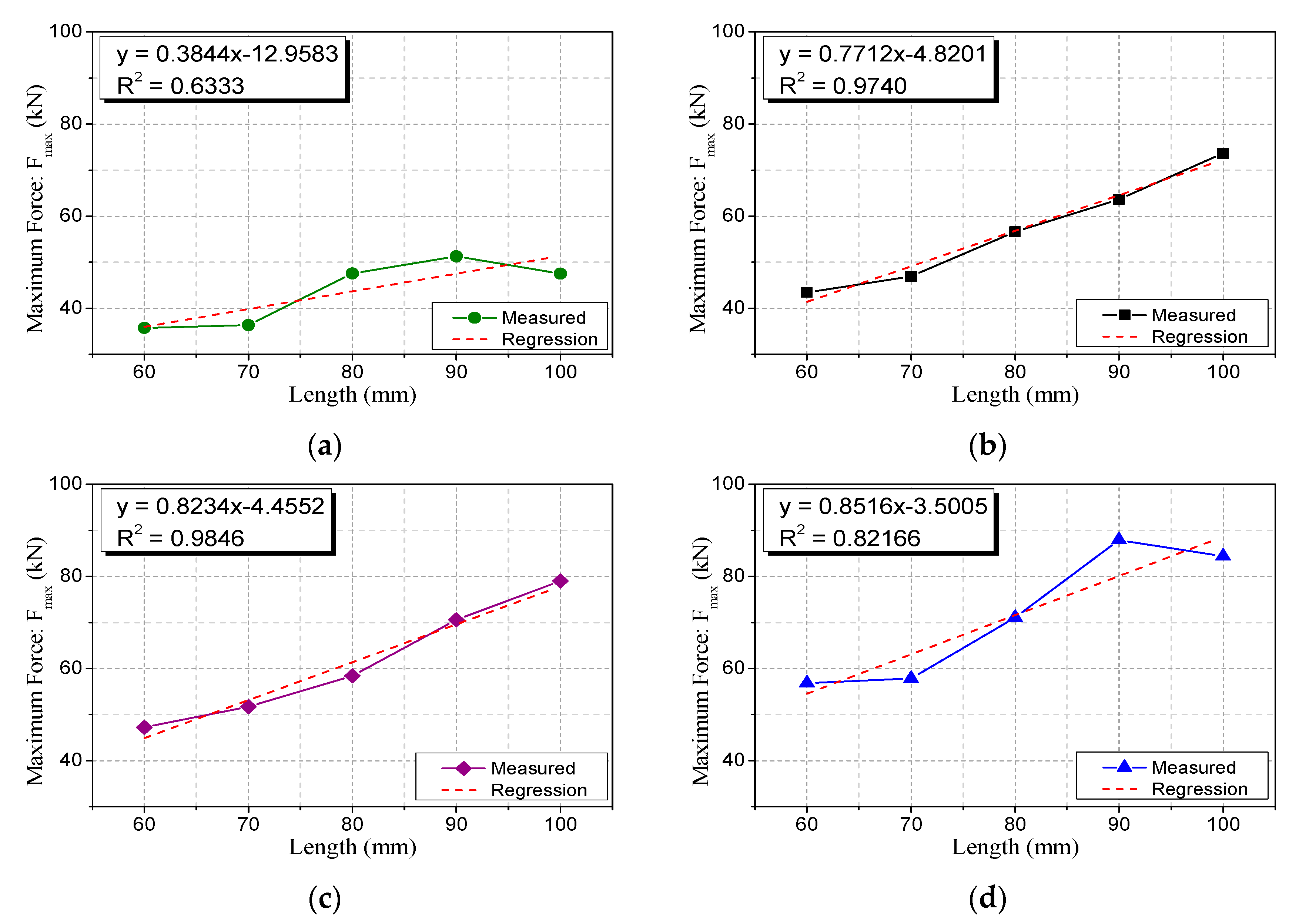
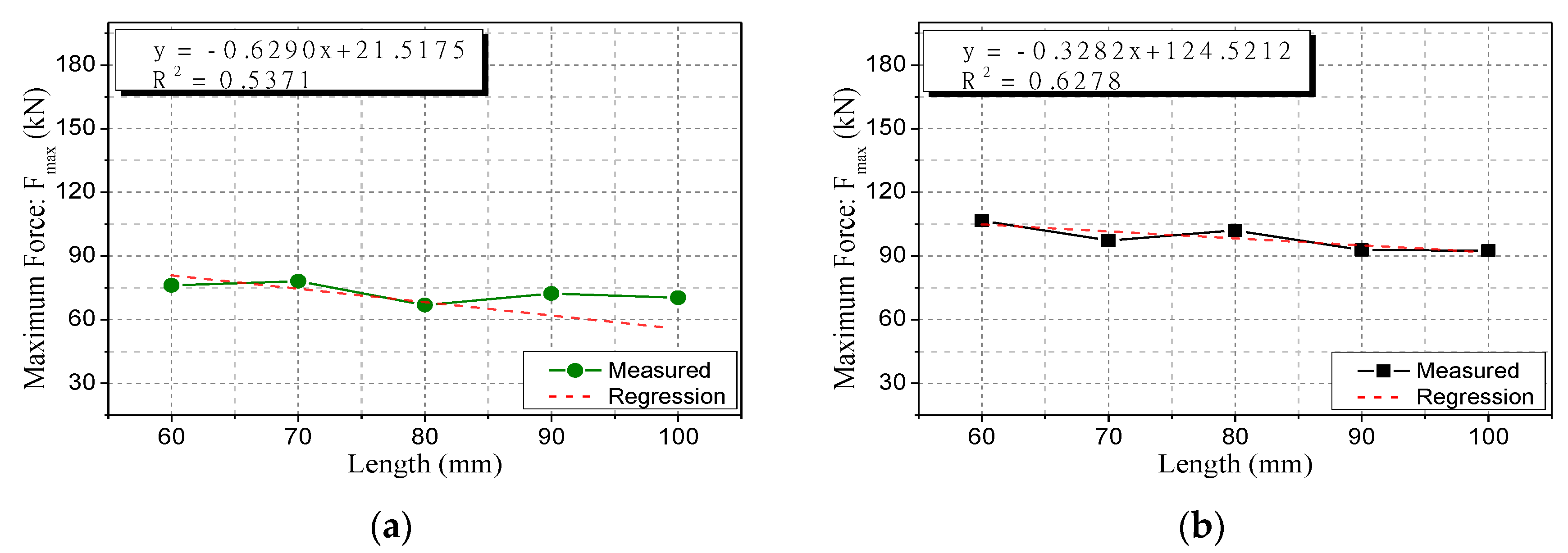
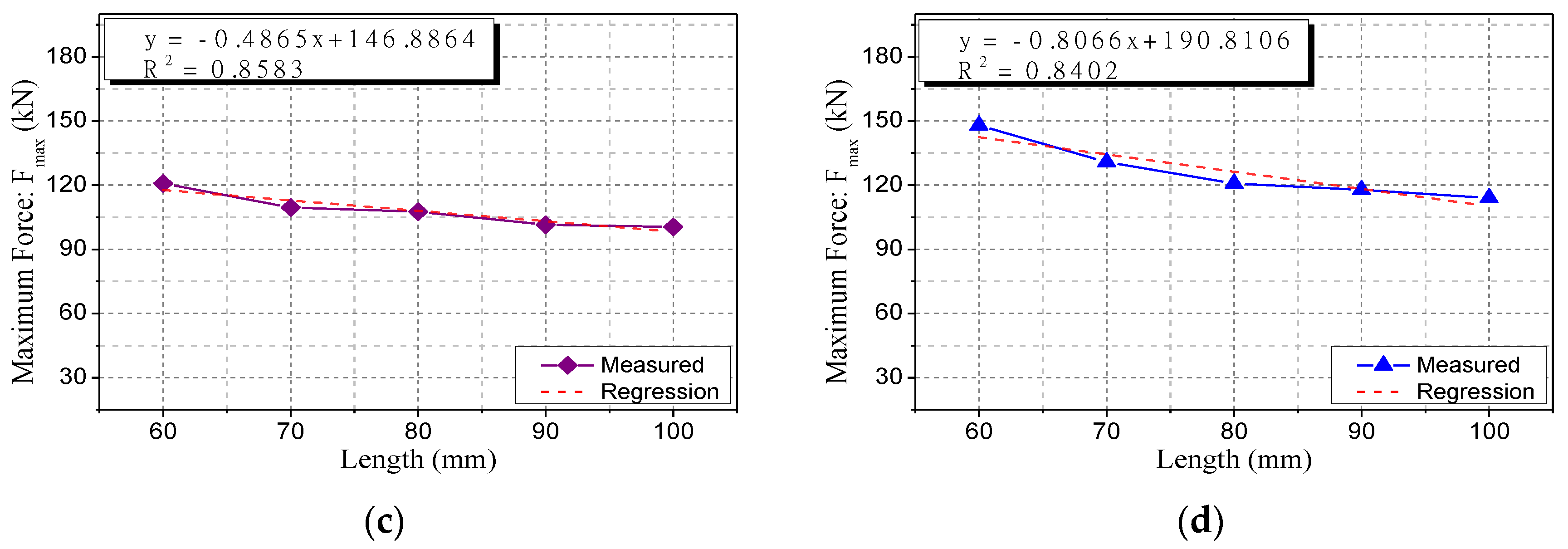
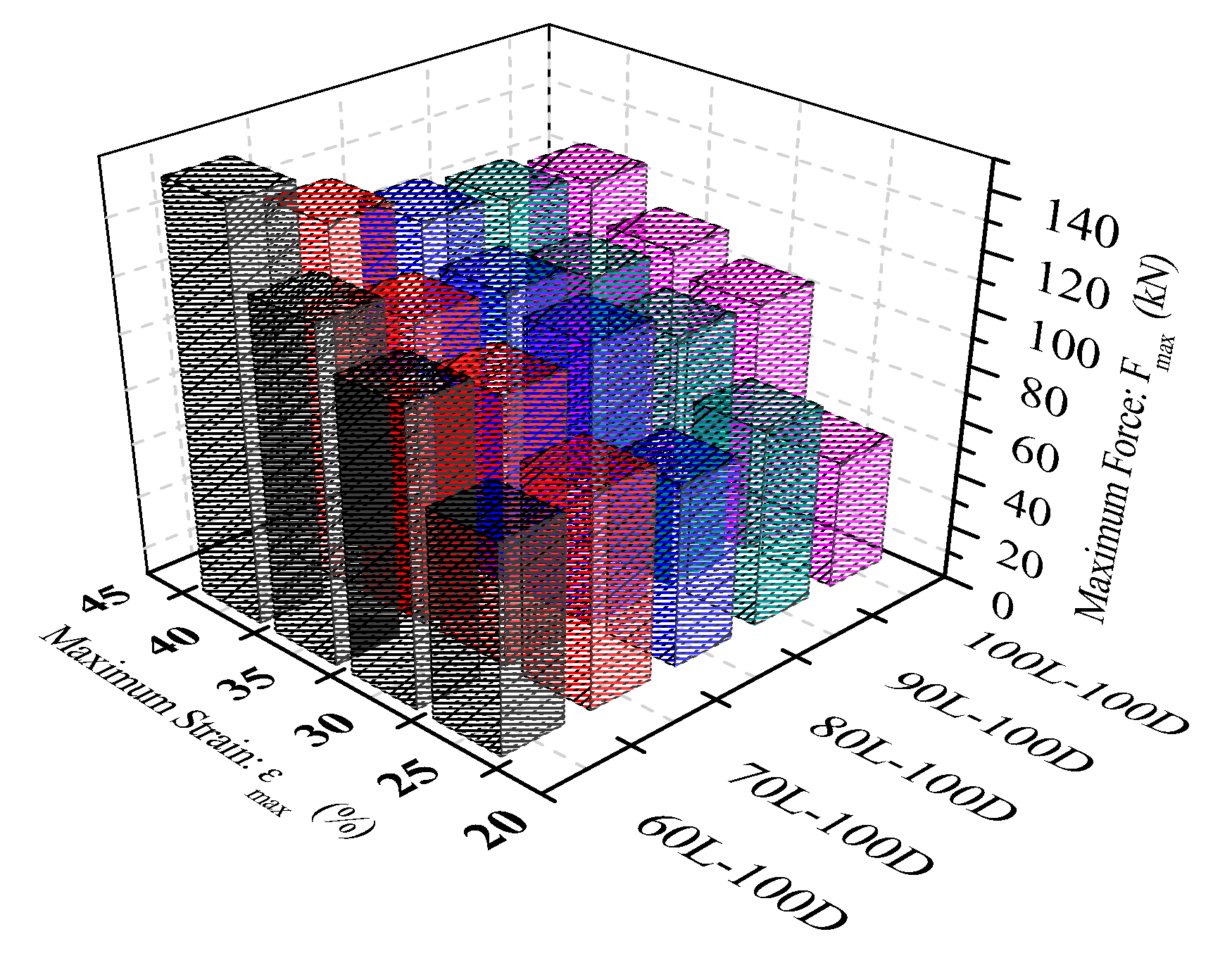
4.1. Type 1 Specimen Size Control
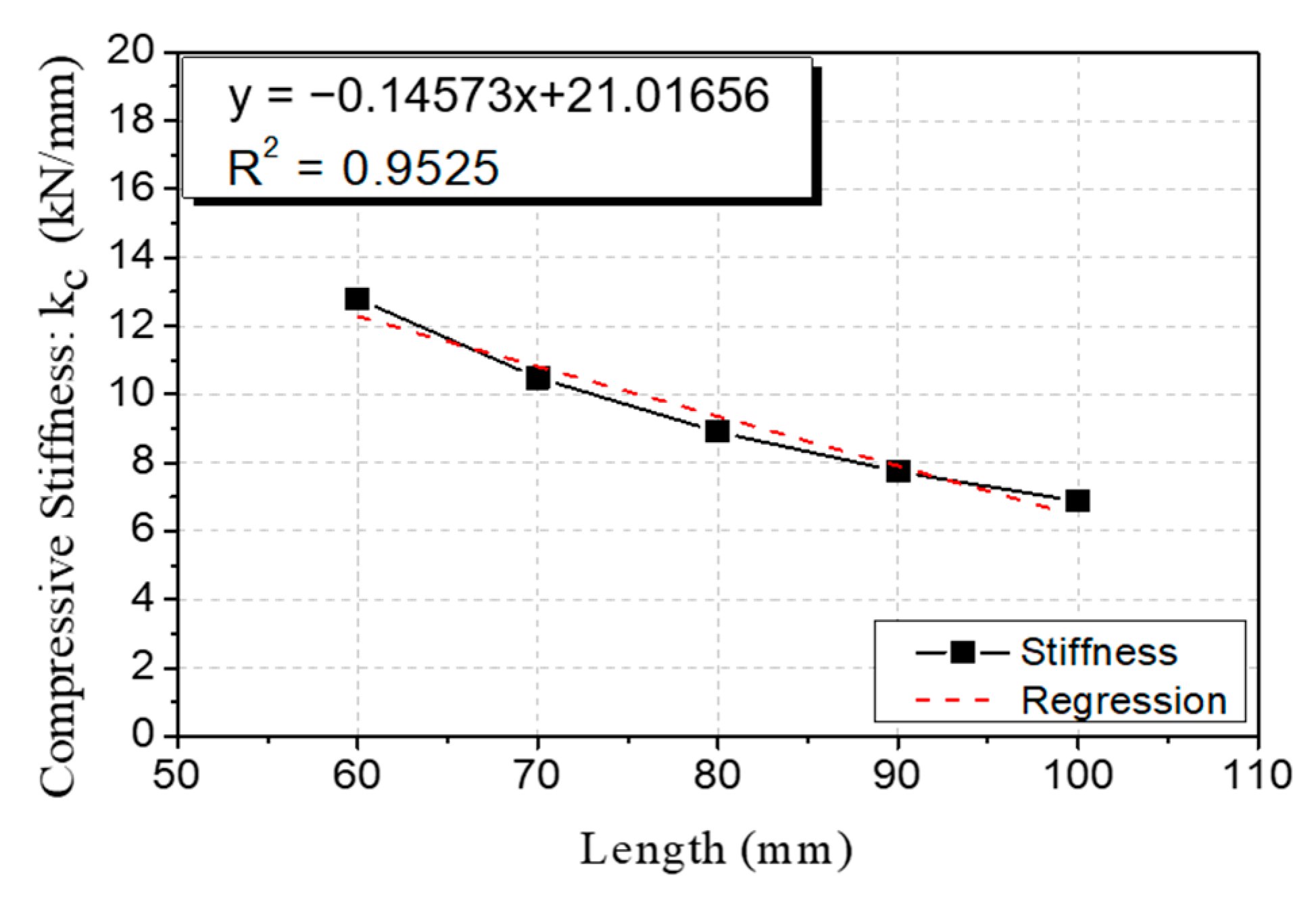
4.2. Type 2 Specimen Compressive Stiffness Contorl
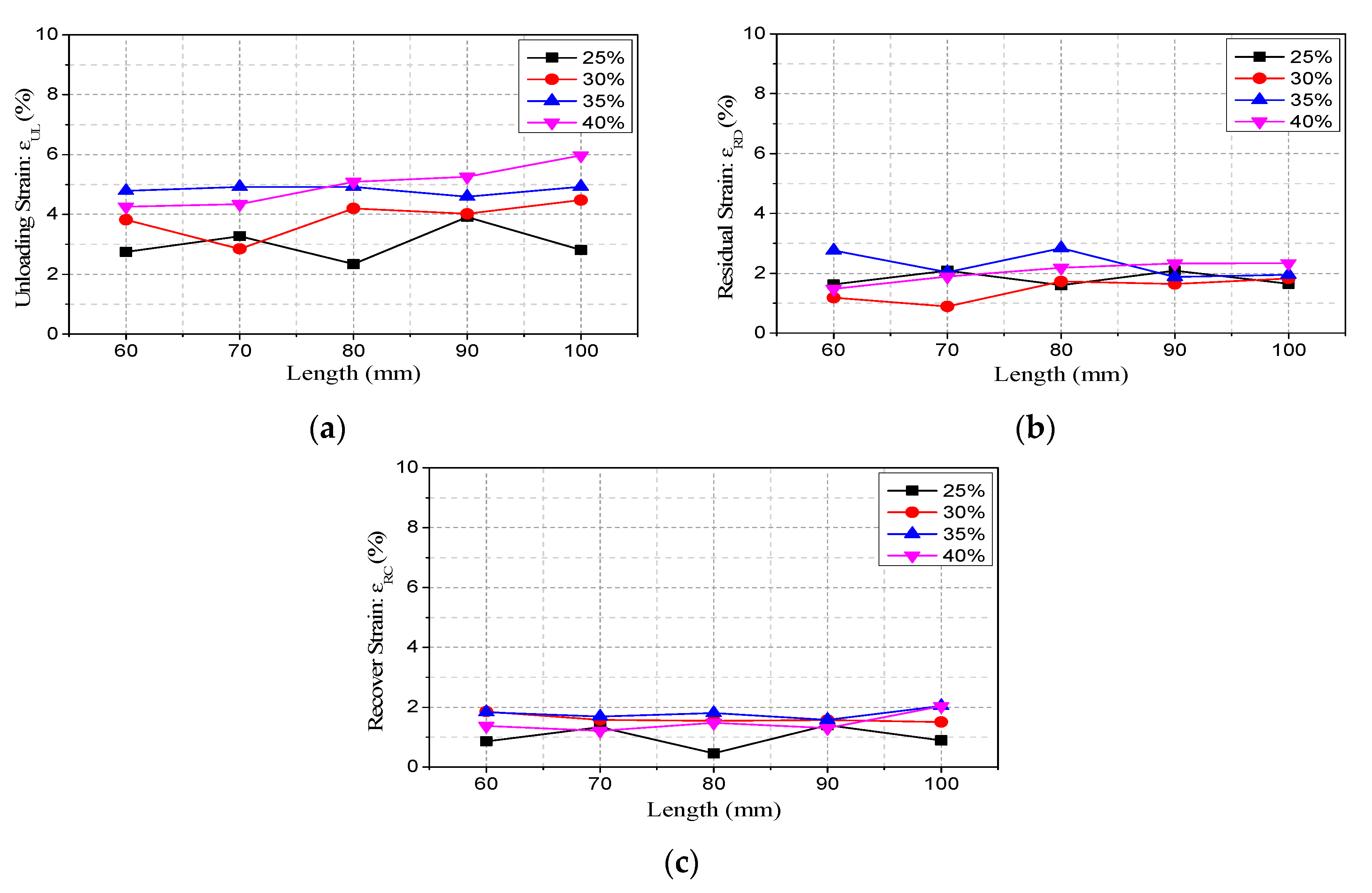
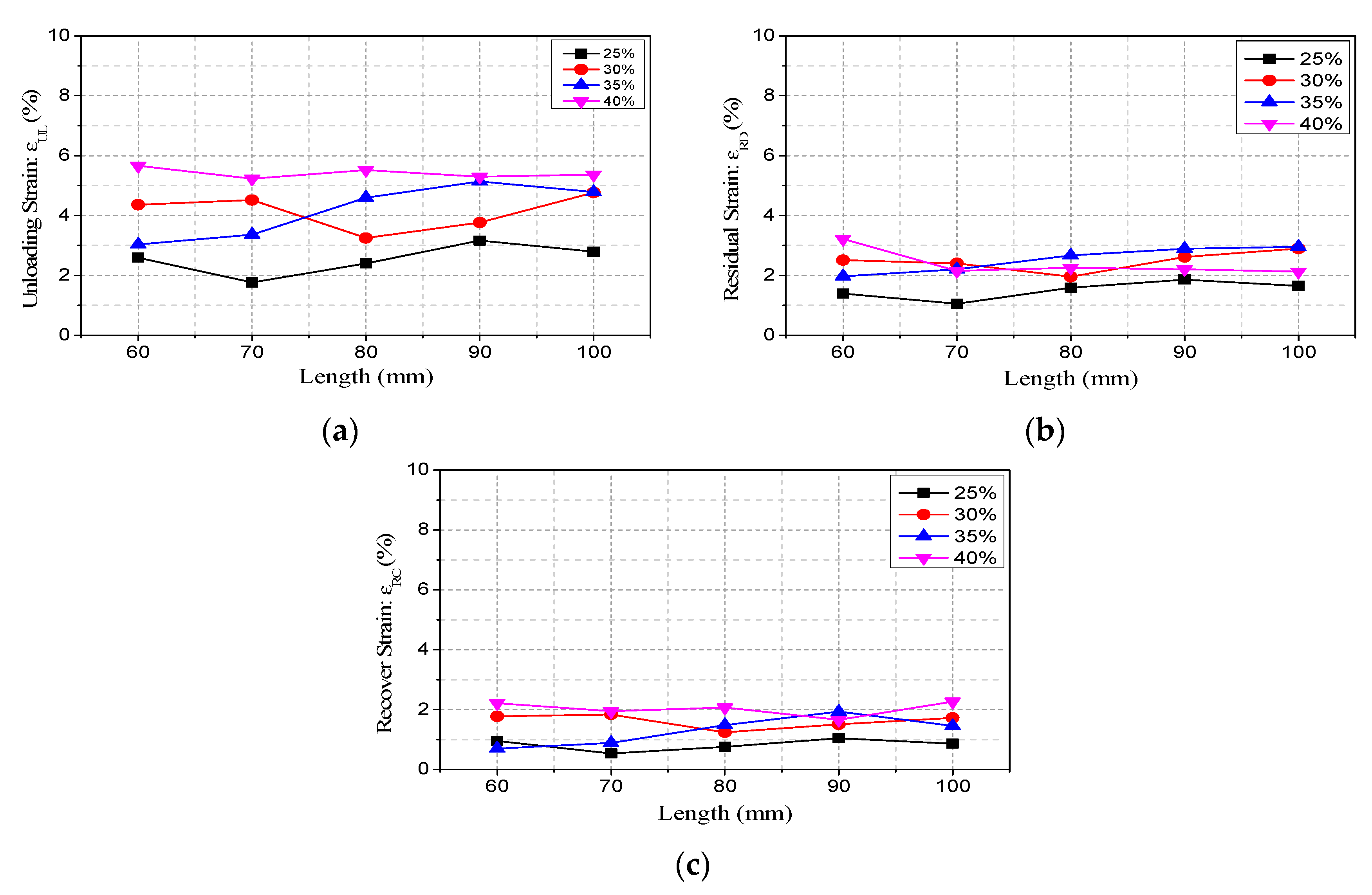
4.3. Energy Dissipation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Somarathna, H.; Raman, S.; Mohotti, D.; Mutalib, A.; Badri, K. The use of polyurethane for structural and infrastructural engineering applications: A state-of-the-art review. Constr. Build. Mater. 2018, 190, 995–1014. [Google Scholar] [CrossRef]
- Somarathna, H.; Raman, S.; Mohotti, D.; Mutalib, A.; Badri, K. Rate dependent tensile behavior of polyurethane under varying strain rates. Constr. Build. Mater. 2020, 254, 119203. [Google Scholar] [CrossRef]
- Damanpack, A.R.; Bodaghi, M.; Liao, W.-H. Contact/impact modeling and analysis of 4D printed shape memory polymer beams. Smart Mater. Struct. 2020, 29, 085016. [Google Scholar] [CrossRef]
- Li, P.; Guo, Y.; Shim, V. A rate-sensitive constitutive model for anisotropic cellular materials—Application to a transversely isotropic polyurethane foam. Int. J. Solids Struct. 2020, 206, 43–58. [Google Scholar] [CrossRef]
- Chou, C.-C.; Tsai, W.-J.; Chung, P.-T. Development and validation tests of a dual-core self-centering sandwiched buckling-restrained brace (SC-SBRB) for seismic resistance. Eng. Struct. 2016, 121, 30–41. [Google Scholar] [CrossRef]
- Fan, X.; Xu, L.; Li, Z. Seismic performance evaluation of steel frames with pre-pressed spring self-centering braces. J. Constr. Steel Res. 2019, 162, 105761. [Google Scholar] [CrossRef]
- Huang, H.; Chang, W.-S. Seismic resilience timber connection-adoption of shape memory alloy tubes as dowels. Struct. Control Health Monit. 2017, 24, e1980. [Google Scholar] [CrossRef] [Green Version]
- Oudah, F.; El-Hacha, R. Joint performance in concrete beam-column connections reinforced using SMA smart material. Eng. Struct. 2017, 151, 745–760. [Google Scholar] [CrossRef]
- Qiu, C.; Du, X. Seismic performance of multistory CBFs with novel recentering energy dissipative braces. J. Constr. Steel Res. 2019, 168, 105864. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Z.; Xie, Q.; Huang, L. Theoretical analysis and experimental investigation of hysteretic performance of self-centering variable friction damper braces. Eng. Struct. 2020, 217, 110779. [Google Scholar] [CrossRef]
- Mirzai, N.M.; Attarnejad, R.; Hu, J.W. Enhancing the seismic performance of EBFs with vertical shear link using a new self-centering damper. Ingegneria Sismica 2018, 35, 57–76. [Google Scholar]
- Mirzai, N.M.; Attarnejad, R.; Hu, J.W. Analytical investigation of the behavior of a new smart recentering shear damper under cyclic loading. J. Intell. Mater. Syst. Struct. 2019, 31, 550–569. [Google Scholar] [CrossRef]
- Hu, J.W.; Leon, R.T. Analyses and evaluations for composite-moment frames with SMA PR-CFT connections. Nonlinear Dyn. 2011, 65, 433–455. [Google Scholar] [CrossRef]
- Song, G.; Ma, N.; Li, H.-N. Applications of shape memory alloys in civil structures. Eng. Struct. 2006, 28, 1266–1274. [Google Scholar] [CrossRef]
- Tamai, H.; Kitagawa, Y. Pseudoelastic behavior of shape memory alloy wire and its application to seismic resistance member for building. Comput. Mater. Sci. 2002, 25, 218–227. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.C.; Hu, J.W. Pilot Study for Investigating the Cyclic Behavior of Slit Damper Systems with Recentering Shape Memory Alloy (SMA) Bending Bars Used for Seismic Restrainers. Appl. Sci. 2015, 5, 187–208. [Google Scholar] [CrossRef]
- McCormick, J.; Desroches, R.; Fugazza, D.; Auricchio, F. Seismic Assessment of Concentrically Braced Steel Frames with Shape Memory Alloy Braces. J. Struct. Eng. 2007, 133, 862–870. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.W.; Lee, J.; Seo, J. Performance-based optimal design of self-centering friction damping brace systems between recentering capability and energy dissipation. J. Mech. Sci. Technol. 2014, 28, 3129–3136. [Google Scholar] [CrossRef]
- Kikuchi, M.; Aiken, I.D. An analytical hysteresis model for elastomeric seismic isolation bearings. J. Int. Assoc. Earthq. Eng. 1997, 26, 215–231. [Google Scholar] [CrossRef]
- Gökçe, T.; Yüksel, E.; Orakdöğen, E. Seismic performance enhancement of high-voltage post insulators by a polyurethane spring isolation device. Bull. Earthq. Eng. 2018, 17, 1739–1762. [Google Scholar] [CrossRef]
- Oertel, G. Polyurethane Handbook; Hanser Publishers: Munich, Germany, 1994. [Google Scholar]
- Jeong, B.; Cheon, J.; Chun, J.; Mok, D.; Lee, H. Synthesis and Characterization of Polyurethane Elastomer. J. Adhes. Interface 2009, 10, 169–173. [Google Scholar]
- Petrovic, Z.S.; Ferguson, J. Polyurethane elastomers. Prog. Polym. Sci. 1991, 16, 695–836. [Google Scholar] [CrossRef]
- Mirzai, N.M.; Hu, J.W. Pilot study for investigating the inelastic response of a new axial smart damper combined with friction devices. Steel Compos. Struct. 2019, 32, 373–388. [Google Scholar] [CrossRef]
- Cui, H.; Wu, G.; Zhang, J.; Xu, J. Experimental study on damage-controllable rocking walls with resilient corners. Mag. Concr. Res. 2019, 71, 1113–1129. [Google Scholar] [CrossRef]
- Szczepański, M.; Migda, W.; Jankowski, R. Experimental Study on Dynamics of Wooden House Wall Panels with Different Thermal Isolation. Appl. Sci. 2019, 9, 4387. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Huang, T. Sliding implant-magnetic bearing for adaptive seismic mitigation of base-isolated structures. Struct. Control Health Monit. 2019, 26, e2431. [Google Scholar] [CrossRef]
- Choi, E.; Lee, J.; Youn, H. An Experimental Study on the Performance of a Damper Fabricated by Dual Rubber Springs. Int. J. Steel Struct. 2020, 20, 1891–1903. [Google Scholar] [CrossRef]
- Migda, W.; Szczepański, M.; Jankowski, R. Increasing the Seismic Resistance of Wood-frame Buildings by Applying PU Foam as Thermal Insulation. Period. Polytech. Civ. Eng. 2019, 63, 480–488. [Google Scholar] [CrossRef] [Green Version]
- Choi, E.; Jeon, J.S.; Seo, J. Cyclic compressive behavior of polyurethane rubber springs for smart dampers. Smart Struct. Syst. 2017, 20, 739–757. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, S.; Tan, P.; Zhu, H. Mechanical performance and shear constitutive model study of a new high-capacity polyurethane elastomeric bearing. Constr. Build. Mater. 2020, 232, 117227. [Google Scholar] [CrossRef]
- Qi, H.; Boyce, M. Stress–strain behavior of thermoplastic polyurethanes. Mech. Mater. 2005, 37, 817–839. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Park, S.-M.; Um, G.-Y.; Bea, J.-W. A Study on Friction-induced Surface Fracture Behaviors of Thermoplastic Polyurethane (TPU)/Rubber Blends. Adhes. Interface 2013, 14, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, P.; Zhang, S.; Wang, Z.; Li, N.; Silva, S.R.P.; Shao, G. A flexible metallic TiC nanofiber/vertical graphene 1D / 2D heterostructured as active electrocatalyst for advanced Li–S batteries. InfoMat 2021, 3, 790–803. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, P.; Li, B.; Zhang, S.; Liu, K.; Hou, R.; Zhang, X.; Silva, S.R.P.; Shao, G. Vertically aligned graphene nanosheets on multi-yolk/shell structured TiC@C nanofibers for stable Li–S batteries. Energy Storage Mater. 2020, 27, 159–168. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Y.; Zhang, Y.; Hou, R.; Zhang, X.; Xue, C.; Wang, S.; Zhu, B.; Li, N.; Shao, G. Photogenerated Electron Transfer Process in Heterojunctions: In Situ Irradiation XPS. Small Methods 2020, 4, 2000214. [Google Scholar] [CrossRef]
- Koblar, D.; Škofic, J.; Boltežar, M. Evaluation of the Young’s Modulus of Rubber-Like Materials Bonded to Rigid Surfaces with Respect to Poisson’s Ratio. Strojniški Vestnik—J. Mechan. Eng. 2014, 60, 506–511. [Google Scholar] [CrossRef] [Green Version]
- Mirzai, N.M.; Attarnejad, R.; Hu, J.W. Experimental investigation of smart shear dampers with re-centering and friction devices. J. Build. Eng. 2021, 35, 102018. [Google Scholar] [CrossRef]
- Darwin, D.; Nmai, C.K. Energy Dissipation in RC Beams Under Cyclic Load. J. Struct. Eng. 1986, 112, 1829–1846. [Google Scholar] [CrossRef]
- Al-Jaberi, Z.; Myers, J.J.; ElGawady, M. Pseudo-static cyclic loading comparison of reinforced masonry walls strengthened with FRCM or NSM FRP. Constr. Build. Mater. 2018, 167, 482–495. [Google Scholar] [CrossRef]







| Type | D (mm) | Din (mm) | L (mm) | S | Ea (MPa) | kc (kN/mm) |
|---|---|---|---|---|---|---|
| 1 | 92 | 20 | 100 | 0.18 | 87.21 | 5.52 |
| 88 | 20 | 90 | 0.20 | 88.03 | 5.85 | |
| 82 | 20 | 80 | 0.20 | 88.37 | 5.72 | |
| 77 | 20 | 70 | 0.21 | 89.03 | 5.80 | |
| 72 | 20 | 60 | 0.23 | 89.97 | 5.96 | |
| 2 | 100 | 20 | 100 | 0.21 | 88.57 | 6.87 |
| 100 | 20 | 90 | 0.23 | 89.94 | 7.75 | |
| 100 | 20 | 80 | 0.26 | 91.86 | 8.90 | |
| 100 | 20 | 70 | 0.29 | 94.65 | 10.48 | |
| 100 | 20 | 60 | 0.34 | 98.95 | 12.79 |
| 25, 30, 35, 40 | |
|---|---|
| Loading Speed , mm/s) | 0.5 |
| Loading Cycle | 3 |
| Temperature (°C) | 25 |
| Specimen | Slop (a) | Const. (b) | |
|---|---|---|---|
| 60L-72D-0P | 6.6998 | 29.097 | 0.9757 |
| 70L-77D-0P | 7.2365 | 40.341 | 0.9299 |
| 80L-82D-0P | 6.9310 | 30.900 | 0.9699 |
| 90L-88D-0P | 11.683 | 39.163 | 0.9731 |
| 100L-92-0P | 11.592 | 42.176 | 0.8388 |
| Specimen | Slop (a) | Const. (b) | |
|---|---|---|---|
| 60L-100D-0P | 22.946 | 55.51 | 0.9826 |
| 70L-100D-0P | 17.044 | 61.312 | 0.9906 |
| 80L-100D-0P | 16.709 | 57.557 | 0.8801 |
| 90L-100D-0P | 14.513 | 59.838 | 0.9784 |
| 100L-100-0P | 20.757 | 36.756 | 0.8649 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, Y.H.; Hu, J.W. Experimental Study on the Behavior of Polyurethane Springs for Compression Members. Appl. Sci. 2021, 11, 10223. https://doi.org/10.3390/app112110223
Ju YH, Hu JW. Experimental Study on the Behavior of Polyurethane Springs for Compression Members. Applied Sciences. 2021; 11(21):10223. https://doi.org/10.3390/app112110223
Chicago/Turabian StyleJu, Young Hun, and Jong Wan Hu. 2021. "Experimental Study on the Behavior of Polyurethane Springs for Compression Members" Applied Sciences 11, no. 21: 10223. https://doi.org/10.3390/app112110223
APA StyleJu, Y. H., & Hu, J. W. (2021). Experimental Study on the Behavior of Polyurethane Springs for Compression Members. Applied Sciences, 11(21), 10223. https://doi.org/10.3390/app112110223







