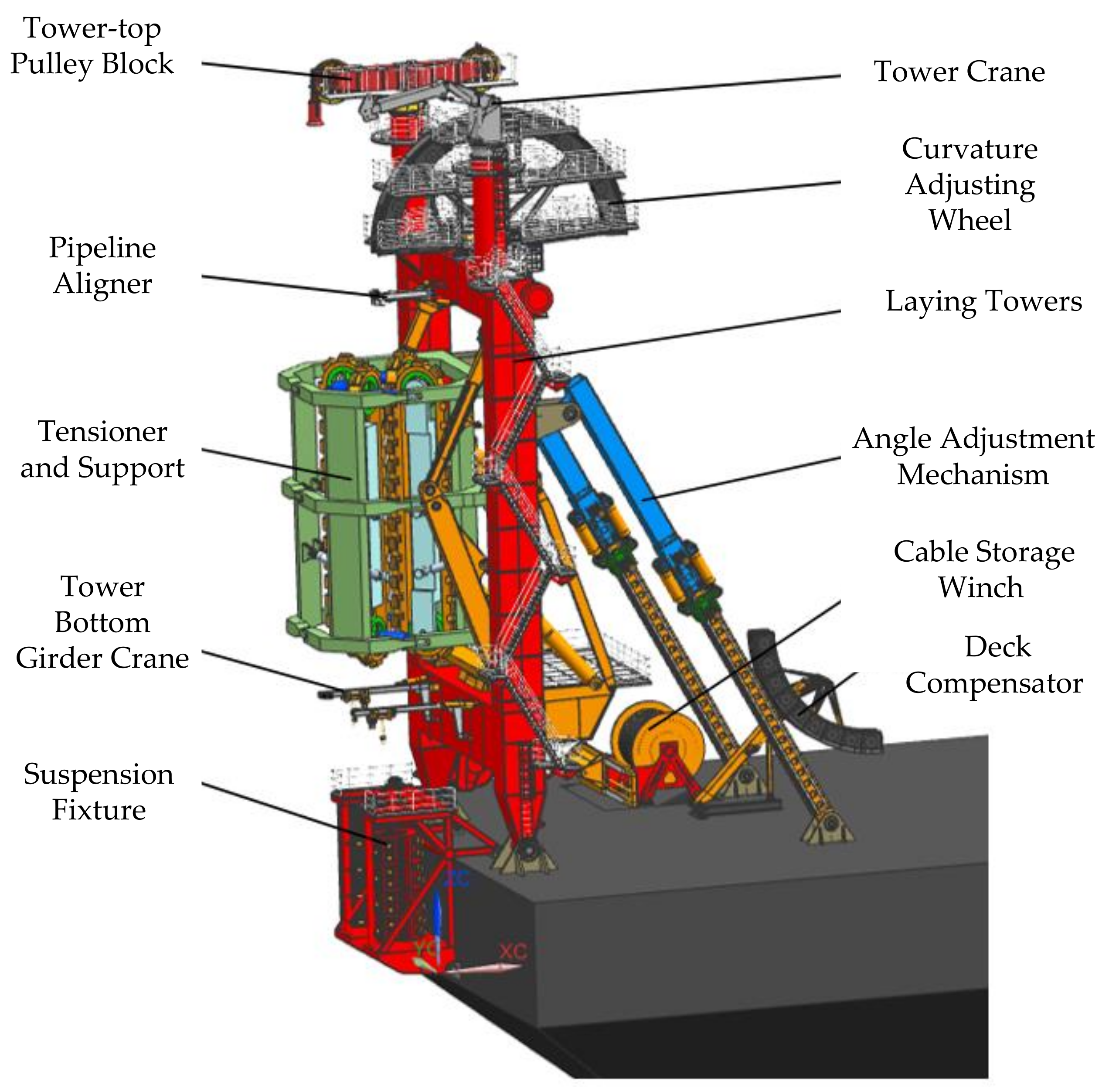
The submarine flexible pipe-laying system is a complex system that includes multiple pieces of equipment working in coordination. The pipes are laid together on the submarine through the cooperation of various subsystems. The paving system mainly consists of tensioners and their supports, curvature adjusting wheels, angle adjusting mechanism, paving tower, and other equipment. The tower mechanism is the main supporting part of the paving system. The tensioner and its bracket, curvature adjusting wheel, pulley set, and other components are fixed on the tower mechanism by welding or bolting. The laying system completes pipe laying by coordinating and working together of various equipment components [
18]. The overall structure of the flexible pipeline-laying system is shown in
Figure 1.
2.1. Ambient Load of Paving System and Ship Motion Response
The laying of subsea pipelines requires collaboration between laying tower system mechanisms. Since it is difficult to predict the marine loads that the laying vessel will be subjected to, analysis of the dynamic characteristics of the pipeline is a prerequisite to ensure that the strength of the designed laying system meets the requirements. In order to carry out this study, data on the marine environmental loads on the laying system and the motion response of the laying vessel under that load are required. When laying pipe, the laying vessel is combined with the flexible pipe for laying pipe, creating a coupling effect. Considering the interaction between the marine load and the motion of the laying vessel, coupling analysis is an effective method to analyze the deep-water flexible pipe-laying process, which allows dynamic analysis of both the vessel and the flexible pipe.
2.1.1. Environmental Load of Paving System
Wind loads on marine structures can generally be calculated by empirical formulas derived from wind tunnel tests on hull models. In this paper, the wind loads of pipe-laying vessels are calculated according to the empirical formulas of wind loads provided by the Oil Companies International Marine Forum (OCIMF) [
19].
Current loads can generally be considered as steady-state planar flows, producing only drag forces on the hull. In order to analyze the force of ocean current on the hull, Equation (1) needs to be used to calculate the superposition of horizontal velocity and wave particle velocity.
where
φcR is the relative angle,
ρc is the density of the seawater in units kg/m
3.
FXC,
FYC, and
MXYC are X-direction, Y-direction, and moment of flow around the vertical axis of the ship, respectively.
d is the average draft depth of the ship, unit m.
vc is the current velocity per m/s, which varies with the depth of the seawater.
VCR is the relative velocity of the ship and the current;
LBP is the vessel vertical length.
CXC,
CYC, and
CXYC are the drag force coefficients. Their values depend on the relationship between the current and the ship, which can also be found from the map data.
Irregular waves are used for the calculation of wave loads. The wave elements are random variables and are usually expressed in terms of their statistical characteristics. According to the principle of linear waves, irregular waves are superimposed by waves with different heights, frequencies, and random phases, which can be defined by energy spectrum. The spectrum selected in this paper is the JONSWAP wave [
20]. JONSWAP spectrum is obtained by Adelman through a large number of data taken in the North Sea. The expression is Equation (2):
where
α is the generalized Philips coefficient,
α = 0.0076(
gx/U
2)
−0.22.
ωp is the peak frequency of the spectrum,
ωp = 22(g/U)(
gx/U
2)
−0.33; σ is the peak parameter,
σ = 0.07 when
ω <
ωp; When
ω >
ωp, σ = 0.09.
γ is the peak enhancement factor with an average value of 3.3. U is the average wind speed, and
x is the length of the wind zone.
Sζ(ω) is a function of the energy density of waves. The expression of wave surface height and time of irregular waves is Equation (3).
where
N represents the number of regular waves and Δ
ω is the interval frequency.
The first-order wave force and the second-order wave force are solved by deriving the transformation and Fourier transformation. The first-order wave force and the second-order wave force can be solved by Equation (4) and Equation (5) respectively.
2.1.2. Research on Mechanical Model of Flexible Pipe
In the analysis of the laying process of flexible deep-sea pipelines, the following four assumptions are required: a. It is assumed that the working ship is stationary when laying the pipeline. b. Current is linear based on the distribution on the longitudinal section of the hull, with zero submarine velocity and maximum surface velocity. c. Integral flexible pipes are laid on the mid-longitudinal plane of the ship. d. Because of the large depth of water laid, the flexible piping can be considered, and the influence of bending rigidity of flexible piping can be ignored.
After laying the pipeline for a period of time, the flexible pipeline in the ocean taken on the form of a catenary, as shown in
Figure 2. The point at which the pipeline passes through the sea level is regarded as origin
O, the x axis as horizontal direction, the y axis as vertical downward direction, the pipeline from contact bottom to
O point at sea level as suspension section, and the bottom contact section on the seabed. When analyzing the suspension section, first intercept the microelement of the dl length of the previous section and analyze its stress, as shown in
Figure 2.
Fn and
Fτ are used to calculate the ocean load per unit length.
τ represents the drag force of the unit pipeline in the ocean by the current in the normal and tangential directions. It can be obtained by Morison’s semi-empirical Equation (6).
where
Cn and
Cτ are the normal and tangential drag force coefficients, respectively;
v represents the current velocity in the horizontal plane where the pipeline unit is located;
θ represents the included angle between the pipe unit and the horizontal direction.
The coordinate axis is established according to the shape of the pipeline. The intersection point between the pipeline and horizontal plane is the origin. The complete pipeline is considered to be composed of a large number of micro-elements. Each microelement is
dy in the
y-direction length. If the depth of seawater is
h, the total microelement segment is
m =
h/dy. For any pipe element
i in the suspension section, the parameters can be calculated by Equation (7), and the parameters at point
i + 1 can be calculated by the parameters at point
i of the pipeline.
Based on the above analysis, the position parameters, tension at each point, line coordinate parameters, and total length of the pipeline can be calculated by computer programming, which can be used as basic parameters for dynamic simulation of pipeline laying. The linearity of pipe laying and the variation of internal force of pipe are calculated by setting the angle, maximum depth, and shape parameters of pipe laying. Several different pipelines are selected for the study, and the parameters are given in
Appendix A.
2.1.3. Research on Dynamic Performance of Pipe-Laying Ship
The ship can be considered as a rigid body when studying its motion in waves. The wave forces acting on the ship are usually solved from two aspects: diffraction and radiation. The motion of the ship is neglected in the calculation of the diffraction method, while the radiation method is mainly used to calculate the influence of the hydrodynamic coefficient on the motion of the ship [
21]. In this paper, the AQWA sub-module of ANSYS is used to analyze the hydrodynamic performance of pipeline-laying ships. Through the frequency domain, hydrodynamic analysis of the ship by AQWA, the hydrostatic stiffness matrix, hull additional mass, hull damping coefficient, first-order wave force, and second-order wave load of the ship can be obtained [
22].
HYSY201 is a pipeline laying vessel of China National Offshore Oil Corporation (CNOOC). Based on the size parameters of HYSY201, the model of pipeline laying vessel is established. The size parameters and physical characteristics of the selected laying vessel are shown in
Appendix B. The parameters provided by the ship’s profile drawing are imported into the DM module of ANSYS to complete the drawing of the ship’s geometric surface by the generated surface, and finally, the ship’s surface model is established. Then the hydrodynamic model can be obtained by meshing the underwater wet surface of the ship with plate units in ANSYS-AQWA, as shown in
Figure 3.
When laying pipelines at sea, the inherent frequency of the hull should avoid the peak frequency of the spectrum under the working sea condition to avoid hull resonance.
RAO is used to describe the motion response of a floating structure under incident waves of unit amplitude [
23,
24]. The definition of RAO is as Equation (8).
where
ζ(ω) is the response of the hull to waves of a certain frequency and
ζ is the amplitude of the corresponding frequency wave.
2.1.4. Time-Domain Coupled Motion Equation
During the laying of flexible pipes, the ship motion is the result of the dynamic coupling between the marine environment and flexible pipes. Based on Newton’s second law, the time-domain coupled motion equation of the ship can be obtained. The relationship between the ship motion and time in waves can be obtained by solving Equation (9).
where
M and
μ represent the mass matrix and additional mass matrix of the system, respectively,
X(t) represents the displacement matrix of ship motion, and
t represents time.
FWA represents the excitation load caused by waves,
FWI represents the drag force of the wind,
FCU represents the drag force of ocean current, and
FP represents the load on the hull caused by the tension generated by laying pipelines. When solving Equation (9), the method of step-by-step integration can be adopted in the time domain. The displacement, velocity, and acceleration of a particle in space can be obtained by the step-by-step integration method over time; thus, the force variation with time can be calculated. The
Newmark-β method can be used to carry out the integration solution.
2.2. Similarity Principle and Derivation of Similar Norms
When testing a designed structure, the prototype design is usually uneconomical and difficult to meet the requirements of the experiment. Therefore, we usually choose a sample similar to the original sample for the experiment. This is called a model experiment. When the scaled model is similar to the prototype, it must be geometrically similar to the prototype and similar in strength [
25]. Since the model is designed in a four-level sea environment, the deformation errors caused by the environment on the prototype and the model can be neglected [
26].
When the prototype and model of flexible pipe-laying system are subjected to corresponding loads, the geometrical and static effects of the variables that can be compared with each other are size
l, external force
F, external moment
M, elastic modulus
E, strain
ε, density
ρ, and stress
σ. According to these variables, the corresponding relationship between prototype and model can be obtained. The relationship between the main physical parameters can be expressed as Equation (10).
For general elastic questions, the characteristics of introducing physical constants are analyzed, and three basic force scales are adopted, namely mass
m, length
L, and time
T. Each variable can be expressed in units of the basic dimension, whose dimension matrix is as Equation (11).
Represent physical parameters from
F,
M,
E,
ρ,
l,
ε,
σ with
a1,
a2,
a3,
a4,
a5,
a6,
a7, respectively. Equation (12) can be simplified by Equation (11).
Equation (13) can be obtained by using
a3,
a4,
a5 as independent variables.
Equation (13) is a statically indeterminate equation with several parameters, including three basic dimensions. The number of independent
π can be known by the
π Theorem to be four (7 − 3 = 4). The Similarly
π Theorem is the Similarly Second Theorem expressed as if a phenomenon can be described by Equation (14).
The equation includes a total of n physical quantities. If
K physical quantities have independent dimensions, the dimension of the last
n −
k physical quantities can be derived from the previous independent dimensions. By means of transformation, the above formula can be transformed into a functional relation between similar criteria
π1,
π2,…
πn−k, that is, Equation (15).
Therefore, Equation (13) can be rewritten as Equation (16).
Then the similarity matrix containing each variable can be obtained as Equation (17).
Then the scale of model scale meets the requirements as Equation (18).
In the design and manufacture of actual models, the model size and material must be selected according to the site of the required experiments. Therefore, the similar constants of geometric size, elastic modulus, and material density (
Cl,
CE,
Cρ) can be determined, and the remaining similar constants can be calculated from these constants. The scaled model uses a scale of 1:20 according to the laboratory conditions. The material used in the prototype is
S690QL high-strength welded structural steel. The material of the model is
Q235 steel. The calculated modulus of elasticity has a similar ratio of 0.996, and the similarity ratio of density is 0.999. The similarity relationship and similarity of the model are shown in
Table 1.
To determine the similarity constants of wave loads, the gravity similarity of fluid flow phenomena needs to be considered, and the Froude number is selected as the similarity criterion [
27]. If the fluid is subjected to a mass force of gravity only, the Froude number (Fr) of the model can be expressed as Equation (19).
where the parameters with angle label m represent the parameters of the model, and those with angle label p represent the parameters of the prototype.
g represents the acceleration of gravity,
l represents the length,
ρ represents the density of the fluid,
v represents the velocity of fluid flow, and
Fi and
Fg represent inertial force and gravity, respectively. From the similarity criteria of the model and the prototype,
Frm =
Frp, and the gravity is constant,
gm =
gp, we can get Equation (20).
It can be derived that, for time
t, there is Equation (21).
Therefore, the period and amplitude of the motion response of the ship to wave load can be reduced in proportion to time and length to obtain the required motion environment for the model.