An Analytical Solution for 2D Dynamic Structure-Soil-Structure Interaction for Twin Flexible Tunnels Embedded in a Homogeneous Half-Space
Abstract
:1. Introduction
2. Methodology
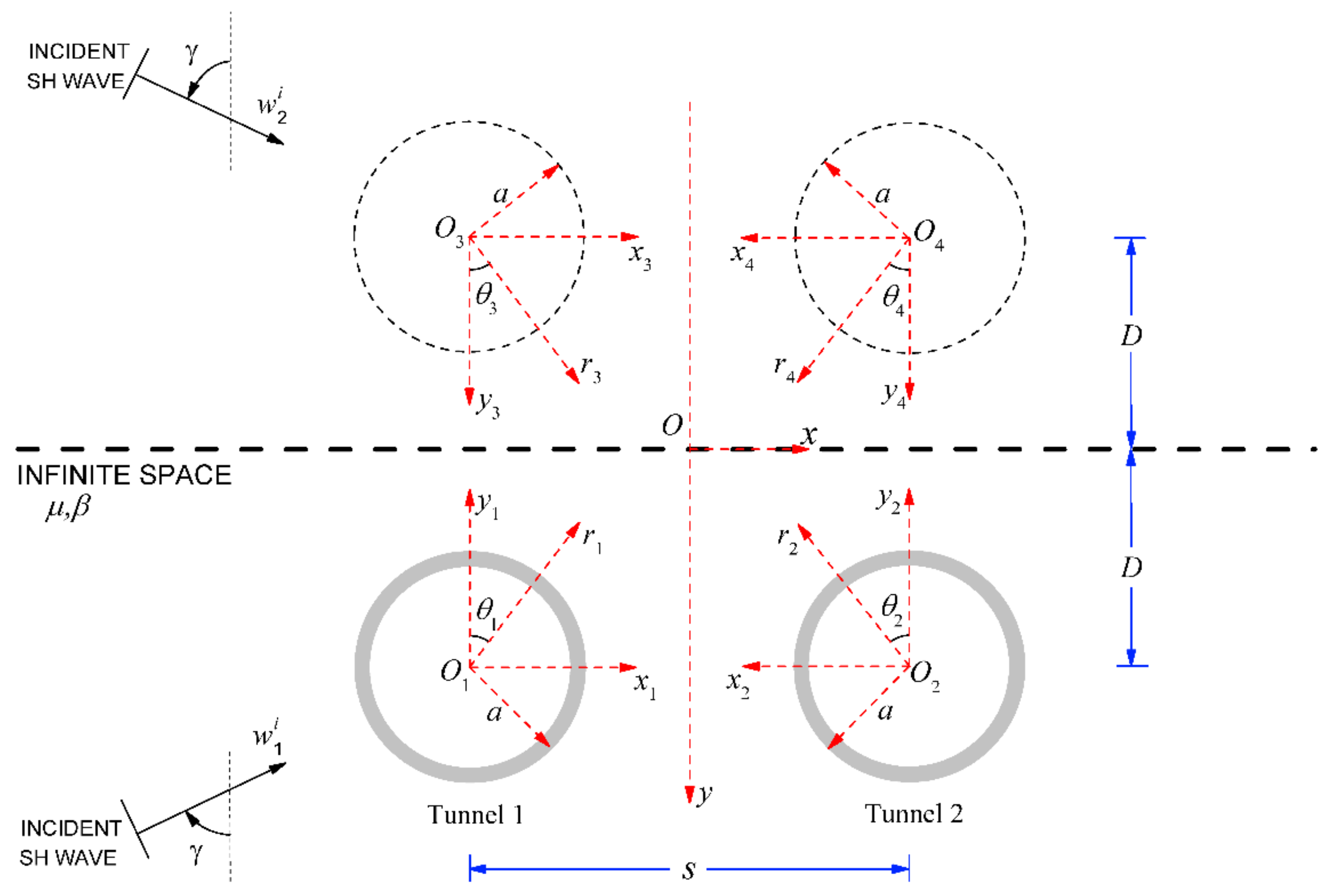
2.1. Analytical Model
2.2. Governing Equations and Boundary Conditions
2.3. Solutions to the Problem
3. Solution Verification
4. Results and Analysis
4.1. Model Parameters
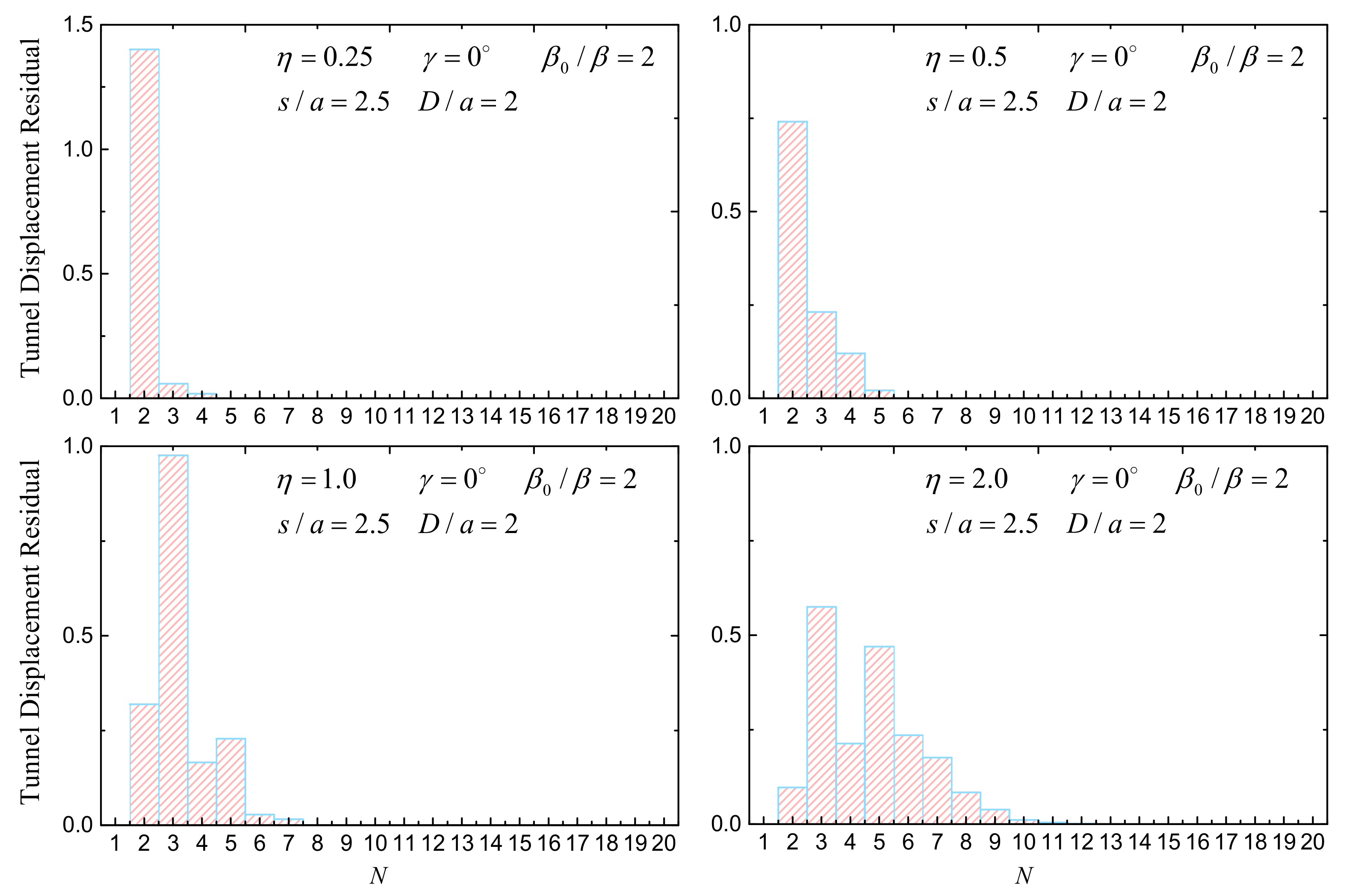
4.2. Influence of Tunnel Stiffness on Tunnel Responses
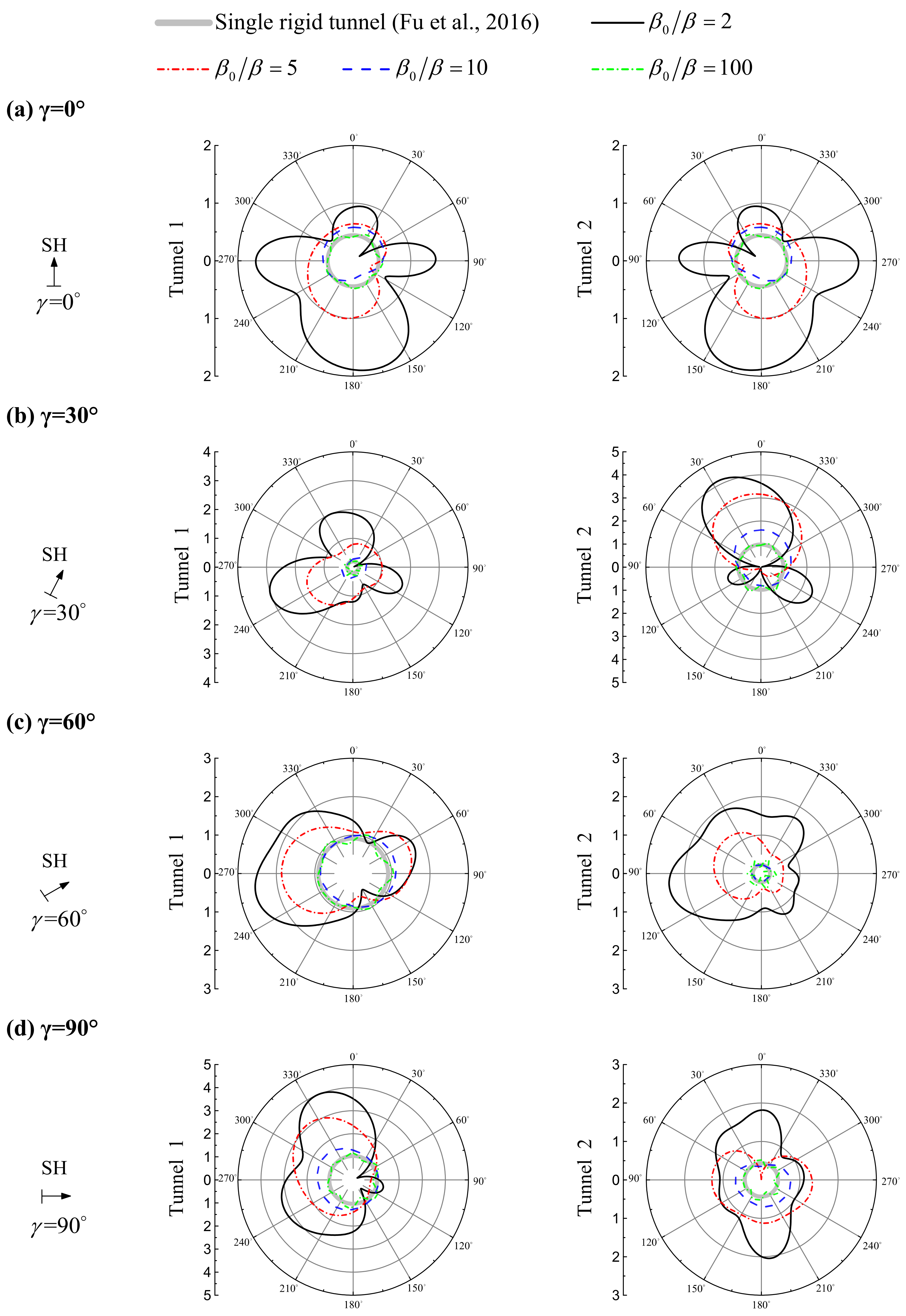
4.3. Influence of Incident Angle
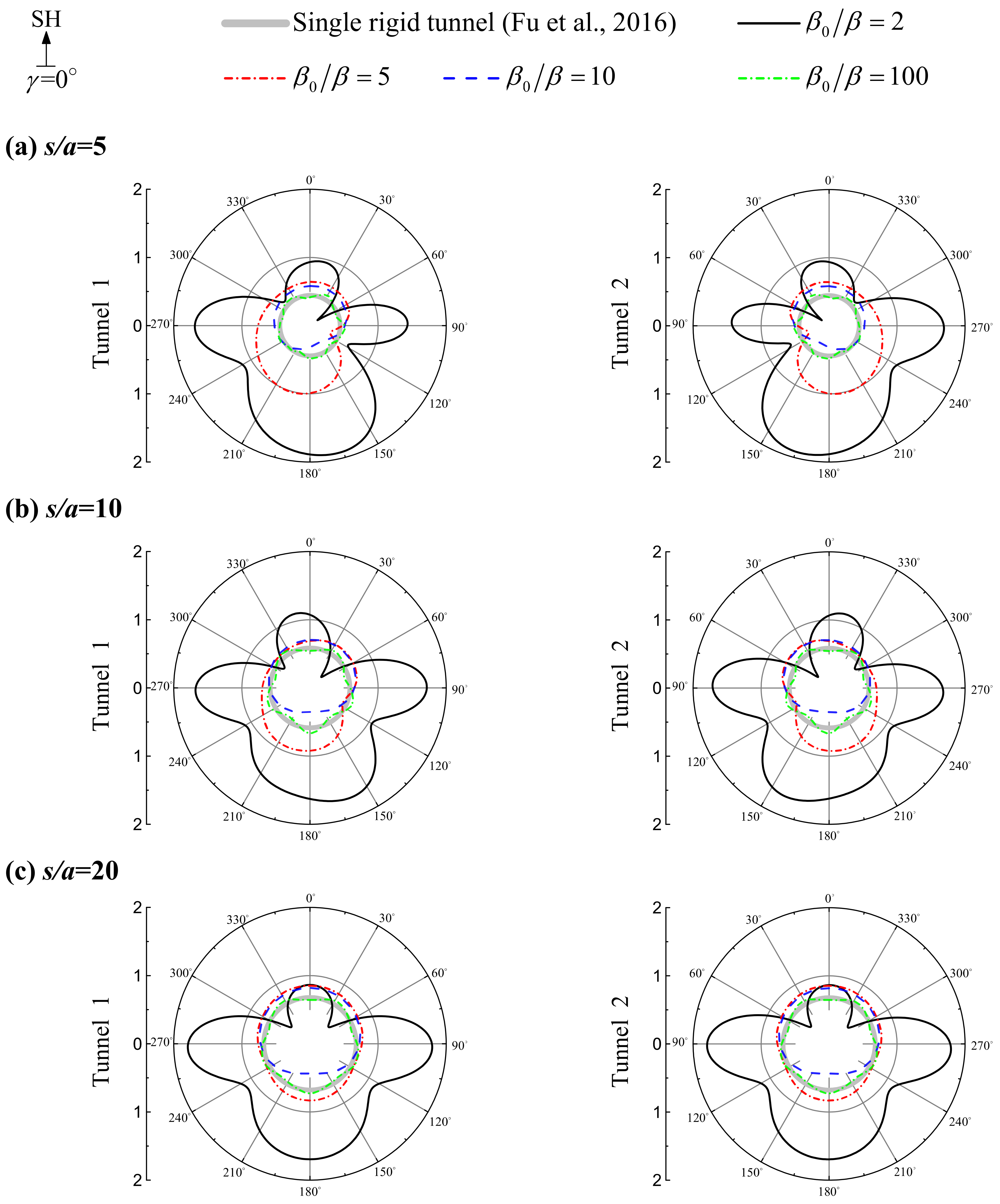
4.4. Influence of Tunnel Distance
5. Conclusions
- (1)
- Tunnel relative stiffness has a great influence on tunnel displacement response. When tunnel relative stiffness is small, tunnel displacement amplitude can reach about 3.3 times larger than that of the single rigid tunnel. A tunnel cannot be treated as a rigid body even for a tunnel relative stiffness that is many times (β0/β = 100) larger than that of the surrounding soil.
- (2)
- The tunnel-soil-tunnel interaction depends not only on the spacing distances between the tunnels but also on the frequency of the incident wave and the incident angle. Especially for higher frequency waves with short wavelength, when the wave is incident obliquely, the tunnel on the incoming wave side has the obvious shielding effect on the tunnel at the outgoing wave side.
- (3)
- The strength of the interaction between the tunnels is highly related to the tunnel spacing distance. The smaller the spacing distance between tunnels, the stronger the interaction between them. When the distance between tunnels reaches s/a = 20, the interaction between tunnels can be ignored. It is worth pointing out that the seismic design of underground tunnels should consider the interaction between tunnels when the tunnel distance is small.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pao, Y.H.; Mow, C.C. Diffraction of Elastic Waves and Dynamic Stress Concentration; Crane Russak and Company: New York, NY, USA, 1973. [Google Scholar]
- Liang, J.W.; Ji, X.D.; Lee, V.W. Effects of an underground lined tunnel on ground motion (I): Series solution. Rock Soil Mech. 2005, 26, 520–524. (In Chinese) [Google Scholar]
- Liang, J.W.; Ji, X.D.; Lee, V.W. Effects of an underground lined tunnel on ground motion (II): Numerical results. Rock Soil Mech. 2005, 26, 687–692. (In Chinese) [Google Scholar]
- Balendra, T.; Thambiratnam, D.P.; Chan, G.K. Dynamic response of twin circular tunnels due to incident SH-waves. Earthq. Eng. Struct. Dyn. 1984, 12, 181–201. [Google Scholar] [CrossRef]
- Hasheminejad, S.M.; Avazmohammadi, R. Dynamic stress concentrations in lined twin tunnels within fluid-saturated soil. J. Eng. Mech. ASCE 2008, 134, 542–554. [Google Scholar] [CrossRef]
- Fu, J.; Liang, J.W.; Du, J.J. Analytical solution of dynamic soil-tunnel interaction for incident plane SH wave. Chin. J. Geotech. Eng. 2016, 38, 588–598. [Google Scholar]
- Fang, Y.G.; Sun, J. Interaction between nonlinear soil and cylindrical structure due to shock wave. Earthq. Eng. Eng. Vib. 1992, 12, 56–64. (In Chinese) [Google Scholar]
- Wong, K.C.; Shah, A.H.; Datta, S.K. Dynamic stresses and displacements in a buried tunnel. J. Eng. Mech. Div. ASCE 1985, 111, 218–234. [Google Scholar] [CrossRef]
- Luco, J.E.; De Barros, F.C.P. Seismic response of a cylindrical shell embedded in a layered viscoelastic half-space. I: Formulation. Earthq. Eng. Struct. Dyn. 1994, 23, 553–567. [Google Scholar] [CrossRef]
- Luco, J.E.; De Barros, F.C.P. Seismic response of a cylindrical shell embedded in a layered viscoelastic half-space. II: Validation and numerical results. Earthq. Eng. Struct. Dyn. 1994, 23, 569–580. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, M.; Wang, L. Scattering of plane P, SV or Rayleigh waves by a shallow lined tunnel in an elastic half space. Soil Dyn. Earthq. Eng. 2013, 49, 52–63. [Google Scholar] [CrossRef]
- Liu, D.; Gai, B.; Tao, G. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Parvanova, S.L.; Dineva, P.S.; Manolis, G.D. Seismic response of lined tunnels in the half-plane with surface topography. Bull. Seismol. Soc. Am. 2014, 12, 981–1005. [Google Scholar] [CrossRef]
- Kumar, N.; Narayan, J.P. Quantification of site-city interaction effects on the response of structure under double resonance condition. Geophys. J. Int. 2018, 212, 422–441. [Google Scholar] [CrossRef]
- Guéguen, P.; Colombi, A. Experimental and Numerical Evidence of the Clustering Effect of Structures on Their Response during an Earthquake: A Case Study of Three Identical Towers in the City of Grenoble, France. Bull. Seismol. Soc. Am. 2016, 106, 2855–2864. [Google Scholar] [CrossRef]
- Schwan, L.; Boutin, C.; Padrón, L.A.; Dietz, M.S.; Bard, P.-Y.; Taylor, C. Site-city interaction: Theoretical, numerical and experimental crossed-analysis. Geophys. J. Int. 2016, 205, 1006–1031. [Google Scholar] [CrossRef] [Green Version]
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Zucca, M.; Crespi, P.G.; Tropeano, G.; Erbì, E. 2D equivalent linear analysis for the seismic vulnerability evaluation of multi-propped retaining structures. In Proceedings of the XVII ECSMGE-2019, Reykjavík, Iceland, 1–6 September 2019. [Google Scholar]
- Zucca, M.; Crespi, P.; Tropeano, G.; Simoncelli, M. On the Influence of Shallow Underground Structures in the Evaluation of the Seismic Signals. Ing. Sismica 2021, 38, 23–35. [Google Scholar]
- Luco, J.E.; Contesse, L. Dynamic structure-soil-structure interaction. Bull. Seismol. Soc. Am. 1973, 63, 1289–1303. [Google Scholar] [CrossRef]
- Liang, J.W.; Han, B.; Todorovska, M.I.; Trifunac, M.D. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space II: Incident SV-waves. Soil Dyn. Earthq. Eng. 2018, 113, 356–390. [Google Scholar] [CrossRef]
- Bybordiani, M.; Arici, Y. Structure-soil-structure interaction of adjacent buildings subjected to seismic loading. Earthq. Eng. Struct. Dyn. 2019, 48, 731–748. [Google Scholar] [CrossRef]
- Vicencio, F.; Alexander, N.A. Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation. Soil Dyn. Earthq. Eng. 2019, 127, 105817. [Google Scholar] [CrossRef]
- Han, B.; Chen, S.L.; Liang, J.W. 2D dynamic structure-soil-structure interaction: A case study of Millikan Library Building. Eng. Anal. Bound. Elem. 2020, 113, 346–358. [Google Scholar] [CrossRef]
- Liang, J.W.; Han, B.; Todorovska, M.I.; Trifunac, M.D. 2D dynamic structure-soil-structure interaction for twin buildings in layered half-space I: Incident SH-waves. Soil Dyn. Earthq. Eng. 2017, 102, 172–194. [Google Scholar] [CrossRef]
- Lou, M.L.; Wang, H.F.; Chen, X.; Zhai, Y.M. Structure-soil-structure interaction: Literature review. Soil Dyn. Earthq. Eng. 2011, 31, 1724–1731. [Google Scholar] [CrossRef]
- Trombetta, N.W.; Mason, H.B.; Hutchinson, T.C.; Zupan, J.D.; Bray, J.D.; Kutter, B.L. Nonlinear soil-foundation-structure and structure-soil-structure interaction: Centrifuge test observations. J. Geotech. Geoenviron. Eng. 2014, 140, 04013057. [Google Scholar] [CrossRef]
- Trombetta, N.W.; Mason, H.B.; Hutchinson, T.C.; Zupan, J.D.; Bray, J.D.; Kutter, B.L. Nonlinear soil-foundation-structure and structure-soil-structure interaction: Engineering demands. J. Struct. Eng. 2015, 141, 04014177. [Google Scholar] [CrossRef]
- Tropeano, G.; Chiaradonna, A.; D’Onofrio, A.; Silvestri, F. An innovative computer code for 1D seismic response analysis including shear strength of soils. Géotechnique 2016, 66, 95–105. [Google Scholar] [CrossRef]
- Jeffery, G.B. Plane Stress and Plane Strain Bipolar Co-ordinates. Philosophical Transactions of the Royal Society A Mathmatical. Phys. Eng. Sci. 1921, 221, 265–293. [Google Scholar]
- Trombetta, N.W.; Mason, H.B.; Chen, Z.; Hutchinson, T.C.; Bray, J.D.; Kutter, B.L. Nonlinear dynamic foundation and frame structure response observed in geotechnical centrifuge experiments. Soil Dyn. Earthq. Eng. 2013, 50, 117–133. [Google Scholar] [CrossRef]
- Lee, V.W.; Trifunac, M.D. Response of tunnels to incident SH-waves. J. Eng. Mech. Div. 1979, 105, 643–659. [Google Scholar] [CrossRef]
- Jin, L.G.; Liang, J.W. Dynamic soil-structure interaction with a flexible foundation embedded in a half-space: Closed-form analytical solution for incident plane SH-waves. J. Earthq. Eng. 2019. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Trifunac, M.D. Dynamic interaction of a shear wall with the soil for incident plane SH Waves. Bull. Seismol. Soc. Am. 1972, 62, 62–83. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, L.; Liu, X.; Sun, H.; Zhou, Z. An Analytical Solution for 2D Dynamic Structure-Soil-Structure Interaction for Twin Flexible Tunnels Embedded in a Homogeneous Half-Space. Appl. Sci. 2021, 11, 10343. https://doi.org/10.3390/app112110343
Jin L, Liu X, Sun H, Zhou Z. An Analytical Solution for 2D Dynamic Structure-Soil-Structure Interaction for Twin Flexible Tunnels Embedded in a Homogeneous Half-Space. Applied Sciences. 2021; 11(21):10343. https://doi.org/10.3390/app112110343
Chicago/Turabian StyleJin, Liguo, Xujin Liu, Hongyang Sun, and Zhenghua Zhou. 2021. "An Analytical Solution for 2D Dynamic Structure-Soil-Structure Interaction for Twin Flexible Tunnels Embedded in a Homogeneous Half-Space" Applied Sciences 11, no. 21: 10343. https://doi.org/10.3390/app112110343
APA StyleJin, L., Liu, X., Sun, H., & Zhou, Z. (2021). An Analytical Solution for 2D Dynamic Structure-Soil-Structure Interaction for Twin Flexible Tunnels Embedded in a Homogeneous Half-Space. Applied Sciences, 11(21), 10343. https://doi.org/10.3390/app112110343





