Efficient Moment-Independent Sensitivity Analysis of Uncertainties in Seismic Demand of Bridges Based on a Novel Four-Point-Estimate Method
Abstract
:1. Introduction
2. An Efficient Algorithm for Moment-Independent Importance Analysis
2.1. Moment-Independent Importance Index
2.2. The Modified 4PEM
2.3. Moment-Independent Sensitivity Analysis Based on 4PEM and SGLD
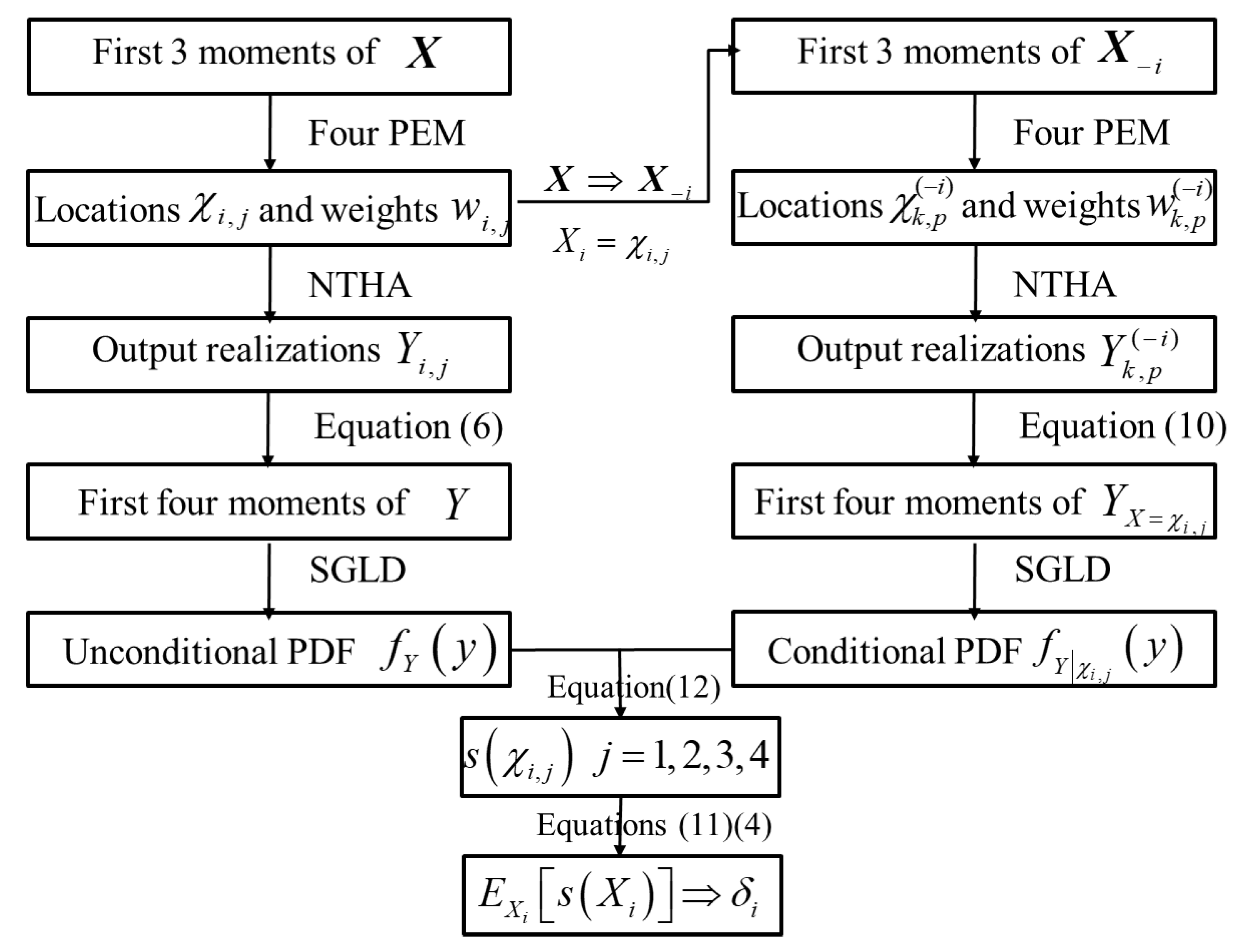
2.4. The Procedures of the Proposed Method
- Set the input vector composed of the uncertain parameters from structural and material properties.
- Implement 4PEM to the structural uncertain parameter vector to obtain the locations and weights .
- Change the uncertain parameters in the structural model according to and obtain the samples of seismic demand through NTHA.
- Calculate the first four moments of by Equation (6).
- Evaluate through SGLD.
- Fix at and implement 4PEM to to obtain the new locations and weights . Repeat step (2)~(4) to obtain .
- Calculate the expectation by Equations (12) and (11) and obtain the MII index by Equation (4).
- Repeat step (5) and (6) until the MII index calculation of all the variables of is finished.
3. Numerical Example
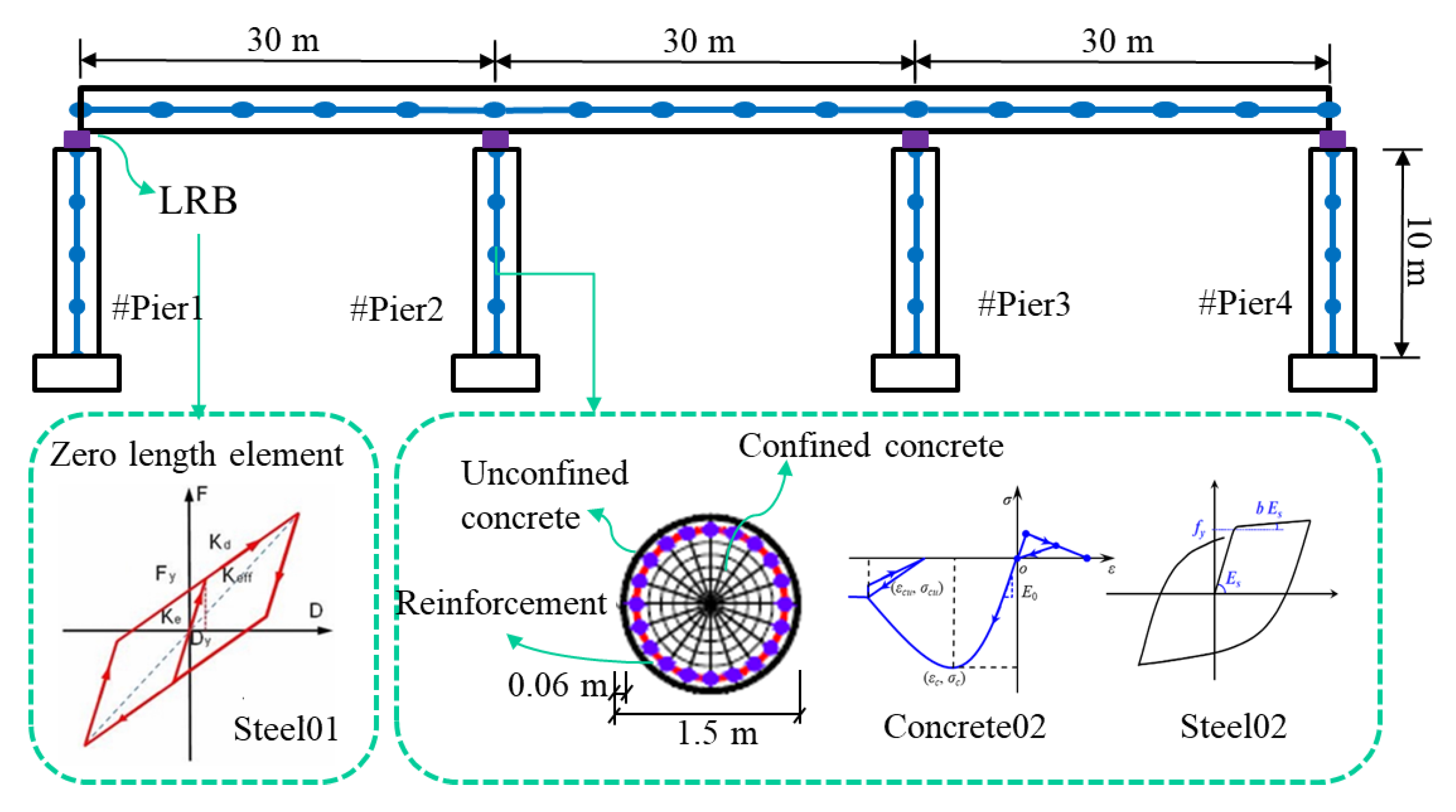
3.1. Bridge Model Description
3.2. Uncertain Parameters
3.3. Characterization of Bridges’ Seismic Demands
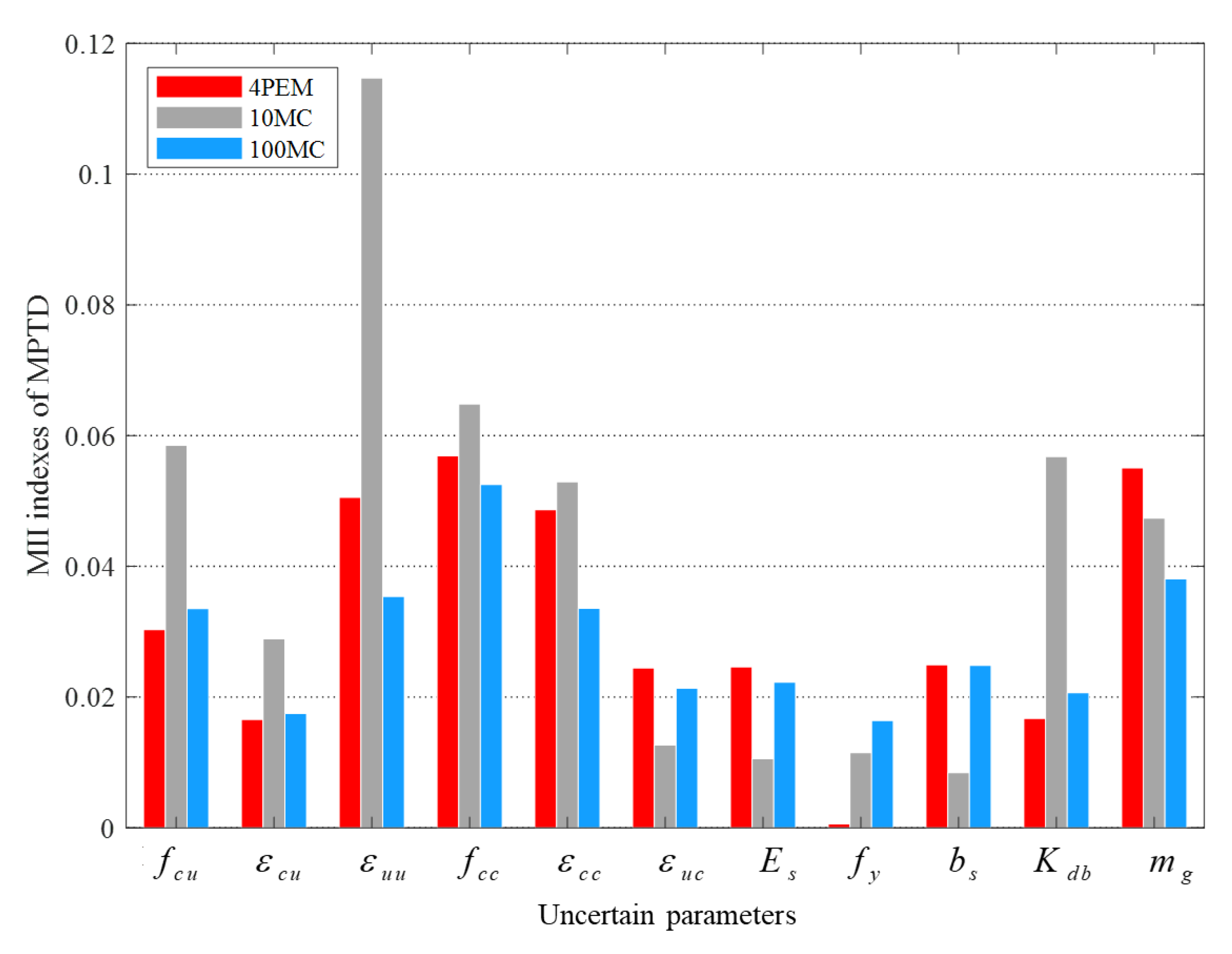
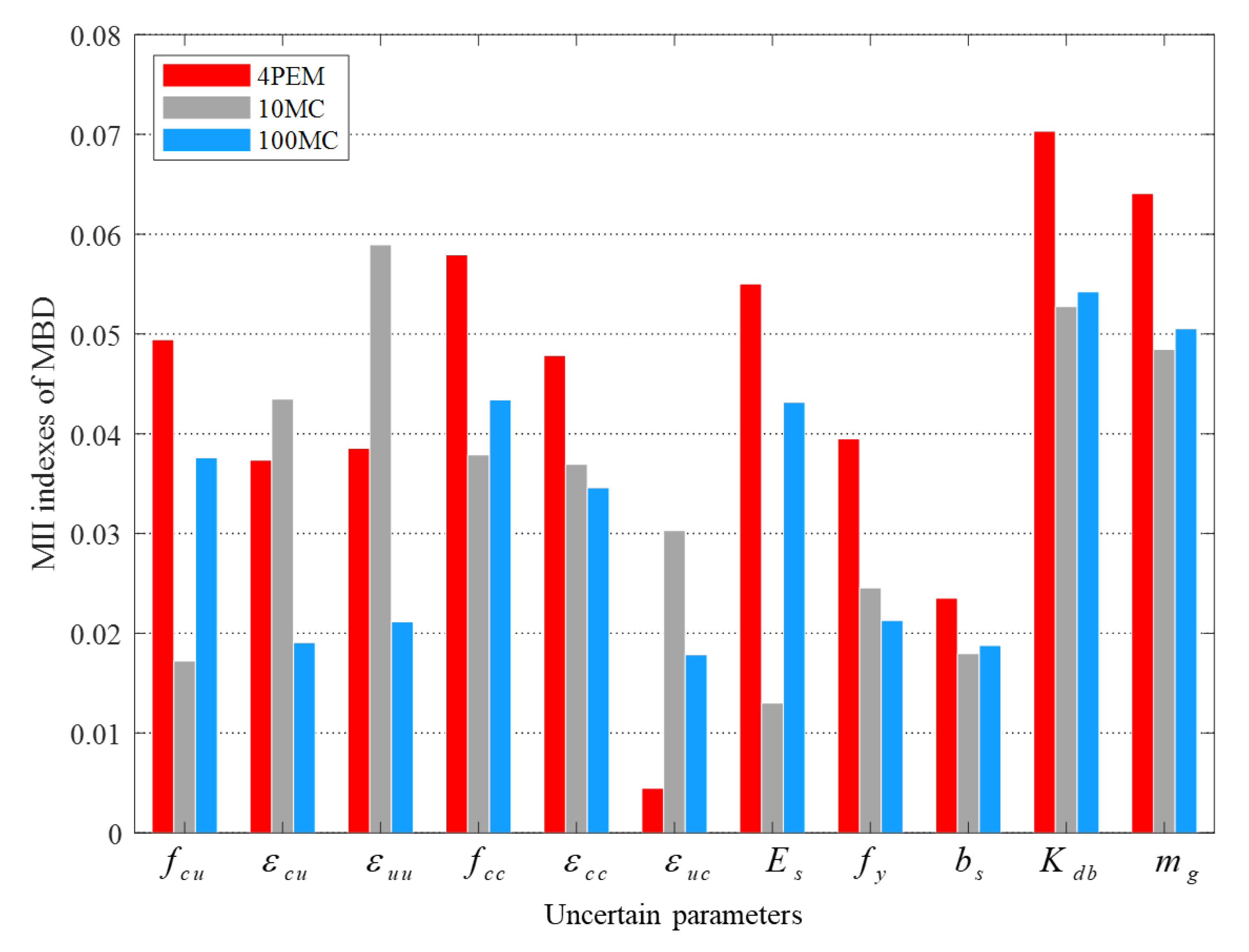
3.4. Moment-Independent Sensitivity Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| the expectation of * | |
| the marginal PDF of | |
| the unconditional PDF of | |
| the conditional PDF by fixing at one implementation value | |
| the conditional PDF under the condition of fixing at its 4PEM locations | |
| nonlinear performance function of the system | |
| the area difference between and | |
| the n-dimensional vector of the structural input variables | |
| (n − 1)-dimensional transformation of by removing | |
| realization of the random variable | |
| the output seismic demand | |
| the realization of by the point-estimated method | |
| the realization of when | |
| the r-th central moment of * | |
| the location of for the point-estimate method | |
| the moment-independent importance index | |
| the ratio of to the -th power of | |
| the mean value of | |
| the point-estimated method’s sampling weight | |
| the point-estimated method’s sampling coefficients |
References
- Xie, Y.; Des Roches, R. Sensitivity of seismic demands and fragility estimates of a typical California highway bridge to uncer-tainties in its soil-structure interaction modeling. Eng. Struct. 2019, 189, 605–617. [Google Scholar] [CrossRef]
- Salkhordeh, M.; Govahi, E.; Mirtaheri, M. Seismic fragility evaluation of various mitigation strategies proposed for bridge piers. Structures 2021, 33, 1892–1905. [Google Scholar] [CrossRef]
- Zhao, N.; Huo, L.; Qu, C.; Li, H. Study on nonlinear vibration control of structures considering parameters uncertainties. J. Disaster Prev. Mitig. Eng. 2015, 35, 477–483. [Google Scholar]
- Saltelli, A. Entropy-based importance measure for uncertain model inputs. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Weng, S.; Tian, W.; Zhu, H.; Xia, Y.; Gao, F.; Zhang, Y.; Li, J. Dynamic condensation approach to calculation of structural respons-es and response sensitivities. Mech. Syst. Signal Process. 2017, 88, 302–317. [Google Scholar] [CrossRef]
- Tang, Z.; Lu, Z.; Jiang, B.; Wang, P.; Feng, Z. Entropy-based importance measure for uncertain model inputs. AIAA J. 2013, 51, 2319–2334. [Google Scholar]
- Liu, Q.; Homma, T. A new computational method of a moment-independent uncertainty importance measure. Reliab. Eng. Syst. Saf. 2009, 94, 1205–1211. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Modeling Comput. Exp. 1993, 55, 112–118. [Google Scholar]
- Feng, K.; Lu, Z.; Pang, C.; Yun, W. An efficient computational method of a moment-independent importance measure using quantile regression. Mech. Syst. Signal Process. 2018, 109, 235–246. [Google Scholar] [CrossRef]
- Yazdani, A.; Nicknam, A.; Dadras, E.Y.; Eftekhari, S.N. Entropy-based sensitivity analysis of global seismic demand of concrete structures. Eng. Struct. 2017, 146, 118–126. [Google Scholar] [CrossRef]
- Song, S.; Qian, Y.J.; Qian, C. Importance analysis of random parameters in seismic demand of bridges. Eng. Mech. 2018, 35, 106–114. (In Chinese) [Google Scholar]
- Xu, Z.; Wang, X. The Moment-Independent Importance Analysis of Structural Seismic Requirements Based on Orthogonal Polynomial Estimation. Math. Probl. Eng. 2020, 2020, 9572192. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Z.; Fan, W.; Ang, A.H.-S.; Liu, R. System reliability assessment of deteriorating structures subjected to time-invariant loads based on improved moment method. Struct. Saf. 2017, 68, 54–64. [Google Scholar] [CrossRef]
- Rosenblueth, E. Point estimates for probability moments. Proc. Natl. Acad. Sci. USA 1975, 72, 3812–3814. [Google Scholar] [CrossRef] [Green Version]
- Rosenblueth, E. Two-point estimates in probabilities. Appl. Math. Model. 1981, 5, 329–335. [Google Scholar] [CrossRef]
- Hong, H. Point-Estimate Moment-Based Reliability Analysis. Civ. Eng. Syst. 1996, 13, 281–294. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Xu, C.; Jiang, C.; Han, X. Probability assessments of dentified parameters for stochastic structures using point es-timation method. Reliab. Eng. Syst. Saf. 2016, 156, 51–58. [Google Scholar] [CrossRef]
- Che, Y.; Wang, X.; Lv, X.; Hu, Y. Probabilistic load flow using improved three point estimate method. Int. J. Electr. Power Energy Syst. 2020, 117, 105618. [Google Scholar] [CrossRef]
- Dang, C.; Xu, J. Novel algorithm for reconstruction of a distribution by fitting its first-four statistical moments. Appl. Math. Model. 2019, 71, 505–524. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Y. Reliability–sensitivity analysis using dimension reduction methods and sadlepoint approximations. Int. J. Numer. Methods Eng. 2013, 93, 857–886. [Google Scholar] [CrossRef]
- Li, G.; Zhou, C.; Zeng, Y.; He, W.; Li, H.; Wang, R. New maximum entropy-based algorithm for structural design optimization. Appl. Math. Model. 2019, 66, 26–40. [Google Scholar] [CrossRef]
- Johnson, N.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Low, Y. A new distribution for fitting four moments and its applications to reliability analysis. Struct. Saf. 2013, 42, 12–25. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Yuan, X. Monte Carlo simulation for moment-independent sensitivity analysis. Reliab. Eng. Syst. Saf. 2013, 110, 60–67. [Google Scholar] [CrossRef]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Earthquake Engineering Research Center (EERC), University of California: Berkeley, CA, USA, 1983; pp. 19–83. [Google Scholar]
- Padgett, J.E.; Desroches, R. Sensitivity of Seismic Response and Fragility to Parameter Uncertainty. J. Struct. Eng. 2007, 133, 1710–1718. [Google Scholar] [CrossRef] [Green Version]
- Tubaldi, E.; Barbato, M.; Dall’Asta, A. Influence of model parameter uncertain-ty on seismic transverse response and vulnerabil-ity of steel–concrete composite bridges with dual load path. J. Struct. Eng. 2012, 138, 363–374. [Google Scholar] [CrossRef]
- Ma, H.-B.; Zhuo, W.-D.; Lavorato, D.; Nuti, C.; Fiorentino, G.; Marano, G.C.; Greco, R.; Briseghella, B. Probabilistic seismic re-sponse and uncertainty analysis of continuous bridges under near-fault ground motions. Front. Struct. Civ. Eng. 2019, 13, 1510–1519. [Google Scholar] [CrossRef]
- Wu, W.; Li, L.; Shao, X. Seismic Assessment of Medium-Span Concrete Cable-Stayed Bridges Using the Component and System Fragility Functions. J. Bridg. Eng. 2016, 21, 04016027. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Zhou, G.; Xu, L. Time-dependent Seismic Fragility Assessment for Aging Highway Bridges Subject to Non-uniform Chloride-induced Corrosion. J. Earthq. Eng. 2020, 1–31. [Google Scholar] [CrossRef]
- De Domenico, D.; Messina, D.; Recupero, A. A Combined Experimental-Numerical Framework for Assessing the Load-Bearing Capacity of Existing PC Bridge Decks Accounting for Corrosion of Prestressing Strands. Materials 2021, 14, 4914. [Google Scholar] [CrossRef]
- Li, H.; Li, L.; Wu, W.; Xu, L. Seismic fragility assessment framework for highway bridges based on an improved uniform de-sign-response surface model methodology. Bull. Earthq. Eng. 2020, 18, 2329–2353. [Google Scholar] [CrossRef]
- Pang, Y.; Wu, X.; Shen, G.; Yuan, W. Seismic Fragility Analysis of Cable-Stayed Bridges Considering Different Sources of Uncertainties. J. Bridg. Eng. 2014, 19, 04013015. [Google Scholar] [CrossRef]
- Hwang, H.; Liu, J.; Chiu, Y. Seismic Fragility Analysis of Highway Bridges; MAEC RR-4 Project; The University of Memphis, Center for Earthquake Research and Information: Memphis, TN, USA, 2001. [Google Scholar]
- Choi, E. Seismic Analysis and Retrofit of Mid-America Bridges; Georgia Institute of Technology: Atlanta, GA, USA, 2002; pp. 1–251. [Google Scholar]
- Nielson, B. Analytical Fragility Curves for Highway Bridges in Moderate Seismic Zones; Georgia Institute of Technology: Atlanta, GA, USA, 2005; pp. 1–260. [Google Scholar]


| Uncertain Parameters | Symbol | Distribution | Mean | COV | Ref. |
|---|---|---|---|---|---|
| Mass per-length of superstructure (kg/m) | Normal | 362 | 0.10 | [26,33] | |
| Post-yield stiffness of LRB (kN/m) | Normal | 96 | 0.14 | [33] | |
| Peak compressive strength of unconfined concrete (MPa) | Lognormal | 26.1 | 0.14 | [32,33] | |
| Strain at the peak strength of unconfined concrete | Lognormal | 0.002 | 0.20 | [32,33] | |
| Strain at the crushing strength of unconfined concrete | Lognormal | 0.005 | 0.20 | [32,33] | |
| Peak compressive strength of confined concrete (MPa) | Lognormal | 33.6 | 0.21 | [32,33] | |
| Strain at the peak strength of confined concrete | Lognormal | 0.004 | 0.2 | [32,33] | |
| Strain at the crushing strength of confined concrete | Lognormal | 0.015 | 0.3 | [32,33] | |
| Young’s modulus of steel rebar (MPa) | Lognormal | 2E5 | 0.02 | [32,34] | |
| Initial yield stress of steel rebar (MPa) | Lognormal | 378 | 0.07 | [32,34] | |
| Strain hardening ratio of steel rebar | Lognormal | 0.01 | 0.20 | [34] |
| MPTD | MBD | |||||||
|---|---|---|---|---|---|---|---|---|
| 4PEM | 10MC | 100MC | Rank | 4PEM | 10MC | 100MC | Rank | |
| 0.0303 | 0.0585 | 0.0335 | 5-3-5 * | 0.0494 | 0.0172 | 0.0376 | 5-10-5 | |
| 0.0165 | 0.0289 | 0.0175 | 10-7-10 | 0.0374 | 0.0435 | 0.0191 | 9-4-9 | |
| 0.0505 | 0.1147 | 0.0354 | 3-1-3 | 0.0385 | 0.0590 | 0.0211 | 8-1-8 | |
| 0.0569 | 0.0648 | 0.0525 | 1-2-1 | 0.0579 | 0.0379 | 0.0434 | 3-5-3 | |
| 0.0487 | 0.0529 | 0.0336 | 4-5-4 | 0.0478 | 0.0369 | 0.0346 | 6-6-6 | |
| 0.0244 | 0.0126 | 0.0214 | 8-8-8 | 0.0045 | 0.0303 | 0.0179 | 11-7-11 | |
| 0.0246 | 0.0106 | 0.0223 | 7-10-7 | 0.0550 | 0.0130 | 0.0431 | 4-11-4 | |
| 0.0006 | 0.0115 | 0.0164 | 11-9-11 | 0.0395 | 0.0246 | 0.0213 | 7-8-7 | |
| 0.0249 | 0.0084 | 0.0248 | 6-11-6 | 0.0235 | 0.0180 | 0.0188 | 10-9-10 | |
| 0.0167 | 0.0568 | 0.0207 | 9-4-9 | 0.0703 | 0.0528 | 0.0542 | 1-2-1 | |
| 0.0551 | 0.0474 | 0.0381 | 2-6-2 | 0.0641 | 0.0484 | 0.0505 | 2-3-2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lei, Y.; Liu, L. Efficient Moment-Independent Sensitivity Analysis of Uncertainties in Seismic Demand of Bridges Based on a Novel Four-Point-Estimate Method. Appl. Sci. 2021, 11, 10405. https://doi.org/10.3390/app112110405
Li X, Lei Y, Liu L. Efficient Moment-Independent Sensitivity Analysis of Uncertainties in Seismic Demand of Bridges Based on a Novel Four-Point-Estimate Method. Applied Sciences. 2021; 11(21):10405. https://doi.org/10.3390/app112110405
Chicago/Turabian StyleLi, Xingyu, Ying Lei, and Lijun Liu. 2021. "Efficient Moment-Independent Sensitivity Analysis of Uncertainties in Seismic Demand of Bridges Based on a Novel Four-Point-Estimate Method" Applied Sciences 11, no. 21: 10405. https://doi.org/10.3390/app112110405






