Dynamic Analysis of the Complex Motion of Three-Section Cudgel in Wushu Sports
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Instrument of the Three-Section Cudgel
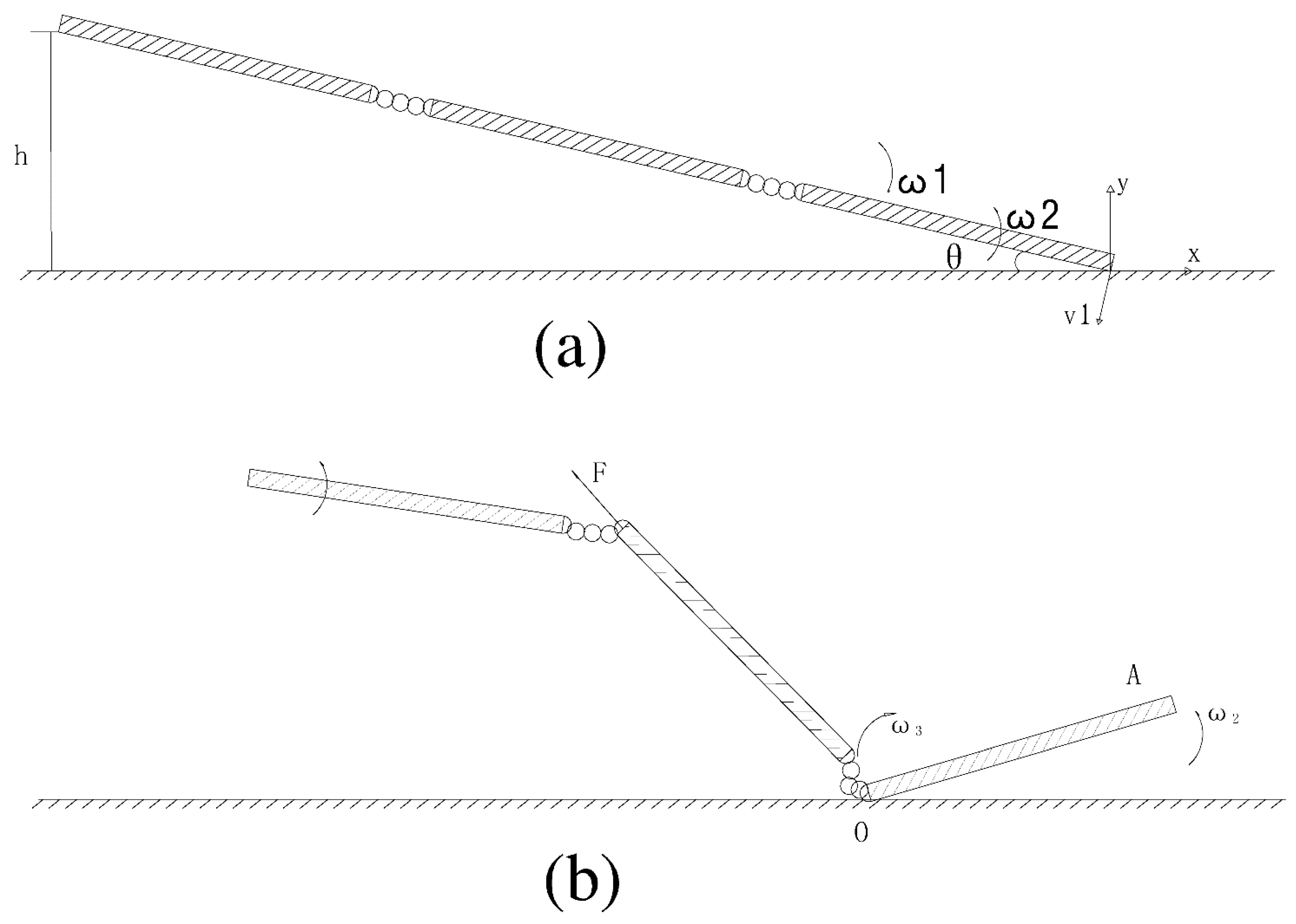
2.2. Dynamic Analysis of Wrestling the Three-Section Cudgel
2.2.1. Mechanical Analysis of Three-Section Cudgel Wrestling Technique
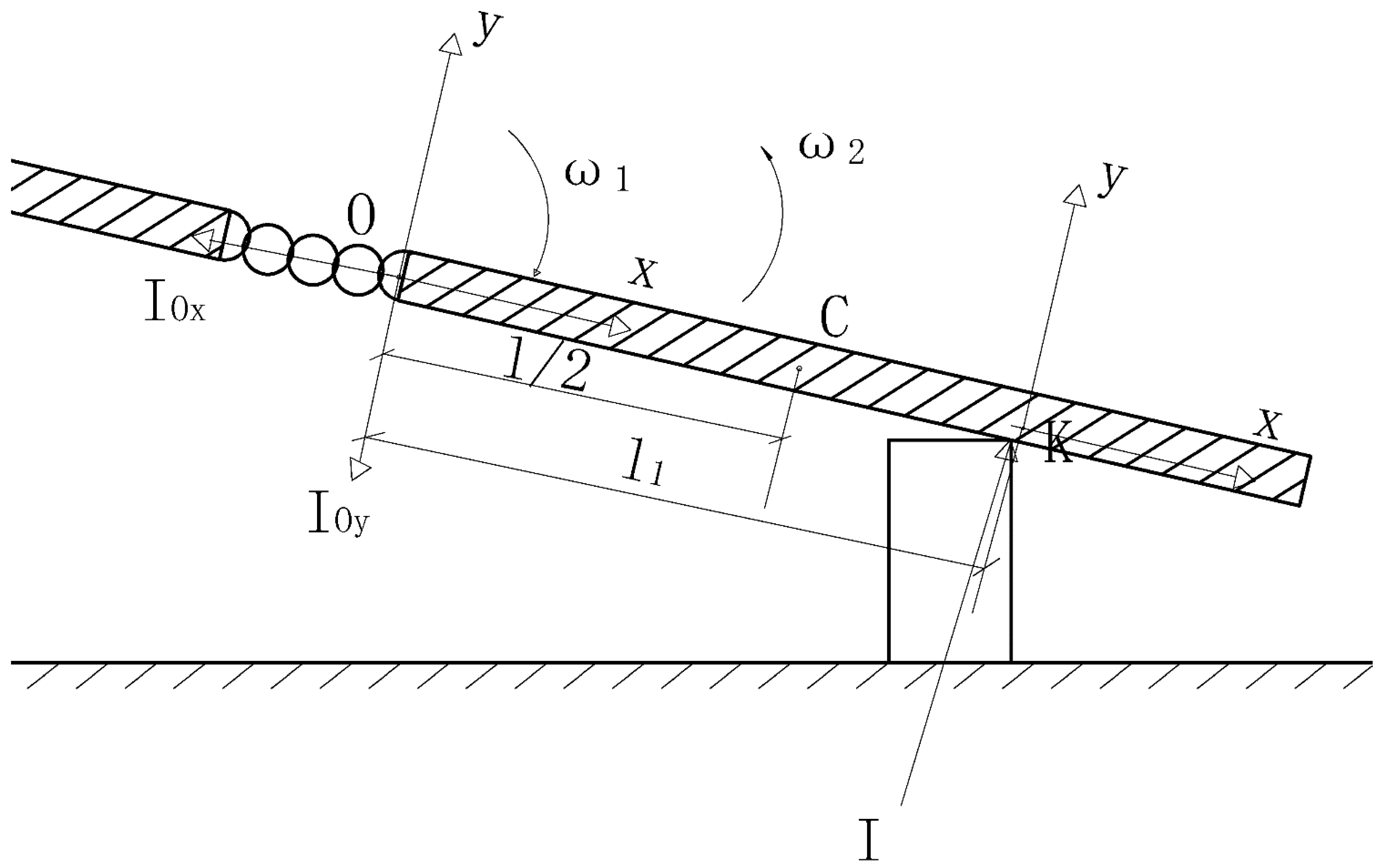
2.2.2. Theoretical Analysis of Impact Impulse of Three-Section Cudgel Wrestling
2.3. Mechanical Analysis of Retrieving Three-Section Cudgel
2.4. ABAQUS Simulation Analysis of Three-Section Cudgels
2.4.1. Explicit Dynamic Analysis Principle of ABAQUS
2.4.2. Finite Element Explicit Dynamic Analysis Method of ABAQUS
- (1)
- Node Calculation
- (2)
- Unit computation
3. Results
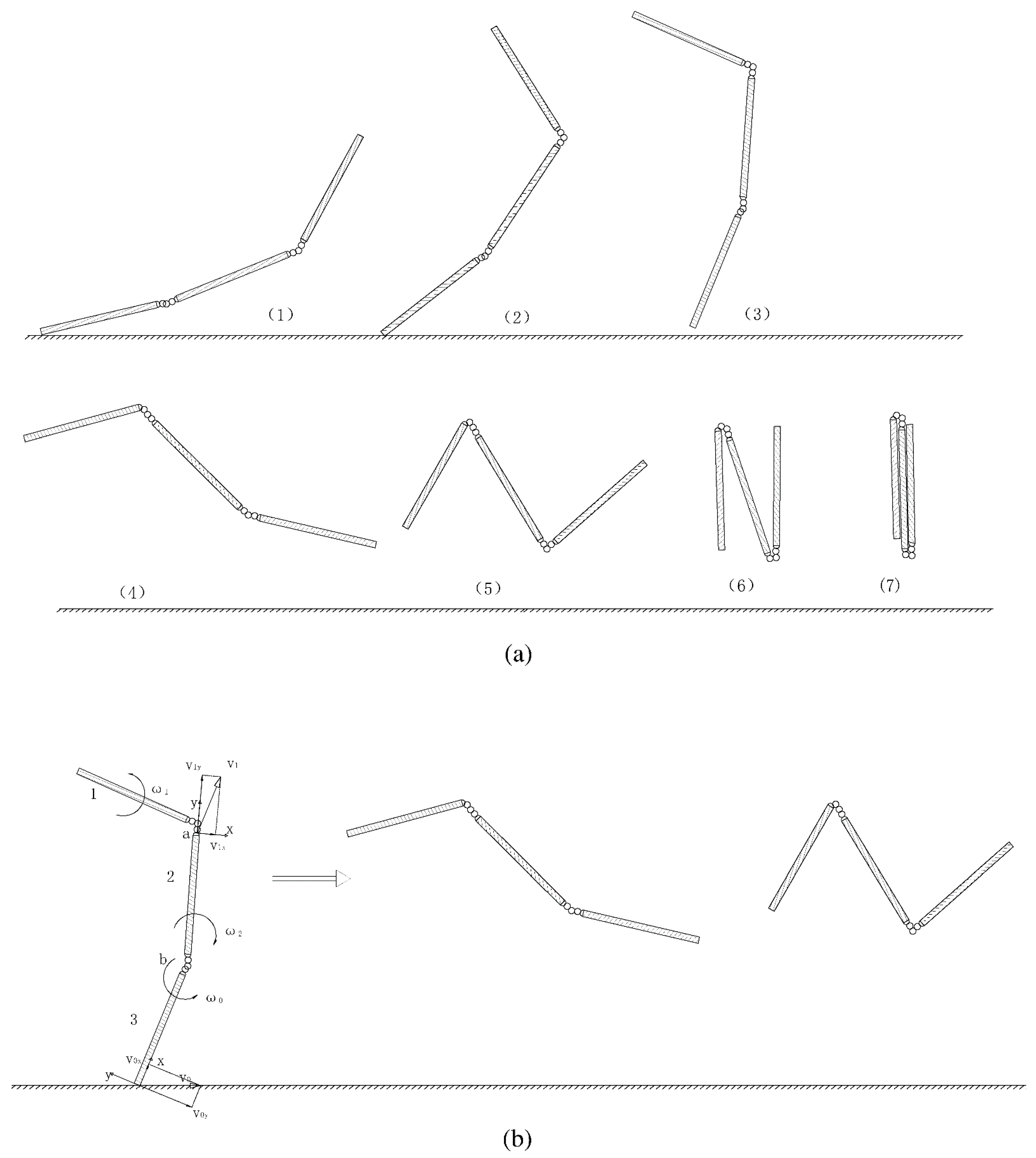
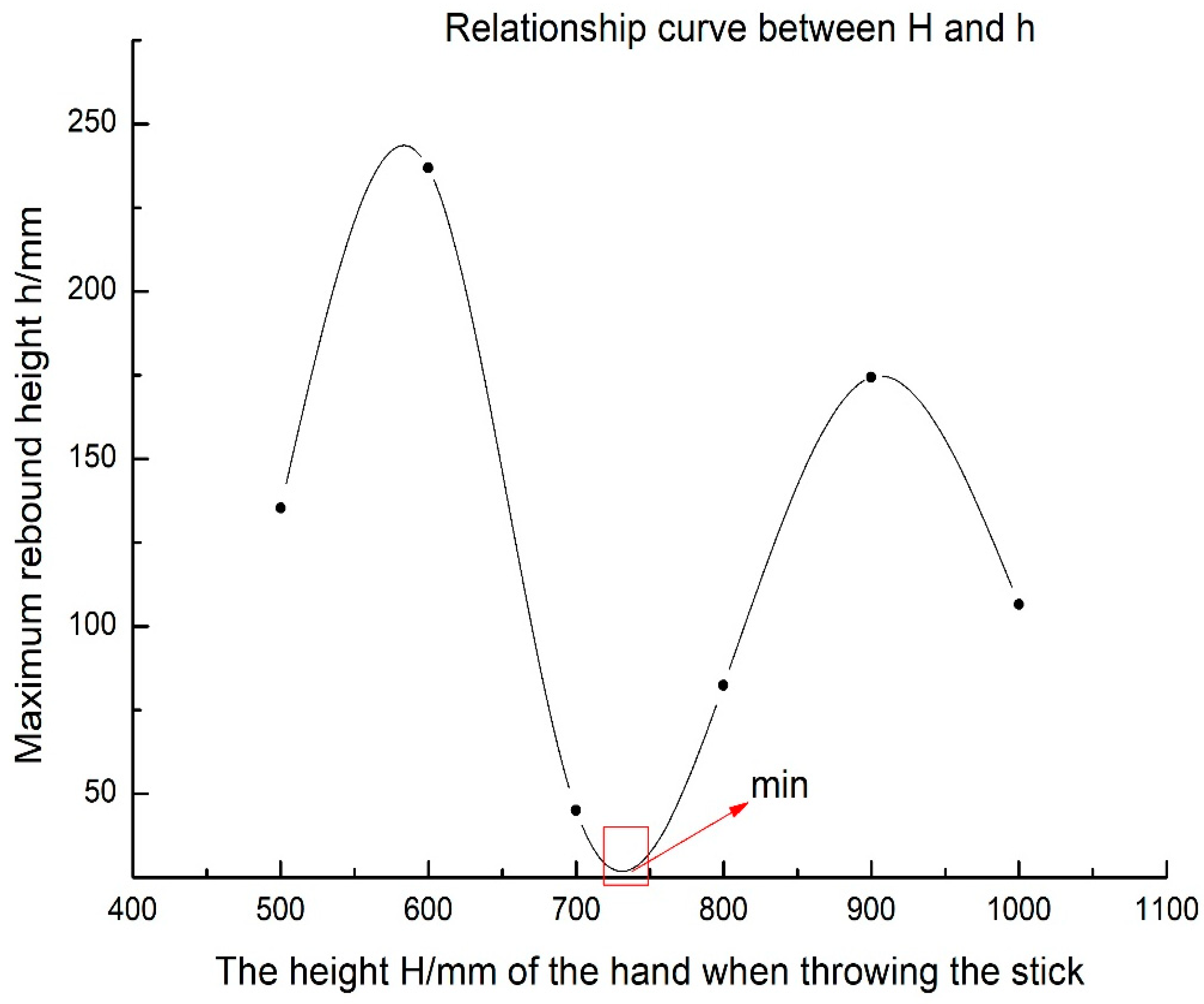
3.1. The Influence of the Height between the Cudgel Holder and the Ground for the Cudgel Wrestling
3.2. The Influence of Initial Angular Velocity of the Three-Section Cudgel for the Cudgel Dropping
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, Y. The historical evolution of two-section stick and the formation of modern technique system. Contemp. Sports Technol. 2017, 7, 197–198. [Google Scholar]
- Longfei, C. Wushu equipment—The cultural connotation of stick and Whip. Wushu Res. 2016, 1, 46–47. [Google Scholar]
- Ma, C. The study of martial arts Instruments in the Northern and Southern Dynasties. J. Shangqiu Teach. Coll. 2014, 30, 112–114. [Google Scholar]
- Li, X.; Liu, D. Eighteen Martial Artsof Martial Arts in Song Dynasty. Fight. Martial Arts Sci. 2014, 12, 23–25, 28. [Google Scholar]
- Zheng, H.; Chuan, K. The influence of Zhao Kuangyin and his Gunshu on the Development of Sports in Northern Song Dynasty. Lantai World 2013, 70–71. [Google Scholar]
- Wang, D.; Lin, X.-M.; Kulmala, J.-P.; Petsola, A.J.; Gao, Y. Can the Functional Movement Screen Method Identify Previously Injured Wushu Athletes? Int. J. Environ. Res. Public Health 2021, 18, 721. [Google Scholar] [CrossRef] [PubMed]
- Shunzi, H. Whip rod—Introduction to wushu equipment. J. Tianshui Teach. Coll. 1985, 01, 69–70. [Google Scholar]
- Beer, F.P.; Johnton, E.R. Mechanics of Materials, 2nd ed.; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Pfeiffer, F.; Glocker, C. Contacts in multibody systems. Pmm J. Appl. Math. Mech. 2000, 64, 773–782. [Google Scholar] [CrossRef] [Green Version]
- Veeraraghavan, S.; Hall, J.F.; Krishnan, S. Modeling the Rocking and Sliding of Free-Standing Objects Using Rigid Body Dynamics. J. Eng. Mech. 2020, 146, 04020041. [Google Scholar] [CrossRef]
- Peters, B. Collision theory. In Reaction Rate Theory and Rare Events Simulations; Elsevier: Amsterdam, The Netherlands, 2017; pp. 147–156. [Google Scholar]
- Stanford, A.L.; Tanner, J.M. Momentum and Collisions. In Physics for Students of Science and Engineering; Stanford, A.L., Tanner, J.M., Eds.; Academic Press: New York, NY, USA, 1985; pp. 145–172. [Google Scholar]
- van Zon, R.; Schofield, J. Numerical implementation of the exact dynamics of free rigid bodies. J. Comput. Phys. 2007, 225, 145–164. [Google Scholar] [CrossRef] [Green Version]
- Skrinjar, L.; Slavic, J.; Boltezar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Wasfy, T.M.; Noor, A.K. Finite element analysis of flexible multibody systems with fuzzy parameters. Comput. Methods Appl. Mech. Eng. 1998, 160, 223–243. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. Equations of motion of the rigid body. In Dynamic Analysis of Structures; Academic Press: New York, NY, USA, 2020; Volume 2, pp. 755–773. [Google Scholar] [CrossRef]
- Langerholc, M.; Česnik, M.; Slavič, J.; Boltežar, M. Experimental validation of a complex, large-scale, rigid-body mechanism. Eng. Struct. 2012, 36, 220–227. [Google Scholar] [CrossRef]
- Ya, S.; Eisenträger, S.; Song, C.; Li, J. An open-source ABAQUS implementation of the scaled boundary finite element method to study interfacial problems using polyhedral meshes. Comput. Methods Appl. Mech. Eng. 2021, 381, 113766. [Google Scholar] [CrossRef]
- Chen, H.; Tan, P. Complex mode superposition method for distributed parameter systems with nonclassical damping. J. Vib. Eng. Technol. 2021, 34, 48–59. [Google Scholar]
- Xu, C.; Cao, X. A direct method for solving a class of nonlinear partial differential equations. Pract. Underst. Math. 2010, 40, 182–187. [Google Scholar]
- Ambrosio, J.A.C. Dynamics of structures undergoing gross motion and nonlinear deformations: A multibody approach. Comput. Struct. 1996, 59, 1001–1012. [Google Scholar] [CrossRef]
- Danielson, K.T.; Browning, R.S.; Adley, M.D. Comparison of second-order serendipity and Lagrange tetrahedral elements for nonlinear explicit methods. Finite Elem. Anal. Des. 2021, 190, 103532. [Google Scholar] [CrossRef]
- Peng, L.; Feng, Z.-Q.; Joli, P. A semi-explicit algorithm for solving multibody contact dynamics with large deformation. Int. J. Non-Linear Mech. 2018, 103, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.J.R.; Taylor, R.L.; Sackman, J.L.; Curnier, A.; Kanoknukulchai, W. A finite element method for a class of contact-impact problems. Comput. Methods Appl. Mech. Eng. 1976, 8, 248–276. [Google Scholar] [CrossRef]
- Vouga, E.; Harmon, D.; Tamstorf, R.; Grinspun, E. Asynchronous variational contact mechanics. Comput. Methods Appl. Mech. Eng. 2011, 200, 2181–2194. [Google Scholar] [CrossRef] [Green Version]
- Anitescu, M.; Potra, F.A.; Stewart, D.E. Time-stepping for three-dimensional rigid body dynamics. Comput. Methods Appl. Mech. Eng. 1999, 177, 183–197. [Google Scholar] [CrossRef]
- Kirk, C.; Clark, D.R.; Langan-Evans, C.; Morton, J.P. The physical demands of mixed martial arts: A narrative review using the ARMSS model to provide a hierarchy of evidence. J. Sports Sci. 2020, 38, 2819–2841. [Google Scholar] [CrossRef] [PubMed]
- Bayril, D.; Selig, J.M. On plane-symmetric rigid-body motions. J. Geom. 2020, 111, 1. [Google Scholar] [CrossRef]
- Liu, Y. The development of the dynamics of rigid body with state variables. Acta Mech. Solida Sin. 1990, 3, 307–314. [Google Scholar]
- Da Silva, G.S.; Kosteski, L.E.; Iturrioz, I. Analysis of the failure process by using the Lattice Discrete Element Method in the Abaqus environment. Theor. Appl. Fract. Mech. 2020, 107, 102563. [Google Scholar] [CrossRef]






| Structure | Elasticity Modulus/(Gpa) | Poisson Ratio | ρ/(g/cm3) | Friction Coefficient (Tangential Direction) |
|---|---|---|---|---|
| The three-section cudgel (The whole) | 2.1 | 0.3 | 7.85 | 0.1 |
| Ground | 2.1 | 0.3 | 7.85 | 0.1 |
| The height of the hand when wrestling a cudgel (H/mm) | 500 | 600 | 700 | 800 | 900 |
| Rebound height (h/mm) | 135.324 | 236.867 | 45.104 | 82.451 | 174.404 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Jiang, Y.; He, X.; Yuan, J.; Gao, Y. Dynamic Analysis of the Complex Motion of Three-Section Cudgel in Wushu Sports. Appl. Sci. 2021, 11, 10407. https://doi.org/10.3390/app112110407
Xu M, Jiang Y, He X, Yuan J, Gao Y. Dynamic Analysis of the Complex Motion of Three-Section Cudgel in Wushu Sports. Applied Sciences. 2021; 11(21):10407. https://doi.org/10.3390/app112110407
Chicago/Turabian StyleXu, Man, Yiran Jiang, Xingfu He, Juntong Yuan, and Ying Gao. 2021. "Dynamic Analysis of the Complex Motion of Three-Section Cudgel in Wushu Sports" Applied Sciences 11, no. 21: 10407. https://doi.org/10.3390/app112110407
APA StyleXu, M., Jiang, Y., He, X., Yuan, J., & Gao, Y. (2021). Dynamic Analysis of the Complex Motion of Three-Section Cudgel in Wushu Sports. Applied Sciences, 11(21), 10407. https://doi.org/10.3390/app112110407






