Comprehensive Study on Surrounding Rock Failure Characteristics of Longwall Roadway and Control Techniques
Abstract
:1. Introduction
2. Engineering Background
3. Methodology
3.1. Theoretical Calculation
3.2. Field Observations
3.3. Numerical Modeling
4. Results
4.1. Distribution Law of Principal Stress
4.2. Developmental Characteristics of the Plastic Zone
4.3. Optimization of Roadway Support Design
5. Discussion
5.1. Different Research Methods and Results
5.2. Excavation Compensation Effect
5.3. Roof Cutting and Pressure Relief
6. Conclusions
- 1.
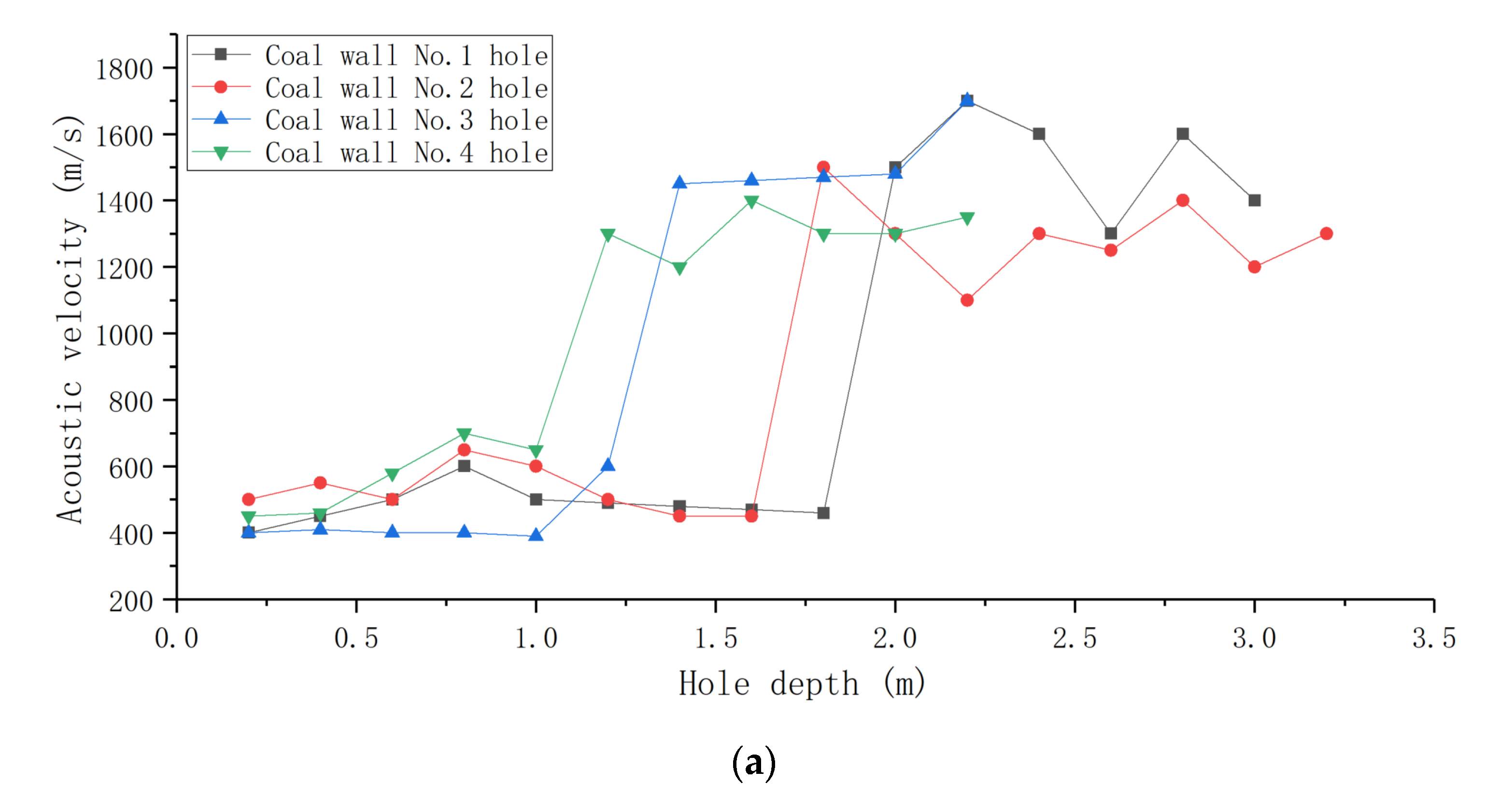
- The shorter the distance is from the working face, the larger is the developmental range of the broken rock zone; the range of the broken rock zone of the coal wall side is larger than that of the coal pillar side. Through formula calculation and field observation, the maximum damage range in surrounding rock on both sides of the roadway can reach 1.8 m.
- 2.
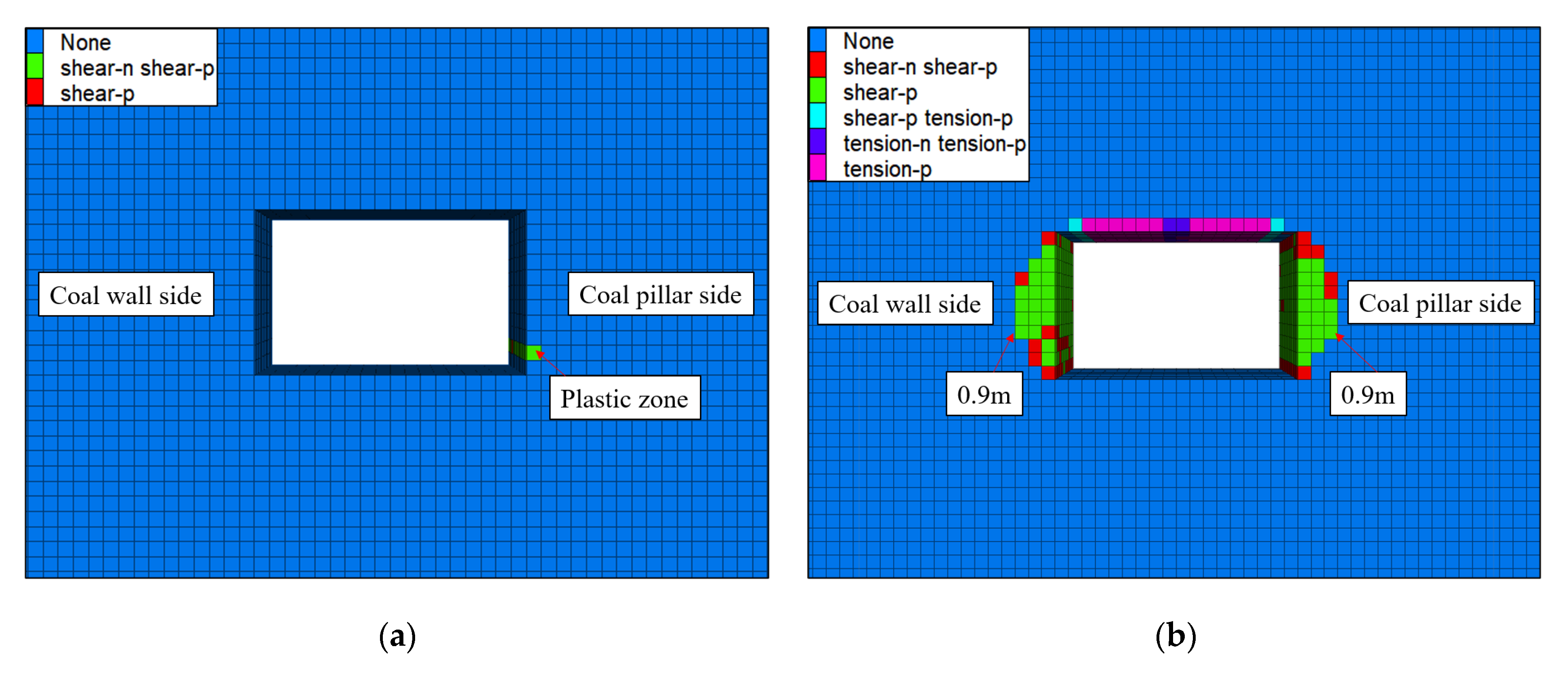
- Under the influence of primary mining, the maximum principal stress of the roadway surrounding rock reaches the maximum value of 6.29 MPa at a distance of 170 m behind the working face. The ratio of the maximum principal stress to the minimum principal stress reaches the maximum value of 1.51 at a distance of 70 m behind the working face. Moreover, the plastic zone of the surrounding rock is less developed, and the surrounding rocks of the roof and floor are relatively complete.
- 3.
- Under the influence of secondary mining, the maximum principal stress of the roadway surrounding rock reaches the maximum value of 19.82 MPa at a distance of 70 m behind the working face. The ratio of the maximum principal stress to the minimum principal stress reaches the maximum value of 1.95 at a distance of 20 m behind the working face. The plastic zone of the surrounding rock is large, the plastic zone of the roof is small, the maximum depth is 0.3 m, the developmental ranges of the two sides are large, the maximum damage depth is 0.9 m, and the floor is relatively intact.
- 4.
- This study demonstrates that a combination of multiple research methods is needed for further comprehensive studies to avoid partial conclusions. The methods and results presented herein are expected to serve as a reference for the analysis of roadway surrounding rock states under similar conditions; optimized support design is also expected to guide field applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Basarir, H.; Sun, Y.; Li, G. Gateway stability analysis by global-local modeling approach. Int. J. Rock Mech. Min. Sci. 2019, 113, 31–40. [Google Scholar] [CrossRef]
- Kang, H.; Wu, L.; Gao, F.; Lv, H.; Li, J. Field study on the load transfer mechanics associated with longwall coal retreat mining. Int. J. Rock Mech. Min. Sci. 2019, 124, 104141. [Google Scholar] [CrossRef]
- Shabanimashcool, M.; Li, C. Vertical stress changes in multi-seam mining under supercritical longwall panels. Int. J. Rock Mech. Min. 2013, 106, 39–47. [Google Scholar]
- Feng, G.; Wang, P.; Chugh, Y.; Zhao, J.; Wang, Z.; Zhang, Z. A Coal Burst Mitigation Strategy for Tailgate during Deep Mining of Inclined Longwall Top Coal Caving Panels at Huafeng Coal Mine. Shock Vib. 2018, 2018, 5929785. [Google Scholar] [CrossRef]
- Paul, A.; Singh, A.; Loui, P.; Singh, A.; Khandelwal, M. Validation of RMR-based support design using roof bolts by numerical modeling for underground coal mine of Monnet Ispat, Raigarh, India—a case study. Arab. J. Geosci. 2012, 5, 1435–1448. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, C.; Tao, Z.; Kang, H.; He, M. Failure mechanism and control technology of large deformation for Muzhailing Tunnel in stratified rock masses. Bull. Eng. Geol. Environ. 2021, 80, 4731–4750. [Google Scholar] [CrossRef]
- Kang, H.; Lin, J.; Fan, M. Investigation on support pattern of a coal mine roadway within soft rocks—A case study. Int. J. Coal Geol. 2015, 140, 31–40. [Google Scholar] [CrossRef]
- Yang, S.; Chen, M.; Jing, H.; Chen, K.; Meng, B. A case study on large deformation failure mechanism of deep soft rock roadway in Xin’An coal mine, China. Eng. Geol. 2017, 217, 89–101. [Google Scholar] [CrossRef]
- Majcherczyk, T.; Niedbalski, Z.; Małkowski, P.; Bednarek, Ł. Analysis of yielding steel arch support with rock bolts in mine roadways stability aspect. Arch. Min. Sci. 2014, 59, 641–654. [Google Scholar] [CrossRef] [Green Version]
- Mahdevari, S.; Shahriar, K.; Sharifzadeh, M.; Tannant, D. Stability prediction of gate roadways in longwall mining using artificial neural networks. Neural Comput. Appl. 2017, 28, 3537–3555. [Google Scholar] [CrossRef]
- Shen, B.; King, A.; Guo, H. Displacement, stress and seismicity in roadway roofs during mining-induced failure. Int. J. Rock Mech. Min. Sci. 2008, 45, 672–688. [Google Scholar] [CrossRef]
- Zhang, G.; Liang, S.; Tan, Y.; Xie, F.; Chen, S.; Jia, H. Numerical modelling for longwall pillar design: A case study from a typical longwall panel in China. J. Geophys. Eng. 2018, 15, 121–134. [Google Scholar] [CrossRef]
- Lawrence, W. A method for the design of longwall gateroad roof support. Int. J. Rock Mech. Min. 2009, 46, 789–795. [Google Scholar] [CrossRef]
- Jiang, Y.; Yoneda, H.; Tanabashi, Y. Theoretical estimation of loosening pressure on tunnels in soft rocks. Tunn. Undergr. Space Technol. 2001, 16, 99–105. [Google Scholar] [CrossRef]
- Leitman, M.; Villaggio, P. Plastic zone around circular holes. J. Eng. Mech. 2009, 135, 1467–1471. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, N.; Chang, Q.; Xu, J.; Zhang, J. Development of ensemble learning models to evaluate the strength of coal-grout materials. Int. J. Min. Sci. Technol. 2021, 31, 153–162. [Google Scholar] [CrossRef]
- Jiang, L.; Kong, P.; Shu, J.; Fan, K. Numerical Analysis of Support Designs Based on a Case Study of a Longwall Entry. Rock Mech. Rock Eng. 2019, 52, 3373–3384. [Google Scholar] [CrossRef]
- Liu, C.; Yue, S.; Wang, M.; Li, J.; Deng, S.; Zhang, G.; Ji, Y.; Li, Z.; Xu, T. Loading Device of Explosive Stress Wave in High Confining Pressure and Dynamic Response of Composite Structure. Compos. Struct. 2021, 258, 113198. [Google Scholar] [CrossRef]
- Liu, H.; Guo, L.; Cao, G.; Zhao, X.; Wang, P.; Huo, T.; Yang, G.; Hao, C.; Wang, Q. Comprehensive Study of Strata Movement Behavior in Mining a Longwall Top Coal Caving Panel of a Composite Coal Seam with Partings. Appl. Sci. 2020, 10, 5311. [Google Scholar] [CrossRef]
- Malkowski, P.; Ostrowski, L.; Bachanek, P. Modelling the small throw fault effect on the stability of a mining roadway and its verification by in situ investigation. Energies 2017, 12, 2082. [Google Scholar]
- Liu, H.; Qiao, B.; Ma, N. Stability analysis and design of roadways in adjacent seams: A case study from Tashan coal mine in China. Arab. J. Geosci. 2020, 13, 308. [Google Scholar] [CrossRef]
- Liu, H.; Guo, L.; Zhao, X.; Wang, P. Effect of Principal Stress Field on the Development of Plastic Zone ahead of the Gateroad. Energies 2020, 13, 4356. [Google Scholar] [CrossRef]
- Li, C.; Guo, X.; Lian, X.; Ma, N. Failure Analysis of a Pre-Excavation Double Equipment Withdrawal Channel and Its Control Techniques. Energies 2020, 13, 6368. [Google Scholar] [CrossRef]
- Gao, F.; Stead, D.; Kang, H. Numerical Simulation of Squeezing Failure in a Coal Mine Roadway due to Mining-Induced Stresses. Rock Mech. Rock Eng. 2015, 48, 1635–1645. [Google Scholar] [CrossRef]
- Ma, N.; Li, J.; Zhao, Z. Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock. J. China Univ. Min. Technol. 2015, 44, 209–213. [Google Scholar]
- Guo, X.; Zhao, Z.; Gao, X.; Wu, X.; Ma, N. Analytical solutions for characteristic radii of circular roadway surrounding rock plastic zone and their application. Int. J. Min. Sci. Technol. 2019, 29, 263–272. [Google Scholar] [CrossRef]
- He, M.; Gao, Y.; Yang, J.; Gong, W. An Innovative Approach for Gob-Side Entry Retaining in Thick Coal Seam Longwall Mining. Energies 2017, 10, 1785. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Wang, Q.; Wu, Q. Innovation and future of mining rock mechanics. J. Rock Mech. Geotech. Eng. 2021, 13, 1–21. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Wang, E.; He, M.; Yang, J. Roof Deformation Characteristics and Preventive Techniques Using a Novel Non-Pillar Mining Method of Gob-Side Entry Retaining by Roof Cutting. Energies 2018, 11, 627. [Google Scholar] [CrossRef]
- Yang, X.; Huang, R.; Yang, G.; Wang, Y.; Cao, J.; Liu, J.; He, M. Validation study of no-pillar mining method without advance tunneling: A case study of a mine in China. Energy Sci. Eng. 2021, 9, 1761–1772. [Google Scholar] [CrossRef]
- Yang, X.; Liu, C.; Sun, H.; Yue, S.; Ji, Y.; Zhang, X.; Hou, L. Research on the Deformation Mechanism and Directional Blasting Roof Cutting Control Measures of a Deep Buried High-Stress Roadway. Shock. Vib. 2020, 2020, 6742504. [Google Scholar] [CrossRef]
- Liu, J.; He, M.; Hou, S.; Zhu, Z.; Wang, Y.; Yang, J. Force change of the gravel side support during gangue heaping under a new non-pillar-mining approach. Geomech Eng. 2021, 27, 31–43. [Google Scholar]

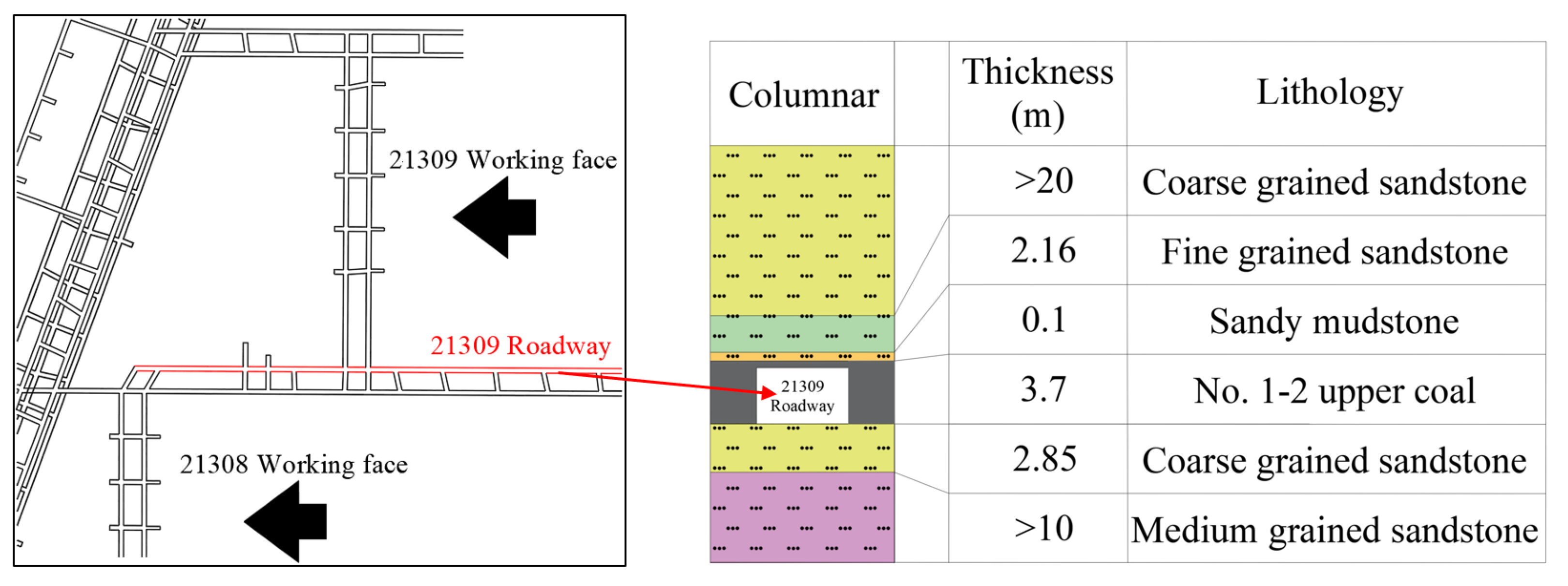




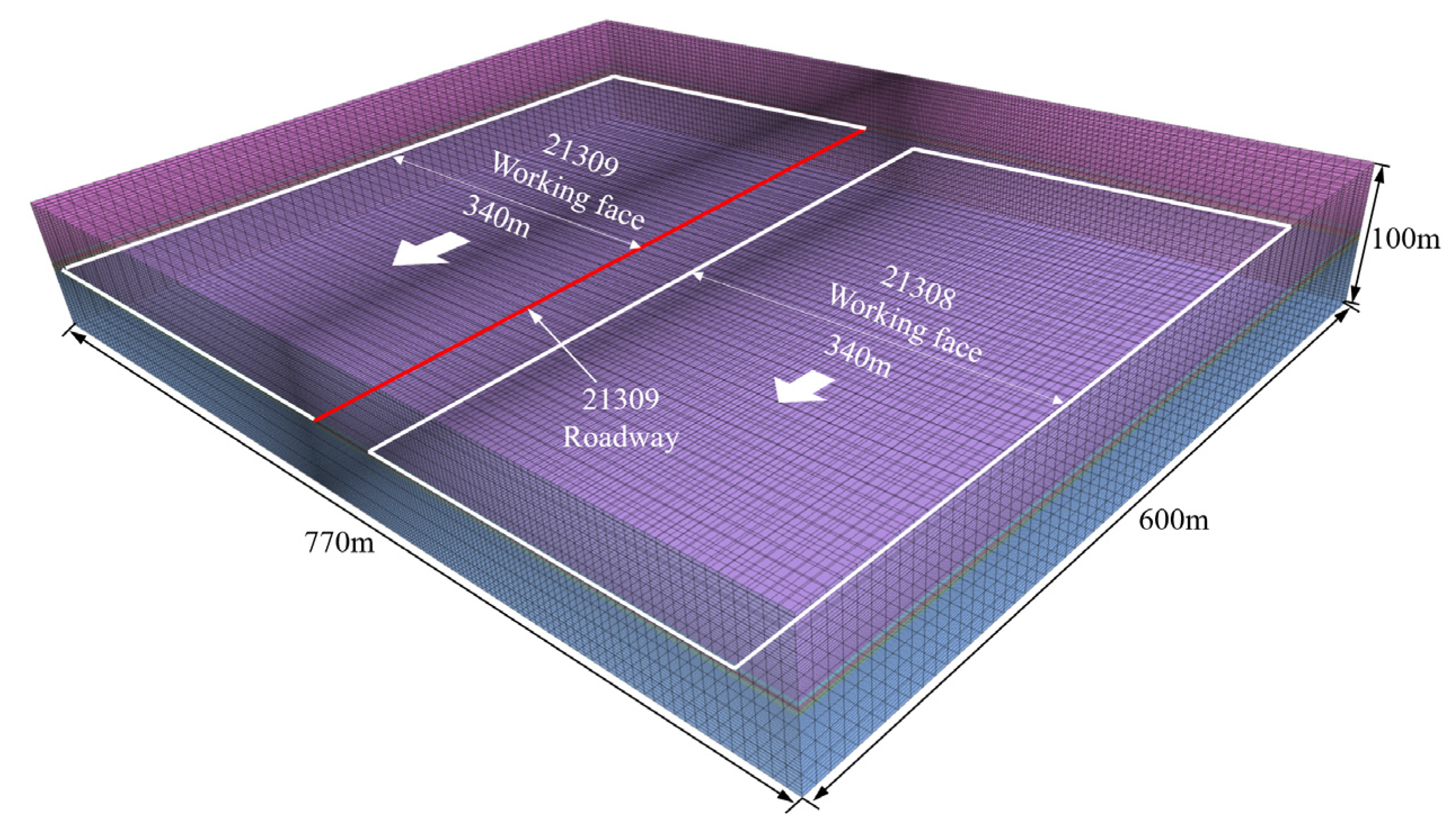


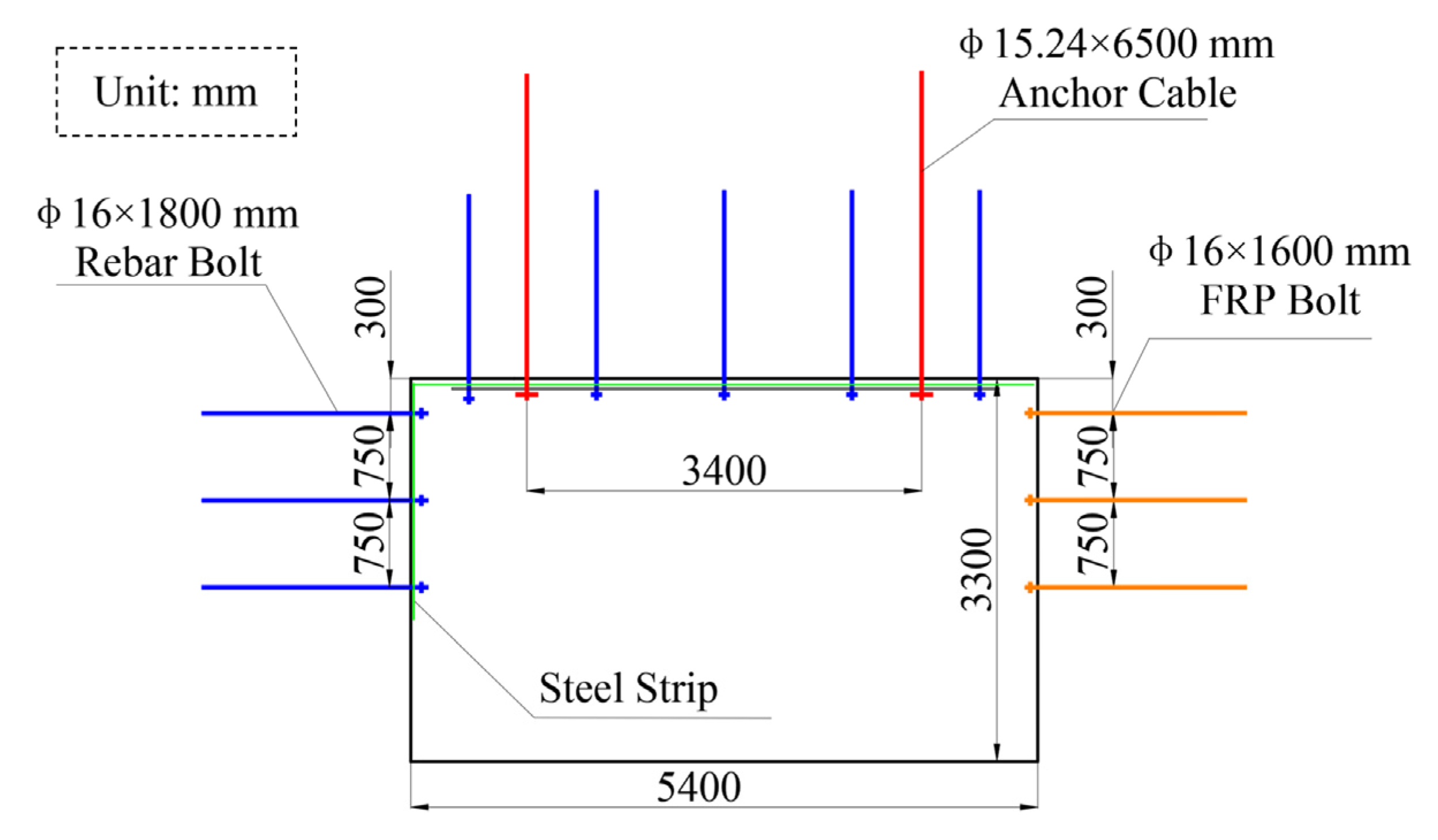
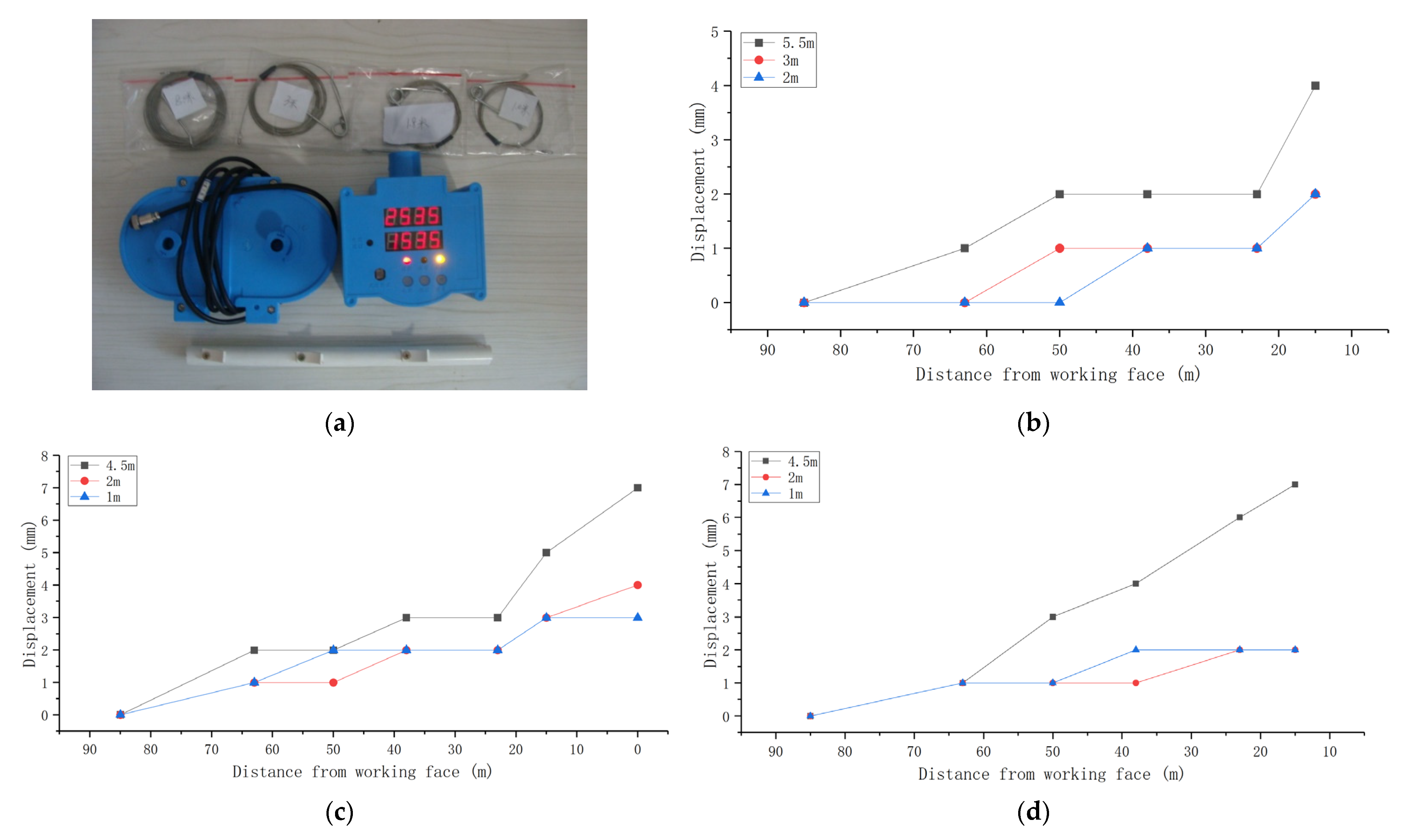


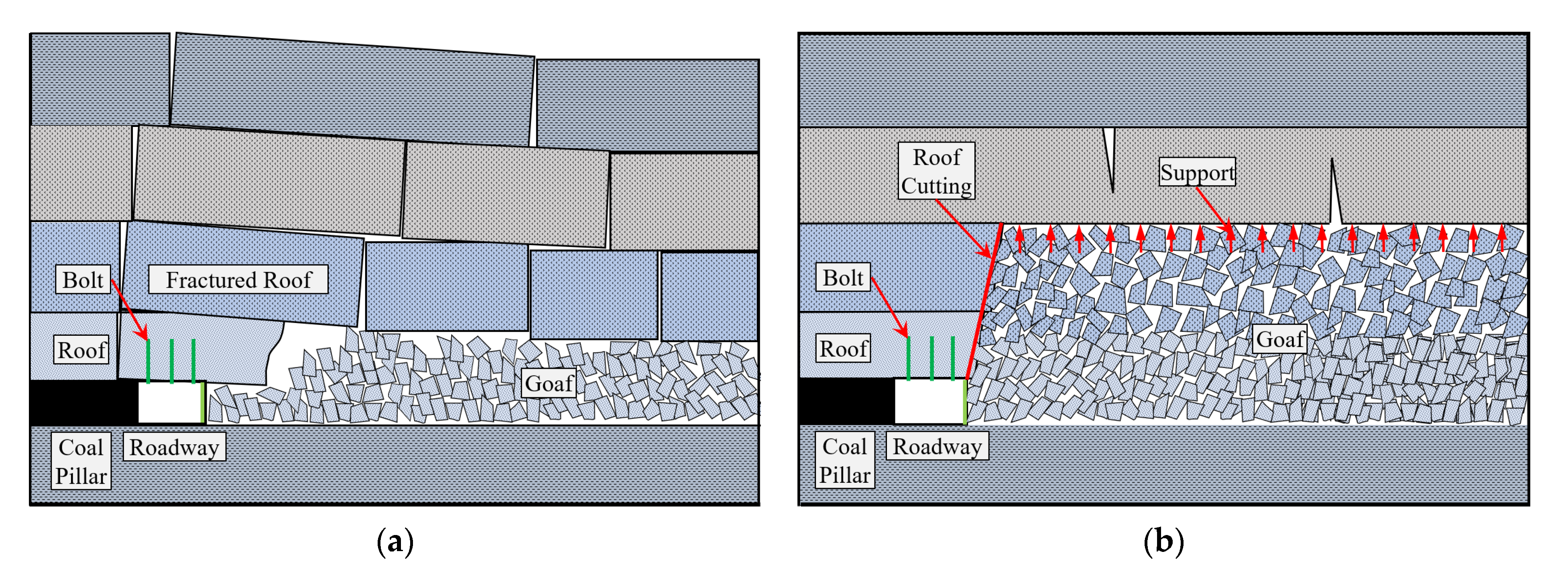
| Lithology | Tensile Strength (MPa) | Compressive Strength (MPa) | Elastic Modulus (MPa) | Poisson Ratio (µ) | Cohesion (MPa) | Internal Friction (°) |
|---|---|---|---|---|---|---|
| Sandstone of basic roof | 3.48 | 37.9 | 9976 | 0.21 | 4.8 | 49 |
| Sandstone of immediate roof | 3.70 | 38.5 | 10,023 | 0.23 | 6.7 | 50 |
| No. 1–2 upper coal | 1.98 | 11.2 | 7087 | 0.35 | 2.85 | 43.2 |
| Sandstone of immediate floor | 4.9 | 47.2 | 11,430 | 0.22 | 7.1 | 52.78 |
| Sandstone of basic floor | 3.89 | 40.1 | 10,477 | 0.23 | 6.8 | 52.09 |
| Distance from Working Face (m) | Broken Rock Zone Range (m) | |
|---|---|---|
| Coal Wall Side | Coal Pillar Side | |
| 15 | 1.8 | 1.4 |
| 25 | 1.6 | - |
| 35 | 1.2 | 1.2 |
| 45 | 1.0 | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yang, G.; Huang, R.; Wang, Y.; Liu, J.; Zhang, J.; Hou, S. Comprehensive Study on Surrounding Rock Failure Characteristics of Longwall Roadway and Control Techniques. Appl. Sci. 2021, 11, 9795. https://doi.org/10.3390/app11219795
Yang X, Yang G, Huang R, Wang Y, Liu J, Zhang J, Hou S. Comprehensive Study on Surrounding Rock Failure Characteristics of Longwall Roadway and Control Techniques. Applied Sciences. 2021; 11(21):9795. https://doi.org/10.3390/app11219795
Chicago/Turabian StyleYang, Xiaojie, Gang Yang, Ruifeng Huang, Yajun Wang, Jianning Liu, Jun Zhang, and Shilin Hou. 2021. "Comprehensive Study on Surrounding Rock Failure Characteristics of Longwall Roadway and Control Techniques" Applied Sciences 11, no. 21: 9795. https://doi.org/10.3390/app11219795
APA StyleYang, X., Yang, G., Huang, R., Wang, Y., Liu, J., Zhang, J., & Hou, S. (2021). Comprehensive Study on Surrounding Rock Failure Characteristics of Longwall Roadway and Control Techniques. Applied Sciences, 11(21), 9795. https://doi.org/10.3390/app11219795







