Revising of the Near Ground Helicopter Hover: The Effect of Ground Boundary Layer Development
Abstract
:1. Introduction
- (i)
- the re-circulation flow in which the starting vortex rolls up ahead of the rotor disk and
- (ii)
- the ground vortex flow in which the starting vortex rolls up below the rotor disk
2. Description of the Numerical Tools
2.1. The Eulerian Solver—MaPFlow
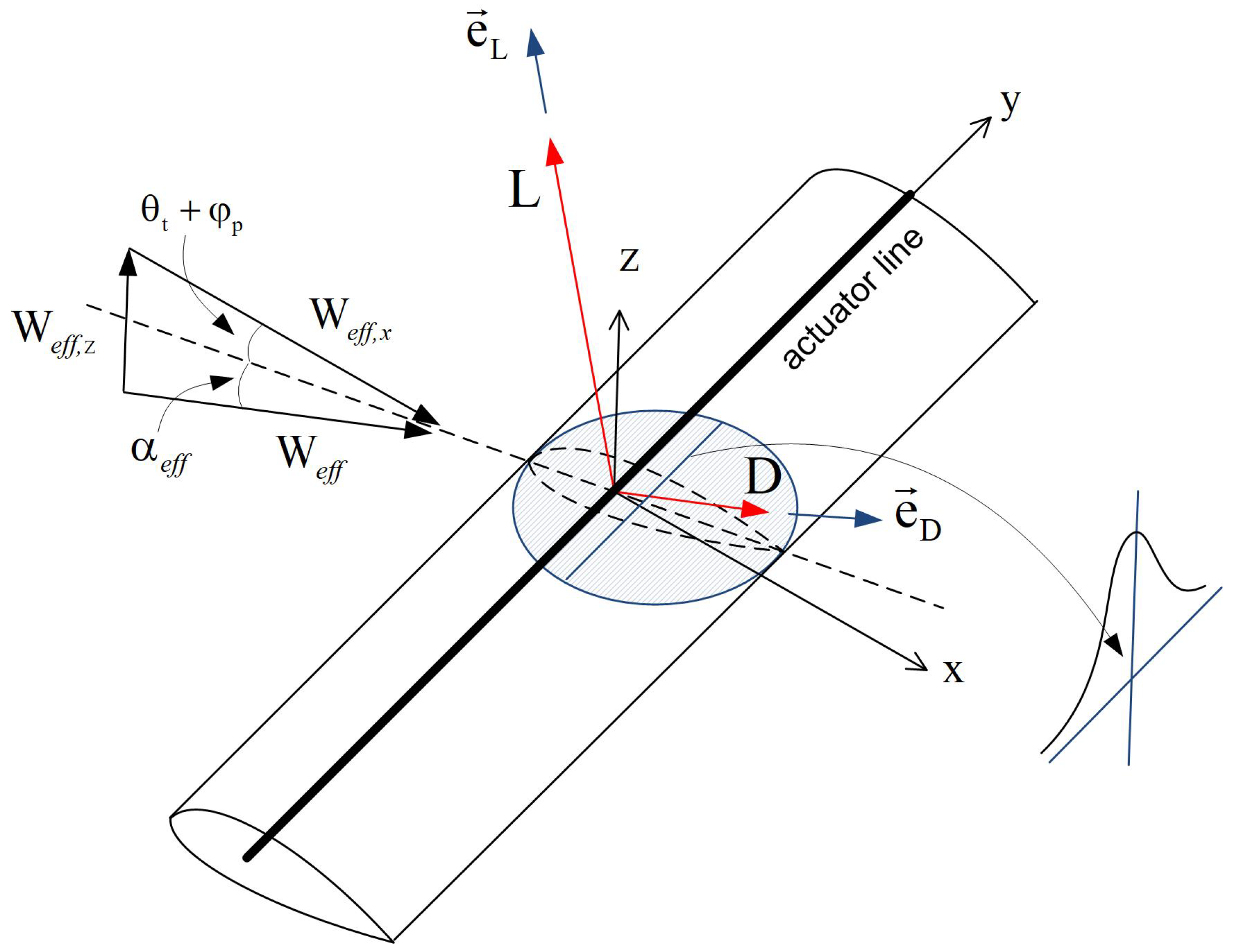
Actuator Line Model
2.2. Lagrangian Solver—Compressible Vortex Particles Approximation
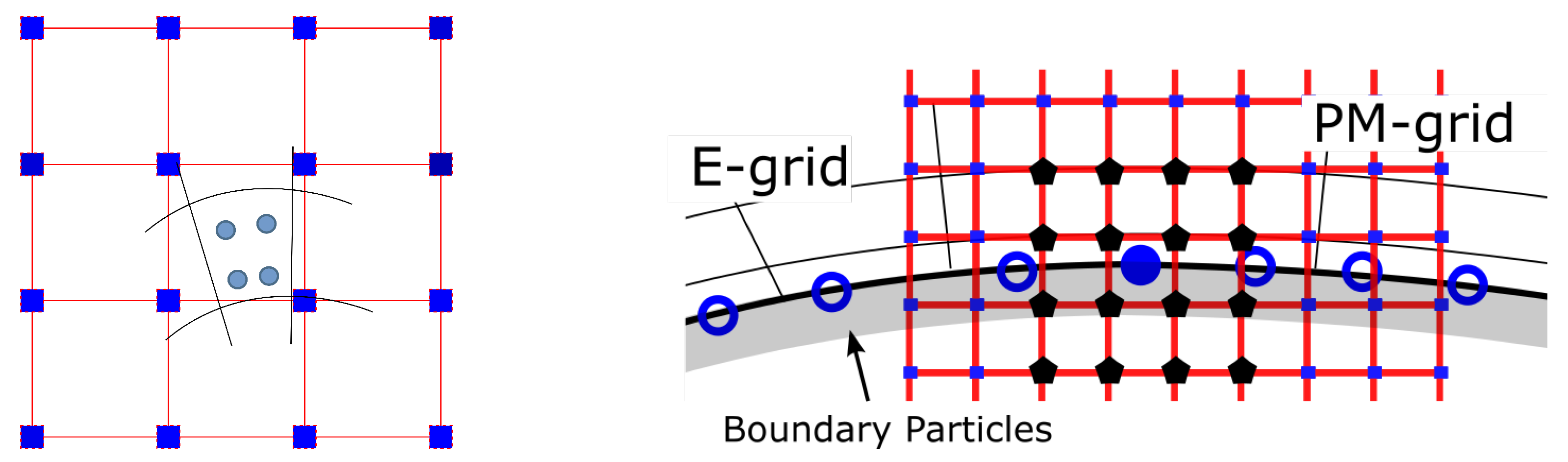
2.3. The Particle Mesh Scheme
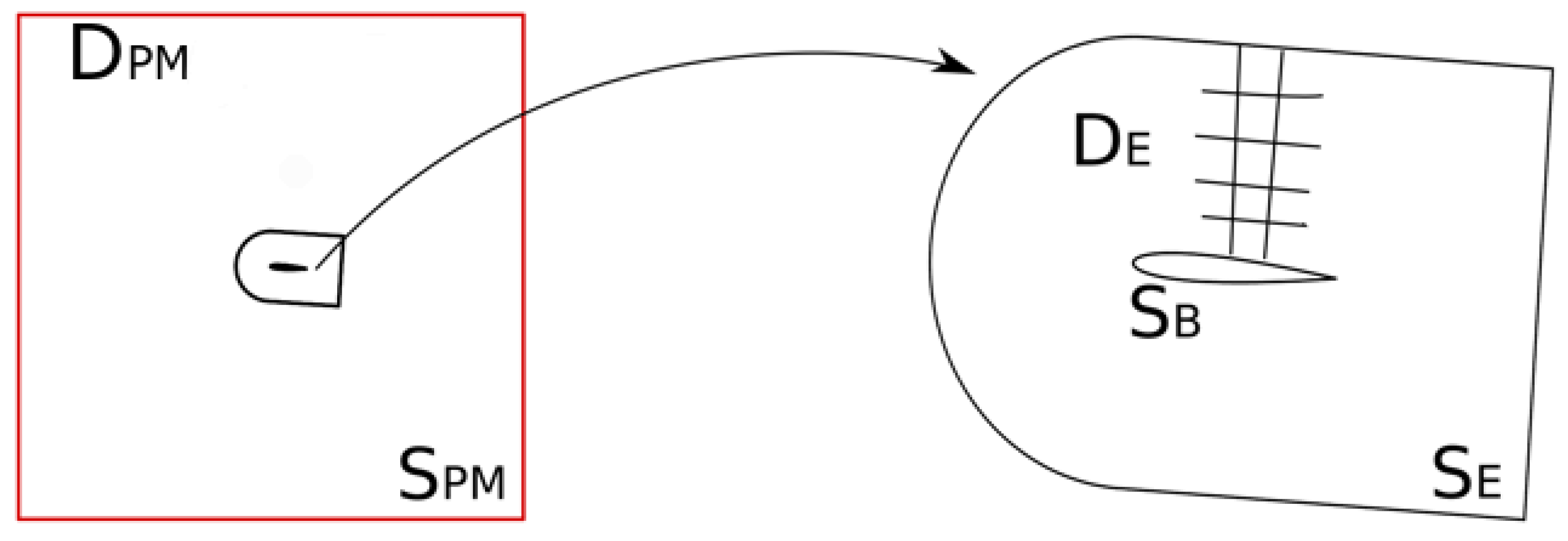
2.4. The Hybrid Solver
2.4.1. Communicating the Boundary Conditions on to the Eulerian Solver
2.4.2. Communicating the Presence of to the Lagrangian Solver
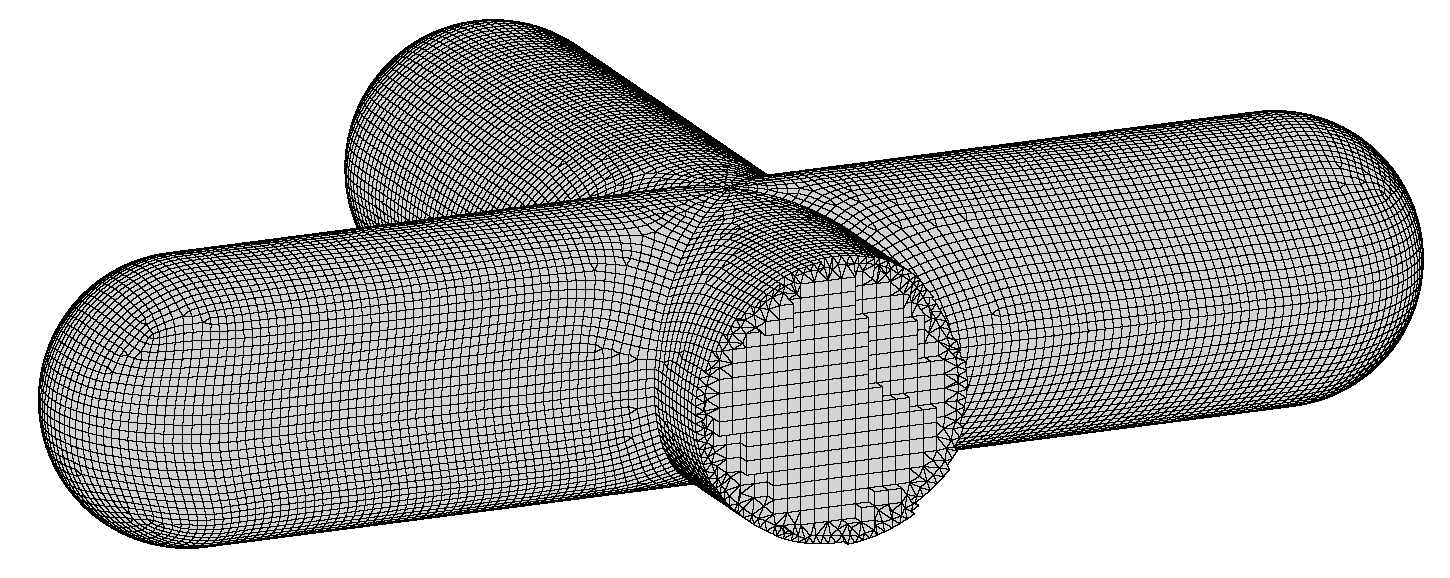
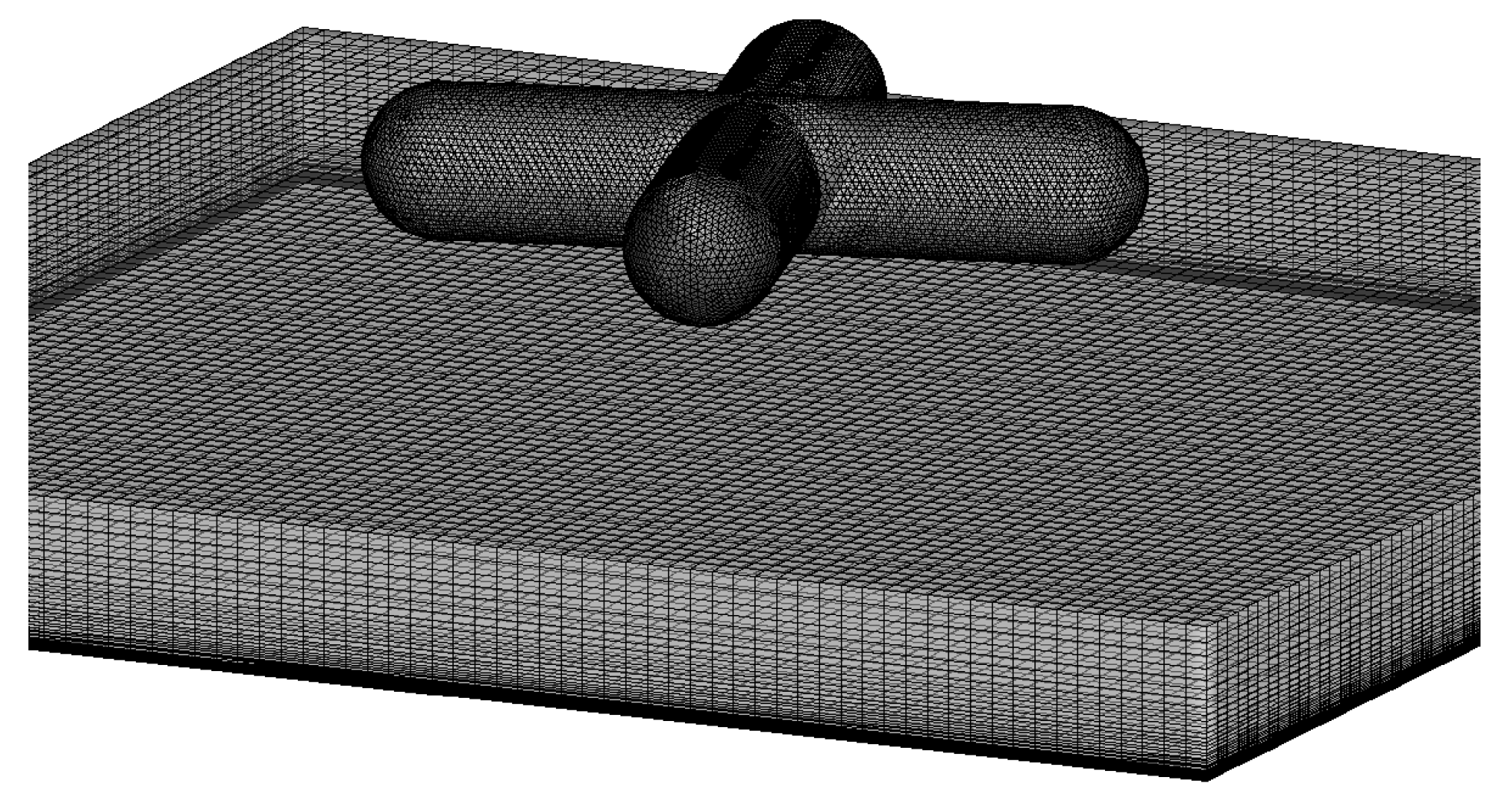
3. Description of the Test Cases
4. Validation against Measurements
4.1. Hover Flight Simulations Outside the Ground Effect (OGE)
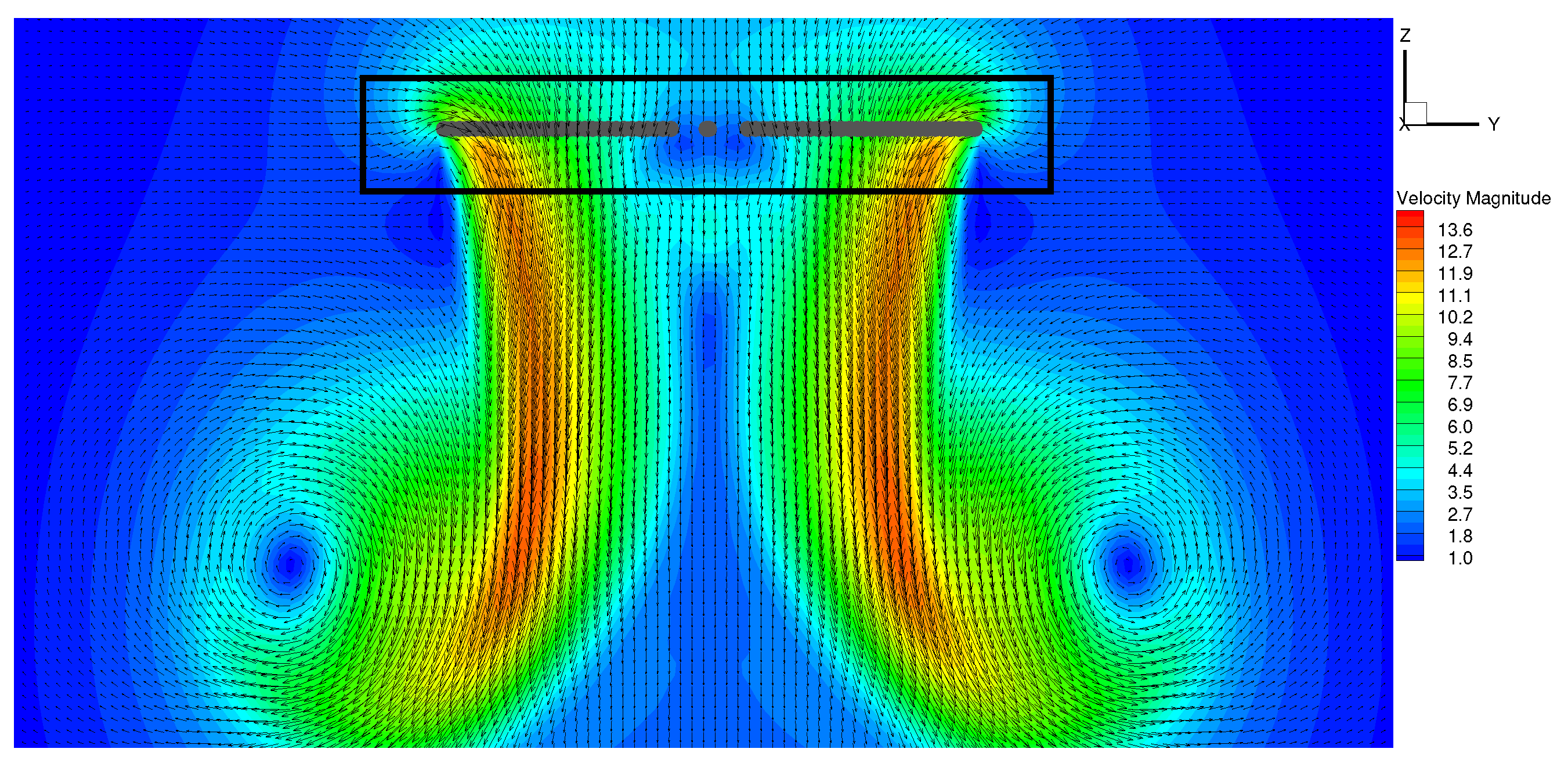
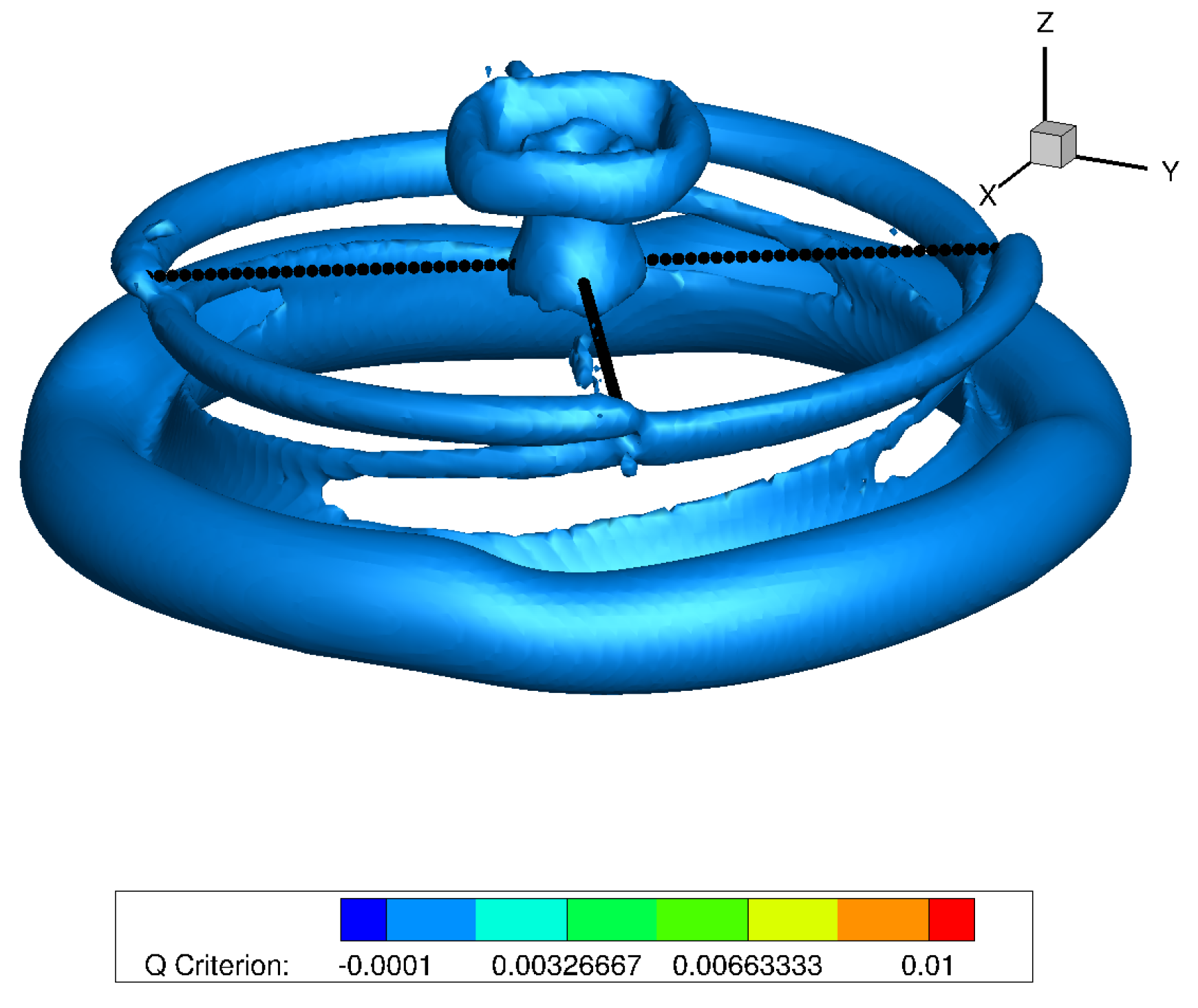
4.2. Hover Flight Simulations in IGE Flight Conditions
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Key, D. Analysis of army helicopter pilot error mishap data and the implications for handling qualities. In Proceedings of the 25th European Rotorcraft Forum, Rome, Italy, 14–16 September 1999. [Google Scholar]
- Curtiss, H.J.; Sun, M.; Putman, W.; Hanker, E.J. Rotor Aerodynamics in Ground Effect At Low Advance Ratios. J. Am. Helicopter Soc. 1984, 29, 48–55. [Google Scholar] [CrossRef]
- Boer, J.; Hermans, C.; Pengel, K. Helicopter Ground Vortex: Comparison of Numerical Predictions with Wind Tunnel Measurement; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Ganesh, B.; Komerath, N. Unsteady Aerodynamics of Rotorcraft in Ground Effect. In Proceedings of the Fluid Dynamics Meeting, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Nathan, N.D.; Green, R. The flow around a model helicopter main rotor in ground effect. Exp. Fluids 2012, 52, 151–166. [Google Scholar] [CrossRef]
- Sugiura, M.; Tanabe, Y.; Sugawara, H.; Matayoshi, N.; Ishii, H. Numerical Simulations and Measurements of the Helicopter Wake in Ground Effect. J. Aircr. 2017, 54, 209–219. [Google Scholar] [CrossRef]
- Sugiura, M.; Tanabe, Y.; Sugawara, H.; Barakos, G.; Matayoshi, N.; Ishii, H. Validation of Cfd Codes for the Helicopter Wake in Ground Effect. In Proceedings of the European Rotorcraft Forum, Milan, Italy, 12–15 September 2017. [Google Scholar]
- Cavallo, S.; Ducci, G.; Barakos, G.; Gibertini, G. CFD Analysis of Helicopter Wakes in Ground effect. In Proceedings of the European Rotorcraft Forum, Delft, The Netherlands, 18–21 September 2018. [Google Scholar]
- Pasquali, C.; Serafini, J.; Bernardini, G.; Milluzzo, J.; Gennaretti, M. Numerical-experimental correlation of hovering rotor aerodynamics in ground effect. Aerosp. Sci. Technol. 2020, 106, 106079. [Google Scholar] [CrossRef]
- Visingardi, A.; De Gregorio, F.; Schwarz, T.; Schmid, M.; Bakker, R.; Voutsinas, S.; Gallas, Q.; Boisard, R.; Gibertini, G.; Zagaglia, D.; et al. Forces on obstacles in rotor wake—A GARTEUR action group. In Proceedings of the 43rd European Rotorcraft Forum, Milan, Italy, 12–15 September 2017. [Google Scholar]
- Gibertini, G.; Grassi, D.; Parolini, C.; Zagaglia, D.; Zanotti, A. Experimental investigation on the aerodynamic interaction between a helicopter and ground obstacles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1395–1406. [Google Scholar] [CrossRef] [Green Version]
- Zagaglia, D.; Giuni, M.; Green, R.B. Rotor-obstacle aerodynamic interaction in hovering flight: An experimental survey. Annu. Forum Proc.-AHS Int. 2016, 1, 356–364. [Google Scholar]
- Andronikos, T.; Papadakis, G.; Riziotis, V.; Prospathopoulos, J.; Voutsinas, S. Validation of a cost effective method for the rotor-obstacle interaction. Aerosp. Sci. Technol. 2021, 113, 106698. [Google Scholar] [CrossRef]
- Voutsinas, S.G. Vortex methods in aeronautics: How to make things work. Int. J. Comput. Fluid Dyn. 2006, 20, 3–18. [Google Scholar] [CrossRef]
- Schmid, M. Simulation of helicopter aerodynamics in the vicinity of an obstacle using a free wake panel method. In Proceedings of the 43rd European Rotorcraft Forum, CEAS, Milan, Italy, 12–15 September 2017. [Google Scholar]
- Papadakis, G. Development of a Hybrid Compressible Vortex Particle Method and Application to External Problems Including Helicopter Flows. Doctoral Dissertation, National Technical University of Athens, Athens, Greece, 2014. [Google Scholar]
- Papadakis, G.; Voutsinas, S.G. A strongly coupled Eulerian Lagrangian method verified in 2D external compressible flows. Comput. Fluids 2019, 195, 104325. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. On the Accuracy of Limiters and Convergence to Steady State Solutions. In Proceedings of the On the Accuracy of Limiters and Convergence to Steady State Solutions, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Spalart, P.; Allmaras, S. One-Equation Turbulence Model for Aerodynamic Flows. Rech. Aerosp. 1994, 5–21. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation k-omega Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Ghosal, S. An analysis of numerical errors in large-eddy simulations of turbulence. J. Comput. Phys. 1996, 125, 187–206. [Google Scholar] [CrossRef] [Green Version]
- Spyropoulos, N.; Prospathopoulos, J.; Manolas, D.; Papadakis, G.; Riziotis, V.A. Development of a fluid structure interaction tool based on an actuator line model. J. Phys. Conf. Ser. 2020, 1618, 052072. [Google Scholar] [CrossRef]
- Schmitz, S.; Chattot, J.J. A coupled Navier–Stokes/Vortex–Panel solver for the numerical analysis of wind turbines. Comput. Fluids 2006, 35, 742–745. [Google Scholar] [CrossRef]
- Martinez-Tossas, L.; Churchfield, M.; Leonardi, S. Large eddy simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy 2015, 18, 1047–1060. [Google Scholar] [CrossRef]
- Jha, P.; Schmitz, S. Actuator curve embedding—An advanced actuator line model. J. Fluid Mech. 2018, 834. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, N.N.; Michelsen, J. Numerical simulations of wake characteristics of a wind turbine in uniform inflow. Wind Energy 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Beale, J.T.; Majda, A. Higher order accurate vortex methods with explicit velocity kernels. J. Comput. Phys. 1985, 58, 188–208. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P. Vortex Methods: Theory and Practice; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wang, K.; Riziotis, V.A.; Voutsinas, S.G. Aeroelastic stability of idling wind turbines. Wind Energy Sci. 2017, 2, 415–437. [Google Scholar] [CrossRef] [Green Version]



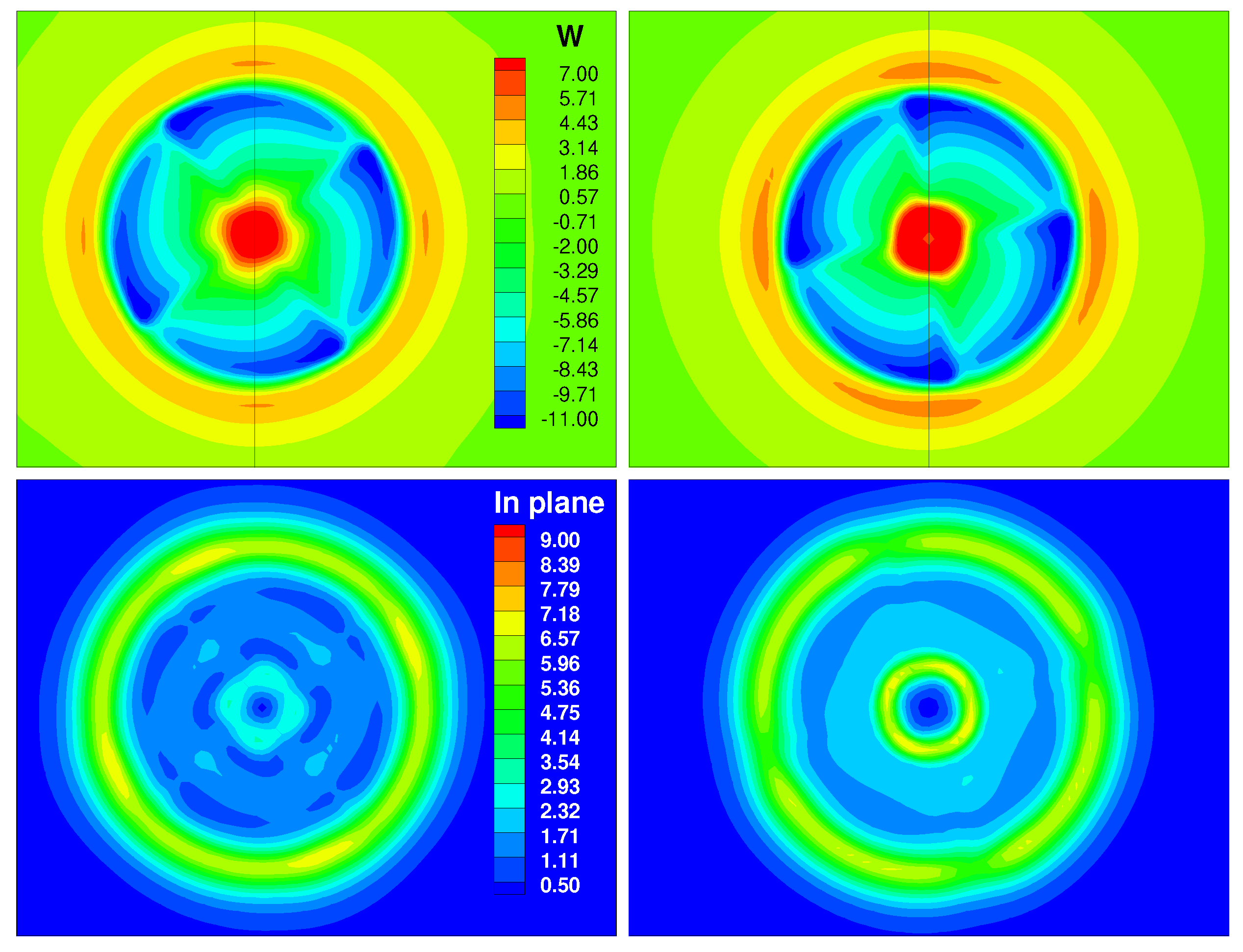
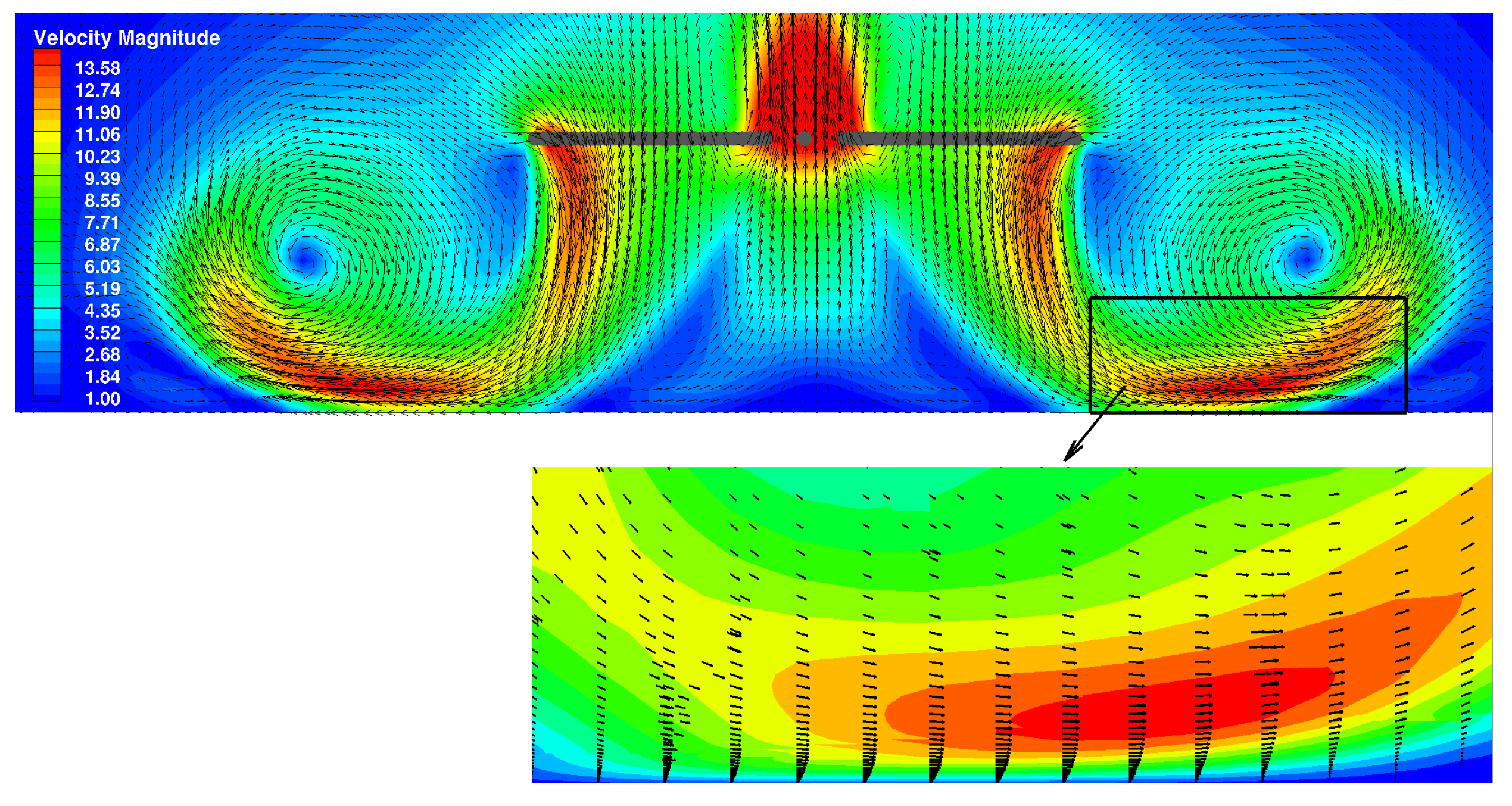
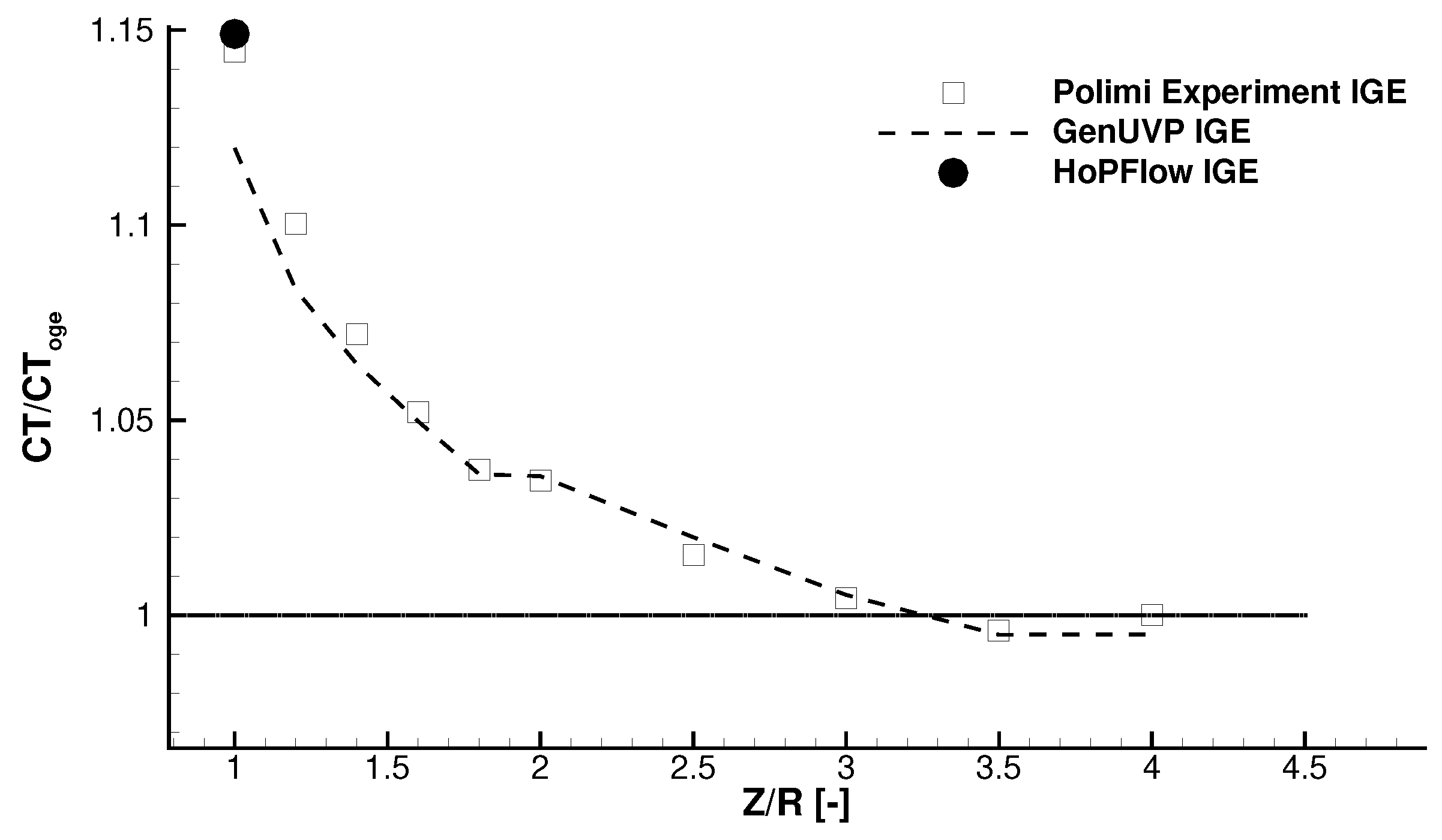

| Measured Thrust Coefficient | Predictions GenUVP | Predictions HoPFlow |
|---|---|---|
| 0.007270 | 0.007290 | 0.007285 |
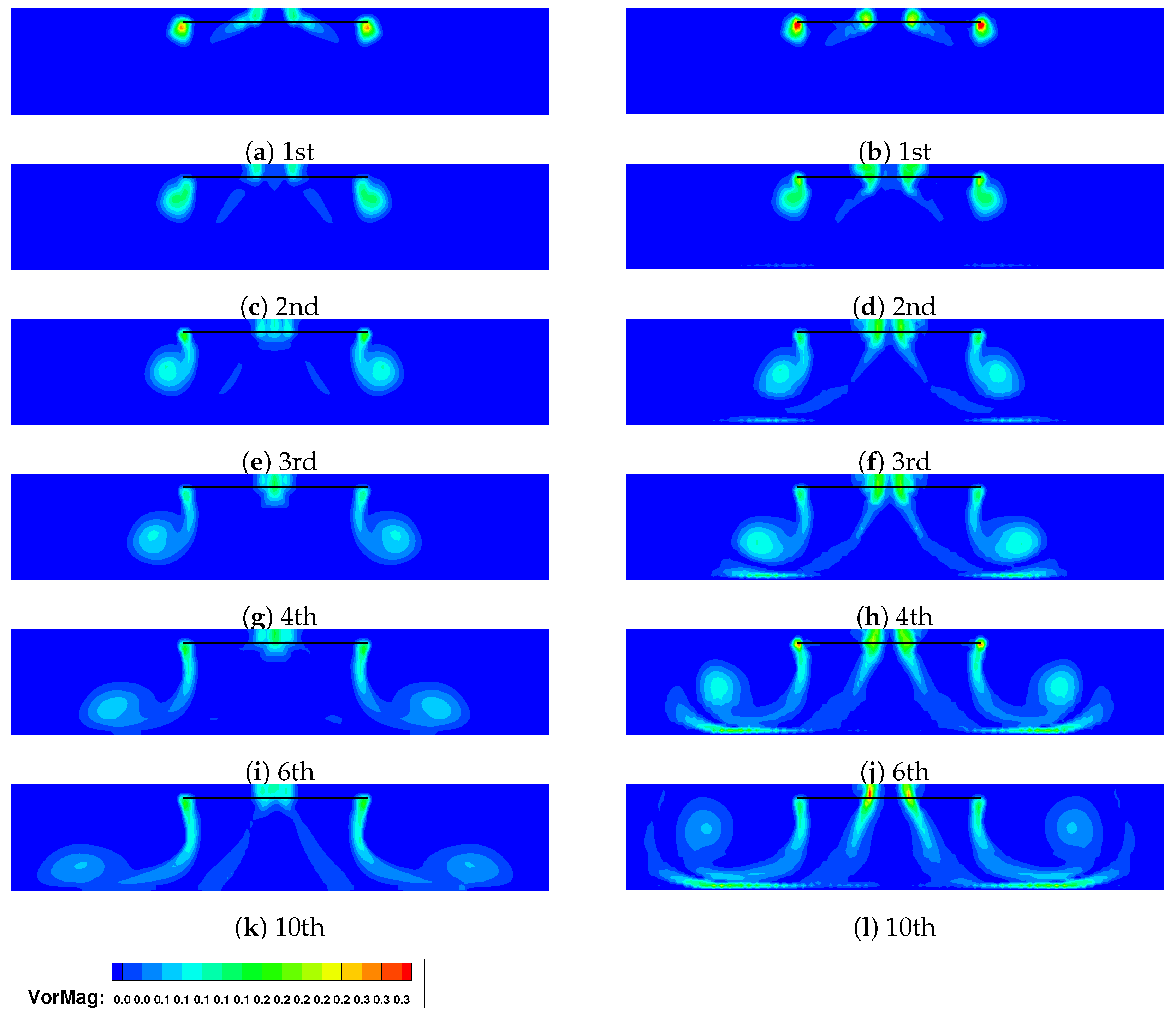
| Period | [Z/R] Inviscid Wall | [r/R] Inviscid Wall | [Z/R] Viscous Wall | [r/R] Viscous Wall |
|---|---|---|---|---|
| 1st | 0.98 | 1.02 | 0.985 | 1.02 |
| 2nd | 0.80 | 1.08 | 0.79 | 1.07 |
| 3rd | 0.58 | 1.18 | 0.53 | 1.19 |
| 4th | 0.45 | 1.34 | 0.39 | 1.41 |
| 6th | 0.28 | 1.76 | 0.51 | 1.86 |
| 10th | 0.22 | 2.14 | 0.65 | 2.00 |
| Experiment | Inviscid Wall | Viscous Wall | GenUVP |
|---|---|---|---|
| 1.1441 | 1.1235 | 1.149 | 1.121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andronikos, T.; Papadakis, G.; Riziotis, V.; Voutsinas, S. Revising of the Near Ground Helicopter Hover: The Effect of Ground Boundary Layer Development. Appl. Sci. 2021, 11, 9935. https://doi.org/10.3390/app11219935
Andronikos T, Papadakis G, Riziotis V, Voutsinas S. Revising of the Near Ground Helicopter Hover: The Effect of Ground Boundary Layer Development. Applied Sciences. 2021; 11(21):9935. https://doi.org/10.3390/app11219935
Chicago/Turabian StyleAndronikos, Theologos, George Papadakis, Vasilis Riziotis, and Spyros Voutsinas. 2021. "Revising of the Near Ground Helicopter Hover: The Effect of Ground Boundary Layer Development" Applied Sciences 11, no. 21: 9935. https://doi.org/10.3390/app11219935
APA StyleAndronikos, T., Papadakis, G., Riziotis, V., & Voutsinas, S. (2021). Revising of the Near Ground Helicopter Hover: The Effect of Ground Boundary Layer Development. Applied Sciences, 11(21), 9935. https://doi.org/10.3390/app11219935








