Experimental Investigations on the Long Term Material Properties of Rubberized Portland Cement Concrete

Featured Application

The use of rubberized concrete in structural applications demands the assessment of its strength and elastic properties. The evolution of these properties in time is important for making pertinent predictions related to the safety of structural elements.

Abstract

The paper presents the results of a research work aimed at assessing the long-term strength and elastic properties of rubberized concrete. The parameters of the research were the rubber replacement of fine aggregates and the age of testing the specimens. Compressive and splitting tensile strength of concrete cylinders were obtained at the age of 5 years, coupled with the static and dynamic modulus of elasticity of all concrete specimens. Additionally, the material damping coefficient was assessed by means of non-destructive tests. The density of the rubberized concrete decreases with the percentage replacement of natural sand by rubber aggregates. A significant drop in the values of density after 5 years was observed for specimens made with rubberized concrete. The static and the dynamic moduli of elasticity decrease with the increase in rubber content. A similar trend is observed for the compressive and tensile splitting strength.

1. Introduction

Concrete, one of the most used construction materials, has been intensively studied due to the complex phenomena governing its behavior from an early age to the long term [1]. Despite its many uncontested advantages as a construction material, concrete also has some drawbacks that prompted an overwhelming research effort to either mitigate or eliminate them entirely. However, perhaps one of the biggest advantages of concrete is its ability to incorporate a variety of wastes from different sources: power plants [2], steel manufacturing processes [3], construction and demolition wastes, municipal wastes, etc.

The latest report of ETRMA (European Tyre and Rubber Manufacturers’ Association) shows that in 2019, a total of 3.55 million tons of tires reached their end of life in Europe alone. Most of them, 95%, according to the same report, were treated through either material or energy recovery (cement kilns, urban heating and power plants) techniques. The application of ELT (end of life tires) derived materials in civil engineering, public works and backfilling amounted to a total of 112 thousand tons, a significant 18% increase compared to 2018.

In view of the continuously stricter regulations in terms of environmental protection and abiding by the concept of circular economy, the construction industry has looked for alternatives in terms of reducing the carbon footprint and preserving the raw materials. The use of rubber crumbs from ELTs as partial substitutes of fine and small coarse aggregates was investigated for the past 25 years. From the early works of Fattuhi and Clark [4] up to the recent research of Wang et al. [5], much effort was invested in understanding the behavior of this new type of concrete.

From the very beginning, it was clear that adding rubber aggregates to concrete resulted in a decrease in the values of mechanical properties [6]. Since strength and elastic properties are the main parameters considered in the design process of structural elements, rubberized concrete has seen limited application in this direction unless special confining solutions were applied [7,8,9]. However, significant deformability was achieved for a material that is inherently brittle [10]. This fact, coupled with the proven ability of rubberized concrete to dampen vibrations, resulted in it being used for various purposes, from road crush barriers to non-structural elements designed to reduce the traffic vibrations or to have enhanced soundproofing properties. Moreover, the durability of concrete incorporating rubber aggregates was found to be higher [11], especially in the case of sulfate corrosion [12].

However, the data presented in the scientific literature focused on the short-term values of the mechanical properties of Portland cement concrete containing rubber aggregates. This is completely understandable given the fact that all design guidelines refer to the strength values and modulus of elasticity obtained by means of standardized tests at the age of 28 days. This allows for a quick and unified approach to assess whether a certain type of concrete is suitable for structural or non-structural applications.

On the other hand, the long-term strength and elastic properties of concrete are rarely investigated, and it is generally assumed they increase in time, provided that there are no deleterious agents acting upon the material. Accelerated durability tests are able to offer information on the ability of concrete to keep its integrity when subjected to chemical attacks and environmental factors (freeze-thaw).

The paper presents the results of a research work aimed at assessing the long-term strength and elastic properties of rubberized concrete. The parameters of the research were the rubber replacement of fine aggregates and the age of testing the specimens. Compressive and splitting tensile strength of concrete cylinders were obtained at the age of 5 years, coupled with a static and dynamic modulus of elasticity of all concrete specimens. Additionally, the material damping coefficient was assessed by means of non-destructive tests.

The significance of the conducted research work relies on the fact that it puts forward data for the material properties of rubberized concrete (RuC) well beyond the standard testing time of 28 days. The main objective was to determine the values of the modulus of elasticity, compressive and tensile splitting strength and their evolution after a significantly longer time interval compared to the standard testing time. Material damping was another important factor considered in the research since it offers an insight into the damping properties of RuC. On the other hand, the data are limited by the number of selected mix proportions, type of aggregate that was replaced by rubber particles as well as storage conditions of the specimens.

2. Materials and Methods

2.1. Materials

The target concrete strength class considered in the research was C30/37. The specimens were cast as part of the FP7-ANAGENNISI (ENV.2013.6.3-1: 603722) project, where large sets of data were obtained for statistical analysis in terms of concrete compressive strength. The target compressive strength for RuC was 20 MPa so that it would actually be used in structural applications. Since replacing natural aggregates with rubber aggregates would result in a decrease of the compressive strength, several strength classes were considered at that time for the reference concrete mix. Based on the experimental data obtained, at the age of 28 days, the C30/37 concrete proved to be the most economical solution in terms of cement consumption. It would lead to the desired compressive strength for the rubberized concrete derived from it at the standard testing age of 28 days.

A CEM I 42.5R type of cement, readily available on the market, was used. The choice of the cement type was based on the fact that high early age compressive strength was sought during the initial experimental plan. River aggregates with rounded edges were used as natural aggregates. The rounded edges prevent the occurrence of stress concentrations and the initiation of early cracking.

The rubber aggregates (Figure 1) came from a local supplier and were obtained from shredding and grinding of the tires from commercial vehicles. The surface texture of the aggregates, as a result of the shredding process, is shown in Figure 1a. Figure 1b gives an overview of the maximum particle size. The rubber aggregates were sorted according to their maximum size and cleaned from any impurities before being delivered in bulk. The impurities refer to any steel parts and/or textiles resulting from the shredding process. The particle size distribution is shown in Figure 1c.

2.2. Methods

The mix proportion considered at the beginning of the experimental program is shown in

Table 1. Mix proportions used in the research.

Mix Designation	Cement (C) CEM I 42.5R	Water (W)	W/C	Aggregates
				Sand	Rubber	Sort 4–8 mm	Sort 8–16 mm
	[kg/m3]	[kg/m3]	-	[kg/m3]	[kg/m3]	[kg/m3]	[kg/m3]
Ref	489	230	0.47	582	-	388	647
RuC40				532	50
RuC60				514.8	67.2
RuC80				492.4	89.6

[6]. The water to cement ratio was kept constant to 0.47 for all mix proportions. The mix proportions were denoted as Ref, for the reference mix without any rubber aggregates, and RuC for rubberized concrete, followed by a number showing the replacement percentage, by volume, of sand by rubber aggregates. The data were converted to mass units when preparing the mix proportions, as presented in Table 1.

The rubber aggregates were set to replace the natural sand, with a maximum dimension of 4 mm. The replacement percentages, by volume, were 40%, 60% and 80%. The apparent density of the rubber aggregates was experimentally determined, 506 kg/m³, and was found to be in line with similar reported data in the scientific literature [13].

A total number of 20 cylinders (ϕ100 × 200 mm) were cast, resulting in a total number of 80 specimens. The specimens were demolded at 24 h after casting and cured in water for 28 days. At the age of 28 days, a cylindrical specimen of each mix proportion was cut in 30 mm thick slices to assess the distribution of the rubber aggregates within the concrete mix, as shown in Figure 2. After 28 days, the samples were kept in laboratory conditions (23 ± 2 °C and relative air humidity of 40–50%) until the day of testing, 5 years later.

The static longitudinal modulus of elasticity was assessed in accordance with specifications of SR EN 12390:13 [14]. Cyclic loading was applied within limits mentioned in the code, and three individual values were obtained for each specimen. One cylinder was loaded in compression until failure in order to set the correct upper and lower limits of the loading cycles, as shown in Figure 3a. Therefore, the static longitudinal modulus of elasticity was assessed for 19 specimens only, with 3 distinct measurements for each specimen. The experimental setup is shown in Figure 3b. A hinge was used between the loading platens of equipment and the concrete cylinder in order to ensure an even distribution of the compressive load.

The compressive and splitting tensile strengths were determined in accordance with SR EN 12390:3 [15] and SR EN 12390:6 [16], respectively. The considered loading rate for determining the compressive strength was 0.6 MPa/s (4.71 kN/s), whereas, for the tensile splitting strength, a loading rate of 0.05 MPa/s (0.4 kN/s) was adopted.

The dynamic longitudinal modulus of elasticity, E_d, was assessed following the guidelines of ASTM C215:14 [17] and was based on the first resonant frequency (FRF) obtained from the Impact Echo Method. The experimental setup is shown in Figure 4. An accelerometer was placed at one end of the concrete cylinder along the longitudinal axis of the specimen to record the response of the sample when subjected to a small impact load at the opposite end. The signal was recorded on a computer via a data acquisition system. The dynamic modulus of elasticity for the cylindrical specimens was computed as shown in Equation (1):

$${\mathrm{E}}_{\mathrm{d}}=\mathrm{D}\cdot \mathrm{m}\cdot {\mathrm{f}}_{\ln }^2$$

(1)

where m is the mass of the sample [kg], f_ln is the fundamental frequency of vibration [Hz] and D is a coefficient that depends on both the diameter and the length of the cylinder (Equation (2)):

$$\mathrm{D}=5.093\cdot \frac{\mathrm{L}}{{\mathrm{d}}^2}$$

(2)

where L is the length of the cylinder [m] and d is the diameter [m].

The material damping properties were assessed by means of the decaying rate function obtained from the damped free vibrations response of the specimens.

3. Results and Discussions

3.1. Density

Figure 5 presents the variation in density with the age of specimens using as reference the values obtained at the standard curing age of 28 days [6]. The presented data are the average value of 20 measurements for the age of 5 years and 30 measurements for the early age.

It can be observed that even though all specimens were kept in the same conditions, the reference kept its value for the density as compared to 28 days. The change from 28 days to 5 years was less than 1%. On the other hand, all three mixes of RuC exhibited a much larger decrease in the density by as much as 12% for RuC80. A possible explanation could be that, even though the same water/cement ratio was used for all mixes, due to the hydrophobic nature of rubber particles, the excess water available for the hydration of the cement paste evaporated due to the storage conditions. Since the amount of cement was the same for all mixes (Table 1) and the curing and storing conditions were identical, it was thought that the rate of hydration was similar for all mixes, and therefore the excess water was lost by evaporation.

According to a recent study on rubberized concrete [18], the porosity and density of micro-cracks in RuC increased with the curing age, although the determined pore radius decreased. All other chemical reactions and rate of strength increase were similar to normal concrete. Earlier findings [19] showed that keeping concrete specimens in hot and, especially, dry conditions would result in overall lower values of the strength and elastic properties that are closely related to the density of the material.

In a similar study [20], it was concluded that the addition of rubber particles increased the number of cracks inside the concrete, which favors the migration of chemically unbound water, weakened the ITZ between the rubber aggregate and cement paste, and entrained more air during the mixing process. As a direct, immediate consequence, the density of rubberized concrete decreased compared to the normal concrete.

The presented trend is in line with data available in the scientific literature and with the general consensus that adding rubber to the concrete mix leads to a decrease in the density of rubberized concrete compared to the equivalent reference mix [11].

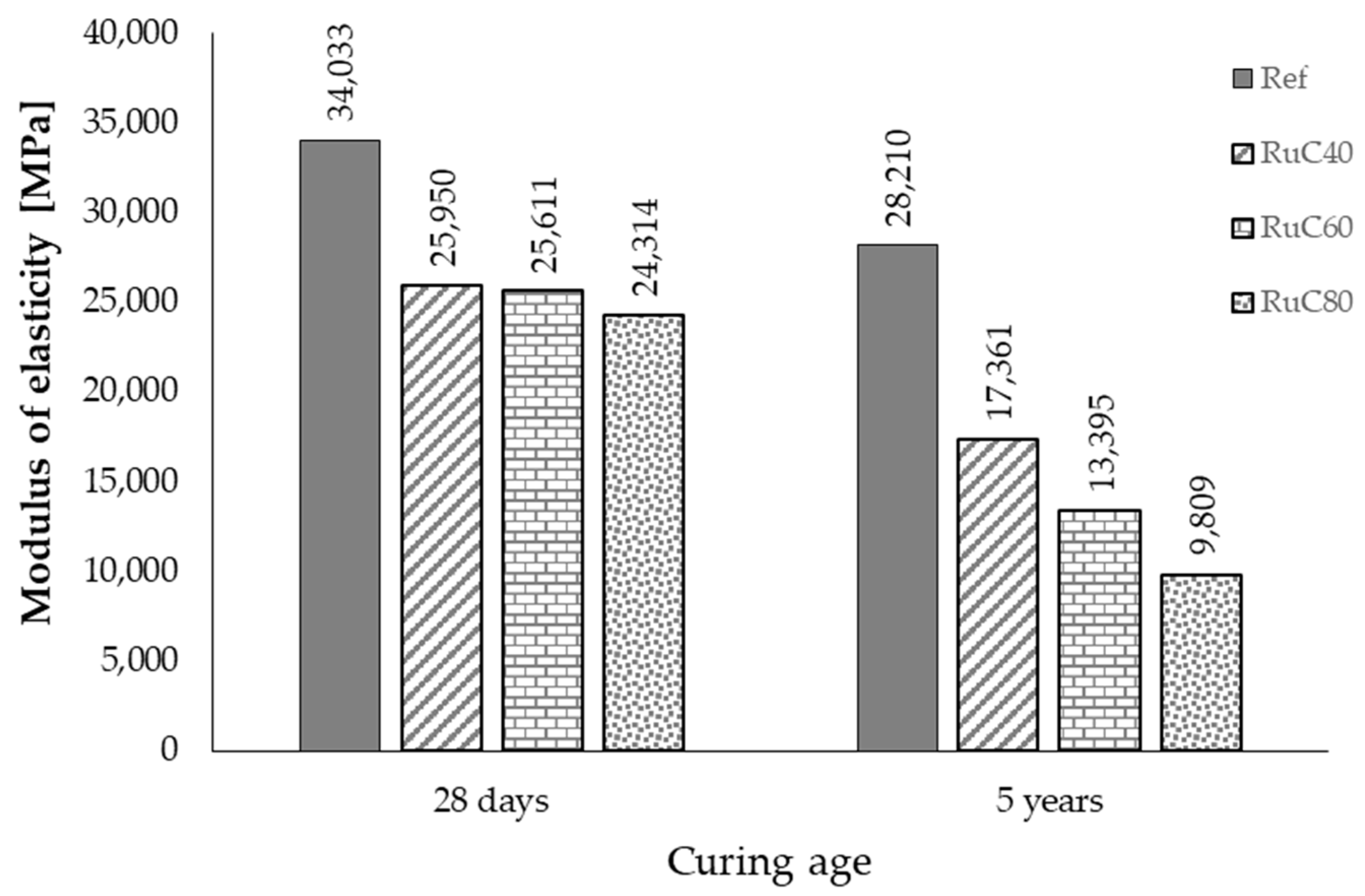
3.2. Static Modulus of Elasticity

As previously mentioned, the static modulus of elasticity in compression was determined in accordance with currently available standards [14]. The results are presented in Figure 6 as the average values of 19 determinations each of these individual values were, in turn, obtained as the average of three measurements, as shown in Figure 3.

It can be observed that irrespective of the mix, there is a decrease in the values of the static modulus of elasticity. The decrease ranged from 17% for the reference mix up to 60% for RuC80. Small variations in the values of modulus of elasticity were reported in the literature for concrete with fly ash, but the curing and exposure conditions were different compared to the present study [21]. The storage conditions of the specimens presented in this study favored the loss of water by evaporation through pores and capillaries.

Rubberized concrete specimens were most affected by this due to the fact that the presence of rubber aggregates favor the occurrence of weak links at the interface between the cement paste and rubber particles, thus favoring migration of water towards the surface of the specimens. A similar decrease in the values of mechanical and elastic properties of RuC was reported in the scientific literature, although for much smaller replacement percentages [22].

The decrease in the values of the static modulus of elasticity ranged from 38.6% for RuC40 to 65.23% for RuC80 mix compared to the reference mix.

3.3. Dynamic Modulus of Elasticity

The determination of the dynamic modulus of elasticity was based on the first resonant frequency of the cylindrical specimen, which was determined by means of the impact echo method. The free vibration response of all specimens (20 for each of the mix proportions presented in Table 1) was recorded, as shown in Figure 7a for the Ref mix, using the experimental setup presented in Figure 4. The Fast Fourier Transform (FFT) was applied to the recorded signal so that to obtain the response spectrum of the specimens, as shown in Figure 7b, from which the fundamental frequency of vibration was identified. For each cylindrical specimen, there were considered at least four measurements from which the fundamental frequency of vibration was calculated, as shown in Figure 8. The different scales used for the vertical axis of the graph were necessary since the response spectrum amplitude varied from one impact to another because the impact energy was different. The use of a single scale for the vertical axis would result in some of the response spectra being displayed with very small peaks. However, the fundamental longitudinal frequency of vibration did not vary by much, proving the consistency of the obtained data.

By applying Equations (1) and (2), the dynamic modulus of elasticity was obtained for all specimens belonging to the considered mix proportions. The data are summarized in

Table 2. Dynamic modulus.

Mix	Length	Diameter	Mass	Freq of Vibration	Ed
	[m]	[m]	[kg]	[Hz]	[MPa]
Ref	0.2	0.1	3.51	10,019	35,863
RuC40	0.199	0.1	3.23	8278	22,381
RuC60	0.2	0.1	3.13	7339	17,128
RuC80	0.199	0.1	3.01	6343	12,298

, where the presented values are the averaged ones from all the measurements.

By taking a look at the data presented in Table 2, it can be observed that the higher the rubber content, the lower the fundamental frequency of vibration (Figure 9). The vertical axis represents the amplitude of the signal, whereas the horizontal axis represents the frequency. Since the amplitude of the peak does not provide valuable information, the unit of measure was not converted into units of measure for acceleration. The information that was relevant for the purpose of the research was the one given on the horizontal axis, the fundamental frequency of vibrations and the downward shift of this frequency with the increase in the content of rubber replacement. Additionally, the lower mass of the cylinders, owing to smaller densities of RuC (Figure 5), leads to lower values for the dynamic modulus of elasticity. The decrease was 37.6% for 40% replacement of sand and reached 65.7% for 80% replacement, similar decrease rates to the static modulus of elasticity.

3.4. Conversion Equations from Dynamic to Static Modulus of Elasticity

The assessment of the dynamic modulus of elasticity has the advantage that involves a non-destructive method, and it can be performed, in general, directly on site. Since, for design and technical assessment purposes, the values of the static modulus of elasticity are considered, conversion equations were proposed. This section is dedicated to checking whether the readily available equations could also be suitable for rubberized concrete.

The considered equations are the one proposed by Popovics [23] (Equation (3)), the equation proposed by Lydon and Balendran [24] (Equation (4)) and the equation available in BS EN 1992-1-1:2004 [25] (Equation (5)).

$${\mathrm{E}}_{\mathrm{c}}=\frac{446.09\times {\mathrm{E}}_{\mathrm{d}}^{1.4}}{{\mathsf{\rho }}_{\mathrm{c}}}$$

(3)

$${\mathrm{E}}_{\mathrm{c}}=0.83\times {\mathrm{E}}_{\mathrm{d}}$$

(4)

$${\mathrm{E}}_{\mathrm{c}}=1.25\times {\mathrm{E}}_{\mathrm{d}}-19$$

(5)

where E_c is the static modulus of elasticity (GPa), E_d is the dynamic modulus of elasticity [GPa] and ρ_c is the density of concrete (kg/m³). The obtained results are summarized in Figure 10.

It can be observed that both Equations (3) and (4) give quite accurate results in terms of the predicted value of the static modulus of elasticity of the reference mix, although they tend to slightly overestimate the experimental results by 6.6% and 5.5%, respectively. When it comes to RuC mixes, Equation (3) underestimates the experimental results by 3.3% for RuC40 up to 20.1% for RuC80. On the other hand, Equation (4) tends to slightly overestimate the experimental results by almost 7% for RuC40 and improve its accuracy with only 4.1% overestimation for RuC80.

Based on the obtained results, it can be concluded that even though Equations (3) and (4) were developed for regular concrete, they are both accurate for 40% replacement of sand by rubber aggregates with Equation (4), keeping its accuracy even for 80% replacement. Equation (5) is very conservative when it comes to the reference mix and quite inaccurate for rubberized concrete.

3.5. Material Damping

One of the key features of rubberized concrete is its ability to dampen vibrations. For this purpose, the material damping was determined by means of the signal decaying function.

From the analysis of the experimental data, it was observed that the recorded signal consisted of a transient part, right after the impact, and a steady-state part. The steady-state part of the signal was fitted by means of a SineDamp equation, as shown in Figure 11. The material damping, ξ, was computed by means of Equation (6):

$$\mathsf{\xi }=\frac{\mathsf{\lambda }}{\sqrt{{\mathsf{\lambda }}^2+{\mathsf{\omega }}^2}}$$

(6)

where λ is the signal rate of decay and ϖ is the pulsation of the signal. Both the rate of decay and the pulsation were extracted from the SineDamp function used to fit the steady-state response.

The obtained values for the material damping ratio are summarized in

Table 3. Material damping.

Mix	Vibration Decay, λ	Pulsation	ξ
	[Hz]	[Hz]	[%]
Ref	471	10,019	0.75
RuC40	1561	8278	3.00
RuC60	1260	7339	2.73
RuC80	1072	6343	2.69

. It can be observed that the replacement of natural sand by rubber particles leads to a three-fold increase in the material damping.

Contrary to what was expected, higher percentages of rubber replacement did not necessarily mean better damping. The explanation may lie in the interfacial transition zone (ITZ) between the rubber particles and the cement matrix. A recent study [26] indicated that even for lower replacement percentages of sand by rubber aggregates, up to 15% replacement, the ITZ exhibited a higher concentration of voids and weaker bonding. The presence of voids was also reflected in lower values for the fundamental frequency of vibration, and further research should be dedicated to this topic.

3.6. Compressive Strength

The compressive strength was measured on 10 cylinders in accordance with SR EN 12390-3 [15]. The load was applied at a constant rate of 0.6 MPa/s (4.71 kN/s). The obtained values are shown in Figure 12.

Compared to the data from [6], the compressive strength of the reference mix increased by 22.64% from 35.56 MPa to 43.61 MPa. However, all other concrete mixes, the ones involving rubber aggregates, showed a decrease in the values of the compressive strength with an almost 35% decrease for RuC80. Only a 3.65% decrease was observed for RuC40. The obtained results are in line with the decreased values of both the static and the dynamic moduli of elasticity and the decrease in the values of the material damping with the increase in the replacement percentage.

A possible explanation may reside in the higher number of voids present at the ITZ level for concrete mixes with large volumes with rubber particles.

The conversion equations from compressive strength to static modulus of elasticity were checked for accuracy and suitability of being applied to rubberized concrete, although they were not specifically developed and proposed for this purpose. Hence, the equation given by Eurocode 2 [27] (Equation (6)) and the equation given in ACI 318-14 [28] (Equation (7)) were investigated. The obtained results are summarized in

Table 4. Predicted values for the static modulus of elasticity as function of the compressive strength.

Mix	Ec (Eurocode 2, Equation (6))	Exp/Ec,6	Ec (ACI 318-14, Equation (7))	Exp/Ec,7
	[MPa]	[%]	[MPa]	[%]
Ref	35,995	78.37	28,825	90.89
RuC40	30,795	56.38	22,711	77.56
RuC60	29,296	45.72	20,978	67.21
RuC80	27,749	35.35	19,180	56.43

.

$${\mathrm{E}}_{\mathrm{c}\mathrm{m}}=22\times {\left(\frac{{\mathrm{f}}_{\mathrm{c}\mathrm{m}}}{10}\right)}^{0.3},\mathrm{where}{\mathrm{f}}_{\mathrm{c}\mathrm{m}}={\mathrm{f}}_{\mathrm{c}\mathrm{k}}+8\left[\mathrm{M}\mathrm{P}\mathrm{a}\right]$$

(7)

$${\mathrm{E}}_{\mathrm{c}}=4.7\sqrt{{{\mathrm{f}}_{\mathrm{c}}}^{\prime }}$$

(8)

where f_c′ and f_ck are the compressive strength of concrete obtained from laboratory investigations [MPa], E_c and E_cm are the static moduli of elasticity [MPa].

It can be observed that the best prediction for the reference mix was given by Equation (7). Equation (6) overestimated the experimental results by as much as 22%. All equations significantly overestimated the experimental results with the increase in the rubber content. The data are in line with the results reported in previous studies [6] and underline the limitation of currently available equations in predicting the modulus of elasticity of rubberized concrete with large volumes of rubber aggregates. Therefore, further studies should be conducted with the aim of proposing accurate prediction equations in view of the increasing use of rubberized concrete in the construction industry.

3.7. Tensile Splitting Strength

The tensile splitting strength was determined on 10 samples in accordance with SR EN 12390:6 [16]. The specimens were loaded by a loading rate of 0.05 MPa/s (0.4 kN/s). The obtained results are shown in Figure 13. It can be seen that the tensile splitting strength decreases with the increase in rubber content. The prediction equation presented in ACI 318:14 [28] was used to check whether or not it can be used in the case of rubberized concrete. The data are summarized in

Table 5. Predicted values for the tensile splitting strength as function of the compressive strength.

Mix	Ec (ACI 318-14)	Exp/Ec
	[MPa]	-
Ref	3.70	1.051
RuC40	2.67	1.041
RuC60	2.37	0.949
RuC80	2.07	0.691

.

From the obtained results, it can be concluded that the equation can accurately predict the tensile splitting strength of both the reference mix and the rubberized concrete mixes with replacement percentages of sand from 40% to 60%. However, it tends to overestimate the values of the tensile splitting strength of RuC80 by 31.9%.

4. Discussions

The obtained results were also investigated from a statistical point of view, namely the spread of the data with respect to the average value. The data are summarized in Table 5 in terms of density, modulus of elasticity and strength values. The coefficient of variation (COV) was used to assess the dispersion of data with respect to the average value obtained from different data set sizes. The static and dynamic moduli of elasticity were determined from 19 specimens, whereas the compressive and tensile splitting strength was from a set of 10 samples each.

It can be observed that the values for the density of all concrete mixes exhibit a very small spread with respect to the median. This proves that the changes in the dimensions of the specimens, as well as the weight of specimens within the same mix proportion, were equally influenced by the storing conditions.

A larger spread of the results was observed for the values of the modulus of elasticity, especially for RuC60 and RuC80 mixes. This could be attributed to the higher content of rubber particles which leads to a larger number of micro-cracks. There is, however, not enough data on this issue, and further research should be conducted in this direction.

The dynamic modulus of elasticity exhibits larger values of COV compared to those obtained for the density but with an almost uniform distribution among the concrete mixes. Taking into account the fact that the vibrations induced by using the Impact Echo Method to assess the fundamental frequency of the specimens have to travel through the material to reach the opposite side and be recorded by the accelerometer, any defect within the material structure would impact the response of the specimens.

Since all cylinders were stored in the same relatively dry environment that favored the evaporation of free water from the concrete pores, this had a direct influence on the material structure, which led to overall lower values for material properties.

By observing the data from

Table 6. Characterization of the experimentally obtained data at the age of 5 years.

Reference Mix (Ref)
	Density	Modulus of Elasticity	Dynamic Modulus of Elasticity	Compressive Strength	Tensile Splitting Strength
	[kg/m3]	[MPa]	[MPa]	[MPa]	[MPa]
Value	2227	28,210	35,863	43.61	3.89
Standard deviation	8.558	456.54	937.57	1.865	0.12
Coefficient of Variation [%]	0.38	1.62	2.61	4.28	3.09
RuC40
	Density	Modulus of Elasticity	Dynamic Modulus of Elasticity	Compressive Strength	Tensile Splitting Strength
	[kg/m3]	[MPa]	[MPa]	[MPa]	[MPa]
Value	2061	17,361	22,381	22.68	2.78
Standard deviation	5.376	240.92	948.37	0.71	0.086
Coefficient of Variation [%]	0.26	1.39	4.24	3.13	3.09
RuC60
	Density	Modulus of Elasticity	Dynamic Modulus of Elasticity	Compressive Strength	Tensile Splitting Strength
	[kg/m3]	[MPa]	[MPa]	[MPa]	[MPa]
Value	1986	13,395	17,128	17.98	2.25
Standard deviation	13.539	1047.3	371.54	0.305	0.091
Coefficient of Variation [%]	0.68	7.82	2.17	1.69	4.06
RuC80
	Density	Modulus of Elasticity	Dynamic Modulus of Elasticity	Compressive Strength	Tensile Splitting Strength
	[kg/m3]	[MPa]	[MPa]	[MPa]	[MPa]
Value	1909	9809	12,298	13.68	1.43
Standard deviation	10.748	590.94	305.26	0.968	0.083
Coefficient of Variation [%]	0.56	6.02	2.48	7.08	5.76

, there is no clear trend in the values of COV as a function of rubber replacement for sand in concrete. This is mainly due to the heterogeneous structure of concrete in general. However, if the values of COV were judged together with the values obtained for the standard deviation with respect to the average values for each investigated material characteristic, the calculated values for COV are in line with those reported in similar research works [29].

5. Conclusions

The paper presents an experimental program aimed at assessing the long-term material properties of rubberized Portland cement concrete. Based on the obtained results, the following conclusions can be drawn:

A significant drop in the values of density after 5 years is observed for specimens made with rubberized concrete, whereas the density of the reference mix changes by a very small amount.

The values of the static modulus of elasticity decrease after 5 years compared to the standard value obtained at 28 days, mainly due to the fact that the specimens were kept indoors, in laboratory conditions and in a relatively dry environment. Therefore, the excess water slowly evaporated during the 5 years. Since the presence of rubber creates a larger amount of excess water, its evaporation left behind voids in the concrete specimens that ultimately leads to lower values of the modulus of elasticity.

Since the dynamic modulus of elasticity is influenced both by the mass of the specimen and by its fundamental longitudinal frequency of vibration, any trend observed for the two parameters is reflected in the evolution in time for this material property. The voids inside the RuC specimens lead to lighter concrete and to lower values for the frequency of vibration. The conversion equations from dynamic modulus to static modulus of elasticity cannot be directly applied to rubberized concrete. Further investigations are deemed necessary in this direction.

Material damping is strongly influenced by the rubber content in concrete. A 40% replacement of sand by rubber aggregates leads to a three-fold increase in the value of the material damping. However, further increase of the replacement percentage has an opposite effect on the damping properties due, primarily, to the occurrence of voids at the ITZ level between rubber particles and cement matrix.

Both compressive and tensile splitting strength are adversely affected by the presence of rubber aggregates. The use of currently available conversion equations from the compressive strength of concrete to the values of the elastic modulus is not applicable to rubberized concrete.

By considering the phenomena observed during the experimental program, further research is necessary, especially at the material level, for a better understanding of the long-term behavior of rubberized concrete. The authors have already taken the first steps in this direction, and a set of SEM and XRD investigations are being conducted. Porosity and absorption assessments are also considered. This may help shed some light on the material structure of normal and rubberized concrete after five years from casting and may provide explanations on the observed behavior pattern.

The structural application of rubberized concrete is currently limited. Based on the obtained data, it can be considered that a 40% replacement of natural sand by rubber aggregates, without any prior surface treatment, leads to acceptable values of the compressive strength after five years of storage in a relatively dry environment. However, the starting mix proportion should be for a higher concrete strength class so that the values obtained for the material properties, after using rubber aggregates, still warrant the use of rubberized concrete in structural applications. Additionally, the large deformation capacity of such concrete should be carefully investigated and considered during the design process as it strongly influences the behavior of connecting elements in a structure. The recommendations are still limited to the mixed proportions used in this research. Other mixes could be considered after careful investigation of their elastic and mechanical properties.