Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns
Abstract
:1. Introduction
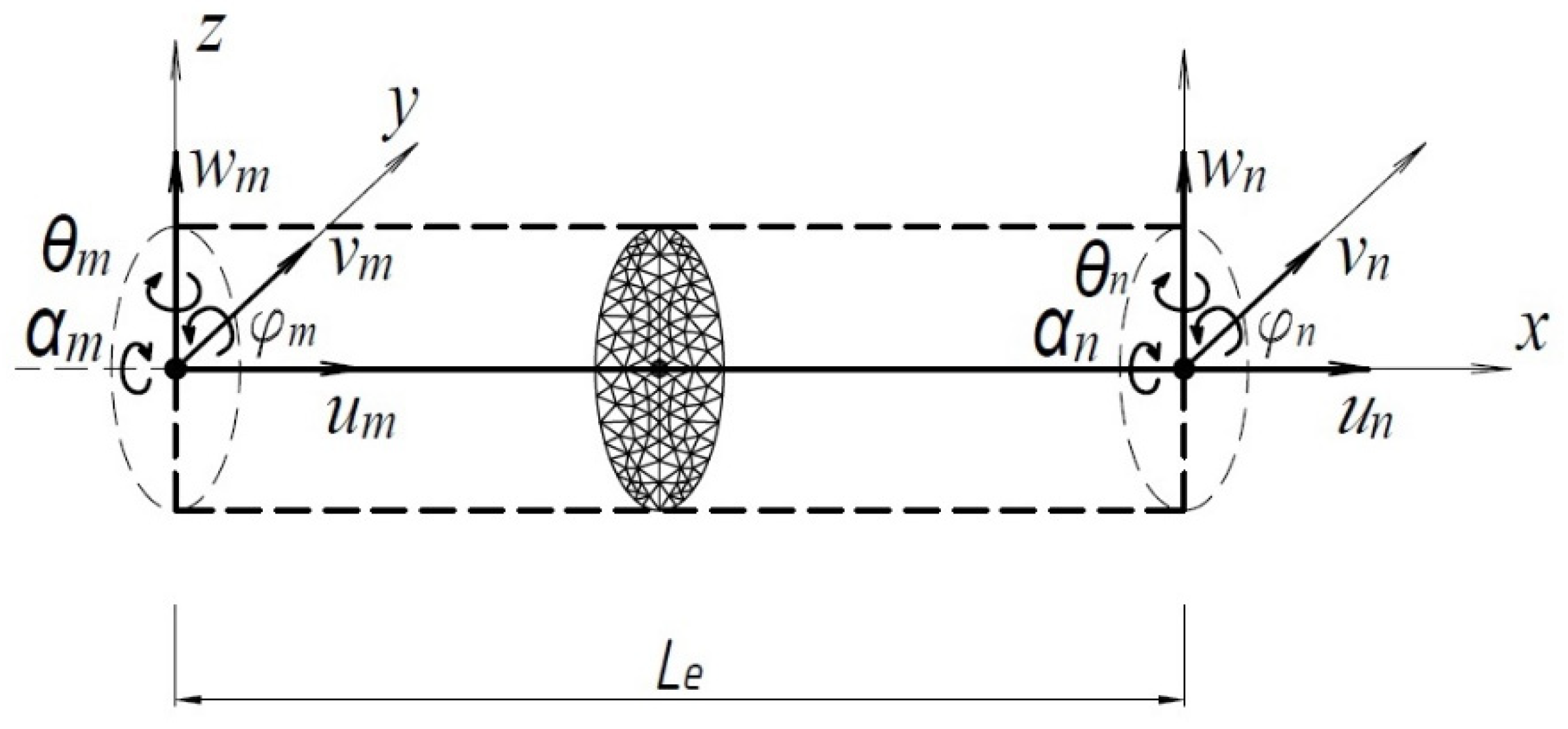
- Derivation of the resolving equations and computer implementation of the method for nonlinear calculation of concrete-filled steel tubular columns by reducing the three-dimensional problem to the two-dimensional one.
- Verification of the method and the developed software by comparison with calculations in existing software complexes in the three-dimensional setting.
- Approbation of the developed method on existing experimental data.
- Study of the peculiarities of the stress–strain state of columns at various eccentricities of the longitudinal force.
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
- 1.
- The method and software for determining the stress–strain state and calculating the bearing capacity of short CFST columns by reducing the three-dimensional problem to the two-dimensional one were developed. The proposed approach leads to significant savings in computational time in comparison with the calculation in the three-dimensional formulation. In the proposed approach, only the displacements of the nodes in the section plane xy and two additional variables and χ act as unknowns.
- 2.
- The proposed method was verified by comparing the solution in the elastic formulation with the solution in the LIRA-SAPR finite element software package based on the three-dimensional model. With the same mesh density in the section plane discrepancy in stresses was 0.6% for σz, 1.6% for σx and 3.1% for σy.
- 3.
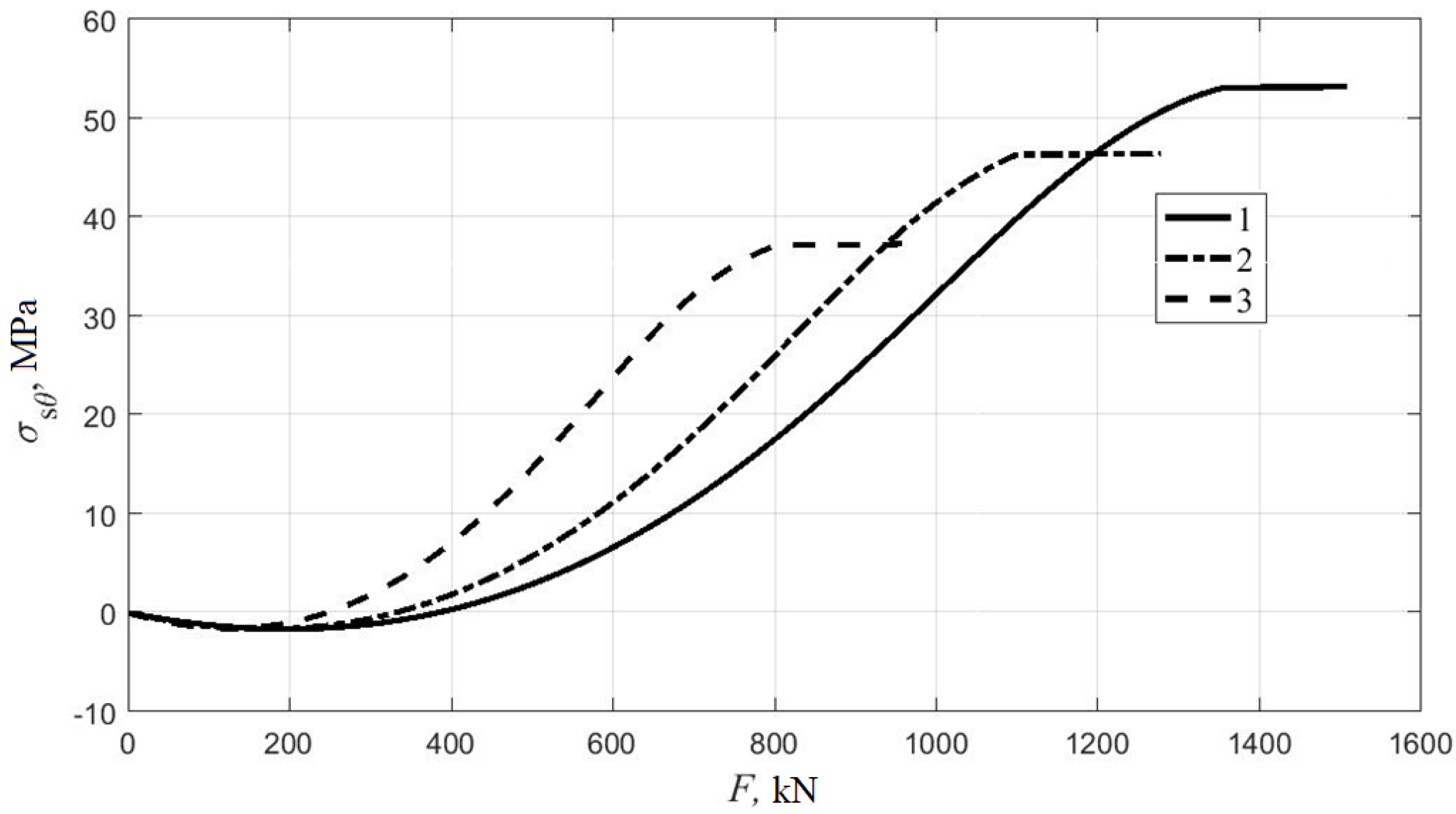
- The developed method was also tested on the experimental data of A.L. Krishan and A.I. Sagadatov for six eccentrically compressed specimens with different eccentricities of the longitudinal force and diameters. The maximum discrepancy between the theoretical and experimental values of the ultimate load was 1.3%. These results also indicate the possibility of applying Geniev’s deformational theory of plasticity of concrete to the calculation of CFST columns.
- 4.
- It was found that, with an increase in the eccentricity of the longitudinal force, the effect of concrete work under conditions of a triaxial stress state in CFST columns with a circular cross-section decrease. The increase in bearing capacity due to the work of concrete under conditions of a triaxial stress state for the samples with D = 159 mm was 19% at e/D = 0.065 and only 3% at e/D = 0.26. Thus, the area of effective work for columns of circular cross-section is small eccentricities of the longitudinal force.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, Y.; Wang, J.; Liu, Y.; Lin, X. Thin-Walled CFST Columns for Enhancing Seismic Collapse Performance of High-Rise Steel Frames. Appl. Sci. 2017, 7, 53. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Liu, J. Application of Steel-tubed Concrete Structures in High-rise Buildings. Int. J. High-Rise Build. 2019, 8, 161–167. [Google Scholar] [CrossRef] [Green Version]
- Krishan, A.L.; Chernyshova, E.P.; Sabirov, R.R. Calculating the Strength of Concrete Filled Steel Tube Columns of Solid and Ring Cross-Section. Procedia Eng. 2016, 150, 1878–1884. [Google Scholar] [CrossRef] [Green Version]
- Krishan, A.L.; Astafeva, M.A.; Chernyshova, E.P. Strength Calculation of Short Concrete-filled Steel Tube Columns. Int. J. Concr. Struct. Mater. 2018, 12. [Google Scholar] [CrossRef]
- Dong, H.; Li, Y.; Cao, W.; Qiao, Q.; Li, R. Uniaxial compression performance of rectangular CFST columns with different internal construction characteristics. Eng. Struct. 2018, 176, 763–775. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, F.; Bie, X. Behaviour of rectangular RACFST slender columns under eccentric compression. J. Build. Eng. 2021, 38, 102236. [Google Scholar] [CrossRef]
- Chen, J.; Chan, T.-M.; Chung, K.-F. Design of square and rectangular CFST cross-sectional capacities in compression. J. Constr. Steel Res. 2021, 176, 106419. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Z.; Sun, G. Axial behaviour of rectangular concrete-filled cold-formed steel tubular columns with different loading methods. Steel Compos. Struct. 2015, 18, 71–90. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Z.; Sun, G. Experimental study of rectangular CFST columns subjected to eccentric loading. Thin-Walled Struct. 2013, 64, 83–93. [Google Scholar] [CrossRef]
- Ma, D.Y.; Han, L.H.; Ji, X.; Yang, W.B. Behaviour of hexagonal concrete-encased CFST columns subjected to cyclic bending. J. Constr. Steel Res. 2018, 144, 283–294. [Google Scholar] [CrossRef]
- Xu, W.; Han, L.H.; Li, W. Performance of hexagonal CFST members under axial compression and bending. J. Constr. Steel Res. 2016, 123, 162–175. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.I.; Bock, M. Behaviour and design of hexagonal concrete-filled steel tubular short columns under axial compression. Eng. Struct. 2017, 153, 732–748. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Patel, V.I. Round-ended rectangular concrete-filled steel tubular short columns: FE investigation under axial compression. J. Constr. Steel Res. 2018, 140, 222–236. [Google Scholar] [CrossRef]
- Fang, H.; Chan, T.M.; Young, B. Structural performance of concrete-filled cold-formed high-strength steel octagonal tubular stub columns. Eng. Struct. 2021, 239, 112360. [Google Scholar] [CrossRef]
- Krishan, A.L.; Rimshin, V.I.; Troshkina, E.A. Strength of Short Concrete Filled Steel Tube columns of Annular Cross Section. IOP Conf. Ser. Mater. Sci. Eng. 2018, 463, 022062. [Google Scholar] [CrossRef]
- Krishan, A.; Astafeva, M. Strength and Deformability of the Concrete Core of Precompressed Concrete Filled Steel Tube Columns of Annular Cross-Section. MATEC Web Conf. 2019, 278, 03002. [Google Scholar] [CrossRef]
- Krishan, A.L.; Narkevich, M.Y.; Sagadatov, A.I.; Rimshin, V.I. The strength of short compressed concrete elements in a fiberglass shell. Mag. Civ. Eng. 2020, 94, 3–10. [Google Scholar] [CrossRef]
- Jamaluddin, N.; Lam, D.; Dai, X.H.; Ye, J. An experimental study on elliptical concrete filled columns under axial compression. J. Constr. Steel Res. 2013, 87, 6–16. [Google Scholar] [CrossRef] [Green Version]
- Uenaka, K. Experimental study on concrete filled elliptical/oval steel tubular stub columns under compression. Thin-Walled Struct. 2014, 78, 131–137. [Google Scholar] [CrossRef]
- Fu, G.; Fu, G.; Yu, C.; Li, S.; Wang, F.; Yang, F. Behaviour of rectangular concrete-filled steel tubular slender column with unequal wall thickness. Eng. Struct. 2021, 236, 112100. [Google Scholar] [CrossRef]
- Weerasinghe, K.A.B.; Gamage, J.C.P.H.; Fawzia, S.; Thambiratnam, D.P. Experimental investigation on flexural behaviour of vertically-curved circular-hollow steel sections strengthened with externally bonded carbon fibre reinforced polymer. Eng. Struct. 2021, 236, 112040. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, L.; Xu, S.; Wang, Q.; Wen, S.; Wang, Y. Study on the mechanical property of low magnesia ore high strength concrete-filled steel tubular columns. J. Phys. Conf. Ser. 2021, 1904, 012021. [Google Scholar] [CrossRef]
- Grigoryan, M.N.; Urvachev, M.; Chepurnenko, A.; Polyakova, T. Determination of the ultimate load for centrally compressed concrete filled steel tubular columns based on the deformation theory of plasticity. IOP Conf. Ser. Mater. Sci. Eng. 2020, 913, 022069. [Google Scholar] [CrossRef]
- Mailyan, D.; Mailyan, L. Ecologically safe and techno economically efficient reinforced concrete constructions of equal resistance. MATEC Web Conf. 2016, 73, 04020. [Google Scholar] [CrossRef] [Green Version]
- Mailyan, L.R.; Stel’makh, S.A.; Shcherban, E.M.; Khalyushev, A.K.; Smolyanichenko, A.S.; Sysoev, A.K.; Parinov, I.A.; Cherpakov, A.V. Investigation of Integral and Differential Characteristics of Variatropic Structure Heavy Concretes by Ultrasonic Methods. Appl. Sci. 2021, 11, 3591. [Google Scholar] [CrossRef]
- Beskopylny, A.; Kadomtseva, E.; Meskhi, B.; Strelnikov, G.; Polushkin, O. Influence of the Cross-Sectional Shape of a Reinforced Bimodular Beam on the Stress-Strain State in a Transverse Impact. Buildings 2020, 10, 248. [Google Scholar] [CrossRef]
- Mailyan, L.; Stel’makh, S.; Shcherban, E.; Komov, V.; Ferrarese, M.; Koposov, A. Calculation of Integral Properties of Vibrated and Centrifugated Concrete. Lect. Notes Civ. Eng. 2021, 150, 97–107. [Google Scholar] [CrossRef]
- Ouyang, Y.; Kwan, A.K.H. Finite element analysis of square concrete-filled steel tube (CFST) columns under axial compressive load. Eng. Struct. 2018, 156, 443–459. [Google Scholar] [CrossRef]
- Geniev, G.; Kissuk, V.; Tupin, G. Theory of Plasticity of Concrete and Reinforced Concrete; Stroyizdat: Moscow, Russia, 1974. [Google Scholar]
- Structural Engineering Software | Liraland Group. Available online: https://www.liraland.com/ (accessed on 5 December 2021).
- Sagadatov, A.I. Stress-Strain State of Compressed Concrete Filled Steel Tubular Elements with an Internal Steel Core. Ph.D. Thesis, Nosov Magnitogorsk State Technical University, Magnitogorsk, Russia, 2006. [Google Scholar]
- Narkevich, M.Y.; Sagadatov, A.I. Strength and deformation property enhancement of compressed steel tube-concrete elements using super concrete and thin-shell structure. IOP Conf. Ser. Mater. Sci. Eng. 2019, 687, 033031. [Google Scholar] [CrossRef]
- Krishan, A.L.; Astafyeva, M.A.; Chernyshova, E.P. Strength of Axially Loaded Concrete Filled Steel Tube Elements of Self-Stressing Concrete. Key Eng. Mater. 2018, 792, 160–165. [Google Scholar] [CrossRef]
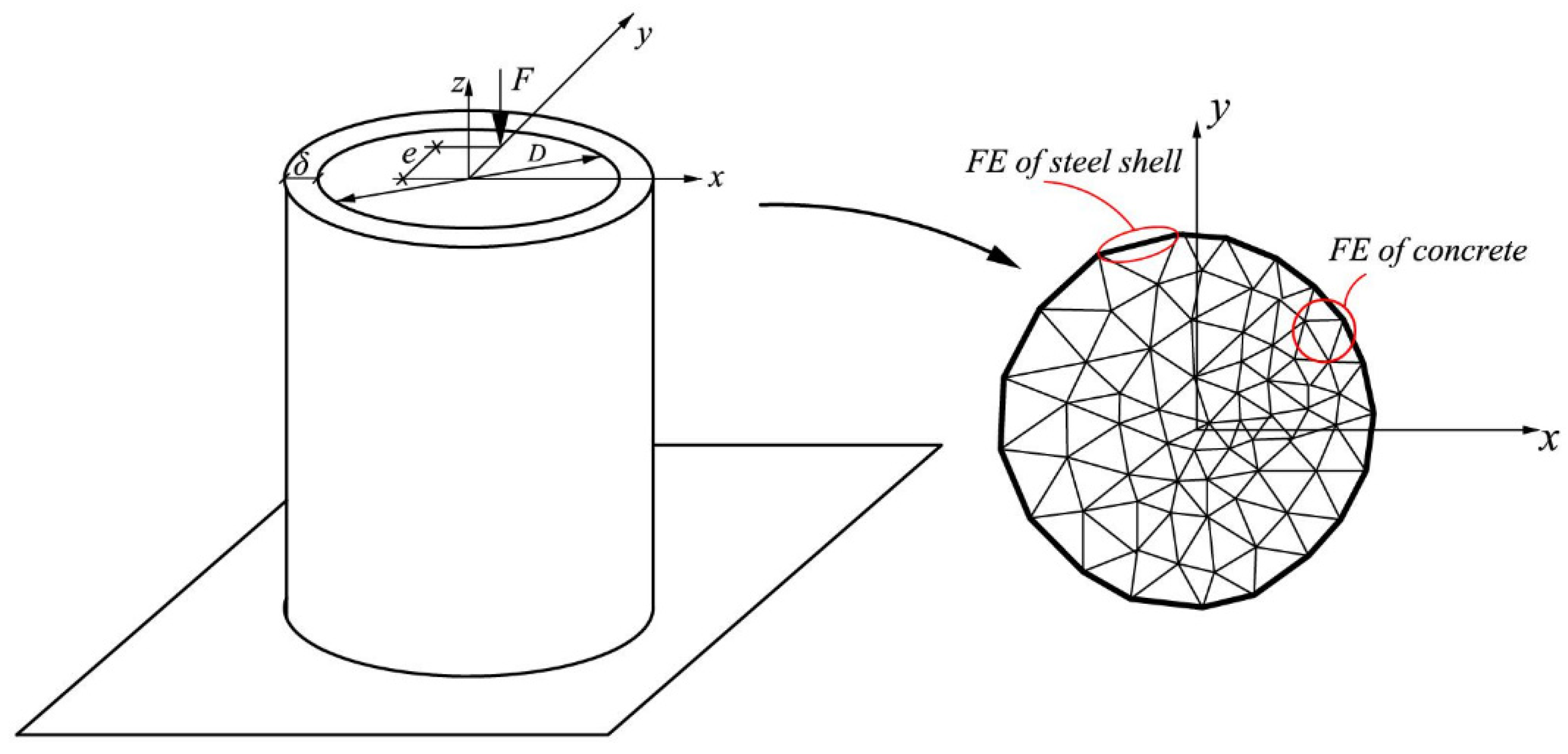
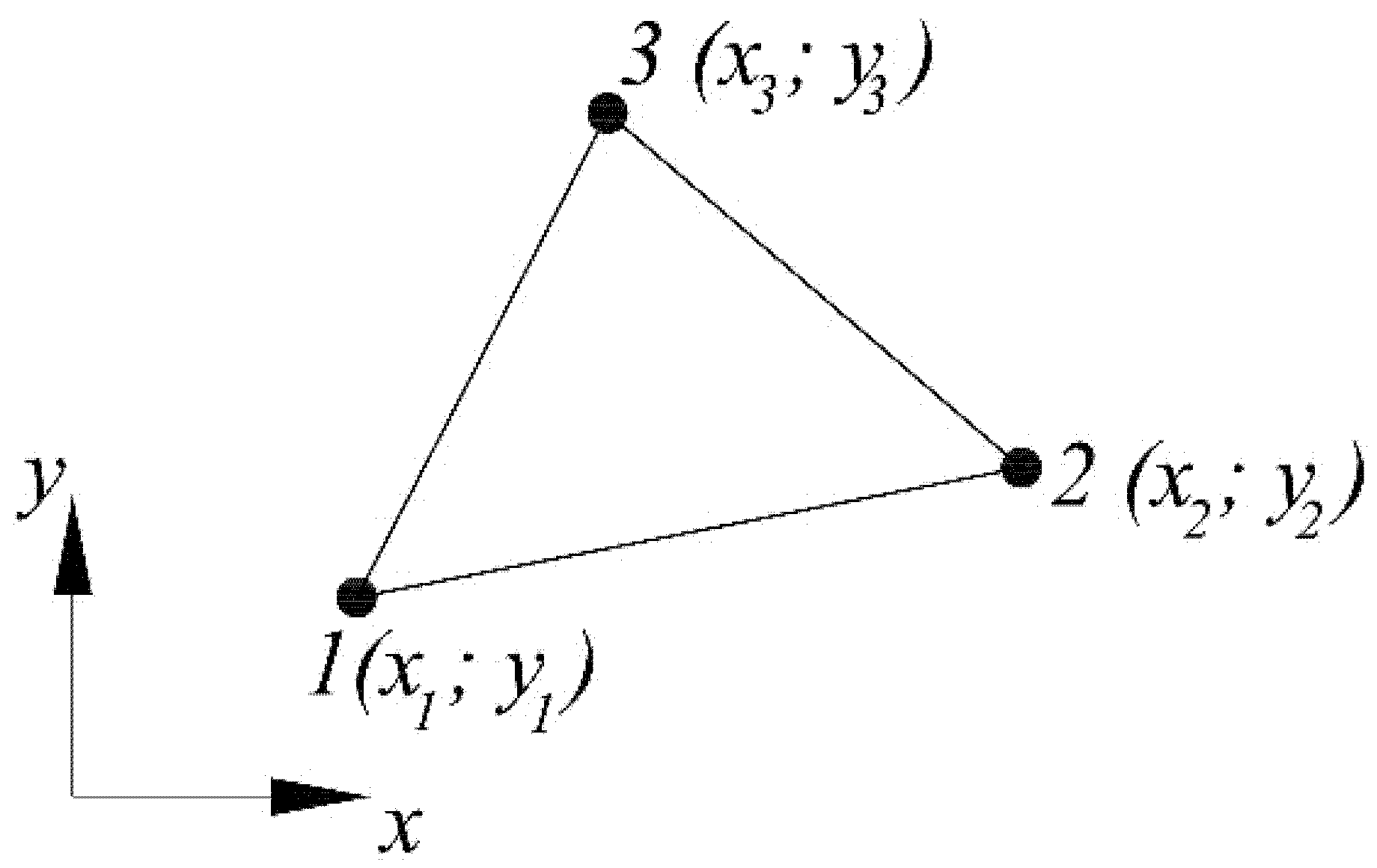
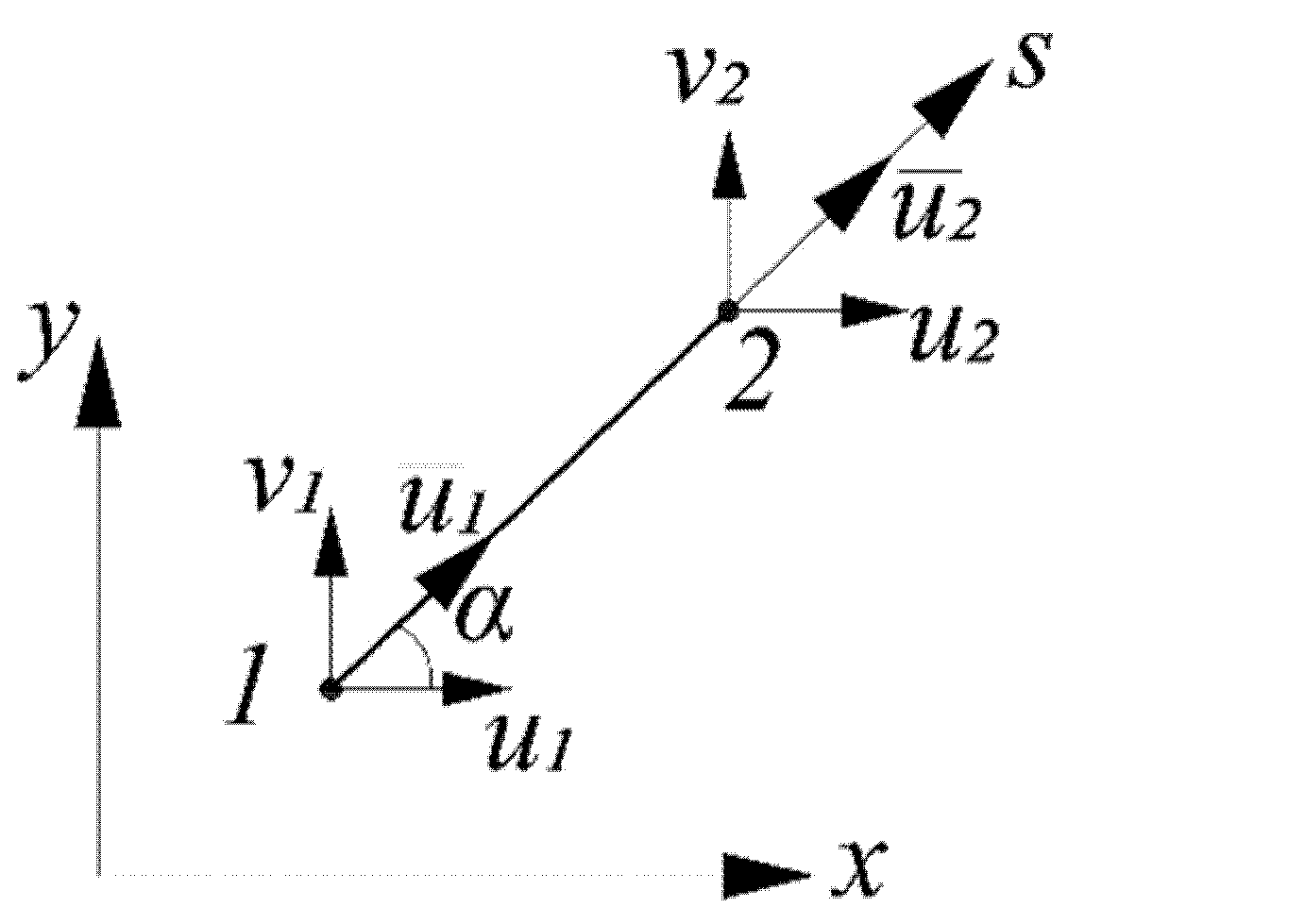

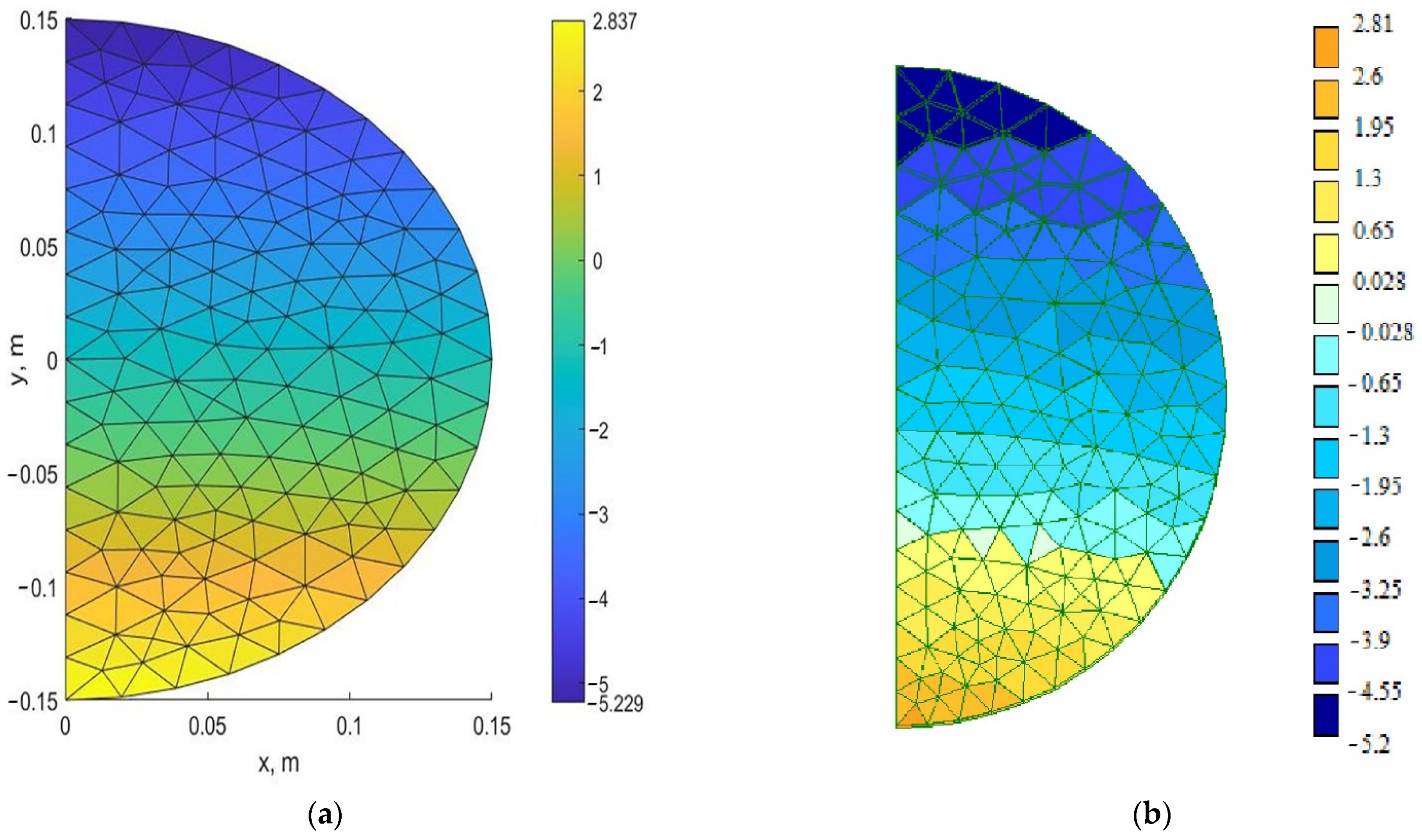
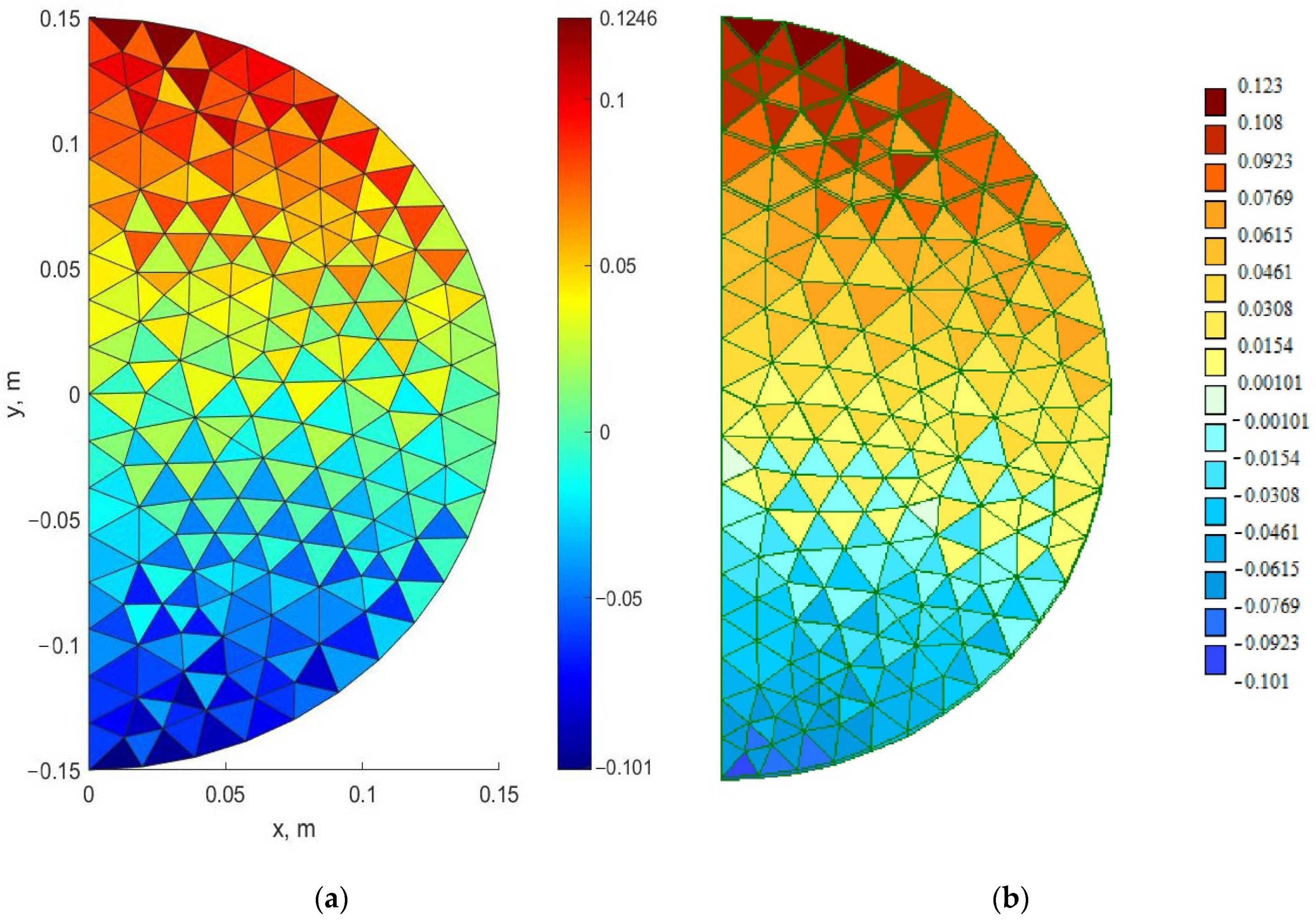
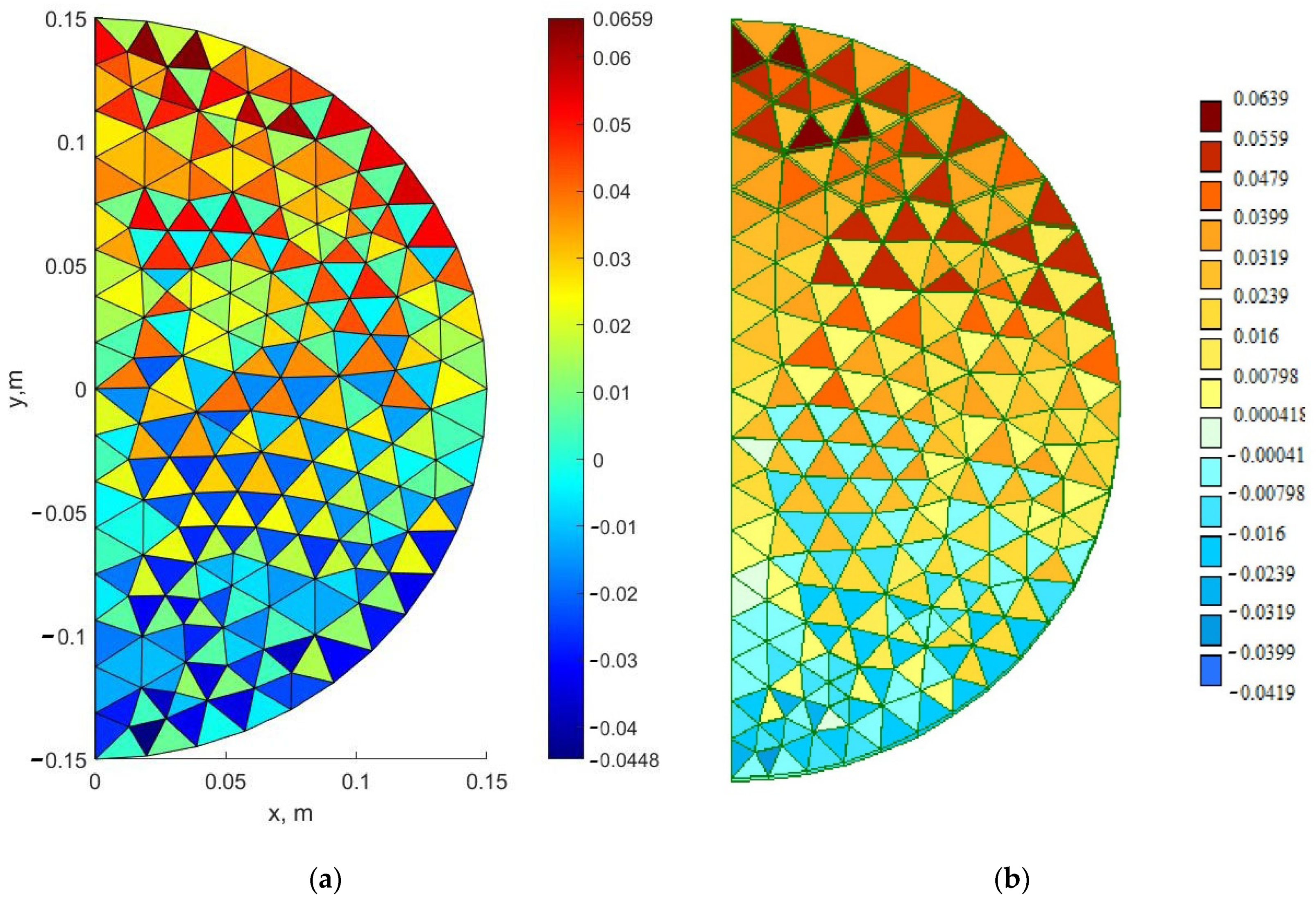
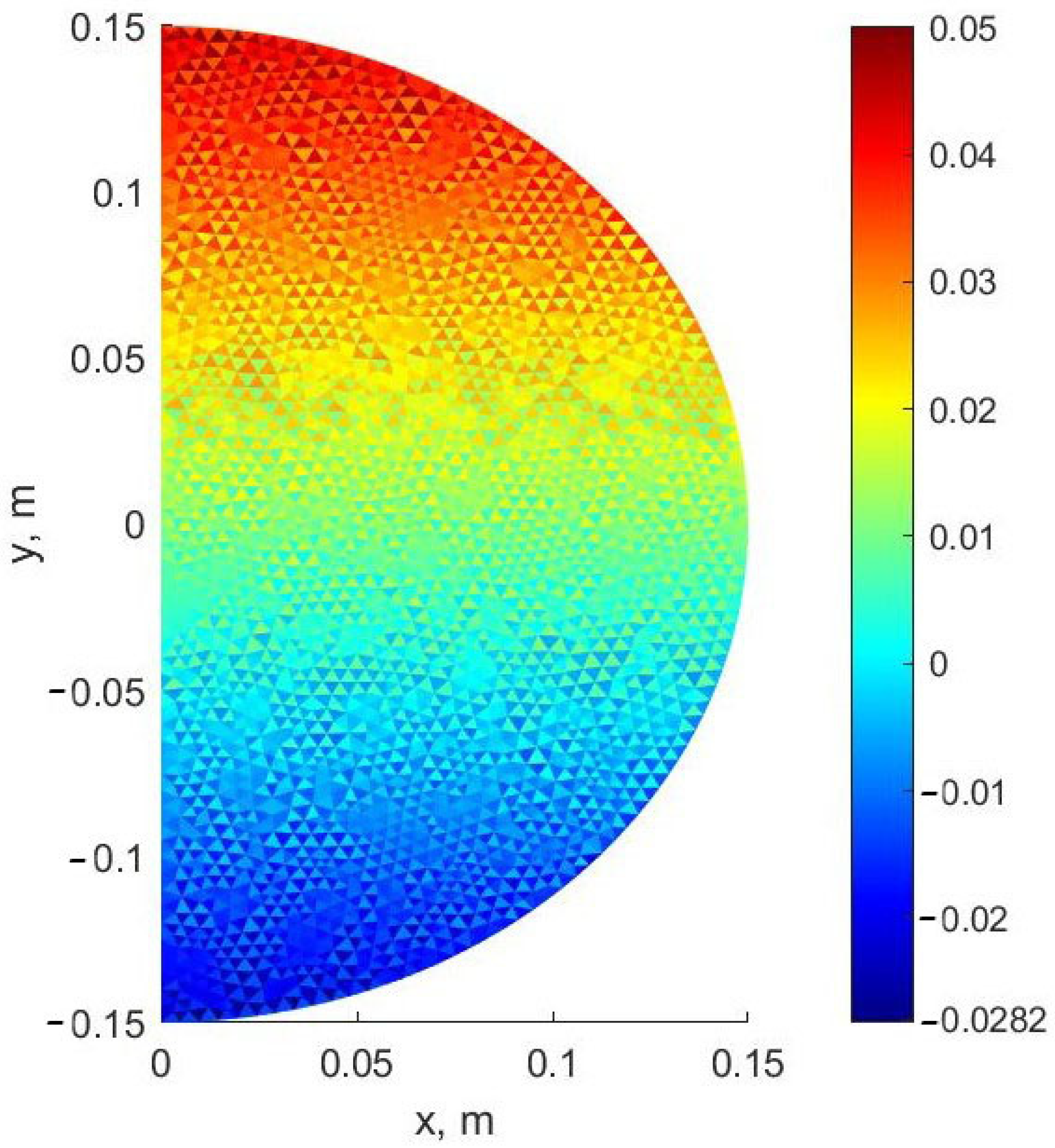

| σz, MPa | σx, MPa | σy, MPa | |
|---|---|---|---|
| MATLAB | 5.23 | 0.125 | 0.0659 |
| LIRA-SAPR | 5.2 | 0.123 | 0.0639 |
| Sample Number | D, mm | δ, mm | Rb, MPa | e/D | Nu,exp, kN | Nu,theor, kN | Nu,bs, kN | Nu,theor/Nu,bs |
|---|---|---|---|---|---|---|---|---|
| 1 | 159 | 6 | 22.0 | 0.065 | 1412 | 1430 | 1200 | 1.19 |
| 2 | 159 | 6 | 22.5 | 0.13 | 1213 | 1210 | 1060 | 1.14 |
| 3 | 159 | 6 | 22.3 | 0.26 | 958 | 950 | 920 | 1.03 |
| 4 | 219 | 8 | 32.5 | 0.065 | 2911 | 2911 | 2780 | 1.05 |
| 5 | 219 | 8 | 30.5 | 0.13 | 2508 | 2515 | 2365 | 1.06 |
| 6 | 219 | 8 | 32.1 | 0.26 | 1945 | 1950 | 1870 | 1.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chepurnenko, A.; Yazyev, B.; Meskhi, B.; Beskopylny, A.; Khashkhozhev, K.; Chepurnenko, V. Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns. Appl. Sci. 2021, 11, 11645. https://doi.org/10.3390/app112411645
Chepurnenko A, Yazyev B, Meskhi B, Beskopylny A, Khashkhozhev K, Chepurnenko V. Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns. Applied Sciences. 2021; 11(24):11645. https://doi.org/10.3390/app112411645
Chicago/Turabian StyleChepurnenko, Anton, Batyr Yazyev, Besarion Meskhi, Alexey Beskopylny, Kazbek Khashkhozhev, and Viacheslav Chepurnenko. 2021. "Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns" Applied Sciences 11, no. 24: 11645. https://doi.org/10.3390/app112411645
APA StyleChepurnenko, A., Yazyev, B., Meskhi, B., Beskopylny, A., Khashkhozhev, K., & Chepurnenko, V. (2021). Simplified 2D Finite Element Model for Calculation of the Bearing Capacity of Eccentrically Compressed Concrete-Filled Steel Tubular Columns. Applied Sciences, 11(24), 11645. https://doi.org/10.3390/app112411645








